New Criteria for Convex-Exponent Product of Log-Harmonic Functions
Abstract
:1. Introduction
2. Main Results
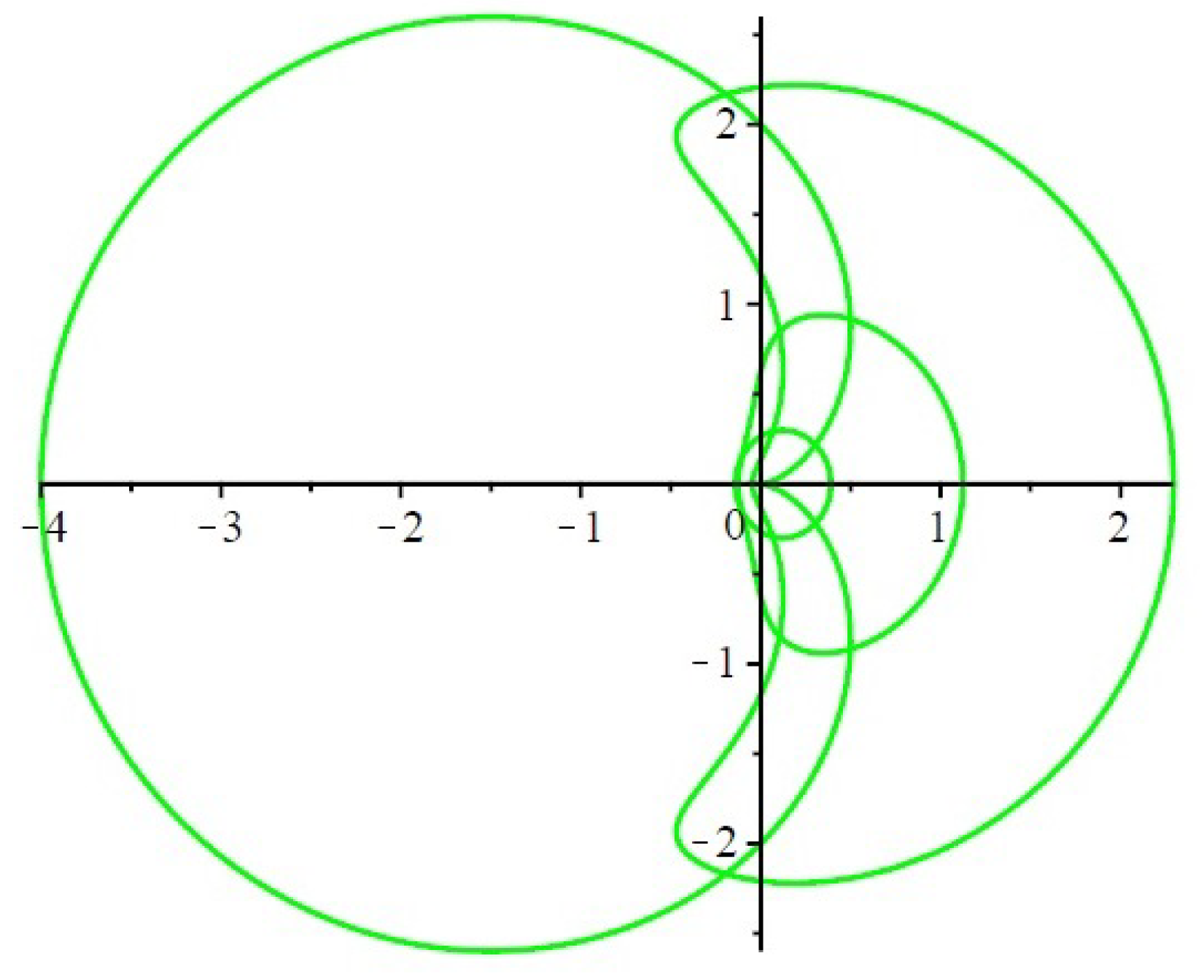
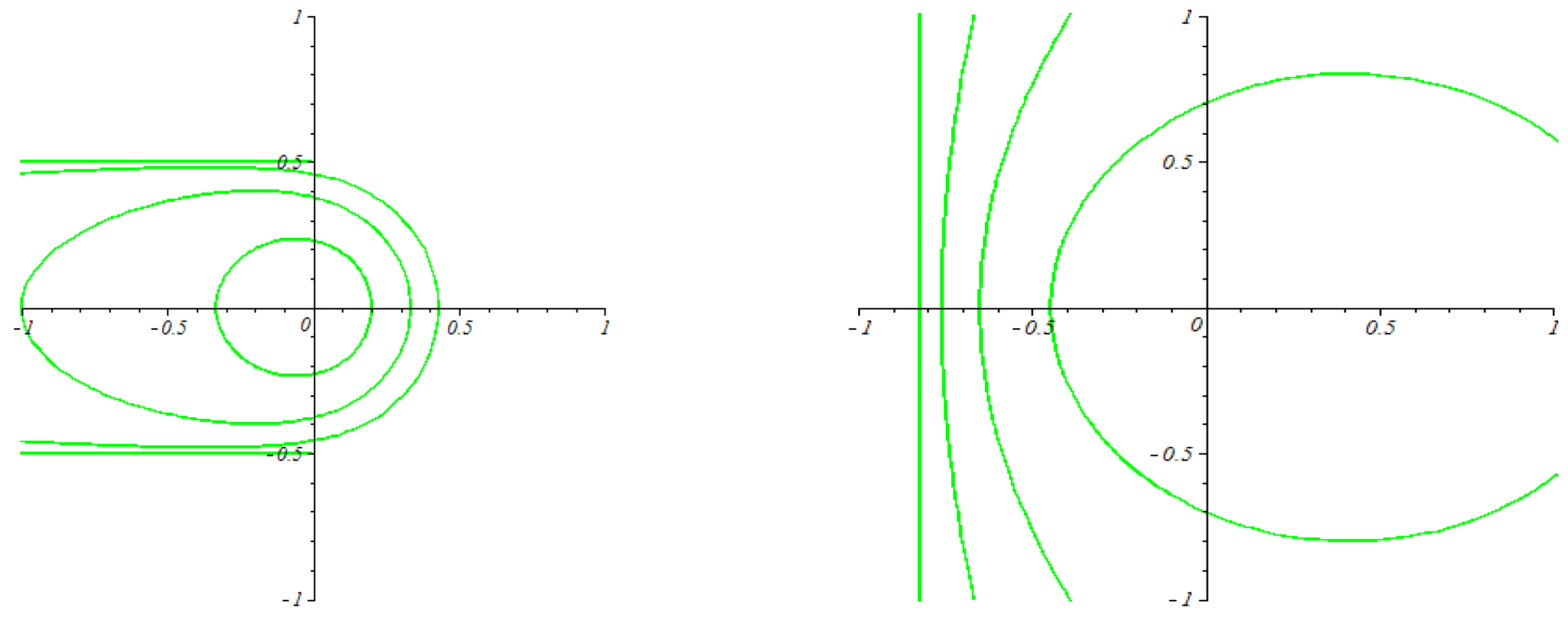
3. Examples
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdulhadi, Z.; Bshouty, D. Univalent functions in H·. Trans. Am. Math. Soc. 1988, 305, 841–849. [Google Scholar]
- Abdulhadi, Z.; Hengartner, W. Spirallike log-harmonic mappings. Complex Var. Theory Appl. 1987, 9, 121–130. [Google Scholar]
- Abdulhadi, Z. Close-to-starlike logharmonic mappings. Internat. J. Math. Math. Sci. 1996, 19, 563–574. [Google Scholar] [CrossRef]
- Aydogan, M.; Polatŏlu, Y. A certain class of starlike log-harmonic mappings. J. Comput. Appl. Math. 2014, 270, 506–509. [Google Scholar] [CrossRef]
- Aydogan, M. Some results on a starlike log-harmonic mapping of order alpha. J. Comput. Appl. Math. 2014, 256, 77–82. [Google Scholar] [CrossRef]
- Abdulhadi, Z.; Ali, R.M. Univalent log-harmonic mapping in the plane. J. Abstr. Appl. 2012, 2012, 721943. [Google Scholar]
- Abdulhadi, Z.; Alareefi, N.M.; Ali, R.M. On the convex-exponent product of log-harmonic mappings. J. Inequal. Appl. 2014, 2014, 485. [Google Scholar] [CrossRef]
- Li, P.; Ponnusamy, S.; Wang, X. Some properties of planar p-harmonic and log-p-harmonic mappings. Bull. Malays. Math. Sci. Soc. 2013, 36, 595–609. [Google Scholar]
- Liu, Z.; Ponnusamy, S. Some properties of univalent log-harmonic mappings. Filomat 2018, 32, 5275–5288. [Google Scholar] [CrossRef]
- Seoudy, T.; Aouf, M.K. Fekete-Szeg problem for certain subclass of analytic functions with complex order defined by q-analogue of Ruscheweyh operator. Constr. Math. Anal. 2020, 3, 36–44. [Google Scholar]
- Clunie, J.; Sheil-Small, T. Harmonic univalent functions. Ann. Acad. Sci. Fenn. Ser. A. I Math. 1984, 9, 3–25. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, Y.; Wang, Z. On the convex combinations of slanted half-plane harmonic mappings. Houst. J. Math. Anal. Appl. 2015, 6, 46–50. [Google Scholar]
- Sun, Y.; Rasila, A.; Jiang, Y. Linear combinations of harmonic quasiconformal mappings convex in one direction. J. Kodai Math. Appl. 2016, 39, 1323–1334. [Google Scholar] [CrossRef]
- Wang, Z.G.; Liu, Z.H.; Li, Y.C. On the linear combinations of harmonic univalent mappings. J. Math. Anal. Appl. 2013, 400, 452–459. [Google Scholar] [CrossRef]
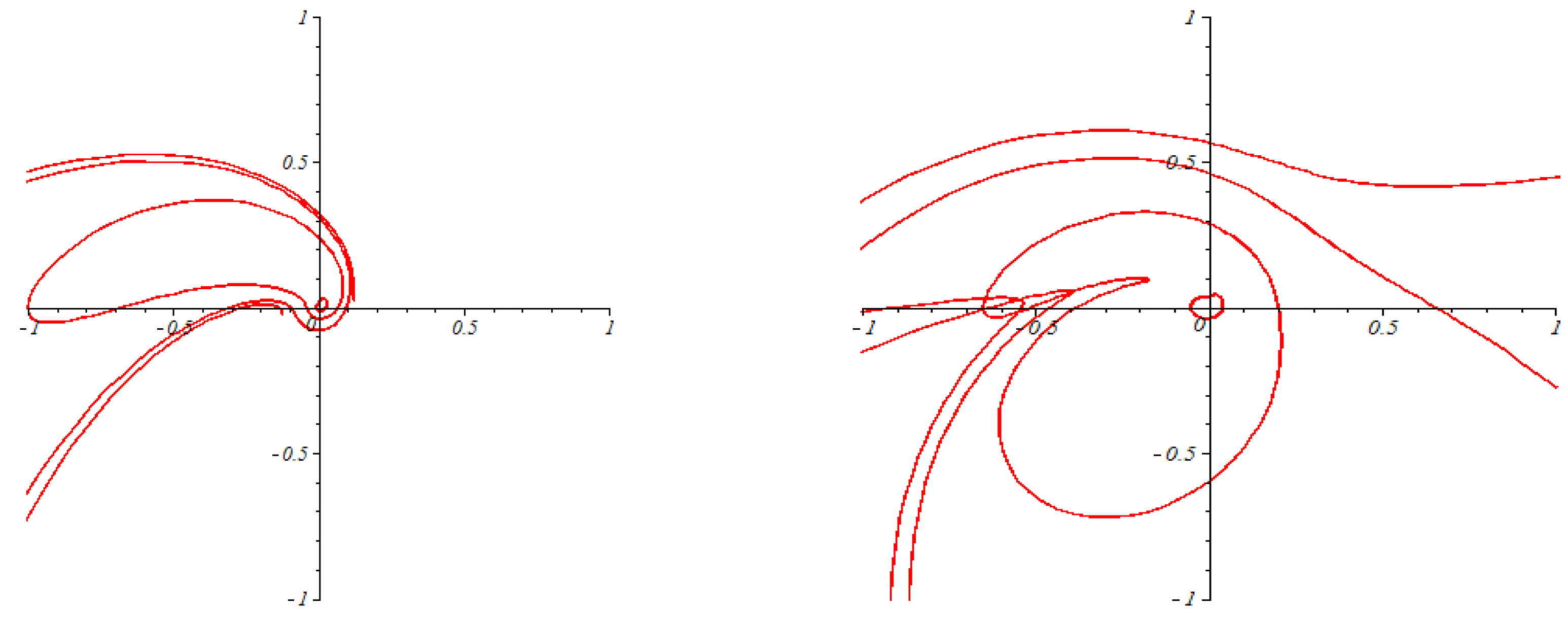

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghalary, R.; Ebadian, A.; Cho, N.E.; Alizadeh, M. New Criteria for Convex-Exponent Product of Log-Harmonic Functions. Axioms 2023, 12, 409. https://doi.org/10.3390/axioms12050409
Aghalary R, Ebadian A, Cho NE, Alizadeh M. New Criteria for Convex-Exponent Product of Log-Harmonic Functions. Axioms. 2023; 12(5):409. https://doi.org/10.3390/axioms12050409
Chicago/Turabian StyleAghalary, Rasoul, Ali Ebadian, Nak Eun Cho, and Mehri Alizadeh. 2023. "New Criteria for Convex-Exponent Product of Log-Harmonic Functions" Axioms 12, no. 5: 409. https://doi.org/10.3390/axioms12050409
APA StyleAghalary, R., Ebadian, A., Cho, N. E., & Alizadeh, M. (2023). New Criteria for Convex-Exponent Product of Log-Harmonic Functions. Axioms, 12(5), 409. https://doi.org/10.3390/axioms12050409




