A Mathematical Analysis of the Stress Statement of the Soil Basis under Complex Loading near the Retaining Wall

Abstract

The present paper describes and provides an analytical solution to the problem of the stress state of a limited-thickness soil basis resting on an incompressible soil base, under the action of two distributed loads of different intensities near the retaining wall of an excavation pit. It is proposed that the method for identifying components of the stress statement within the framework of the engineering problem in question is improved, and the solution is based on the trigonometric Ribiere–Fileon series. The results obtained by the authors allow for an evaluation of the supplementary effect on a retaining wall produced by loads from heavy machinery and materials stored near this retaining wall. These findings are useful for the design of underground constructions of buildings and structures. Theoretical results are provided together with those of numerical experiments to validate the research reliability.

1. Introduction

In conditions of dense urban development during the construction of underground transport infrastructure using an open method, as well as construction of underground parts of buildings and structures, including unique and high-rise ones, the most important problem in their design is to ensure the safety and possibility of the further operation of objects located in the zone of influence of a new construction. Often, the construction of station complexes, transfer hubs, and tunnel structures occurs in dense urban developments, which inevitably affects the development of additional deformations of the surrounding soil basis and the foundations of buildings and structures. Thus, when designing underground structures, as well as underground multi-level parts of buildings, it is necessary to carry out a quantitative assessment of changes in the stress–strain statement of the soil basis, including the foundations of buildings and structures located in the previously designated zone of influence of construction. A scientific and practical approach to solving this problem makes it possible to ensure the safe operation of these buildings and structures in the zone of influence of the construction of buried structures. This zone of influence significantly depends on the dimensions, depth, and shape of the pit (square or rectangular, etc.), as well as on the physical and mechanical properties of the surrounding soils.

Assessing the impact of new construction on existing buildings and structures is one of the most difficult geotechnical tasks. Solutions to engineering problems, based on the theory of elasticity, have been devised in the course of the development of theoretical and applied soil mechanics. Many of them remain relevant today because they can serve as the basis for new analytical solutions in nonlinear soil mechanics, and they allow for a wide range of factors triggering the stress–strain state of soil basis to be taken into account. Moreover, an accurate analytical solution can be applied to verify the findings of the numerical modeling of an engineering problem, which is widely used in the practice of designing the bases and foundations of buildings and structures.

The Flaman solution (1892) is among the first solutions focused on evaluating the stress state under the action of linear loading on the surface of a half-space [1]. Other well-known problems are the Mitchell problem (1902), which is focused on the action of a uniformly distributed strip load having an intensity q; the Boussinesque problem (1885), which concerns a unit force P acting on a linearly deformed half-space; the Kelvin problem, which is about unit force being applied to an infinitely long body; and several other problems.

Subsequently, solutions focused on evaluating the stress–strain state of soil basis under loading have been further refined and improved by M.I. Gorbunov-Posadov [2], G.K. Klein [3], N.A. Tsytovich [4], N.M. Gersevanov [5], Schleicher [6], K.E. Egorov [7], S.P. Timoshenko [8], Z.G. Ter-Martirosyan [9], and others [10,11,12,13], who took into account various factors such as stress distribution, stiffness, and the shape of foundation structures, etc. It is noteworthy that the works of A.V. Pilyagin [14] and D.V. Rachkov [15] focused on evaluating the SSS of soil bases with various shapes, with respect to different loading patterns and cases of application (surface or deep effects). Additionally, a number of scientists [16,17,18,19,20,21,22,23,24,25,26,27] are developing methods based on the inverse problems of identifying stresses in soil bases, using software packages for field testing and the numerical modeling of problems. In estimating stress strain field research has been made in terms of evolving methods in the scientific fields of uncertainty quantification and Machine Learning. Specifically, Savvides and Papadopoulos formed a Feed Forward Neural Network that estimate failure stresses and strains in Shallow Foundations formed through Stochastic Finite Element Analysis following Savvides and Papadrakakis [28,29] which estimated stress strain field through uncertainty estimation. Moreover, Chwala and Pula [30] has provided an analysis for the bearing capacity and the stress strain field in two layered soil with uncertainty while Fenton and Griffiths [31] did the same for the Mohr Coulomb φ-c parameters.

According to the extensive long-term data on the geodetic monitoring of the settlements of the foundations of buildings and structures, their predicted values, calculated using the elastic half-space model, exceed the actual values many times. This overestimation of the calculated values of precipitation is directly related to the absence of boundaries for the deformation areas in terms of width and depth. Previously, S.P. Timoshenko [8] gave a solution using a Fourier series for the case of a continuously distributed, infinitely long beam. The first application of a trigonometric series to problems in bending beams was performed by M. Ribiere (1899). The further development of this method was continued by L. Fileon (1903). Many scientists [3,4,7] have developed various models with the possibility of limiting the compressible soil layer both in depth and width. Based on the decision of S.P. Timoshenko [8], Z.G. Ter-Martirosyan developed a model for the model of a layer with a limited width and thickness [9]. This model was based on the assumption that the formation of a stress–strain state in a soil mass under the action of a local load has a certain specificity, which was confirmed by the results of theoretical and long-term experimental studies. A closed area with a finite width is formed under the distributed load, within which, the stresses exceed the values of the soil strength. In addition, in this area, there is an extreme value of soil deformation (Figure 1). The soil’s mechanical properties and the strength of the soil particles, as well as the width of the load (b = 2a), have an impact on the shape and size of such an area.

Analytical methods for calculating such problems in a linear and elastic formulation make it possible to take into account these factors and provide solutions to the simple formulas used in the design in the first approximation. Many theoretical solutions remain relevant today, since on their basis, it is possible to develop new analytical solutions for nonlinear soil mechanics. However, there are still no theoretical solutions that allow for taking into account, at the same time, the large range of factors that form the stress–strain statement of a soil basis. These are the distance of the building from the pit, the load on the foundation, and the width and length of the foundation. In this paper, the authors propose a variation and evolution of the method for determining the components of a stress state within a particular engineering problem, based on the trigonometric Ribiere–Fileon series [32,33]. For comparison purposes, a similar calculation was performed using the PLAXIS 2D software package with the boundary conditions provided below.

2. Materials and Methods

In earlier works [32,34], authors have analyzed the effect of a distributed load q = const on an area with a width of b = 2a, located at distance d from the edge of a rectangular retaining wall on a soil foundation resting on an incompressible base. This paper offers the statement of and a solution to the problem of the simultaneous application of two distributed loads with different values of intensity (q₁ и q₂) and different or similar widths (b₁ и b₂), at a distance d from the retaining wall. The case of the application of the distributed loads q₁ = 30 kPa, b₁ = 7 m and q₂ = 15 kPa, b₂ = 7 m at distance d = 2 m is considered. This problem corresponds to the case of a location of the load from construction machinery near the edge of the excavation pit (q₁ = 30 kPa) and the load from the materials stockpiled nearby (q₂ = 15 kPa). The loading pattern is shown in Figure 2.

It is assumed that the vertical wall is secured with strut elements, but vertical displacements of soil are allowed (Figure 1). When solving problems of the elasticity theory from a mathematical point of view, the conditions of equilibrium and equations of compatibility (continuity of deformations) must be satisfied. In addition, the condition of the linear dependence between stresses and deformations must be satisfied.

According to the theory of elasticity, the solution of the plane problem consists of finding some function φ(x,y) (Airy function) that is related to the stress components and volumetric weight of the soil by the following dependencies [4,8,9,32]:

$${\sigma }_x=\frac{{\partial }^2\phi }{\partial y^2}-\rho gy; {\sigma }_y=\frac{{\partial }^2\phi }{\partial x^2}-\rho gy; {\tau }_{xy}=-\frac{{\partial }^2\phi }{\partial x\partial y}$$

(1)

and satisfies the biharmonic equation:

$$\frac{{\partial }^4\phi }{\partial x^4}+2\frac{{\partial }^4\phi }{\partial x^2\partial y^2}+\frac{{\partial }^4\phi }{\partial y^4}=0$$

(2)

The solution to the problem formulated is obtained using the Ribiere–Fileon trigonometric series method. This method has a better convergence of the series for stress functions. The general solution of the biharmonic Equation (2) can be represented as an infinite trigonometric series [8,9,32]:

$$\begin{gathered} \phi \left(x,y\right)={\displaystyle \sum _{m=1}^{\infty }[\cos \alpha x\left(A_{m}ch\alpha y+B_{m}ych\alpha y+C_{m}sh\alpha y+D_{m}ysh\alpha y\right)+} \\ +\sin \alpha x\left({A^{\prime }}_{m}ch\alpha y+{B^{\prime }}_{m}ych\alpha y+{C^{\prime }}_{m}sh\alpha y+{D^{\prime }}_{m}ysh\alpha y\right)] \end{gathered}$$

(3)

The constants A_m, B_m,…, C’_m, and D’_m are determined from the boundary conditions. Using the stress function (2), adding, if necessary, power polynomials, it is possible to obtain the final analytical solutions [32].

For the problem, we assume the following boundary conditions on the upper and lower boundaries of the area of the soil basis:

$$\begin{array}{l}\mathrm{at} y=0\mathrm{and} y=2h: {\sigma }_y\left(x,0\right)={\sigma }_y\left(x,2h\right)=q\\ \left(-a\le x\le a\right);{\sigma }_y\left(x,0\right)={\sigma }_y\left(x,2h\right)=0\left(-l\le x\le -a\right)\mathrm{and} \left(a\le x\le l\right)\\ \mathrm{at} y=0 \mathrm{and} y=2h: {\tau }_{xy}\left(x,0\right)=0; {\tau }_{xy}\left(x,2h\right)=0\end{array}$$

(4)

Horizontal displacements on the right boundary $x=\pm l$ are absent. We have another boundary condition in the form:

$$u\left(\pm l\right)=0\hspace{1em}\hspace{1em}\nu \left(\pm l\right)\ne 0$$

(5)

The components of the stress statement of the soil basis outside the enclosing structure are calculated using the method of Z.G. Ter-Martirosyan [7,8,33,34] and are applied to the Ribiere–Fileon trigonometric series in the following manner:

$$\begin{array}{l}{\sigma }_y\left(x,y\right)=\frac{qa}{l}+\\ +\frac{4q}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\sin \frac{m\pi a}{l}}{m}\frac{\left[\left(\frac{m\pi h}{l}ch\frac{m\pi h}{l}+sh\frac{m\pi h}{l}\right)ch\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\cos \frac{m\pi x}{l}}\end{array}$$

(6)

$$\begin{array}{l}{\sigma }_x\left(x,y\right)=\frac{qa}{l}\frac{\nu }{1-\nu }-\\ -\frac{4q}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\sin \frac{m\pi a}{l}}{m}\frac{\left[\left(\frac{m\pi h}{l}ch\frac{m\pi h}{l}-sh\frac{m\pi h}{l}\right)ch\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}}\cos \frac{m\pi x}{l}\end{array}$$

(7)

$${\tau }_{xy}\left(x,y\right)=-\frac{4q}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\sin \frac{m\pi a}{l}}{m}}\frac{\left[\frac{m\pi h}{l}ch\frac{m\pi h}{l}sh\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}ch\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\sin \frac{m\pi x}{l}$$

(8)

$${\sigma }_m(x,y)=\frac{1+\nu }{3}\left[\frac{qa}{l}\frac{1}{1-\nu }+\frac{8q}{\pi }{\displaystyle \sum _{m=1}^{\propto }\frac{\sin \frac{m\pi a}{l}}{m}}\frac{\mathrm{s}h\frac{m\pi a}{l}ch\frac{m\pi (y-h)}{l}}{\mathrm{s}h\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\cos \frac{m\pi x}{l}\right]$$

(9)

where:

q—the distributed load, kPa;

b—the width of the strip of the distributed load, m;

l—the width of the estimated area;

m—any integer, m = 1;

h—the depth of the estimated area;

ν—Poisson’s ratio

In the first approximation, this problem can be solved using the symmetrically oriented load principle, similar to the problem of SSS in the elastic soil layer with a thickness h, under the action of the distributed load q = const along the strip with a width of b = 2a, whose bottom boundary rests on an incompressible soil base [33]. When the symmetrical loads q = const are applied to the layer of 2h thickness along the strip with a width of b = 2a y = ±h, the solution to the problem turns out to be symmetrical in relation to y = 0; in this case, ε_x = 0, σ_x ≠ 0 is the condition that is satisfied at the boundary.

For presenting a uniformly distributed load at a distance d from the vertical recess, we use a calculation scheme as a result of the simultaneous action of the uniformly distributed loads, with an intensity q addition over a strip with a width of b₁ = 2a₁ and b₂ = 2a₂ and an intensity of −q over a strip with a width of d and d + b₁ [32].

The final solution aimed at determining the stress components is as follows:

$$\begin{array}{l}{\sigma }_y\left(x,y\right)=\left(\frac{q_1(b_1+b_2+d)}{l}-\frac{q_{2}d}{l}+\frac{q_3(b_1+d)}{l}-\frac{q_3{b}_1}{l}\right)+\\ +\frac{4q}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\left(\sin \frac{m\pi a}{l}-\sin \frac{m\pi b}{l}\right)}{m}\frac{\left[\left(\frac{m\pi h}{l}ch\frac{m\pi h}{l}+sh\frac{m\pi h}{l}\right)ch\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\cos \frac{m\pi x}{l}}\end{array}$$

(10)

$$\begin{array}{l}{\sigma }_x\left(x,y\right)=\left(\frac{q_1(b_1+b_2+d)}{l}-\frac{q_{2}d}{l}+\frac{q_3(b_1+d)}{l}-\frac{q_3{b}_1}{l}\right)\frac{\nu }{1-\nu }-\\ -\frac{4q}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\left(\sin \frac{m\pi a}{l}-\sin \frac{m\pi b}{l}\right)}{m}\frac{\left[\left(\frac{m\pi h}{l}ch\frac{m\pi h}{l}-sh\frac{m\pi h}{l}\right)ch\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}}\cos \frac{m\pi x}{l}\end{array}$$

(11)

$${\tau }_{xy}\left(x,y\right)=-\frac{4(q_1-q_2+q_3)}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\left(\sin \frac{m\pi ((b_1+b_2+d)-d+(b_1+d))}{l}-\sin \frac{m\pi b}{l}\right)}{m}}\frac{\left[\frac{m\pi h}{l}ch\frac{m\pi h}{l}sh\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}ch\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\sin \frac{m\pi x}{l}$$

(12)

$${\sigma }_m(x,y)=\frac{1+\nu }{3}\left[\left(\frac{q_1(b_1+b_2+d)}{l}-\frac{q_{2}d}{l}+\frac{q_3(b_1+d)}{l}-\frac{q_3{b}_1}{l}\right)\frac{1}{1-\nu }+\frac{8q}{\pi }{\displaystyle \sum _{m=1}^{\propto }\frac{\sin \frac{m\pi a}{l}}{m}}\frac{\mathrm{s}h\frac{m\pi a}{l}ch\frac{m\pi (y-h)}{l}}{\mathrm{s}h\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\cos \frac{m\pi x}{l}\right]$$

(13)

where d is the distance from the distributed load to the retaining wall, according to Figure 2.

3. Results

The analytical calculation, obtained using the MathCAD software package, allowed for a determination of the stress components throughout the plane at y > 0 and ±x. For the purpose of the comparative analysis, a similar calculation was performed by applying the PLAXIS 2D software package to the quarter plane with the boundary condition on the y axis.

The design scheme in the PLAXIS 2D software included a single-layer soil basis with a lateral boundary condition, under which ε_x = 0, σ_x ≠ 0, simulating an absolutely rigid enclosure of the pit in the absence of horizontal movements. The lower boundary of the calculated model was fixed in the vertical and horizontal directions by default. The mesh size was fine. A mesh sensitivity analysis was conducted. A general view of the calculation scheme is shown in Figure 3. In Figure 4a, Figure 5a, Figure 6a and Figure 7a, isolines of these stress components for the case of the distributed loads of q₁ = 30 kPa, b₁ = 7 m and q₂ = 15 kPa, b₂ = 7 m at distance of d = 2 m are presented. The given values were randomly selected based on the experience of designing similar structures in order to quantify the proposed solution.

A calculation in PS PLAXIS was carried out to verify the isolines of the vertical, horizontal, shear, and mean stresses obtained earlier, using an analytical calculation with the formulas (10–13). We used the Linear Elastic model in PS PLAXIS with the parameters E = 25,000 kPa, _ = 0.37, and γ = 0 kN/m³ The results of the numerical calculations are shown in Figure 4b, Figure 5b, Figure 6b and Figure 7b.

Graphs showing the supplementary horizontal (Figure 8a) and vertical stresses (Figure 8b) at the contact between “the soil basis and the retaining wall” were also constructed.

4. Discussion

An analysis of the existing analytical models of foundations showed that the real structural behavior of soil bases is best conveyed by an analytical model that allows for taking into account the limited width and depth of the deformation area. The results of the solution also demonstrated that the stresses caused by the action of a distributed load near the retaining wall of a pit shifted to the boundary of the pit with increasing values. A characteristic feature was the asymmetric distribution of the stress isofields relative to the center of the distributed load when it was located at a distance from the side of the retaining wall of the pit, with an offset towards the enclosure of the pit. In cases of simple and complex loading, the solution to the problem, based on the trigonometric Ribiere–Fileon series, demonstrated a satisfactory convergence with the results of the numerical solution obtained using the PLAXIS 2D software package, which confirms the possibility of using this solution to evaluate the SSS of bases and foundations near retaining walls.

5. Conclusions

Having generalized the results of the research, we can make the following conclusions:

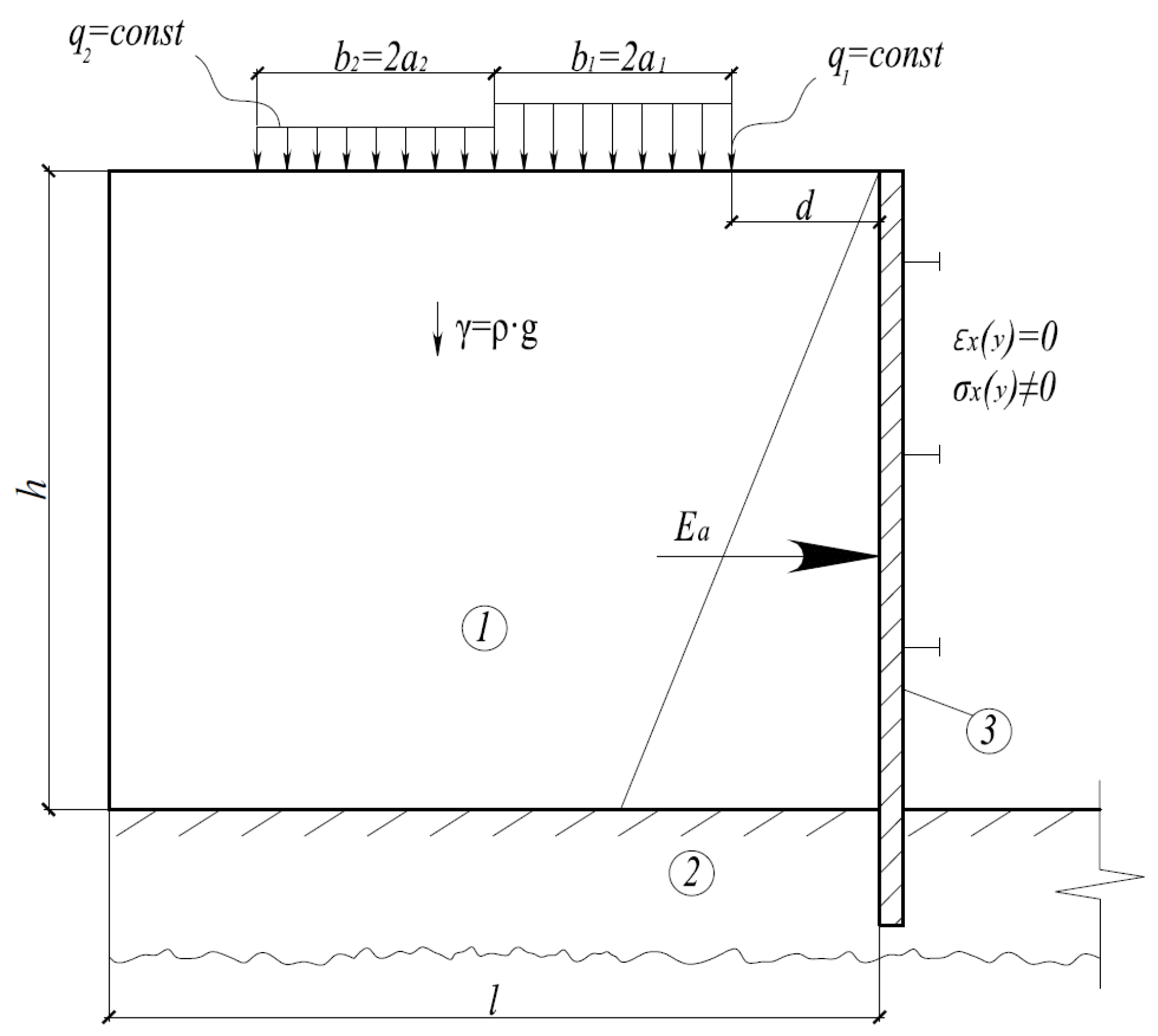
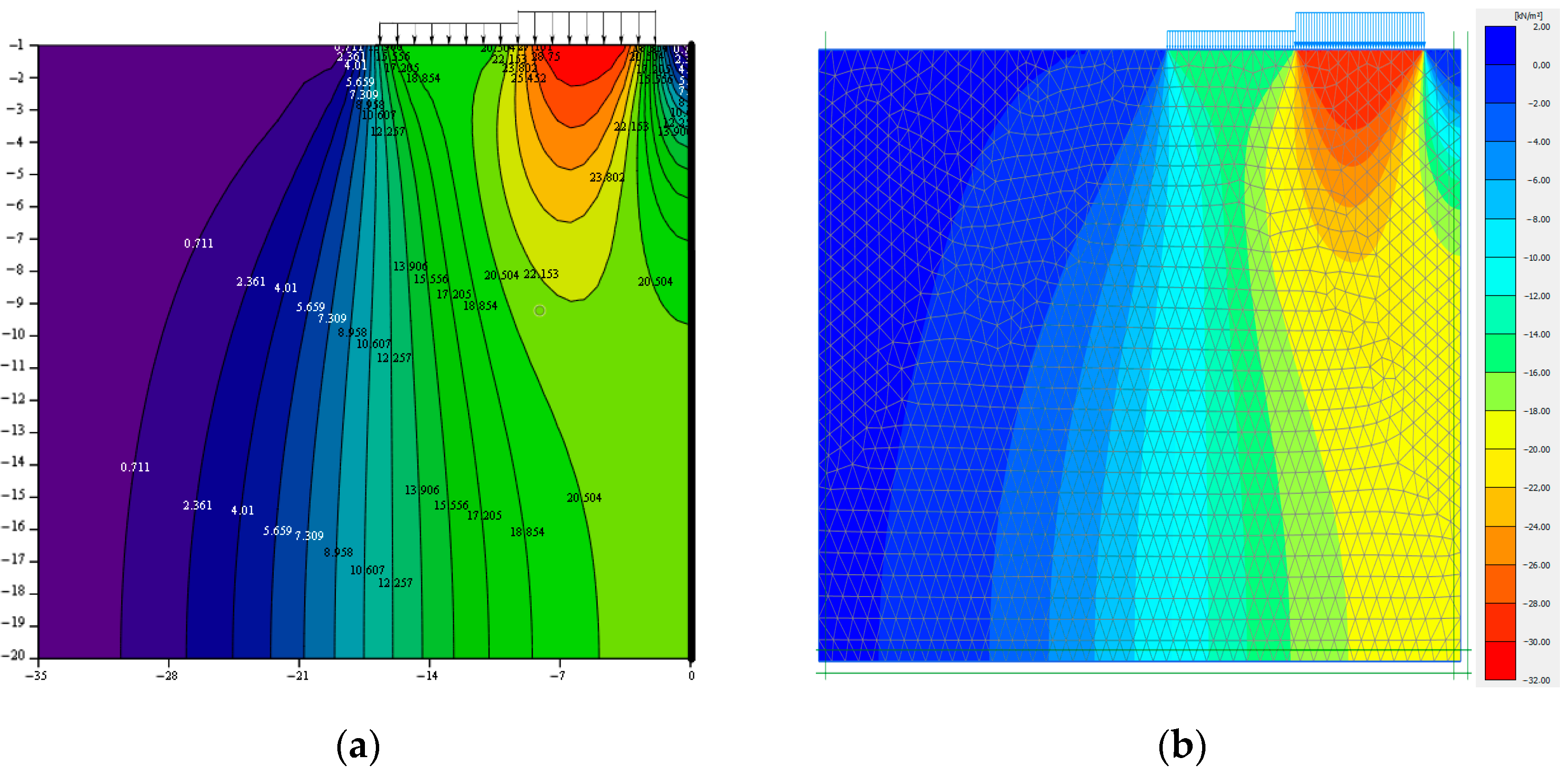
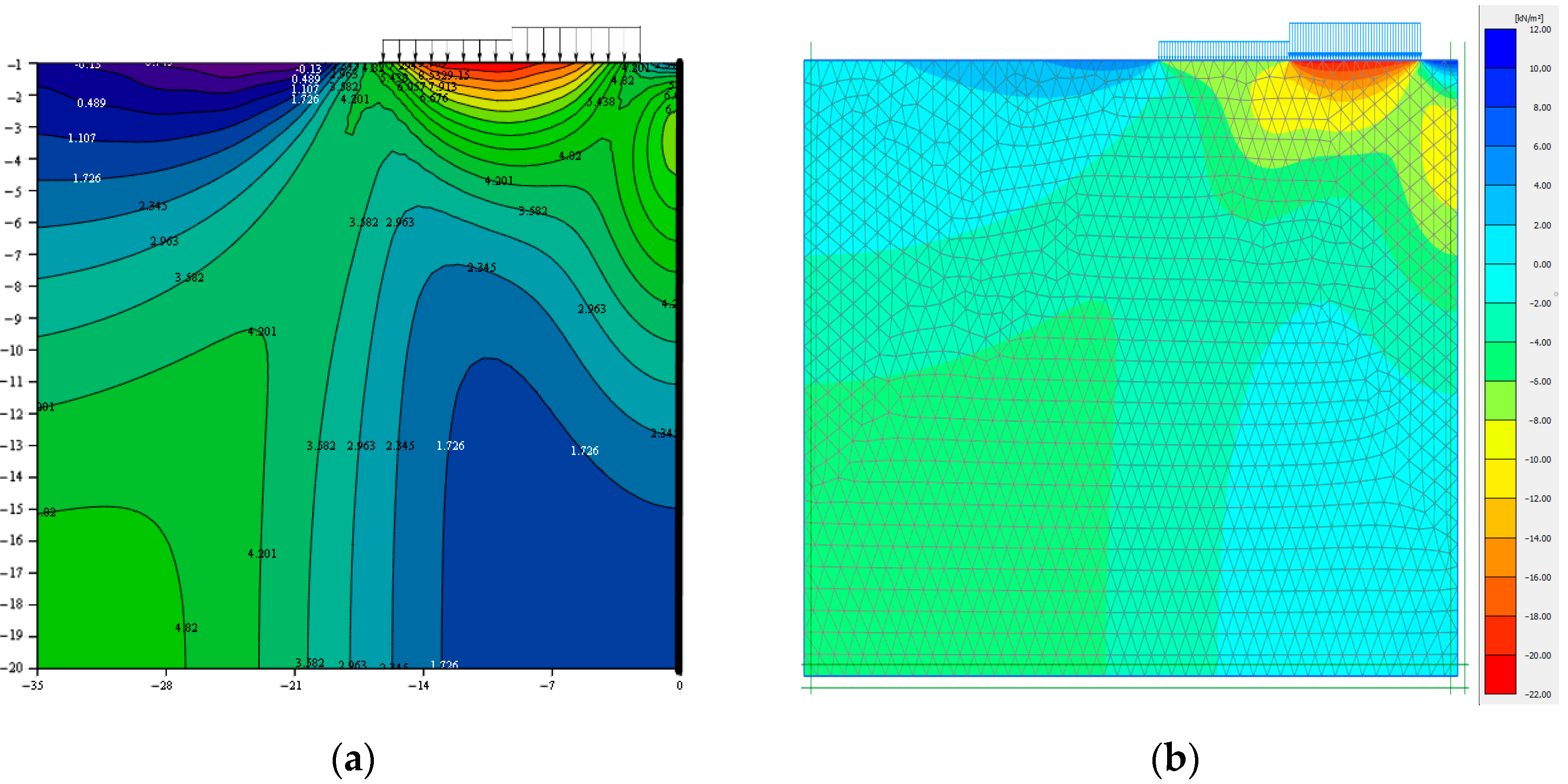
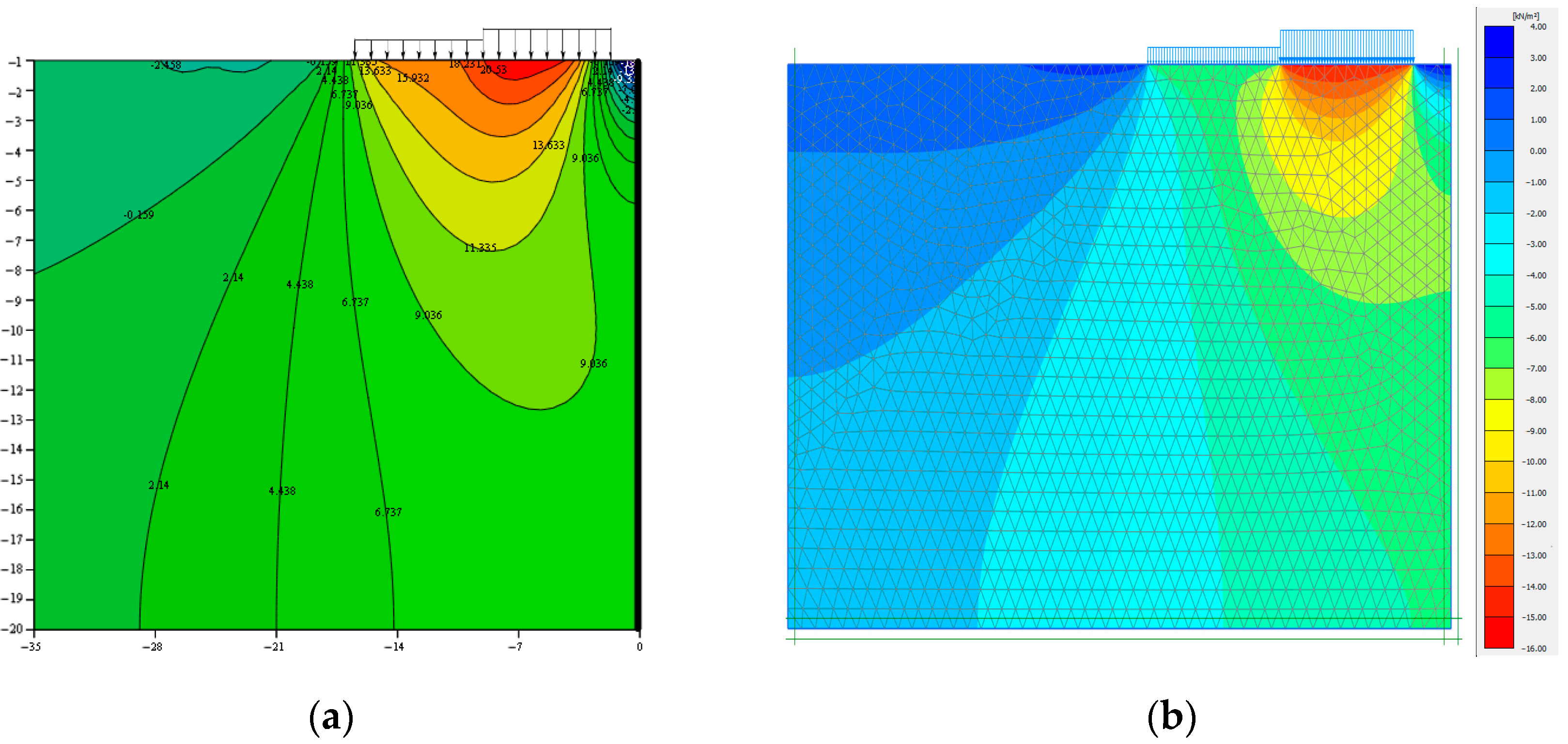
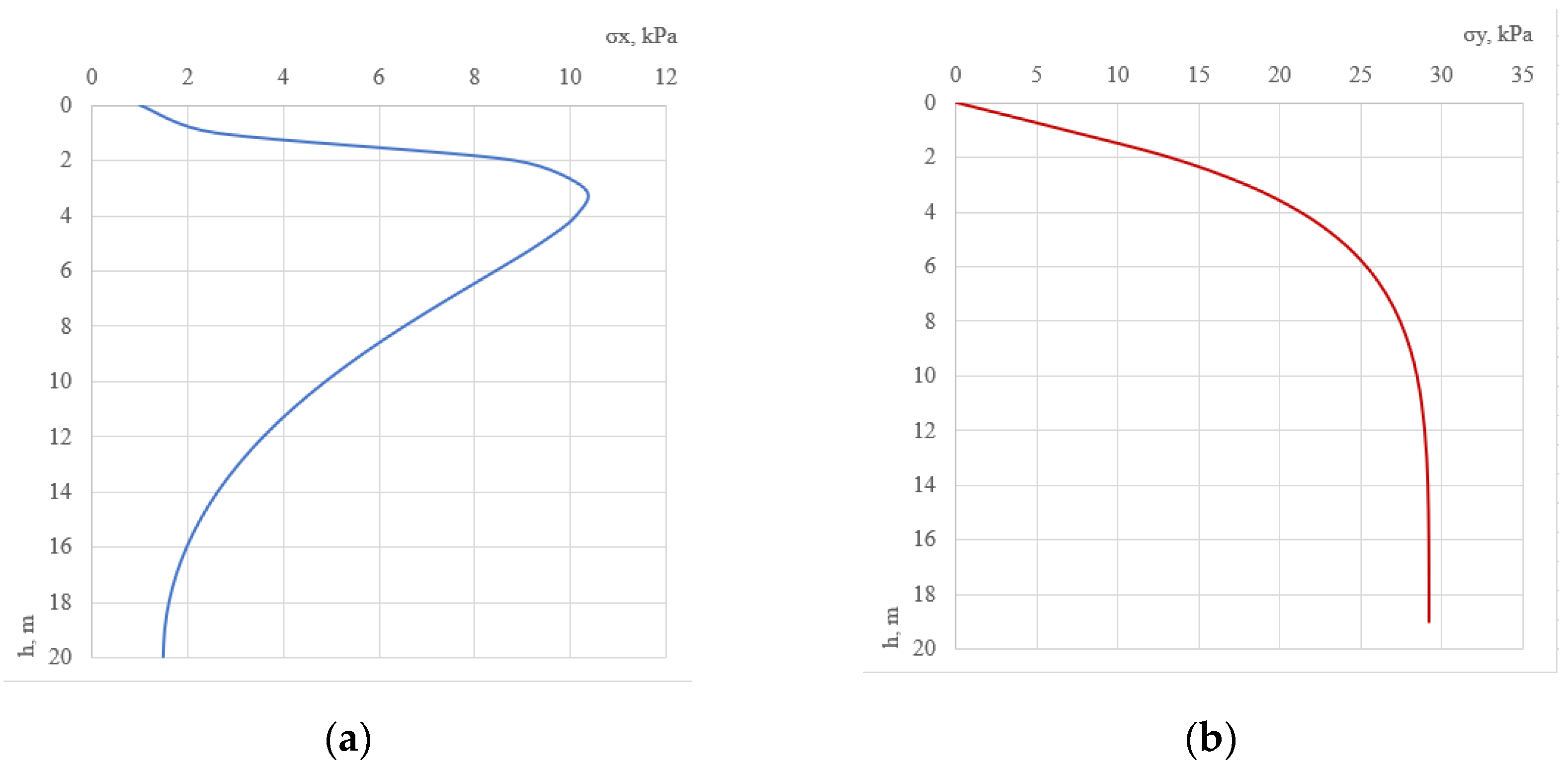
• It follows from the analysis of the results of the accurate mathematical solution to the problem that supplementary horizontal and vertical stresses in the range of 10–30 kPa arise on the y axis in the absence of horizontal displacements. At x = 0, shear stresses τ_xy = 0;
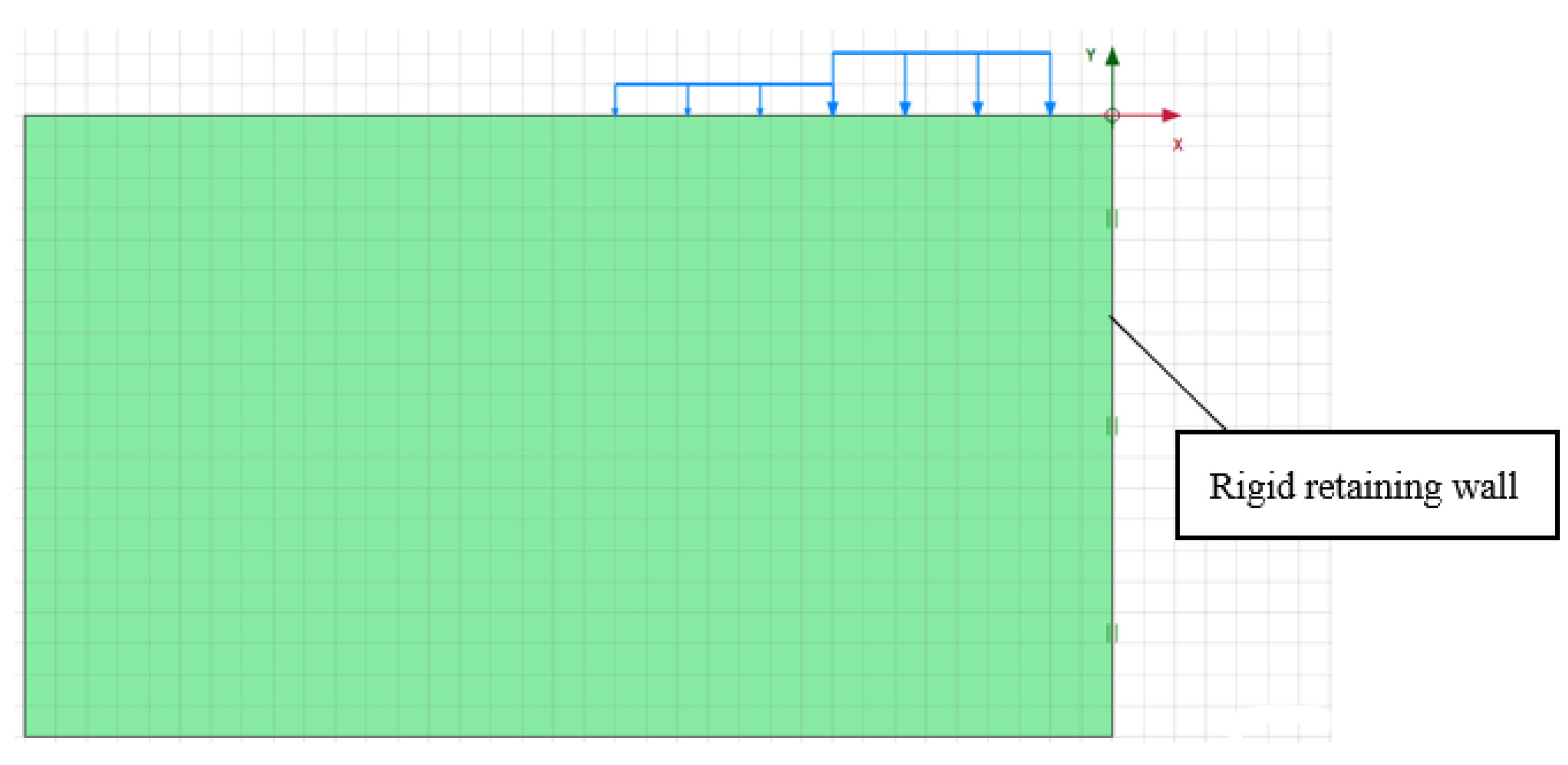
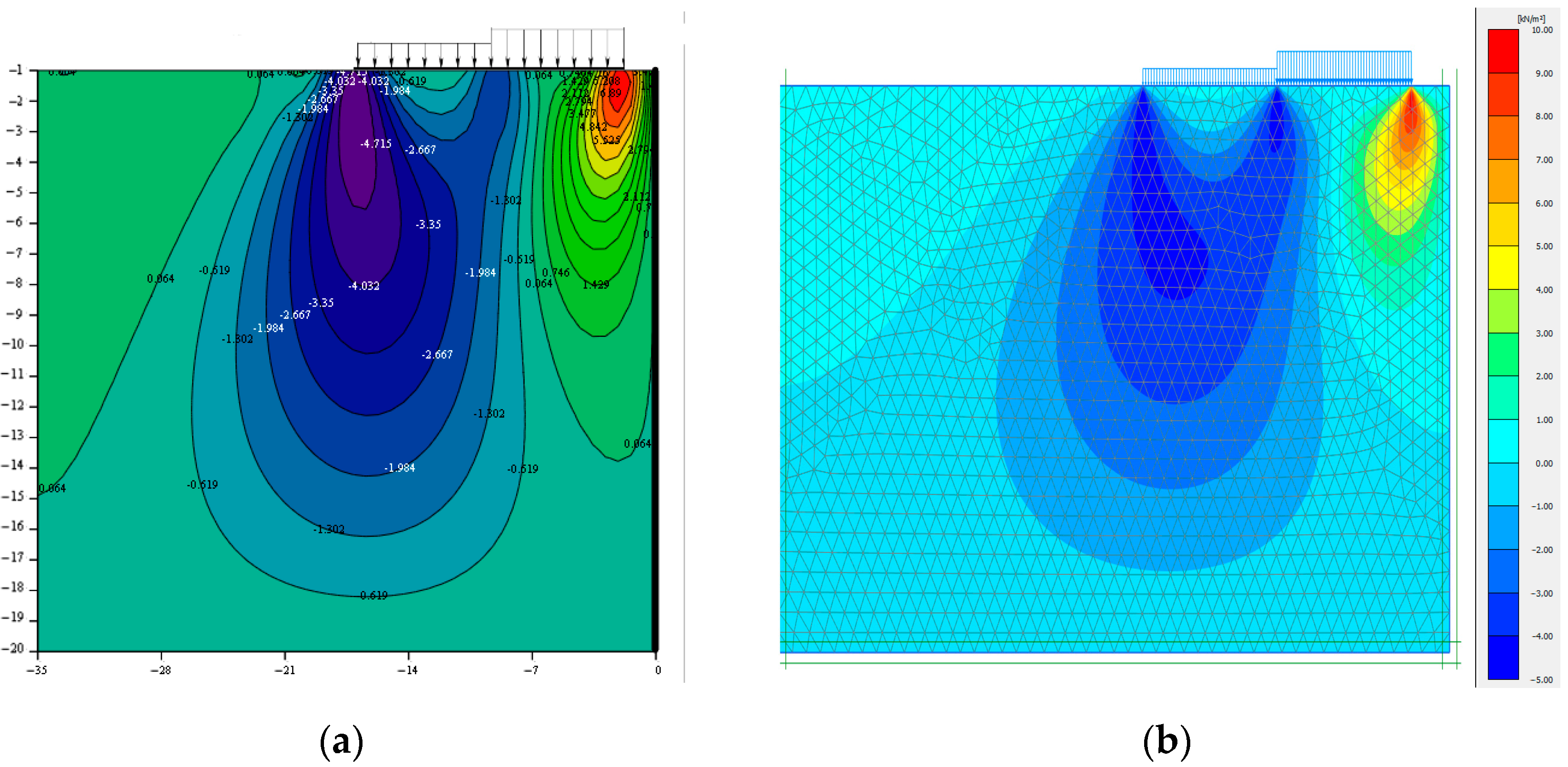
• Based on a comparative analysis of the obtained solution to the problem of stress distribution in an array of soils with finite widths and thicknesses based on an incompressible base, using the method of the Ribiere–Fileon trigonometric series and the solution obtained in the PLAXIS 2D software, it was shown that the actual behaviour of soil bases under a load, in particular at a distance from the side of the pit, corresponded closely to the model of soil basis, which allows for taking into account the limitations of the deformation area in terms of width and depth.
• It is noteworthy that the obtained isofields of stresses may also be used in practical engineering and geotechnical studies for forecasting the settlements of two adjacent buildings or structures near a retaining wall, by supplementing the solution with deformation components.
• When designing excavations for buildings and structures, one can use this solution to obtain the isofields of stresses under distributed loads, e.g., from adjacent construction machinery and stockpiled materials. It is worth noting that the displacement of horizontal stresses towards a retaining wall triggers supplementary internal forces in the retaining wall, which should be considered when selecting reinforcements for reinforced concrete retaining walls or a metal retaining wall made of pipes or sheeting of Larsen and similar types.
• In further studies, it is assumed that there should be a comparison of the theoretical and numerical solutions with the results of the geodetic monitoring of stresses in a soil basis.