Vanishing Property of BRST Cohomology for Modified Highest Weight Modules

Abstract

We construct certain modified highest weight modules which are called quasi highest weight modules in this paper. Using the quasi highest weight modules, we introduce a new category of modules over an affine Lie superalgebra which contains projective covers. We also prove that both these projective covers and the quasi highest weight modules satisfy the vanishing property of BRST cohomology.

1. Introduction

Let $\mathfrak{g}$ be a simple finite-dimensional complex Lie superalgebra and f be its any even nilpotent element. Then, we can construct an associated algebra denoted by $W\left(\mathfrak{g},f\right)$ through the cohomology of Becchi-Rouet-Strora-Tyutin (shortly BRST) complex (see [1]). We call this associated algebra a W-algebra. W-algebras appeared around 80’s in the study of rational conformal field theories and can be considered as a generalization of vertex algebras [2,3,4,5].

Let $\widehat{\mathfrak{g}}$ be the affinization of $\mathfrak{g}$, and fix its positive root system ${\widehat{\Delta }}_{+}$ in the root system $\widehat{\Delta }$ of $\widehat{\mathfrak{g}}$. Let $\widehat{\mathfrak{h}}$ be the associated Cartan subalgebra of $\widehat{\mathfrak{g}}$ (see Section 2.2 for the details). Then, we obtain the full subcategory ${\mathcal{O}}_k$ of the category of left $\widehat{\mathfrak{g}}$-modules with level k whose objects satisfy the following conditions (see [6]):

1.

$V={⨁}_{\mu \in {\widehat{\mathfrak{h}}}^{*}}{V}^{\mu }$ and dim $V^{\mu }<\infty \mathrm{for}\mathrm{all}\mu \in {\widehat{\mathfrak{h}}}^{*}$, where $V^{\mu }$ is the weight space of weight $\mu \in {\widehat{\mathfrak{h}}}^{*}$.

2.

The set of weights of V is contained in ${\bigcup }_{i=1}^n\left({\lambda }_i-{\mathbb{Z}}_{\ge 0}{\widehat{\Delta }}_{+}\right)$ for some finite subset $\left\{{\lambda }_1,\cdots ,{\lambda }_n\right\}$ of ${\widehat{\mathfrak{h}}}^{*}$, where ${\mathbb{Z}}_{\ge 0}{\widehat{\Delta }}_{+}$ is the ${\mathbb{Z}}_{\ge 0}$-span of ${\widehat{\Delta }}_{+}$.

Through the theory of BRST cohomology, one can construct a functor H from the category ${\mathcal{O}}_k$ to the category of $W\left(\mathfrak{g},f\right)$-modules. More explicitly, the $W\left(\mathfrak{g},f\right)$-module corresponding to a $\widehat{\mathfrak{g}}$-module M is the cohomology $H\left(M\right)$ of the BRST complex associated to M (see [7,8,9]). This functor was studied in [1,10,11,12] in order to compute the characters of $W\left(\mathfrak{g},f\right)$-modules. In addition, it is known that the vanishing property of BRST cohomology is satisfied in the category ${\mathcal{O}}_k$ (see [13,14,15]). Namely, for any object of ${\mathcal{O}}_k$ its BRST cohomology is vanished except for the degree 0. In [16], this vanishing property of BRST cohomology was extended to a certain larger category containing ${\mathcal{O}}_k$.

One of the main purposes of this article was to search for another category of $\widehat{\mathfrak{g}}$-modules which satisfies the vanishing property of BRST cohomology. For this purpose, we shall construct a new category ${\mathcal{Q}}_k$ of modules over an affine Lie superalgebra based on certain modified highest weight modules. We shall call these modified highest weight modules the quasi highest weight modules in this paper. The quasi highest weight modules are motivated from the the generalized Verma modules introduced in [17] (Section 6). We are particularly interested in a certain specific quasi highest weight modules $P_{\lambda }$ (see Section 3.2), and we shall prove that they satisfy the vanishing property of BRST cohomology (see Theorem 5).

However, we should point out that it is necessary to know if the category ${\mathcal{Q}}_k$ contains projective covers satisfying the vanishing property of BRST cohomology in order to prove the vanishing property of BRST cohomology for any object in ${\mathcal{Q}}_k$. For this reason, we are also interested in constructing projective covers in ${\mathcal{Q}}_k$ which satisfy the vanishing property of BRST cohomology. In fact we shall prove that there exist projective covers in ${\mathcal{Q}}_k$, and they yield the composition series whose successive factors are equal to the quasi highest weight modules $P_{\lambda }$ (see Theorem 4). In addition, it turns out that these composition series give rise to the vanishing property of BRST cohomology (see Theorem 6).

In the forthcoming article, we shall show how the projective covers constructed in this article can be used to prove the vanishing property of BRST cohomology for any object of ${\mathcal{Q}}_k$.

2. Preliminaries

2.1. Setting-Up

Assume that $\mathfrak{g}$ is a simple finite-dimensional complex Lie superalgebra with a nondegenerate even supersymmetric bilinear form $\left(|\right)$. Let $\left\{e,x,f\right\}$ be an ${\mathfrak{sl}}_2$-triple of even elements of $\mathfrak{g}$ normalized as $\left[ef\right]=x,\left[xe\right]=e,\left[xf\right]=-f$. Then, we obtain the following properties from the representation theory of ${\mathfrak{sl}}_2$:

(P1) There exists the eigenspace decomposition $\mathfrak{g}={⨁}_{j\in \frac{1}{2}\mathbb{Z}}{\mathfrak{g}}_j$ with respect to the action of adx.

(P2) ad$f:{\mathfrak{g}}_{\frac{1}{2}}⟶{\mathfrak{g}}_{-\frac{1}{2}}$ yields a vector space isomorphism.

We should notice that the element f gives rise to a skew-supersymmetric even bilinear form $〈,〉$ on ${\mathfrak{g}}_{\frac{1}{2}}$ defined by the formula $〈a,b〉=\left(f|\left[ab\right]\right)$. In addition, we obtain from (P2) that $〈,〉$ is a nondegenerate bilinear form on ${\mathfrak{g}}_{\frac{1}{2}}$.

Write ${\mathfrak{g}}^f$ for the centralizer of f in $\mathfrak{g}$. In other words, ${\mathfrak{g}}^f=\left\{x\in \mathfrak{g}|\left[fx\right]=0\right\}$. Then, it follows from the representation theory of ${\mathfrak{sl}}_2$ that ${\mathfrak{g}}^f={\oplus }_{j\in \frac{1}{2}{\mathbb{Z}}_{\le 0}}{\mathfrak{g}}_j^f$, where ${\mathfrak{g}}_j^f={\mathfrak{g}}^f\cap {\mathfrak{g}}_j$ (see [18]).

Consider a Cartan subalgebra $\mathfrak{h}\subset {\mathfrak{g}}_0$ of $\mathfrak{g}$ containing x. Let $\Delta \subset {\mathfrak{h}}^{*}$ be the set of roots of $\mathfrak{g}$. Fix the root vector $u_{\alpha }\in {\mathfrak{g}}_{\alpha }$ satisfying $\left(u_{\alpha }|u_{-\alpha }\right)=1$ for each $\alpha \in \Delta$. It is well-known that each root space ${\mathfrak{g}}_{\alpha }$ is one-dimensional except for the case of type $A(1,1)$ (see [19]). To avoid this exceptional case, we shall always assume that $\mathfrak{g}$ is a simple basic Lie superalgebra different from the type $A(1,1)$ in the remaining part of this paper.

For each $j\in \frac{1}{2}\mathbb{Z}$, define ${\Delta }_j=\left\{\alpha \in \Delta \left|\alpha \right(x)=j\right\}$. Then, this implies that $\Delta ={\cup }_{j\in \frac{1}{2}\mathbb{Z}}{\Delta }_j$. Also, we see that ${\Delta }_0$ is the set of roots of the subalgebra ${\mathfrak{g}}_0$ (see [18]). Write ${\Delta }_{0,+}$ and ${\Delta }_{0,-}$ for the set of positive and negative roots of ${\Delta }_0$, respectively. Then, we check that ${\Delta }_{+}={\Delta }_{0,+}\bigsqcup {\Delta }_{>0}$ (resp. ${\Delta }_{-}={\Delta }_{0,-}\bigsqcup {\Delta }_{<0}$) is the set of positive (resp. negative) roots of $\mathfrak{g}$, where ${\Delta }_{>0}={\bigsqcup }_{j>0}{\Delta }_j$ (resp. ${\Delta }_{<0}={\bigsqcup }_{j<0}{\Delta }_j$). Hence, we obtain the following triangular decompositions

$$\mathfrak{g}={\mathfrak{n}}_{-}\oplus \mathfrak{h}\oplus {\mathfrak{n}}_{+}$$

and

$${\mathfrak{g}}_0={\mathfrak{n}}_{0,-}\oplus \mathfrak{h}\oplus {\mathfrak{n}}_{0,+},$$

where ${\mathfrak{n}}_{\pm }={\oplus }_{\alpha \in {\Delta }_{\pm }}{\mathfrak{g}}_{\alpha }$ and ${\mathfrak{n}}_{0,\pm }={\oplus }_{\alpha \in {\Delta }_{0,\pm }}{\mathfrak{g}}_{\alpha }$.

Next, define ${\mathfrak{g}}_{>0}={⨁}_{j>0}{\mathfrak{g}}_j$ and ${\mathfrak{g}}_{<0}={⨁}_{j<0}{\mathfrak{g}}_j$. Notice from definitions that ${\mathfrak{g}}_{>0}={⨁}_{\alpha \in {\Delta }_{>0}}{\mathfrak{g}}_{\alpha }$ and ${\mathfrak{g}}_{<0}={⨁}_{\alpha \in {\Delta }_{<0}}{\mathfrak{g}}_{\alpha }$, and hence we get

$$\mathfrak{g}={\mathfrak{g}}_{<0}\oplus {\mathfrak{n}}_{0,-}\oplus \mathfrak{h}\oplus {\mathfrak{n}}_{0,+}\oplus {\mathfrak{g}}_{>0}.$$

2.2. Affine Lie Superalgebras [20,21]

Let $\widehat{\mathfrak{g}}$ be the Kac-Moody affinization of $\mathfrak{g}$. In other words, $\widehat{\mathfrak{g}}$ is the Lie superalgebra defined by $\widehat{\mathfrak{g}}=\mathfrak{g}\otimes \mathbb{C}\left[t,t^{-1}\right]\oplus \mathbb{C}K\oplus \mathbb{C}D$ with commutation relations

1.

$\left[u\left(m\right)v\left(n\right)\right]=\left[uv\right](m+n)+m{\delta }_{m+n,0}\left(u|v\right)K$,

2.

$\left[Du\left(m\right)\right]=mu\left(m\right),\left[K\widehat{\mathfrak{g}}\right]=0$,

where $u,v\in \mathfrak{g}$; $m,n\in \mathbb{Z}$; $u\left(m\right):=u\otimes t^m$.

Recall that the bilinear form $\left(|\right)$ is extended from $\mathfrak{g}$ to $\widehat{\mathfrak{g}}$ by the rules

1.

$\left(u\left(m\right)\left|v\right(n)\right)=\left(u\right|v){\delta }_{m+n,0}$,

2.

$\left(\mathfrak{g}\otimes \mathbb{C}\left[t,t^{-1}\right]|\mathbb{C}K\oplus \mathbb{C}D\right)=0$,

3.

$\left(K|K\right)=\left(D|D\right)=0$ and $\left(K|D\right)=\left(D|K\right)=1$.

In the remaining part of this paper, we shall fix the triangular decomposition $\widehat{\mathfrak{g}}={\widehat{\mathfrak{n}}}_{-}\oplus \widehat{\mathfrak{h}}\oplus {\widehat{\mathfrak{n}}}_{+}$, where

$$\begin{array}{ccc}\hfill \widehat{\mathfrak{h}}& =& \mathfrak{h}\oplus \mathbb{C}K\oplus \mathbb{C}D,\hfill \\ \hfill {\widehat{\mathfrak{n}}}_{-}& =& \left({\mathfrak{n}}_{-}\otimes \mathbb{C}\left[t^{-1}\right]\right)\oplus \left(\mathfrak{h}\otimes \mathbb{C}\left[t^{-1}\right]t^{-1}\right)\oplus \left({\mathfrak{n}}_{+}\otimes \mathbb{C}\left[t^{-1}\right]t^{-1}\right),\hfill \\ \hfill {\widehat{\mathfrak{n}}}_{+}& =& \left({\mathfrak{n}}_{-}\otimes \mathbb{C}\left[t\right]t\right)\oplus \left(\mathfrak{h}\otimes \mathbb{C}\left[t\right]t\right)\oplus \left({\mathfrak{n}}_{+}\otimes \mathbb{C}\left[t\right]\right).\hfill \end{array}$$

We also write $\widehat{\Delta }$, ${\widehat{\Delta }}_{+}$ and ${\widehat{\Delta }}_{-}$ for the set of roots, positive roots and negative roots of $\widehat{\mathfrak{g}}$, respectively. In addition, we denote by ${\widehat{\mathfrak{h}}}_k^{*}$ the set $\left\{\lambda \in {\widehat{\mathfrak{h}}}^{*}|\lambda \left(K\right)=k\right\}$ for a complex number k.

3. Quasi Highest Weight Modules

3.1. New Category

We first introduce a new triangular decomposition of $\widehat{\mathfrak{g}}$.

Definition 1.

1.

The quasi triangular decomposition of $\widehat{\mathfrak{g}}$ is

$$\widehat{\mathfrak{g}}=\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\oplus {\mathfrak{n}}_{0,+}\right)\oplus \widehat{\mathfrak{h}}\oplus \left({\mathfrak{n}}_{0,-}\oplus {\mathfrak{g}}_{>0}\oplus {\widehat{\mathfrak{g}}}^{>}\right),$$

where ${\widehat{\mathfrak{g}}}^{<}=\mathfrak{g}\otimes \mathbb{C}\left[t^{-1}\right]t^{-1}$ and ${\widehat{\mathfrak{g}}}^{>}=\mathfrak{g}\otimes \mathbb{C}\left[t\right]t$.

2.

A simultaneous eigenvector of $\widehat{\mathfrak{h}}$ that is annihilated by ${\mathfrak{n}}_{0,-}\oplus {\mathfrak{g}}_{>0}\oplus {\widehat{\mathfrak{g}}}^{>}$ is called a quasi highest weight vector of $\widehat{\mathfrak{g}}$.

3.

A $U\left(\widehat{\mathfrak{g}}\right)$-module generated by a single quasi highest weight vector is called a quasi highest weight $U\left(\widehat{\mathfrak{g}}\right)$-module, where $U\left(\widehat{\mathfrak{g}}\right)$ denotes the universal enveloping algebra of $\widehat{\mathfrak{g}}$.

Example 1.

Let $\mathbb{C}v$ be the 1-dimensional $U\left(\mathfrak{g}\right)$-module generated by a single vector v such that v is a simultaneous eigenvector of $\mathfrak{h}$ and ${\mathfrak{n}}_{0,-}\oplus {\mathfrak{g}}_{>0}$ acts trivially. Set

$${\widehat{\mathfrak{g}}}^{\ge }={\widehat{\mathfrak{g}}}^{>}\oplus \mathfrak{g}$$

and

$$V=U\left(\widehat{\mathfrak{g}}\right)\underset{U\left({\widehat{\mathfrak{g}}}^{\ge }\oplus \mathbb{C}D\oplus \mathbb{C}K\right)}{⨂}\mathbb{C}v,$$

where

1.

${\widehat{\mathfrak{g}}}^{>}\oplus \mathbb{C}D$ acts trivially on $\mathbb{C}v$.

2.

K acts as scalar k on $\mathbb{C}v$.

Then, we see that V is the quasi highest weight $U\left(\widehat{\mathfrak{g}}\right)$-module with quasi highest weight vector $1\otimes v$. We also point out that V is an example of the generalized Verma modules defined in [17] (Section 6).

Now, we introduce new categories of $U\left(\widehat{\mathfrak{g}}\right)$-modules containing quasi highest weight modules.

Definition 2.

The category ${\mathcal{Q}}_k$ is the full subcategory of the category of the left $U\left(\widehat{\mathfrak{g}}\right)$-modules at level k which has objects V satisfying the following conditions:

1.

$V={⨁}_{\lambda \in {\widehat{\mathfrak{h}}}_k^{*}}{V}^{\lambda }$ with dim$V^{\lambda }<\infty$ for all $\lambda \in {\widehat{\mathfrak{h}}}_k^{*}$.

2.

There exists a finite subset $\left\{{\mu }_1,\cdots ,{\mu }_n\right\}$ of ${\widehat{\mathfrak{h}}}_k^{*}$ such that

$$wt\left(V\right)\subset \bigcup _{i=1}^n\left({\mu }_i-{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}\right),$$

where ${\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)$ and ${\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$ denote the ${\mathbb{Z}}_{\ge 0}$-span of ${\widehat{\Delta }}_{+}-{\Delta }_{0,+}$ and ${\Delta }_{0,+}$, respectively.

Definition 3.

Let ${\mathcal{Q}}_k\left(\Lambda \right)$ be the full subcategory of ${\mathcal{Q}}_k$ whose objects are those modules V of ${\mathcal{Q}}_k$ satisfying

(1)

$V={⨁}_{\mu \in {\widehat{\mathfrak{h}}}^{*}}{V}^{\mu }$,

(2)

$V^{\mu }=0$ if $\mu \notin \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$.

Definition 4.

Let $F{\mathcal{Q}}_k\left(\Lambda \right)$ be the full subcategory of ${\mathcal{Q}}_k\left(\Lambda \right)$ whose objects are finitely generated $U\left(\widehat{\mathfrak{g}}\right)$-modules.

For each$\mu \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$, set

$$P_1=\left\{\alpha \in {\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)|\mu +\alpha \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}\right\}$$

and

$$P_2={\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)-P_1.$$

Lemma 1.

For each $\mu \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$, one has

1.

$P_1$ is a finite set.

2.

If $\alpha \in P_2$ and $\beta \in {\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)$, then $\alpha +\beta \in P_2$.

Proof. 

$\left(1\right)$ is immediate from the definition of $P_1$.

In oder to prove $\left(2\right)$, assume that $\alpha +\beta \notin P_2$. Then, we have $\alpha +\beta \in P_1$ since $\alpha +\beta \in {\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)$. So we get $\mu +\alpha +\beta \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$, and hence $\mu +\alpha \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$. This contradicts to $\alpha \in P_2$. □

Let us now consider the decomposition

$$U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)=\left(\underset{\alpha \in P_1}{⨁}U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha }\right)\oplus \left(\underset{\alpha \in P_2}{⨁}U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha }\right),$$

where $U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)$ is graded by declaring that each monomial

$$x_{j_1}{x}_{j_2}\cdots x_{j_n}\left(x_{j_i}\in {\mathfrak{g}}_{{\alpha }_{j_i}}\mathrm{for}{\alpha }_{j_i}\in {\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)$$

is of degree ${\alpha }_{j_1}+\cdots +{\alpha }_{j_n}$.

For a given $\mu \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$, we define a $U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}\oplus \widehat{\mathfrak{h}}\right)$-module structure on $U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)$ as follows:

$${\mathfrak{n}}_{0,-}\mathrm{acts}\mathrm{trivially}\mathrm{on}U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right),$$

(1)

$$\left(x+h\right)·v=\left(\mu +\alpha \right)\left(h\right)v+xv,$$

(2)

where $x\in {\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0},h\in \widehat{\mathfrak{h}}\mathrm{and}v\in U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha }$.

On the other hand, we see from Lemma 1, (2) that ${⨁}_{\alpha \in P_2}U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha }$ is an ideal of $U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)$. Set

$$W\left(\mu \right)=U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)/\underset{\alpha \in P_2}{⨁}U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha },$$

and define a $U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}\oplus \widehat{\mathfrak{h}}\right)$-module structure on $W\left(\mu \right)$ via the action $x·\left[u\right]=\left[x·u\right]$ for $x\in {\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}\oplus \widehat{\mathfrak{h}}$ and $u\in U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)$, where $\left[\right]:U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)⟶W\left(\mu \right)$ is the natural quotient map.

Next, we introduce the induced $U\left(\widehat{\mathfrak{g}}\right)$-module

$$P\left(\mu \right)=U\left(\widehat{\mathfrak{g}}\right)\underset{U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}\oplus \widehat{\mathfrak{h}}\right)}{⨂}W\left(\mu \right).$$

(3)

Theorem 1.

Let $\mu \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$. Then, $P\left(\mu \right)$ defined in (3) is an object of $F{\mathcal{Q}}_k\left(\Lambda \right)$.

Proof. 

We first notice that $W\left(\mu \right)\simeq {⨁}_{\alpha \in P_1}U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha }$ as vector spaces and $P_1$ is finite due to Lemma 1. So, dim$W\left(\mu \right)$ is finite because dim $U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha }<\infty$ for each $\alpha \in {\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)$. Let us now take a basis ${\left\{w_i\right\}}_{1\le i\le n}$ of $W\left(\mu \right)$. Then, $P\left(\mu \right)$ becomes a left free $U\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\oplus {\mathfrak{n}}_{0,+}\right)$-module with a basis ${\left\{1\otimes w_i\right\}}_{1\le i\le n}$. This yields that $P\left(\mu \right)$ is a finitely generated $U\left(\widehat{\mathfrak{g}}\right)$-module.

On the other hand, we obtain from (1) and (2) that all weights of $P\left(\mu \right)$ are contained in

$$\bigcup _{\alpha \in P_1}\left(\mu +\alpha -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}\right),$$

(4)

and (4) is contained in $\Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$ due to the definition of $P_1$. Furthermore, ${⨁}_{i=1}^{n}U\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\oplus {\mathfrak{n}}_{0,+}\right)\left(1\otimes w_i\right)$ has finite dimensional weight spaces because $-{\Delta }_{0,+}\cap \left({\widehat{\Delta }}_{-}-{\Delta }_{0,-}\right)=\varnothing$. The result now follows. □

Lemma 2.

Let V be an object of ${\mathcal{Q}}_k\left(\Lambda \right)$ and $\mu \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$. Then, we have

$$Ho{m}_{\widehat{\mathfrak{g}}}\left(P\left(\mu \right),V\right)\simeq Ho{m}_{\widehat{\mathfrak{h}}}\left({\mathbb{C}}_{\mu },V\right),$$

where ${\mathbb{C}}_{\mu }$ is the 1-dimensional $\widehat{\mathfrak{h}}$-module with basis $\mathbf{1}$ whose action is $h·\mathbf{1}=\mu \left(h\right)\mathbf{1}$.

Proof. 

Define

$$\Phi :Ho{m}_{U\left(\widehat{\mathfrak{g}}\right)}\left(P\left(\mu \right),V\right)⟶Ho{m}_{U\left(\widehat{\mathfrak{h}}\right)}\left({\mathbb{C}}_{\mu },V\right)$$

by $\Phi \left(A\right)\left(\mathbf{1}\right)=A\left(1\otimes \left[1\right]\right)$ for $A\in Ho{m}_{U\left(\widehat{\mathfrak{g}}\right)}\left(P\left(\mu \right),V\right)$, and

$$\Psi :Ho{m}_{U\left(\widehat{\mathfrak{h}}\right)}\left({\mathbb{C}}_{\mu },V\right)⟶Ho{m}_{U\left(\widehat{\mathfrak{g}}\right)}\left(P\left(\mu \right),V\right)$$

by $\Psi \left(f\right)\left(x\otimes \left[y\right]\right)=x·y·f\left(\mathbf{1}\right)$ for $f\in Ho{m}_{U\left(\widehat{\mathfrak{h}}\right)}\left({\mathbb{C}}_{\mu },V\right)$, $x\in U\left(\widehat{\mathfrak{g}}\right)$ and $y\in U\left(\widehat{\mathfrak{g}}\oplus {\mathfrak{g}}_{>0}\right)$.

We first should check that $\Phi \left(A\right)$ is an $U\left(\widehat{\mathfrak{h}}\right)$-module homomorphism. In fact, for $h\in \widehat{\mathfrak{h}}$ we get

$$\begin{array}{ccc}\hfill h·\Phi \left(A\right)\left(\mathbf{1}\right)& =& h·A\left(1\otimes \left[1\right]\right)\hfill \\ & =& A\left(1\otimes h·\left[1\right]\right)\hfill \\ & =& A\left(1\otimes \mu \left(h\right)\left[1\right]\right)\hfill \\ & =& \Phi \left(A\right)\left(\mu \left(h\right)\mathbf{1}\right)\hfill \\ & =& \Phi \left(A\right)\left(h·\mathbf{1}\right).\hfill \end{array}$$

This implies that $\Phi$ is well-defined.

We now prove that $\Psi$ is well-defined. We first show that $x·y·f\left(\mathbf{1}\right)$ is independent of the choice of $y\in U\left(\widehat{\mathfrak{g}}\oplus {\mathfrak{g}}_{>0}\right)$. Let $y^{{}^{\prime }}=y+u$ for $u\in {⨁}_{\alpha \in P_2}U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha }$. Since $V\in \mathrm{Obj}\left({\mathcal{Q}}_k\left(\Lambda \right)\right)$, we should have

$$U{\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\right)}^{\alpha }·f\left(\mathbf{1}\right)\in V^{\mu +\alpha }=\left\{0\right\}$$

for $f\in Ho{m}_{U\left(\widehat{\mathfrak{h}}\right)}\left({\mathbb{C}}_{\mu },V\right)$ and $\alpha \in P_2$. This yields that $u·f\left(\mathbf{1}\right)=0$, and $\Psi \left(f\right)\left(x\otimes \left[y\right]\right)$ is independent of the choice of y. In addition,

$$\begin{array}{ccc}\hfill z·\Psi \left(f\right)\left(x\otimes \left[y\right]\right)& =& z·\left(x·y·f\left(\mathbf{1}\right)\right)\hfill \\ & =& \left(zx\right)·y·f\left(\mathbf{1}\right)\hfill \\ & =& \Psi \left(f\right)\left(zx\otimes \left[y\right]\right)\hfill \\ & =& \Psi \left(f\right)\left(z·\left(x\otimes \left[y\right]\right)\right).\hfill \end{array}$$

Thus, one has $\Psi \left(f\right)\in Ho{m}_{U\left(\widehat{\mathfrak{g}}\right)}\left(P\left(\mu \right),V\right)$ and hence $\Psi$ is well-defined.

Finally, we see that

$$\Phi \left(\Psi \left(f\right)\right)\left(\mathbf{1}\right)=\Psi \left(f\right)\left(1\otimes \left[1\right]\right)=f\left(\mathbf{1}\right)$$

and

$$\begin{array}{ccc}\hfill \Psi \left(\Phi \left(A\right)\right)\left(x\otimes \left[y\right]\right)& =& x·y·\Phi \left(A\right)\left(\mathbf{1}\right)\hfill \\ & =& x·y·A\left(1\otimes \left[1\right]\right)\hfill \\ & =& A\left(x·y·\left(1\otimes \left[1\right]\right)\right)\hfill \\ & =& A\left(x\otimes \left[y\right]\right)\left(\sin \mathrm{ce}y\in U\left(\widehat{\mathfrak{g}}\oplus {\mathfrak{g}}_{>0}\right)\right).\hfill \end{array}$$

This shows that $\Phi$ and $\Psi$ are inverse of one another. The result now follows. □

The following result shows that $P\left(\mu \right)$ is a projective object in the category $F{\mathcal{Q}}_k\left(\Lambda \right)$.

Theorem 2.

$P\left(\mu \right)$ is a projective object in the category $F{\mathcal{Q}}_k\left(\Lambda \right)$.

Proof. 

Consider a diagram in the category ${\mathcal{Q}}_k\left(\Lambda \right)$. By Lemma 2, we obtain the associated diagram

.	$$\hspace{1em}$$ (5)

It is obvious that we can find $f\in Ho{m}_{\widehat{\mathfrak{g}}}\left({\mathbb{C}}_{\mu },N\right)$ making the diagram (5) commutes. So, by Lemma 2 the homomorphism f gives rise to the associated homomorphism $\Psi \left(f\right)\in Ho{m}_{\widehat{\mathfrak{g}}}\left(P\left(\mu \right),N\right)$. Moreover, for $x\otimes \left[y\right]\in P\left(\mu \right)$ we see that

$$\begin{array}{ccc}\hfill g\circ \Psi \left(f\right)\left(x\otimes \left[y\right]\right)& =& g\left(x·y·f\left(\mathbf{1}\right)\right)\hfill \\ & =& x·y·g\left(f\left(\mathbf{1}\right)\right)\hfill \\ & =& x·y·\Phi \left(h\right)\left(\mathbf{1}\right)\hfill \\ & =& \Psi \left(\Phi \left(h\right)\right)\left(x\otimes \left[y\right]\right)\hfill \\ & =& h\left(x\otimes \left[y\right]\right).\hfill \end{array}$$

The result now follows. □

In the following theorem, we prove that the category $F{\mathcal{Q}}_k\left(\Lambda \right)$ contains enough projective objects.

Theorem 3.

Let V be an object of $F{\mathcal{Q}}_k\left(\Lambda \right)$. Then, there exists a surjective $U\left(\widehat{\mathfrak{g}}\right)$-module homomorphism $\psi :{⨁}_{i=1}^{n}P\left({\mu }_i\right)⟶V$ for some ${\mu }_1,\cdots ,{\mu }_n\in {\widehat{\mathfrak{h}}}^{*}$.

Proof. 

Let $\left\{v_1,\cdots ,v_n\right\}$ be a set of generators of V consisting of weight vectors, say $v_i\in V^{{\mu }_i}$. By Lemma 2, we obtain

$$\Psi \left(f_i\right)\in Ho{m}_{U\left(\widehat{\mathfrak{g}}\right)}\left(P\left({\mu }_i\right),V\right)$$

from the $U\left(\widehat{\mathfrak{h}}\right)$-module homomorphism $f_i:{\mathbb{C}}_{{\mu }_i}\to V^{{\mu }_i}\subset V$ defined by $f_i\left(\mathbf{1}\right)=v_i$. By adding $\Psi \left(f_i\right)$ for $1\le i\le n$, we get a surjective $U\left(\widehat{\mathfrak{g}}\right)$-module homomorphism $\psi :{⨁}_{i=1}^{n}P\left({\mu }_i\right)\to V$. The result now follows. □

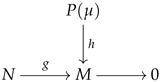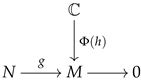3.2. Composition Series

For $\lambda \in {\widehat{\mathfrak{h}}}_k^{*}$, we define an 1-dimensional $U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}\oplus \widehat{\mathfrak{h}}\right)$-module structure on ${\mathbb{C}}_{\lambda }$ with basis $\mathbf{1}$ as follows:

• ${\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}$ acts trivially on ${\mathbb{C}}_{\lambda }$,
• $h·\mathbf{1}=\lambda \left(h\right)\mathbf{1}$ for $h\in \widehat{\mathfrak{h}}$.

Set

$$P_{\lambda }=U\left(\widehat{\mathfrak{g}}\right)\underset{U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}\oplus \widehat{\mathfrak{h}}\right)}{⨂}{\mathbb{C}}_{\lambda },$$

(6)

Notice that $P_{\lambda }$ is a free $U\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\oplus {\mathfrak{n}}_{0,+}\right)$-module of rank 1 with basis $1\otimes \mathbf{1}$. We also point out that $P_{\lambda }$ is a quasi highest weight $U\left(\widehat{\mathfrak{g}}\right)$-module with quasi highest weight vector $1\otimes \mathbf{1}$.

In the following theorem, we construct an analogue of a Verma composition series for the $U\left(\widehat{\mathfrak{g}}\right)$-module $P\left(\mu \right)$ defined in (3).

Theorem 4.

Let $\mu \in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$. Then, $P\left(\mu \right)$ has a finite series of submodules

$$P\left(\mu \right)=M_1\supset M_2\supset \cdots \supset M_n\supset M_{n+1}=\left\{0\right\}$$

such that $M_j/M_{j+1}\simeq P_{{\lambda }_j}$, where $P_{{\lambda }_j}$ is an object of $F{\mathcal{Q}}_k\left(\Lambda \right)$ for $j=1,\cdots ,n$.

Proof. 

By (2), the weights of $W\left(\mu \right)$ are of the form $\mu +{\alpha }_k$ for ${\alpha }_k\in P_1$. Choose a basis $\left\{w_1,\cdots ,w_n\right\}$ of $W\left(\mu \right)$ so that $w_i\in W{\left(\mu \right)}^{\mu +{\alpha }_i}$ for ${\alpha }_i\in P_1$. We arrange $w_i$ so that ${\alpha }_r\ge {\alpha }_s$ implies $r\ge s$, and define $W_j={⨁}_{i\ge j}\mathbb{C}{w}_i$. Then, we have

$$W\left(\mu \right)=W_1\supset W_2\supset \cdots \supset W_n\supset W_{n+1}=\left\{0\right\}.$$

(7)

Notice that $U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}\oplus \widehat{\mathfrak{h}}\right)W_j\subset W_{j+1}$ since ${\mathfrak{n}}_{0,-}$ acts trivially on $W\left(\mu \right)$ and ${\mathfrak{g}}_{\beta }{w}_j\in W{\left(\mu \right)}^{\mu +{\alpha }_j+\beta }$ for all $\beta \in {\widehat{\Delta }}_{+}-{\Delta }_{0,+}$. This implies that each $W_j$ is a $U\left({\widehat{\mathfrak{g}}}^{>}\oplus {\mathfrak{g}}_{>0}\oplus {\mathfrak{n}}_{0,-}\oplus \widehat{\mathfrak{h}}\right)$-module. Inside $P\left(\mu \right)$, consider

$$M_j=U\left(\widehat{\mathfrak{g}}\right)·\left(1\otimes W_j\right)=U\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\oplus {\mathfrak{n}}_{0,+}\right)·\left(1\otimes W_j\right).$$

Then, we obtain from (7) that

$$P\left(\mu \right)=M_1\supset M_2\supset \cdots \supset M_n\supset M_{n+1}=\left\{0\right\}.$$

Notice that $M_j/M_{j+1}$ is a free $U\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\oplus {\mathfrak{n}}_{0,+}\right)$-module of rank 1 with basis $\left\{1\otimes w_j\right\}$, and hence $M_j/M_{j+1}$ is isomorphic to the quasi highest weight module $P_{{\lambda }_j}$, where ${\lambda }_j=\mu +{\alpha }_j$. Since each ${\alpha }_j\in P_1$, one has ${\lambda }_j=\mu +{\alpha }_j\in \Lambda -{\mathbb{Z}}_{\ge 0}\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge 0}{\Delta }_{0,+}$. This implies that $P_{{\lambda }_j}$ is an object of $F{\mathcal{Q}}_k\left(\Lambda \right)$. The result now follows. □

4. BRST Cohomology

4.1. BRST Complex

Set $L{\mathfrak{g}}_{>0}={\mathfrak{g}}_{>0}\otimes \mathbb{C}\left[t,t^{-1}\right]$ and $L{\mathfrak{g}}_{>0}^{*}={\mathfrak{g}}_{>0}^{*}\otimes \mathbb{C}\left[t,t^{-1}\right]$. Write $CL\left(L{\mathfrak{g}}_{>0}\oplus L{\mathfrak{g}}_{>0}^{*}\right)$ for the Clifford superalgebra associated with $L{\mathfrak{g}}_{>0}\oplus L{\mathfrak{g}}_{>0}^{*}$ (see [22]). In other words, $CL\left(L{\mathfrak{g}}_{>0}\oplus L{\mathfrak{g}}_{>0}^{*}\right)$ is spanned by ${\psi }_{\alpha }\left(m\right)$ and ${\psi }^{\alpha }\left(n\right)\left(\alpha \in {\Delta }_{>0};m,n\in \mathbb{Z}\right)$ and satisfies the following relations

• $\left[{\psi }_{\alpha }\left(m\right){\psi }^{\beta }\left(n\right)\right]={\delta }_{\alpha ,\beta }{\delta }_{m+n,0}$,
• $\left[{\psi }_{\alpha }\left(m\right){\psi }_{\beta }\left(n\right)\right]=\left[{\psi }^{\alpha }\left(m\right){\psi }^{\beta }\left(n\right)\right]=0$,

where ${\left\{{\psi }_{\alpha }\right\}}_{\alpha \in {\Delta }_{>0}}$ and ${\left\{{\psi }^{\alpha }\right\}}_{\alpha \in {\Delta }_{>0}}$ are the associated bases of $\sqcap {\mathfrak{g}}_{>0}$ and $\sqcap {\mathfrak{g}}_{>0}^{*}$ corresponding to the basis ${\left\{u_{\alpha }\right\}}_{\alpha \in {\Delta }_{>0}}$ of ${\mathfrak{g}}_{>0}$, respectively. (Recall that ⊓ is the parity reversing functor on the category of superspaces.)

Let $F\left(L{\mathfrak{g}}_{>0}\right)$ be the irreducible representation of $CL\left(L{\mathfrak{g}}_{>0}\oplus L{\mathfrak{g}}_{>0}^{*}\right)$ generated by the vector $\mathbf{1}$ satisfying the relations

$${\psi }_{\alpha }\left(n\right)\mathbf{1}=0\mathrm{for}\alpha \in {\Delta }_{>0}\mathrm{and}n\ge 0,$$

$${\psi }^{\beta }\left(n\right)\mathbf{1}=0\mathrm{for}\beta \in {\Delta }_{>0}\mathrm{and}n>0.$$

Define deg$\mathbf{1}=0$, deg${\psi }_{\alpha }\left(n\right)=-1$ and deg${\psi }^{\alpha }\left(n\right)=1$ for $\alpha \in {\Delta }_{>0}$ and $n\in \mathbb{Z}$. Then, one obtain the induced decomposition of $F\left(L{\mathfrak{g}}_{>0}\right)$:

$$F\left(L{\mathfrak{g}}_{>0}\right)=\underset{i\in \mathbb{Z}}{⨁}{F}^i\left(L{\mathfrak{g}}_{>0}\right).$$

Recall that ${\mathfrak{g}}_{\frac{1}{2}}$ is a superspace with the nondegenerate skew-supersymmetric bilinear form $〈,〉$ (see Section 2.1). Denote by ${\mathfrak{g}}_{\frac{1}{2}}^{ne}$ the superspace ${\mathfrak{g}}_{\frac{1}{2}}$ equipped with the nondegenerate skew-supersymmetric bilinear form $〈,〉$. Let ${\left\{{\Phi }_{\alpha }\right\}}_{\alpha \in {\Delta }_{\frac{1}{2}}}$ be the corresponding basis of ${\mathfrak{g}}_{\frac{1}{2}}^{ne}$ associated with the basis ${\left\{u_{\alpha }\right\}}_{\alpha \in {\Delta }_{\frac{1}{2}}}$ of ${\mathfrak{g}}_{\frac{1}{2}}$. Define $L{\mathfrak{g}}_{\frac{1}{2}}^{ne}={\mathfrak{g}}_{\frac{1}{2}}^{ne}\otimes \mathbb{C}\left[t,t^{-1}\right]$, and let $CL\left(L{\mathfrak{g}}_{\frac{1}{2}}^{ne}\right)$ be the Clifford superalgebra associated with $L{\mathfrak{g}}_{\frac{1}{2}}^{ne}$. Then, the superalgebra $CL\left(L{\mathfrak{g}}_{\frac{1}{2}}^{ne}\right)$ is generated by ${\Phi }_{\alpha }\left(n\right)\left(\alpha \in {\Delta }_{\frac{1}{2}},n\in \mathbb{Z}\right)$ with the relation

$$\left[{\Phi }_{\alpha }\left(m\right){\Phi }_{\beta }\left(n\right)\right]=〈u_{\alpha },u_{\beta }〉{\delta }_{m+n+1,0}.$$

(8)

Write ${\left\{u^{\alpha }\right\}}_{\alpha \in {\Delta }_{\frac{1}{2}}}$ for the dual basis of ${\left\{u_{\alpha }\right\}}_{\alpha \in {\Delta }_{\frac{1}{2}}}$ with respect to $〈,〉$; that is $〈u_{\alpha },u^{\beta }〉={\delta }_{\alpha ,\beta }$, and denote by ${\Phi }^{\alpha }$ the corresponding dual basis of ${\mathfrak{g}}_{\frac{1}{2}}^{ne}$ associated with $u^{\alpha }$. It is immediate from (8) that

$$\left[{\Phi }_{\alpha }\left(m\right){\Phi }^{\beta }\left(n\right)\right]={\delta }_{\alpha ,\beta }{\delta }_{m+n+1,0}.$$

Let $F^{ne}\left(f\right)$ be the irreducible representation of $CL\left(L{\mathfrak{g}}_{\frac{1}{2}}^{ne}\right)$ generated by the vector $\mathbf{1}$ with the property ${\Phi }_{\alpha }\left(n\right)\mathbf{1}=0$ for $\alpha \in {\Delta }_{\frac{1}{2}}$ and $n\ge 0$.

For an object V${\mathcal{Q}}_k$, set

$$C\left(V\right)=V\otimes F\left(L{\mathfrak{g}}_{>0}\right)\otimes F^{ne}\left(f\right)=\underset{i\in \mathbb{Z}}{⨁}{C}^i\left(V\right),$$

(9)

where $C^i\left(V\right)=V\otimes F^i\left(L{\mathfrak{g}}_{>0}\right)\otimes F^{ne}\left(f\right)$.

Define the operator d on $C\left(V\right)$ by

$$\begin{array}{ccc}\hfill & & d=\sum _{\begin{array}{c}\alpha \in {\Delta }_{>0}\\ n\in \mathbb{Z}\end{array}}{(-1)}^{p\left(\alpha \right)}{u}_{\alpha }(-n)\otimes {\psi }^{\alpha }\left(n\right)\otimes 1\hfill \\ & & -\frac{1}{2}\sum _{\begin{array}{c}\\ \alpha ,\beta ,\gamma \in {\Delta }_{>0}\\ k+l+m=0\end{array}}{(-1)}^{p\left(\alpha \right)p\left(\gamma \right)}\left(\left[u_{\alpha }{u}_{\beta }\right]|u_{-\gamma }\right)\otimes {\psi }^{\alpha }\left(k\right){\psi }^{\beta }\left(l\right){\psi }_{\gamma }\left(m\right)\otimes 1\hfill \\ & & +\sum _{\alpha \in {\Delta }_1}\left(f|u_{\alpha }\right)\otimes {\psi }^{\alpha }\left(1\right)\otimes 1+\sum _{\begin{array}{c}\alpha \in {\Delta }_{\frac{1}{2}}\\ n\in \mathbb{Z}\end{array}}{(-1)}^{p\left(\alpha \right)}1\otimes {\psi }^{\alpha }\left(n\right)\otimes {\Phi }_{\alpha }(-n),\hfill \end{array}$$

(10)

where $p\left(\alpha \right)$ denotes the parity of $u_{\alpha }$.

Notice that the operator d is an odd operator, and $d{C}^i\left(V\right)\subset C^{i+1}\left(V\right)$. In addition, we obtain $\left[dd\right]=2d^2=0$ from Theorem 2.1 in [17]. Thus $\left(C\left(V\right),d\right)$ becomes a cohomology complex. The cohomology

$$H^i\left(V\right):=H^i\left(C\left(V\right),d\right)\mathrm{for}i\in \mathbb{Z}.$$

(11)

given by the complex $\left(C\left(V\right),d\right)$ is called the cohomology of the BRST complex of the quantized Drinfeld-Sokolov reduction.

4.2. Main Results

We first prove the vanishing property of BRST cohomology for the quasi highest weight module $P_{\lambda }$ defined in (6).

Theorem 5.

For $\lambda \in {\widehat{\mathfrak{h}}}_k^{*}$, we have $H^i\left(P_{\lambda }\right)=0$ for all $i\ne 0$.

Proof. 

Let ${\omega }_0$ be the Chevalley involution on $U\left({\mathfrak{g}}_0\right)$ defined by ${\omega }_0\left(u_{\alpha }\right)=-u_{-\alpha }$ for $\alpha \in {\Delta }_0$ and ${\omega }_0\left(h\right)=-h$ for $h\in \mathfrak{h}$ (see [20], Chapter 1). Then, we have the induced algebra isomorphism

$$1\otimes {\omega }_0:U\left({\widehat{\mathfrak{n}}}_{-}\right)⟶U\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\right)\otimes U\left({\mathfrak{n}}_{0,+}\right)$$

(12)

via identification $U\left({\widehat{\mathfrak{n}}}_{-}\right)\simeq U\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\right)\otimes U\left({\mathfrak{n}}_{0,-}\right)$.

Recall from (6) that $P_{\lambda }$ is a free $U\left({\widehat{\mathfrak{g}}}^{<}\oplus {\mathfrak{g}}_{<0}\oplus {\mathfrak{n}}_{0,+}\right)$-module of rank 1. Thus, due to the isomorphism $1\otimes {\omega }_0$ defined in (12), $P_{\lambda }$ is isomorphic to the Verma module $M\left(\lambda \right)$ with highest weight $\lambda$. Since the boundary operator d in (10) commutes with the isomorphism $1\otimes {\omega }_0$, we have $H^i\left(P_{\lambda }\right)=H^i\left(M\left(\lambda \right)\right)$ for all i. The result now follows from Theorem 6.3.1 in [14]. □

The following result is immediate from Theorems 4 and 5.

Theorem 6.

Let $\Lambda \in {\widehat{\mathfrak{h}}}^{*}$ and $\mu \in \Lambda -{\mathbb{Z}}_{\ge }\left({\widehat{\Delta }}_{+}-{\Delta }_{0,+}\right)+{\mathbb{Z}}_{\ge }{\Delta }_{0,+}$. Then, we have $H^i\left(P\left(\mu \right)\right)=0$ for all $i\ne 0$.