Noninteger Dimension of Seasonal Land Surface Temperature (LST)
Abstract
:1. Introduction
2. Materials, Methods, and Results
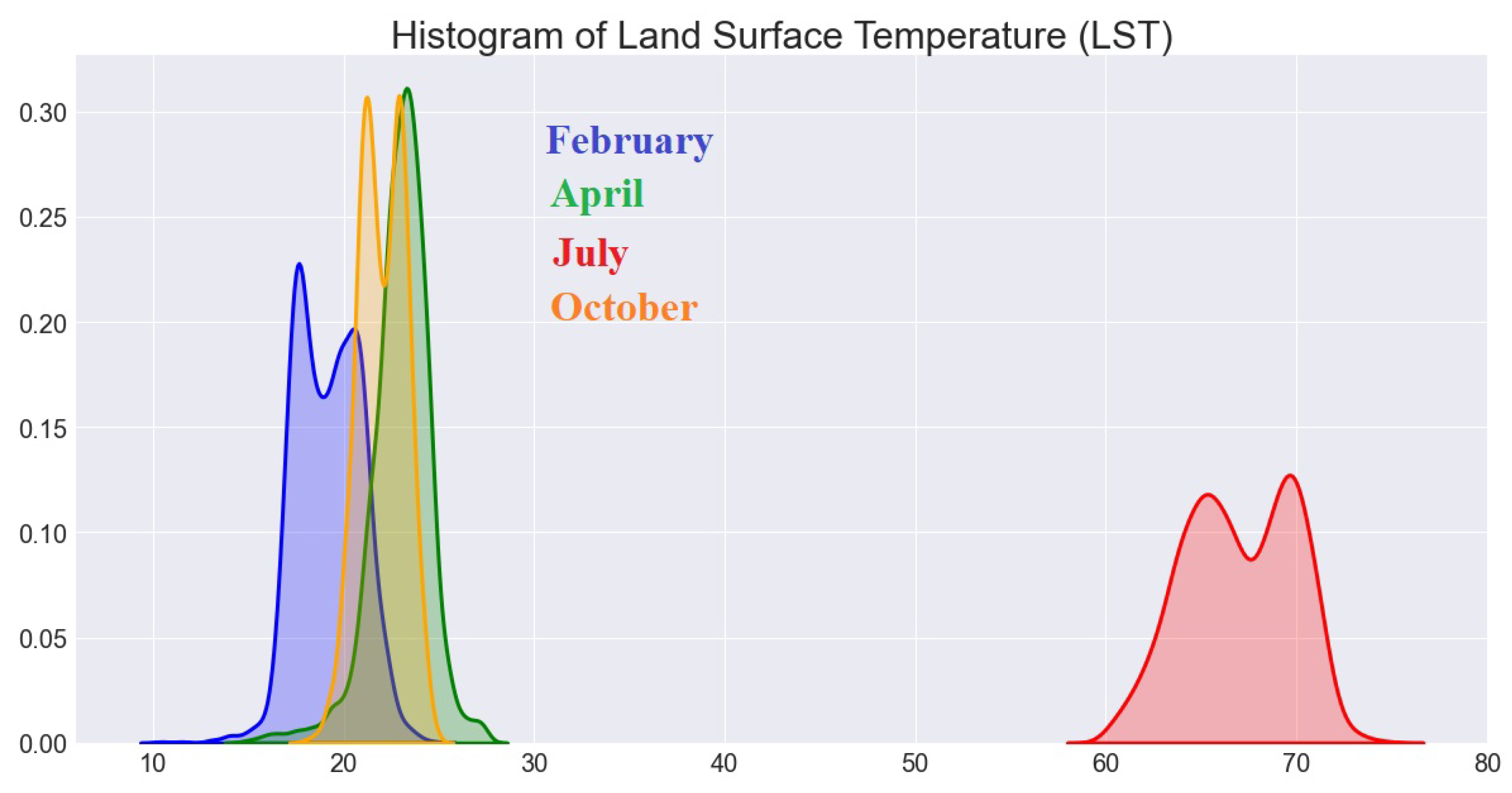
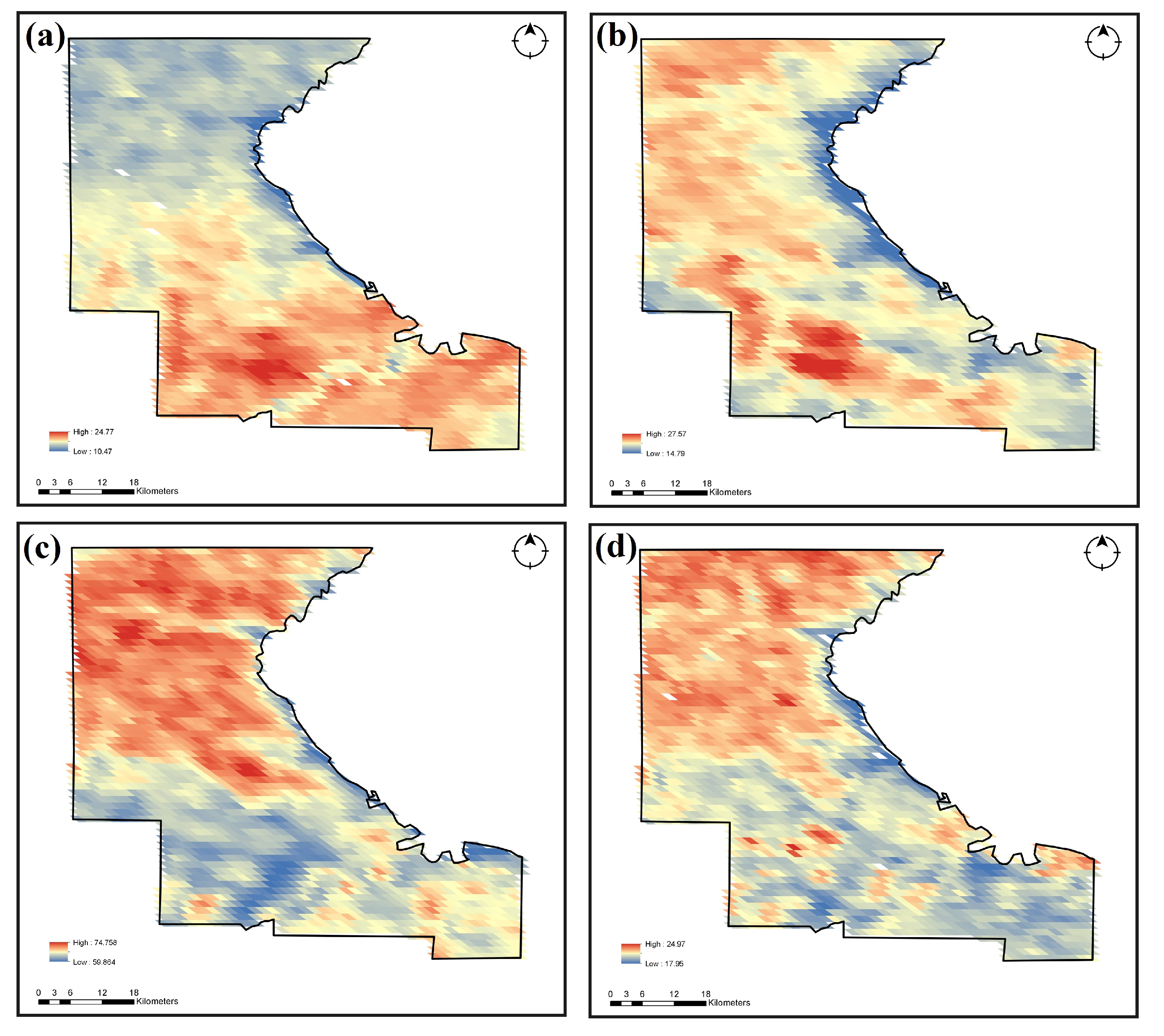
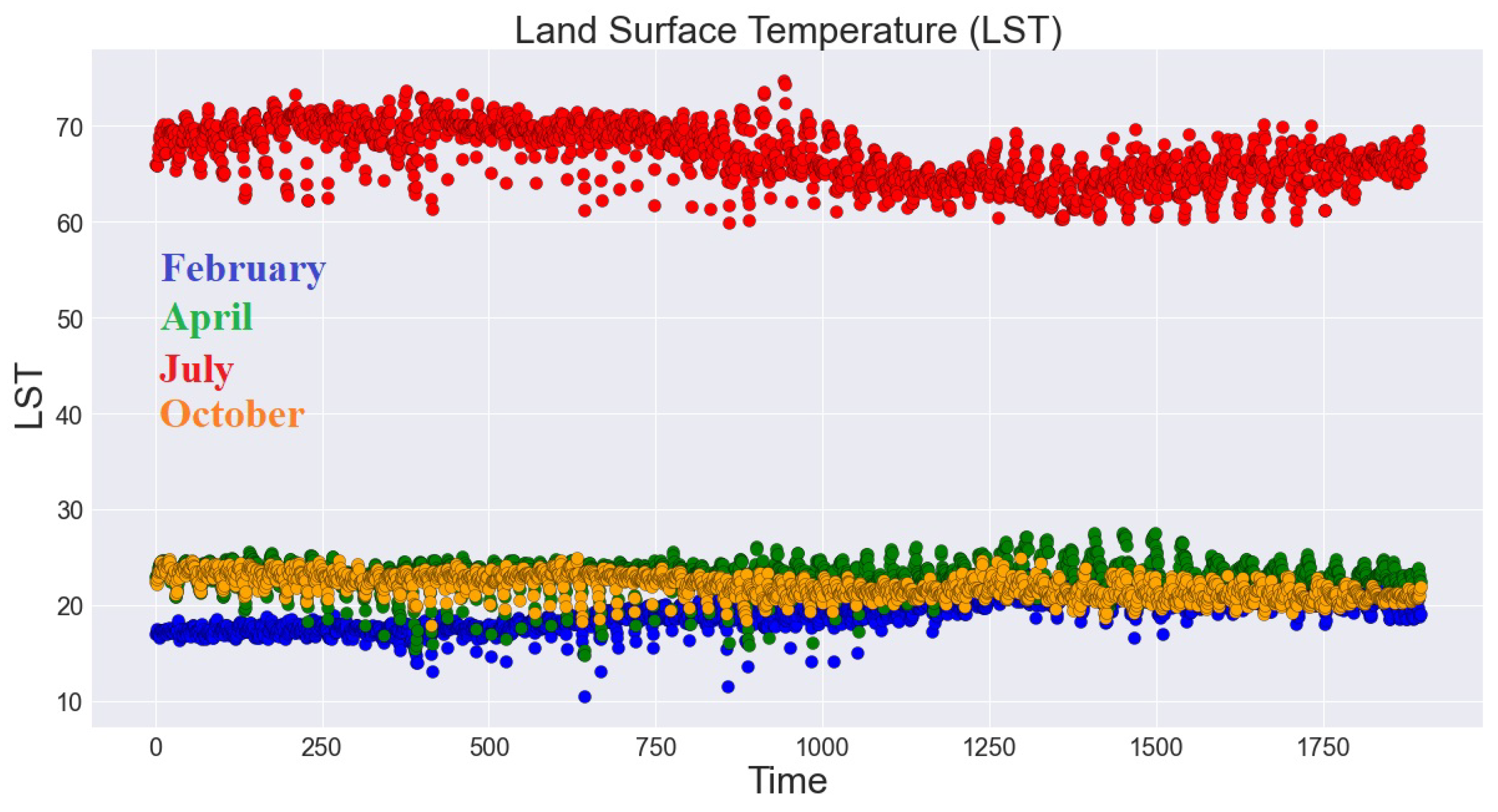
2.1. Data: The Land Surface Temperature (LST) of Riley County for February, April, July, and October (2021)
2.1.1. Time Series Regression Analysis
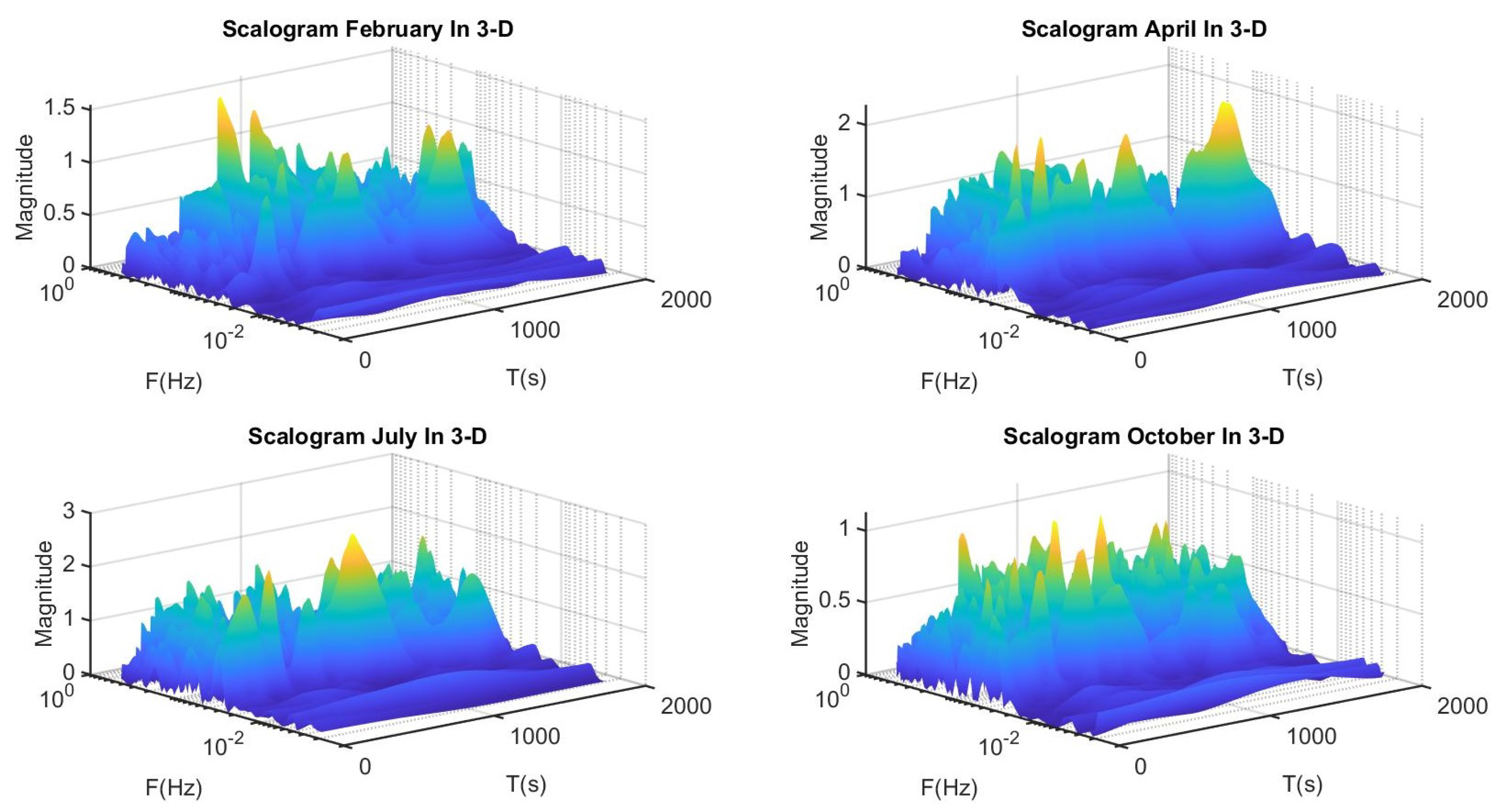
2.1.2. Time–Frequency Analysis Using Continuous Wavelet Transform (CWT) and Wavelet-Based Semblance Analysis
2.1.3. Vibration Frequency Analysis via the Power Spectral Density (PSD)
2.2. Fractal Geometry and the World’s Weather and Climate Patterns
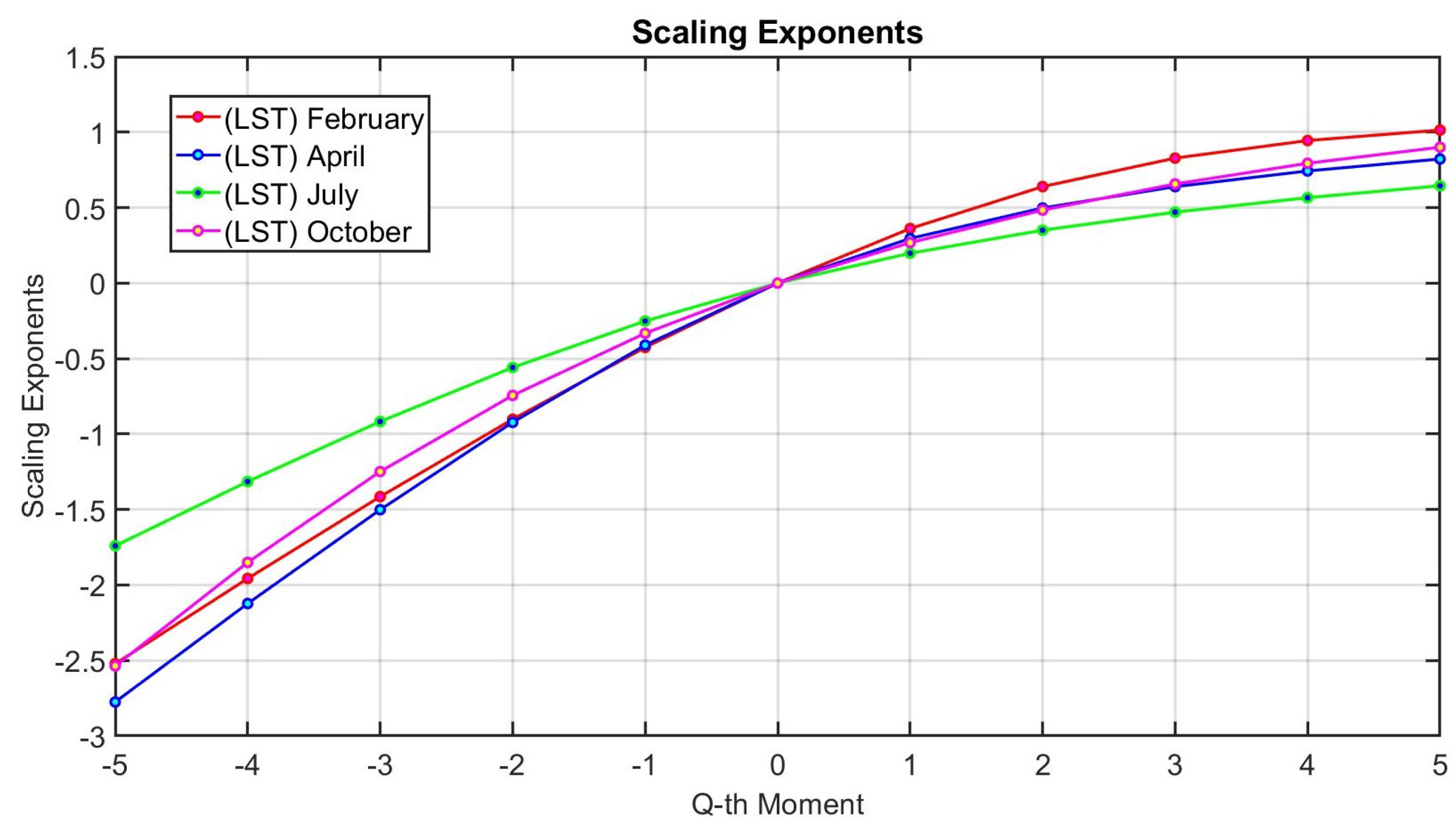
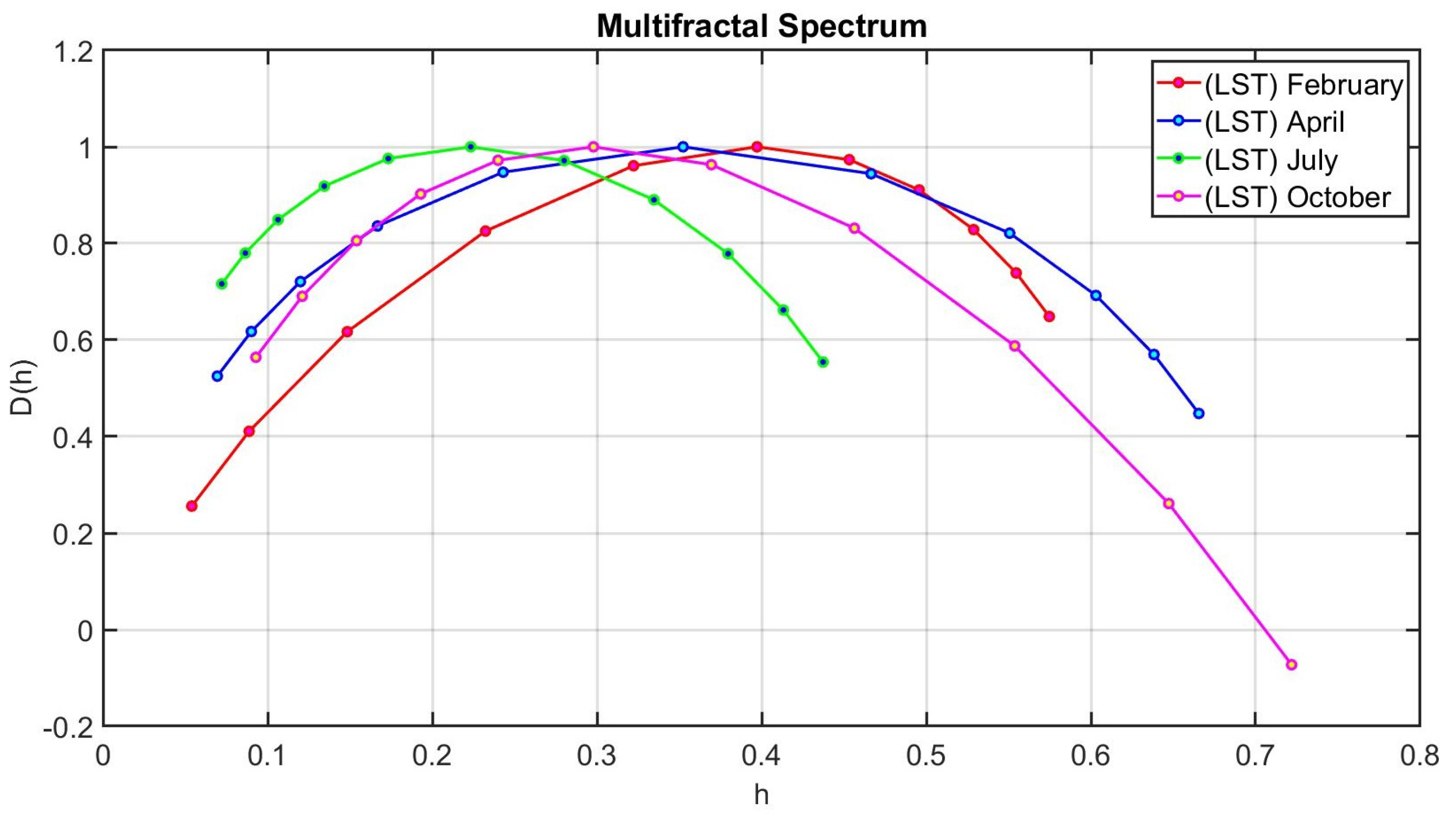
2.2.1. Multifractal Analysis and the Discrete Wavelet Transform (DWT)
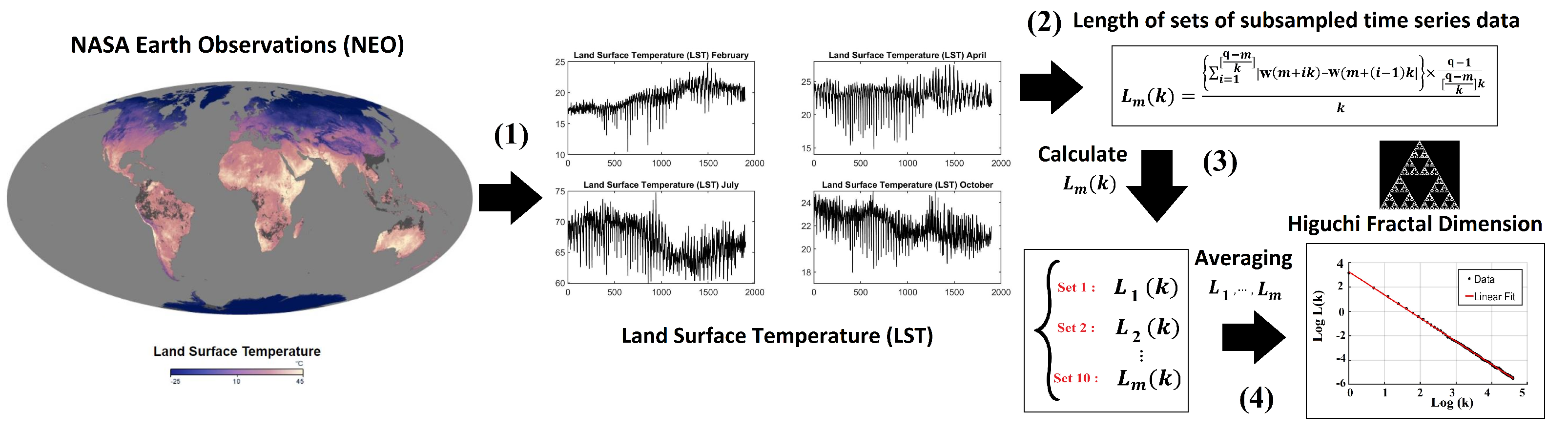
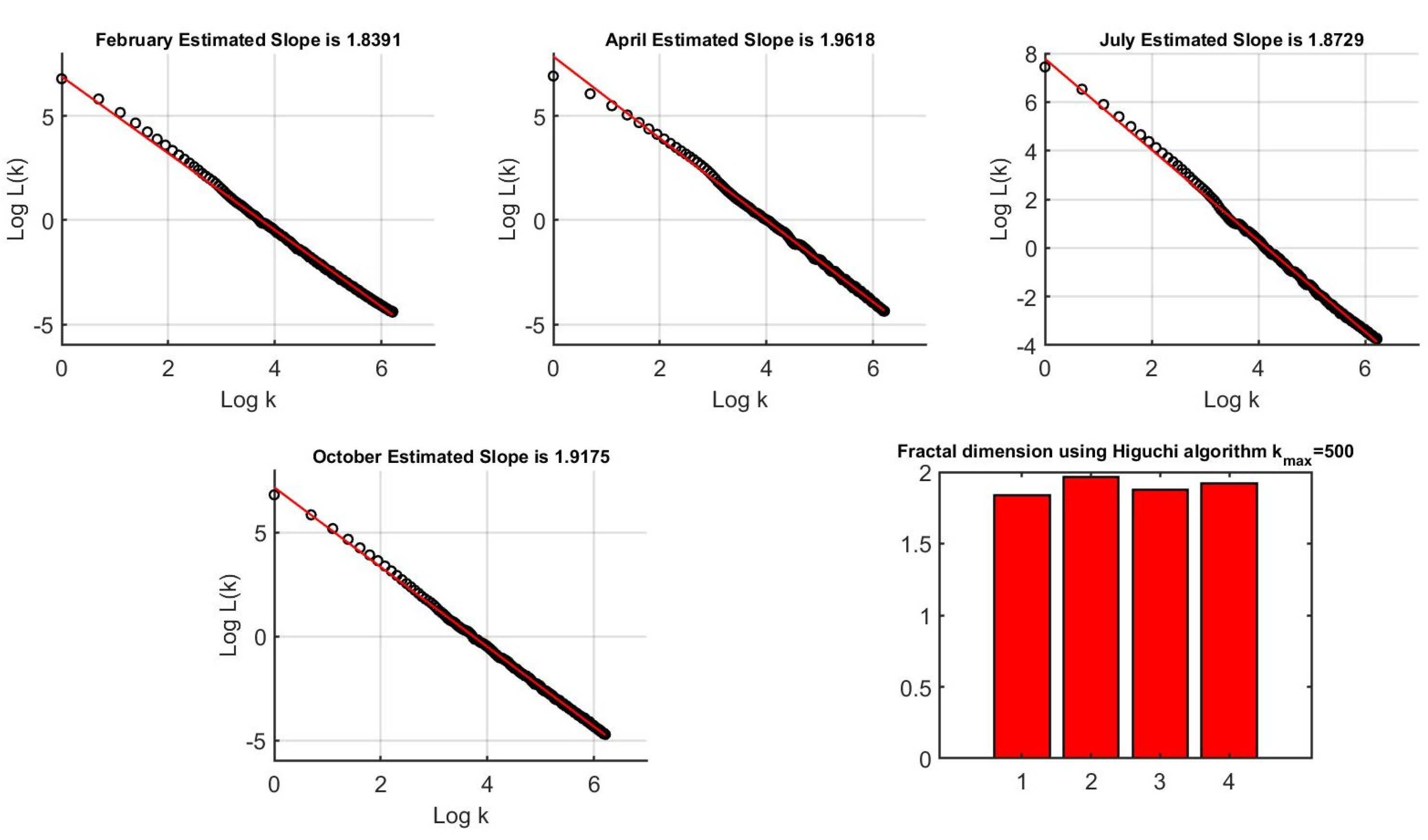
2.2.2. Higuchi Fractal Dimension Algorithm
3. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
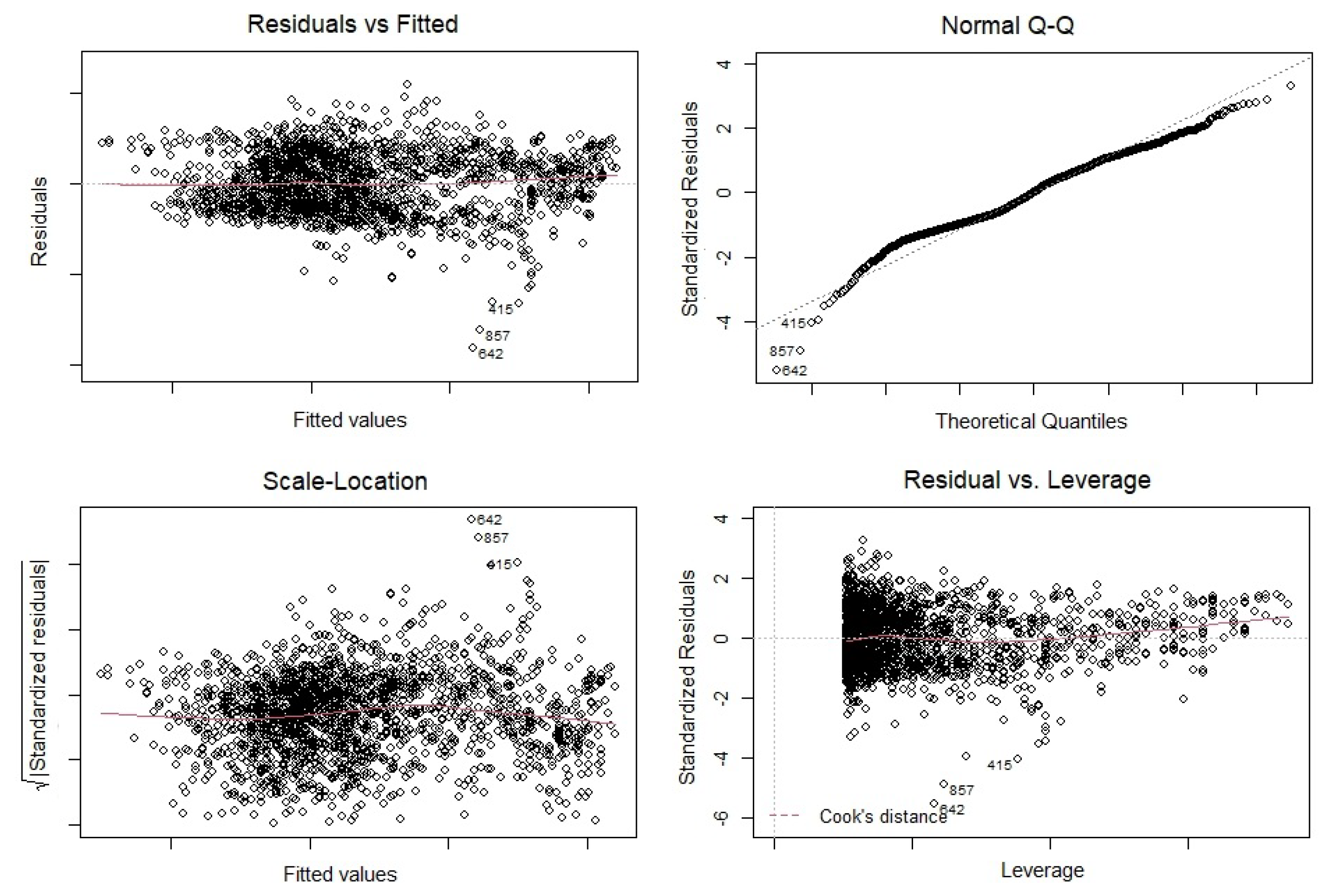
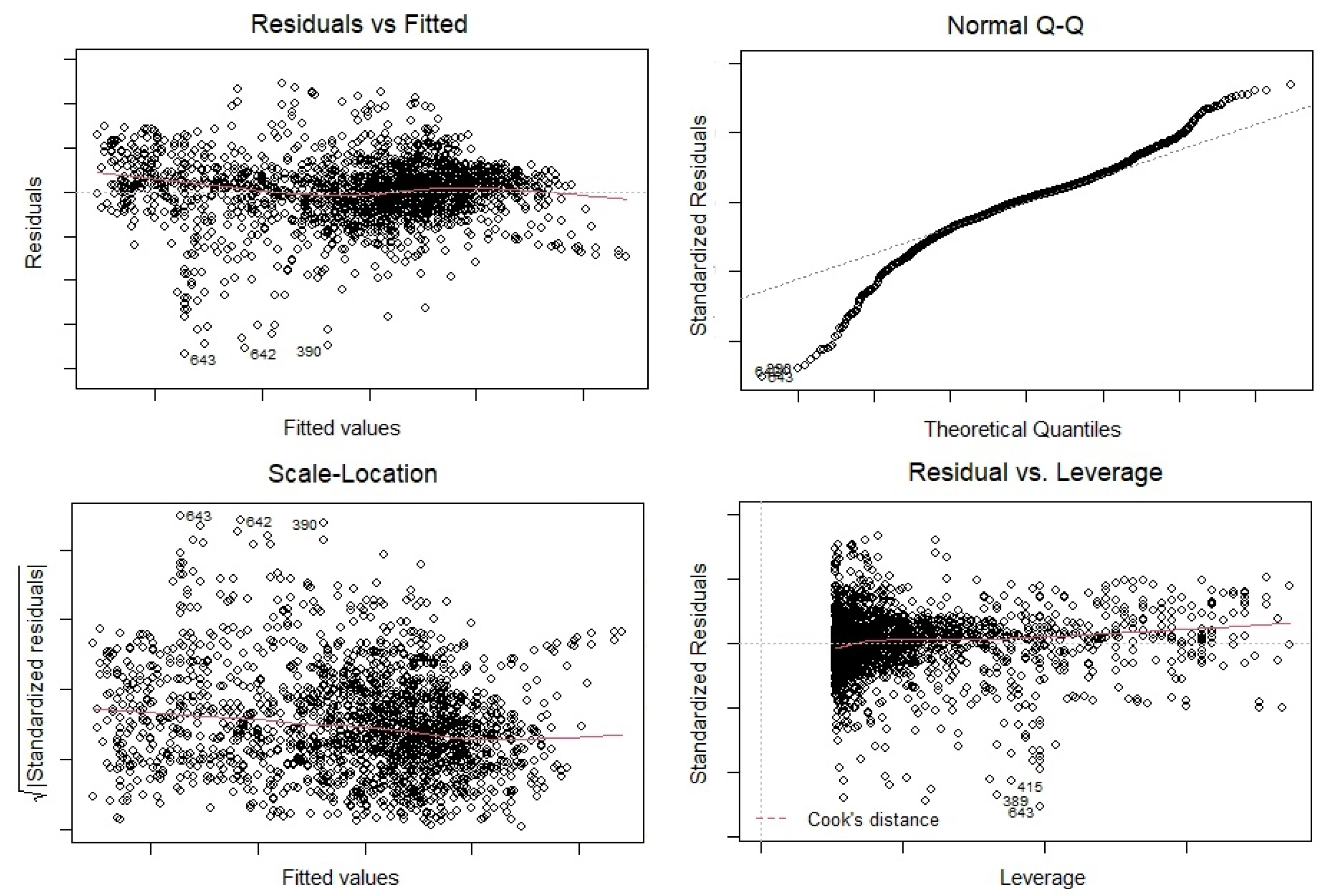
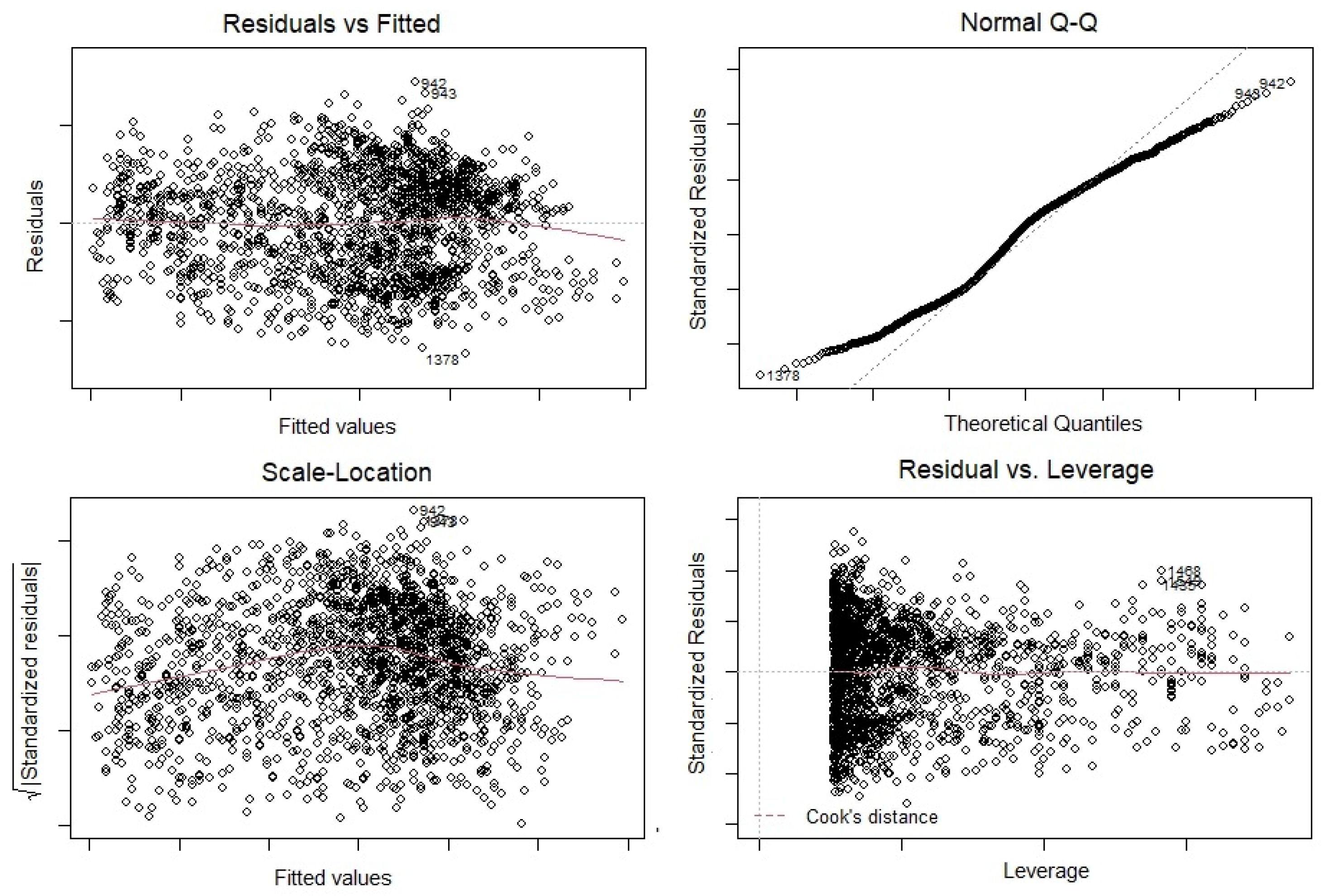
Appendix A. Traditional Statistical Analysis


References
- Houghton, J.T.; Jenkins, G.J.; Ephraums, J.J. Climate change: The ipcc scientific assessment. Am. Sci. 1990. Available online: https://www.osti.gov/biblio/6819363 (accessed on 14 April 2023).
- Azizi, S.; Azizi, T. The fractal nature of drought: Power laws and fractal complexity of arizona drought. Eur. J. Math. Anal. 2022, 2, 17. [Google Scholar] [CrossRef]
- Eleftheriou, D.; Kiachidis, K.; Kalmintzis, G.; Kalea, A.; Bantasis, C.; Koumadoraki, P.; Spathara, M.E.; Tsolaki, A.; Tzampazidou, M.I.; Gemitzi, A. Determination of annual and seasonal daytime and nighttime trends of modis lst over greece-climate change implications. Sci. Total Environ. 2018, 616, 937–947. [Google Scholar] [CrossRef] [PubMed]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Tayyebi, A.; Jenerette, G.D. Increases in the climate change adaption effectiveness and availability of vegetation across a coastal to desert climate gradient in metropolitan los angeles, ca, usa. Sci. Total Environ. 2016, 548, 60–71. [Google Scholar] [CrossRef]
- Sy, S.; de Noblet-Ducoudré, N.; Quesada, B.; Sy, I.; Dieye, A.M.; Gaye, A.T.; Sultan, B. Land-surface characteristics and climate in west africa: Models’ biases and impacts of historical anthropogenically-induced deforestation. Sustainability 2017, 9, 1917. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Luo, G.; Chen, C.; Ochege, F.U.; Hellwich, O.; Zheng, H.; Hamdi, R.; Wu, S. Quantifying the contribution of climate change and human activities to biophysical parameters in an arid region. Ecol. Indic. 2021, 129, 107996. [Google Scholar] [CrossRef]
- Boisier, J.; de Noblet-Ducoudré, N.; Ciais, P. Inferring past land use-induced changes in surface albedo from satellite observations: A useful tool to evaluate model simulations. Biogeosciences 2013, 10, 1501–1516. [Google Scholar] [CrossRef] [Green Version]
- Boisier, J.; de Noblet-Ducoudré, N.; Pitman, A.; Cruz, F.; Delire, C.; den Hurk, B.V.; der Molen, M.V.; Müller, C.; Voldoire, A. Attributing the impacts of land-cover changes in temperate regions on surface temperature and heat fluxes to specific causes: Results from the first lucid set of simulations. J. Geophys. Res. Atmos. 2012, 117, D12116. [Google Scholar] [CrossRef]
- de Noblet-Ducoudré, N.; Boisier, J.-P.; Pitman, A.; Bonan, G.; Brovkin, V.; Cruz, F.; Delire, C.; Gayler, V.; den Hurk, B.V.; Lawrence, P.; et al. Determining robust impacts of land-use-induced land cover changes on surface climate over north america and eurasia: Results from the first set of lucid experiments. J. Clim. 2012, 25, 3261–3281. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.; Shekhar, S. Statistical analysis of land surface temperature–vegetation indexes relationship through thermal remote sensing. Ecotoxicol. Environ. Saf. 2015, 121, 39–44. [Google Scholar] [CrossRef]
- Mostovoy, G.V.; King, R.L.; Reddy, K.R.; Kakani, V.G.; Filippova, M.G. Statistical estimation of daily maximum and minimum air temperatures from modis lst data over the state of mississippi. GISci. Remote Sens. 2006, 43, 78–110. [Google Scholar] [CrossRef] [Green Version]
- Taheri, M.; Mohammadian, A.; Ganji, F.; Bigdeli, M.; Nasseri, M. Energy-based approaches in estimating actual evapotranspiration focusing on land surface temperature: A review of methods, concepts, and challenges. Energies 2022, 15, 1264. [Google Scholar] [CrossRef]
- Chen, J.; Chen, B.; Black, T.A.; Innes, J.L.; Wang, G.; Kiely, G.; Hirano, T.; Wohlfahrt, G. Comparison of terrestrial evapotranspiration estimates using the mass transfer and penman-monteith equations in land surface models. J. Geophys. Res. Biogeosci. 2013, 118, 1715–1731. [Google Scholar] [CrossRef]
- Zhao, W.; Li, A. A review on land surface processes modelling over complex terrain. Adv. Meteorol. 2015, 2015, 607181. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B.; Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Mandelbrot, B.B. Fractal Geometry and Applications: A Jubilee of Benoît Mandelbrot; American Mathematical Soc.: Providence, RI, USA, 2004. [Google Scholar]
- Ivanov, P.C.; Amaral, L.A.N.; Goldberger, A.L.; Havlin, S.; Rosenblum, M.G.; Struzik, Z.R.; Stanley, H.E. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461–465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, D.; Sharif, A. Common multifractality in the heart rate variability and brain activity of healthy humans. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 023121. [Google Scholar] [CrossRef]
- Sassi, R.; Signorini, M.G.; Cerutti, S. Multifractality and Heart Rate Variability. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 028507. [Google Scholar] [CrossRef] [PubMed]
- Burrough, P.A. Fractal dimensions of landscapes and other environmental data. Nature 1981, 294, 240–242. [Google Scholar] [CrossRef]
- Azizi, T. Mathematical modeling of stress using fractal geometry; the power laws and fractal complexity of stress. Adv. Neurol. Sci. 2022, 5, 140–148. [Google Scholar]
- Azizi, T. Measuring fractal dynamics of fecg signals to determine the complexity of fetal heart rate. Chaos Solitons Fractals X 2022, 9, 100083. [Google Scholar] [CrossRef]
- Azizi, T. On the fractal geometry of different heart rhythms. Chaos Solitons Fractals X 2022, 9, 100085. [Google Scholar] [CrossRef]
- Laguna, P.; Moody, G.B.; Mark, R.G. Power spectral density of unevenly sampled data by least-square analysis: Performance and application to heart rate signals. IEEE Trans. Biomed. Eng. 1998, 45, 698–715. [Google Scholar] [CrossRef] [PubMed]
- Martin, R. Noise power spectral density estimation based on optimal smoothing and minimum statistics. IEEE Trans. Speech Audio Process. 2001, 9, 504–512. [Google Scholar] [CrossRef] [Green Version]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google earth engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Greene, W.H. The econometric approach to efficiency analysis. Meas. Product. Effic. Product. Growth 2008, 1, 92–250. [Google Scholar]
- Cohen, L. Time-Frequency Analysis; Prentice Hall: Hoboken, NJ, USA, 1995; Volume 778. [Google Scholar]
- Gröchenig, K. Foundations of Time-Frequency Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Cooper, G.; Cowan, D. Comparing time series using wavelet-based semblance analysis. Comput. Geosci. 2008, 34, 95–102. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Blackledge, J. Electromagnetic Scattering Solutions for Digital Signal Processing. Ph.D. Thesis, University of JyväSkylä, JyväSkylä, Finland, 2010. [Google Scholar]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Christensen, A.N. Semblance filtering of airborne potential field data. Aseg Ext. Abstr. 2003, 2003, 1–5. [Google Scholar] [CrossRef]
- von Frese, R.R.; Jones, M.B.; Kim, J.W.; Kim, J.-H. Analysis of anomaly correlations. Geophysics 1997, 62, 342–351. [Google Scholar] [CrossRef]
- Banerjee, S.; Hassan, M.K.; Mukherjee, S.; Gowrisankar, A. Fractal Patterns in Nonlinear Dynamics and Applications; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Arneodo, A.; Manneville, S.; Muzy, J.; Roux, S. Revealing a lognormal cascading process in turbulent velocity statistics with wavelet analysis. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 357, 2415–2438. [Google Scholar] [CrossRef]
- Bacry, E.; Muzy, J.-F.; Arneodo, A. Singularity spectrum of fractal signals from wavelet analysis: Exact results. J. Stat. Phys. 1993, 70, 635–674. [Google Scholar] [CrossRef] [Green Version]
- Muzy, J.-F.; Bacry, E.; Arneodo, A. The multifractal formalism revisited with wavelets. Int. J. Bifurc. Chaos 1994, 4, 245–302. [Google Scholar] [CrossRef]
- Abry, P.; Baraniuk, R.; Flandrin, P.; Riedi, R.; Veitch, D. Multiscale nature of network traffic. IEEE Signal Process. Mag. 2002, 19, 28–46. [Google Scholar] [CrossRef] [Green Version]
- Abry, P.; Flandrin, P.; Taqqu, M.S.; Veitch, D. Wavelets for the analysis, estimation, and synthesis of scaling data. In Self-Similar Network Traffic and Performance Evaluation; Wiley: Hoboken, NJ, USA, 2000; pp. 39–88. [Google Scholar]
- Abry, P.; Flandrin, P.; Taqqu, M.S.; Veitch, D. Self-similarity and long-range dependence through the wavelet lens. Theory Appl.-Long-Range Depend. 2003, 1, 527–556. [Google Scholar]
- Veitch, D.; Abry, P. A wavelet-based joint estimator of the parameters of long-range dependence. IEEE Trans. Inf. Theory 1999, 45, 878–897. [Google Scholar] [CrossRef] [Green Version]
- Jaffard, S. Wavelet Techniques in Multifractal Analysis; Technical Report; Paris University: Paris, France, 2004. [Google Scholar]
- Wendt, H.; Abry, P. Multifractality tests using bootstrapped wavelet leaders. IEEE Trans. Signal Process. 2007, 55, 4811–4820. [Google Scholar] [CrossRef] [Green Version]
- Wendt, H.; Abry, P.; Jaffard, S. Bootstrap for empirical multifractal analysis. IEEE Signal Process. Mag. 2007, 24, 38–48. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 3, 1141. [Google Scholar] [CrossRef]
- Hentschel, H.G.E.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Phys. D Nonlinear Phenom. 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Riedi, R. An improved multifractal formalism and self-similar measures. J. Math. Anal. Appl. 1995, 189, 462–490. [Google Scholar] [CrossRef] [Green Version]
- Riedi, R.H. Multifractal Processes; Technical Report; Rice Univ Houston Tx Dept of Electrical and Computer Engineering: Houston, TX, USA, 1999. [Google Scholar]
- Panigrahy, C.; Garcia-Pedrero, A.; Seal, A.; Rodríguez-Esparragón, D.; Mahato, N.K.; Gonzalo-Martín, C. An approximated box height for differential-box-counting method to estimate fractal dimensions of gray-scale images. Entropy 2017, 19, 534. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Cao, Y.; Tung, W.-W.; Hu, J. Multiscale Analysis of Complex Time Series: Integration of Chaos and Random fractal Theory, and Beyond; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Öztürk, Y. Fractal dimension as a diagnostic tool for cardiac diseases. Int. J. Curr. Eng. Technol. 2019, 9, 425–431. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Katz, M.J. Fractals and the analysis of waveforms. Comput. Biol. Med. 1988, 18, 145–156. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azizi, S.; Azizi, T. Noninteger Dimension of Seasonal Land Surface Temperature (LST). Axioms 2023, 12, 607. https://doi.org/10.3390/axioms12060607
Azizi S, Azizi T. Noninteger Dimension of Seasonal Land Surface Temperature (LST). Axioms. 2023; 12(6):607. https://doi.org/10.3390/axioms12060607
Chicago/Turabian StyleAzizi, Sepideh, and Tahmineh Azizi. 2023. "Noninteger Dimension of Seasonal Land Surface Temperature (LST)" Axioms 12, no. 6: 607. https://doi.org/10.3390/axioms12060607



