Fluid Dynamics Calculation in SF6 Circuit Breaker during Breaking as a Prerequisite for the Digital Twin Creation
Abstract
1. Introduction
- -
- Thus, the following requirements are imposed on the CB:
- -
- Low resistance in normal conditions (in the normally closed contact);
- -
- High-voltage proof of external and internal insulation, which makes it possible to withstand lightning and switching overvoltage, as well as transient recovering voltage (TRV) after the arc is extinguished;
- -
- The ability of both making and breaking the short-circuit currents —the CB must reliably extinguish the arc without its re-ignition;
- -
- Ensuring fast transition from the closed to open position and vice versa, especially in automatic reclosing cycles.
2. Switching of SF6 Circuit Breakers
2.1. Interrupter Types in SF6 Circuit Breakers
2.2. Models of Switching Arc Interaction with SF6 Gas Flow
- -
- Continuity equation (law of conservation of mass);
- -
- Equation of the second law (law of conservation of momentum);
- -
- Energy equation (law of conservation of energy).
- 1.
2.3. Methods for Calculating the Processes of Interaction between Arc and the SF6 Flow
3. Analytical Calculation of SF6 Circuit Breaker Breaking
- (1)
- There was no supply and removal of heat during the outflow of gas (adiabatic process);
- (2)
- The process of gas outflow had a steady character;
- (3)
- There were no friction losses;
- (4)
- The gas was considered ideal;
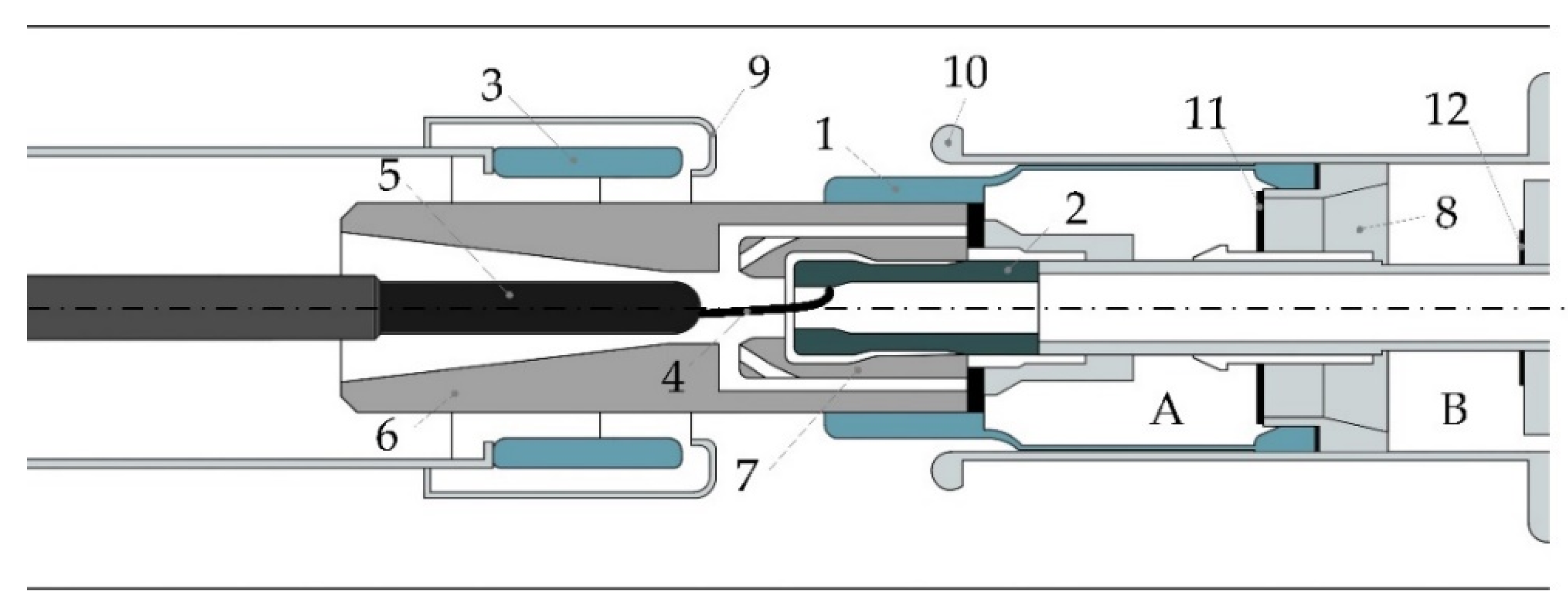
3.1. SF6 Circuit Breaker under Study
3.2. Computational Model of the Circuit Breaker under Study
- -
- Full contact separation ;
- -
- The contact separation before blast start is ;
- -
- Piston cross section ;
- -
- Ambient medium temperature
- -
- Pressure inside CB ;
- -
- The flow coefficient μ at all stages of the outflow was assumed to be 0.9 (the outflow coefficient, which took into account the decrease in the actual cross section of the hole due to the compression of the jet in it);
- -
- Adiabatic exponent for SF6 gas ;
- -
- We set the discretization step of the calculation; for this, we divided the entire piston stroke into 20 identical sections: . The contact separation in each section would be:
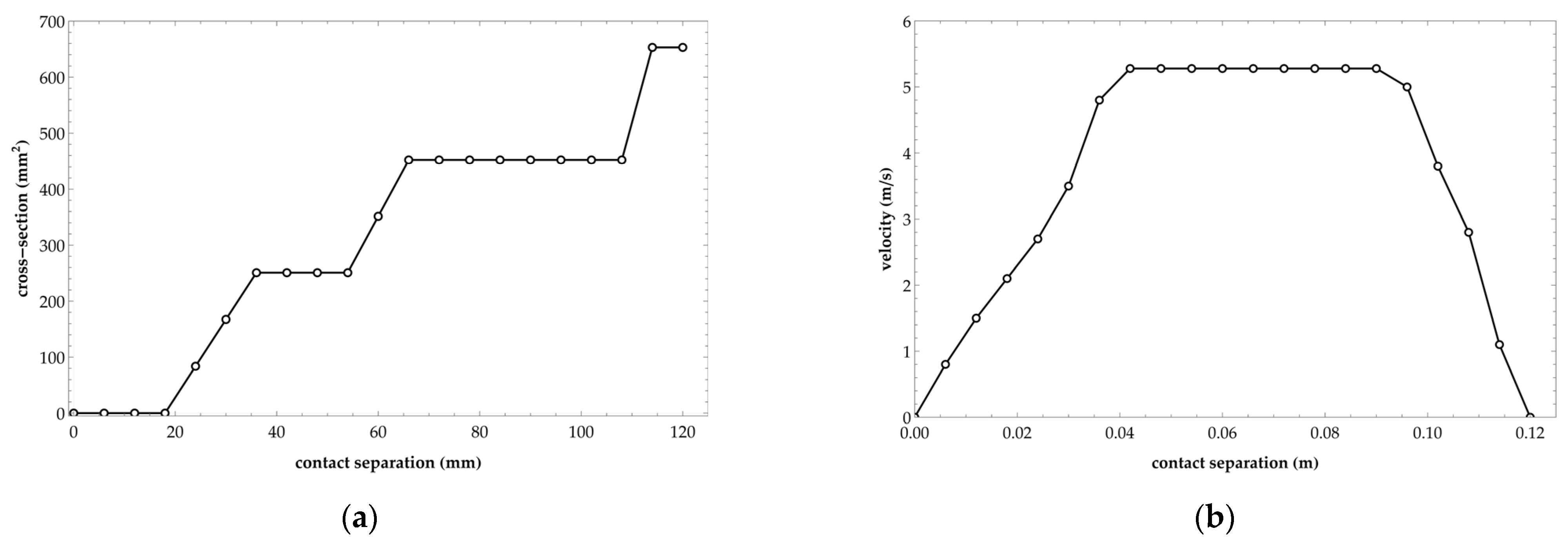
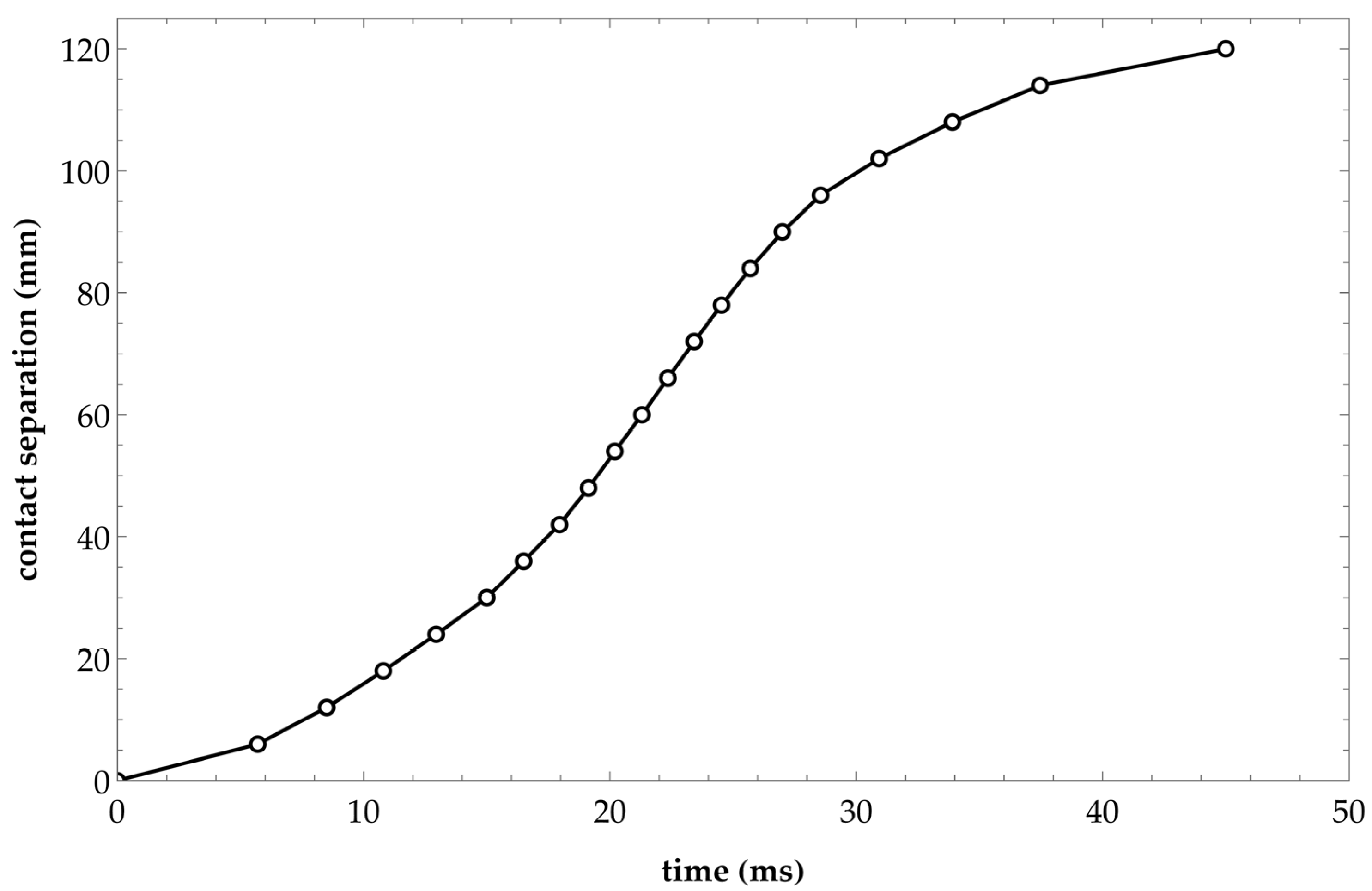
3.3. Calculation Results
4. Numerical Calculation of SF6 Gas Circuit Breaker Switching
- -
- The Boussinessq model;
- -
- The Spallart–Allmaras model;
- -
- The model;
- -
- The model;
- -
- The Reynolds stress model;
- -
- The direct numerical simulation (DNS);
- -
- The large eddy simulation.
4.1. The Model of Turbulent Flow
4.2. The Model of Turbulent Flow
4.3. The Computational Model of the Object under Study
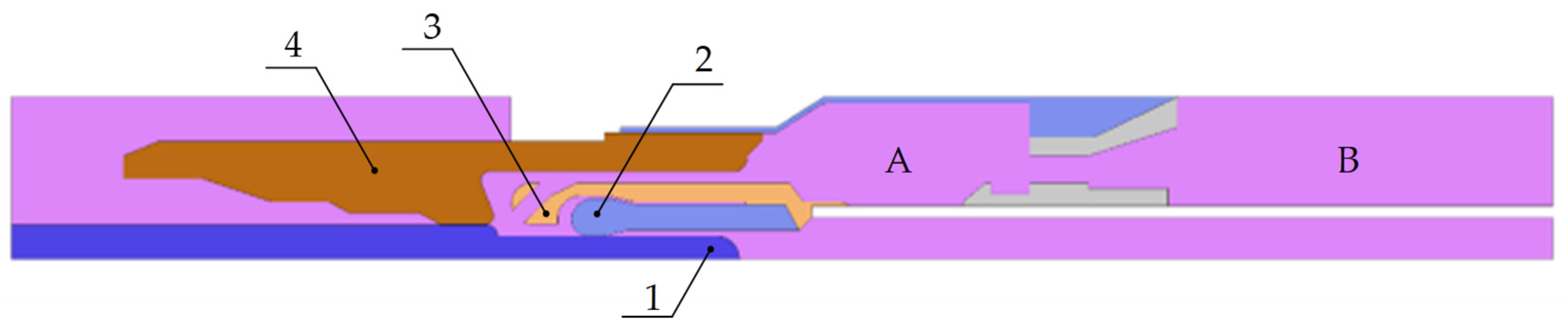
4.4. The Proposed Model of Interaction between SF6 Gas Flow and Arc
4.5. Calculation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Küchler, A. High Voltage Engineering. Fundamentals—Technology—Applications; Springer-Verlag GmbH Germany: Schweinfurt, Germany, 2018; 650p. [Google Scholar] [CrossRef]
- GOST 52565-2006; Alternating-Current Circuit Breakers for Voltages from 3 to 750 kV. General Specifications. National standard of Russia. Rosstandart: Moscow, Russia, 2007; 91p. (In Russian)
- IEC 62271-100; High-Voltage Switchgear and Controlgear—Part 100: Alternating-Current Circuit-Breakers. IEC: Geneva, Switzerland, 2008; 695p.
- IEC 62271-110; High Voltage Switchgear and Controlgear—Part 110: Inductive Load Switching, Ed. 2.0. IEC: Geneva, Switzerland, 2017; 60p.
- IEEE Std C37.015–2017 (Revision of IEEE Std C37.015-2009); Guide for the Application of Shunt Reactor Switching. IEEE: New York, NY, USA, 2018; 62p. [CrossRef]
- Zalesskiy, A. Electric Arc; Gosenergoizdat: Leningrad, Russia, 1963; 267p. (In Russian) [Google Scholar]
- Engelsht, V.; Gurovich, V.; Desyatkov, G. Electric Arc Column Theory; AN USSR, Siberian department, Thermal physics institute: Novosibirsk, Russia, 1990; 373p. (In Russian) [Google Scholar]
- Agafonov, G.; Babkin, I. High Voltage Electrical Apparatus with SF6 Insulation; Energoatomizdat: St. Petersburg, Russia, 2002; 728p. (In Russian) [Google Scholar]
- Tonkonogov, E. The Design of Electrical Apparatus. High Voltage SF6 Circuit Breakers; Izdatelstvo of Peter the Great St. Petersburg Polytechnic University: St. Petersburg, Russia, 2008; 160p. (In Russian) [Google Scholar]
- Averyanova, S.A. Theory of Arc Extinguishing in Electrical Apparatuses. Interaction of the Electric Arc with the Gas Flow in High Voltage Circuit Breakers; Izdatelstvo of Peter the Great St. Petersburg Polytechnic University: St. Petersburg, Russia, 2015; 68p. (In Russian) [Google Scholar]
- Poltev, A. Design and Calculation of SF6 High Voltage Apparatus; Energiya, Leningrad department: Leningrad, Russia, 1979; 240p. (In Russian) [Google Scholar]
- Eroshenko, S. Calculation of Short Circuit Currents in Power Systems; Izdatelstvo of Ural Federal University: Ekaterinburg, Russia, 2019; 104p. (In Russian) [Google Scholar]
- Khalyasmaa, A.I.; Eroshenko, S.A.; Zinovyev, K.A.; Bolgov, V. Improvement of Short-Circuit Calculation Results Reliability for Large Electric Power Systems. In 2019 Electric Power Quality and Supply Reliability Conference and 2019 Symposium on Electrical Engineering and Mechatronics, PQ and SEEM 2019; IEEE: Kärdla, Estonia, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Il’in, A.S. Mathematical Modeling of Thermodynamic Processes of Arc Extinguishing in SF6 flow in Electrical Apparatus; Candidate of Technical Science Dissertation, Ural Federal University: Ekaterinburg, Russia, 2012. (In Russian) [Google Scholar]
- Chunikhin, A.; Zhavoronkov, M. High Voltage Apparatus; Energoatomizdat: Moscow, Russia, 1985; 432p. (In Russian) [Google Scholar]
- Smeets, R.; Van Der Sluis, L.; Kapetanović, M.; Peelo, D.; Janssen, A. Switching in Electrical Transmission and Distribution Systems, 1st ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2015; 425p. [Google Scholar]
- Kapetanović, M. High Voltage Circuit Breakers; Faculty Electrotech. Eng., Univ. Sarajevo: Sarajevo, Bosnia and Herzegovina, 2011; 648p. [Google Scholar]
- Kukekov, G. High Voltage AC Circuit Breakers, 2nd ed.; revised; Energiya, Leningrad Department: Leningrad, Russia, 1972; 336p. (In Russian) [Google Scholar]
- Cassie, A.M. A new theory of rupture and circuit severity. CIGRE Rep. 1939, 102, 588–608. [Google Scholar]
- Mayr, O. Beitrage zur Theorie des Statischen und des Dynamischen Lichtbogens. Arch. Für Elektrotechnik 1943, 37, 588–608. (In German) [Google Scholar] [CrossRef]
- Browne, T.E. A study of A-C. arc behavior near currents zero by means of mathematical models. AIEE Trans. 1948, 67, 147–153. [Google Scholar] [CrossRef]
- Browne, T.E. An Approach to Mathematical Analysis of A-C Arc Extinction in Circuit Breakers. AIEE Trans. 1959, 77, 1508–1517. [Google Scholar] [CrossRef]
- Ragaller, K. Current Interruption in High-Voltage Networks, 1st ed.; Springer: New York, NY, USA, 1978; 360p. [Google Scholar] [CrossRef]
- Hermann, W.; Kogelschatz, U.; Niemeyer, L.; Ragaller, K.; Schade, E. Experimental and theoretical study of a stationary high-current arc in a supersonic nozzle flow. J. Phys. D (Appl. Phys.) 1974, 7, 1703–1723. [Google Scholar] [CrossRef]
- Hermann, W.; Ragaller, K. Theoretical description of the current interruption in HV gas blast breakers. IEEE Trans. Power Appar. Syst. 1977, 96, 1546–1555. [Google Scholar] [CrossRef]
- Tuma, D.T.; Lowke, J.J. Prediction of properties of arcs stabilized by forced convection. J. Appl. Phys. 1975, 46, 3361–3367. [Google Scholar] [CrossRef]
- Lowke, J.J.; Ludwig, H.C. A simple model for high-current arcs stabilized by forced convection. J. Appl. Phys. 1975, 46, 3352–3360. [Google Scholar] [CrossRef]
- EI-Akkari, F.R.; Tuma, D.T. Simulation of transient and zero current behavior of arcs stabilized by forced convection. IEEE Trans. Power Appar. Syst. 1977, 96, 1784–1788. [Google Scholar] [CrossRef]
- Swanson, B.W. Nozzle arc interruption in supersonic flow. IEEE Trans. Power Appar. Syst. 1977, 96, 1697–1706. [Google Scholar] [CrossRef]
- Il’in, A.S. Numerical simulation of arc quenching processes in a high-voltage SF6 circuit breaker and comparison of results with real tests. Sci. Tech. Bull. Povolzhye 2011, 5, 140–146. (In Russian) [Google Scholar]
- Il’in, A.S. Model of arc quenching processes in high voltage circuit breaker. Electrotekhnika 2011, 12, 36–42. (In Russian) [Google Scholar]
- Park, S.H.; Kim, H.K.; Bae, C.Y.; Jung, H.K. Evaluation on Short Line Fault Breaking Performance of SF6 Gas Circuit Breaker Considering Effects of Ablated Nozzle Vapor. IEEE Trans. Magn. 2009, 45, 1836–1839. [Google Scholar] [CrossRef]
- Park, J.H.; Kim, K.H.; Yeo, C.H.; Kim, H.K. CFD Analysis of Arc-Flow Interaction in a High-Voltage Gas Circuit Breaker Using an Overset Method. IEEE Trans. Plasma Sci. 2014, 42, 175–184. [Google Scholar] [CrossRef]
- Schavemaker, P.H.; Van Der Sluis, L. An Improved Mayr-Type Arc Model Based on Current-Zero Measurements. IEEE Trans. Power Deliv. 2000, 15, 580–584. [Google Scholar] [CrossRef]
- Smeets, R.P.P.; Kertész, V. Evaluation of High-Voltage Circuit Breaker Performance with a Validated Arc Model. IEEE Proc. Gener. Transm. Distrib. 2000, 147, 121–125. [Google Scholar] [CrossRef]
- Ahmethodžić, A.; Kapetanović, M.; Sokolija, K.; Smeets, R.P.P.; Kertész, V. Linking a Physical Arc Model with a Black Box Arc Model and Verification. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1029–1037. [Google Scholar] [CrossRef]
- Ohtaka, T.; Kertesz, V.; Smeets, R.P.P. Novel Black-Box Arc Model Validated by High-Voltage Circuit Breaker Testing. IEEE Trans. Power Deliv. 2018, 33, 1835–1844. [Google Scholar] [CrossRef]
- Sinkevich, O.A.; Stahanov, I.P. Plasma Physics. Stationary Processes in a Partially Ionized Gas; Graduate school: Moscow, Russia, 1991; 191p. (In Russian) [Google Scholar]
- Cherednichenko, V.S.; Anshakov, A.S.; Kuzmin, M.G. Plasma Electrotechnological Installations; Izdatelstvo of Novosibirsk State University: Novosibirsk, Russia, 2009; 508p. (In Russian) [Google Scholar]
- Boulos, M.I.; Fauchais, P.L.; Pfender, E. Handbook of Thermal Plasmas; Springer: Cham, Switzerland, 2020; p. 1500. [Google Scholar] [CrossRef]
- Zhong, L.; Cressault, Y.; Teulet, P. Evaluation of Arc Quenching Ability for a Gas by Combining 1-D Hydrokinetic Modeling and Boltzmann Equation Analysis. IEEE Trans. Plasma Sci. 2019, 47, 1835–1840. [Google Scholar] [CrossRef]
- Zhong, L.; Gu, Q.; Zheng, S. An Improved Method for Fast Evaluating Arc Quenching Performance of a Gas Based on 1D Arc Decaying Model. Phys. Plasmas. 2019, 26, 103507. [Google Scholar] [CrossRef]
- Zhong, L.; Wang, J.; Wang, X.; Rong, M. Comparison of Dielectric Breakdown Properties for Different Carbon-Fluoride Insulating Gases as SF6 Alternatives. AIP Adv. 2018, 8, 085122. [Google Scholar] [CrossRef]
- Ivanov, M.F.; Galburt, V.A. Numerical Simulation of Gas and Plasma Dynamics by Particle Methods; Izdatelstvo of Moscow Institute of Physics and Technology: Moscow, Russia, 2000; 168p. (In Russian) [Google Scholar]
- Klimontonovich, Y.L. Kinetic Theory of Non-Ideal Gas and Non-Ideal Plasma; Science: Moscow, Russia, 1975; 352p. (In Russian) [Google Scholar]
- Fridman, A.; Kennedy, L.A. Plasma Physics and Engineering, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2021; 724p. [Google Scholar] [CrossRef]
- Muratović, M.; Kapetanović, M.; Ahmethodzić, A.; Delic, S.; Suh, W.B. Nozzle Ablation Model: Calculation of Nozzle Ablation Intensity and Its Influence on State of SF6 Gas in Thermal Chamber. In Proceedings of the 2013 IEEE International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; pp. 692–697. [Google Scholar] [CrossRef]
- Park, J.H.; Ha, M.J. Experimental and Numerical Studies of Nozzle Ablation and Geometric Change in Real Gas Circuit Breakers. IEEE Trans. Power Deliv. 2022, 37, 4506–4514. [Google Scholar] [CrossRef]
- Kuroda, M.; Urai, H.; Terada, M.; Ishii, T.; Kojima, Y.; Yokomizu, Y. Evaluation of Dielectric Interruption Performance in Gas Circuit Breaker with Ablated PTFE/BN Vapor. In Proceedings of the 2019 5th International Conference on Electric Power Equipment—Switching Technology: Frontiers of Switching Technology for a Future Sustainable Power System, ICEPE-ST 2019, Kitakyushu, Japan, 13–16 October 2019; pp. 551–554. [Google Scholar] [CrossRef]
- Jianying, Z.; Zhijun, W.; Bo, Z.; Yongqi, Y.; Yapei, L. Research on Parameters Optimization of High Voltage Circuit Breaker Nozzle Based on Image Recognition and Deep Learning. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 496–504. [Google Scholar] [CrossRef]
- Kwak, C.S.; Kim, H.K.; Lee, S.H. Bezier Curve-Based Shape Optimization of SF6 Gas Circuit Breaker to Improve the Dielectric Withstanding Performance for Both Medium and Maximum Arcing Time. In Proceedings of the ICEPE-ST 2017—4th International Conference on Electric Power Equipment-Switching Technology, Xi’an, China, 22–25 October 2017; Volume 2017-Decem, pp. 61–65. [Google Scholar] [CrossRef]
- Bang, B.H.; Lee, Y.S.; Choi, J.U.; Ahn, H.S.; Park, S.W. Prediction and Improvement of Dielectric Breakdown between Arc Contacts in Gas Circuit Breaker. In Proceedings of the 2013 2nd International Conference on Electric Power Equipment—Switching Technology, ICEPE-ST 2013, Matsue, Japan, 20–23 October 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Homaee, O.; Gholami, A. Prestrike Modeling in SF6 Circuit Breakers. Int. J. Electr. Power Energy Syst. 2020, 114, 105385. [Google Scholar] [CrossRef]
- Zhang, H.; Yao, Y.; Wang, Z.; Zhang, B.; Hao, X.; Liu, Y.; Du, Y. Application of Arc Breaking Simulation in Development of Extra High Voltage SF6 Circuit Breaker. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online, 2–3 July 2020; pp. 842–845. [Google Scholar] [CrossRef]
- Dhotre, M.T.; Ye, X.; Seeger, M.; Schwinne, M.; Kotilainen, S. CFD Simulation and Prediction of Breakdown Voltage in High Voltage Circuit Breakers. In Proceedings of the 2017 IEEE Electrical Insulation Conference, EIC 2017, Baltimore, MD, USA, 11–14 June 2017; pp. 201–204. [Google Scholar] [CrossRef]
- Ha, M.J.; Kim, J.; Yeo, C.H.; Kweon, K.Y. Influence of PTFE Ablation on the Performance of High Voltage Self-Blast Circuit Breaker. In Transmission and Distribution Conference and Exposition: Asia and Pacific, T and D Asia 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Iordanidis, A.A.; Franck, C.M. Simulation of Ablation ARCS in Realistic Nozzles. In GD 2008—17th International Conference on Gas Discharges and Their Applications; IEEE: Piscataway, NJ, USA, 2008; pp. 209–212. [Google Scholar]
- Zhang, J.; Lan, J.; Tian, L. Influence of DC Component of Short-Circuit Current on Arc Characteristics during the Arcing Period. IEEE Trans. Power Deliv. 2014, 29, 81–87. [Google Scholar] [CrossRef]
- Ahmethodžić, A.; Kapetanović, M.; Gajić, Z. Computer Simulation of High-Voltage SF6 Circuit Breakers: Approach to Modeling and Application Results. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1314–1322. [Google Scholar] [CrossRef]
- Choi, Y.K.; Shin, J.K. Arc Gas-Flow Simulation Algorithm Considering the Effects of Nozzle Ablation in a Self-Blast GCB. IEEE Trans. Power Deliv. 2015, 30, 1663–1668. [Google Scholar] [CrossRef]
- Iordanidis, A.A.; Franck, C.M. Self-Consistent Radiation-Based Simulation of Electric Arcs: II. Application to Gas Circuit Breakers. J. Phys. D Appl. Phys. 2008, 41, 135206. [Google Scholar] [CrossRef]
- Zhang, J.L.; Yan, J.D.; Fang, M.T.C. Investigation of the Effects of Pressure Ratios on Arc Behavior in a Supersonic Nozzle. IEEE Trans. Plasma Sci. 2000, 28, 1720–1724. [Google Scholar] [CrossRef]
- Park, Y.; Song, T. Plasma Arc Simulation of High Voltage Circuit Breaker with a Hybrid 2D/3D Model. In Proceedings of the 2022 6th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Seoul, Republic of Korea, 15–18 March 2022; Volume 4, pp. 190–193. [Google Scholar] [CrossRef]
- Golovin, S.V. Partially Invariant Solutions of the Magnetohydrodynamics Equations. Doctor of Physical-Mathematical Science Dissertation, Novosibirsk State University, Novosibirsk, Russia, 2009. (In Russian). [Google Scholar]
- Lie, S. Vorlesungen über Continuierliche Gruppen mit Geometrischen und Anderen Anwendungen; B.G. Teubner: Leipzig, Germany, 1893; 805p. (In German) [Google Scholar]
- Ovsyannikov, L.V. Group Properties of Differential Equations; AN USSR, Siberian department: Novosibirsk, Russia, 1962; 239p. (In Russian) [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics, 2nd ed.; Pearson Education Ltd.: Harlow, UK, 2007; 520p. [Google Scholar]
- Najm, H.N. Uncertainty Quantification and Polynomial Chaos Techniques in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Loycanskiy, L.G. Fluid and Gas Mechanics, 7th ed.; revised; Drofa: Moscow, Russia, 2003; 840p. (In Russian) [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2012; 658p. [Google Scholar] [CrossRef]
- Averyanova, S.A. Numerical Simulation of Gas Flow in the Arcing Device of a High-Voltage Circuit Breaker; Candidate of Physical-Mathematical Science Dissertation, Peter the Great St. Petersburg Polytechnic University: St. Petersburg, Russia, 2005. (In Russian) [Google Scholar]
- Swanson, B.W.; Roidt, R.M. Thermal Analysis of an SF6 Circuit Breaker ARC. IEEE Trans. Power Appar. Syst. 1971, PAS-91, 381–389. [Google Scholar] [CrossRef]
- Pei, Y. Computer Simulation of Fundamental Processes in High Voltage Circuit Breakers Based on an Automated Modelling Platform. Ph.D. Thesis, The University of Liverpool, Liverpool, UK, November 2014. [Google Scholar]
- Liu, J. Modelling and Simulation of Air and SF6 Switching Arcs in High Voltage Circuit Breakers. Ph.D. Thesis, The University of Liverpool, Liverpool, UK, May 2016. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries: La Cañada, CA, USA, 2006; 522p. [Google Scholar]
- Bai, S.; Luo, H.; Guan, Y.; Liu, W. Arc Shape and Arc Temperature Measurements in SF6 High-Voltage Circuit Breakers Using a Transparent Nozzle. IEEE Trans. Plasma Sci. 2018, 46, 2120–2125. [Google Scholar] [CrossRef]
- Chernoskutov, D.; Popovtsev, V.; Sarapulov, S. Analysis of SF6 Circuit Breakers Failures Related to Missing Current Zero. Part I. In 2020 Ural Smart Energy Conference (USEC); IEEE: Ekaterinburg, Russia, 2020; pp. 51–54. [Google Scholar] [CrossRef]
- Chernoskutov, D.; Popovtsev, V.; Sarapulov, S. Analysis of SF6 Circuit Breakers Failures Related to Missing Current Zero. Part II. In 2020 Ural Smart Energy Conference (USEC); IEEE: Ekaterinburg, Russia, 2020; pp. 55–58. [Google Scholar] [CrossRef]
- Thomas, R. Three Phase Controlled Fault Interruption Using High Voltage SF6 Circuit Breakers. Ph.D. Thesis, The University of Liverpool, Göteborg, Sweden, 2007. [Google Scholar]
- Kays, W.M. Turbulent Pratidtl Number—Where Are We? J. Heat Transfer. 1994, 116, 284–295. [Google Scholar] [CrossRef]
- Lacasse, D.; Turgeon, É.; Pelletier, D. On the Judicious Use of the k-ε Model, Wall Functions and Adaptivity. Int. J. Therm. Sci. 2004, 43, 925–938. [Google Scholar] [CrossRef]
- Gonzalez, J.J.; Freton, P.; Reichert, F.; Petchanka, A. PTFE Vapor Contribution to Pressure Changes in High-Voltage Circuit Breakers. IEEE Trans. Plasma Sci. 2015, 43, 2703–2714. [Google Scholar] [CrossRef]
- Chernoskutov, D.V. Increasing the Switching Capacity of High-Voltage Electrical Equipment; Candidate of Technical Science Dissertation, Ural Federal University: Ekaterinburg, Russia, 2017. (In Russian) [Google Scholar]
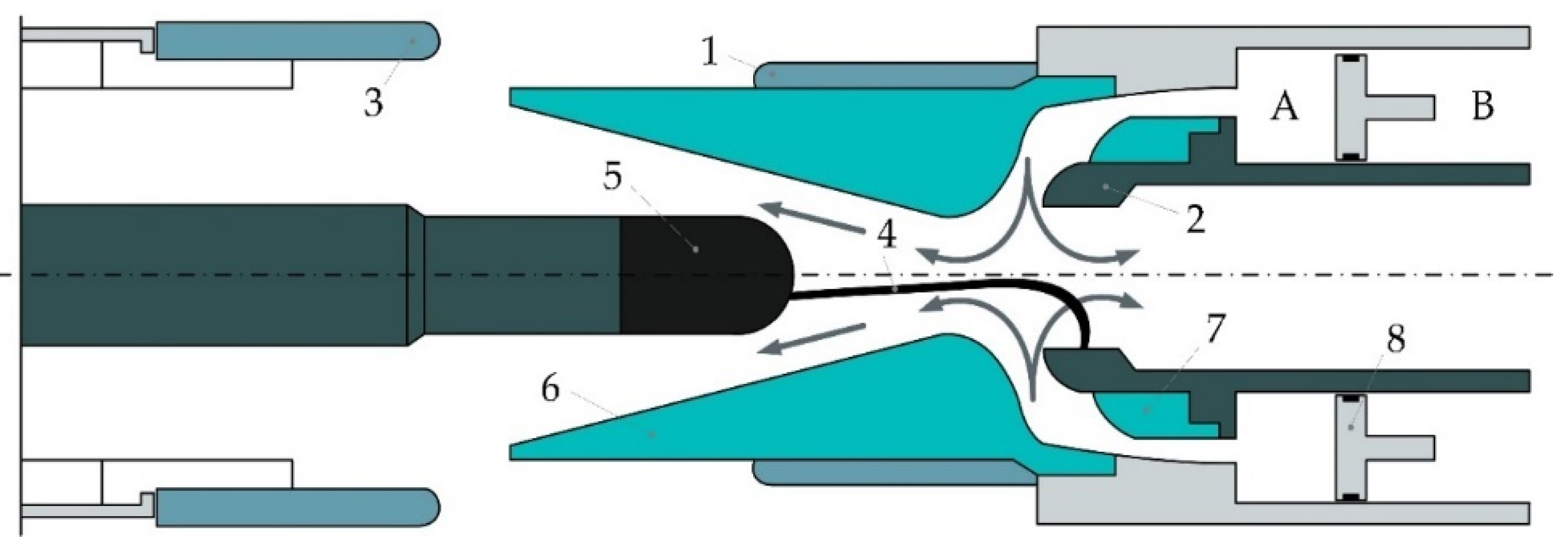
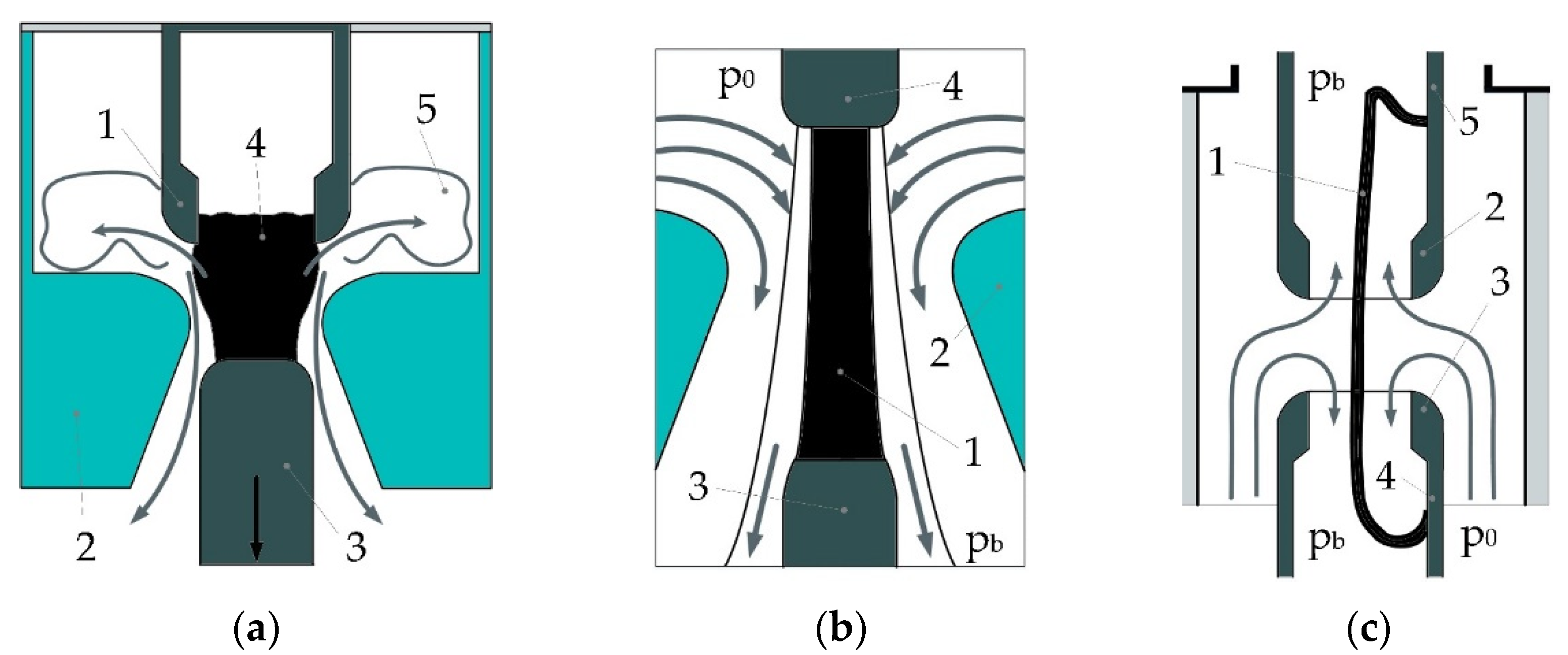
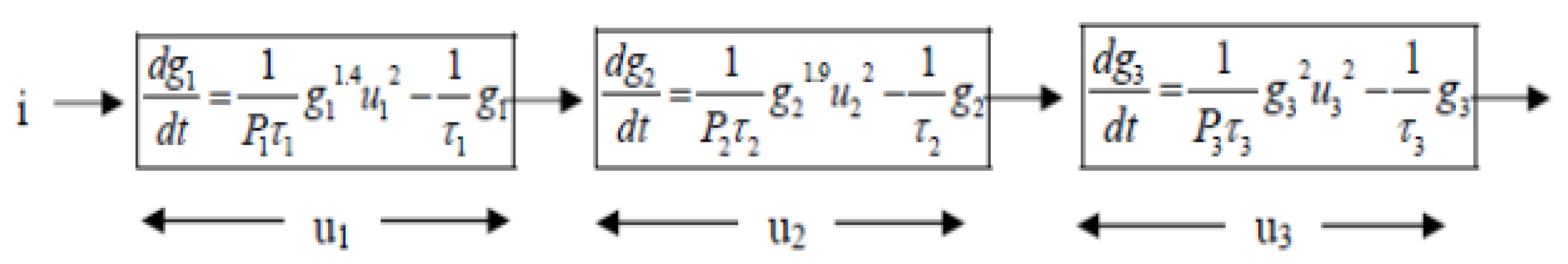
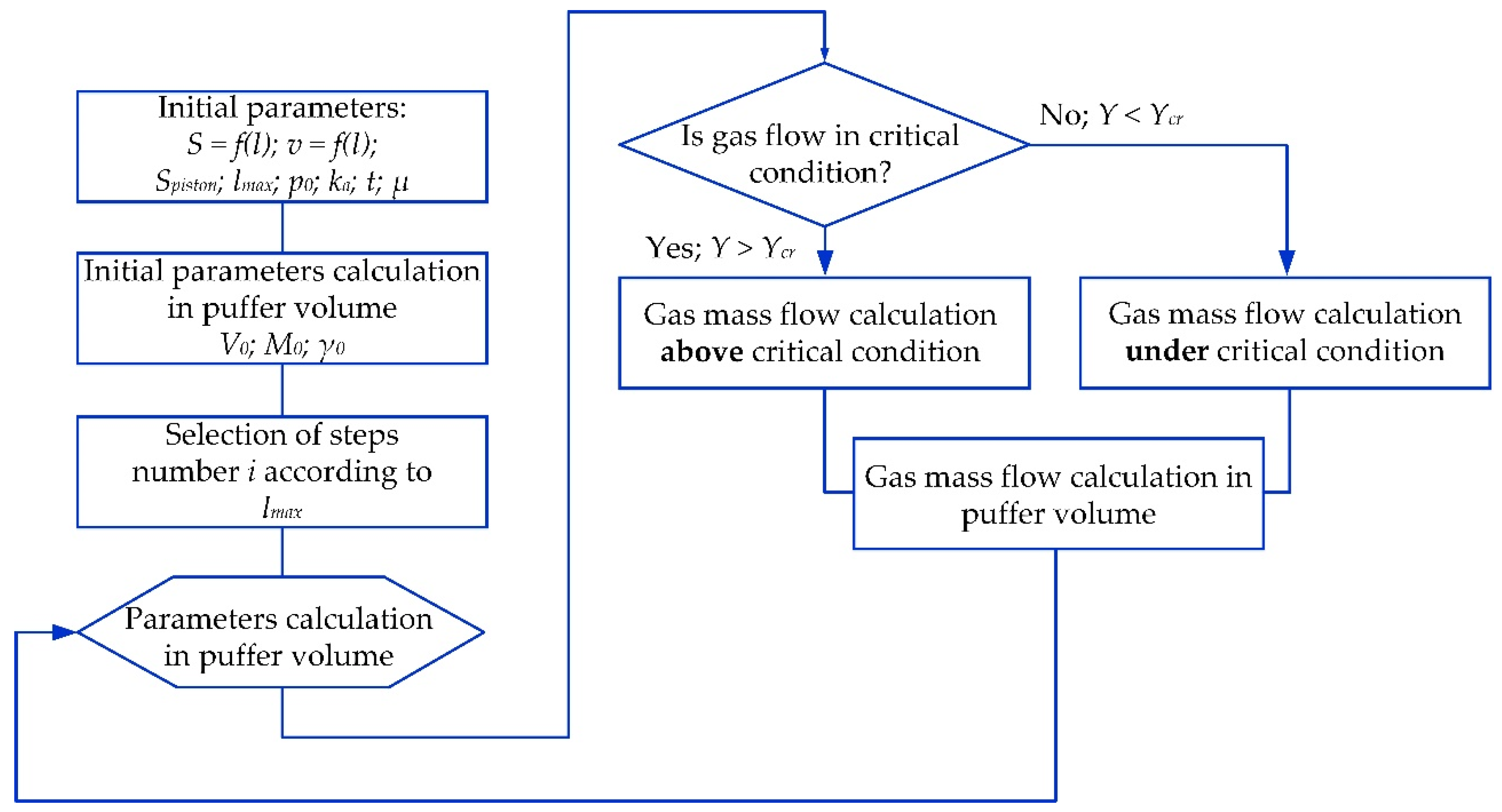
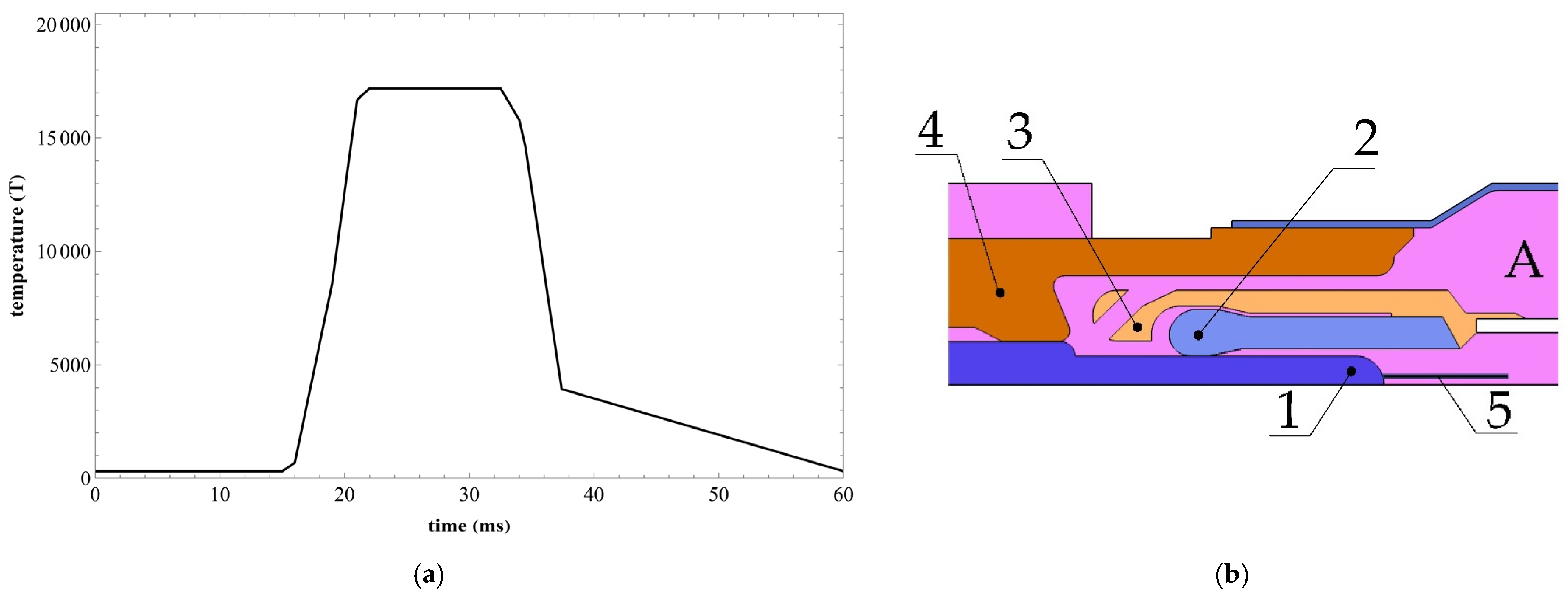



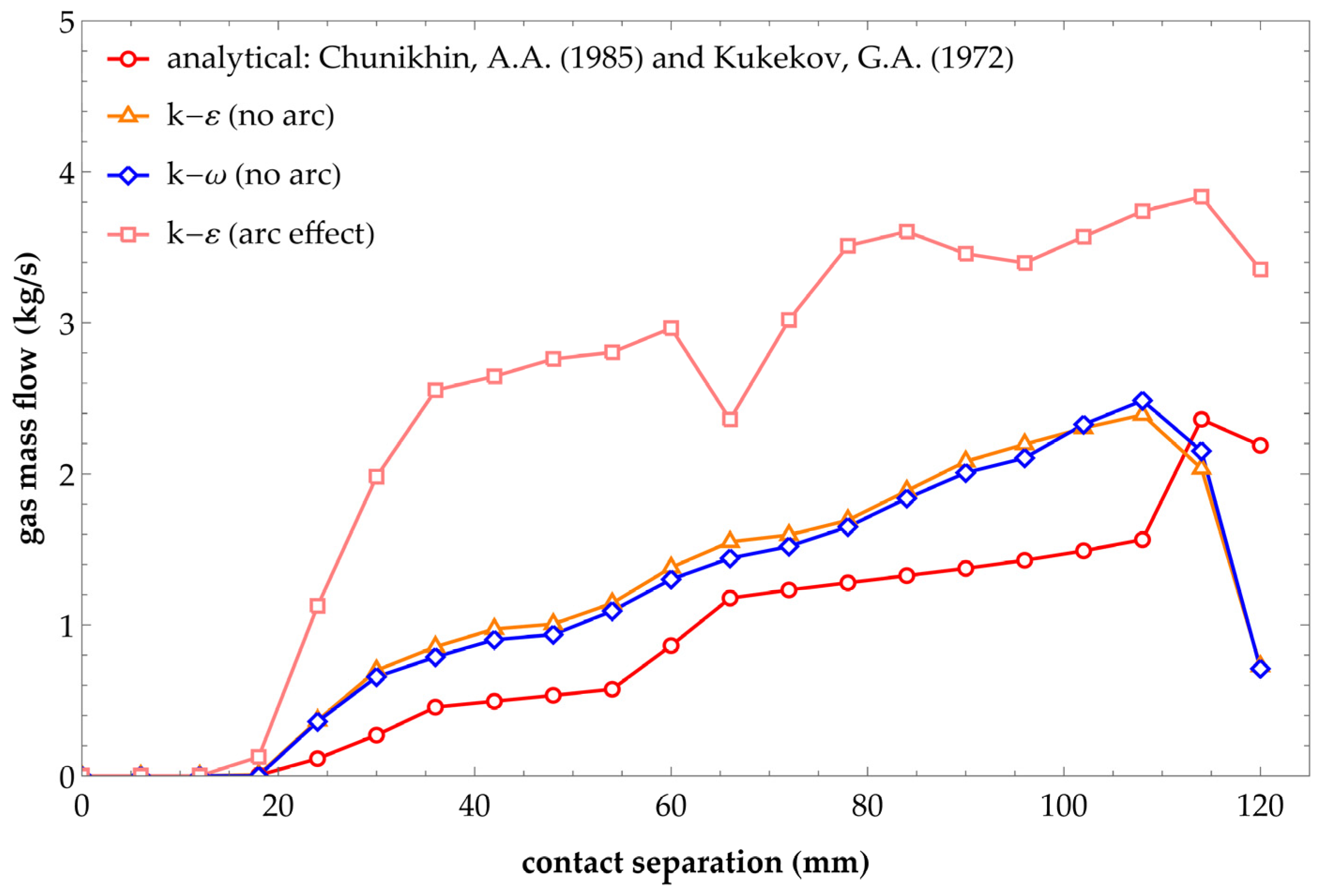




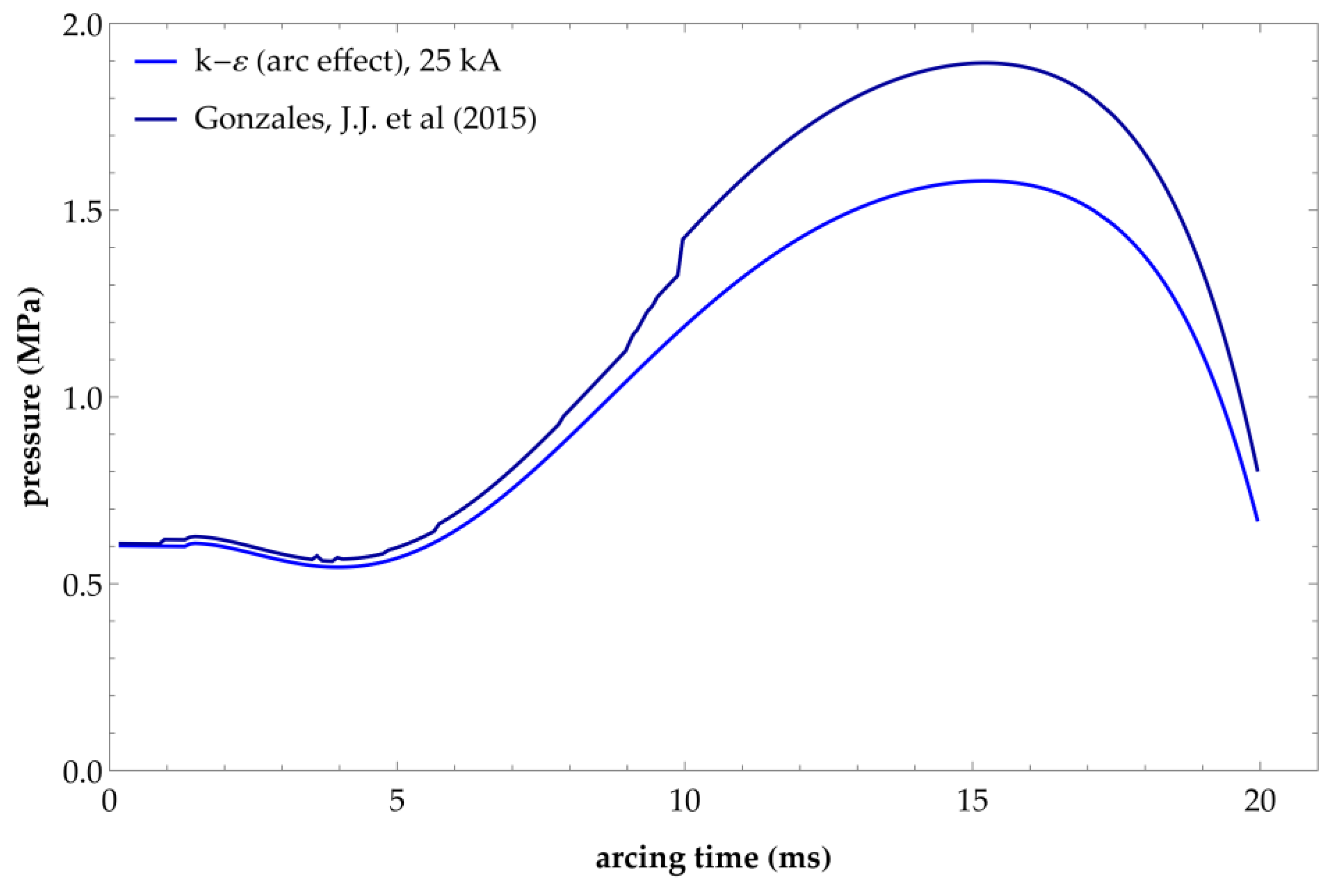
| Parameter Description | Parameter | |
|---|---|---|
| Symbol | Formula | |
| Arc parameters (varying from test to test) | ||
| Time constant | ||
| Cooling power constants | – | |
| – | ||
| Parameters related to CB design | ||
| Distance between arcing contacts | – | |
| Empirical constant (depends on tested CB and for conditions of the short-line fault) | According to [3] | |
| Time constants | ||
| Constants representing the breaker design | According to [37] | |
| According to [37] | ||
| According to [37] | ||
| Cooling power | ||
| № | Ref. | Problem under Study | The Model of Arc Interaction with SF6 Flow | Computational Numerical Model |
|---|---|---|---|---|
| 1 | [32] | Predicting arc extinction by simulating outgassing with nozzle ablation | Conservation equations, Joule heating, and radiation transfer | A two-dimensional axisymmetric |
| 2 | [33] | Exploration of the arc extinguishing process, when the capacitive current is turned off by a self-generating switch | Conservation equations, Joule heating, radiation transfer | A two-dimensional axisymmetric |
| 3 | [47] | Exploration of the nozzle ablation process for breaking capacity | Conservation equations, radiation transfer | A two-dimensional planar |
| 4 | [54] | Elimination of an impulse wave in front of a stationary arcing contact inside the nozzle, causing a decrease in the flow rate of SF6 gas in the nozzle | Conservation equations | A two-dimensional planar |
| 5 | [55] | Arc re-ignition prediction | Conservation equations, Joule heating and radiation transfer | A two-dimensional axisymmetric |
| 6 | [56] | Influence of impurities, arising in the process of nozzle ablation on the process of arc quenching | Conservation equations | A two-dimensional planar |
| 7 | [57] | The reconstruction of a digital model of an arc in cylindrical nozzles | Conservation equations | A two-dimensional planar |
| 8 | [58] | Exploration of the influence of the aperiodic component of the tripping current on the process of arcing | Magnetohydrodynamic: conservation equations, Maxwell’s equations | A two-dimensional axisymmetric |
| 9 | [59] | Creation of a software package for modeling arc extinguishing processes | Conservation equations, Joule heating | A two-dimensional planar |
| 10 | [60] | Exploration of the process of arc extinguishing by a self-blast CB, taking into account the ablation of the nozzle | Conservation equations | A two-dimensional axisymmetric |
| 11 | [61] | Investigation of the process of arc extinguishing by a self-generated switch, taking into account the ablation of the nozzle | Conservation equations, radiation transfer | A two-dimensional axisymmetric |
| 12 | [62] | Exploration of the arc extinguishing process in a supersonic nozzle | Conservation equations | A two-dimensional axisymmetric |
| 13 | [63] | Improved accuracy at low breaking currents (wire arc). | Magnetohydrodynamic: conservation equations, Maxwell’s equations | 3D |
| l, mm | Vi, mm3 | pi, MPa | Yi | Ψi | vavg.i, m/s | Gi, kg/s | ||
|---|---|---|---|---|---|---|---|---|
| 6 | 1.209 | 0.420 | 1.000 | 0 | 0 | 0 | 0 | 29.674 |
| 12 | 1.155 | 0.441 | 0.975 | 0.218 | 0.40 | 0 | 0 | 29.674 |
| 18 | 1.101 | 0.465 | 0.938 | 0.336 | 1.15 | 0 | 0 | 29.674 |
| 24 | 1.048 | 0.491 | 0.895 | 0.424 | 1.80 | 0.114 | 0.380 | 29.294 |
| 30 | 0.994 | 0.512 | 0.856 | 0.482 | 2.40 | 0.271 | 0.676 | 28.617 |
| 36 | 0.940 | 0.530 | 0.823 | 0.520 | 3.10 | 0.455 | 0.881 | 27.736 |
| 42 | 0.886 | 0.547 | 0.795 | 0.546 | 4.15 | 0.494 | 0.715 | 27.022 |
| 48 | 0.833 | 0.569 | 0.766 | 0.569 | 5.04 | 0.533 | 0.635 | 26.387 |
| 54 | 0.779 | 0.596 | 0.734 | 0.588 | 5.28 | 0.574 | 0.652 | 25.735 |
| 60 | 0.725 | 0.627 | 0.701 | 0.604 | 5.28 | 0.863 | 0.981 | 24.755 |
| 66 | 0.671 | 0.653 | 0.671 | 0.614 | 5.28 | 1.177 | 1.337 | 23.417 |
| 72 | 0.618 | 0.673 | 0.646 | 0.620 | 5.28 | 1.231 | 1.399 | 22.019 |
| 78 | 0.564 | 0.695 | 0.625 | 0.623 | 5.28 | 1.279 | 1.453 | 20.565 |
| 84 | 0.510 | 0.719 | 0.604 | 0.625 | 5.28 | 1.326 | 1.507 | 19.058 |
| 90 | 0.457 | 0.747 | 0.582 | 0.625 | 5.28 | 1.374 | 1.561 | 17.497 |
| 96 | 0.403 | 0.780 | 0.559 | 0.625 | 5.28 | 1.427 | 1.622 | 15.875 |
| 102 | 0.349 | 0.820 | 0.535 | 0.625 | 5.14 | 1.491 | 1.740 | 14.135 |
| 108 | 0.295 | 0.867 | 0.508 | 0.625 | 4.40 | 1.564 | 2.133 | 12.002 |
| 114 | 0.242 | 0.902 | 0.486 | 0.625 | 3.30 | 2.360 | 4.291 | 7.711 |
| 120 | 0.188 | 0.733 | 0.526 | 0.625 | 1.95 | 2.188 | 6.732 | 0.979 |
| Description | Parameter | |
|---|---|---|
| Designation | Value | |
| Pressure inside the interrupter | p | 0.42 MPa |
| Initial gas flow velocity | u | 0 m/s |
| Ambient temperature | T | 313 K |
| Von Karman constant | 0.41 | |
| Parameters of k-e turbulence model | ||
| – | 1.44 | |
| – | 1.92 | |
| – | 0.09 | |
| Turbulent kinetic energy | 1 | |
| Turbulent dissipation rate | 1.3 | |
| Constant parameters of k-w turbulence model | ||
| – | 0.12 | |
| – | 0.072 | |
| – | 0.09 | |
| Turbulent kinetic energy | 0.5 | |
| Specific turbulent dissipation rate | 0.5 | |
| Number of Elements | Vertex Elements | Edge Elements | Average Element Quality | Automatic Remeshing | Relative Tolerance | Tolerance Factor | Termination Technique | Max Iterations |
|---|---|---|---|---|---|---|---|---|
| 4737 | 92 | 1090 | 0.4474 | 0.08 | 0.1 | 1 | Tolerance | 20 |
| l, mm | t, ms | , MPa | , MPa | , m/s | , m/s | , kg/s | , kg/s |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.420 | 0.420 | 0 | 0 | 0 | 0 |
| 6 | 5.70 | 0.441 | 0.441 | 0 | 0 | 0 | 0 |
| 12 | 8.50 | 0.462 | 0.462 | 0 | 0 | 0 | 0 |
| 18 | 10.80 | 0.484 | 0.484 | 6.0 | 6.0 | 0 | 0 |
| 24 | 12.95 | 0.507 | 0.507 | 31.0 | 30.0 | 0.367 | 0.360 |
| 30 | 15.00 | 0.523 | 0.523 | 59.0 | 55.5 | 0.699 | 0.656 |
| 36 | 16.50 | 0.533 | 0.533 | 83.0 | 74.5 | 0.855 | 0.787 |
| 42 | 17.95 | 0.552 | 0.554 | 105.0 | 89.5 | 0.973 | 0.902 |
| 48 | 19.13 | 0.572 | 0.575 | 121.0 | 103.0 | 1.005 | 0.936 |
| 54 | 20.20 | 0.590 | 0.596 | 121.0 | 105.0 | 1.143 | 1.092 |
| 60 | 21.30 | 0.607 | 0.613 | 123.0 | 106.0 | 1.380 | 1.301 |
| 66 | 22.35 | 0.626 | 0.631 | 105.0 | 103.0 | 1.550 | 1.442 |
| 72 | 23.42 | 0.644 | 0.665 | 119.0 | 124.0 | 1.595 | 1.520 |
| 78 | 24.53 | 0.659 | 0.666 | 126.0 | 111.0 | 1.693 | 1.650 |
| 84 | 25.70 | 0.673 | 0.681 | 119.0 | 118.0 | 1.888 | 1.838 |
| 90 | 27.00 | 0.682 | 0.690 | 145.0 | 129.0 | 2.083 | 2.007 |
| 96 | 28.55 | 0.676 | 0.687 | 98.0 | 105.0 | 2.196 | 2.105 |
| 102 | 30.93 | 0.645 | 0.658 | 105.0 | 105.0 | 2.303 | 2.327 |
| 108 | 33.90 | 0.590 | 0.600 | 83.0 | 95.0 | 2.391 | 2.486 |
| 114 | 37.46 | 0.511 | 0.514 | 65.0 | 75.0 | 2.036 | 2.151 |
| 120 | 45.00 | 0.383 | 0.378 | 20.0 | 21.0 | 0.727 | 0.710 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popovtsev, V.V.; Khalyasmaa, A.I.; Patrakov, Y.V. Fluid Dynamics Calculation in SF6 Circuit Breaker during Breaking as a Prerequisite for the Digital Twin Creation. Axioms 2023, 12, 623. https://doi.org/10.3390/axioms12070623
Popovtsev VV, Khalyasmaa AI, Patrakov YV. Fluid Dynamics Calculation in SF6 Circuit Breaker during Breaking as a Prerequisite for the Digital Twin Creation. Axioms. 2023; 12(7):623. https://doi.org/10.3390/axioms12070623
Chicago/Turabian StylePopovtsev, Vladislav V., Alexandra I. Khalyasmaa, and Yurii V. Patrakov. 2023. "Fluid Dynamics Calculation in SF6 Circuit Breaker during Breaking as a Prerequisite for the Digital Twin Creation" Axioms 12, no. 7: 623. https://doi.org/10.3390/axioms12070623
APA StylePopovtsev, V. V., Khalyasmaa, A. I., & Patrakov, Y. V. (2023). Fluid Dynamics Calculation in SF6 Circuit Breaker during Breaking as a Prerequisite for the Digital Twin Creation. Axioms, 12(7), 623. https://doi.org/10.3390/axioms12070623








