Abstract
To the existing list of alternative formulations of quantum mechanics, a new version of the non-Hermitian interaction picture is added. What is new is that, in contrast to the more conventional non-Hermitian model-building recipes, the primary information about the observable phenomena is provided not only by the Hamiltonian but also by an additional operator with a real spectrum (say, ) representing another observable. In the language of physics, the information carried by opens the possibility of reaching the exceptional-point degeneracy of the real eigenvalues, i.e., a specific quantum phase transition. In parallel, the unitarity of the system remains guaranteed, as usual, via a time-dependent inner-product metric . From the point of view of mathematics, the control of evolution is provided by a pair of conjugate Schrödiner equations. This opens the possibility od an innovative dyadic representation of pure states, by which the direct use of is made redundant. The implementation of the formalism is illustrated via a schematic cosmological toy model in which the canonical quantization leads to the necessity of working with two conjugate Wheeler-DeWitt equations. From the point of view of physics, the “kinematical input” operator may represent either the radius of a homogeneous and isotropic expanding empty Universe or, if you wish, its Hubble radius, or the scale factor emerging in the popular Lemaitre-Friedmann-Robertson-Walker classical solutions, with the exceptional-point singularity of the spectrum of mimicking the birth of the Universe (“Big Bang”) at .
Keywords:
quantum theory of unitary systems; non-Hermitian interaction representation; non-stationary physical inner products; dyadic representation of pure states; schematic quantum model of Big Bang MSC:
83C47
1. Introduction
Around the turn of millennium it had widely been accepted that the various existing formulations of quantum mechanics (QM) “differ dramatically in mathematical and conceptual overview, yet each one makes identical predictions for all experimental results” [1]. In the cited review the authors emphasized the historical as well as methodical importance of the Heisenberg’s alias “matrix” formulation of QM (in which the states do not change in time) as well as the economy of the most common Schrödinger’s alias “wavefunction” formulation (which “shifts the focus from measurable quantity to state”).
In loc. cit. the catalogue of formulations was not exhaustive. The authors did not mention the “universal” interaction picture (IP) in which the observables (say, ) and the states (say, ) are both allowed to vary with time, and . In the general Hermitian IP framework of conventional textbooks [2], one can easily re-derive both the Heisenberg-picture (HP) or Schrödinger-picture (SP) methodical extremes when setting or , respectively.
The review also did not reflect the quick developments in the field in the direction initiated by Bender and Boettcher [3]. The latter innovation turned attention to the overrestrictive role played by the Stone theorem [4]. By this theorem, indeed, the evolution described by the Schrödinger equation
is unitary in if and only if the Hamiltonian is self-adjoint in , . In our present paper, we intend to offer a further extension of the latter methodical developments in which the Hermiticity restrictions imposed by the Stone theorem were circumvented.
In the introduction, we have to remind the readers that the origin of the idea can in fact be traced back to the paper by Dyson [5]. Long before the turn of the millennium, this author revealed that the goal of having the theory non-Hermitian but still unitary can be achieved via a non-unitary, time-independent preconditioning of the SP wavefunctions,
In applications, the non-unitarity of the stationary Dyson’s map led to an efficient description of correlations in various complicated many-body systems [5,6,7,8].
Along this line, the potentially user-unfriendly Hamiltonian has been replaced by its user-friendlier isospectral avatar defined as acting in the new, potentially user-friendlier Hilbert space ,
The conventional Hermiticity gets lost () so that Hilbert space has to be declared unphysical. Importantly, due to the time-independence of , the loss is just formal, with the Hermiticity of in merely replaced by Dieudonné’s [9] metric-mediated quasi-Hermiticity of in ,
On a more abstract quantum-theoretical level, the isospectrality between a pre-selected, sufficiently user-friendly non-Hermitian Hamiltonian and its self-adjoint reconstructed partner opened multiple new model-building strategies, first of all in quantum field theory [10,11]. The possibility of reconstruction of the “missing” physical inner-product metrics from a given non-Hermitian Hamiltonian H led also, in the framework of relativistic QM, to the completion of the years-long efforts of a consistent probabilistic interpretation of the Klein-Gordon fields [12,13,14,15] and/or of the Proca fields [16,17].
A few other successful applications can be found mentioned in the recent review of the field by Mostafazadeh [18]. Still, the author had to admit there that after a tentative transition from the Klein-Gordon equation to a formally not too different Wheeler-DeWitt (WDW) equation of quantum gravity [19,20], the applicability of the reconstruction of appears to be limited. In the Mostafazadeh’s own words, “the lack of a satisfactory solution of this problem has been one of the major obstacles in transforming canonical quantum gravity and quantum cosmology into genuine physical theories” (cf. p. 1291 in loc. cit.).
For this reason, the review [18] of quasi-Hermitian QM only marginally mentioned the WDW models. An analogous skepticism can also be found expressed in the quantum-gravity-dedicated monographs [21,22]). The main mathematical obstacle can be seen in the fact that the operators “that arise in quantum cosmological models” have to be manifestly time-dependent and that such a choice “requires a more careful examination” [18].
More recently, the problem has been reopened, and the latter challenge was re-addressed in [23]. Still, the main methodical and conceptual challenges were, from our present point of view, circumvented. For this reason, we felt urged to complement the theory in our present paper with a new analysis in which the manifest t-dependence of the quasi-Hermitian operators would prove tractable in a more satisfactory manner.
As we already indicated in the Abstract, an important source of inspiration of our present project was that the vast majority of the conventional applications of the non-Hermitian model-building recipes starts from the assumption of our knowledge of the Hamiltonian H. In most cases, this operator is assumed to be observable, i.e., constrained by relation (4). At the same time, the more abstract theory of review [7] admits the existence of “input information” knowledge of at least one other, independent operator (i.e., in our present notation, of ) with a real spectrum.
In some sense (cf. [24]), an attempt of a feasible and, at the same time, purposeful incorporation of in the formalism was one of the main driving forces behind the present work. On the side of physics, we decided to motivate it by the needs of quantum cosmology, in which notions such as Hubble radius or scale factor play a key role in the classical-physics toy-model descriptions of the empty, homogeneous, and isotropically expanding Universe. Nevertheless, for our present purposes, we found it sufficient to speak just about an entirely schematic observable “radius of an expanding toy-model Universe” which is allowed to vary with the so-called cosmological time t.
The presentation of our results starts in Section 2, where we briefly review the existing stationary and non-stationary versions of the quasi-Hermitian quantum mechanics. In Section 3, we then turn attention to the WDW equation and review and emphasize the recent progress in its study. A deeper insight into its role is then provided in Section 4, in which we introduce our present highly schematic but instructive toy model of the quantum Universe.
For the sake of simplicity, just the radius will be considered quantized, i.e., represented, just shortly after Big Bang, by a (quasi-Hermitian) operator . Subsequently, the related basic technical questions of the construction of the physical Hilbert-space metric and of the evolution equations in the non-Hermitian interaction picture (NIP) are addressed and reviewed in Section 5. Several conceptual aspects of the theory are finally discussed in Section 6 and summarized in Section 7.
2. Two Quasi-Hermitian Formulations of Quantum Theory
The introduction in quantum mechanics usually starts, in textbooks, from its formulation in the Schrödinger “representation” alias “picture” (SP, [2]). In this language, the states are represented by the ket-vector elements of a suitable Hilbert space . The unitary evolution of the system is prescribed by Equation (1), i.e., by Schrödinger equation in which the Hamiltonian is required to be self-adjoint, . In such a setting, a decisive simplification of the solution of Equation (1) can be achieved, in principle at least, via the (usually just numerical) diagonalization of the Hamiltonian.
2.1. Non-Hermitian Schrödinger Picture (NSP)
In many realistic models, the diagonalization of may happen to be prohibitively difficult. More than half a century ago, fortunately, Freeman Dyson [5] revealed that whenever the “maximal” simplification remains, due to its complexity, unavailable, the underlying realistic Schrödinger Equation (1) might still be made tractable via a “partial” simplification of the Hamiltonian. He just recommended that the “inaccessible” diagonalization be replaced by any other (i.e., just invertible) auxiliary time-independent isospectrality mapping which need not even be required to be unitary.
One just has to redefine the states as well as, whenever necessary or useful, the Hilbert space itself (cf. Equation (2) above). The original conventional Schrödinger equation is replaced by its equivalent representation in ,
As long as , it also makes sense to introduce the “alternative ket vectors”
evolving, in , according to a complementary Schrödinger equation,
The main benefit of the resulting formalism using two Schrödinger equations and two different Hamiltonians (viz., H and ) is that for pure states, the predictions of the results of measurements have a fully analogous form in and in . Indeed, once one considers any stationary and self-adjoint operator representing an observable in , and once one defines its NSP avatar in , the validity of the elementary mathematical identity
implies the coincidence of the predictions (i.e., of the probability densities) when computed via the single textbook Schrödinger Equation (1) or via the conjugate pair (5) + (6).
2.2. Non-Hermitian Interaction Picture (NIP)
Once we admit the dependence of Dyson’s mapping on time, , it is sufficient to follow the description of the necessary (i.e., NIP) amendments to the theory as described in [25,26]. After such a generalization of the formalism, the main changes result from the emergence, in both of the non-Hermitian Schrödinger equations, of the non-vanishing Coriolis-force term.
The non-stationary generalization of the observable non-Hermitian Hamiltonian (or, in the standard language of mathematics, of quasi-Hermitian Hamiltonian) remains, by definition, isospectral with the self-adjoint (though now, admissibly, non-stationary). Hamiltonian of textbooks. Nevertheless, the price to pay for the non-stationarity is that the non-stationary upgrade of the two NIP Schrödinger equations reads
where the generator of evolution contains the Coriolis term and ceases to be observable, therefore (cf., e.g., p. 1272 in [18]).
The admissibility of the non-stationarity of the prototype textbook Hamiltonian is, in some sense, exceptional [27]. For all of the other non-Hermitian and non-stationary operators of observables defined, in , by their pull-down from , the formalism would become prohibitively complicated unless we assumed that , i.e., unless we require that
where the self-adjoint avatars of the non-Hamiltonian observables remain time-independent (see also [23] for a detailed discussion of this subtlety).
Under the latter assumption, one can re-establish a complete parallelism between the conventional Hermitian quantum mechanics in the interaction picture and its non-Hermitian alternative, in which the two NIP Schrödinger Equations (9) and (10) control the evolution of states. Naturally, a complete picture is only obtained when one also takes into consideration the manifest and necessary time-dependence of the observables. The most straightforward guarantee of the internal consistency of the theory is then provided by the following result.
Lemma 1.
The time-dependence of observables (11) can be reconstructed from their initial values by the solution of Heisenberg equation
Proof.
One has to notice that the role of the NIP generator of evolution is played here by the Coriolis force. The solution of the equation specifies the (by definition, non-stationary) operator in consistent manner. At the same time, our knowledge of this solution immediately opens the possibility of an ultimate evaluation of the matrix elements entering the following nonstationary upgrade of Equation (7),
This formula expresses the probabilistic contents of the non-stationary theory and quantifies the prediction of the results of the measurement at time .
3. Samples of Application
In the preface to the ambitious theoretical monograph [22], we read that “despite an enormous effort of work by a vast amount of physicists over the past 70 years, we still do not have a credible quantum general relativity theory” (QGR). “What we do have today are candidate theories; …for each of them, one still has to show …that it reduces to the presently known …classical general relativity at low energies” [22].
3.1. Wheeler-DeWitt Equation
The incompleteness of the candidate QGR theories is best illustrated by the canonical quantum gravity based on WDW equation. In this field, incidentally, the progress is significant. On p. 1291 of [18], for example, it is emphasized that “in the 1960’s the discovery of the Hamiltonian formulation of the General Theory of Relativity …provided the necessary means to apply Dirac’s method of constrained quantization”. We believe that in this context, the NIP-based study of the not-too-realistic WDW equation has not yet told us its last word yet.
The skepticism of the theoreticians is in sharp contrast with the experimental side of the QGR problem, where the efforts of physicists were amazingly successful. For example, the age of our Universe is currently widely agreed to be finite and equal to cca 13.8 billion years [28]. It is worth adding that the determination of the latter value belongs to one of the most impressive recent experimental results in physics. Under the self-explanatory name “Cosmic Background Radiation Anisotropy Satellite/Satellite for Measurement of Background Anisotropies” (COBRAS/SAMBA, [28]) the measurement was initiated around 1996 and operated by the European Space Agency between the years 2009 and 2013. The necessary sensitivity and resolution were further improved by the NASA Wilkinson Microwave Anisotropy Probe (WMAP).
This resulted in the data summarized in the so-called Lambda cold dark matter (CDM) model alias “standard” cosmological model” [29]. In the acronym, the first Greek letter refers to the cosmological constant, while the use of the word “standard” emphasizes that its parameters fit not only the expansion of the universe or the distribution laws of the atomic nuclei and/or galaxies but also the fairly contradictory hypothesis of the existence of the initial point-like Big-Bang singularity.
Once we reopen the question of the compatibility of the CDM hypotheses with the basic principles of quantum theory, we only have to return to a moderate skepticism. The applicability of the underlying classical-physics-based concepts finds its first natural limitation in a restriction to their far-from-Big-Bang verifications. The experiments remain persuasively compatible with the classical GR theory as the correct theory of gravity at macroscopic distances.
In this context, we found our basic theoretical inspiration and encouragement in the comprehensive review paper [18]. We read there that in quantum cosmology “the relevant …second order differential equations” (i.e., WDW equations) resemble the Klein-Gordon equations and “have the following general form”
(cf. Equation Nr. 377 and the related comments in [18]). The symbol denotes here a “wave function of the Universe” which would be “void of a physical meaning” without “an appropriate inner product” [18].
In the near future, the quantum effects emerging at the singularities (as sampled by black holes or the hypothetical Big Bang) will have to be re-analyzed. In other words, there is still a broad gap between our understanding of the correspondence between the well-confirmed classical singularities and their internally consistent quantum analogues. A model-based description of their mechanism and dynamics is still, in light of Equation (14), one of the most important subjects of research and one of the sources of open questions that motivated our forthcoming considerations.
In a way explained in review [18] (cf., in particular, section Nr. 9.2), a full formal analogy between the Klein-Gordon and WDW equations only exists when the operator part of Equation (14) remains time-independent, . In this case, indeed, the Klein-Gordon-type equation can be transformed into its NSP equivalent (5) of Section 2.1 (cf. also equation Nr. 378 in loc. cit.). The second NSP Schrödinger Equation (6) of Section 2.1 is then easily written in terms of the conjugate Hamiltonian operator . The correct physical (i.e., probabilistic) interpretation of the evolution then follows from the one-to-one correspondences (2) and (3) between the states and operators in the respective Hilbert spaces and .
After a transition (of our present interest) to the genuine WDW version of Equation (14), the operator must necessarily be kept manifestly time-dependent. This forces us to make use of the non-stationary NIP formalism of Section 2.2. The main innovation is that any quasi-Hermitian observable of interest (say, A in Equation (7)) becomes, by definition, time-dependent (cf. Equation (11)). As a consequence, the prediction of any measurement (i.e., the evaluation of the overlap (13)) requires, suddenly, not only the solution of the two comparatively friendly Schrödinger-like evolution equations for the state (i.e., the construction of the two vectors in ) but, first of all, also the solution of another maximally user-unfriendly Heisenberg-like evolution Equation (12) for the operator.
3.2. Closed versus Open Quantum Systems
Many authors proved discouraged by the latter technical obstacles, and so they redirected their attention, typically, to the exactly solvable models (later, we will pick up the letter [30] for illustration). Frequently, people also simplify the model-building process by giving up unitarity. They declare their quantum system, in the spirit of Refs. [31,32], “open”. In some sense, the newly acquired freedom becomes abused because, by definition of the open quantum systems (formulated, basically, in Feshbach’s spirit [33,34]) the resulting “effective” non-Hermitian descriptions are, in the sense of fundamental theory, incomplete [35,36].
This being said, one should add that the use of the effective operators of observables really enables one to pay more attention to the ever-present noise and fluctuations in the quantum systems living in the real world (cf., e.g., [37,38]). In the future, in this sense, it will certainly be necessary to try to move beyond the restrictive closed-system models, indeed.
In our present paper the consequent fundamental-theory approach is not abandoned. In its framework, nevertheless, even the operator-evolution nature of the Heisenberg-like Equation (12) need not be the main technical problem. Indeed, difficulties also emerge in connection with the corresponding non-stationary upgraded doublet of Schrödinger-like Equations (9) and (10). As long as the generator of the evolution of the states becomes defined as the difference between the Hamiltonian (which is, by definition, observable) and the Coriolis force (which is, in general, not observable), also the generator itself is not observable (once more, we may recall Theorem Nr. 2 in [18] for details). Moreover, many examples (cf., e.g., [39,40]) show that the elements of its spectrum need not even form the complex conjugate pairs. For this reason, it also makes hardly any sense to try to simplify the model by imposing, upon this operator, the popular -symmetry constraint. Nevertheless, in the search for innovations, this is what is often being completed—see, e.g., [41,42].
Recently, new light has been shed on these problems by the two studies of several solvable and manifestly time-dependent “wrong-sign” anharmonic oscillators [30,43]. Surprisingly enough, it has been shown there that it may still make good sense to impose the -symmetry constraint directly upon the observable Hamiltonian . At the first sight, the motivation seems missing because this operator only enters the pair of the NIP Schrödinger equations in combination with Coriolis force. Nevertheless, the toy-model studies reconfirmed that the main advantage of using the concept of -symmetry lies in its capability of a clear separation of the unitary dynamical regime (in which the symmetry remains unbroken) from its unphysical non-unitary complement (in which the -symmetry becomes spontaneously broken).
3.3. Pure States in Dyadic Representation
A clarification of the slightly complicated NIP situation becomes provided when one imagines that Schrödinger’s, the Heisenberg’s and Dirac’s intermediate alias interaction pictures describe the same physics. All of them characterize the same evolution of a quantum system, which is initiated by the preparation of a pure state at , which finally leads to the prediction of the results of the measurement at . In the language of mathematics, this means that once we complement the Dyson map (2) (or, more precisely, its non-stationary, time-dependent amendment) by a complementary, alternative replacement
We may immediately deduce that . Thus, whenever we decide to work with the two different state-vector elements and of the Hilbert space , it appears sufficient to work just with the information about the metric encoded in the double-ket vector .
The latter trick leads, in a way emphasized in the review [23], to an enormous simplification of the NIP formalism. The statement may also be given a more compact mathematical form in which the pure state is represented, in , by the rank-one (i.e., dyadic) projector
with (or even without) the conventional assumptions of the biorthonormality and bicompleteness
this enables us to re-derive the fundamental measurement-prediction Formula (13).
4. Quantum Gravity in a Toy Model
In the preceding context, it is worth adding that, in spite of a certain resemblance of our state-representing formulae with the Aharonov’s and Vaidman’s time-symmetric two-state-vector formalism [44,45], the parallels are purely formal because the present approach remains safely traditional and time-asymmetric (see also a few other comments in Section 6.1 below). This means that we just stay in the framework of a traditional non-relativistic quantum cosmology in which the t-dependent state (and, say, the pure state) of the Universe would have to be prepared at a suitable time . One can expect that the state of the Universe evolves and gets measured at another instant . Now, our task is to explain how one might realize such an evolution scenario, in principle at least, when making the pure states represented by the rank-one projectors (16).
4.1. Classical Singularities
There are not too many results in which one would really succeed in making the space-time background of QGR quantized (i.e., represented by an operator) and, simultaneously, time-dependent. In our present considerations, we decided to emphasize, therefore, just a few preselected methodical aspects of quantum gravity, with our attention paid, predominantly, to the requirement of the background independence of the theory, in which even the measurements of the distances in an empty Universe would be of a strictly quantum, probabilistic nature [46].
We will test our ideas in the non-covariant kinematical regime in which the time t will still be treated as a parameter [47]. Moreover, even the strictly quantum Universe will be assumed to be simplified and existing just in a very small vicinity of its classical Big-Bang singularity. After such a specification of the simplified dynamical regime, we will add several further, methodically motivated reductions to the picture.
- The classical space-time geometry of the Universe has to remain “next to trivial”. We will employ the not exceedingly revolutionary kinematics working with the non-covariant concept of absolute time. The quantum-theory-controlled evolution of the Universe will then be assumed to be unitary, i.e., unitary in the language of the more or less conventional quantum mechanics of the so-called closed systems.
- In both the classical and quantum settings, the naively physical non-relativistic parameter of time t will be assumed positive and set equal to zero at Big Bang. On the classical non-relativistic level also the 3D spatial coordinates will be assumed time-dependent, therefore, , and .
- All this would lead to a still nontrivial version of the background independence because the observable values of the spatial nodes , , and (i.e., say, point-particle positions [47]) have to be defined (i.e., prepared and/or measured) as eigenvalues of operators, in principle at least.
- The last three operators have to be self-adjoint in a physical Hilbert space in which the inner product has the property of being time-dependent and degenerating at . In other words, a “non-Hermitian” NIP version of QM will have to be used.
For the sake of simplicity in our toy-model-based considerations, we will assume that the kinematics of the expanding Universe will be just one-parametric. The purpose of such a choice is twofold. In the context of mathematics, the maximal simplicity of our methodical considerations has to be achieved. In this sense, one can simply speak about a homogeneous and isotropic, centrally symmetric expanding empty Universe characterized, say, by its volume or radius . Thus, in our present minimal project, just such a real function would have to be reinterpreted as an eigenvalue of an ad hoc operator .
In parallel, in the context of physics, the interpretation of the parameter might be made more sophisticated, with the details to be found, e.g., in the dedicated monograph [48]. Thus, for example, one could identify its t-dependent value with the scale factor emerging in the popular Lemaitre-Friedmann-Robertson-Walker classical solvable model, or with the closely related function of t called Hubble radius, etc.
In any case, the reduction of the description of the classical dynamics to a single real parameter implies that in the centrally symmetric picture with we will have to replace, firstly, the three spatial Cartesian coordinates , , and by the equivalent spherical coordinates , and . Secondly, for the sake of simplicity, this will enable us to assume, in another reasonable approximation, the stationarity and of the angles. Moreover, we will treat the latter two values as fixed and not quantized. Thus, both of the spherical angular coordinates will be kept “frozen” and “irrelevant”, i.e., classical and time-independent.
All of the latter simplifications have a methodical motivation. In contrast, the radius of the Universe itself will be defined, after quantization, as one of the available real eigenvalues of a time-dependent “dynamical-geometry” operator . At any suitable Hilbert-space dimension we will have to write where the “multiverse-counting” quantum number specifies the hypothetical “prepared” pure quantum state of the Universe.
The quantum radius of the Universe must be time-dependent. At Big Bang, we have to guarantee the existence of an “unavoidable” degeneracy (also called “exceptional point”, EP, [49]), for all n. Our time-dependent “dynamical-geometry” operator must be, in our working Hilbert space , non-Hermitian but Hermitizable alias quasi-Hermitian, i.e., such that
In the literature, interested readers may find a number of the generic methodical comments on the latter equation (cf., e.g., [7,18,50]). In what follows, we intend to work just with an illustrative family of certain non-numerically tractable N by N matrices . This will enable us to keep the related discussion sufficiently short and specific.
4.2. The Radius of the Universe in a Solvable Toy Model
A mathematical inspiration for our present project of the realization of a schematic quantum model of the Universe dates back to the unpublished preprint [51]. We considered there, in an entirely different context, a one-parametric family of non-Hermitian (but Hermitizable, quasi-Hermitian) matrices with the real spectra that represented the discrete bound-state energies. The purpose of the preprint (to be cited as PI in what follows) was a study of the slow, adiabatic unitary-evolution process resulting in a fall of the level systems into an exceptional-point singularity (EPN, [49]).
Not the same, but analogous matrices will be used here in another role, viz., in the role of a non-stationary operator with the eigenvalues representing the observable instantaneous radii of the Universe. For the sake of simplicity, we will assume that the dimension N of our schematic Hilbert space is finite. We will consider and postulate that our “kinematical”, geometric-background-representing input matrices have the following respective forms,
Here, and are suitable real and smooth functions of time t. Thus, for illustration we may choose the shift , the dimension and the parameter . This would yield the spectrum as displayed in Figure 1. We may see that the model is “realistic” in the sense that at any quantum number n our toy-model empty Universe exhibits a point-like singularity (Big Bang) at and a quick expansion at .
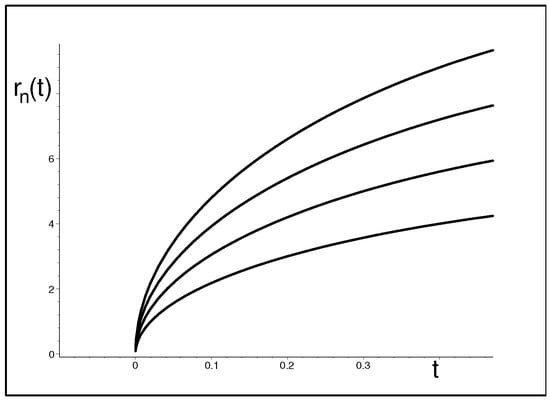
Figure 1.
The “multiverse” eigenvalues of the toy-model operator of Equation (19) representing the eligible instantaneous size of the quantized Universe expanding after Big Bang.
A number of comments are to be made in advance. First, we have to keep in mind that once we start from the hypothetical knowledge of the kinematics, it need not be easy to combine the underlying space-evolution ansatzs (i.e., in our toy-model case, the specification of parameters in Equation (19)) with the requirements of the dynamics (sampled, in our case, by the WDW Equation (14)).
5. The Consistent Model-Building Process
Our model-building philosophy is based on the Big-Bang-admitting ansatz (19). Thus, our very first task is to make the corresponding choice of the kinematics (i.e., of the time-dependent matrix ) compatible with the unitarity of the evolution (in this sense, we assume that the quantum system under consideration is a closed system). This means that we have to take into account, first of all, the Dieudonné’s Hermitizability constraint (18).
5.1. The First Step: The Construction of the Metric
From the point of view of physics all of the sufficiently ambitious quantum-Big-Bang-related models have to mimic a quasi-static phase transition. Naturally, the concept of the phase transition itself is very broad (see, e.g., the comprehensive review paper [52], where the authors list more than 400 further relevant references). In comparison, the range of physics behind our present Big-Bang-related project is perceivably narrower. In a way discussed more thoroughly in papers [53,54] we will only deal here with the more specific philosophy of quantum phase transitions, the realization of which is based on the presence, in the space of parameters, of a suitable Kato’s [49] exceptional point. Moreover, just marginal attention will be paid to the energy levels and to the Hamiltonians. Our study will be redirected to the background-representing operator (or rather non-Hermitian N-by-N-matrix) . Depending on a real time-simulating parameter (such that ) and preceding the case of a more realistic time-dependent (i.e., non-relativistic) triplet of N by N matrices , , representing a dynamical, fully quantized (and, at finite , just discretized) three-dimensional space-time-grid background.
We will require that the spectra of all of these matrices be complex at the negative times (this has to reflect the unobservable status of the space before the Big Bang), real but EPN-degenerate at (i.e., at the hypothetical non-relativistic Big-Bang instant), and real and non-degenerate at (for pragmatic reasons we will just keep in mind the not too large times, i.e., say, ). Moreover, in the three-dimensional space of the hypothetical expanding Universe we will also reparametrize the coordinates and replace their time-dependent and system-dependent Cartesian grid by the spherical triplet . For the sake of simplicity, the angular coordinates will be assumed fixed, and just the radial one will be treated as the expanding-Universe spatial background and quantized, i.e., treated as one of the eligible eigenvalues of an ad hoc, kinematical-input operator .
For methodical purposes (as well as for the sake of definiteness), we will assume that the latter, geometry-representing operator, is given in advance, having the form resembling closely the Hamiltonians in PI. Thus, once we abbreviate or introduce a new variable , the parallels become complete.
All of our toy-model matrices will be chosen as real, non-Hermitian, and, whenever , Hermitizable. This means that at any preselected matrix dimension N there exists an inner-product-metric operator (which need not be unique; see [7]) such that our spatial-grid-simulating operator satisfies the quasi-Hermiticity condition (18). In PI, we worked with the close analogues of our present matrices (19) so that we could just recall and modify Theorem Nr 1 of PI and formulate the following result.
The values of these matrix elements had to be computed as solutions of Equation (18)—for the first few Hilbert-space dimensions N, the results may be found in PI.
Theorem 1.
In PI we also recommended to arrange the non-vanishing matrix elements into the k by arrays,
At every finite Hilbert-space dimension the metric compatible with the respective radii (19) may be sought in the following generic form
containing the sparse-matrix coefficients
etc.
5.2. Coriolis Force and the Evolution Equations
At a fixed Hilbert-space dimension N the general inner-product-metric solution of Equation (18) is non-unique. It varies with an plet of free parameters, the variability of which is only restricted by the condition of the necessary positivity of the metric. In ref. [54], we studied a special “zero-spectral-shift” sub-family of our present time-dependent models (19) with . At arbitrary N, we described certain “optimal” solutions (24) that exhibited a number of desirable features. From our present point of view the most important one was that the positivity of the metric (i.e., of all of its time-dependent eigenvalues ) proved guaranteed at all of the dimensions and at all of the times of interest.
Easily, the latter result can be re-adapted to our present needs. Irrespective of the radius-positivity-guaranteeing ad hoc shift parameters , the following Theorem can be easily proved by mathematical induction.
Theorem 2.
All of the time-dependent eigenvalues of the optimal-radius-dependent inner-product metric are given, at any matrix-dimension N, by the following closed formula,
where , and, in general,
The main consequence of this result is that all of the eigenvalues of the metric are positive. This means that we may recall Equation (4) (in which we reconstructed the “unknown” metric as a product of the two “known” Dyson maps) and that we may try to invert the recipe (assuming that the metric is “known” and that the Dyson map is to be reconstructed, say, in the form of a real square root of [54]). This means that we can factor the metric into the product.
representing a time-dependent generalization of the stationary factorization formula of Equation (4).
This enables us to treat the Coriolis-force matrix (as defined by Equation (8) as known. One can conclude that the construction of the toy model is almost completed. Indeed, any plet of its other observable features can be represented by the respective operators (say, , with, if needed, assigned to the energy-representing Hamiltonian). All of these operators must be, in terms of the same “correct and physical” Hilbert-space metric, quasi-Hermitian,
Secondly, any one of them (and, in particular, the Hamiltonian ) can be used to define the basis that can be biorthonormalized (cf. [55] or Equation (17)). The purpose may be served, in the real-spectrum dynamical regime, by the doublet of eigenvalue problems
Thirdly, the knowledge of the metric also facilitates the search for other candidates for the observables (denoted, say, as without a subscript). Indeed, once we consider the product , we immediately see that is Hermitian. Thus, any Hermitian “input-information” matrix can be treated as a set of free parameters defining a quasi-Hermitian operator eligible as an observable.
The observables of the latter type may be required to correspond to their conventional SP avatars which are stationary, conserved, and time-independent. In such a case, the process of the definition of the operator (at all times) can be facilitated and replaced by the definition of the operator just at a single instant, , with the completion of the construction of (at all times) provided by the solution of the corresponding Heisenberg Equation (12).
In the last step of our considerations, we may preselect a Hermitian matrix and use it as the parameters defining the energy-representing observable Hamiltonian . Then we may immediately reconstruct the generator of the evolution of the states, which enters, finally, the two conjugate Schrödinger Equations (9) and (10). The construction of the model is complete.
6. Discussion
In a way summarized in reviews [11,18,56], the recent theoretical developments in quantum mechanics threw new light on many traditional model-building strategies. The main idea of the innovation lies in an extension of the concept of the so-called observable from its traditional form (i.e., from its self-adjoint representation) to an unconventional alternative that is non-Hermitian but which happens to be Hermitizable. The Hermitization is still needed, mediated by an amended Hilbert-space inner-product metric which, “it it exists” [7], varies with our choice of the observable.
In applications, one often works with an observable Hamiltonian. Whenever its most standard self-adjoint SP version happens to be user-unfriendly, the desirable user-friendliness can be recovered after transition to its suitable non-Hermitian avatar. A full compatibility of the resulting hiddenly Hermitian NSP reformulation of quantum mechanics is achieved when, with a suitable , the new, non-Hermitian Hamiltonian remains quasi-Hermitian,
We already reminded the readers that in Section 9.2 of the review [18], it has been pointed out that the NSP-based construction of the stationary inner-product matric plays a particularly important role in relativistic quantum mechanics (with being the Klein-Gordon operator) and in the various versions of application of Dirac’s method of constrained quantization to gravity (with being the Wheeler-DeWitt operator). It is only desirable to add now that after a transition to the more advanced NIP version of the theory in which one decides to work with the time-dependent Hilbert-space metrics , most of the above-cited statements must be thoroughly reformulated. In particular, the most general non-stationary version of the Klein-Gordon operator of the relativistic QM cannot remain consistently identified with the observable operator anymore.
In our present paper, the same change of paradigm has been described and shown to be necessary in the NIP approach to the genuine, non-stationary Wheeler-DeWitt equation of quantum gravity. For this purpose, naturally, multiple technical simplifying assumptions had to be accepted.
6.1. Conventional Time-Asymmetric QM Concept of the Evolution
The description of a quantum system in which the observables are represented by operators is, certainly, richer than the description of its classical limit [57]. One of the related paradoxes is that a substantial part of the success of quantum theory is, in some sense, serendipitous, based on a lucky choice of one of many eligible “quantizations”. In this sense, we are currently not too lucky when trying to quantize Einstein’s general relativity (see, e.g., the Isham’s foreword to the Thiemann’s monograph [22]).
One of the problems is, in Thiemann’s words, that the “quantum theory of the non-gravitational interactions …completely ignores General Relativity” while the latter classical theory alias geometry “completely ignores quantum mechanics” (see p. 9 in loc. cit.). In our present paper, in this sense, we tried to stay firmly in the framework of non-relativistic quantum mechanics.
After such a simplification, the survival of the concept of time t enables one to order evolution in a strictly causal manner. Incidentally, the “fixed-frame” restriction of such a type can be softened by a change of perspective working with another, “non-time” evolution parameter [46]. In an extreme case as presented and discussed in a methodical study [47], one can even quantize the time itself, i.e., one can treat t as a “pure-state” eigenvalue of a “quantum clock” operator.
The idea of such a type is also presented in the Rovelli’s monograph [21]. We can read there that only in conventional approaches does one believe that “the Schrödinger picture is only viable for theories where there is a global observable time variable t”. Naturally, “this conflicts with GR [general relativity], where no such variable exists” (cf. pp. 10 and 11 in loc. cit.). One has to conclude that a properly covariant formulation of the unitary quantum evolution near Big Bang is still not well understood and formulated at present, especially because after the replacement of quantum mechanics by quantum field theory (QFT), one reveals that “most of the conventional machinery of perturbative QFT is profoundly incompatible with the general-relativistic framework” [21]. Thus, only the traditional perturbation-approximation-based pragmatic approaches to predictive cosmology seem to be available at present [48].
In this sense, we propose here that one of the possible schematic keys to the puzzle might be sought in the quantization of the classical GR singularities (like Big Bang) using, on a quantum level, Kato’s [49] concept of the exceptional-point degeneracy of the schematic, non-covariant Universe at .
6.2. More Realistic Frameworks like Loop Quantum Gravity
The current progress in experimental astronomy is amazing: we already mentioned the measurements of the cosmic microwave background [28]. This confirmed the Big Bang hypothesis experimentally. In parallel, its mathematically singular nature also motivated an intensification of the efforts of making Einstein’s classical general relativity (GR) compatible with the first principles of quantum mechanics (QM) [21,22].
The recent progress in this direction is remarkable. We already mentioned the studies of the conventional canonical recipes aimed, according to Wheeler [19] and DeWitt [20], at the construction of a “wave-function of the Universe”. Among the more recent related theoretical results, one must also mention the formalism of the so called loop quantum gravity (LQG, [58]). In this setting, one is really able to work with the modified QM called “relational”, with some basic details mentioned in Section Nr. 5.6 of the monograph [21]. Nevertheless, we read there that the relational reformulation of QM “has aspects that need to be investigated further” (cf. p. 367 in [21]).
On these grounds, our interest in the problem has been born. During one of the seminars on the subject (dedicated to the description of quantum Big Bang), we imagined that people very often come to a quick conclusion that the classical GR singularities (like, typically, the Big-Bang-mediated “abrupt” birth of the Universe) must necessarily get, according to the conventional wisdom, “smeared” (i.e., in the mathematical sense, “regularized”) after quantization.
For a long time, the latter intuitive expectation had been widely accepted. A replacement of the Big-Bang singularity by the so-called Big Bounce was advocated by the widest LQG community [59,60]. Only very recently has this assertion been reconsidered and opposed [61]. This means that the competition between the Big Bang and Big Bounce hypotheses may currently be considered to have reopened.
In our present toy model, the quantum Big Bang instant remains singular. Counterintuitive as such a possibility seems to be, one could see its multiple analogues, say, in the physics of phase transitions. Naturally, many forms of the description of conventional phase transitions are more or less standard, not requiring the use of the sophisticated mathematics of the LQG approach. At the same time, the newly emerging undecided status of the quantum Big Bang hypothesis represents a challenge. We believe that the new forms of insight were also provided by our present paper.
6.3. A Broader Physical Context
One of the main formal supports for optimism may be seen in the fact that one of the key formal features of our present NIP theory is in its richer representation of quantum dynamics. Indeed, in the conventional version of QM, the flexibility of the model-building processes is strongly restricted by the fact that the (pure) state of a unitary quantum system of interest is merely represented by a ket-vector element of a preselected and time-independent Hilbert space . In contrast, the mathematical and phenomenological roles of the ket-vectors in the NIP Hilbert space become separated. The amended theory works with the two non-equivalent versions of the latter space, viz., with (where the inner product is elementary but unphysical) and with . In the latter case one can say that either the definition of the correct, physical inner product contains the operator of metric or that the operation of the physical Hermitian conjugation is realized as the less conventional antilinear map . This, indeed, simplifies the formalism because the mathematically user-friendly space (which must be declared “unphysical”) can also serve as a representation space for .
From such a perspective, the NIP approach comes with the new possibility of making the family of the gravity-related quantum field theories “background-independent”(cf. p. 22 in [21], or the more detailed comments in [22]). From a purely pragmatic point of view, this simply means that in the conventional models (i.e., say, in the point-particle wave functions ), even the parameters (i.e., in this case, the coordinates ) have to be perceived as eigenvalues of a suitable operator (let us note that many of the associated technical problems are discussed in the framework of the so-called non-commutative-geometry [62]).
In our present paper, an innovative realization of the background-independence requirement has been achieved by making the time-dependent radius of the expanding Universe quantized, i.e., identified, in the pure-state multiverse-philosophy spirit, with one of the eigenvalues of an ad hoc quasi-Hermitian operator .
7. Conclusions
At present, the use of non-Hermitian operators in quantum theory is remarkably diversified, ranging from the traditional and pragmatic effective-operator descriptions of the open and resonant quantum systems [31] up to the new horizons opened by the studies of the abstract mathematical aspects of the formalism [56].
In a narrower domain of the description of closed (i.e., unitary) quantum systems using non-Hermitian operators, the main division line is the one that separates the stationary and non-stationary theories. In the former subdomain, the Coriolis forces vanish so that . There emerge no problems with calling the Schrödinger-equation generator a Hamiltonian [18].
In the latter, non-stationary-theory subdomain the situation is different. We have to work there with the less elementary relation.
(called, by some authors, the time-dependent Dyson equation [41,63,64,65,66,67]). The term “Hamiltonian” must then be allocated, interpreted, and used with much more care [68].
In the stationary NSP setting, the idea of the acceptability of the various non-Hermitian forms of quantum Hamiltonians has its origin in Dyson’s paper [5]. The knowledge of a standard stationary self-adjoint Hamiltonian of textbooks (which is, by definition, safely self-adjoint in ) was simply complemented there by a tentative, “trial and error” choice of . Via the isospectrality constraint (3), one was immediately able to define a preconditioned, friendlier stationary representation H of the conventional Hamiltonian. This made the innovative “Dyson’s picture” of QM complete.
The encouraging experience with the mediated simplifications of multiple conventional Schrödinger equations (say, in nuclear physics [6]) inspired Scholtz et al. [7] to invert the paradigm. They assumed that what we are given are just the “tractable” time-independent operators of the observables (including, first of all, the Hamiltonian H) which are non-Hermitian but which possess the real spectra. The core of the idea (i.e., of the “quasi-Hermitian” reformulation of quantum mechanics called non-Hermitian Schrödinger picture (NSP)) was that once we recall the respective quasi-Hermiticity constraints (cf., e.g., Equation (4) or (18) above), we may reconstruct (not always uniquely) and factorize (also not always uniquely) the correct physical Hilbert-space metric “if it exists” (cf. p. 74 in [7]). The resulting “quasi-Hermitian-input” version of the NSP formalism is then again a consistent theory.
The authors of the paper [7] were well aware of the main weaknesses of their NSP recipe. They identified them as lying, in the sufficiently realistic models, not only in the ambiguity of the assignment of to a given Hamiltonian H but also in the technically rather complicated nature of an explicit construction of any such a metric (cf. also a few related comments in [18]). Fortunately, a way out of the dead end has been found by Bender and coauthors [3,11] who proposed to narrow the class of the eligible non-Hermitian stationary Hamiltonians H. The more user-friendly subfamily of the Hamiltonians was required to be -symmetric, i.e., such that . Originally, the symbol denoted here just the operator of parity while the antilinear operator mediated the time reversal. Later, it became clear that after a suitable generalization of these concepts, the physics-motivated property of the -symmetry of H can be also perceived as mathematically equivalent to the self-adjointness of H with respect to a suitable pseudo-metric, i.e., as the self-adjointness of H in Krein space [69,70].
The success of the -symmetric models was enormous [11]. Paradoxically, it also appeared to have two not entirely pleasant consequences. The first one was that around the year 2007, mainstream research left the rather narrow area of quantum physics. Beyond this area (i.e., typically in classical optics), the idea of -symmetry found a large number of new and exciting applications (for reviews, see [71] or the recent monographs [72,73]). The second paradox connected with the deep appeal of the idea of the -symmetry of H can be seen in the above-mentioned narrowing of the scope and perspective. In the words written on p. 1198 of the review [18], “the adopted terminology is rather unfortunate” because the “-symmetric QM is an example of a more general class of theories …in which -symmetry does not play a basic role”.
As another unwanted consequence of the reduction of the scope of the -symmetric version of the theory there emerged (and, for a long time, survived) several “no-go” theorems (sampled, e.g., by Theorem Nr. 2 in [18]) that claimed the impossibility of a sufficiently satisfactory non-stationary extension of the quasi-Hermitian quantum mechanics. It took several years before the correct and consistent non-stationary extension of the quasi-Hermitian quantum mechanics as described in [25,26] has finally been accepted as correct (cf., e.g., [74]). The process of acceptance was also slowed down by certain purely terminological misunderstandings (cf., e.g., their brief account in [23]). At present, fortunately, the situation seems clarified. Different groups of authors (using still very different notation conventions, cf., e.g., papers [42] or [75]) accepted, ultimately, the same (or at least practically the same) interpretation of the non-stationary NIP theory.
The related developments enriched the field with a number of new and highly relevant applications. Virtually all of them can be characterized by the role played by the time-dependent Dyson Equation (29) (cf., e.g., section Nr. 5 in [43]). The build-up of the theory may then start either from the knowledge of (so that one can speak about a “dynamical-information” (DI) input), or from the knowledge of (one then relies upon a purely kinematical or “Coriolis-force” (CF) input information), or, finally, from (let us call this option a “Schrödinger-generator” (SG) input knowledge).
In all of these alternative approaches, their users decided to call their preferred preselected component of Equation (29) “the Hamiltonian”. In fact, the above-cited words that “the adopted terminology is rather unfortunate” applied again. The main reason is that even in the unitary evolution dynamical regime, the spectra of and/or of need not be real or even complex conjugate in general [39,40,68]. In this sense, calling the generator a Hamiltonian (which was, originally, the proposal by one of my PhD students [76,77]) is far from optimal because only the spectrum of the observable-energy component of can consistently be assumed real.
On these grounds, the most natural implementation of the NIP approach seems to be provided by its DI model-building realization. In our recent paper [43], such a conjecture has been tested using the exactly solvable wrong-sign-oscillator model of Fring and Tenney [30]. We came to a not quite expected conclusion, that for the model in question, by far the most convenient and efficient construction strategy appeared to be the innocent-looking “kinematical” CF approach.
This observation can be perceived as one of the sources of inspiration of our present paper. It forced us to reconsider the theory and to re-read one of the oldest studies in the field, viz., paper [7], in which the authors always kept in mind the need to work with a complete set of observables rather than just with a Hamiltonian. We imagined that precisely this idea also offers the “missing source” of a deeper understanding of the non-stationary NIP theory.
The return to the roots helped us resolve at least some of the paradoxes. For example, once one starts thinking about unitary systems characterized by more than one observable [7,24], the build-up of the theory starting from the mere single operator appears to be conceptually less satisfactory. During the build-up of a more satisfactory theory one must keep in mind both the dynamics (i.e., the influence of upon the states as mediated by Schrödinger equation(s)) and the kinematics (due to the fact that only appears in Schrödinger equation(s) in combination with the Coriolis force).
In our present paper, we managed to show that the initial choice of a “non-dynamical” observable (i.e., in our present notation, of ) simplifies the construction significantly. This is, after all, our main methodical message. We saw that our innovative strategy does not only simplify, decisively, the “introductory-step” reconstruction of the kinematics (i.e., of the metric as well as of the Dyson map and of from ), but that it also leaves an entirely unrestricted space for the subsequent choice of the “dynamics”, i.e., for an independent specification of the instantaneous energy , etc.
We may only add that our other, serendipitous, physicists-addressing message is that the independence of the initial choice of the non-dynamical observable might very well serve the purpose of the extension of the applicability of the unitary NIP quantum theory to the “exotic”, exceptional-point-related dynamical regimes. This is sampled in our schematic cosmological toy model by the demonstration of the possibility of an internal consistence of the hypothetical point-like Big Bang singularity even after quantization.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Styer, D.F.; Balkin, M.S.; Becker, K.M.; Burns, M.R.; Dudley, C.E.; Forth, S.T.; Gaumer, J.S.; Kramer, M.A.; Oertel, D.C.; Park, L.H.; et al. Nine formulations of quantum mechanics. Am. J. Phys. 2002, 70, 288–297. [Google Scholar] [CrossRef]
- Messiah, A. Quantum Mechanics; North Holland: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- Stone, M.H. On one-parameter unitary groups in Hilbert Space. Ann. Math. 1932, 33, 643–648. [Google Scholar] [CrossRef]
- Dyson, F.J. General theory of spin-wave interactions. Phys. Rev. 1956, 102, 1217–1230. [Google Scholar] [CrossRef]
- Janssen, D.; Dönau, F.; Frauendorf, S.; Jolos, R.V. Boson description of collective states. Nucl. Phys. A 1971, 172, 145–165. [Google Scholar] [CrossRef]
- Scholtz, F.G.; Geyer, H.B.; Hahne, F.J.W. Quasi-Hermitian Operators in Quantum Mechanics and the Variational Principle. Ann. Phys. 1992, 213, 74–101. [Google Scholar] [CrossRef]
- Bishop, R.F.; Znojil, M. Non-Hermitian coupled cluster method for non-stationary systems and its interaction-picture reinterpretation. Eur. Phys. J. Plus 2020, 135, 374. [Google Scholar] [CrossRef]
- Dieudonne, J. Quasi-Hermitian Operators. In Proc. Int. Symp. Lin. Spaces; Pergamon: Oxford, UK, 1961; pp. 115–122. [Google Scholar]
- Bender, C.M.; Milton, K.A. Nonperturbative calculation of symmetry breaking in quantum field theory. Phys. Rev. 1997, D55, 3255–3259. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1118. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Hilbert Space Structures on the Solution Space of Klein-Gordon Type Evolution Equations. Class. Quantum Grav. 2003, 20, 155–171. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Quantum mechanics of Klein-Gordon-type fields and quantum cosmology. Ann. Phys. 2004, 309, 1–48. [Google Scholar] [CrossRef]
- Znojil, M. Relativistic supersymmetric quantum mechanics based on Klein-Gordon equation. J. Phys. A Math. Gen. 2004, 37, 9557–9571. [Google Scholar] [CrossRef]
- Mostafazadeh, A.; Zamani, F. Quantum Mechanics of Klein-Gordon fields I: Hilbert space, localized states, and chiral symmetry. Ann. Phys. 2006, 321, 2183–2209. [Google Scholar] [CrossRef]
- Jakubský, V.; Smejkal, J. A positive-definite scalar product for free Proca particle. Czech. J. Phys. 2006, 56, 985. [Google Scholar] [CrossRef]
- Zamani, F.; Mostafazadeh, A. Quantum Mechanics of Proca fields. J. Math. Phys. 2009, 50, 052302. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermitian Representation of Quantum Mechanics. Int. J. Geom. Meth. Mod. Phys. 2010, 7, 1191–1306. [Google Scholar] [CrossRef]
- Wheeler, J.A. Battelle Rencontres; DeWitt, C.M., Wheeler, J.A., Eds.; Bejamin: New York, NY, USA, 1968. [Google Scholar]
- DeWitt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Thiemann, T. Introduction to Modern Canonical Quantum General Relativity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Znojil, M. Non-Hermitian interaction representation and its use in relativistic quantum mechanics. Ann. Phys. 2017, 385, 162–179. [Google Scholar] [CrossRef]
- Znojil, M.; Semorádová, I.; Rŭžička, F.; Moulla, H.; Leghrib, I. Problem of the coexistence of several non-Hermitian observables in PT-symmetric quantum mechanics. Phys. Rev. 2017, A 95, 042122. [Google Scholar] [CrossRef]
- Znojil, M. Time-dependent version of cryptohermitian quantum theory. Phys. Rev. 2008, D78, 085003. [Google Scholar]
- Znojil, M. Three-Hilbert-space formulation of Quantum Mechanics. Symm. Integ. Geom. Meth. Appl. SIGMA 2009, 5, 001. [Google Scholar] [CrossRef]
- Fring, A.; Frith, T. Exact analytical solutions for time-dependent Hermitian Hamiltonian systems from static unobservable non-Hermitian Hamiltonians. Phys. Rev. 2017, A 95, 010102(R). [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Available online: https://en.wikipedia.org/wiki/Lambda-CDM_model (accessed on 1 March 2023).
- Fring, A.; Tenney, R. Spectrally equivalent time-dependent double wells and unstable anharmonic oscillators. Phys. Lett. A 2020, 384, 126530. [Google Scholar] [CrossRef]
- Rotter, I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A Math. Theor. 2009, 42, 153001. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Feshbach, H. Unified theory of nuclear reactions. Ann. Phys. 1958, 5, 357–390. [Google Scholar] [CrossRef]
- Feshbach, H. A unified theory of nuclear reactions II. Ann. Phys. 1962, 19, 287–313. [Google Scholar] [CrossRef]
- Jones, H.F. Scattering from localized non-Hermitian potentials. Phys. Rev. 2007, D76, 125003. [Google Scholar] [CrossRef]
- Jones, H.F. Interface between Hermitian and non-Hermitian Hamiltonians in a model calculation. Phys. Rev. 2008, D 78, 065032. [Google Scholar] [CrossRef]
- Stassi, R.; De Liberato, S.; Garziano, L.; Spagnolo, B. Quantum control and long-range quantum correlations in dynamical Casimir arrays. Phys. Rev. 2015, A 92, 013830. [Google Scholar] [CrossRef]
- Valenti, D.; Carollo, A.; Spagnolo, B. Stabilizing effect of driving and dissipation on quantum metastable states. Phys. Rev. A 2018, 97, 042109. [Google Scholar] [CrossRef]
- Znojil, M. Hybrid form of quantum theory with non-Hermitian Hamiltonians. Phys. Lett. A 2023, 457, 128556. [Google Scholar] [CrossRef]
- Znojil, M. Systematics of quasi-Hermitian representations of non-Hermiitan quantum models. Ann. Phys. 2023, 448, 169198. [Google Scholar] [CrossRef]
- Fring, A.; Frith, T. Eternal life of entropy in non-Hermitian quantum systems. Phys. Rev. 2019, A 100, 010102(R). [Google Scholar] [CrossRef]
- Fring, A.; Taira, T.; Tenney, R. Real energies and Berry phases in all PT regimes in time-dependent non-Hermitian theories. J. Phys. A Math. Theor. 2023, 56, 12LT01. [Google Scholar] [CrossRef]
- Znojil, M. Non-stationary non-Hermitian “wrong-sign” quantum oscillators and their meaningful physical interpretation. Entropy 2023, 25, 692. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Bergmann, P.G.; Lebowitz, J.L. Time Symmetry in the Quantum Process of Measurement. Phys. Rev. 1964, 134, B1410–B1416. [Google Scholar] [CrossRef]
- Aharonov, Y.; Vaidman, L. The Two-State Vector Formalism: An Updated Review. Available online: https://arxiv.org/pdf/quant-ph/0105101.pdf (accessed on 1 March 2023).
- Brody, D.C.; Hughston, L.P. Quantum measurement of space-time events. J. Phys. A Math. Theor. 2021, 54, 235304. [Google Scholar] [CrossRef]
- Hilgevoord, J. Time in quantum mechanics. Am. J. Phys. 2002, 70, 301–306. [Google Scholar] [CrossRef]
- Mukhanov, V.; Feldman, H.;; Brandenberger, R. Theory of Cosmological Perturbations. Phys. Rep. 1992, 215, 203–233. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Znojil, M. On the role of the normalization factors κn and of the pseudo-metric P in crypto-Hermitian quantum models. arXiv 2008, arXiv:0710.4432. [Google Scholar] [CrossRef]
- Znojil, M. Quantum catastrophes II. Generic pattern of the fall into instability. arXiv 2023, arXiv:1212.0734v1. [Google Scholar]
- Carollo, A.; Valenti, D.; Spagnolo, B. Geometry of quantum phase transitions. Phys. Rep. 2020, 838, 1–72. [Google Scholar] [CrossRef]
- Znojil, M. A return to observability near exceptional points in a schematic PT-symmetric model. Phys. Lett. 2007, B 647, 225–230. [Google Scholar] [CrossRef]
- Znojil, M. Passage through exceptional point: Case study. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190831. [Google Scholar] [CrossRef]
- Brody, D.C. Biorthogonal quantum mechanics. J. Phys. A Math. Theor. 2013, 47, 035305. [Google Scholar] [CrossRef]
- Bagarello, F.; Gazeau, J.-P.; Szafraniec, F.; Znojil, M. (Eds.) Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Brody, D.C.; Hughston, L.P. Geometric quantum mechanics. J. Geom. Phys. 2001, 38, 19–53. [Google Scholar] [CrossRef]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A status report. Class. Quantum Grav. 2004, 21, R53–R152. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of a singularity in loop quantum cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef]
- Malkiewicz, P.; Piechocki, W. Turning Big Bang into Big Bounce: II. Quantum dynamics. Class. Quant. Gravity 2010, 27, 225018. [Google Scholar] [CrossRef]
- Wang, C.; Stankiewicz, M. Quantization of time and the big bang via scale-invariant loop gravity. Phys. Lett. B 2020, 800, 135106. [Google Scholar] [CrossRef]
- Bagarello, F.; Fring, A. A non selfadjoint model on a two dimensional noncommutative space with unbound metric. Phys. Rev. 2013, A88, 042119. [Google Scholar] [CrossRef]
- Figueira de Morisson Faria, C.; Fring, A. Time evolution of non-Hermitian Hamiltonian systems. J. Phys. A Math. Gen. 2006, 39, 9269–9289. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Time-dependent pseudo-Hermitian Hamiltonians defining a unitary quantum system and uniqueness of the metric operator. Phys. Lett. B 2007, 650, 208–212. [Google Scholar] [CrossRef]
- Gong, J.-B.; Wang, Q.-H. Geometric Phase in PT-Symmetric Quantum Mechanics. Phys. Rev. 2010, A 82, 012103. [Google Scholar] [CrossRef]
- Gong, J.-B.; Wang, Q.-H. Time-dependent PT-symmetric quantum mechanics. J. Phys. A Math. Theor. 2013, 46, 485302. [Google Scholar] [CrossRef]
- Luiz, F.S.; Pontes, M.A.; Moussa, M.H.Y. Unitarity of the time-evolution and observability of non-Hermitian Hamiltonians for time-dependent Dyson maps. Phys. Scr. 2020, 95, 065211. [Google Scholar] [CrossRef]
- Znojil, M. Composite quantum Coriolis forces. Mathematics 2023, 11, 1375. [Google Scholar] [CrossRef]
- Langer, H.; Tretter, C. A Krein space approach to PT symmetry. Czech. J. Phys. 2004, 54, 1113–1120. [Google Scholar] [CrossRef]
- Albeverio, S.; Kuzhel, S. PT-symmetric operators in quantum mechanics: Krein spaces methods. In Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Bagarello, F., Gazeau, J.-P., Szafraniec, F., Znojil, M., Eds.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Berry, M.V. Physics of nonhermitian degeneracies. Czech. J. Phys. 2004, 54, 1039–1047. [Google Scholar] [CrossRef]
- Christodoulides, D.; Yang, J.-K. (Eds.) Parity-Time Symmetry and Its Applications; Springer: Singapore, 2018. [Google Scholar]
- Bender, C.M. PT Symmetry in Quantum and Classical Physics; World Scientific: Singapore, 2018. [Google Scholar]
- Fring, A.; Moussa, M.H.Y. Unitary quantum evolution for time-dependent quasi-Hermitian systems with non-observable Hamiltonians. Phys. Rev. 2016, A 93, 042114. [Google Scholar] [CrossRef]
- Ju, C.-Y.; Miranowicz, A.; Minganti, F.; Chan, C.-T.; Chen, G.-Y.; Nori, F. Einstein’s Quantum Elevator: Hermitization of Non-Hermitian Hamiltonians via a generalized vielbein Formalism. Phys. Rev. Res. 2022, 4, 023070. [Google Scholar] [CrossRef]
- Bíla, H. Adiabatic time-dependent metrics in PT-symmetric quantum theories. arXiv 2009, arXiv:0902.0474. [Google Scholar]
- Bíla, H. Pseudo-Hermitian Hamiltonians in Quantum Physics. Ph.D. Thesis, Czech Technical University, Prague, Czech Republic, 2009. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).