Abstract
In this study, a modified anisotropic elastic Weiskopf model for a sandy medium was introduced, satisfying the highest rotational symmetry compatible with a Weiskopf sandiness parameter greater than the unity. The developed approach was applied for computing and comparing head SP waves propagating along the free surface of the halfspace. The comparison revealed a substantial discrepancy in the SP wave pulses detected at the points of observation. The developed models for the generation and detection of SP waves are based on the FEA (finite element analysis) of the inner Lamb problem.
MSC:
74J15
1. Introduction
1.1. Weiskopf Sandy Model
The constitutive equation for modeling sandy materials was proposed by Weiskopf (1945) [1]. The model reflects an experimental observation [2,3,4,5,6,7] that sandy materials, or more generally, granular materials, exhibit a ratio between Young’s and shear moduli larger than that predicted by Hook’s law:
where and are Young’s and shear moduli, respectively, is a parameter, known as the “soil constant” [8], and is Poisson’s ratio.
Another useful representation for Equation (1), found by Weiskopf, is as follows:
where is a parameter known as “sandiness”; at , the sandy medium becomes elastic and isotropic. Equation (1) and its natural generalization is discussed in more detail in the next section.
The concept of constitutive Equation (1) proposed in [1] was applied to analyze (i) the soil pressure on retaining walls [5,6,9]; (ii) the propagation of the horizontally polarized SH and Love waves in a medium containing a sandy layer [10,11,12,13,14]; (iii) the propagation of the polarized, in the vertical (sagittal) plane, Rayleigh and Lamb waves [15,16,17]; and (iv) the propagation of the edge waves [18].
1.2. Head SP Waves
Head SP waves, discovered by Jeffreys (1926), play an important role in transmitting wave energy in the close vicinity of the epicentral zone of an earthquake or undersurface blast loading [8,19,20,21]. SP waves are also the subject of extensive studies on the acoustics of layered composites [22,23]. In this respect, also see applications of energy dissipation for SP head waves along with Rayleigh, Rayleigh–Lamb, and other types of SAWs [24,25,26,27,28].
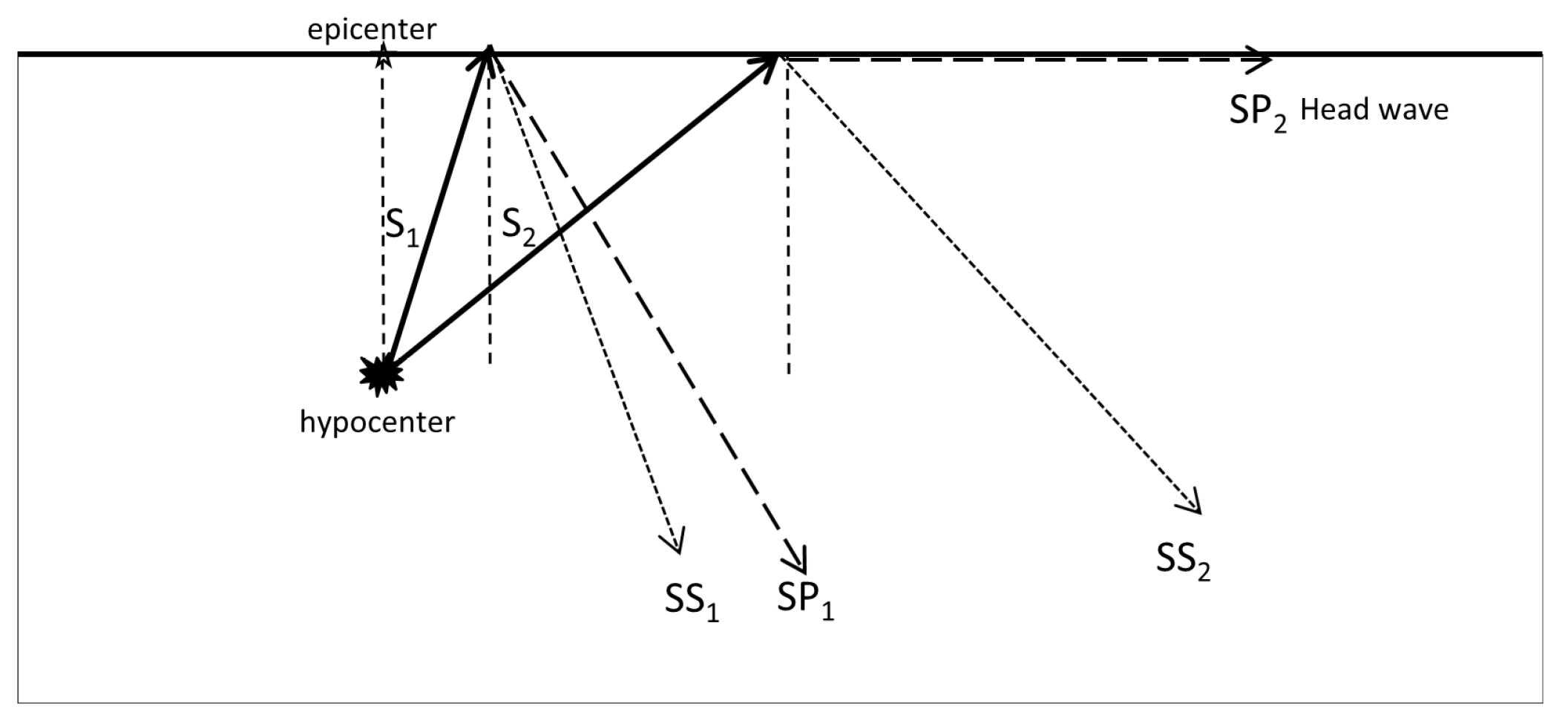
The considered head SP waves (bulk S wave being converted into P wave at the free surface) propagating along a free surface of a substrate arise at the reflection of bulk S waves from the free surface of a substrate at the critical angle. Figure 1 displays the application of Snell’s law for the incident and reflected waves.
where the upper indices and refer to the incident and reflected waves, correspondingly, ; is the angle of the reflected P wave; and and are the corresponding velocities, and ; herein, and are Lame constants, and is the material density. It is assumed that and , which ensures positive definiteness of the elasticity tensor [19,24].
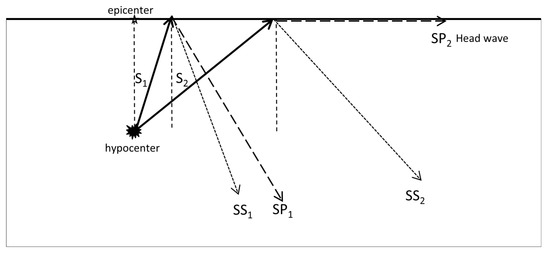
Figure 1.
A scheme for the head SP wave origination: S1 wave propagates at the subcritical angle, giving rise to the reflected SS1 and SP1 waves; S2 wave propagates at the critical angle, giving rise to the reflected SS2 wave and SP2 head wave.
Assuming yields the critical angle of incidence for the S wave:
At the angle , the incident S wave gives rise to the P wave that travels along the free surface; such a wave is known as the SP head wave [19,20].
By applying ray methods [29,30], the critical distance from the epicenter, where the SP head wave starts to propagate, was found:
where is the depth of the buried pulse.
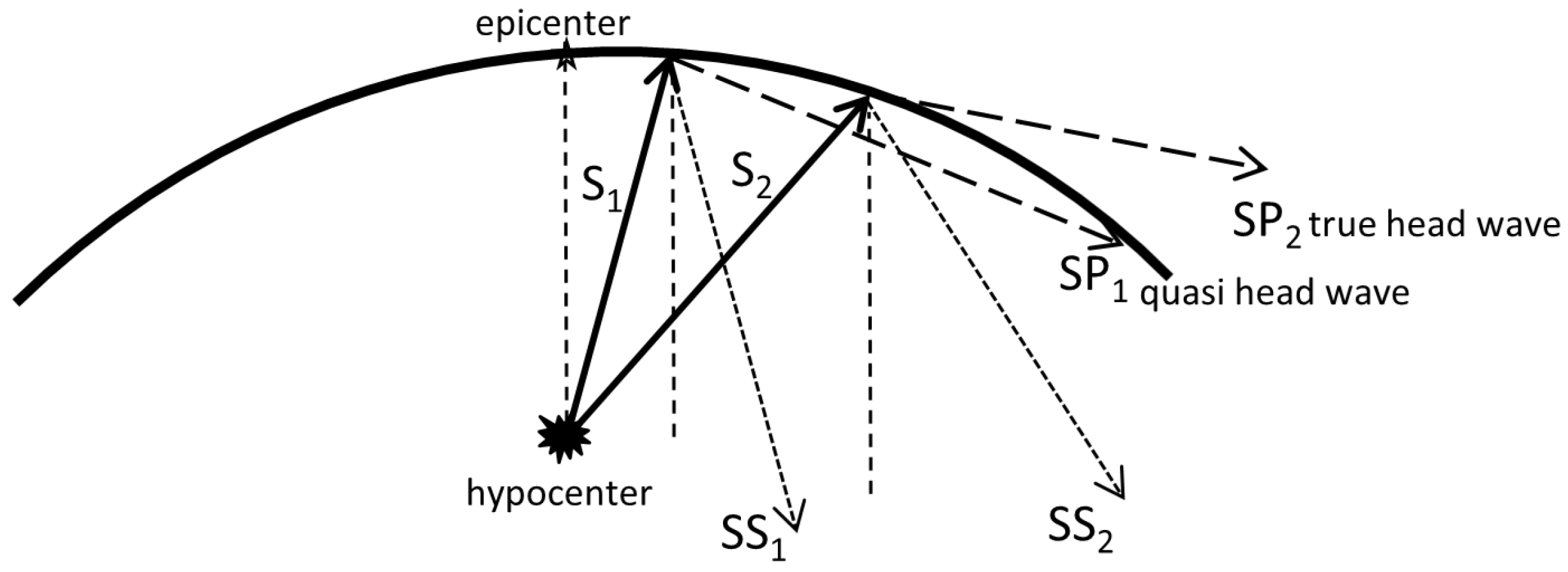
The principal scheme, in a case accounting for the Earth’s curvature, requires a modification; see Figure 2.
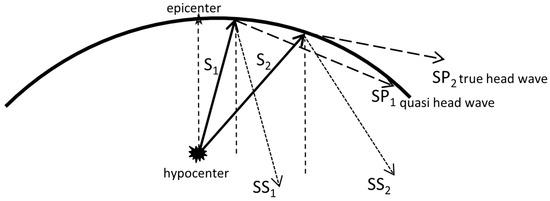
Figure 2.
A scheme for the head and quasi head SP wave origination at a curved surface: S1 wave propagates at the subcritical angle, giving rise to the reflected SS1 wave and SP1 quasi head waves; S2 wave propagates at the critical angle, giving rise to the reflected SS2 wave and SP2 true head wave.
Thus, in order to account for the Earth’s curvature, we require angles of the S wave incident that are slightly smaller than the critical angle defined by Equation (4). Some other problems related to finding the dynamic displacement field from the buried pulse loading are analyzed in [31,32,33,34]. While the curvature effects are important in geophysical large-scale models, the current research is confined by a simpler model with a plain boundary.
It should be noted that head waves have been intensively studied in quite a large number of works [19,20] related to seismic wave analyses of nearby earthquakes, geophysical prospecting, and explosion seismology over the past 100 years or so. In seismic exploration, it is customary to call the SP waves the refracted or refractive waves, and the method based on them is called the refractive method [20]. In this respect, Mohorovicic (1910) appears to have been the first to use head waves in earthquake records to infer the layering of the continental Earth’s crust. While his analysis was based on geometrical optic considerations, thus limiting to high frequency waves, it was later revealed [19,20] that his analysis remains valid in waves of an arbitrary frequency.
And the final remark concerns the validity of the ray methods, which are mainly used in the discussed works [19,20,22]. It is assumed that (i) the velocity gradients are much smaller than the circular frequency, which is not the case in most real situations; (ii) the radii of the curvature of the interfaces are significantly greater than the wavelength, which is applicable to the nearby regions to the epicenter; and (iii) there is no possibility to derive an exact formula relating the frequency and degree of accuracy of the results for a given number of members of the ray series [19,20,22]. Actually, the accuracy of ray formulas depends not only on the parameters of the media but also on the direction of the ray and other conditions. These shortcomings eminent to the ray method will be overcome in the next sections, where the FE method is applied to constructing the solutions for the analysis of SP wave arrivals at the points of observation located on a free surface.
1.3. Current Research
Herein, presumably for the first time, a comparative analysis of propagating true SP head waves in isotropic and sandy media is performed with FE (finite element) modeling coupled with constructing analytical expressions for the (apparent) velocities of head waves. The applied FE models utilize solutions to the inner Lamb problem of the buried pulse, allowing for the generation of desired SP head waves along with P and S bulk and Rayleigh waves. In this respect, please see [35,36,37,38].
The analysis reveals a substantial discrepancy in both velocities of the propagating bulk and head waves along with magnitudes of the SP head waves, indicating (i) a slower apparent SP head wave velocity in sandy media than in the equivalent isotropic one; (ii) decreasing velocity values with an increasing sandiness parameter value; (iii) an increasing critical distance with the increase in the sandiness parameter value; and (iv) an increase in the SP head wave magnitudes compared with the magnitudes of the same waves in the equivalent isotropic medium. The latter fact is of special importance in estimating SP wave magnitudes in the vicinity of the epicenters of shallow earthquakes and undersurface blast loadings.
Thus, the current research targeting the analysis of bulk and SP wave arrivals at a free surface of a Weiskopf halfspace under the action of an impulse delta-like force load, which is applied in the interior of the halfspace, becomes, apparently, the first study of such a problem. It should be emphasized that this research differs from a number of previous studies related to the analysis of the so-called inner Lamb problem of a point force load inside a homogeneous isotropic halfspace [36], and studies of surface acoustic wave propagation in layered media, including ones containing Weiskopf layers [39]. Another remark concerns the performed analysis of the displacement fields in two principally different Weiskopf media, differing by the Weiskopf parameter, and the latter specifies the so-called “sandiness” [1] and is of special importance in geophysics [5]. Again, as the literature review shows, the current research is presumably the first study related to the analysis of head waves appearing in Weiskopf media.
2. The Modified Weiskopf Model
The original Weiskopf theory [1] was applied to solve static problems for a sandy halfspace, satisfying the equations of state Equation (1). Considering these equations in the framework of anisotropic elasticity reveals that the Weiskopf medium is eventually an anisotropic one characterized by three independent elastic constants: . Such a three-constant medium possesses cubic symmetry with the elasticity tensor in the principal crystallographic axes, written as [40]
Following [40], only the upper triangular part is shown in the expressions of Equation (6).
Introducing three other material parameters,
yields
where relations in Equation (8) follow from the positive definite condition imposed on elasticity tensor Equation (6). Indeed, the positive definite condition for the elasticity tensor corresponding to an arbitrary elastic anisotropy reads as
where is an arbitrary non-vanishing second-order tensor, and stands for the fourth-order elasticity tensor, which is symmetric with respect to its outer pairs of indices. Note also that the positive definite condition implies the strong ellipticity condition of the elasticity tensor; however, the reverse implication is not true.
The latter expressions are convenient in comparing the components of the elasticity tensor for the considered cubic medium with ones for an isotropic medium, for which an additional relation holds:
Now, the Weiskopf soil and sandy constants [1] in Equation (1), written in terms of parameters , and , become
note that for an isotropic medium at , Equation (11) yields and .
Applying Equation (11), the elastic modulus can be expressed in terms of other elastic moduli and the corresponding soil and sandy parameters:
Equation (12) can be used for computing the elastic modulus for the variation in the parameter .
3. Mathematical Model
3.1. Inner Plain Lamb Problem
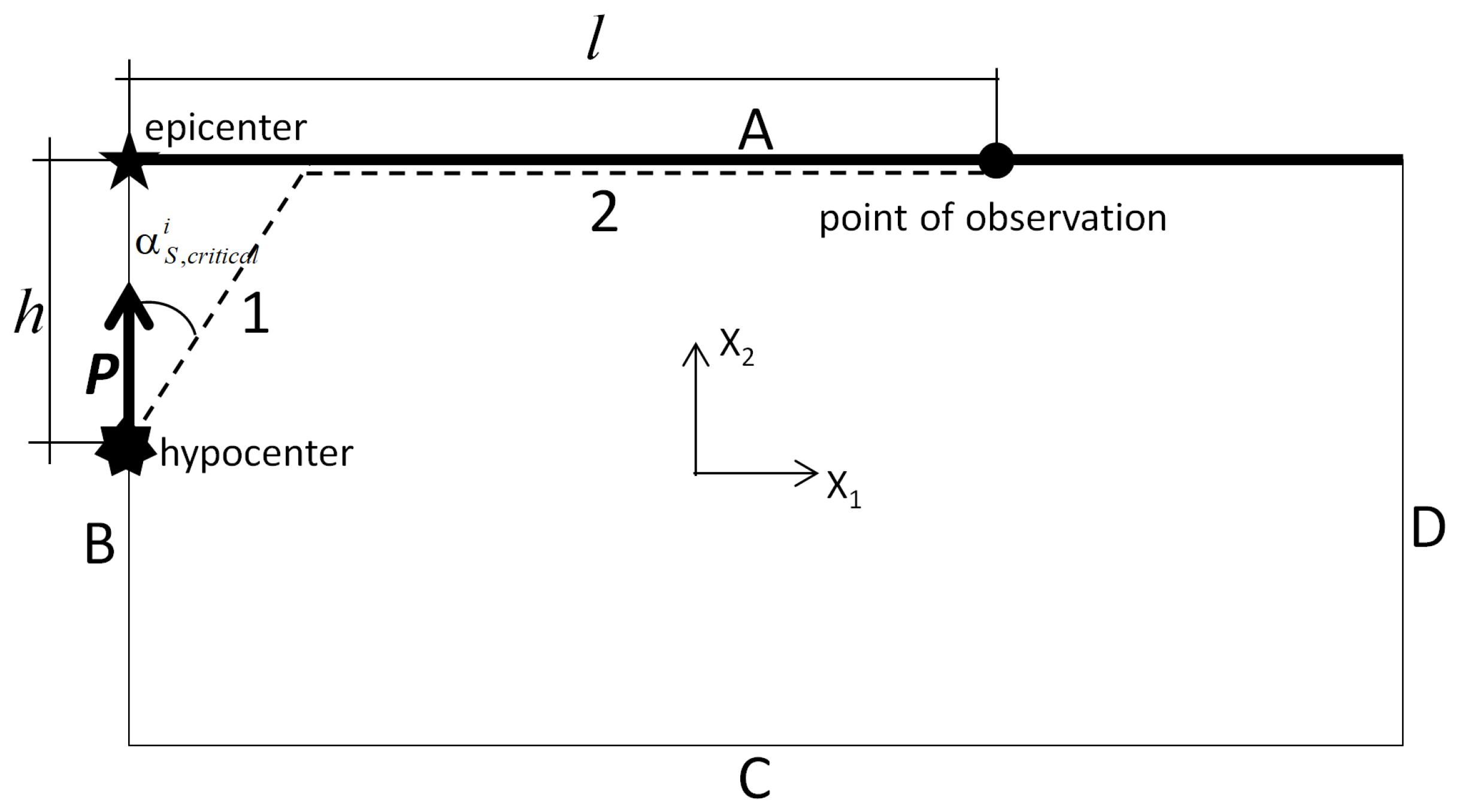
To analyze head SP waves, the plane (strain) inner Lamb problem with a buried vertical pulse load was considered (Figure 3).
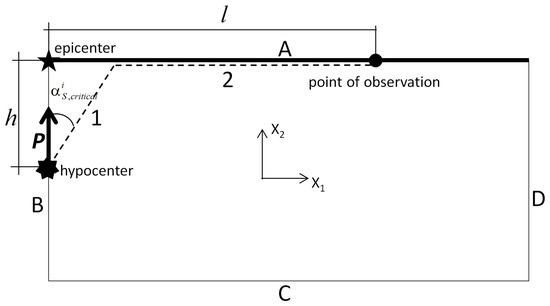
Figure 3.
The plain strain inner Lamb problem for modeling the arrival of SP head waves: the dashed line indicates the pass of the SP wave travelling to a point of observation located on the free surface, h is the depth of the buried pulse, and l is the distance from the epicenter to the point of observation.
According to the theory of head waves, in the first part, the wave traveling past the SP wave travels at the speed of ; in the second part, the wave travels at the speed of . Taking into account the expression in Equation (4) for the critical angle and an easy verified relation,
the arrival time of the SP wave to a point of observation on the free surface becomes
Now, Equation (14) allows us to define the apparent velocity of the SP head wave:
Equation (15) shows that the apparent velocity of the SP head wave depends upon the relative depth of the origin and distance from the epicenter.
3.2. Boundary Conditions
For the FEA (finite element analysis), the following boundary conditions were imposed.
Regarding edge A (Figure 3), the traction free boundary conditions are as follows:
where is the surface traction field and is the normal unit outward to the upper boundary .
Regarding edge B (Figure 3), symmetry boundary conditions are as follows:
where a comma denotes the corresponding partial derivative.
Along edges C and D (Figure 3), the non-reflecting (absorbing) boundary conditions based on the perfectly matched layers (PML) were specified; see [41,42]. The PML ensures efficient absorbing even at oblique angles of incidence [43,44].
3.3. Initial Conditions 22
The initial conditions at were assumed as corresponding to the state of rest:
3.4. Force Loading
The applied force representing the buried delta pulse can be represented as a multiplication of the two delta functions:
where is the force magnitude, is the unit vector directed along the axis (Figure 3), and is the point on edge B where the force was applied.
3.5. Numerical Implementation
As was pointed out earlier, the governing equation of motion is solved by the FE method for spatial discretization and the FD (finite difference) numerical scheme for the time–domain discretization. These were implemented with the explicit Lax–Wendroff energy-preserving numerical scheme [45,46]. To achieve a conditionally stable numerical algorithm, the Courant–Friedrichs–Lewi condition was imposed on the time increment [46].
where stands for the so-called Courant–Friedrichs–Lewi time increment, ensuring the numerical stability condition for the initially conditionally stable numerical scheme; is the minimal linear size of the finite element used; and is the maximal P wave velocity, if multiple materials are considered, or if the considered single material has varied physical properties. Thus, all the numerical computations were (mechanical) energy-preserving and numerically stable, which is extremely important for modeling and analyzing shock wave propagation [47,48]. It should also be noted that the hourglass control was used for increasing element stiffness and avoiding the appearance of non-physical self-balanced stress fields, associated with the hourglass type deformation of the adjacent finite elements [45]. Another remark concerns the use of four-node linear quadrilateral elements with reduced integration, which are reasonably accurate in a FEA related to solving plane problems of non-stationary dynamics [49].
To minimize the non-physical oscillations behind the wave fronts, the time parameter was chosen to satisfy the following empirical condition [36]:
where is the Courant number [50].
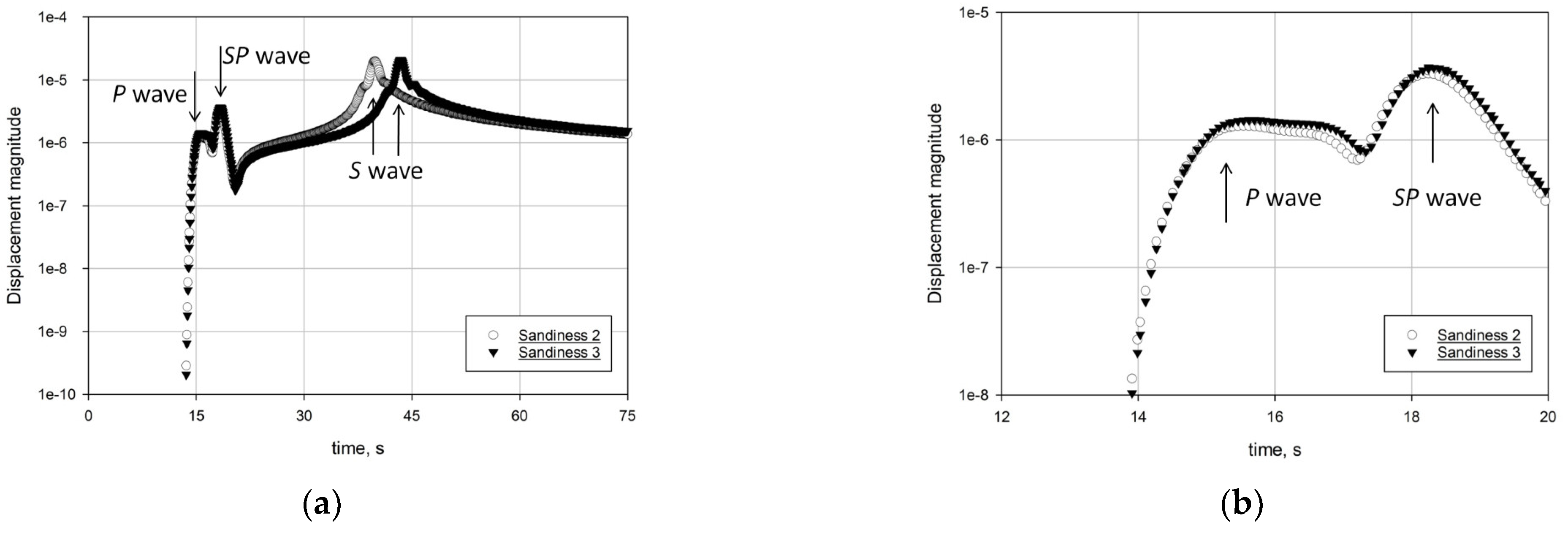
The magnitudes of the displacement fields, which arrived at the free surface, are shown in Figure 4 for a point located from the epicenter at 6h (h is the depth of the buried pulse). The plots characterizing the arrivals of the SP waves at other points of observation are analogous.
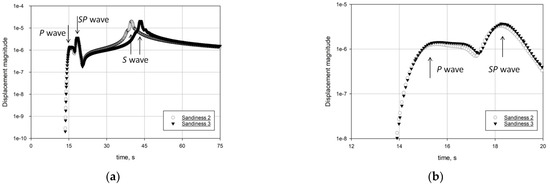
Figure 4.
Displacement magnitudes in a point of observation located at 6h from the epicenter: (a) an overview; (b) in the vicinity of SP wave arrival.
Analyzing the peaks related to the arrival of P and SP waves in both sandy media shows that the peaks arrive at the same time and have almost identical magnitudes. Actually, the velocities of P waves traveling along the horizontal pass are exactly identical, while the velocities of S waves traveling along the inclined pass are substantially different due to a difference in shear moduli; this gives an explanation for the notable difference in the arrival times of the S wave signals. Another remark concerns the apparent lack of dispersion of SP waves in the considered media; see Figure 4. This phenomenon is also discussed in [8,19,20,21].
4. Concluding Remarks
As the presented literature review shows, the problem of bulk wave propagation in a laminated anisotropic halfspace is analyzed apparently for the first time; previous studies are mainly related to the bulk wave propagation in either isotropic halfspaces, e.g., [36], or to the dispersive SAW (surface acoustic waves) in anisotropic layered media [39,51,52,53,54].
The performed analysis reveals the timings and amplitudes of both bulk and SP head waves, which either arrive at the free surface (bulk P and S waves) or travel along the free surface (SP head waves). One of the most important findings is associated with a noticeable discrepancy between the arrival times of the considered waves propagating in the Weiskopf media with different sandiness parameters. Moreover, it is found that the wave amplitudes are also prone to the sandiness parameter value; it is actually observed that in a vicinity of the SP wave arrivals, the wave amplitudes differ enough to distinguish one type of the Weiskopf material from another.
Another remark concerns the adopted FE modeling techniques, which are based on the explicit Lax–Wendroff energy-preserving numerical scheme [45,46]. To achieve a conditionally stable numerical algorithm, the Courant–Friedrichs–Lewi condition was imposed on the time increments. Thus, all the numerical computations were (mechanical) energy-preserving and numerically stable, which is extremely important for modeling and analyzing shock wave propagation [47,48].
In works on the analysis of head waves [55,56,57], Snell’s law is quite often used to obtain the so-called critical angle, which is necessary for the appearance of SP head waves. In this respect, it was found by both theoretical and experimental studies that Snell’s law is valid for not only geometrical optic approximations, when the elastic wavelength is (infinitely) small compared with the distances from the interface [58], but this law remains applicable in cases of low frequencies, when the wavelength becomes sufficiently large [19]. Also note that the spectral decomposition of the considered impact loadings produces a broad range of circular frequencies [7,35]; however, due to the previous results, Snell’s law remains valid for impact pulses.
And, finally, SP head waves arise in quite a large number of problems related to solid-state acoustics. For example, in the course of deep Earth exploration, these waves are observed at the seismic wave propagation in the geophysical formations [59,60,61,62,63,64,65,66,67,68,69], enabling the identification of both the Earth’s crust and mantle fine structure [66,68]. On a smaller scale, SP waves propagating along the free Earth’s surface are generated by shallow earthquakes and undersurface explosions [36,70,71,72,73,74,75]. These waves play an important role in the identification of underground or surface explosions from shallow earthquakes with the corresponding seismograms [36]; even very shallow earthquakes with focuses lying at a depth of several kilometers produce prominent SP waves, while explosions, especially near surface ones, produce no SP waves in seismograms [20,36]. SP head waves are also observed at smaller scales, when different (technogenic) underground vibrating sources produce SP waves [76,77,78].
Author Contributions
Conceptualization, A.K. and S.K.; methodology, A.K.; software, S.K.; validation, A.K. and S.K.; formal analysis, A.K.; investigation, S.K.; resources, A.K.; data curation, A.K.; writing—original draft preparation, S.K.; writing—review and editing, A.K.; visualization, A.K.; supervision, A.K.; project administration, S.K.; funding acquisition, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education RF, grant number FSWG-2023-0004.
Data Availability Statement
No data was used for the current research.
Acknowledgments
This research was supported by the Ministry of Science and Higher Education of the Russian Federation (project no. FSWG-2023-0004, «A system of territorial seismic protection of critical infrastructure facilities based on granular metamaterials with the properties of wide-range phonon crystals».
Conflicts of Interest
The authors declare no conflict of interest.
References
- Weiskopf, W.H. Stresses in soils under a foundation. J. Franklin Inst. 1945, 239, 445–465. [Google Scholar] [CrossRef]
- Pentis, E.A.; White, L. Underpinning, Its Practice and Applications; Columbia University Press: New York, NY, USA, 1931. [Google Scholar]
- Cernica, J.N. Geotechnical Engineering: Foundation Design; John Wiley & Sons, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Georgiadis, M.; Anagnostopoulos, C. Lateral pressure on sheet pile walls due to strip load. J. Geotech. Geoenviron. Eng. 1998, 124, 95–98. [Google Scholar] [CrossRef]
- Gotoh, K.; Yamanouchi, T. Stress and displacement characteristics of soil mass as Weiskopf’s body due to surface load. Soils Found. 1979, 19, 97–107. (In Japanese) [Google Scholar] [CrossRef]
- Misra, B. Lateral pressures on retaining walls due to loads on surfaces of granular backfills. Soils Found. 1981, 20, 33–44. [Google Scholar] [CrossRef] [PubMed]
- Motta, E. Generalized Coulomb active-earth pressure for distanced surcharge. J. Geotech. Eng. 1994, 120, 1072–1079. [Google Scholar] [CrossRef]
- Tsvankin, I. Properties of evanescent waves in anisotropic media. J. Seism. Explor. 2008, 17, 67–74. [Google Scholar]
- Goldshtein, M.N. Some problems in soil mechanics and foundation engineering today. Soil Mech. Found. Eng. 1971, 8, 86–90. [Google Scholar] [CrossRef]
- Deep, S.; Sharma, V. Love type waves in a dry sandy layer lying over an isotropic elastic halfspace with imperfect interface. J. Phys. Conf. Ser. 2020, 1531, 012069. [Google Scholar] [CrossRef]
- Dey, S.; Gupta, A.K.; Gupta, S. Propagation of torsional surface waves in dry sandy medium under gravity. Math. Mech. Solids 1998, 3, 229–235. [Google Scholar] [CrossRef]
- Gupta, S.; Ahmed, M. On propagation of Love waves in dry sandy medium sandwiched between fiber-reinforced layer and prestressed porous half-space. Earthq. Struct. 2017, 12, 619–628. [Google Scholar]
- Pal, P.C.; Kumar, S.; Mandal, D. Surface wave propagation in sandy layer overlying a liquid saturated porous half-space and lying under a uniform liquid layer. Mech. Adv. Mater. Struct. 2014, 23, 59–65. [Google Scholar] [CrossRef]
- Pandit, D.K.; Kundu, S. Propagation of Love wave in viscoelastic sandy medium lying over pre-stressed orthotropic half-space. Procedia Eng. 2017, 173, 996–1002. [Google Scholar] [CrossRef]
- Dey, S.; Chandra, A. Surface waves in a dry sandy medium under gravity. Acta Geophys. Pol. 1983, 31, 395–404. [Google Scholar]
- Kakar, R.; Kakar, S. Rayleigh wave in an anisotropic heterogeneous crustal layer lying over a gravitational sandy substratum. Geomech. Eng. 2016, 10, 137–154. [Google Scholar] [CrossRef]
- Pal, P.C.; Kumar, S.; Bose, S. Propagation of Rayleigh waves in anisotropic layer overlying a semi-infinite sandy medium. Ain Shams Eng. J. 2015, 6, 621–627. [Google Scholar] [CrossRef]
- Kumar, P.; Chattopadhyay, A.; Singh, A.K. Propagation of edge wave in homogeneous viscoelastic sandy media. In Advances in Structural Vibration. Lecture Notes in Mechanical Engineering; Dutta, S., Inan, E., Dwivedy, S.K., Eds.; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology Theory and Methods; W.H. Freeman & Co.: New York, NY, USA, 1980. [Google Scholar]
- Cerveny, V.; Ravindra, R. Theory of Seismic Head Waves; University of Toronto Press: Toronto, ON, Canada, 1971. [Google Scholar]
- Doruelo, J.; Hilterman, F.; Goloshubin, G. Head Waves as Mechanism for Azimuthal PP AVO Magnitude Anomalies; SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2006; pp. 199–203. [Google Scholar]
- Angelsky, O.V.; Zenkova, C.Y.; Hanson, S.G.; Zheng, J. Extraordinary manifestation of evanescent wave in biomedical application. Front. Phys. 2020, 8, 159. [Google Scholar] [CrossRef]
- Somekh, M.G.; Pechprasarn, S. Surface Plasmon, Surface Wave, and Enhanced Evanescent Wave Microscopy. In Handbook of Photonics for Biomedical Engineering; Ho, A.P., Kim, D., Somekh, M., Eds.; Springer: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Djeran-Maigre, I.; Kuznetsov, S.V. Velocities, dispersion, and energy of SH-waves in anisotropic laminated plates. Acoust. Phys. 2014, 60, 200–207. [Google Scholar] [CrossRef]
- Dudchenko, A.V.; Dias, D.; Kuznetsov, S.V. Vertical wave barriers for vibration reduction. Arch. Appl. Mech. 2021, 91, 257–276. [Google Scholar] [CrossRef]
- Goldshtein, R.V.; Dudchenko, A.V.; Kuznetsov, S.V. The modified Cam-Clay (MCC) model: Cyclic kinematic deviatoric loading. Arch. Appl. Mech. 2016, 86, 2021–2031. [Google Scholar] [CrossRef]
- Goldshtein, R.V.; Kuznetsov, S.V. Long-wave asymptotics of Lamb waves. Mech. Solids 2017, 52, 700–707. [Google Scholar] [CrossRef]
- Ilyashenko, A.V.; Kuznetsov, S.V. Theoretical aspects of applying Lamb waves in nondestructive testing of anisotropic media. Russ. J. Nondestruct. Test. 2017, 53, 243–259. [Google Scholar] [CrossRef]
- Pekeris, C.L. The seismic buried pulse. Proc. Natl. Acad. Sci. USA 1955, 41, 629–639. [Google Scholar] [CrossRef] [PubMed]
- Pekeris, C.L.; Lifson, H. Motion of the surface of a uniform elastic half-space produced by a burried pulse. J. Acoust. Soc. Am. 1957, 29, 1233–1238. [Google Scholar] [CrossRef]
- Garvin, W.W. Exact transient solution of the buried line source problem. Proc. R. Soc. Lond. Ser. A 1956, 234, 528–541. [Google Scholar]
- Kausel, E.; Manolis, G. Wave Motion in Earthquake Engineering; WIT Press: Southampton, UK, 1999. [Google Scholar]
- Kausel, E. Lamb’s problem at its simplest. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 469, 20120462. [Google Scholar] [CrossRef]
- Sánchez-Sesma, F.; Iturrarán-Viveros, U. The classic Garvin’s problem revisited. Bull. Seism. Soc. Am. 2006, 96, 1344–1351. [Google Scholar] [CrossRef]
- Kuznetsov, S.V. Fundamental and singular solutions of Lamé equations for media with arbitrary elastic anisotropy. Q. Appl. Math. 2005, 63, 455–467. [Google Scholar] [CrossRef]
- Kuznetsov, S.V.; Terentjeva, E.O. Planar internal Lamb problem: Waves in the epicentral zone of a vertical power source. Acoust. Phys. 2015, 61, 356–367. [Google Scholar] [CrossRef]
- Moczo, P.; Kristek, J.; Vavrycuk, V.; Archuleta, R.J.; Halada, L. 3D heterogeneous staggered-grid finite-difference modeling of seismic motion with volume harmonic and arithmetic averaging of elastic moduli and densities. Bull. Seism. Soc. Am. 2002, 92, 3042–3066. [Google Scholar] [CrossRef]
- Shuo, M.; Archuleta, R.J.; Liu, P. Hybrid modeling of elastic P-SV wave motion: A combined finite-element and staggered-grid finite-difference approach. Bull. Seism. Soc. Am. 2004, 94, 1557–1563. [Google Scholar]
- Kuznetsov, S.V. Detection of a hidden sandy layer in a stratified substrate by dispersion analysis. In Mechanics of High-Contrast Elastic Solids; Contributions from Euromech Colloquium 626; Springer International Publishing: Cham, Switzerland, 2023; pp. 119–132. [Google Scholar]
- Gurtin, M.E. The Linear Theory of Elasticity. In Linear Theories of Elasticity and Thermoelasticity; Truesdell, C., Ed.; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Li, S.; Brun, M.; Djeran-Maigre, I.; Kuznetsov, S. Explicit/implicit multi-time step co-simulation in unbounded medium with Rayleigh damping and application for wave barrier. Eur. J. Environ. Civ. Eng. 2018, 24, 2400–2421. [Google Scholar] [CrossRef]
- Li, S.; Brun, M.; Djeran-Maigre, I.; Kuznetsov, S. Hybrid asynchronous absorbing layers based on Kosloff damping for seismic wave propagation in unbounded domains. Comp. Geotech. 2019, 109, 69–81. [Google Scholar] [CrossRef]
- Fathi, A.; Poursartip, B.; Kallivokas, L. Time-domain hybrid formulations for wave simulations in three-dimensional PML-truncated heterogeneous media. Int. J. Numer. Meth. Eng. 2015, 101, 165–198. [Google Scholar] [CrossRef]
- Pettit, J.; Walker, A.; Cawley, P.; Lowe, M. A stiffness reduction method for efficient absorption of waves at boundaries for use in commercial finite element codes. Ultrasonics 2014, 54, 1868–1879. [Google Scholar] [CrossRef] [PubMed]
- Lax, P.D. Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves; SIAM: Philadelphia, PL, USA, 1972. [Google Scholar]
- Lax, P.D.; Wendroff, B. Difference schemes for hyperbolic equations with high order of accuracy. Commun. Pure Appl. Math. 1964, 17, 381–398. [Google Scholar] [CrossRef]
- Winnicki, I.; Jasinski, J.; Pietrek, S. New approach to the Lax-Wendroff modified differential equation for linear and nonlinear advection. Numer. Methods Partial. Differ. Equ. 2019, 35, 2275–2304. [Google Scholar] [CrossRef]
- Zubeldia, M. Energy concentration and explicit Sommerfeld radiation condition for the electromagnetic Helmholtz equation. J. Funct. Anal. 2012, 263, 2832–2862. [Google Scholar] [CrossRef]
- Rathod, H.D. Some analytical integration formulae for a four node isoparametric element. Comput. Struct. 1988, 30, 1101–1109. [Google Scholar] [CrossRef]
- Finlayson, B.A. Numerical Methods for Problems with Moving Fronts; Ravenna Park Pub: Seattle, WT, USA, 1992. [Google Scholar]
- Craster, R.V.; Joseph, L.M.; Kaplunov, J. Long-wave asymptotic theories: The connection between functionally graded waveguides and periodic media. Wave Motion 2014, 51, 581–588. [Google Scholar] [CrossRef]
- Djeran-Maigre, I.; Kuznetsov, S. Solitary SH waves in two-layered traction-free plates. Comptes Rendus Mécanique 2008, 336, 102–107. [Google Scholar] [CrossRef]
- Kuznetsov, S.V. Low frequency limits for Lamb waves in homogeneous, stratified and functionally graded anisotropic plates. Mech. Adv. Mater. Struct. 2022, 29, 4252–4258. [Google Scholar] [CrossRef]
- Aloisio, A.; Totani, F.; Alaggio, R.; Totani, G. Dispersion curves of transverse waves propagating in multi-layered soils from experimental tests in a 100 m deep borehole. Geosciences 2021, 11, 207. [Google Scholar] [CrossRef]
- Palmer, D. An introduction to the generalized reciprocal method of seismic refraction interpretation. Geophysics 1981, 46, 1508–1518. [Google Scholar] [CrossRef]
- Briickl, E. The interpretation of traveltime fields in refraction seismology. Geophys. Prospect. 1987, 35, 973–992. [Google Scholar] [CrossRef]
- Merzer, A.M. Head waves, normal waves, and the shapes of transition layers. Geophys. J. Int. 1974, 37, 1–7. [Google Scholar] [CrossRef]
- Coulombel, J.-F.; Williams, M. Amplification of pulses in nonlinear geometric optics. J. Hyperbolic Differ. Equ. 2014, 11, 749–793. [Google Scholar] [CrossRef]
- Berryman, J.G. Seismic velocity decrement ratios for regions of partial melt in the lower mantle. Geophys. Res. Lett. 2000, 27, 421–424. [Google Scholar] [CrossRef]
- Braile, L.W. Crustal structure of the continental interior, in Geophysical Framework of the Continental United States. Mem. Geol. Soc. Am. 1989, 172, 285–315. [Google Scholar]
- Buffett, B.A.; Garnero, E.J.; Jeanloz, R. Sediments and the top of Earth’s core. Science 2000, 288, 2007–2012. [Google Scholar] [CrossRef]
- Cagniard, L. Reflection and Refraction of Progressive Seismic Waves; Flinn, E.A., Dix, C.H., Eds.; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Choy, G.L. Theoretical seismograms of core phases calculated by frequency-dependent full wave theory, and their interpretation. Geophys. J. R. Astron. Soc. 1977, 51, 275–312. [Google Scholar] [CrossRef]
- Davies, D.; Kelly, E.J.; Filson, J.R. Vespa process for analysis of seismic signals. Nat. Phys. Sci. 1971, 232, 1971. [Google Scholar] [CrossRef]
- de Hoop, A.T. A modification of Cagniard’s method for solving seismic pulse problems. Appl. Sci. Res. Ser. B 1960, 8, 349–356. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model (PREM). Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Frederiksen, A.W.; Bostock, M.G. Modelling teleseismic waves in dipping anisotropic structures. Geophys. J. Int. 2000, 141, 401–412. [Google Scholar] [CrossRef]
- Fuchs, K.; Muller, G. Computation of synthetic seismograms with the reflectivity method and comparison with observations. Geophys. J. R. Astron. Soc. 1971, 23, 417–433. [Google Scholar] [CrossRef]
- Garnero, E.J.; Helmberger, D.V. A very slow basal layer underlying large-scale low-velocity anomalies in the lower mantle beneath the Pacific—Evidence from core phases. Phys. Earth Planet. Inter. 1995, 91, 161–176. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Y.; Zhow, S.; Zhang, H. Detection of fault zone head waves and the fault interface imaging in the Xianshuihe–Anninghe Fault zone (Eastern Tibetan Plateau). Geophysi. J. Int. 2023, 234, 1157–1167. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Z. Automatic identification of fault zone head waves and direct P waves and its application in the Parkfield section of the San Andreas Fault, California. Geophys. J. Int. 2016, 205, 1326–1341. [Google Scholar] [CrossRef]
- Nardoni, C.; De Siena, L.; Magrini, F.; Cammarano, F.; Maeda, T.; Mattei, E. Earthquake characteristics and structural properties of the Southern Tyrrhenian Basin from full seismic wave simulations. Surv. Geophys. 2023, 44, 925–945. [Google Scholar] [CrossRef]
- Zhao, P.; Peng, Z.; Shi, Z.; Lewis, M.; Ben-Zion, Y. Variations of the velocity contrast and rupture properties of M6 earthquakes along the Parkfield section of the San Andreas fault. Geophys. J. Int. 2010, 180, 765–780. [Google Scholar] [CrossRef]
- Ben-Zion, Y.; Malin, P. San Andreas fault zone head waves near Parkfield, California. Science 1991, 251, 1592–1594. [Google Scholar] [CrossRef] [PubMed]
- Bennington, N.; Thurber, C.; Feigl, K.; Murray-Moraleda, J. Aftershock distribution as a constraint on the geodetic model of coseismic slip for the 2004 Parkfield earthquake. Pure Appl. Geophys. 2011, 168, 1553–1565. [Google Scholar] [CrossRef]
- Kurzweil, L.G. Ground-borne noise and vibration from underground rail systems. J. Sound Vib. 1979, 66, 363–370. [Google Scholar] [CrossRef]
- Di, H.; Zhou, S.; Luo, Z.; He, C.; Xiao, J.; Li, X. A vehicle-track-tunnel-soil model for evaluating the dynamic response of a double-line metro tunnel in a poroelastic half-space. Comp. Geotech. 2017, 101, 245–263. [Google Scholar] [CrossRef]
- Benech, N.; Negreira, C.A. Longitudinal and lateral low frequency head wave analysis in soft media. J. Acoust. Soc. Am. 2005, 117, 3424–3431. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).