Quantum Circuit Template Matching Optimization Method for Constrained Connectivity
Abstract
1. Introduction
2. Preliminaries
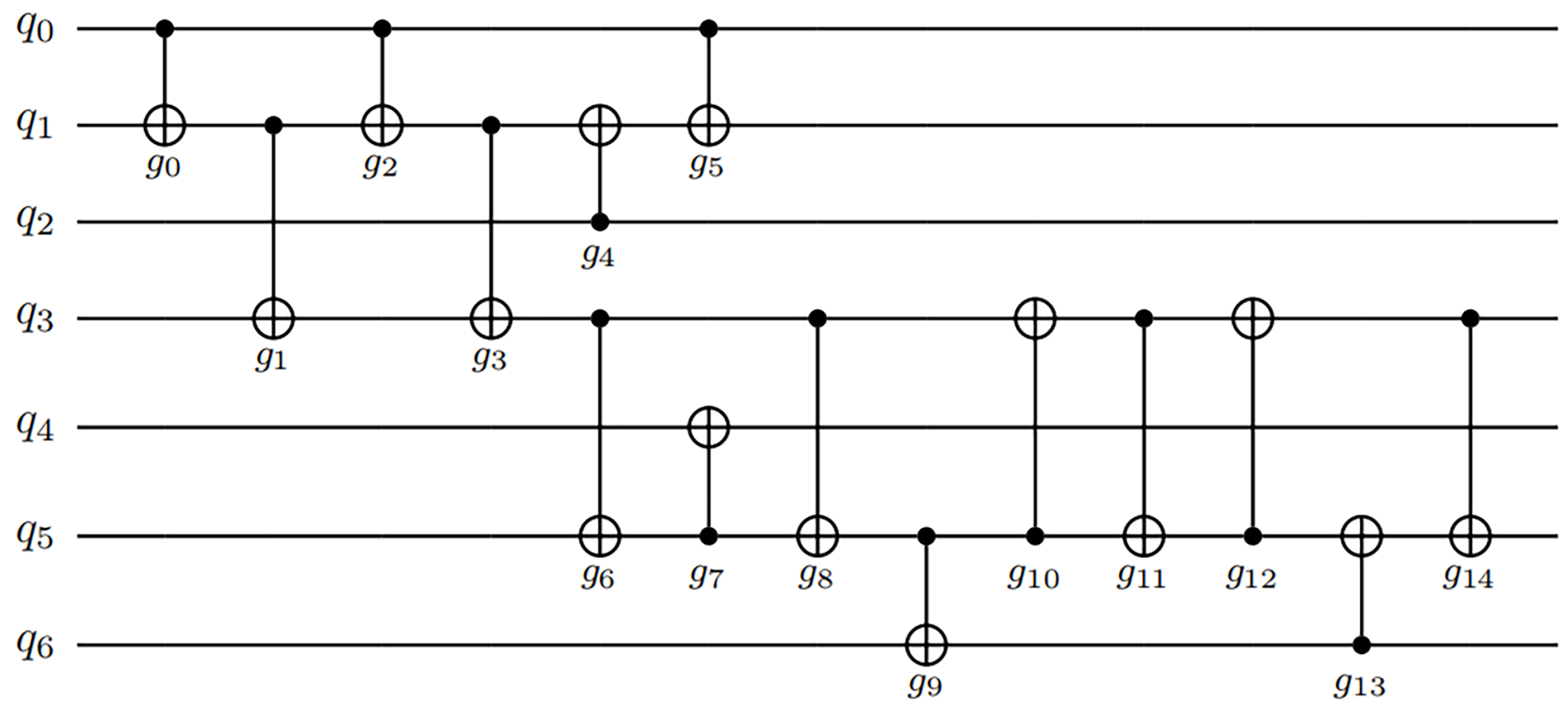
2.1. Quantum Gate and Quantum Circuit
2.2. Quantum Cost
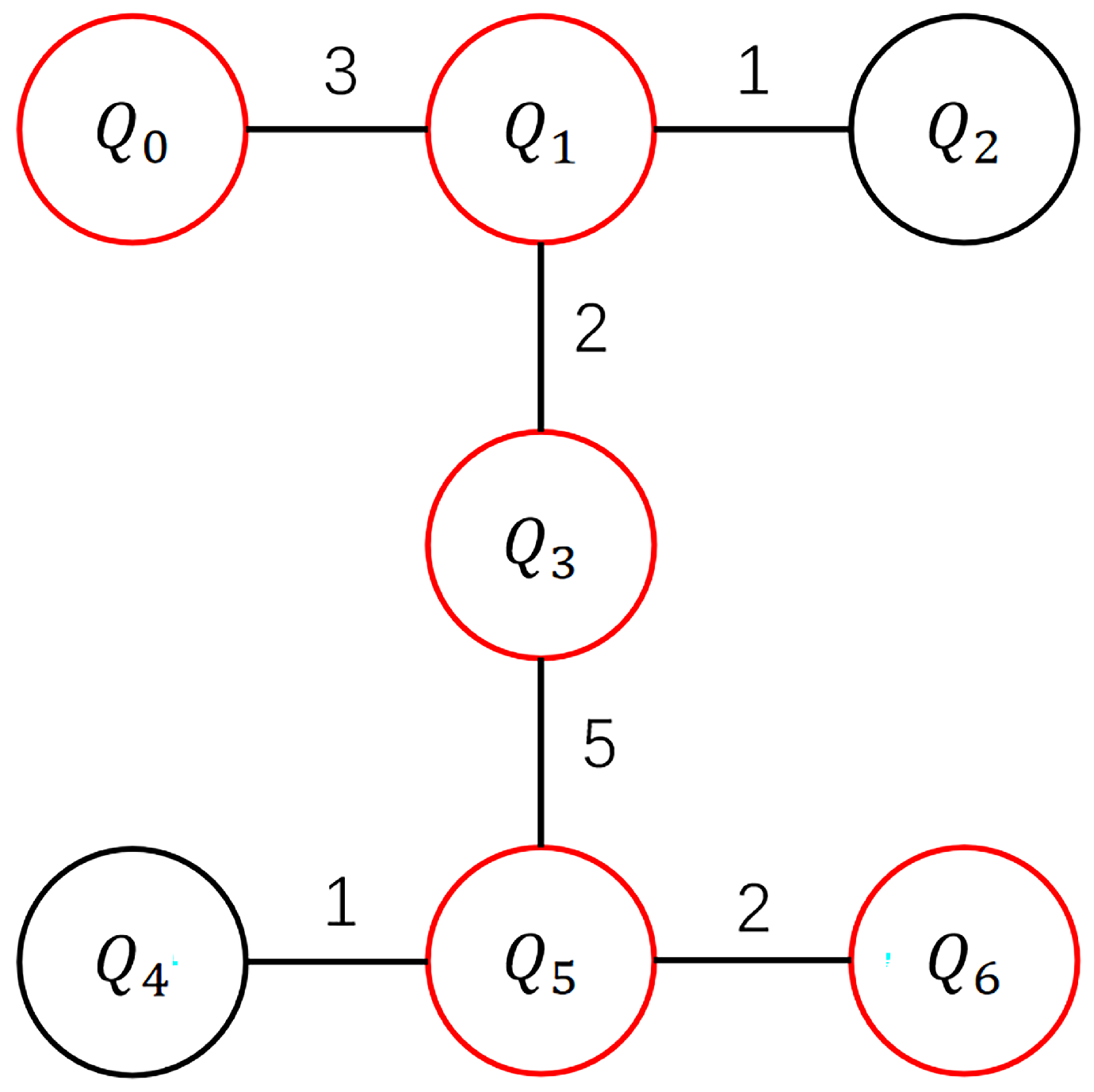
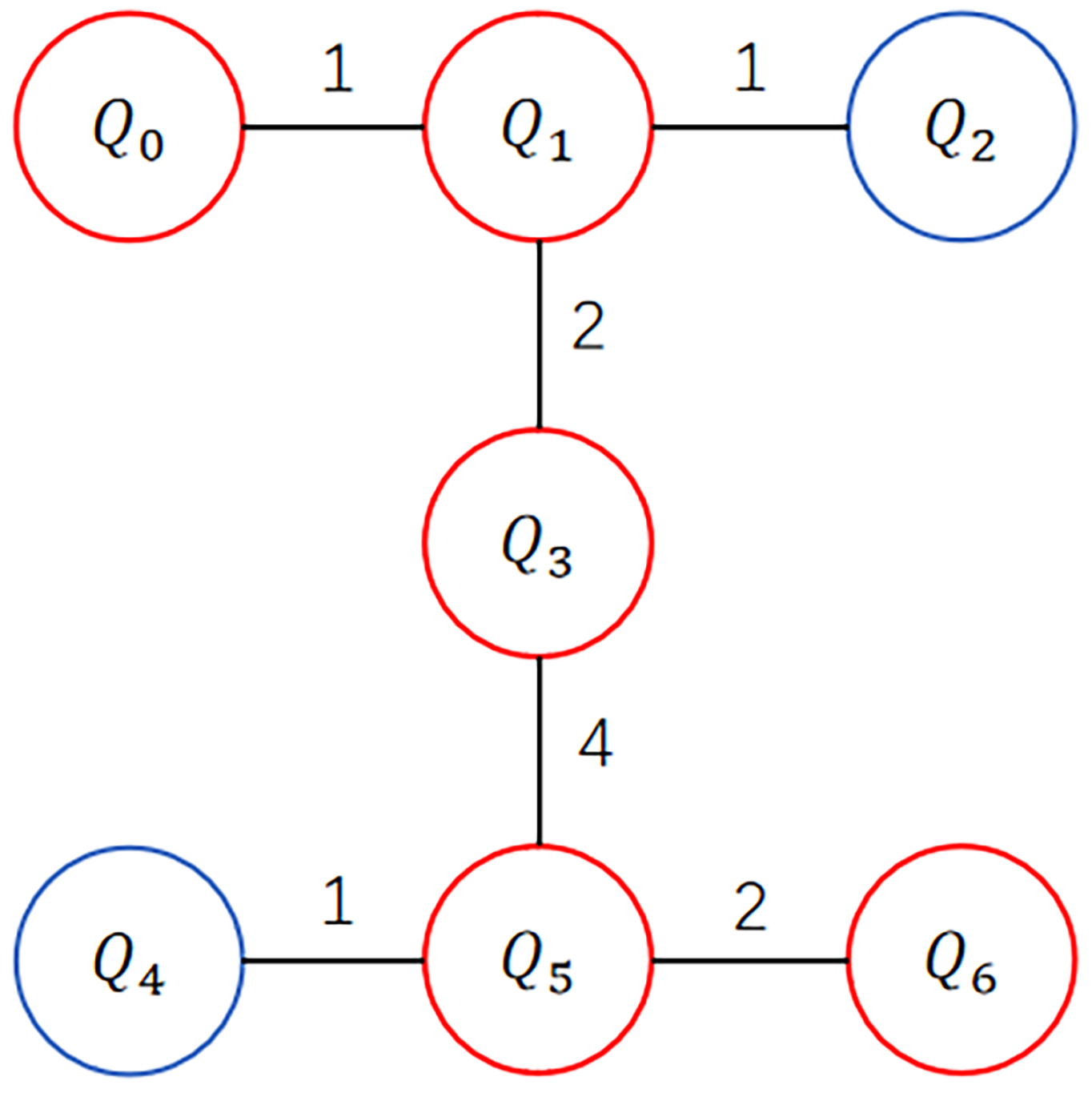
2.3. Quantum Topology
2.4. Quantum Circuit Mapping
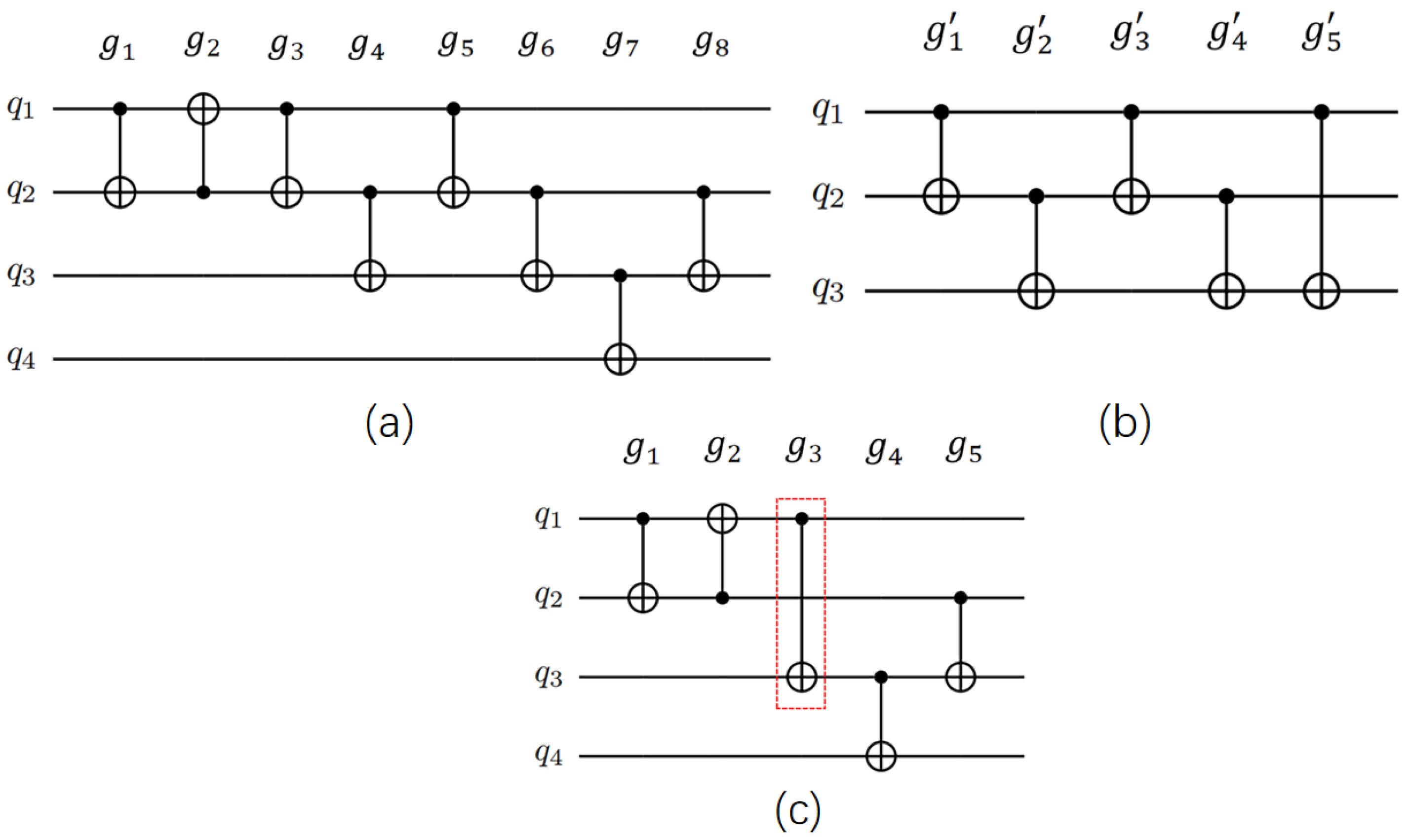
2.5. Quantum Circuit Templates
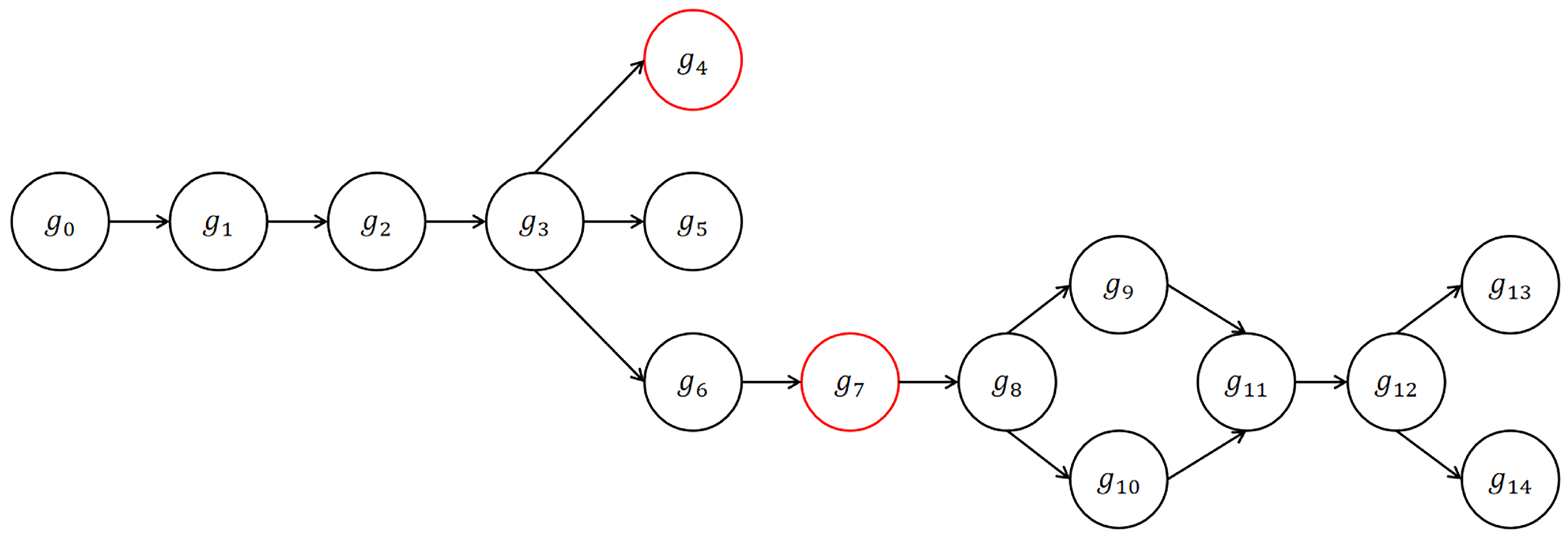
2.6. Gate Dependency Graph
3. Selection of Linear Substructure
Topological Linear Substructure Selection
| Algorithm 1: The first round of linear substructure selection algorithm |
Input: Topology , the number of gates between qubits Output: The selected substructure qubits 1. Initialize a list W to store qubits 2. for do 3. for do 4. if have the least adjacent connection nodes then 5. for connection points do 6. if has maximum weight then 7. Add to to the list of W 8. else if no adjacent nodes can be selected then 9. break 10. end if 11. end for 12. end for 13. return W |
4. Circuit Zoning Optimization and Reorganization
4.1. Circuit Zoning
| Algorithm 2: Circuit zoning |
Input: Gate dependency graph Output: Zoning circuits 1. Initialize a list C to store gates 2. for do 3. if min gates on selected qubit then 4. Add to the list of C 5. if one successor gate of block gates then 6. continue 7. else if one successor gate of gates on selected qubit then 8. Add the successor gate to the list of C 9. else if the only successor gate of block gates then 10. break 11. end if 12. if one successor gate of block gates then 13. continue 14. else if one successor gate of gates on selected qubit then 15. Add the successor gate to the list of C 16. else if the only successor gate of block gates then 17. break 18. end if 19. end if 20. end for 21. return C |
4.2. Circuit Optimization and Reorganization
| Algorithm 3: The second round of linear substructure selection algorithm |
Input: Topology , qubits have been selected Output: The selected substructure qubits 1. Initialize a list to store qubits 2. for do 3. for do 4. if have the least adjacent connection nodes then 5. for connection points do 6. if has maximum weight or not selected then 7. Add to to the list of 8. else if no adjacent nodes can be selected then 9. break 10. end if 11. end for 12. end for 13. return |
5. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information, 10th ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Iten, R.; Moyard, R.; Metger, T.; Sutter, D.; Woerner, S. Exact and practical pattern matching for quantum circuit optimization. ACM Trans. Quantum Comput. 2022, 3, 2643–6808. [Google Scholar] [CrossRef]
- Pointing, J.; Padon, O.; Jia, Z.; Ma, H.; Hirth, A.; Palsberg, J. Quanto: Optimizing Quantum Circuits with Automatic Generation of Circuit Identities. arXiv 2021, arXiv:2111.11387. [Google Scholar]
- Bandyopadhyay, C.; Wille, R.; Drechsler, R.; Rahaman, H. Post Synthesis-Optimization of Reversible Circuit using Template Matching. In Proceedings of the 24th International Symposium on VLSI Design and Test (VDAT), Bhubaneswar, India, 23–25 July 2020. [Google Scholar]
- Bravyi, S.; Shaydulin, R.; Hu, S.; Maslov, D. Clifford Circuit Optimization with Templates and Symbolic Pauli Gates. Quantum 2021, 5, 580. [Google Scholar] [CrossRef]
- Li, G.; Ding, Y.; Xie, Y. Tackling the qubit mapping problem for NISQ-era quantum devices. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems, Providence, RI, USA, 13–17 April 2019; pp. 1001–1014. [Google Scholar]
- Itoko, T.; Raymond, R.; Imamichi, T.; Matsuo, A. Optimization of quantum circuit mapping using gate transformation and commutation. Integration 2020, 70, 43–50. [Google Scholar] [CrossRef]
- Wille, R.; Burgholzer, L.; Zulehner, A. Mapping quantum circuits to IBM QX architectures using the minimal number of SWAP and H operations. In Proceedings of the 2019 56th ACM/IEEE Design Automation Conference (DAC), Las Vegas, NV, USA, 2–6 June 2019; pp. 1–6. [Google Scholar]
- Zhu, P.; Zheng, S.; Wei, L. The complexity of quantum circuit mapping with fixed parameters. Quantum Inf. Process. 2022, 21, 361. [Google Scholar] [CrossRef]
- Zhu, P.; Guan, Z.; Cheng, X. A dynamic look-ahead heuristic for the qubit mapping problem of NISQ computers. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 4721–4735. [Google Scholar] [CrossRef]
- Sivarajah, S.; Dilkes, S.; Cowtan, A.; Edgington, W.S.A.; Duncan, R. T|ket〉: A retargetable compiler for nisq devices. Quantum Sci. Technol. 2020, 6, 014003. [Google Scholar] [CrossRef]
- Steane, A. Quantum computing. Rep. Prog. Phys. 1997, 61, 117. [Google Scholar] [CrossRef]
- Barenco, A.; Bennett, C.H.; Cleve, R.; Divincenzo, D.P.; Margolus, N.; Shor, P. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Lee, S.J.; Kim, T. The cost of quantum gate primitives. J. Mult.-Valued Log. Soft Comput. 2006, 12, 561–573. [Google Scholar]
- Kliuchnikov, V.; Maslov, D.; Mosca, M. Asymptotically optimal approximation of single qubit unitaries by Clifford and T circuits using a constant number of ancillary qubits. Phys. Rev. Lett. 2013, 110, 19. [Google Scholar] [CrossRef] [PubMed]
- Nam, Y.; Ross, N.J.; Su, J.; Child, A.M.; Maslow, D. Automated optimization of large quantum circuits with continuous parameters. NPJ Quantum Inf. 2018, 4, 1. [Google Scholar] [CrossRef]
- Patel, T.; Younis, E.; Iancu, C.; Jong, W.D.; Tiwari, D. Robust and Resource-Efficient Quantum Circuit Approximation. arXiv 2021, arXiv:2108.12714. [Google Scholar]
- Janzing, D.; Wocjan, D.; Beth, T. “Non-Identity-Check” Is Qma-Complete. Int. J. Quantum Inf. 2005, 3, 463–473. [Google Scholar] [CrossRef]
- Prasad, A.K.; Shende, V.V.; Markov, I.L.; Hayes, J.P.; Patel, K.N. Data structures and algorithms for simplifying reversible circuits. ACM J. Emerg. Technol. Comput. Syst. 2006, 2, 277–293. [Google Scholar] [CrossRef]
- Maslov, D.; Dueck, G.W.; Miller, D.M.; Negrevergne, C. Quantum circuit simplification and level compaction. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2008, 27, 436–444. [Google Scholar] [CrossRef]
- Duncan, R.; Kissinger, A.; Pedrix, S.; Wetering, J. Graph-theoretic Simplification of Quantum Circuits with the ZX-calculus. Quantum 2020, 4, 279. [Google Scholar] [CrossRef]
- IBM Quantum Experience. Available online: https://quantum-computing.ibm.com/ (accessed on 11 December 2022).
- Qiskit—An Open-Source Framework for Working with Noisy Quantum Computers at the Level of Pulses, Circuits, and Algorithms. Available online: https://github.com/Qiskit (accessed on 14 May 2023).
- Rahman, M.M.; Dueck, G.W. Properties of quantum templates. In Proceedings of the 4th International Workshop, RC 2012, Berlin/Heidelberg, Germany, 2–3 July 2012; pp. 125–137. [Google Scholar]
- Rahman, M.M.; Dueck, G.W.; Horton, J.D. An Algorithm for Quantum Template Matching; Association for Computing Machinery: New York, NY, USA, 2015; Volume 11, pp. 1550–4832. [Google Scholar]
- Nath, R.K.; Sharma, M.; Dutta, P.; Shang, Y. On r-Noncommuting Graph of Finite Rings. Axioms 2021, 10, 233. [Google Scholar] [CrossRef]
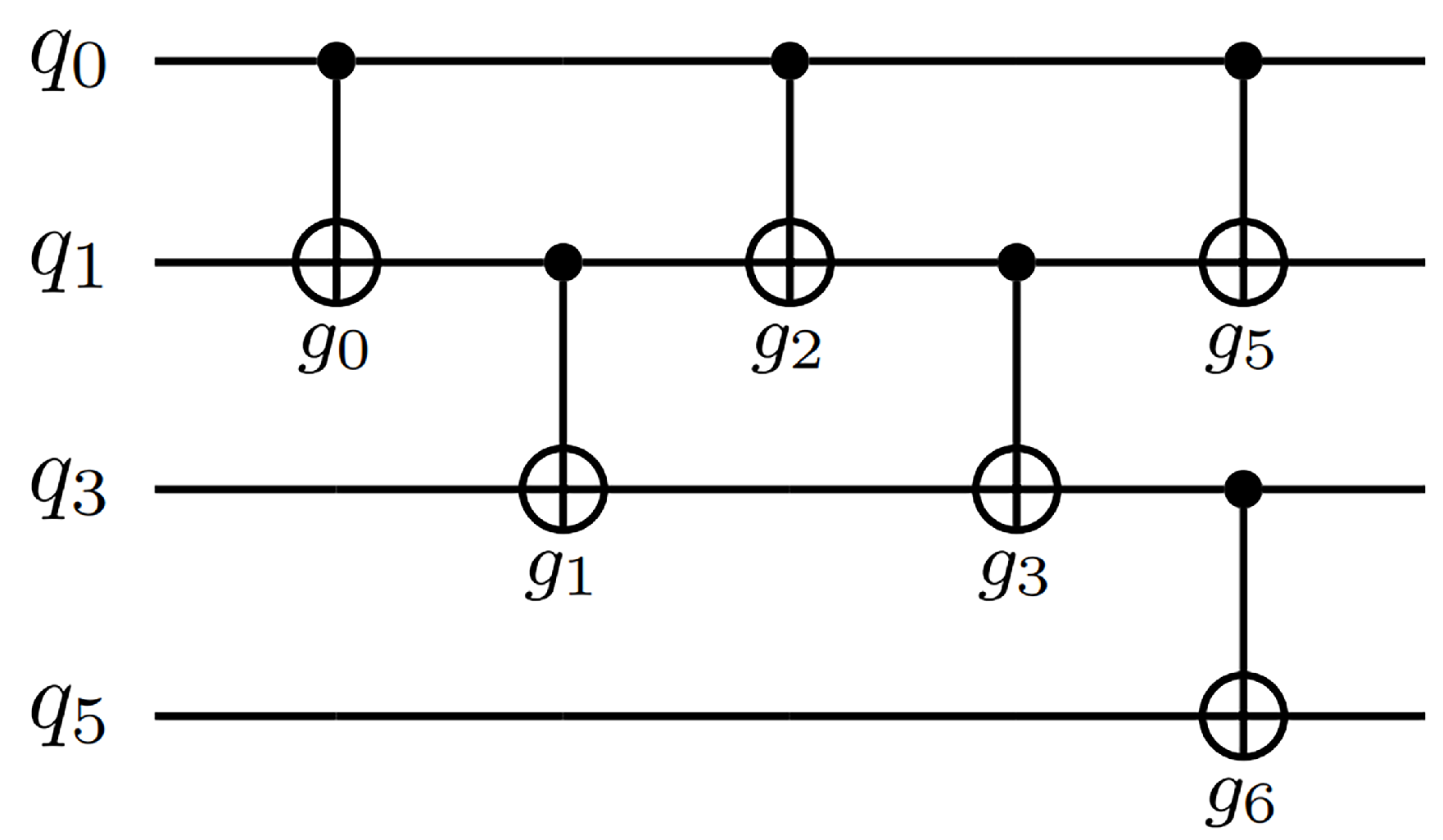
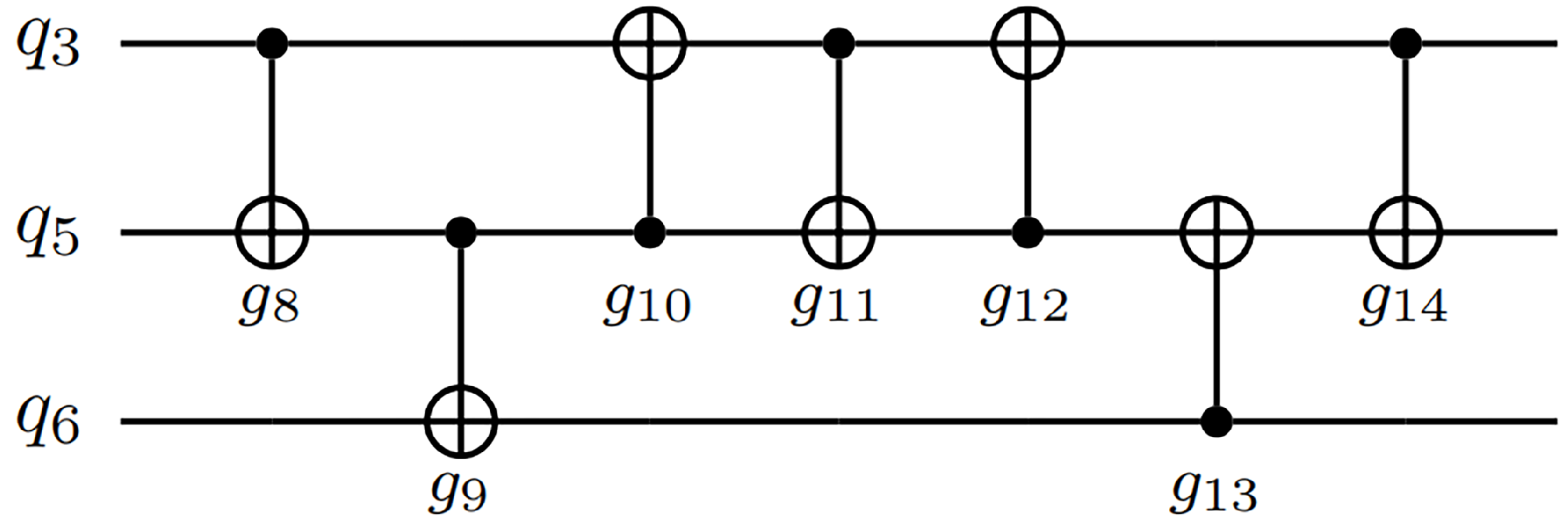
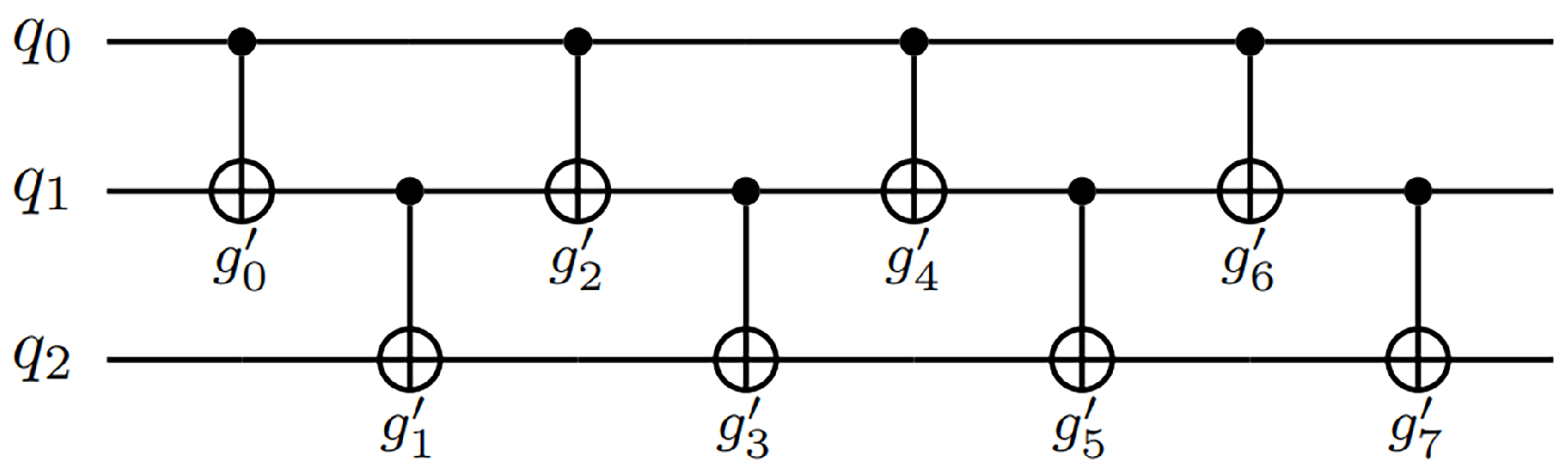
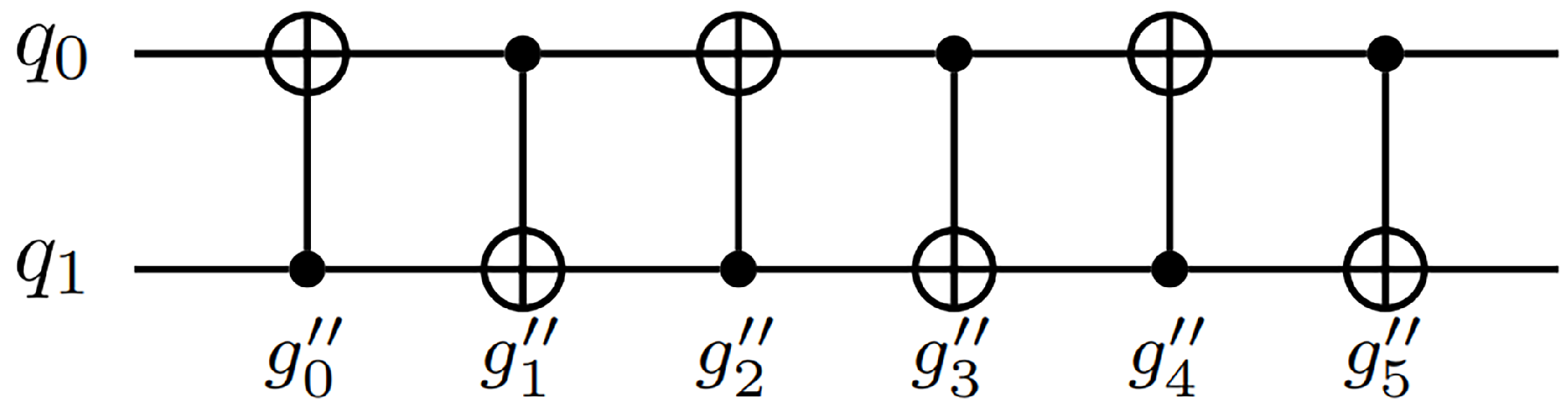
| Circuit Name | n | Original CNOTs | Mapped CNOTs | Tket [12] | Qiskit [24] | Topt CNots | % | |
|---|---|---|---|---|---|---|---|---|
| With [12] | With [24] | |||||||
| 4gt5_75 | 5 | 38 | 63 | 63 | 64 | 38 | 39.68 | 40.63 |
| 4gt13_90 | 5 | 53 | 64 | 62 | 84 | 45 | 27.42 | 46.43 |
| 4gt13_91 | 5 | 49 | 64 | 64 | 88 | 48 | 25.00 | 45.45 |
| 4gt4-v0_78 | 6 | 109 | 180 | 189 | 174 | 131 | 24.71 | 30.69 |
| 4gt4-v0_79 | 6 | 105 | 163 | 173 | 157 | 113 | 28.03 | 34.68 |
| 4gt4-v0_80 | 6 | 79 | 151 | 129 | 145 | 131 | 9.66 | −1.55 |
| Average | 25.75 | 32.72 | ||||||
| Circuit Name | n | Original CNOTs | Mapped CNOTs | Tket [12] | Qiskit [24] | Topt CNots | % | |
|---|---|---|---|---|---|---|---|---|
| With [12] | With [24] | |||||||
| 4gt5_75 | 5 | 38 | 49 | 47 | 58 | 33 | 29.79 | 43.10 |
| 4gt13_90 | 5 | 53 | 57 | 57 | 72 | 43 | 24.56 | 40.28 |
| 4gt4-v0_80 | 6 | 79 | 131 | 127 | 141 | 85 | 33.07 | 39.75 |
| alu_bdd_288 | 7 | 38 | 75 | 73 | 66 | 60 | 17.81 | 9.09 |
| majority_239 | 7 | 267 | 429 | 423 | 403 | 358 | 15.37 | 11.17 |
| C17_204 | 7 | 205 | 332 | 330 | 332 | 272 | 17.58 | 18.07 |
| ham7_104 | 7 | 149 | 212 | 210 | 266 | 155 | 26.19 | 41.73 |
| rd53_131 | 7 | 200 | 339 | 331 | 338 | 296 | 10.57 | 12.43 |
| rd53_135 | 7 | 134 | 219 | 219 | 248 | 185 | 15.53 | 25.40 |
| Average | 21.16 | 26.78 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Guan, Z.; Feng, S.; Jiang, Y. Quantum Circuit Template Matching Optimization Method for Constrained Connectivity. Axioms 2023, 12, 687. https://doi.org/10.3390/axioms12070687
Gao X, Guan Z, Feng S, Jiang Y. Quantum Circuit Template Matching Optimization Method for Constrained Connectivity. Axioms. 2023; 12(7):687. https://doi.org/10.3390/axioms12070687
Chicago/Turabian StyleGao, Xiaofeng, Zhijin Guan, Shiguang Feng, and Yibo Jiang. 2023. "Quantum Circuit Template Matching Optimization Method for Constrained Connectivity" Axioms 12, no. 7: 687. https://doi.org/10.3390/axioms12070687
APA StyleGao, X., Guan, Z., Feng, S., & Jiang, Y. (2023). Quantum Circuit Template Matching Optimization Method for Constrained Connectivity. Axioms, 12(7), 687. https://doi.org/10.3390/axioms12070687





