Convergence of Collocation Methods for One Class of Impulsive Delay Differential Equations
Abstract
:1. Introduction
- ;
- for , the function is differentiable and ;
- the function is left-continuous in I, and if and , then , ;
- are constants, .
2. Collocation Methods
3. Global Convergence
4. Global Superconvergence and Local Superconvergence
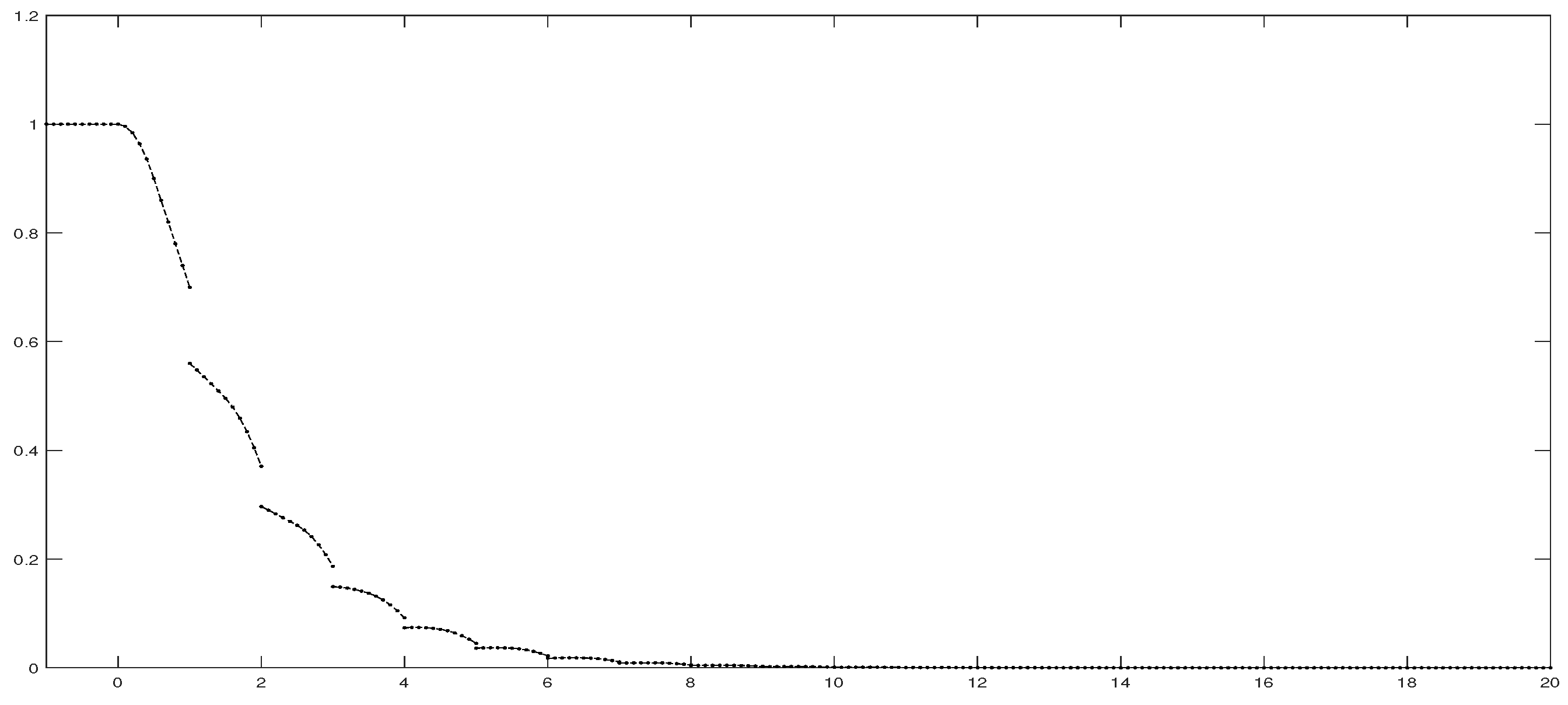
5. Numerical Experiments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akgöl, S.D. Oscillation of impulsive linear differential equations with discontinuous solutions. Bull. Aust. Math. Soc. 2023, 107, 112–124. [Google Scholar] [CrossRef]
- Liu, M.Z.; Liang, H.; Yang, Z.W. Stability of Runge-Kutta methods in the numerical solution of linear impulsive differential equations. Appl. Math. Comput. 2007, 192, 346–357. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, G.L.; Liu, M.Z. Analytic and numerical exponential asymptotic stability of nonlinear impulsive differential equations. Appl. Numer. Math. 2014, 81, 40–49. [Google Scholar] [CrossRef]
- Stamova, I.M.; Stamov, T.G. Impulsive effects on global stability of models based on impulsive differential equations with “supremum” and variable impulsive perturbations. Appl. Math. Mech. 2014, 35, 85–96. [Google Scholar] [CrossRef]
- Wen, Q.; Wang, J.R.; O’Regan, D. Stability analysis of second order impulsive differential equations. Qual. Theory Dyn. 2022, 21, 54. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Karakoç, F. Oscillation of impulsive linear differential equations with discontinuous solutions. Comput. Math. Appl. 2010, 60, 1648–1685. [Google Scholar] [CrossRef] [Green Version]
- Bainov, D.D.; Dimitrova, M.B.; Dishliev, A.B. Oscillation of the solutions of a class of impulsive differential equations with deviating argument. J. Appl. Math. Stoch. Anal. 1998, 11, 95–102. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.R. Stability for impulsive delay differential equations. Nonlinear Anal. Theory Methods Appl. 2005, 63, 66–80. [Google Scholar] [CrossRef]
- Yan, J.; Kou, C. Oscillation of solutions of impulsive delay differential equations. J. Math. Anal. Appl. 2001, 254, 358–370. [Google Scholar] [CrossRef] [Green Version]
- You, Z.L.; Wang, J.R. Stability of impulsive delay differential equations. J. Appl. Math. Comput. 2018, 56, 253–268. [Google Scholar] [CrossRef]
- You, Z.L.; Wang, J.R.; O’Regan, D. Asymptotic stability of solutions of impulsive multi-delay differential equations. Trans. Inst. Meas. Control 2018, 40, 4143–4152. [Google Scholar] [CrossRef]
- Zhang, G.L.; Song, M.H.; Liu, M.Z. Exponential stability of the exact solutions and the numerical solutions for a class of linear impulsive delay differential equations. J. Comput. Appl. Math. 2015, 285, 32–44. [Google Scholar] [CrossRef]
- Gao, H.C.; Liang, H. Discontinuous piecewise polynomial collocation methods for integral-algebraic equations of hessenberg type. Comput. Appl. Math. 2022, 41, 291. [Google Scholar] [CrossRef]
- Liang, H.; Brunner, H. Integral-algebraic equations: Theory of collocation methods I. SIAM J. Numer. Anal. 2013, 51, 2238–2259. [Google Scholar] [CrossRef]
- Liang, H.; Brunner, H. Integral-algebraic equations: Theory of collocation methods II. SIAM J. Numer. Anal. 2016, 54, 2640–2663. [Google Scholar] [CrossRef]
- Zhang, T.T.; Liang, H.; Zhang, S.J. On the convergence of multistep collocation methods for integral-algebraic equations of index 1. Comput. Appl. Math. 2020, 39, 294. [Google Scholar] [CrossRef]
- Brunner, H. Collocation Methods for Volterra Integral and Related Functional Differential Equations; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Li, Y.P.; Yang, Z.W.; Liang, H. Analysis of collocation methods for a class of third-kind auto-convolution Volterra integral equations. Math. Comput. Simul. 2022, 199, 341–358. [Google Scholar] [CrossRef]
- Zhang, R.; Liang, H.; Brunner, H. Analysis of collocation methods for generalized auto-convolution Volterra integral equations. SIAM J. Numer. Anal. 2016, 54, 899–920. [Google Scholar] [CrossRef]
- Brunner, H.; Liang, H. Stability of collocation methods for delay differential equations with vanishing delays. BIT Numer. Math. 2010, 50, 693–711. [Google Scholar] [CrossRef]
- Liang, H.; Brunner, H. Collocation methods for differential equations with piecewise linear delays. Commun. Pure Appl. Anal. 2012, 11, 1839–1857. [Google Scholar] [CrossRef]
- Yi, L.J.; Wang, Z.Q. A legendre-gauss-radau spectral collocation method for first order nonlinear delay differential equations. Calcolo 2016, 53, 691–721. [Google Scholar] [CrossRef]
- Liang, H.; Brunner, H. The convergence of collocation solutions in continuous piecewise polynomial spaces for weakly singular Volterra integral equations. SIAM J. Numer. Anal. 2019, 57, 1875–1896. [Google Scholar] [CrossRef]
- Liang, H.; Brunner, H. Discrete superconvergence of collocation solutions for first-kind Volterra integral equations. J. Integral Equ. Appl. 2012, 24, 359–391. [Google Scholar] [CrossRef]
- Liang, H.; Brunner, H. On the convergence of collocation solutions in continuous piecewise polynomial spaces for Volterra integral equations. BIT Numer. Math. 2016, 56, 1339–1367. [Google Scholar] [CrossRef]

| p | 2-Lobatto IIIA | 2-Gauss | ||
|---|---|---|---|---|
| t = 0.5 | t = 1 | t = 0.5 | t = 1 | |
| 2 | 1.7240 × 10−2 | 1.2168 × 10−2 | 2.7472 × 10−4 | 2.0228 × 10−4 |
| 4 | 3.9397 × 10−3 | 2.8676 × 10−3 | 1.4879 × 10−5 | 1.0948 × 10−5 |
| 8 | 9.3972 × 10−4 | 7.0782 × 10−4 | 1.0017 × 10−6 | 7.3700 × 10−7 |
| 16 | 2.3991 × 10−4 | 1.7640 × 10−4 | 6.2500 × 10−8 | 4.6000 × 10−8 |
| Ratio | 3.9170 | 4.0125 | 16.0272 | 16.0217 |
| p | 2-Radau IIA | 3-Gauss | ||
|---|---|---|---|---|
| t = 0.5 | t = 1 | t = 0.5 | t = 1 | |
| 2 | 2.1397 × 10−3 | 1.5676 × 10−3 | 1.8968 × 10−6 | 1.3955 × 10−6 |
| 4 | 2.3972 × 10−4 | 1.6764 × 10−4 | 2.8791 × 10−8 | 2.1183 × 10−8 |
| 8 | 3.7523 × 10−5 | 2.7605 × 10−5 | 4.4659 × 10−10 | 3.2858 × 10−10 |
| 16 | 4.8319 × 10−6 | 3.5550 × 10−6 | 6.9650 × 10−12 | 5.1240 × 10−12 |
| Ratio | 7.7657 | 7.7651 | 64.1195 | 64.1261 |
| p | 2-Lobatto IIIA | 2-Gauss | ||
|---|---|---|---|---|
| t = 0.5 | t = 1 | t = 0.5 | t = 1 | |
| 2 | 1.0600 × 10−2 | 1.6060 × 10−2 | 1.6962 × 10−4 | 2.6848 × 10−4 |
| 4 | 2.7996 × 10−3 | 3.8603 × 10−3 | 1.0462 × 10−5 | 1.5195 × 10−5 |
| 8 | 6.9520 × 10−4 | 9.6125 × 10−4 | 6.5040 × 10−7 | 9.2360 × 10−7 |
| 16 | 1.7417 × 10−4 | 2.3971 × 10−4 | 4.0600 × 10−8 | 5.7300 × 10−8 |
| Ratio | 3.9915 | 4.0101 | 16.0197 | 16.1187 |
| p | 2-Radau IIA | 3-Gauss | ||
|---|---|---|---|---|
| t = 0.5 | t = 1 | t = 0.5 | t = 1 | |
| 2 | 1.4042 × 10−3 | 1.5269 × 10−3 | 3.1785 × 10−7 | 4.0601 × 10−6 |
| 4 | 1.9795 × 10−4 | 2.1244 × 10−4 | 8.6487 × 10−8 | 6.6899 × 10−8 |
| 8 | 2.5980 × 10−5 | 2.8380 × 10−5 | 1.4918 × 10−10 | 1.0551 × 10−9 |
| 16 | 3.3200 × 10−6 | 3.6800 × 10−6 | 2.3850 × 10−12 | 1.6521 × 10−11 |
| Ratio | 7.8253 | 7.7120 | 62.5489 | 63.8865 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, G.; Sun, Y. Convergence of Collocation Methods for One Class of Impulsive Delay Differential Equations. Axioms 2023, 12, 700. https://doi.org/10.3390/axioms12070700
Wang Z, Zhang G, Sun Y. Convergence of Collocation Methods for One Class of Impulsive Delay Differential Equations. Axioms. 2023; 12(7):700. https://doi.org/10.3390/axioms12070700
Chicago/Turabian StyleWang, Zhiwei, Guilai Zhang, and Yang Sun. 2023. "Convergence of Collocation Methods for One Class of Impulsive Delay Differential Equations" Axioms 12, no. 7: 700. https://doi.org/10.3390/axioms12070700
APA StyleWang, Z., Zhang, G., & Sun, Y. (2023). Convergence of Collocation Methods for One Class of Impulsive Delay Differential Equations. Axioms, 12(7), 700. https://doi.org/10.3390/axioms12070700






