Proposed Shaft Coupling Based on RPRRR Mechanism: Positional Analysis and Consequences
Abstract
:1. Introduction
2. Materials and Methods
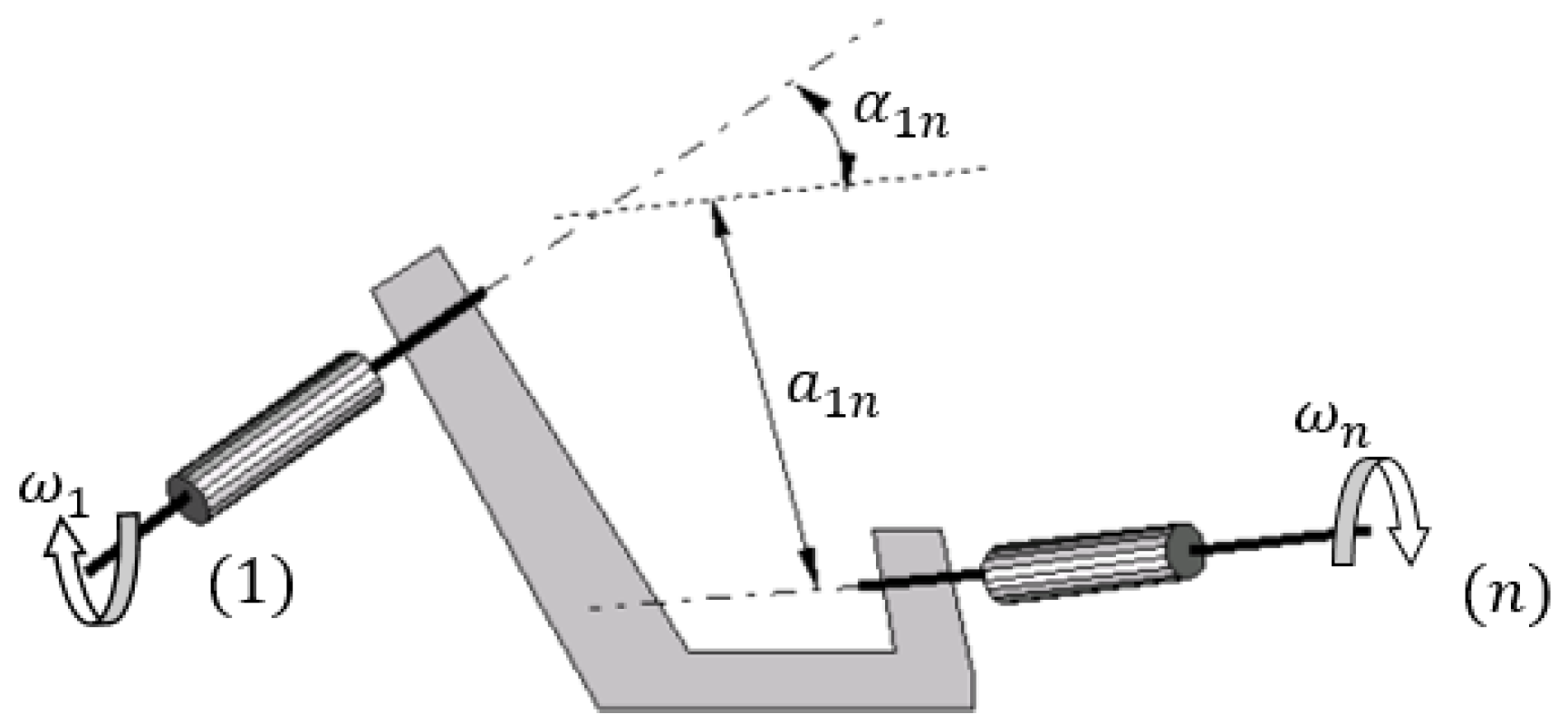
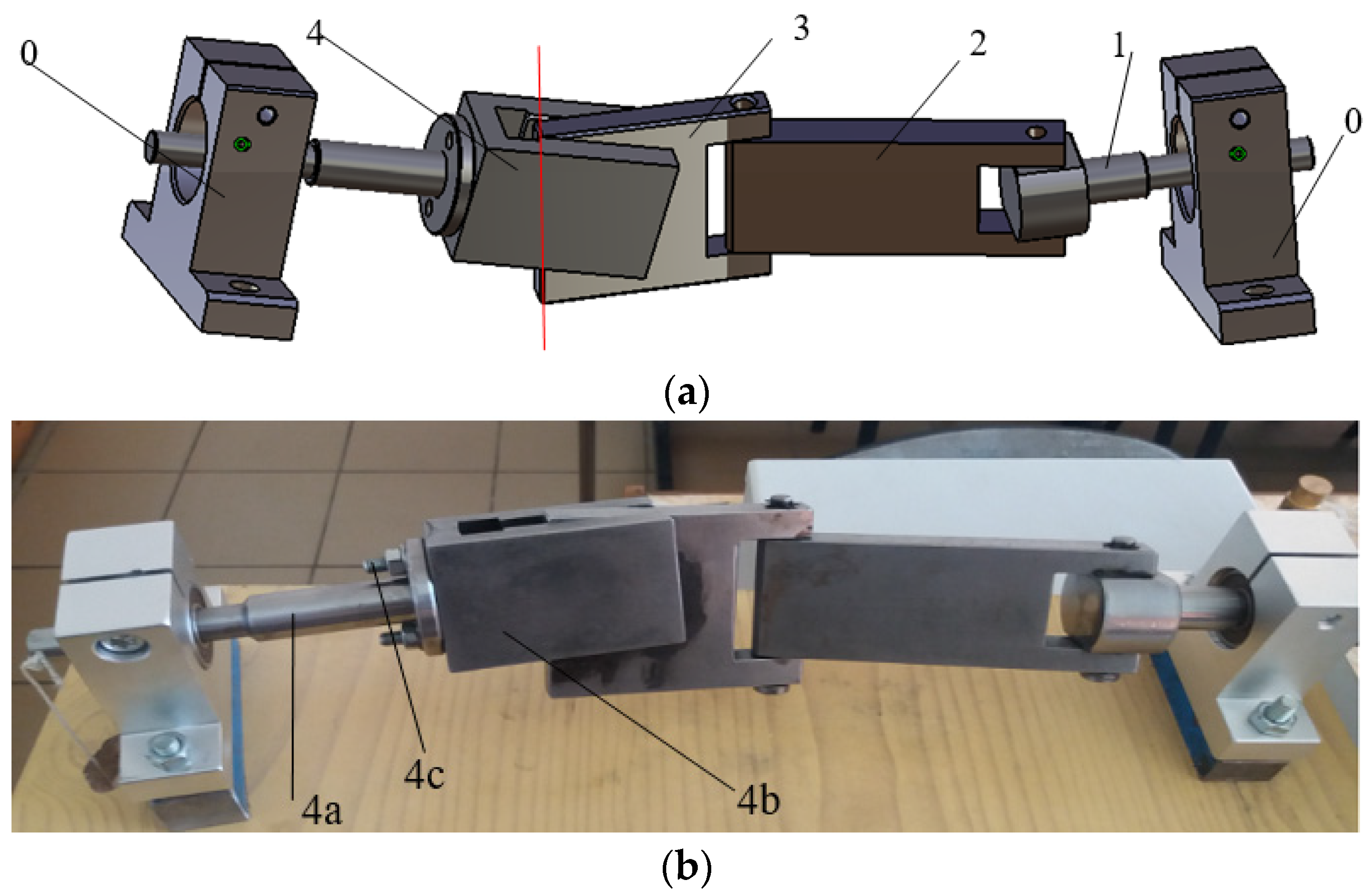
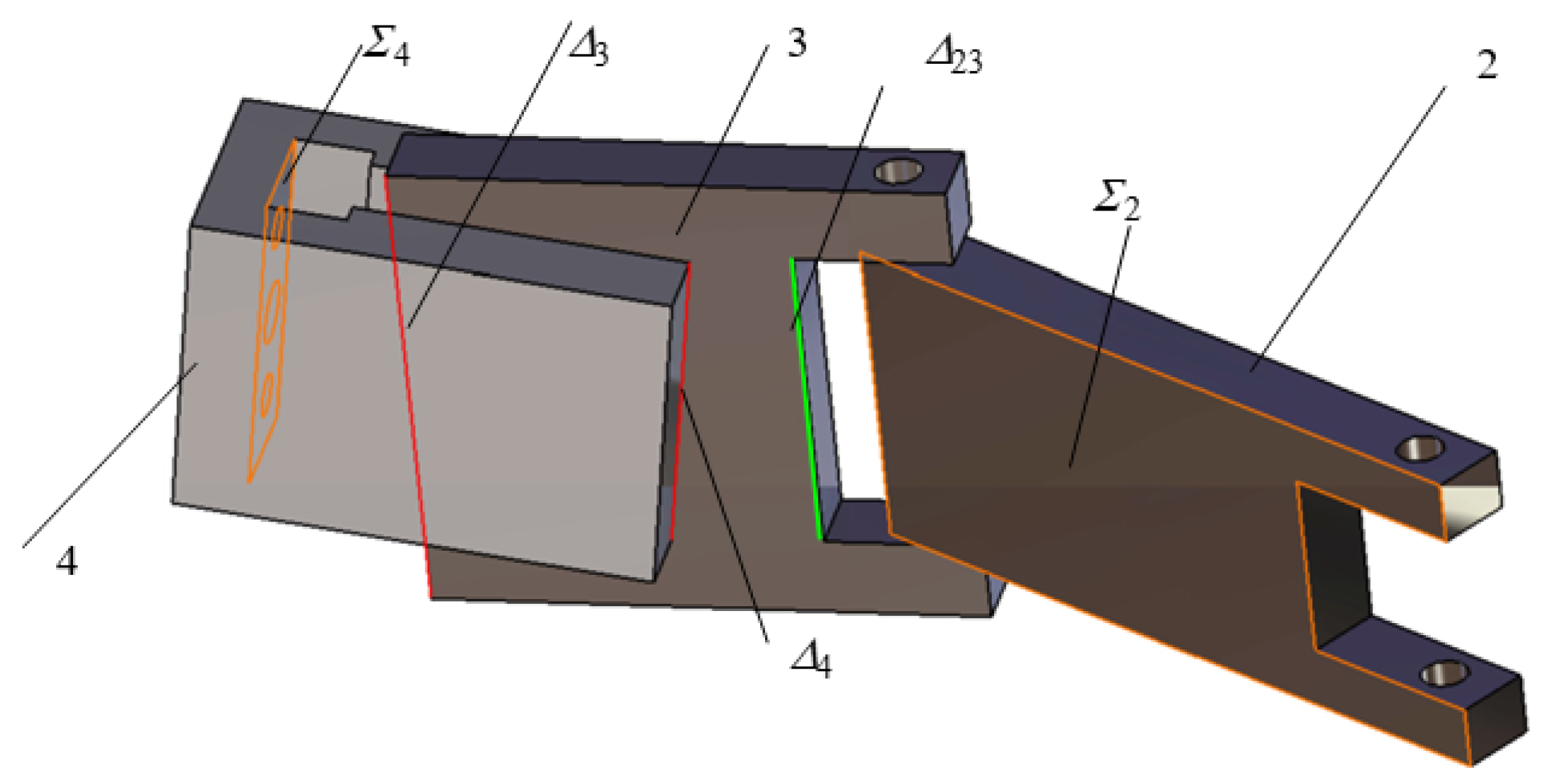
2.1. Structural Considerations
2.2. Kinematic Analysis of the Proposed Structural Solution
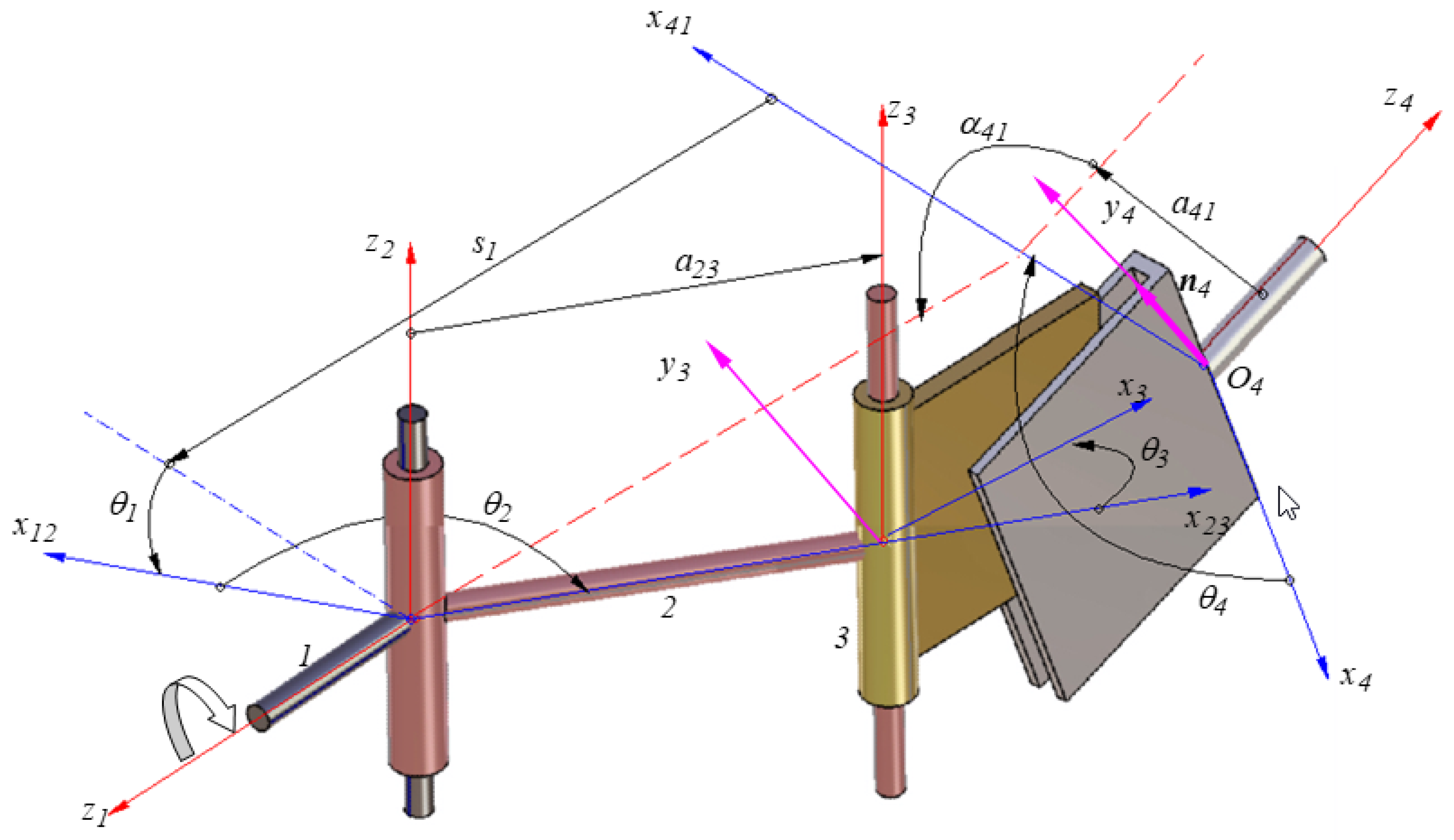
2.2.1. Principle of the Denavit–Hartenberg Methodology
2.2.2. Kinematic Analysis of the Proposed Mechanism
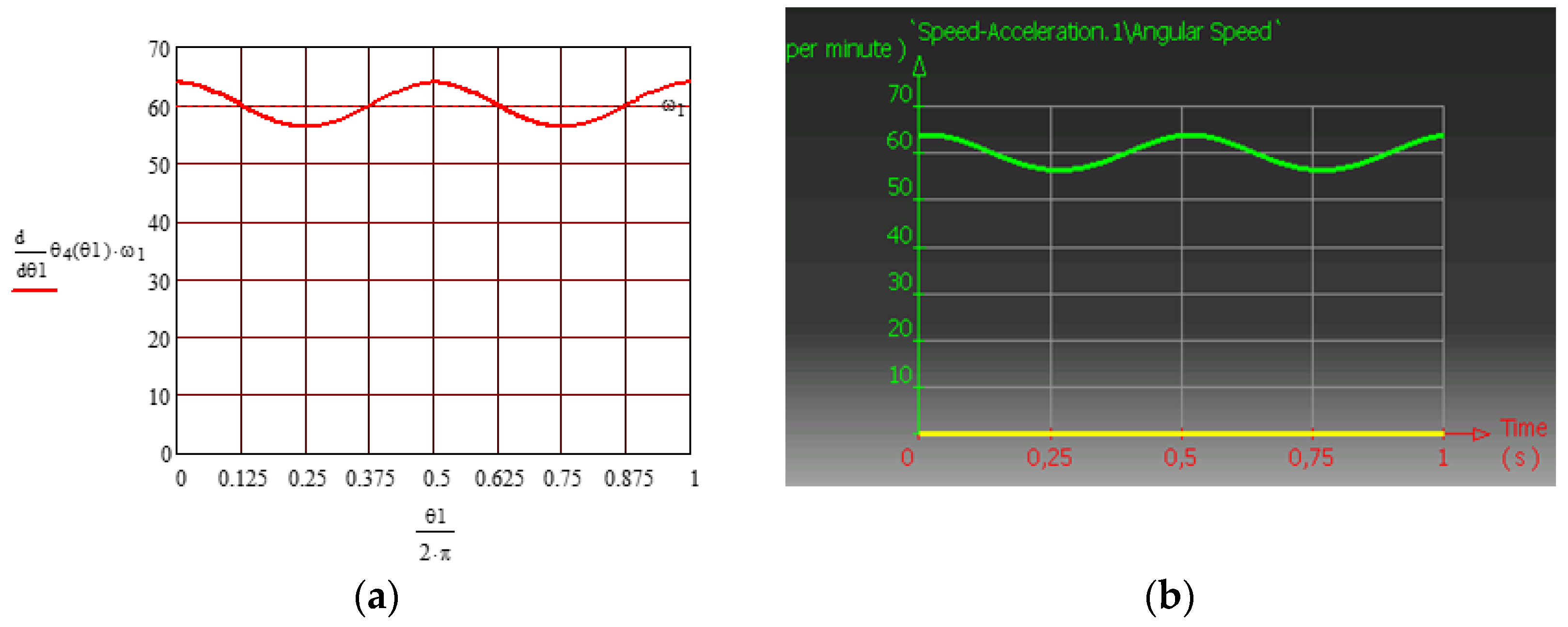
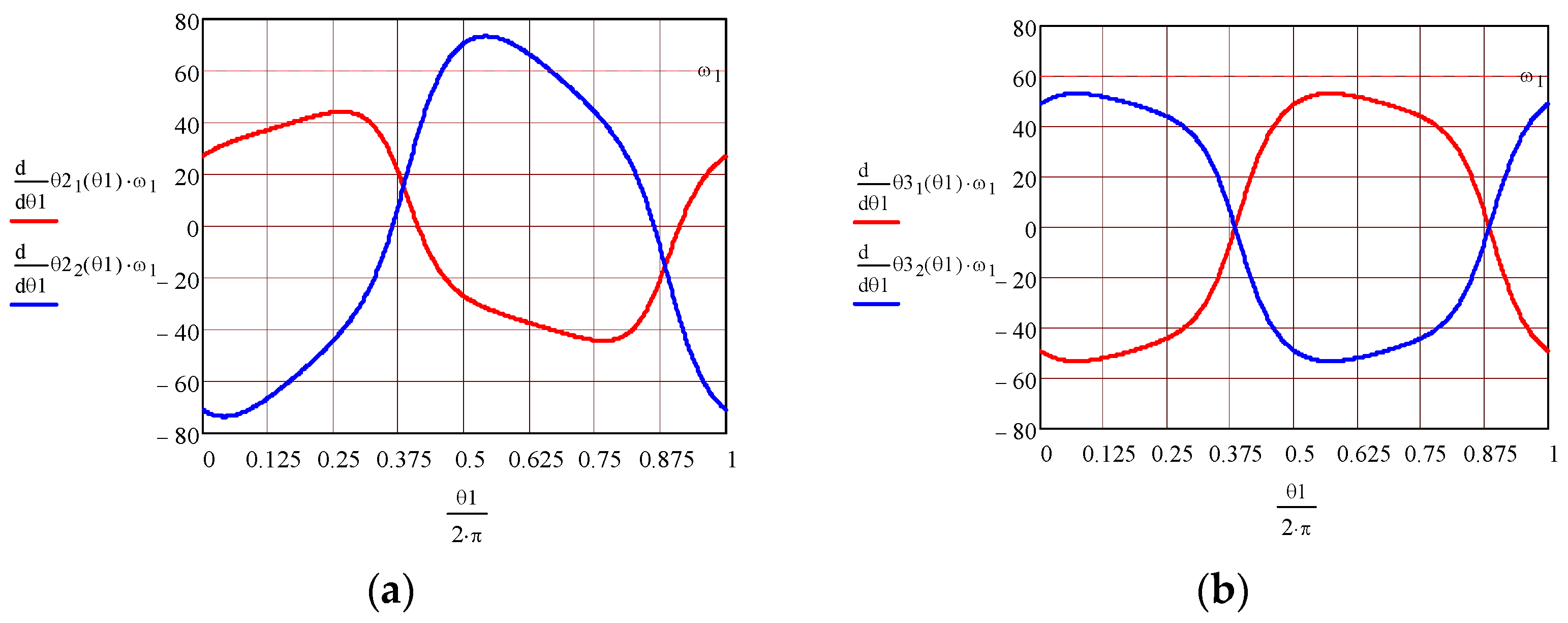
2.2.3. Finding the Motions from the Revolute Pairs
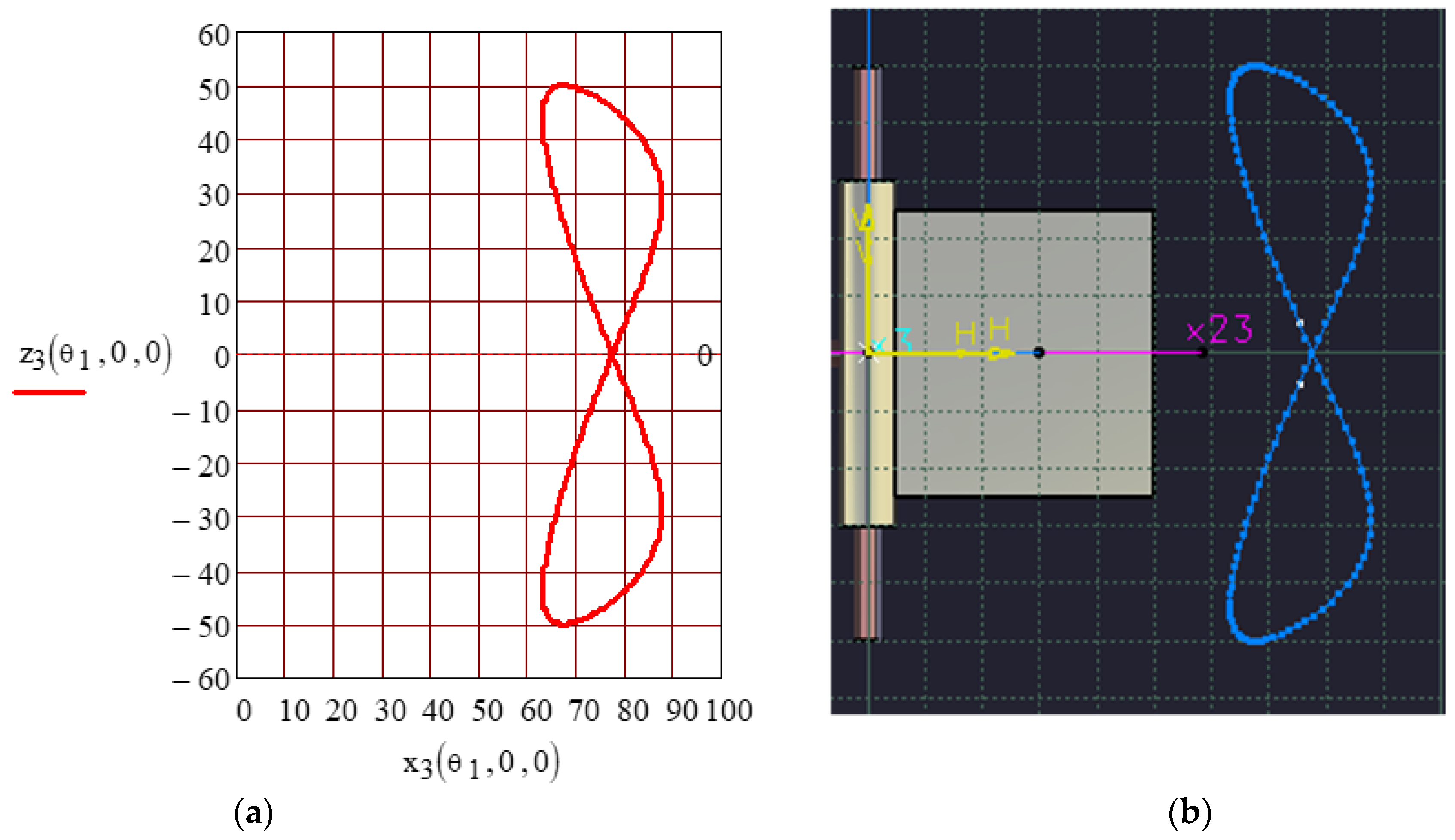
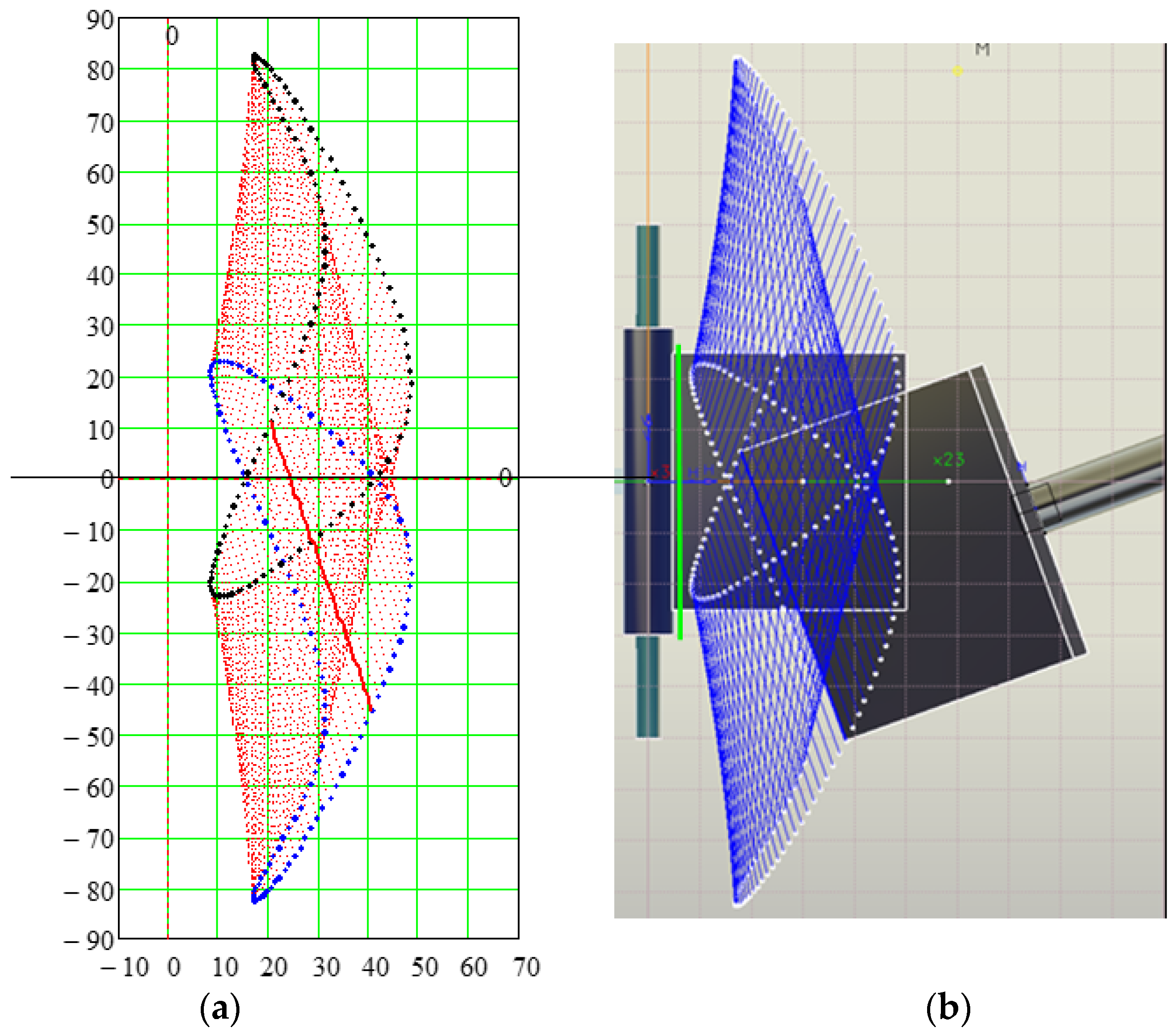
2.2.4. Finding the Motion from the Planar Pair
- The angular velocity has a constant sign and presents a periodic variation, which attests to the fact that, in the final pair, the motion is rotatory (Figure 7).
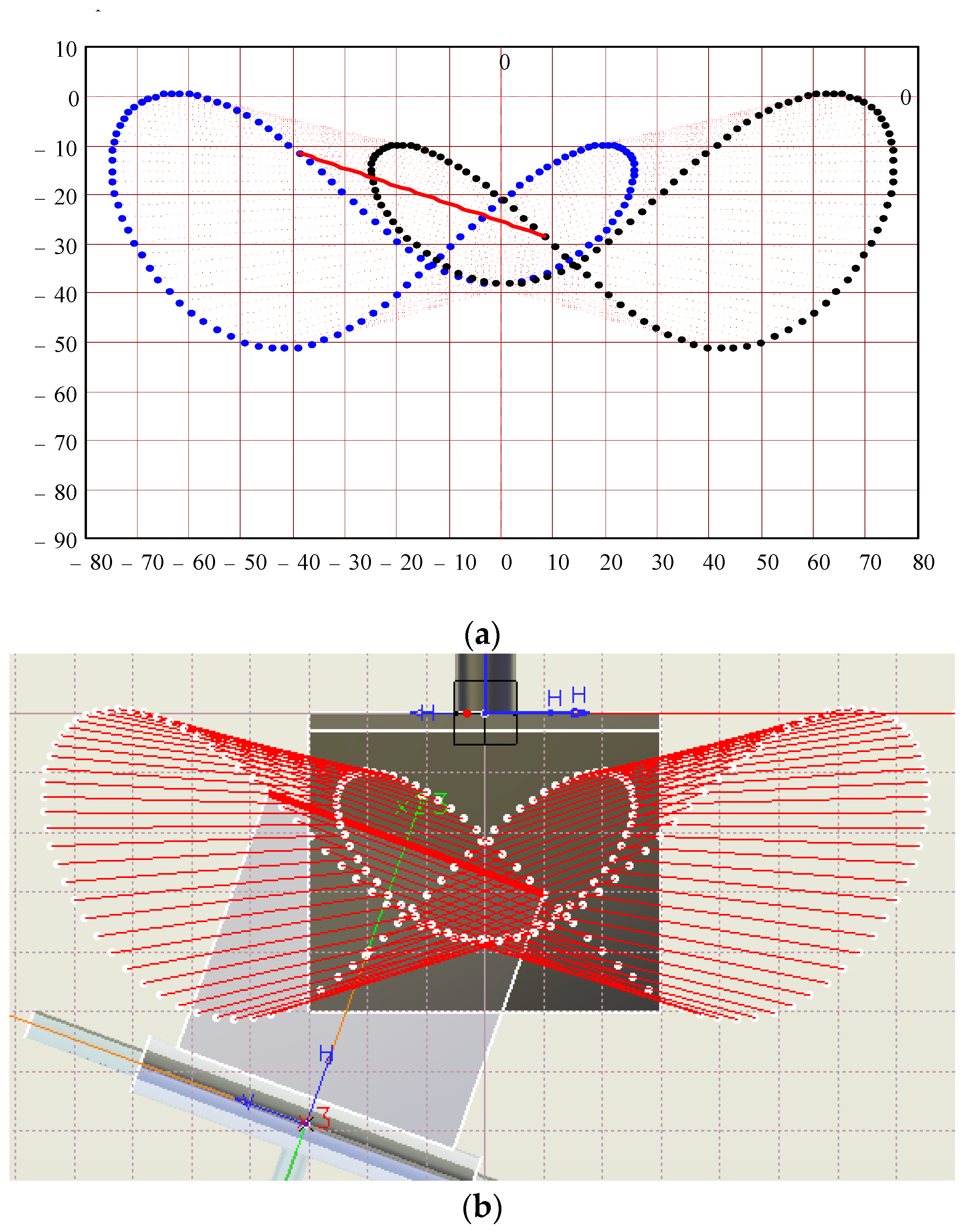
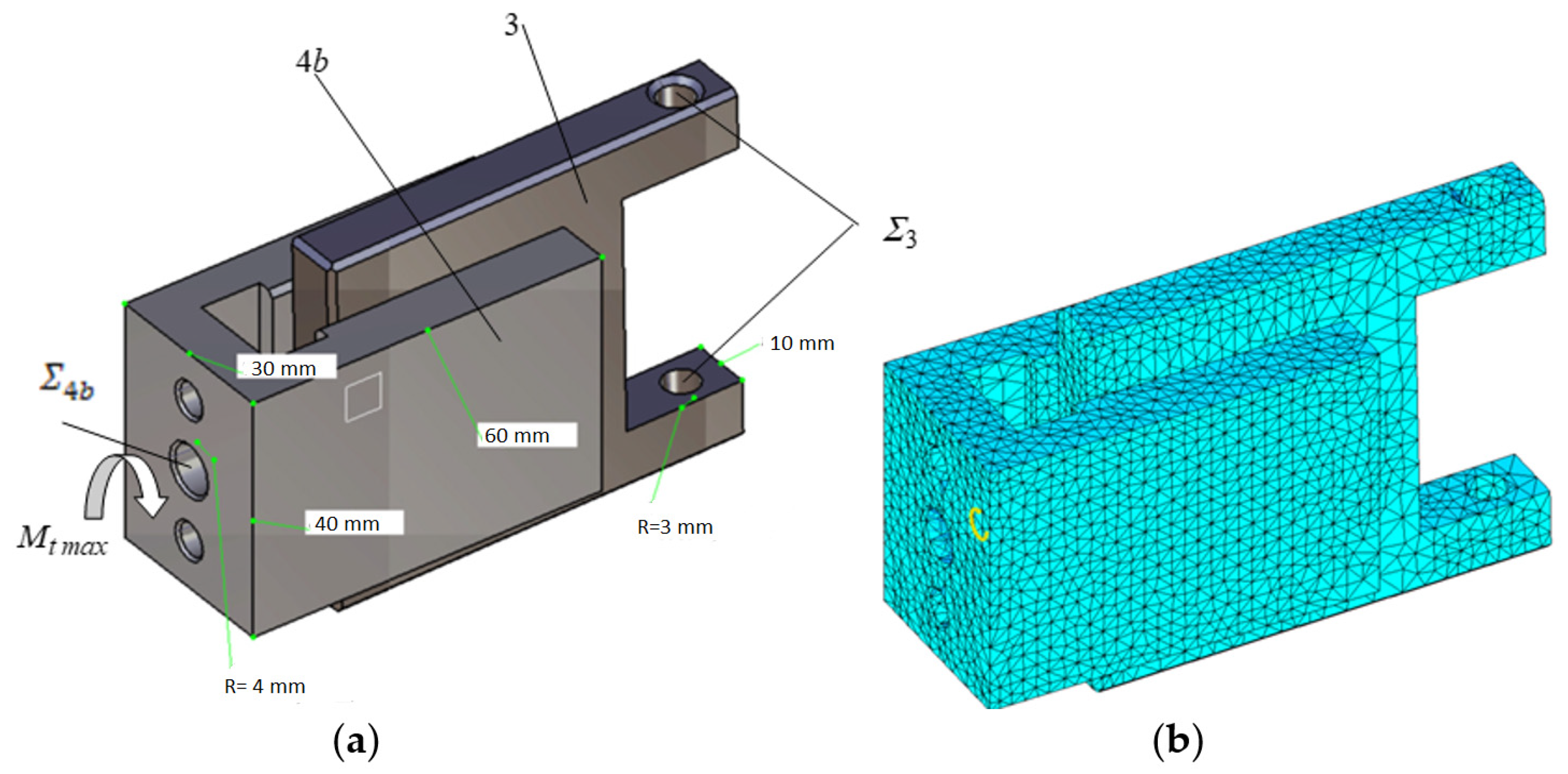
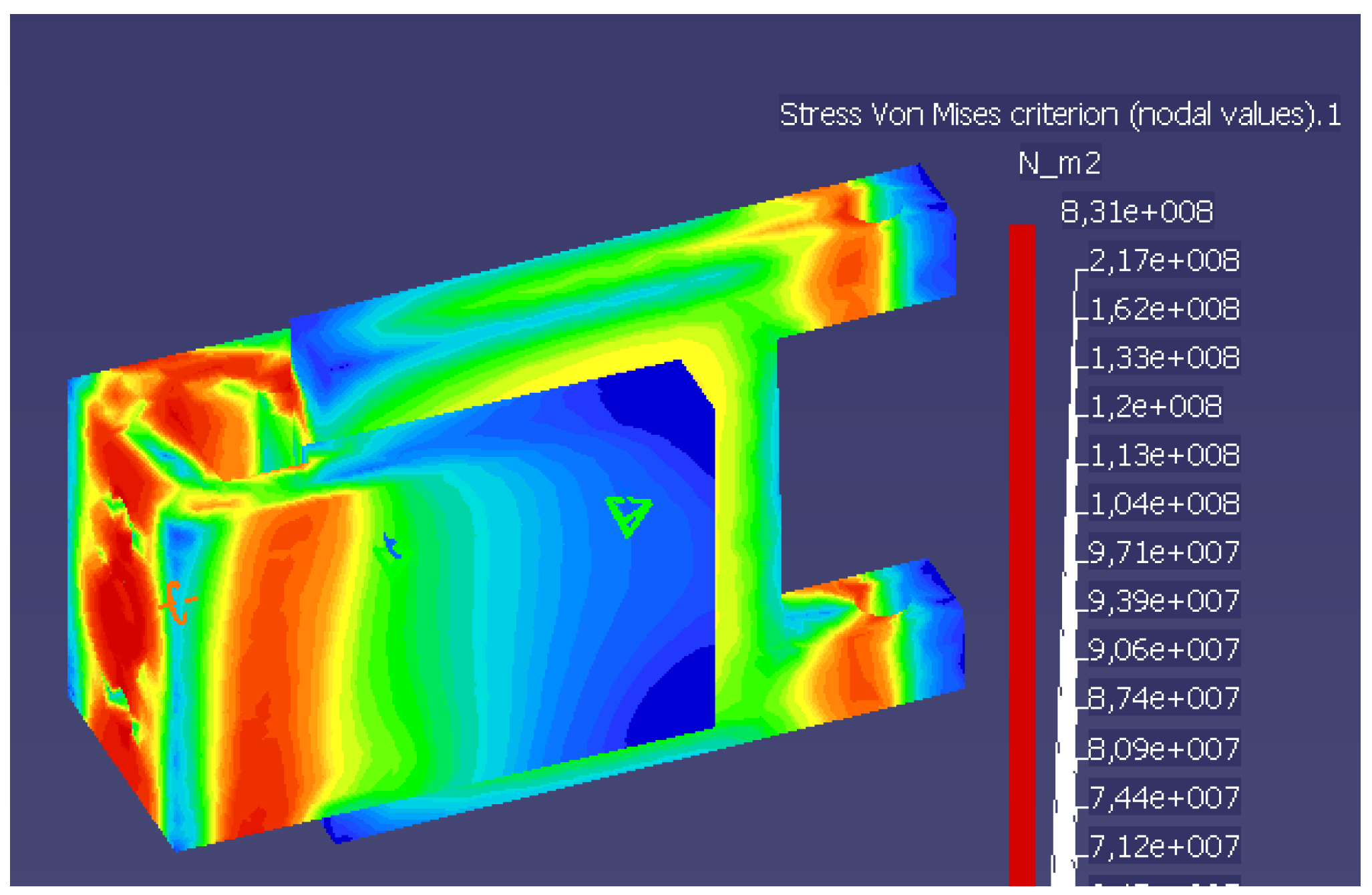
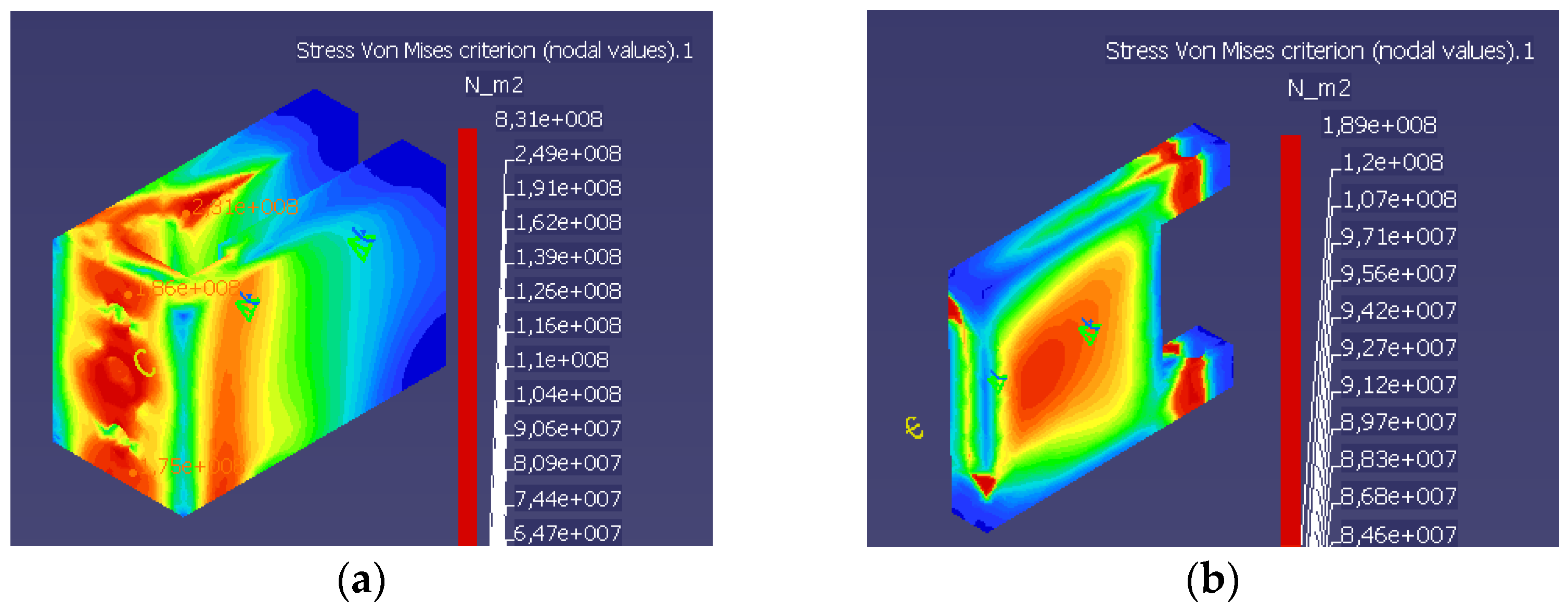
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uicker, J.J., Jr.; Pennock, G.R.; Shigley, J.E. Theory of Machines and Mechanisms, 4th ed.; Oxford University Press: New York, NY, USA, 2010; pp. 368–370. [Google Scholar]
- Sclater, N. Mechanisms and Mechanical Devices Sourcebook, 5th ed.; McGraw Hill: New York, NY, USA, 2011; pp. 109–110. [Google Scholar]
- Tsai, L.-W. Mechanism Design: Enumeration of Kinematic Structures According to Function; CRC Press: Boca Raton, FL, USA, 2000; 328p. [Google Scholar]
- Phillips, J. Freedom in Machinery; Cambridge University Press: Cambridge, UK, 2007; 448p. [Google Scholar]
- Schwartz, L. Theorie des distributions et transformation de Fourier. Ann. Univ. Grenoble-Sect. Sci. Math. Phys. 1948, 23, 7–24. [Google Scholar]
- Ata, E.; Kıymaz, O. New generalized Mellin transform and applications to partial and fractional differential equations. Int. J. Math. Comput. Eng. 2023, 1, 45–66. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012; pp. 43–75. [Google Scholar]
- Dilao, R. Dynamical System and Chaos: An Introduction with Applications; Springer Nature Switzerland AG: Cham, Switzerland, 2023; pp. 105–132. [Google Scholar]
- Lorenzi, M.G.; Francaviglia, M. Art & Mathematics in Antoni Gaudi’s architecture: “La Sagrada Família”. J. Appl. Math. 2010, 3, 125–146. [Google Scholar]
- Zhu, N.; Tian, J. Numerical simulation of vortex vibration in main girder of cable-stayed bridge based on bidirectional fluid–structure coupling. Appl. Math. Nonlinear Sci. 2022. ahead of print. [Google Scholar] [CrossRef]
- Yan, L. Application of renewable energy decorative materials in modern architectural design under low-carbon concept. Appl. Math. Nonlinear Sci. 2022. ahead of print. [Google Scholar] [CrossRef]
- Bi, S.; Ye, X.; Shao, Y. Electronic properties of diamond semiconductor materials: Based on response surface model. Appl. Math. Nonlinear Sci. 2023. ahead of print. [Google Scholar] [CrossRef]
- Irgens, F. Rheology and Non-Newtonian Fluids; Springer: New York, NY, USA, 2013; pp. 143–167. [Google Scholar]
- Wang, Y. Numerical Simulation and Characteristic Analysis of Music Based on Nonlinear Equations. Appl. Math. Nonlinear Sci. 2023. ahead of print. [Google Scholar] [CrossRef]
- Chi, J.; Alahmadi, D. Badminton players’ trajectory under numerical calculation method. Appl. Math. Nonlinear Sci. 2022, 7, 217–228. [Google Scholar] [CrossRef]
- Ball, R.S. The Theory of Screws; A Study in the Dynamics of Rigid Body; Hodges, Foster and CO: Dublin, Ireland, 1876; pp. 38–43. [Google Scholar]
- Phillips, J. Freedom in Machinery; Cambridge University Press: Cambridge, UK, 1984; pp. 45–58. [Google Scholar]
- Clifford, W.K. Preliminary Sketch of Bi-quaternions. Proc. Lond. Math. Soc. 1873, 4, 381–395. [Google Scholar]
- Angeles, J. The Application of Dual Algebra to Kinematic Analysis. In Computational Methods in Mechanical Systems—NATO ASI Series F; Springer-Verlag Berlin Heidelberg: Berlin, Germany, 1998; Volume 161, pp. 3–32. ISBN 978-3-662-03729-4_1. [Google Scholar]
- Hamilton, W.R. On quaternions, or on a new system of imaginaries in algebra. Phil. Magaz. J. Sci. 2009, 25, 489–495. [Google Scholar]
- Yang, A.T. Application of Quaternion Algebra and Dual Numbers to the Analysis of Spatial Mechanisms. Ph.D. Thesis, Columbia University, New York, NY, USA, 1963. [Google Scholar]
- Ho, C.Y. Tensor analysis of spatial mechanisms. IBM J. Res. Dev. 1966, 10, 207–212. [Google Scholar] [CrossRef]
- Mangeron, D.; Drăgan, B. Kinematic study with new matrix-tensor methods for four link spatial mechanisms. Rev. Mech. Appl. 1962, 7, 1539–1551. [Google Scholar]
- Baigunchekov, Z.; Laribi, M.A.; Carbone, G.; Mustafa, A.; Amanov, B.; Zholdassov, Y. Structural-Parametric Synthesis of the RoboMech Class Parallel Mechanism with Two Sliders. Appl. Sci. 2021, 11, 9831. [Google Scholar] [CrossRef]
- Barbin, E.; Menghini, M.; Volkert, K. Descriptive Geometry, The Spread of a Polytechnic Art—The Legacy of Gaspard Monge; Springer Nature: Cham, Switzerland, 2019; pp. 3–18. [Google Scholar]
- Yoshikawa, T. Foundations of Robotics: Analysis and Control; MIT Press: Cambridge, MA, USA, 2003; pp. 259–262. [Google Scholar]
- Davidson, J.K.; Hunt, K.H. Robots and Screw Theory: Applications of Kinematics and Statics to Robotics; Oxford University Press Inc.: New York, NY, USA, 2004; pp. 59–94. [Google Scholar]
- Lee, R.S.; Lin, Y.H. Development of universal environment for constructing 5-axis virtual machine tool based on modified D–H notation and OpenGL. Robot. Comput.-Integr. Manuf. 2010, 26, 253–262. [Google Scholar] [CrossRef]
- Tsai, C.Y.; Lin, P.D. The mathematical models of the basic entities of multi-axis serial orthogonal machine tools using a modified Denavit–Hartenberg notation. Int. J. Adv. Manuf. Technol. 2009, 42, 1016–1024. [Google Scholar] [CrossRef]
- Benignus, C.; Buschner, P.; Meier, M.K.; Wilken, F.; Rieger, J.; Beckmann, J. Patient Specific Instruments and Patient Individual Implants—A Narrative Review. J. Pers. Med. 2023, 13, 426. [Google Scholar] [CrossRef]
- Greco, C.; Weerakkody, T.H.; Cichella, V.; Pagnotta, L.; Lamuta, C. Lightweight Bioinspired Exoskeleton for Wrist Rehabilitation Powered by Twisted and Coiled Artificial Muscles. Robotics 2023, 12, 27. [Google Scholar] [CrossRef]
- Lenarčič, J.; Bruno Siciliano, B. Advances in Robot Kinematics; Springer: Cham, Switzerland, 2020; pp. 1–6, 98–108. [Google Scholar] [CrossRef]
- Doroftei, I.; Cazacu, C.-M.; Alaci, S. Design and Experimental Testing of an Ankle Rehabilitation Robot. Actuators 2023, 12, 238. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, H.; Zhang, L. Study of frictional wear properties of materials for mechanical seals. Appl. Math. Nonlinear Sci. 2023. ahead of print. [Google Scholar] [CrossRef]
- Vorro, J.; Bush, T.R.; Rutledge, B.; Li, M. Kinematic measures during a clinical diagnostic technique for human neck disorder: Inter- and intraexaminer comparisons. BioMed Res. Int. 2013, 2013, 950719. [Google Scholar] [CrossRef]
- Yoon, K.; Cho, S.-M.; Kim, K.G. Coupling Effect Suppressed Compact Surgical Robot with 7-Axis Multi-Joint Using Wire-Driven Method. Mathematics 2022, 10, 1698. [Google Scholar] [CrossRef]
- Zhang, J.; Ng, N.; Scott, C.E.H.; Blyth, M.J.G.; Haddad, F.S.; Macpherson, G.J.; Patton, J.T.; Clement, N.D. Robotic arm-assisted versus manual unicompartmental knee arthroplasty. Bone Jt. J. 2022, 104, 541–548. [Google Scholar] [CrossRef]
- Hunt, K.H. Kinematic Geometry of Mechanisms; Oxford University Press: Oxford, UK, 1990; pp. 30–51. [Google Scholar]
- Angeles, J. Spatial Kinematic Chains: Analysis–Synthesis–Optimization; Springer: Berlin/Heidelberg, Germany, 1982; pp. 189–218. [Google Scholar]
- McCarthy, J.M.; Soh, G.S. Geometric Design of Linkages; Springer: Berlin/Heidelberg, Germany, 2010; pp. 253–279. [Google Scholar]
- Yi, L.; Leinonen, T. On the Dimensional Synthesis of Spatial Four-and Five-Bar Linkage, Romansy 14: Theory and Practice of Robots and Manipulators, Proceedings of the Fourteenth CISM-IFToMM Symposium; Bianchi, G., Guinot, J.-C., Rzymkowski, C., Eds.; Springer: Vienna, Austria, 2002; pp. 407–419. [Google Scholar] [CrossRef]
- Segreti, A. Mechanism for the Transmission of Rotary Movement between two Shafts having Non-Parallel, Non-Coplanar Axes. U.S. Patent WO 02/103220 A2, 27 December 2002. [Google Scholar]
- Seherr-Thoss, H.C.; Schmelz, F.; Aucktor, E. Universal Joints and Driveshafts. Analysis, Design, Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 53–79; discussion 109–245. [Google Scholar]
- Gladwel, G.M.L. Contact Problems in the Classical Theory of Elasticity; Sijthoff & Noordhoff: Hague, The Netherlands, 1980; p. 716. [Google Scholar]
- Hills, D.A.; Nowell, D.; Sackfield, A. Mechanics of Elastic Contacts; Elsevier Butterworth-Heinemann: Oxford, UK, 1993; pp. 198–226. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; pp. 84–106. [Google Scholar] [CrossRef]
- Gonzales-Palacios, M.A.; Angeles, J. Cam Synthesis; Springer: Dordrecht, The Netherlands, 1993; pp. 37–53. [Google Scholar]
- Inurritegui, A.; Larranaga, J.; Arana, A.; Ulacia, U. Load distribution and tooth root stress of highly crowned spherical gear couplings working at high misalignment angles. J. Mech. Mach. Theory 2023, 179, 105104. [Google Scholar] [CrossRef]
- Inurritegui, A.; Larranaga, J.; Arana, A.; Ulacia, U. Numerical-experimental analysis of highly crowned spherical gear couplings working at high misalignment angles. J. Mech. Mach. Theory 2023, 183, 105260. [Google Scholar] [CrossRef]
- Inurritegui, A.; Larranaga, J.; Arana, A.; Ulacia, U. Spherical gear coupling design space analysis for high misalignment applications. Mech. Mach. Theory 2022, 173, 104837. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004; pp. 441–474. [Google Scholar]
- Vullo, V. Gears, Volume 1: Geometric and Kinematic Design; Springer: Cham, Switzerland, 2021; pp. 139–151. [Google Scholar]
- Alaci, S.; Muscă, I.; Pentiuc, Ș.-G. Study of the Rolling Friction Coefficient between Dissimilar Materials through the Motion of a Conical Pendulum. Materials 2020, 13, 5032. [Google Scholar] [CrossRef] [PubMed]
- Popov, V.L. Contact Mechanics and Friction. Physical Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 55–69. [Google Scholar]
- Alaci, S.; Cerlinca, D.A.; Ciornei, F.C.; Filote, C.; Frunza, G. Experimental Highlight of Hysteresis Phenomenon in Rolling Contact. J. Phys. Conf. Ser. 2015, 585, 012010. [Google Scholar] [CrossRef]
- Hayes, M.J.D.; Rotzoll, M.; Bucciol, Q.; Copeland, A.A. Planar and spherical four-bar linkage vi−vj algebraic input–output equations. J. Mech. Mach. Theory 2023, 182, 105222. [Google Scholar] [CrossRef]
- Luzi, L.; Sancisi, N.; Parenti-Castelli, V. The Potential of the 7R-R Closed Loop Mechanism to Transfer Motion Between Two Shafts with Varying Angular Position. In Interdisciplinary Applications of Kinematics. Mechanisms and Machine Science; Kecskeméthy, A., Geu Flores, F., Carrera, E., Elias, D., Eds.; Springer: Cham, Switzerland, 2019; Volume 71, pp. 185–195. [Google Scholar] [CrossRef]
- Watanabe, K.; Sekine, T.; Nango, J. Kinematic Analysis of RSCR Spatial Four-Link Mechanisms. Trans. Jpn. Soc. Mech. Eng. Ser. C 1997, 63, 2482–2489. [Google Scholar] [CrossRef] [Green Version]
- Urbinati, F.; Pennestrì, E. Kinematic and Dynamic Analyses of the Tripode Joint. Multibody Syst. Dyn. 1998, 2, 355–367. [Google Scholar] [CrossRef]
- Akbil, E.; Lee, T.W. On the motion characteristics of tripode joints. Part 1: General case; Part 2: Applications. ASME J. Mech. Transm. Autom. Des. 1984, 106, 228–241. [Google Scholar] [CrossRef]
- Lobontiu, N.; Hunter, J.; Keefe, J.; Westenskow, J. Tripod mechanisms with novel spatial Cartesian flexible hinges. J. Mech. Mach. Theory 2022, 167, 104521. [Google Scholar] [CrossRef]
- Wang, X.F.; Chang, D.G.; Wang, J.Z. Kinematic investigation of tripod sliding universal joints based on coordinate transformation. Multibody Syst. Dyn. 2009, 22, 97–113. [Google Scholar] [CrossRef]
- Alaci, S.; Ciornei, F.C.; Filote, C. Considerations upon a New Tripod Joint Solution. Mechanika 2013, 19, 567–574. [Google Scholar] [CrossRef]
- Alaci, S.; Pentiuc, R.D.; Ciornei, F.C.; Buium, F.; Rusu, O.T. Kinematics analysis of the swash plate mechanism. IOP MSE 2019, 568, 012017. [Google Scholar]
- Hartenberg, R.; Denavit, J. Kinematic Synthesis of Linkages, 1st ed.; McGraw-Hill Inc.: New York, NY, USA, 1964; pp. 343–368. [Google Scholar]
- Denavit, J.; Hartenberg, R.S. A kinematic notation for lower-pair mechanisms based on matrices. J. Appl. Mech. 1955, 22, 215–221. [Google Scholar] [CrossRef]
- Alaci, S.; Pentiuc, R.D.; Doroftei, I.; Ciornei, F.C. Use of dual numbers in kinematical analysis of spatial mechanisms. Part II: Applying the method for the generalized Cardan mechanism. IOP MSE 2019, 568, 12032. [Google Scholar] [CrossRef] [Green Version]
- Fischer, I. Dual-Number Methods in Kinematics, Statics and Dynamics; CRC Press: New York, NY, USA, 1999; pp. 54–95. [Google Scholar]
- McCarthy, J.M. Introduction in Theoretical Kinematics, 3rd ed.; MIT Press: Cambridge, MA, USA, 2018; pp. 103–108. [Google Scholar]
- Yang, A.T.; Freudenstein, F. Application of Dual-Number Quaternion Algebra to the Analysis of Spatial Mechanisms. J. Appl. Mech. 1964, 31, 300–308. [Google Scholar] [CrossRef]
- Dimentberg, F.M. The Screw Calculus and Its Applications in Mechanics; Foreign Technology Division Translation FTD-HT-23-1965; U.S. Department of Commerce: Washington, DC, USA, 1969; pp. 1632–1667.
- Angeles, J. Rational Kinematics; Springer: New York, NY, USA, 1998; pp. 12–34. [Google Scholar]
- Cao, A.; Jing, Z.; Ding, H. A general method for kinematics analysis of two-layer and two-loop deployable linkages with coupling chains. J. Mech. Mach. Theory 2020, 152, 103945. [Google Scholar] [CrossRef]
- Molotnikov, V.; Molotnikova, A. Kinematic Analysis of Mechanisms. In Theoretical and Applied Mechanics; Springer Nature: Cham, Switzerland, 2023; pp. 299–310. [Google Scholar] [CrossRef]
- Roupa, I.; Gonçalves, S.B.; Silva, M.T. Kinematics and dynamics of planar multibody systems with fully Cartesian coordinates and a generic rigid body. J. Mech. Mach. Theory 2023, 180, 105134. [Google Scholar] [CrossRef]
- Uicker, J.J., Jr.; Denavit, J.; Hartenberg, R.S. An Iterative Method for the Displacement Analysis of Spatial Mechanisms. J. Appl. Mech. 1964, 31, 309–314. [Google Scholar] [CrossRef]
- EN ISO 3952-1; Kinematic Diagrams—Graphical Symbols. Part 1. The European Standard: Geneva, Switzerland, 2019; pp. 1–25.
- Maxfield, B. Engineering with Mathcad; Butterworth-Heinemann, Elsevier: Oxford, UK, 2006; pp. 287–289. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alaci, S.; Doroftei, I.; Ciornei, F.-C.; Romanu, I.-C.; Ciocirlan, T.-M.; Ciornei, M.-C. Proposed Shaft Coupling Based on RPRRR Mechanism: Positional Analysis and Consequences. Axioms 2023, 12, 707. https://doi.org/10.3390/axioms12070707
Alaci S, Doroftei I, Ciornei F-C, Romanu I-C, Ciocirlan T-M, Ciornei M-C. Proposed Shaft Coupling Based on RPRRR Mechanism: Positional Analysis and Consequences. Axioms. 2023; 12(7):707. https://doi.org/10.3390/axioms12070707
Chicago/Turabian StyleAlaci, Stelian, Ioan Doroftei, Florina-Carmen Ciornei, Ionut-Cristian Romanu, Toma-Marian Ciocirlan, and Mariana-Catalina Ciornei. 2023. "Proposed Shaft Coupling Based on RPRRR Mechanism: Positional Analysis and Consequences" Axioms 12, no. 7: 707. https://doi.org/10.3390/axioms12070707
APA StyleAlaci, S., Doroftei, I., Ciornei, F.-C., Romanu, I.-C., Ciocirlan, T.-M., & Ciornei, M.-C. (2023). Proposed Shaft Coupling Based on RPRRR Mechanism: Positional Analysis and Consequences. Axioms, 12(7), 707. https://doi.org/10.3390/axioms12070707






