Abstract
In this paper, we discuss some of the key properties of sum-free subsets of abelian groups. Our discussion has been designed with a broader readership in mind and is hence not overly technical. We consider answers to questions like the following: How many sum-free subsets are there in a given abelian group G? What are its sum-free subsets of maximum cardinality? What is the maximum cardinality of these sum-free subsets? What does a typical sum-free subset of G look like?
1. Introduction
Here, we present the key progress made on sum-free subsets of abelian groups. Our main aim is to convey this information without being overly technical in order to make the topic accessible to a broader readership. Let us begin with a definition.
Definition 1.
Let G be an abelian group. A subset S of G is sum-free if for all , we have that .
In the case of , under the usual addition, one can easily come up with simple examples. For instance, , , and any set composed solely of odd numbers. In 1916, Schur [1] was the first to start work that would eventually lead to the study of sum-free sets. He did so by proving that for a sufficiently high , every finite colouring of the integers in the interval contains a monochromatic triple , usually referred to as a Schur triple, such that [2]. Cameron and Erdős [3] also made a considerable contribution to this topic, focusing in particular on sum-free subsets of positive integers (for details, see Section 3).
The literature on sum-free sets presents very interesting questions. For instance, Alon et al. [4] and Green and Ruzsa [5] posed the following questions: How many sum-free subsets are there in G? What are the sum-free subsets of maximum cardinality? What is the maximum cardinality of these sum-free subsets? What does a typical sum-free subset of G look like? Here, we address these questions, among others.
We organised our paper as follows. Section 2 presents the basic methods, both computational and algebraic, capable of identifying sum-free sets. In addition, we discuss periodic sum-free sets, presenting methods to generate infinite sum-free subsets of positive integers. Section 3 considers the bounds on the quantity of sum-free sets. It first discusses these bounds on subsets of positive integers and then provides a more general account regarding any finite abelian group. Section 4 deals with maximal sum-free sets, that is, a broader class of sum-free sets that includes sum-free sets of maximum cardinality. Section 5 reviews our main findings and presents our conclusions.
2. Identifying Sum-Free Sets
In this section, we are particularly interested in the following question: Given an abelian group G, finite or not, are there methods to identify its sum-free subsets? Before we can explore potential answers, it is helpful to present the bounds that follow. In the case of sum-free integer subsets of , Erdős [6] showed that this interval contains a sum-free set of cardinality . Alon and Kleitman [7] went even further by devising the more general theorem below.
Theorem 1.
Let G be a finite abelian group. For every , there exists a sum-free subset of B with cardinality greater than .
Alon and Kleitman proved the above theorem by first observing that the sets and are sum-free subsets of . Given that is cyclic, it has a subgroup for every d dividing n, with an order of . They then provided a case analysis, computing for all divisors d of n and , finding that
The above result eventually led to the bound in Theorem 1. Alon and Kleitman then made use of a theorem by Rhemtulla and Street [8] regarding the maximum cardinality of sum-free subsets of elementary abelian groups to show that is, in fact, optimal.
Theorem 1 provides a lower bound for the cardinality of the largest sum-free subset of G. This can be helpful if one is trying to identify all of its sum-free subsets. That is, if no sum-free set of cardinality greater than has been identified, then the list is not complete.
The rest of this section discusses methods for helping with the identification of sum-free sets. We explore three simple algorithms (for completeness) capable of generating sum-free sets, periodic sum-free sets, and other useful algebraic methods.
2.1. Computational Approaches
Cameron [9] described an algorithm to identify sum-free subsets of positive integers. As he put it, when examining a number a, if this is not the sum of two elements of a set S, then choose uniformly at random whether to put a in S. This informal description does not clarify how a is selected or what criteria should be used to stop the algorithm. Although these points may seem negative, his approach makes the algorithm easily adaptable to particular cases.
We formalise the above steps in Algorithm 1. We decided to set the first value to be user-defined (it could be chosen at random). We also introduced a condition regarding the cardinality of the sum-free set to be identified to ensure an eventual completion. This naive algorithm is capable of identifying a sequence of nested sum-free subsets of . If applied to a finite group, it can be easily modified to identify the maximal sum-free sets (for details on the latter, see Section 4), which is what we mean by adaptable. Unfortunately, this algorithm cannot identify all sum-free sets. For instance, it is unable to identify two sum-free sets with an empty intersection.
Considering the above information, one may wonder if it is possible to have an algorithm capable of identifying all sum-free sets. The obvious approach would be to test each of the possible subsets of G and list those that are sum-free. However, this is rather computationally expensive, running at . Algorithm 2, where we use a sequence of binary numbers to identify each subset, formalises the steps. Note that this algorithm can be made parallel by supplying k computers with different sets of binary numbers.
Taking into account the above prohibitively high exponential bound, Kolountzakis [10] provided a partial solution that applies to integer sum-free sets. We have that every set of integers contains a sum-free subset S with (see Theorem 1). Kolountzakis proposed an algorithm capable of identifying S in polynomial time. Note that S is a large sum-free set that contains more sum-free sets if (any subset of a sum-free set is sum-free), but it may not contain all; hence, our use of the word partial. Kolountzakis’ algorithm is based on the following theorem.
| Algorithm 1: Cameron’s algorithm to identify sum-free sets. |
Require: , where a is the initial element to be considered, and b is the cardinality of the sum-free subset of to be identified. Ensure: S is a sum-free subset of such that . while
do Identify an element uniformly at random. . rand(). if and then . end if end while |
| Algorithm 2: Identifying all sum-free sets. |
Require: An additive non-trivial finite abelian group G, with identity e. Ensure: S is a set containing all sum-free subsets of G. Put each element of in a vector . for to do Create a vector containing the binary value of i spread over its components. Create a set A such that the element if b, for . if then Put A in S. end if end for |
Theorem 2.
Let be a prime and , where is non-negative and defined on . Then, there exists a sum-free set such that .
In the above theorem, refers to the multiplicative group over . Kolountzakis proved the above theorem by first noticing that is sum-free in and . Kolountzakis then built on B by identifying an element for which . Finally, he defined the sum-free set , proving S is sum-free and has the required cardinality. Algorithm 3 presents the steps used to identify S, which defines , with A being a set of integers.
Kolountzakis made some considerations regarding the computational cost of his algorithm. He noted that the number of prime factors of an integer x is at most . Hence, the number of primes in the factorisation of any is at most . He then applied the Prime Number Theorem of arithmetic progressions to state that there is a prime , which does not divide any , concluding that the algorithm can be carried out in polynomial time.
| Algorithm 3: Identifying a large sum-free set (Kolountzakis). |
| Require: A set of integers . Ensure: S is a sum-free subset of A. Identify a prime with such that it divides no . Compute for all . Identify a for which . Construct the set Construct the set . |
2.2. Periodic Sum-Free Sets
The set of odd integers is probably the most well-known example of a periodic sum-free set. There are, of course, other periodic sum-free subsets of integers.
Lemma 1.
Let , with , S is sum-free.
Proof.
Let . Then, and for some . Let us assume, for a contradiction, that . This would mean that for some , which can be simplified to . However, the latter is a contradiction, as we have . □
Tran [11] stated that the sets and are sum-free. This is indeed the case, and we can devise another more general result.
Lemma 2.
Let A be a sum-free subset of and , S is sum-free.
Proof.
Let . Then, and for some and . We have that . Given , we have that . □
2.3. Other Algebraic Approaches
In this section, we explore other algebraic approaches to identify sum-free subsets of G. This task becomes considerably easier if one already knows one such, preferably large, sum-free set.
Proposition 1.
Let S be a sum-free subset of G, then any is sum-free.
Proof.
A can only contain elements that are in S. Hence, A is sum-free. □
Proposition 2.
Let A and B be sum-free subsets of an abelian group G. The intersection of A and B is sum-free.
Proof.
We have that . Hence, Proposition 1 tells us that is sum-free. □
Proposition 2 has an interesting consequence, first pointed out by Cameron and Erdős [3] for the case of integer sum-free subsets of , which we show in a more general form below.
Corollary 1.
Let be a family of sum-free subsets of an abelian group G. is closed under intersection.
If there is no known sum-free subset for the group in question but this group is finite and a subgroup H is known, then one can use the lemma below to identify sum-free sets.
Lemma 3.
Let H be a proper subgroup of a finite group G. Given an element , the coset is sum-free.
Proof.
Let us assume that is not sum-free. Then, for some and . This implies , and by consequence, . However, this contradicts the hypothesis. Hence, is sum-free. □
3. Counting Sum-Free Sets
We begin this section by discussing the foundational work of Cameron and Erdős [3], further restricting the definition of sum-free sets to focus solely on positive integers (see Section 3.1–Section 3.3). Section 3.4 generalises our discussion to any abelian group.
3.1. The Cameron and Erdős Conjecture
Let S be a sum-free set of integers, such that with the largest element k. In their seminal work, Cameron and Erdős [3] started their analysis of sum-free sets like S with a straightforward remark, leading to interesting consequences. For each integer , S contains at most one component of the pair . Hence, , and, consequently, .
This is rather interesting because it easily gives us an upper bound for . Cameron and Erdős [3] continued stating that, in the case of positive integers, the only sum-free sets of cardinality are:
- The odd numbers in the interval ;
- If n is odd, ;
- If n is even, and .
Any set composed solely of odd numbers is sum-free, and it is straightforward to see that any of the above sets have the required cardinality of . Freiman [12] proved that the above rules hold for . However, using Algorithm 2, we have found the following exceptions for : , ; , and ; and , . These are the only exceptions to the above rules.
Clearly, the existence of the above exceptions does not invalidate the stated upper bound for . Let be the number of sum-free sets in . In this regard, Cameron and Erdős stated that
Other authors, such as Calkin [13], reached a similar conclusion that but via a completely different path (for details, see Section 3.2). Cameron and Erdős [3] went further and conjectured that is, in fact, bounded. They believed that this ratio tends to the limits of approximately and , depending on whether n tends to infinity through odd or even numbers. They then introduced the following theorem.
Theorem 3.
There is an absolute constant c such that the number of sum-free sets of whose least element is greater than does not exceed .
The complete proof for the above theorem can be found in [3]. Generally speaking, it begins by fixing and counting the sum-free subsets of , with no element lower than . This proof shows that such sum-free sets fall within three categories and that if one were to sum the quantity of all possible such sets, the answer would be at most . Given that c is a constant, Cameron and Erdős conjectured that is .
3.2. Advances on the Cameron and Erdős Conjecture
The Cameron and Erdős conjecture that is is rather difficult to prove in full. An attempt by Freiman [12] addressed a weaker version of this conjecture. Freiman showed that the number of sum-free sets for which has the bound , where k is the largest element in the set. This is not quite the same as showing that this bound applies to , that is, the number of all sum-free sets in , but it is certainly a good start. His approach was to first prove the following.
Theorem 4.
If S is a sum-free set of positive integers such that , where , then either (i) S is composed solely of odd numbers, or (ii) S contains both odd and even numbers, , and .
Freiman began his proof by defining that a set S is difference-free if , where . He then briefly showed that sum-free and difference-free are equivalent properties of a set. Note that implies that there are such that . This also means that if a is positive, then as . Hence, contains positive differences , negative differences , and zero. We have that ; thus, . Freiman also stated that S and are subsets of . This is true for S by definition.
Freiman continued by stating that if S is difference-free, then . This is indeed the case because it could only be false if S and shared elements; however, the definition of difference-free tells us that they do not. Freiman went on to prove Theorem 4 by analysing the different possible greatest common divisors over the elements of S subtracted by min(), and using the above inequality.
Calkin [13] provided another step for proving the Cameron and Erdős conjecture with the theorem below.
Theorem 5.
The number of sum-free sets of integers contained in is for every .
Again, this is not quite the same as the original conjecture that is , but it is certainly close. Calkin proved the above theorem using a theorem guaranteeing the existence of a function such that every integer subset of of size contains an arithmetic progression of a certain length (for details, see [14]), and introducing other three lemmas. The general idea behind Calkin’s proof is that it is possible to find a particular arithmetic progression shared by all integer sum-free sets of a particular size. Then, one can count how many possible sum-free sets in contain this particular arithmetic progression.
Alon [15] also made constructive steps towards proving the Cameron and Erdős conjecture with the following theorem.
Theorem 6.
Any (finite, undirected, and simple) k-regular graph on n vertices has no more than independent sets.
The above theorem is essentially an upper bound on the number of non-adjacent vertices in a graph. Alon proved Theorem 6 by showing that the upper bound for the probability of a certain event happening on a set of mutually independent events is exponentially small. By combining this with random two-colourings of a graph (which are mutually independent), he showed that certain colourings would not take place; hence, the upper bound in Theorem 6. By applying Theorem 6 on Cayley graphs, Alon reached the following corollary.
Corollary 2.
Let G be a group and . Then, the number of A-free subsets of G does not exceed .
Alon defined an A-free set as follows. Let with G finite. S is A-free if . That is, if there is no and such that . The concept of sum-free is just a special case of the above definition, in which .
There are two important things to note in Corollary 2. First, it implies Theorem 5; Alon presented the latter as a further corollary. Second, this corollary makes no mention of our usual interval but instead talks of a group; thus, it is more general. We decided to leave it in this section rather than Section 3.4 (which discusses sum-free subsets of abelian groups) because of its link to the Cameron and Erdős conjecture.
3.3. Proving the Cameron and Erdős Conjecture
The Cameron and Erdősconjecture was finally proven independently by Green [16] and Sapozhenko [17]. Green did so by proving the following.
Theorem 7.
The number of sum-free sets of integers in is asymptotically , where takes two different constant values depending on the parity of n.
Green first identified a family of subsets of with three properties:
- Each is almost sum-free. That is, the number of 3-tuples with and is .
- . That is, does not contain too many sets.
- Every sum-free set of integers in is a subset of a member of .
Let S be a sum-free set of integers in ; property (3) of tells us that for some . Property (2) ensures that the number of sets in is only , so the number of sum-free sets S in for which is . By supposing , Green was able to determine that with an that is , S either belongs to an interval of a particular length (with an error of elements) or it has even elements. Green then showed that with exceptions, all sum-free S in fall under two categories:
- S consists entirely of odd numbers.
- S is contained in the interval .
Green then applied a result by Cameron and Erdős [3], which estimates the number of sum-free sets in the interval , thereby proving Theorem 7 and, consequently, the conjecture by Cameron and Erdős.
The original proof of the Cameron and Erdős conjecture by Sapozhenko has been published in Russian [17], with a later version in English [18]. In the latter, Sapozhenko reached the same conclusion for Theorem 7. To do so, he defined to be the number of sum-free subsets in the interval , with the shorthand for (matching our previous notation), and for the number of sum-free subsets of odd numbers also in . He then proved the following theorem using a purely combinatorial approach.
Theorem 8.
.
We have that relates to half of all subsets in , so . The above theorem implies that almost all sum-free sets in are either composed entirely of odd numbers or are contained in the interval . This is a rather similar finding to that of Green [16]. Sapozhenko pointed out that Theorem 8 implies Theorem 7. To prove the former, Sapozhenko first made a couple of important definitions. Let and be families of subsets of . The family covers if, for any , there exists a such that .
Sapozhenko defined some conditions that must hold for to be called correct. He then defined to be an almost correct system of containers of , if is correct for some subfamily such that . With these definitions at hand, we can now go back to Theorem 8.
Let and represent the families of all sum-free sets in the intervals and , respectively, and represent the family of all sum-free sets composed of odd numbers in . Now, let . Sapozhenko showed that has an almost correct system of containers. Hence, there exists a subfamily of , , with a correct system of containers. Thus, . Sapozhenko proved that , and, consequently, . So, , leading to Theorem 8.
One could be forgiven for thinking that given the conjecture by Cameron and Erdős has been proven (so, it is now a theorem), mathematicians would no longer be interested. However, in 2014, Alon et al. [19] returned to this problem from a different perspective. This time, they presented a refinement rather than a proof of the old conjecture, which takes the following form.
Theorem 9.
There exists a constant such that for every and every , the interval contains at most sum-free sets of size m.
The above theorem presents a considerable difference compared to Theorems 7 and 8, as the bound is now specific to the cardinality of the sum-free sets. In order to prove Theorem 9, Alon et al. made use of a general bound on the number of independent sets with cardinality m in uniform hypergraphs (this bound has been proven by the same authors, see [4]). Such sets have a clear relation to sum-free sets. Alon et al. obtained a hypergraph to encode Schur triples, and eventually proved Theorem 9.
More recently, Hancock et al. [20] worked on a slightly different counting problem: How many subsets S of , sum-free or not, can be partitioned into two sum-free sets (this is sometimes referred to as a two-wise sum-free set)? They proposed the following theorem.
Theorem 10.
The number of integer subsets of that can be partitioned into two sum-free sets is .
The above theorem means that the number of these subsets grows asymptotically as fast as , which is a tighter bound than if using . The proof for the above theorem, similar to that for Theorem 8, makes use of advancements in container theory. Perhaps the most important sum-free-set-related outcome of Hancock et al. is the conjecture that the number of sets in that can be partitioned into two sum-free sets is . This conjecture was finally proven by Tran [11] with the following theorem.
Theorem 11.
The number of two-wise sum-free sets of is .
Clearly, (this inequality is strictly greater because ). The fact there are more two-wise sum-free sets in than sum-free sets is not particularly surprising. We have that:
- Every subset of a sum-free set is sum-free, so all sum-free sets with cardinality two or greater can be partitioned into two sum-free sets.
- Some sets that are not sum-free can be partitioned into two sum-free sets.
Hence, point 1 gives us n sets that are not two-wise sum-free in (the singletons). However, point 2 gives us more than n two-wise sum-free sets. There are many examples we could provide to show that this is indeed the case. For instance, we can join any singleton S containing an even number to any set composed of odd numbers, and partition this union into two sum-free sets (one with the even numbers and the other with the odd numbers). For any singleton S containing an odd number, we can join S to any set composed of odd numbers that is disjoint from S. This union would also be two-wise sum-free.
The proof of Theorem 11 also makes use of the method of containers. The fact that this method has been used so often to count sum-free sets, leading to new bounds (see, for instance, [11,17,18,20]), is unsurprising. Tan explained that this is a powerful tool to deal with combinatorial problems. In essence, this shows that independent sets tend to cluster together in many types of hypergraphs. The advantage is that this allows for counting the independent sets one cluster at a time.
We conclude this section by empirically showing how close the bound conjectured by Cameron and Erdős actually is in a small sample. Using Algorithm 2, we counted all sum-free sets for . Figure 1a shows two curves in the logarithmic scale, the number of sum-free sets for a particular n (in blue) and the bound conjectured by Cameron and Erdős (in orange). These two curves seem to become parallel as n grows, which is what one would expect. Figure 1b shows the difference between the two curves in Figure 1a. The “spiky” shape in Figure 1b is also expected as the convergence depends on the parity of n (see Theorem 7).
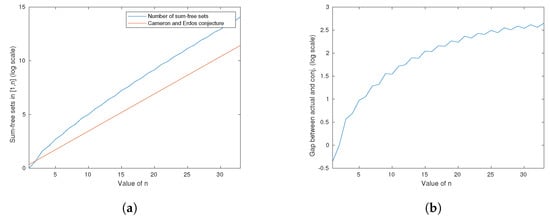
Figure 1.
A comparison, using the logarithmic scale, of the number of sum-free sets for a particular n (for ) and the bound conjectured by Cameron and Erdős. (a) The quantity of sum-free sets for each value of n (blue), and the bound conjectured by Cameron and Erdős (orange). (b) The difference between the number of sum-free sets for each n and the bound conjectured by Cameron and Erdős.
3.4. Counting Sum-Free Subsets of Abelian Groups
In Section 3.1, we considered Cameron and Erdős’ proposition that if S is a sum-free integer subset of , then . Kedlaya [21] showed, with a simple proof, that this also applies to finite groups.
Proposition 3.
Let S be the largest sum-free subset of a finite group G, then .
Proof.
Let . Given S is sum-free, we have that . Hence, . □
Recall that given a proper subset H of a finite abelian group G, if , then the coset is sum-free (see Lemma 3). Using this, Babai and Sós [22] refined the bound in Proposition 3 by proving the proposition below.
Proposition 4.
Let G be a group of order n, H be a proper subgroup of G, and S be the largest sum-free subset of G. If with , then .
Proof.
In this case, there are k cosets of cardinality . We have that at least one of these cosets follows the format with . Lemma 3 tells us that any coset under this format is sum-free. □
Using the above propositions, we can prove the following Lemma.
Lemma 4.
Let G be an abelian group of order n. If is sum-free, then with equality if and only if S is a non-trivial coset of a subgroup of index 2 in G.
Proof.
Proposition 3 tells us that holds. Regarding the equality statement, if S is a non-trivial coset of a subgroup of index 2 in G, then Proposition 4 tells us that . Let us analyse the converse. Let S be a sum-free subset of G with , and . Clearly, and . Note that as well. Hence, by the finite subgroup criteria, is a subgroup of G. Let H be this subgroup, and we have that and . Hence, S is, in fact, a coset with . □
The above proposition can be helpful in finding the largest sum-free subset of a group G, which, in turn, can be helpful in counting the number of sum-free subsets in G (a subset of a sum-free set is sum-free) but let us go in order.
We previously discussed a result by Alon [15] that directly applies to any finite abelian group (see Corollary 2). His corollary implies there are at most sum-free subsets in any finite abelian group G. Lev, Łuczak, and Schoen [23] extended the work of Alon by providing a sharp result.
Theorem 12.
Let G be an abelian group of order n. There is an absolute constant such that the number of sum-free sets in G is , where is the number of even-order components in the canonical decomposition of G into a direct sum of its cyclic groups, and the implicit constant in the sign is absolute.
G is a finite abelian group and, we assume, non-trivial, so it can be decomposed to the direct product of cyclic p-groups. This decomposition is of the form , where each with is a prime number. The only even prime is 2, so for . Hence, Theorem 12 applies solely to finite abelian groups of even order.
In order to prove Theorem 12, the original authors first proved that the number of “primitive” sum-free subsets of a finite abelian group G of order n is for an absolute constant . A sum-free set S is primitive if there is a homomorphism mapping S to a sum-free , where . They then combined this result with a lemma stating that there are at most subgroups in G and a second lemma stating that there are subgroups of index two in G. Noting that if , then any sum-free sets in G that are not primitive are all subsets of (this is a consequence of Lemma 4), they eventually proved Theorem 12.
Green and Ruzsa [5] went further in the analysis of sum-free subsets of finite abelian groups. In their work, they first identified the maximum density of a sum-free set.
Definition 2.
Let S be the largest sum-free subset of a finite abelian group G, and the density of S. That is, and . We call the maximum density of a sum-free set in G.
Green and Ruzsa analysed the inequality , and by using the Rhemtulla and Street [24] result that for all m, they concluded that holds for any finite abelian group. Green and Ruzsa defined a function mapping any given finite abelian group to the density of its largest sum-free set, as follows.
Definition 3.
Let v be the function , where G is any finite abelian group, be defined as follows.
The authors then divided sum-free sets into three types (matching the three cases in the definition of v, above), and eventually proved that .
The above definition gives us the cardinality of the largest sum-free set in any finite abelian group G (something we take further when discussing maximal sum-free sets in Section 4). Noting that any subset of a sum-free set is sum-free, Green and Ruzsa continued. Let be the number of sum-free sets in G, then . That is, the number of sum-free sets in G is at least as high as the number of subsets in its largest sum-free set. They then showed that nearly all sum-free sets in G are contained in some sum-free subset of maximum cardinality. The general idea that nearly all sum-free sets are, in fact, subsets of a small number of other sum-free sets is not completely alien. Green [16] and Sapozhenki [18] had previously shown that nearly all integer sum-free subsets of are either entirely composed of odd numbers or contained in the interval (see Section 3.3). With the above results, Green and Ruzsa proved the following theorem.
Theorem 13.
Let G be a finite abelian group, be the number of sum-free subsets of G, and be the density of the largest sum-free subset of G. Then, .
Note that calculating the above is relatively easy given the existence of function v (see Definition 3).
It can also be interesting to count sum-free subsets carrying a particular property. With this in mind, Alon et al. [4] extended the work of Green and Ruzsa by counting sum-free sets with a particular cardinality m, as we can see in their theorem below.
Theorem 14.
Let G be an abelian group of order n. Then,
In the above theorem, is the number of sum-free subsets of G with cardinality m. Alon et al.’s proof of Theorem 14 is rather long and involved. They were able to determine an upper bound for independent sets of cardinality m on a particular type of graph. They then partitioned sum-free subsets of G into two sets based on the intersection between these sets and the subgroups of G with index 2. By modelling the sets using graphs, Alon et al. were able to use the found upper bound to eventually prove Theorem 14.
4. Maximal Sum-Free Sets
In the previous section, we saw that Green and Ruzsa [5] proved that nearly all sum-free subsets of a finite abelian group G are contained in a sum-free subset of G of maximum cardinality (see the discussion of Theorem 13). This sum-free subset of maximum cardinality belongs to a well-known class of sum-free sets called maximal sum-free.
Definition 4.
Let G be a group and be sum-free. We call S maximal sum-free if there is no sum-free such that . That is, S is not properly contained in any other sum-free subset of G.
4.1. Maximal Sum-Free Subsets of Positive Integers
Cameron and Erdős [25] investigated maximal sum-free integer subsets of . They explained that they expected the number of maximal sum-free sets, , to be substantially lower than the number of sum-free sets. This expectation seems to be supported by Theorem 8 and the proof of Theorem 7, which imply that almost all sum-free integer subsets of are either composed entirely of odd numbers (i.e. subsets of a maximal sum-free set of all odd numbers) or are contained in the interval . The latter is not sum-free but it contains the maximal sum-free sets (for an odd n), and , as well as (both of them for an even n), identified in their previous work (see [3] and the discussion in Section 3.1). Cameron and Erdős then proved the following.
Theorem 15.
The number of maximal sum-free integer subsets of is equal to or greater than .
Interestingly, their proof of the above theorem does not require the identification of all maximal sum-free sets of . This is probably easier to explain using an example (an interested reader can find the proof itself in [25]).
Example 1.
Let us analyse with . Let or , whichever leads to an even m. Hence, . Let us now build sum-free sets consisting of m and only one component of each pair for any odd . The only suitable value of x is one, leading to the pair . With this, we obtain the sum-free sets and . Note that these sets are not necessarily maximal; however, no further odd number less than m can be added to any of them. For instance, if you take and add to it either 3 or 5, this set will cease to be sum-free. Hence, both and are subsets of different maximal sum-free sets. In this example, we found the following maximal sum-free sets, among others: , , and . These show that (i) the sets and are indeed subsets of different maximal sum-free sets, and (ii) a set may, in fact, be a subset of more than one maximal sum-free set.
The problem of finding an upper bound for has attracted some attention. uczak and Schoen [26] devised a probabilistic proof showing that . Note that every maximal sum-free set is, of course, sum-free, and the latter grows at in (see Section 3.3). Hence, the above result by uczak and Schoen is an improvement but intuition would indicate there is room for more. Wolfovitz [27] took this further and proved that . His proof made use of the family of sum-free sets devised by Green [16] when proving Theorem 7 (for a description, see Section 3.3), and another family of sum-free sets whose union is maximal sum-free. Using these he eventually reached the stated bound.
Balogh et al. [28] made a considerable improvement on the above result with the following theorem.
Theorem 16.
There are at most maximal sum-free integer subsets of .
The proof of the above theorem makes use of containers and the family of sum-free sets (see Section 3.3). Container theory is, in fact, a quite popular approach for counting sum-free sets, maximal or not. We have seen it used by Sapozhenko [18], Hancock et al. [20], and Tran [11] when proving Theorems 8, 10, and 11, respectively. Each element of is a container. Balogh et al. then proved that each one of these containers has at most maximal sum-free sets, leading to Theorem 16.
Recently, Balogh et al. [29] took the above even further by providing an exact answer, instead of a bound, to the number of maximal sum-free sets. They proved the theorem below using containers and the family of sum-free sets (see Section 3.3). However, they were forced to make improvements in container theory in order to avoid over-counting the number of maximal sum-free sets thanks to an error term in the original theory.
Theorem 17.
For each , there is a constant such that given any (mod 4), contains maximal sum-free sets.
The proof of the above theorem also sheds some light on the structure of the maximal sum-free subsets of . For instance, if contains Schur triples (such triple consists of such that ), then S falls under one of three categories:
- and , where and is sum-free.
- and , where and B contains solely odd numbers.
Note that S is not necessarily sum-free; however, a family of such sets would be nearly sum-free. With this, Balogh et al. were able to describe the general properties of maximal sum-free sets. Here, we state those we found to be the most interesting. There are only a small number of maximal sum-free subsets of in category 1. This seems well aligned with intuition. The cardinality of every sum-free set of maximum cardinality is , and these are also maximal sum-free sets. One would then expect the majority of maximal sum-free sets that are not of maximum cardinality to not be much lower than . Regarding category 2, Balogh et al. showed that the number of maximal sum-free sets under this category with two or more even numbers amounts to only . This also follows intuition. Such a set would have a cardinality higher than (otherwise it would be category 1), and the sum of two even numbers is even. The more even numbers a sum-free set has, the harder it is to achieve such high cardinality. Finally, by analysing the sets in categories 2 and 3, they found that the number of maximal sum-free subsets of containing at most one even number is . This is rather close to the bound established in Theorem 16. Hence, the majority of maximal sum-free sets fall under these categories and follow this configuration.
4.2. Maximal Sum-Free Subsets of Abelian Groups
In this section, we explore maximal sum-free subsets of finite abelian groups. Here, represents the number of maximal sum-free sets in a group G.
Theorem 18.
Let G be a group of order n, .
Wolfovitz [27] proved the above by first identifying a sum-free and constructing a Cayley graph. This graph is k-regular (i.e., each vertex has degree k) with . Wolfovitz continued by stating that there are at most maximal sum-free subsets of G with cardinality less than and concluded that to prove Theorem 18, it suffices to count those with cardinality of at least . Each maximal sum-free subset is an independent set in at least one Cayley graph. Since there are such graphs, it is enough to fix a sum-free of size and upper bound the number of independent sets that correspond to the maximal sum-free sets. This eventually leads to Theorem 18.
Balogh et al. [29] argued that Theorem 18 only shows that is exponentially smaller than if G is of even order (as its largest sum-free subset will have cardinality ). They then produced a proof for the improvement below.
Theorem 19.
Let G be an abelian group of order n, and S be the largest sum-free subset of G. Then, .
To prove the above, Balogh et al. constructed a family of containers that is slightly different than that devised by Green to prove Theorem 7. Recall that , where S is the largest sum-free subset of a group G (see Definition 2). In this new version, we have that for any , , where B is sum-free in G, and , and with . The other previous requirements of and that any sum-free subset of G is contained in at least one element of remain. A sum-free cannot have a cardinality that is higher than that of the largest sum-free subset of G.
Balogh et al. then fixed and stated that every maximal sum-free subset of G contained in F can be formed by picking a sum-free (at most choices, using the above definition) and extending it with B. Regarding the latter, Balogh et al. stated that the number of maximal independent sets in a graph is at most . These two results eventually lead to Theorem 19.
If a sum-free set S is of maximum cardinality, then S is maximal sum-free. Such S is of particular importance because nearly all sum-free subsets of the same group are contained in a set like S (see the discussion of Theorem 13). Also, in the case of subsets of , Balogh et al. [29] showed that only a small number of maximal sum-free sets have cardinality less than or equal to (see our discussion of Theorem 17). Hence, it is interesting to study the exceptions, that is, groups with small maximal sum-free sets.
Giudici and Hart [30] explored the world of small maximal sum-free sets. Their work proved various interesting theorems. Here, we present some of their main findings.
Theorem 20.
Let G be a group and be a maximal sum-free set of cardinality one. Then, , or , and the element in S is of prime order in G.
Giudici and Hart proved the above by analysing S, a maximal sum-free set containing a single element g. They noticed that if g does not have order 2, then . This is clear, as if , we would have , and, consequently, and . By using the result and a previous corollary in their work ([30], Corollary 3.10) stating that in this case, , they reached . Then, after testing all possibilities, they concluded that . Afterwards, they examined the case . In this case, they found that every has order 4 and is the only subgroup of G with order 2. They then concluded that and or .
Giudici and Hart also proved that only certain groups have a sum-free subset of cardinality 2. They provided a list containing 11 such groups and their respective sum-free sets (note that a group may have more than one sum-free set with cardinality 2). is one of the groups in the list, as one would expect (given that ), but it is very interesting to see there are various other groups listed, one with order 16. Finally, Giudici and Hart conjectured that any group G with does not contain a maximal sum-free set of size 3. This conjecture was later proved by Anabanti and Hart [31].
5. Conclusions
In this paper, our main aim was to present and discuss some interesting properties of sum-free subsets of abelian groups to a broader readership. More specifically, we set out to discuss answers to questions like those raised by Alon et al. [4] and Green and Ruzsa [5]: How many sum-free subsets are there in a given abelian group G? What are its sum-free subsets of maximum cardinality? What is the maximum cardinality of these sum-free subsets? What does a typical sum-free subset of G look like?
In order to address the above questions, as well as others, we first asked ourselves the following question: Given an abelian group G, how can we identify its sum-free subsets? In Section 2, we addressed this by presenting different methods, both computational and algebraic, that can be employed to identify such sum-free sets. In Section 3, we discussed the considerable amount of work carried out on counting sum-free sets. We also identified that Cameron and Erdős’ list of integer sum-free subsets of with cardinality was incomplete (we found exceptions for three values of n and these are the only exceptions that exist, see Section 3.1). In Section 3, we explained that nearly all sum-free subsets of G are contained in some sum-free set of maximum cardinality (see the discussion of Theorem 13). This clearly demonstrated the importance of sum-free sets of maximum cardinality, providing a reason for us to focus on maximal sum-free sets in Section 4. In Section 4, we discussed proofs regarding the bounds of maximal sum-free sets, which sheds some light on the structure of maximal sum-free sets (see Theorem 17). Within these sections, we covered what we believe to be the main areas pertinent to sum-free subsets of abelian groups.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analysed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Schur, I. Uber die Kongruenz xm+ym≡zm( mod p). Jahresber. Dtsch. Math.-Ver. 1916, 25, 114–117. [Google Scholar]
- Cameron, P.J. Portrait of a Typical Sum-Free Set; Cambridge University Press: Cambridge, UK, 1987; Volume 123. [Google Scholar]
- Cameron, P.J.; Erdős, P. On the number of sets of integers with various properties. In Number Theory; Mollin, R.A., Ed.; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 1990; pp. 61–79. [Google Scholar]
- Alon, N.; Balogh, J.; Morris, R.; Samotij, W. Counting sum-free sets in Abelian groups. Isr. J. Math. 2014, 199, 309–344. [Google Scholar] [CrossRef]
- Green, B.; Ruzsa, I.Z. Sum-free sets in abelian groups. Isr. J. Math. 2005, 147, 157–188. [Google Scholar] [CrossRef]
- Erdős, P. Extremal problems in number theory. In Proceedings of Symposia in Pure Mathematics; American Mathematical Society: Providence, RI, USA, 1965; pp. 181–189. [Google Scholar]
- Alon, N.; Kleitman, D.J. Sum-free subsets. In A Tribute to Paul Erdős; Cambridge University Press: Cambridge, UK, 1990; pp. 13–26. [Google Scholar]
- Rhemtulla, A.; Street, A.P. Maximal sum-free sets in elementary abelian p-groups. Can. Math. Bull. 1971, 14, 73–80. [Google Scholar] [CrossRef]
- Cameron, P.J. Clive Sinclair. Available online: http://cameroncounts.wordpress.com/2021/09/18/clive-sinclair/ (accessed on 15 August 2022).
- Kolountzakis, M.N. Selection of a large sum-free subset in polynomial time. Inf. Process. Lett. 1994, 49, 255–256. [Google Scholar] [CrossRef]
- Tran, T. On the structure of large sum-free sets of integers. Isr. J. Math. 2018, 228, 249–292. [Google Scholar] [CrossRef]
- Freiman, G.A. On the structure and the number of sum-free sets. In Proceedings of the Journées Arithmétiques, Geneva, Switzerland, 9–13 September 1991; pp. 195–201. [Google Scholar]
- Calkin, N.J. On the number of sum-free sets. Bull. Lond. Math. Soc. 1990, 22, 141–144. [Google Scholar] [CrossRef]
- Szemerédi, E. On sets of integers containing no k elements in arithmetic progression. Acta Arith 1974, 27, 503–505. [Google Scholar]
- Alon, N. Independent sets in regular graphs and sum-free subsets of finite groups. Isr. J. Math. 1991, 73, 247–256. [Google Scholar] [CrossRef]
- Green, B. The Cameron–Erdős conjecture. Bull. Lond. Math. Soc. 2004, 36, 769–778. [Google Scholar] [CrossRef]
- Sapozhenko, A. The Cameron-Erdős conjecture. Dokl. Math. 2003, 68, 438–441. [Google Scholar] [CrossRef]
- Sapozhenko, A.A. The Cameron–Erdős conjecture. Discret. Math. 2008, 308, 4361–4369. [Google Scholar] [CrossRef]
- Alon, N.; Balogh, J.; Morris, R.; Samotij, W. A refinement of the Cameron–Erdős conjecture. Proc. Lond. Math. Soc. 2014, 108, 44–72. [Google Scholar] [CrossRef]
- Hancock, R.; Staden, K.; Treglown, A. Independent sets in hypergraphs and Ramsey properties of graphs and the integers. SIAM J. Discret. Math. 2019, 33, 153–188. [Google Scholar] [CrossRef]
- Kedlaya, K.S. Product-free subsets of groups. Am. Math. Mon. 1998, 105, 900–906. [Google Scholar] [CrossRef]
- Babai, L.; Sós, V.T. Sidon sets in groups and induced subgraphs of Cayley graphs. Eur. J. Comb. 1985, 6, 101–114. [Google Scholar] [CrossRef]
- Lev, V.F.; Łuczak, T.; Schoen, T. Sum-free sets in abelian groups. Isr. J. Math. 2001, 125, 347–368. [Google Scholar] [CrossRef]
- Rhemtulla, A.; Street, A.P. Maximal sum-free sets in finite abelian groups. Bull. Aust. Math. Soc. 1970, 2, 289–297. [Google Scholar] [CrossRef]
- Cameron, P.J.; Erdős, P. Notes on sum-free and related sets. Comb. Probab. Comput. 1999, 8, 95–107. [Google Scholar] [CrossRef][Green Version]
- Łuczak, T.; Schoen, T. On the number of maximal sum-free sets. Proc. Am. Math. Soc. 2001, 129, 2205–2207. [Google Scholar] [CrossRef]
- Wolfovitz, G. Bounds on the number of maximal sum-free sets. Eur. J. Comb. 2009, 30, 1718–1723. [Google Scholar] [CrossRef]
- Balogh, J.; Liu, H.; Sharifzadeh, M.; Treglown, A. The number of maximal sum-free subsets of integers. Proc. Am. Math. Soc. 2015, 143, 4713–4721. [Google Scholar] [CrossRef]
- Balogh, J.; Liu, H.; Sharifzadeh, M.; Treglown, A. Sharp bound on the number of maximal sum-free subsets of integers. J. Eur. Math. Soc. 2018, 20, 1885–1911. [Google Scholar] [CrossRef]
- Giudici, M.; Hart, S. Small maximal sum-free sets. Electron. J. Comb. 2009, 16, R59. [Google Scholar] [CrossRef] [PubMed]
- Anabanti, C.S.; Hart, S. Locally maximal product-free sets of size 3. arXiv 2015, arXiv:1503.06509. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).