Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models
Abstract
:1. Introduction
2. Materials and Methods
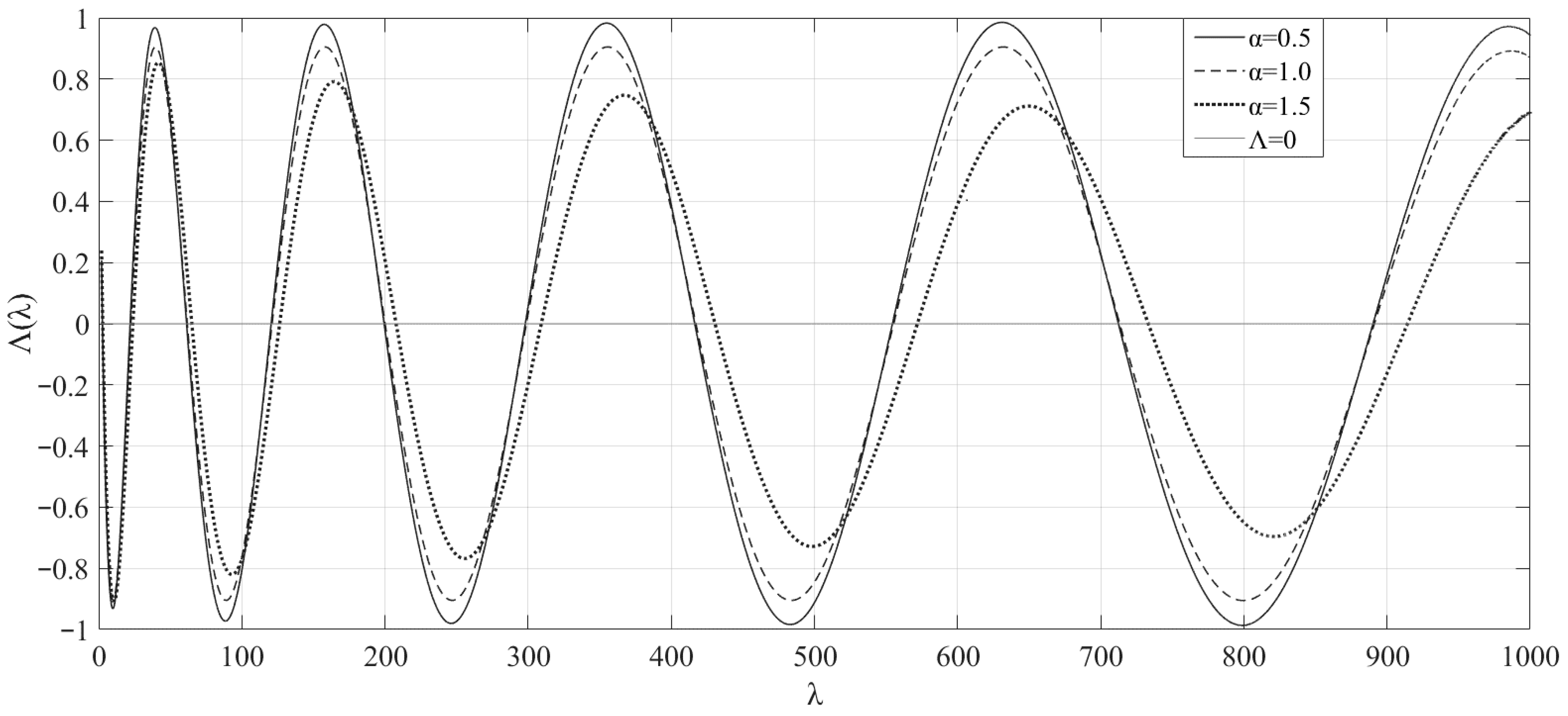
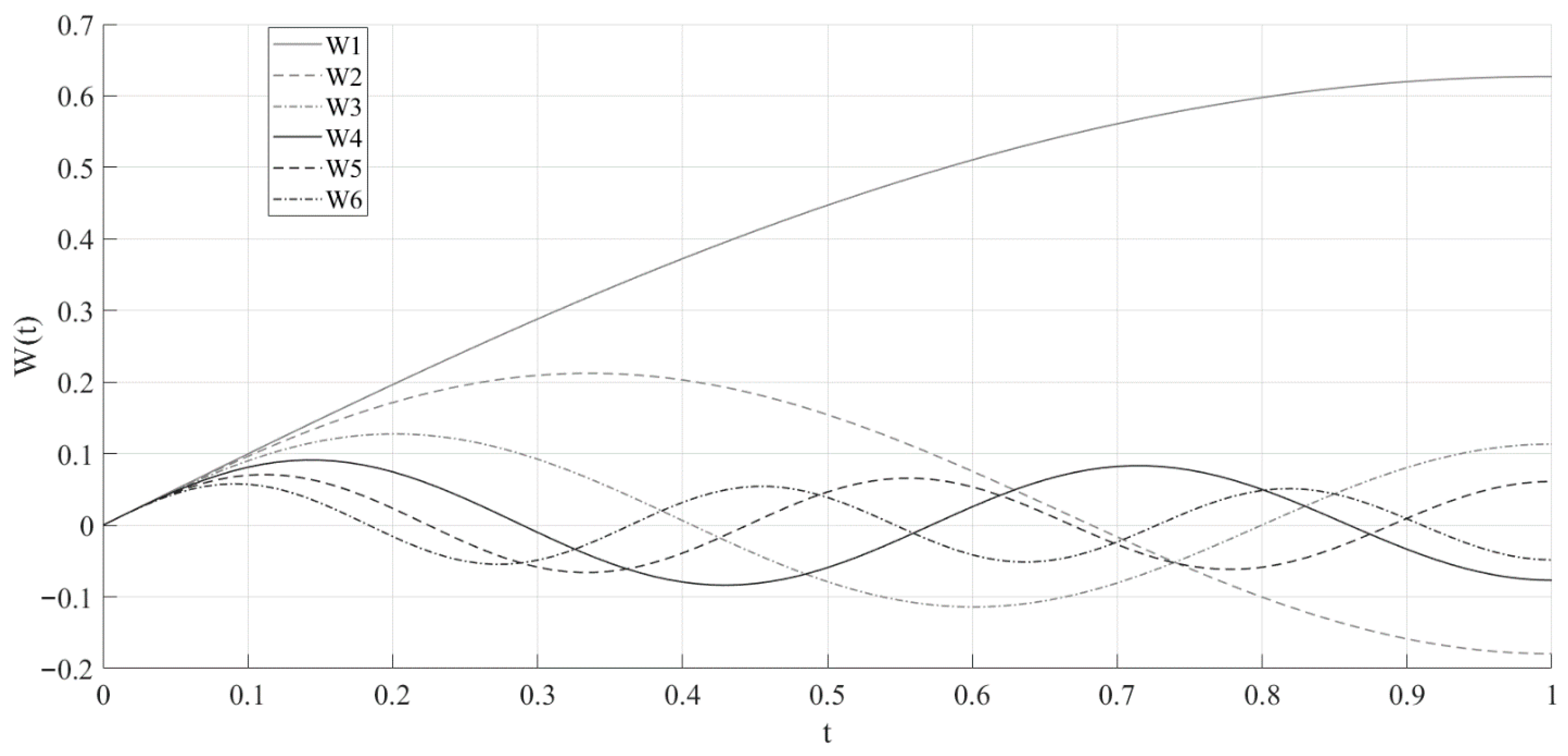
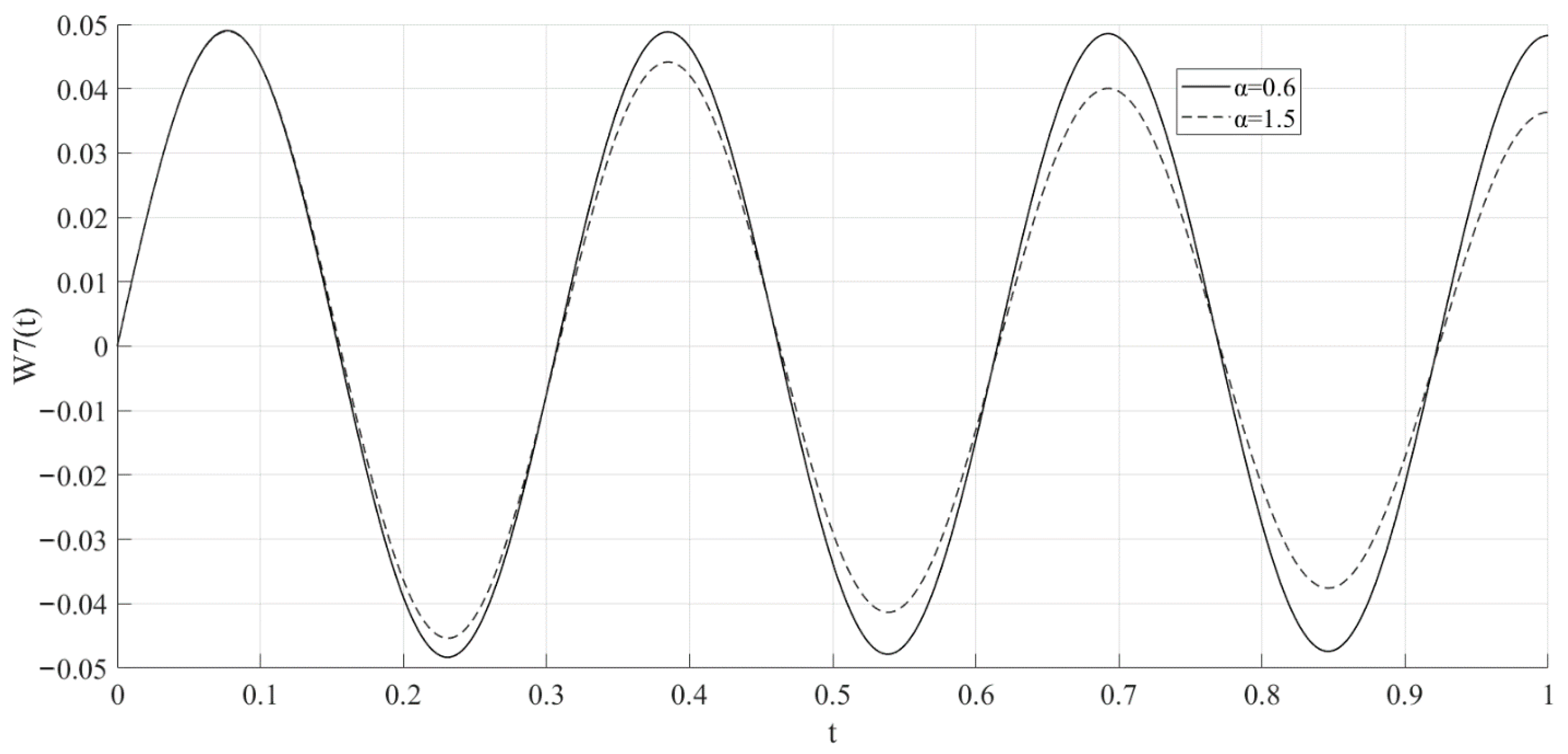
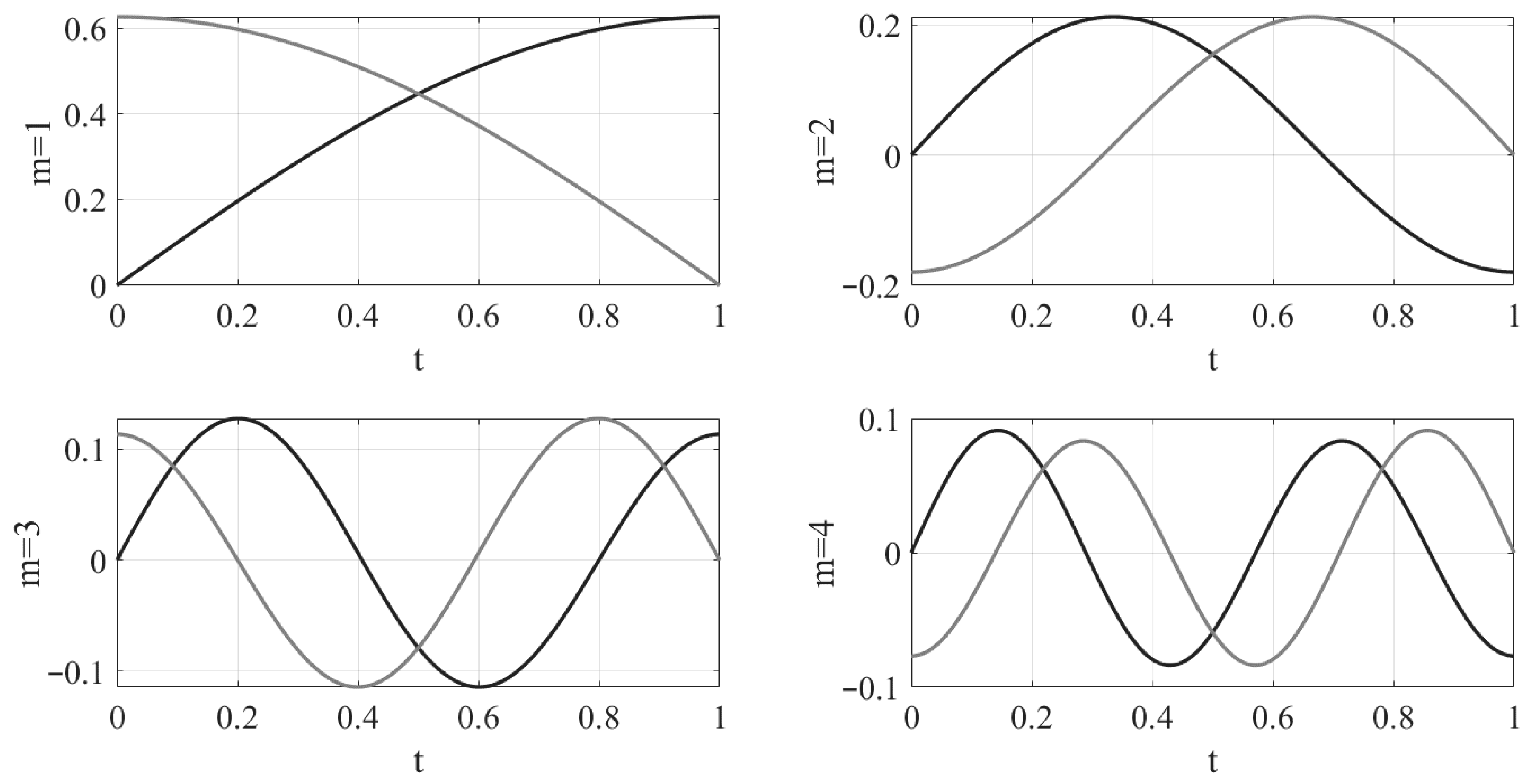
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Nauka i Tekhnika, M., Ed.; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1988. (In Russian) [Google Scholar]
- Machado, J.A.T. Handbook of Fractional Calculus with Applications; De Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2019; Volume 1–8. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, A.T. Advances in Fractional Calculus. In Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010; 314p. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Wave Propagation, Impact and Variational Principles; Wiley: London, UK, 2014; 406p. [Google Scholar]
- Sandev, T.; Tomovshi, Z. Fractional Equations and Models: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Alotta, G.; Barrera, O.; Cocks, A.; Di Paola, M. The finite element implementation of 3D fractional viscoelastic constitutive models. Finite Elements Anal. Des. 2018, 146, 28–41. [Google Scholar] [CrossRef]
- Alotta, G.; Barrera, O.; Pegg, E.C. Viscoelastic material models for more accurate polyethylene wear estimation. J. Strain Anal. Eng. Des. 2018, 53, 302–312. [Google Scholar] [CrossRef]
- Shitikova, M.V. Fractional Operator Viscoelastic Models in Dynamic Problems of Mechanics of Solids: A Review. Mech. Solids 2022, 57, 1–33. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Krusser, A.I. Models of viscoelastic materials: A review on historical development and formulation. Adv. Struct. Mater. 2022, 175, 285–326. [Google Scholar] [CrossRef]
- Shabani, M.; Jahani, K.; Di Paola, M.; Sadeghi, M.H. Frequency domain identification of the fractional Kelvin-Voigt’s parameters for viscoelastic materials. Mech. Mater. 2019, 137, 103099. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorazyczewski, B. Identification of the parameters of the Kelvin-Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Di Paola, M.; Pirrotta, A.; Valenza, A. Visco-elastic behavior through fractional calculus: An easier method for best fitting ex-perimental results. Mech. Mat. 2011, 43, 799–806. [Google Scholar] [CrossRef]
- Popov, I.I.; Chang, T.-P.; Rossikhin, Y.A.; Shitikova, M.V. Experimental Study of Concrete Aging Effect on the Contact Force and Contact Time During the Impact Interaction of an Elastic Rod with a Viscoelastic Beam. J. Mech. 2016, 33, 317–322. [Google Scholar] [CrossRef]
- Lagos-Varas, M.; Movilla-Quesada, D.; Arenas, J.; Raposeiras, A.; Castro-Fresno, D.; Calzada-Perez, M.A.; Vega-Zamanillo, A.; Maturana, J. Study of the mechanical behavior of asphalt mixtures using fractional rheology to model their viscoelasticity. Constr. Build. Mater. 2018, 200, 124–134. [Google Scholar] [CrossRef]
- Wang, Y.; Harris, J.M. Seismic attenuation models: Multiple and fractional generalizations. In SEG Technical Program Expanded Abstracts; SEG: Houston, TX, USA, 2020; pp. 2754–2758. [Google Scholar]
- Popov, I.I.; Shitikova, M.V.; Levchenko, A.V.; Zhukov, A.D. Experimental identification of the fractional parameter of the fractional derivative standard linear solid model for fiber-reinforced rubber concrete. Mech. Adv. Mater. Struct. 2023, 30, 1–9. [Google Scholar] [CrossRef]
- Popov, I.I.; Shitikova, M.V. Impulse excitation technique and its application for identification of material damping: An over-view. IOP Conf. Ser. Mater. Sci. Eng. 2020, 962, 022025. [Google Scholar] [CrossRef]
- Erokhin, S.V.; Aleroev, T.S. Parametric identification of the order of a fractional derivative in the Begley–Torvik model. Math. Model. 2018, 30, 93–102. [Google Scholar]
- Ungarova, L.G.; Ogorodnikov, E.N. Identification of the parameters of non-linear fractional mathematical models of a hered-itarily elastic body based on experimental data on the creep of PVC-compound samples. In Proceedings of the XI All-Russian Scientific Conference “Mathematical Modeling and Boundary Value Problems”, Samara, Russia, 27–30 May 2019; Volume 1, pp. 359–363. [Google Scholar]
- Xu, Y.; He, Q.; Guo, Y.-Q.; Huang, X.-H.; Dong, Y.-R.; Hu, Z.-W.; Kim, J. Experimental and Theoretical Investigation of Viscoelastic Damper by Applying Fractional Derivative Method and Internal Variable Theory. Buildings 2023, 13, 239. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional Calculus—A Different Approach to the Analysis of Viscoelastically Damped Struc-tures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the Fractional Calculus Model of Viscoelastic Behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Caputo, M. Vibrations of an infinite viscoelastic layer with a dissipative memory. J. Acoust. Soc. Am. 1974, 56, 897–904. [Google Scholar] [CrossRef]
- Ingman, D.; Suzdalnitsky, J. Control of damping oscillations by fractional differential operator with time-dependent order. Comput. Methods Appl. Mech. Eng. 2004, 193, 5585–5595. [Google Scholar] [CrossRef]
- Naber, M. Linear Fractionally Damped Oscillator. Int. J. Differ. Equ. 2010, 2010, 197020. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications; Academic Press: London, UK, 1999; 340p. [Google Scholar]
- Watanabe, S. An Approach to Visco-Elastic Behaviors with a Mathematical Method. J. Text. Mach. Soc. Jpn. 1959, 5, 10–13. [Google Scholar] [CrossRef]
- Gerasimov, A.N. Generalisation of linear laws of deformation and its application to internal friction problems. PMM 1948, 12, 251–260. [Google Scholar]
- Aleroev, T.; Aleroeva, H. Problems of Sturm-Liouville type for diferential equations with fractional derivatives. In Fractional Diferential Equations; Kochubei, A., Luchko, Y., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; pp. 21–46. [Google Scholar]
- Kirianova, L. The fractional derivative type identification for the modelling deformation and strength characteristics of polymer concrete. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1030, 012094. [Google Scholar] [CrossRef]
- Aleroev, T.S.; Kirane, M.; Tang, Y.F. Boundary-value problems for dirential equations of fractional order. J. Math. Sci. 2013, 10, 158–175. [Google Scholar]
- Nashif, A.D.; Jones, D.I.G.; Henderson, J.P. Vibration Damping; John Wiley & Sons: Hoboken, NJ, USA, 1991; 472p, ISBN 978-0-471-86772-2. [Google Scholar]
| 2.59 | 21.99 | 61.41 | 120.47 | 199.37 | 297.97 | 416.35 | 554.43 | 712.29 | 890.15 | |
| 2.65 | 22.27 | 61.67 | 120.81 | 199.69 | 298.31 | 416.69 | 554.79 | 712.63 | 890.37 | |
| 2.73 | 22.85 | 62.67 | 122.29 | 201.63 | 300.75 | 419.61 | 558.23 | 716.59 | 894.83 | |
| 2.81 | 23.87 | 65.05 | 126.41 | 207.77 | 309.17 | 430.55 | 571.91 | 733.21 | 914.29 |
| 2.23 | 21.87 | 61.27 | 120.41 | 199.31 | 297.95 | 416.33 | 554.47 | 712.33 | 890.12 | |
| 2.27 | 22.01 | 61.49 | 120.71 | 199.67 | 298.37 | 416.81 | 554.97 | 712.89 | 890.73 | |
| 2.51 | 23.23 | 64.27 | 125.45 | 206.71 | 307.99 | 427.27 | 570.53 | 731.75 | 912.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiryanova, L.; Matseevich, T. Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models. Axioms 2023, 12, 779. https://doi.org/10.3390/axioms12080779
Kiryanova L, Matseevich T. Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models. Axioms. 2023; 12(8):779. https://doi.org/10.3390/axioms12080779
Chicago/Turabian StyleKiryanova, Ludmila, and Tatiana Matseevich. 2023. "Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models" Axioms 12, no. 8: 779. https://doi.org/10.3390/axioms12080779
APA StyleKiryanova, L., & Matseevich, T. (2023). Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models. Axioms, 12(8), 779. https://doi.org/10.3390/axioms12080779





