Pricing of Credit Risk Derivatives with Stochastic Interest Rate

Abstract

This paper deals with a credit derivative pricing problem using the martingale approach. We generalize the conventional reduced-form credit risk model for a credit default swap market, assuming that the firms’ default intensities depend on the default states of counterparty firms and that the stochastic interest rate follows a jump-diffusion Cox–Ingersoll–Ross process. First, we derive the joint Laplace transform of the distribution of the vector process $(r_t,R_t)$ by applying piecewise deterministic Markov process theory and martingale theory. Then, using the joint Laplace transform, we obtain the explicit pricing of defaultable bonds and a credit default swap. Lastly, numerical examples are presented to illustrate the dynamic relationships between defaultable securities (defaultable bonds, credit default swap) and the maturity date.

1. Introduction

Efficient tools for the management of credit risk in portfolios are always in high demand in financial institutions. This leads to a specialized market for credit derivatives. Due to the initiation of the credit derivatives market in the early 1990s, credit derivatives have maintained robust growth in the past decades. Being an enormous market that already surpasses the debt one, it has been attracting increasing research interest. For the modeling of credit risk in credit-risky securities markets, depending on the formulation, there are two well-established fundamental models available at present, i.e. the so-called reduced-form model [1,2,3] and the structural model [4,5]. In the reduced-form model, the influences on the default are assumed to be dominated by exogenous factors, for example, policies from the government; meanwhile, structural models mainly focus on endogenous factors—more specifically, the asset allocation of firms. Compared with the structural one, the reduced-form model is believed to be easier for constructing a tractable formula explaining the price of credit-risky securities in terms of economic covariates, which facilitates the estimation. In this work, we mainly focus on the reduced-form model.

There is a long history of insights into credit risk in the credit derivatives market with the reduced-form model, going back to the 1990s. When describing dependency default risks, bottom-up models as well as top-down models are commonly used. Bottom-up models focus on modeling default intensities of individual reference entities to characterize a portfolio default intensity. For more developments of bottom-up models, references [6,7,8] are highly recommended. The top-down models mainly focus on modeling default at the portfolio level; in other words, the default intensity of the entire investment portfolio is modeled without reference to the constituent names. Some works on top-down models are included in [9,10,11]. In our paper, we focus on bottom-up models.

In bottom-up models, the default intensity is generally assumed to be a stochastic process, while the relevant randomness is built up from state variables. Moreover, a further consideration of credit contagion is then pioneered by [12] (the so-called DL model) to incorporate the concentration risk in credit portfolios. In the meantime, the emergence of certain special phenomena—for instance, the banking crisis—reveals one of the defects of the conventional reduced-form models, which did not possess a full consideration of credit risk sources. Accordingly, a model with the concept of counterparty risk was brought forward by [7]. In recent years many scholars have considered this factor, for example in [13,14,15,16,17,18]. In conjunction with the credit contagion, this model emphasizes the so-called primary–secondary framework, which simplifies the payoff structure. The default intensity in such a framework is assumed to be mainly decided by the default state of the counterparty and the economy-wide state variables that follow the Vasicek process (see e.g., [19]). In addition, [13,15,16,20,21] also involved the effects of various other factors (such as the settlement risk, the replacement cost, credit rating, Markov Regime-Switching) in the pricing of CDSs. However, further effects are still desired for improving these models to better characterize the credit derivatives market.

One of the essential aspects of a fine modeling of credit risk is the proper addressing of the dynamic changes of economy-wide state variables. Among all economy-wide state variables, we only consider the risk-free interest rate in this work. As the mean reversion may come from the underlying macro-economic currents, or the corrections on account of bond market overreaction, the Cox–Ingersoll–Ross (CIR) process (for more details, see [22]) is applied to characterize the interest rate fluctuation [23,24,25,26,27]. This process covers the defect of the Vasicek model that makes it possible to get negative interest rates. In the CIR process, the volatility term $\theta \sqrt{r\left(t\right)}$ will approach zero when the interest rate gets close to zero, which cancels the effects of the randomness. Thus, the interest rate in such a case remains positive. Meanwhile, the volatility takes high value when the interest rate is high, which is a desired property for modeling. Moreover, in practice, when a primary event takes place, e.g., a change in monetary policies, there will be a positive jump in the interest rate process. Such a jump will be suppressed by the government over time. Then, the process continues until it is taken over by another jump caused by a new event. Therefore, to depict such a phenomenon, we consider a jump-diffusion Cox–Ingersoll–Ross (JCIR) process.

In this paper, we propose a revised reduced-form model [28]. It incorporates the assumption that the firms’ default intensities are related to the default states of counterparty firms and the stochastic interest rate driven by the jump-diffusion Cox–Ingersoll–Ross (JCIR) process. This model, to some extent, is more in accordance with the actual CDS market than that of classical work [7]. The primary intention of this article is to derive an explicit expression for the joint Laplace transform of the distribution of the risk-free interest rate-related vector process $(r_t,R_t)$ by applying the piecewise deterministic Markov process theory. The piecewise deterministic Markov process theory was developed by [29] and has been proven to be a very powerful mathematical tool in the field of non-diffusion models. Using the joint Laplace transform, we obtain the explicit pricing of defaultable bonds and default swap rates. Finally, according to this explicit expression, we present the dynamic relations between defaultable securities and the maturity date.

The rest of this paper is organized as follows. In Section 2, we present the setup of the counterparty structure. In Section 3, we derive the joint Laplace transform of the distribution of the vector process $(r_t,R_t)$, and the pricing formulae for defaultable bonds are derived. Meanwhile, with several examples, we also explore the impact of counterparty risk and spot interest rate on bond pricing. In Section 4, we extend our model to the pricing of credit default swaps and the importance of default correlation and spot interest rate models in pricing a default swap. In Section 5, conclusive remarks and further academic challenges are presented.

2. Reduced-Form Model

In this section, to construct the model, a collection of doubly stochastic Poisson processes are assumed to represent the default. Then, the primary–secondary framework is applied to further simplify the subsequent exposition.

2.1. Model Setup

To set up the model, the filtered probability space $(\Omega ,\mathcal{F},{\left\{\mathcal{F}\right\}}_{t=0}^{T^{*}},\mathbb{P})$ is used for the uncertainty in the economy, while $X_t$, an ${\mathbb{R}}^d$-valued process, and point processes $N^i$ ($i=1,\cdots ,I$) are assumed to indicate the d economy-wide state variables and the default processes of firm i, respectively. $N^i$ is 0 initially and changes to 1 once the default takes place. Denoting ${\tau }_i$ as the relevant default time, the default process of firm i could be presented as $N_t^i=1_{\{{\tau }^i\le t\}}$. Then, the filtration could be generated according to $X_t$ and $N_t^i$ as

$$\begin{array}{c}\hfill {\mathcal{F}}_t={\mathcal{F}}_t^X\vee {\mathcal{F}}_t^1\vee \cdots \vee {\mathcal{F}}_t^I,\end{array}$$

with

$$\begin{array}{c}\hfill {\mathcal{F}}_t^X=\sigma (X_s,0\le s\le t)\mathrm{and}{\mathcal{F}}_t^i=\sigma (N_s^i,0\le s\le t)\end{array}$$

being the filtrations obtained from $X_t$ and $N_t^i$, respectively.

In addition, we indicate the filtration generated by the default process of all firms but the ith one as

$$\begin{array}{c}\hfill {\mathcal{F}}_t^{-i}={\mathcal{F}}_t^1\vee \cdots \vee {\mathcal{F}}_t^{i-1}\vee {\mathcal{F}}_t^{i+1}\vee \cdots \vee {\mathcal{F}}_t^I.\end{array}$$

Thus, ${\mathcal{F}}_{T^{*}}^X\vee {\mathcal{F}}_{T^{*}}^{-i}$ embraces the full information up to time $T^{*}$ on the state variables and the default processes of all firms other than that of the ith. We could also choose an intensity process ${\lambda }_t^i$, for $t\in [0,T^{*}]$, being non-negative and ${\mathcal{F}}_{T^{*}}^X\vee {\mathcal{F}}_{T^{*}}^{-i}$-measurable, with

$${\int }_0^t{\lambda }_s^{i}ds<\infty ,\mathbb{P}-a.s.,$$

so that a Poisson process $N^i$ can be defined.

2.2. Primary–Secondary Framework

As a typical case, in this work, we discuss the default probability of a commercial bank. We assume that bank A owns a large amount of debt from firm B. However, it is normally not vice versa, and thus not possible to affect B’s default probability. Thus, we implement the constraints as follows. All I firms considered could be separated into two incompatible types, i.e., $S_1$ primary firms and the rest $I-S_1$ secondary firms. The default processes of the primary firms only depend on state variables, while those of secondary firms depend on both the state variables and the default status of the primary firms.

To start with, under probability measure $\mathbb{P}$, for the $S_1$ primary firms, there is a sequence of independent unit exponential random variables, $\{e^i,1\le i\le S_1\}$, being also independent of $X_t$. Thus, the relevant default times can be defined as

$$\begin{array}{c}\hfill {\tau }^i=inf\{t:{\int }_0^t{\lambda }_s^{i}ds\ge e^i\},1\le i\le S_1,\end{array}$$

(1)

with ${\lambda }_t^i$ adapted to ${\mathcal{F}}_t^X$, while the conditional and unconditional survival probability distributions of primary firm i are given by

$$\begin{array}{cc}\hfill & \mathbb{P}({\tau }^i>t|{\mathcal{F}}_{T^{*}}^X)=exp(-{\int }_0^t{\lambda }_s^{i}ds),t\in [0,T^{*}],\end{array}$$

(2)

$$\begin{array}{cc}& \mathbb{P}({\tau }^i>t)=\mathbb{E}[exp(-{\int }_0^t{\lambda }_s^{i}ds)],t\in [0,T^{*}].\end{array}$$

(3)

Since the primary firms’ default processes only depend on $X_t$, we denote their default intensities by

$$\begin{array}{c}\hfill {\lambda }_t^i=a_{0,t}^i,1\le i\le S_1.\end{array}$$

(4)

Then, we proceed to the secondary default processes. Similarly, for the $I-S_1$ secondary firms, there is also a sequence of relevant independent variables, $\{e^j,S_1+1\le j\le I\}$, being independent of $X_t$ and $\{{\tau }^i,1\le i\le S_1\}$ as well. Hence, the default times can be defined as

$$\begin{array}{c}\hfill {\tau }^j=inf\{t:{\int }_0^t{\lambda }_s^{j}ds\ge e^j\},S_1+1\le j\le I,\end{array}$$

(5)

with ${\lambda }_t^j$ adapted to ${\mathcal{F}}_t^X\vee {\mathcal{F}}_t^1\vee \cdots \vee {\mathcal{F}}_t^{S_1}$, while the conditional and unconditional survival probability distributions of secondary firm j are expressed as

$$\begin{array}{cc}\hfill & \mathbb{P}({\tau }^j>t|{\mathcal{F}}_{T^{*}}^X\vee {\mathcal{F}}_{T^{*}}^1\vee \cdots \vee {\mathcal{F}}_{T^{*}}^{S_1})=exp(-{\int }_0^t{\lambda }_s^{j}ds),t\in [0,T^{*}],\end{array}$$

(6)

$$\begin{array}{cc}& \mathbb{P}({\tau }^j>t)=\mathbb{E}[exp(-{\int }_0^t{\lambda }_s^{j}ds)],t\in [0,T^{*}].\end{array}$$

(7)

Since the default processes of secondary firms depend on $X_t$ and the default processes of primary firms, we denote the default intensities by

$$\begin{array}{c}\hfill {\lambda }_t^j=a_{0,t}^j+{\displaystyle \sum _{k=1}^{S_1}}{a}_{k,t}^j{1}_{\{{\tau }^k\le t\}},S_1+1\le j\le I,\end{array}$$

(8)

with $a_{k,t}^j$ adapted to ${\mathcal{F}}_t^X$. The default of firm k, according to the sign of $a_{k,t}^j$, can either increase ($a_{k,t}^j>0$) or decrease ($a_{k,t}^j<0$) the default probability of firm j. In addition, a more general default intensity can be achieved by involving the interactions of the indicator functions.

According to the assumptions above, we now derive the explicit pricing formulae of defaultable bonds and default swap rates in Section 3 and Section 4, respectively.

3. Defaultable Bonds

In this section, we derive the pricing formulae for defaultable bonds. First, we present the general formulae for bonds in the primary–secondary framework that fulfills the assumptions in the previous sections. Under the equivalent martingale measure $\mathbb{P}$, the prices of the default-free and defaultable bonds are, respectively, given by

$$\begin{array}{ccc}\hfill p(t,T)& =& \mathbb{E}[exp(-{\int }_t^T{r}_{s}ds)|{\mathcal{F}}_t],\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill V^i(t,T)& =& {\beta }^{i}p(t,T)+1_{\{{\tau }^i>t\}}(1-{\beta }^i)\mathbb{E}[exp(-{\int }_t^T(r_s+{\lambda }_s^i)ds)|{\mathcal{F}}_t],\hfill \end{array}$$

(10)

where ${\beta }^i$ is the recovery rate of defaultable bond i, and $t\le T<T^{*}$. Here, to reduce derivation complexity, we assume the recovery rate to be a constant for obtaining a simple martingale pricing formula. Obviously, due to (10), the prices of risky bonds consist of two parts, i.e., the recovery rate ${\beta }^i$ and the rest factor $1-{\beta }^i$, both discounted to t. The first part could be calculated explicitly, while the second one could be obtained in the absence of default. Moreover, the second part, being discounted at the adjusted spot rate, presents the default risk in the model. Therefore, the pricing under $\mathbb{P}$ depends on the expectation in (10).

Then, in the following, we assume firm A and B to be the primary and secondary firm, respectively. The default of firm A is independent of the default risk of others, while that of firm B depends on the default risk of firm A. Both firm A and B’s default risk depends on the interest rate, which could be owing to the firms’ big cash demands for debt repayments. In this work, we only consider the simple case, with the default intensities following the linear relations:

$$\begin{array}{ccc}\hfill {\lambda }_t^A& =& b_0^A+b_1^A{r}_t,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\lambda }_t^B& =& b_0^B+b_1^B{r}_t+b{1}_{\{{\tau }^A\le t\}},\hfill \end{array}$$

(12)

where $b_0^A$, $b_1^A$, $b_0^B$, $b_1^B$, and b are positive constants. The only economy-wide state variable we account for here is the risk-free interest rate, which, more specifically, follows an extended CIR process with positive jumps:

$$\begin{array}{c}\hfill d{r}_t=\alpha (\eta -r_t)dt+\theta \sqrt{r_t}d{W}_t+d{J}_t,\end{array}$$

(13)

where we assume that $\alpha ,\eta ,\theta \ge 0$, $J_t={\sum }_{i=1}^{M_t}{Y}_i$. $M_t$ is a Poisson process with frequency $\rho$, which indicates the total number of jumps up to time t. $\{Y_i,i\ge 1\}$ are the sizes of the jumps and are assumed to be independent and identically distributed random variables following a distribution function $F\left(x\right)(x>0)$. When the value of the CIR process approaches 0, the behavior of such a process relies on its parameters. There are several conditions that assure that the jump-CIR process (13) remains strictly positive. We list those conditions as follows:

• ${\theta }^2\le 2\alpha \eta$. This condition is needed to guarantee $r_t>0$ with probability 1 if $r_0>0$, 0 is not accessible, and the process never blows up to ∞. Since $r_t$ follows a classical CIR process, the Feller condition ${\theta }^2\le 2\alpha \eta$ assures that $r_t>0$. Specifically, the probability of no jumps on a given time interval is positive, which also strengthens the importance of ${\theta }^2\le 2\alpha \eta$. If ${\theta }^2>2\alpha \eta$, the process $r_t$ will repeatedly cross zero and reflect at zero.
• $F\left(Y_i\right)\in {\mathcal{F}}_{t^{-}}$$F\left(Y_i\right)$ is the distribution of $Y_i$, which ensures the Markov property of the $r_t$. That is, if one can predict the exact jump timing and jump-size at an instant before a jump occurs, one can make an arbitrarily large profit with certainty.
• $E{Y}_i\in [0,\infty ),-r_{t-}<Y_i<\infty$ at $M_t=1$, which preserves non-negative jump intensity and a positive instantaneous volatility. For a more specific description about the conditions where the jump-CIR process remains strictly positive, one can refer to [30].

Comparing with the Vasicek model, the CIR process possesses the properties of mean-reverting and non-negativity, which is of better modeling for interest rates. When $\eta =\theta =0$, then JCIR processes reduce to shot noise processes, which are widely used in various fields, e.g., actuarial science, mathematical finance and electronics. Accordingly, investigating JCIR processes has important academic value and application value.

In the following, a critical lemma is brought out to price credit securities. We can refer to [31] for specific proof methods via martingale theory as well as piecewise deterministic Markov process theory.

Lemma 1.

Assume that $\mu \ge 0$, $k\ge 0$, then the joint Laplace transform of the distribution of $(r_t,R_t)$ (let $R_t={\int }_0^t{r}_{u}du$) is

$$\begin{array}{ccc}\hfill g(\mu ,k,t,T)& =& \mathbb{E}\left\{e^{-\mu r_T}{e}^{-k(R_T-R_t)}\right|{\mathcal{F}}_t^r\}\hfill \\ & =& exp(-B_{\mu ,k}(t,T)r_t)exp\left(\frac{{\alpha }^2\eta (T-t)}{{\theta }^2}\right){\left(C_{\mu ,k}(t,T)\right)}^{-\frac{2\alpha \eta }{{\theta }^2}}\hfill \\ & & \times exp(-\rho {\int }_0^{T-t}[1-h\left(B_{\mu ,k}(0,u)\right)]du),\hfill \end{array}$$

(14)

where

$$\begin{array}{c}\hfill h\left(B_{\mu ,k}(0,u)\right)={\int }_0^{\infty }{e}^{-B_{\mu ,k}(0,u)x}dF\left(x\right),\end{array}$$

(15)

$$\begin{array}{c}\hfill B_{\mu ,k}(t,T)=\frac{(2k-\alpha \mu )+\mu \sqrt{{\alpha }^2+2k{\theta }^2}coth(\sqrt{{\alpha }^2+2k{\theta }^2}(T-t)/2)}{({\theta }^2\mu +\alpha )+\sqrt{{\alpha }^2+2k{\theta }^2}coth(\sqrt{{\alpha }^2+2k{\theta }^2}(T-t)/2)},\end{array}$$

(16)

$$\begin{array}{ccc}\hfill C_{\mu ,k}(t,T)& =& cosh(\sqrt{{\alpha }^2+2k{\theta }^2}(T-t)/2)\hfill \\ & & +({\theta }^2\mu +\alpha ){({\alpha }^2+2k{\theta }^2)}^{-\frac{1}{2}}sinh(\sqrt{{\alpha }^2+2k{\theta }^2}(T-t)/2).\hfill \end{array}$$

(17)

Proof. 

$1.$ (Construct a martingale) Setting the infinitesimal generator operator $\mathcal{A}$ to 0, we construct a martingale. Let $f(R,r,t)=exp\{-G(t)r-kR+H(t\left)\right\}$. By [32], letting $\mathcal{A}f(R,r,t)=0$, we have

$$\begin{array}{c}\hfill -G^{{}^{\prime }}\left(t\right)r+H^{{}^{\prime }}\left(t\right)-kr-\alpha (\eta -r)G\left(t\right)+\frac{1}{2}{\theta }^{2}r{G}^2\left(t\right)+\rho [y\left(G\left(t\right)\right)-1]=0.\end{array}$$

(18)

Solving Equation (18), we get

$$\begin{array}{c}\hfill \left\{\begin{array}{c}-G^{{}^{\prime }}\left(t\right)-k+\alpha G\left(t\right)+\frac{1}{2}{\theta }^2{G}^2\left(t\right)=0,\hfill \\ H^{{}^{\prime }}\left(t\right)-\alpha \eta G\left(t\right)+\rho [y\left(G\left(t\right)\right)-1]=0.\hfill \end{array}\right.\end{array}$$

(19)

By solving the above coupled equations, we can get the explicit expression of $G\left(t\right)$ and $H\left(t\right)$. Then for $l>0$ and $k\ge 0$, when $0\le t<\frac{l}{\sqrt{{\alpha }^2+2k{\theta }^2}}$, $exp\{-G\left(t\right)r_t-k{R}_t+\rho {\int }_0^t[1-y\left(G\left(u\right)\right)]du+\alpha \eta {\int }_0^{t}G\left(u\right)du\}$ is a martingale, where

$$\begin{array}{c}\hfill y\left(\varphi \right)={\int }_0^{\infty }{e}^{-\varphi x}dF\left(x\right),\end{array}$$

(20)

and

$$\begin{array}{c}\hfill G\left(t\right)=-\frac{\alpha }{{\theta }^2}-\frac{\sqrt{{\alpha }^2++2k{\theta }^2}}{{\theta }^2}coth\left(\frac{\sqrt{{\alpha }^2+2k{\theta }^2}t-l}{2}\right).\end{array}$$

(21)

$2.$ (Laplace transforms of the distributions of $r_t$ and $R_t$) For an arbitrary fixed time $t(0\le s\le t<\frac{l}{\sqrt{{\alpha }^2}+2k{\theta }^2})$, by the properties of martingale, we have

$$\begin{array}{ccc}\hfill & & \mathbb{E}\{exp\{-G\left(t\right)r_t-k{R}_t+\rho {\int }_0^t[1-y\left(G\left(u\right)\right)]du+\alpha \eta {\int }_0^{t}G\left(u\right)du\}|{\mathcal{F}}_s^r\}\hfill \\ & & =exp\{-G\left(s\right)r_s-k{R}_s+\rho {\int }_0^s[1-y\left(G\left(u\right)\right)]du+\alpha \eta {\int }_0^{s}G\left(u\right)du\}.\hfill \end{array}$$

(22)

Then,

$$\begin{array}{ccc}\hfill & & \mathbb{E}\{exp\{-G\left(t\right)r_t-k(R_t-R_s)\}|{\mathcal{F}}_s^r\}\hfill \\ & & =exp\{-G\left(s\right)r_s\}exp\{-\rho {\int }_s^t[1-y\left(G\left(u\right)\right)]du\}exp\{-\alpha \eta {\int }_s^{t}G\left(u\right)du\}.\hfill \end{array}$$

(23)

Set $G\left(t\right)=\mu \ge 0$. By (21), we have

$$\begin{array}{c}\hfill l=\sqrt{{\alpha }^2+2k{\theta }^2}t-ln\frac{\mu {\theta }^2+\alpha -\sqrt{{\alpha }^2+2k{\theta }^2}}{\mu {\theta }^2+\alpha +\sqrt{{\alpha }^2+2k{\theta }^2}}.\end{array}$$

(24)

From (24), we easily get that $l>\sqrt{{\alpha }^2+2k{\theta }^2}t$, i.e., $t<\frac{l}{\sqrt{{\alpha }^2+2k{\theta }^2}}$. Substituting (24) in to $G\left(s\right)$, we get

$$\begin{array}{ccc}\hfill G\left(s\right)& =& B_{\mu ,k}(s,t)\hfill \\ & =& \frac{(2k-\alpha \mu )+\mu \sqrt{{\alpha }^2+2k{\theta }^2}coth(\sqrt{{\alpha }^2+2k{\theta }^2}(t-s)/2)}{({\theta }^2\mu +\alpha )+\sqrt{{\alpha }^2+2k{\theta }^2}coth(\sqrt{{\alpha }^2+2k{\theta }^2}(t-s)/2)},\hfill \end{array}$$

(25)

then, we have

$$\begin{array}{ccc}\hfill & & \mathbb{E}\{exp\{-G\left(t\right)r_t-k(R_t-R_s)\}|{\mathcal{F}}_s^r\}\hfill \\ & & =exp\{-B_{\mu ,k}(s,t)r_s\}exp\{-\rho {\int }_s^t[1-y\left(B_{\mu ,k}(u,t)\right)]du\}exp\{-\alpha \eta {\int }_s^t{B}_{\mu ,k}(u,t)du\}.\hfill \end{array}$$

(26)

For the right side of (26), letting $v=t-u$ and by integral calculation, we get the results of Lemma 1. □

Until now, the closed-form solution of the Laplace transforms of $r_t$ and $R_t$ are derived. Setting $\mu =0$ and $k=0$ in (14) gives the following corollaries.

Corollary 1.

Assume that $\mu \ge 0$, $k\ge 0$; then, the Laplace transforms of the distributions of $r_t$ and $R_t$ are, respectively,

$$\begin{array}{ccc}\hfill & & \mathbb{E}\left\{e^{-\mu r_T}\right|{\mathcal{F}}_t^r\}\hfill \\ & =& exp(-B_{\mu ,0}(t,T)r_t)exp\left(\frac{{\alpha }^2\eta (T-t)}{{\theta }^2}\right){\left(C_{\mu ,0}(t,T)\right)}^{-\frac{2\alpha \eta }{{\theta }^2}}\hfill \\ & & \times exp(-\rho {\int }_0^{T-t}[1-h\left(B_{\mu ,0}(0,u)\right)]du),\hfill \end{array}$$

(27)

and

$$\begin{array}{ccc}\hfill & & \mathbb{E}\left\{e^{-k(R_T-R_t)}\right|{\mathcal{F}}_t^r\}\hfill \\ & =& exp(-B_{0,k}(t,T)r_t)exp\left(\frac{{\alpha }^2\eta (T-t)}{{\theta }^2}\right){\left(C_{0,k}(t,T)\right)}^{-\frac{2\alpha \eta }{{\theta }^2}}\hfill \\ & & \times exp(-\rho {\int }_0^{T-t}[1-h\left(B_{0,k}(0,u)\right)]du).\hfill \end{array}$$

(28)

For mathematical simplicity, the jump size $\{Y_i,i\ge 1\}$ is assumed to be exponentially distributed; in other words,

$$F\left(x\right)=1-e^{-\omega x}(\omega >0,x>0).$$

As a special case of Corollary 1, the following corollary is presented.

Corollary 2.

Assume that $\mu \ge 0$, $k\ge 0$, and the distribution of jump sizes is $F\left(x\right)=1-e^{-\omega x}(\omega >0,x>0)$; then, the Laplace transforms of the distributions of $r_t$ and $R_t$ are

$$\begin{array}{ccc}\hfill & & \mathbb{E}\left\{e^{-\mu r_T}\right|{\mathcal{F}}_t^r\}\hfill \\ & =& exp(-B_{\mu ,0}(t,T)r_t)exp\left(\frac{{\alpha }^2\eta (T-t)}{{\theta }^2}\right){\left(C_{\mu ,0}(t,T)\right)}^{-\frac{2\alpha \eta }{{\theta }^2}}\hfill \\ & & \times {\left(\frac{2\alpha (\omega +\mu )exp\left(\alpha \right(T-t\left)\right)}{\omega ({\theta }^2\mu +2\alpha )exp\left(\alpha (T-t)\right)+(2\alpha \mu -\omega {\theta }^2\mu )}\right)}^{-\frac{2\rho }{2\alpha -\omega {\theta }^2}},\hfill \end{array}$$

(29)

and

$$\begin{array}{ccc}\hfill & & \mathbb{E}\left\{e^{-k(R_T-R_t)}\right|{\mathcal{F}}_t^r\}\hfill \\ & =& exp(-B_{0,k}(t,T)r_t)exp\{H_1\left(k\right)(T-t)+H_2\left(k\right)ln{D}_k(t,T)-H_{3}ln{C}_{0,k}(t,T)\}.\hfill \end{array}$$

(30)

where

$$\begin{array}{c}\hfill D_k(t,T)=cosh(\sqrt{{\alpha }^2+2k{\theta }^2}(T-t)/2)+\frac{\omega \alpha +2k}{\alpha \sqrt{{\alpha }^2+2k{\theta }^2}}sinh({\alpha }^2+2k{\theta }^2(T-t)/2),\end{array}$$

$$\begin{array}{c}\hfill H_1\left(k\right)=\frac{{\alpha }^2\eta (T-t)}{{\theta }^2}-\frac{2k\rho }{\omega (\sqrt{{\alpha }^2+2k{\theta }^2}+\alpha )+2k}-\frac{\omega \rho \sqrt{{\alpha }^2+2k{\theta }^2}}{2k+2\omega \alpha -{\omega }^2{\theta }^2},\end{array}$$

$$\begin{array}{c}\hfill H_2\left(k\right)=\frac{2\omega \rho }{2k+2\omega \alpha -{\omega }^2{\theta }^2},\end{array}$$

$$\begin{array}{c}\hfill H_3=\frac{2\alpha \eta }{{\theta }^2}.\end{array}$$

Thus, from (10) and Lemma 1, we can derive the pricing formulae of defaultable bonds. The time-t prices of the A- and B-bond with maturity date T will be shown in the following theorem.

Theorem 1.

In the primary–secondary framework, assume that firm A and firm B have the same maturity date with 0-valued recovery rate $({\beta }^A=0,{\beta }^B=0)$. Suppose that intensity process ${\lambda }_t^A$ satisfies (11) and process ${\lambda }_t^B$ satisfies (12); then, the time-t prices of the bonds issued by primary firm A and secondary firm B, respectively, are

$$\begin{array}{c}\hfill V^A(t,T)=\mathbb{E}\left[e^{-(1+b_1^A)(R_T-R_t)}\right|{\mathcal{F}}_t^r]e^{-b_0^A(T-t)}=g(0,1+b_1^A,t,T)e^{-b_0^A(T-t)},\end{array}$$

(31)

and

$$\begin{array}{ccc}\hfill V^B(t,T)& =& e^{-(b_0^B+b)(T-t)}g(0,1+b_1^B,t,T)+b{e}^{-(b_0^B+b)T+(b_0^B+b_0^A)t}\hfill \\ & & \times {\int }_t^T{e}^{-(b_0^A-b)s}·exp\left(\frac{{\alpha }^2\eta (T-s)}{{\theta }^2}\right){\left(C_{0,1+b_1^B}(s,T)\right)}^{-\frac{2\alpha \eta }{{\theta }^2}}\hfill \\ & & \times exp(-\rho {\int }_0^{T-s}[1-h\left(B_{0,1+b_1^B}(0,u)\right)]du)\hfill \\ & & \times g(B_{0,1+b_1^B}(s,T),1+b_1^B+b_1^A,t,s)ds.\hfill \end{array}$$

(32)

Proof. 

Firstly, from (11) and Lemma 1, we can easily illustrate that (31) holds. Secondly, according to (10), (12), and the property of conditional expectation, we obtain the time-t price of the bond with maturity date T issued by firm B

$$\begin{array}{ccc}\hfill V^B(t,T)& =& \mathbb{E}[exp(-{\int }_t^T(r_s+{\lambda }_s^B)ds)|{\mathcal{F}}_t]\hfill \\ & =& \mathbb{E}[exp(-b_0^B(T-t)-(1+b_1^B)(R_T-R_t)-b(T-{\tau }^A)1_{\{{\tau }^A\le T\}})|{\mathcal{F}}_t]\hfill \\ & =& \mathbb{E}[exp(-b_0^B(T-t)-(1+b_1^B)(R_T-R_t))\hfill \\ & & \times \mathbb{E}[exp(-b(T-{\tau }^A)1_{\{{\tau }^A\le T\}})|{\mathcal{F}}_t\vee {\mathcal{F}}_{T^{*}}^r]\left|{\mathcal{F}}_t\right].\hfill \end{array}$$

(33)

To calculate the time-t price of the B-bond with maturity T, we need to evaluate the conditional expectation embedded in (33). According to (2) and the law of integration by parts, we obtain that

$$\begin{array}{ccc}\hfill & & \mathbb{E}[exp(-b(T-{\tau }^A)1_{\{{\tau }^A\le T\}})|{\mathcal{F}}_t\vee {\mathcal{F}}_{T^{*}}^r]\hfill \\ & =& ({\int }_t^T+{\int }_T^{\infty })e^{-b(T-s)1_{\{s\le T\}}}d(1-e^{-b_0^A(s-t)-b_1^A(R_s-R_t)})\hfill \\ & =& e^{-b(T-t)}(1+b{\int }_t^T{e}^{-(b_0^A-b)(s-t)-b_1^A(R_s-R_t)}ds).\hfill \end{array}$$

(34)

Hence, according to the expectation obtained, we get

$$\begin{array}{ccc}\hfill V^B(t,T)& =& e^{-(b_0^B+b)(T-t)}\mathbb{E}\left[e^{-(1+b_1^B)(R_T-R_t)}\right|{\mathcal{F}}_t]+b{e}^{-(b_0^B+b)T+(b_0^B+b_0^A)t}\hfill \\ & & \times {\int }_t^T{e}^{-(b_0^A-b)s}\mathbb{E}\left[e^{-(1+b_1^B+b_1^A)(R_s-R_t)-(1+b_1^B)(R_T-R_s)}\right|{\mathcal{F}}_t]ds.\hfill \end{array}$$

(35)

For the first expectation term, we easily obtain

$$\begin{array}{c}\hfill \mathbb{E}\left[e^{-(1+b_1^B)(R_T-R_t)}\right|{\mathcal{F}}_t]=g(0,1+b_1^B,t,T).\end{array}$$

(36)

Furthermore, using the properties of iterated conditional expectation, we get

$$\begin{array}{ccc}\hfill & & \mathbb{E}\left[e^{-(1+b_1^B+b_1^A)(R_s-R_t)-(1+b_1^B)(R_T-R_s)}\right|{\mathcal{F}}_t]\hfill \\ & =& \mathbb{E}[e^{-(1+b_1^B+b_1^A)(R_s-R_t)}·\mathbb{E}\left[e^{-(1+b_1^B)(R_T-R_s)}\right|{\mathcal{F}}_s]|{\mathcal{F}}_t]\hfill \\ & =& exp\left(\frac{{\alpha }^2\eta (T-s)}{{\theta }^2}\right){\left(C_{0,1+b_1^B}(s,T)\right)}^{-\frac{2\alpha \eta }{{\theta }^2}}\hfill \\ & & \times exp(-\rho {\int }_0^{T-s}[1-h\left(B_{0,1+b_1^B}(0,u)\right)]du)g(B_{0,1+b_1^B}(s,T),1+b_1^B+b_1^A,t,s).\hfill \end{array}$$

(37)

Now, substituting (36) and (37) into (35), (32) holds. The proof of Theorem 1 is complete. Next, we will present the numerical results of the yield spread. □

Until now, within the primary–secondary framework, we obtain the explicit pricing of defaultable bonds. Now, we pay attention to the yield spread, which is a function of maturity to explore the effect of counterparty risk on firm B’s bond price. In continuous-time modeling, we define the yield spread $\psi$ between defaultable bond v and default-free bond p as

$$\begin{array}{c}\hfill \psi (t,T)=-\frac{1}{T-t}ln\frac{v(t,T)}{p(t,T)}.\end{array}$$

(38)

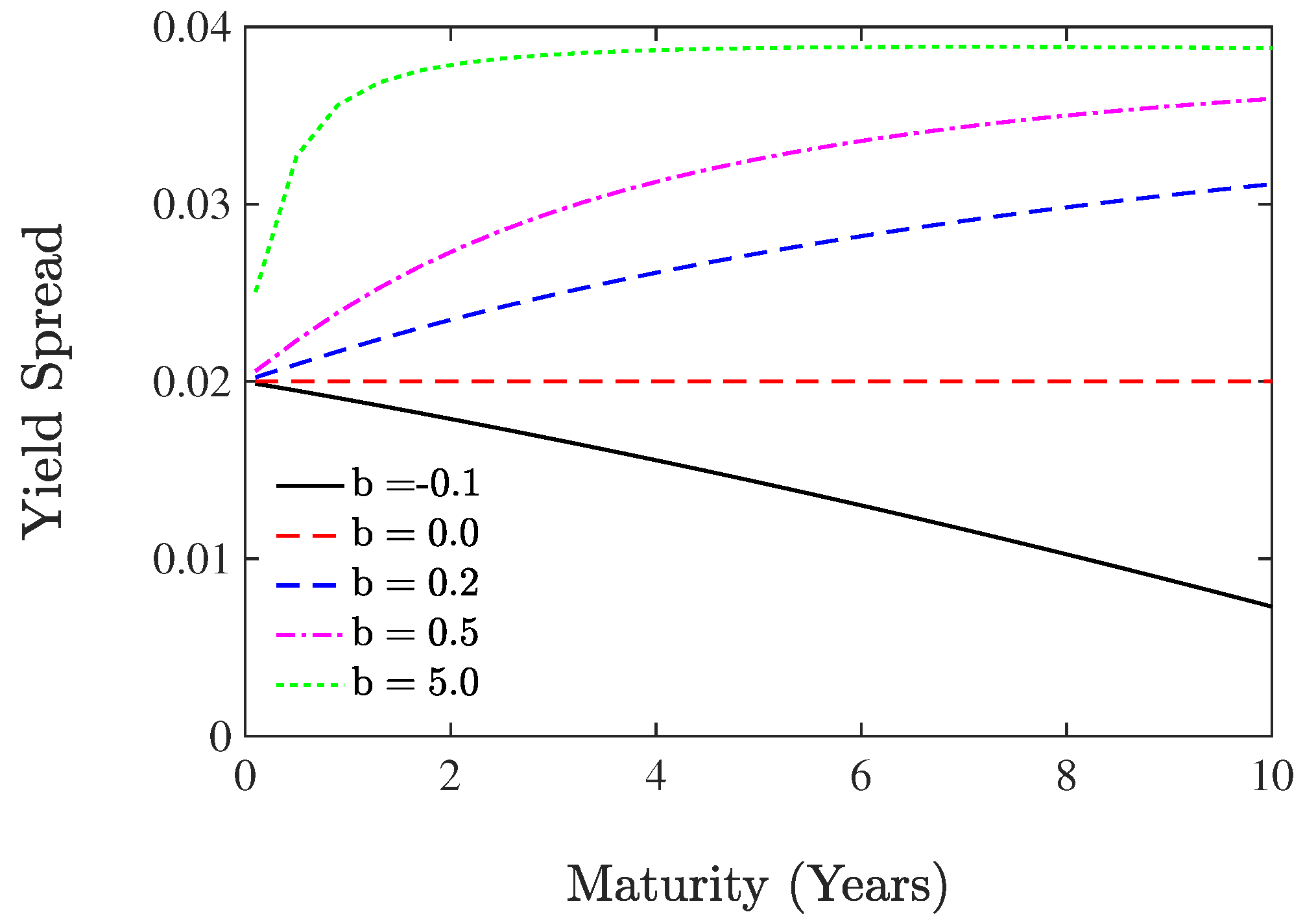
In the following, we present an example to discuss the term structure of yield spreads between primary firm A and secondary firm B.

Example 1.

Assume that ${\beta }^A={\beta }^B=0$, then the yield spread of firm B’s bond is the corresponding martingale default probability averaged over $T-t$. In the economy, if we ignore the counterparty risk and the short-term interest rate, mathematically speaking, $b=0$ and $b_1^B=0$; then, the yield spread will be the constant $b_0^B$. When $b>0$ ($b_1^B=0$), firm B’s default is “accelerated" by firm A’s default with an increasing pattern in the yield spread. In contrast, a “deceleration" holds when $b<0$ ($b_1^B=0$), with the yield spread being a decreasing function of maturity. These effects are illustrated in Figure 1 with some given parameters.

In contrast with the Markov model based on the ratings of Jarrow et al. [33], in our model, we ignore the interaction between market risk and credit risk. Usually investment-grade issuers’ credit spread curves are upward-sloping, while those of speculative-level issuers are tilted downward. However, when the possibility of default is affected by economy-wide risk factors, there will be additional aspects to this problem, as illustrated in Figure 1. Except for Panel (a), obviously, the shape of the default-free term structure and the coefficient $b_1^A$ jointly determine the term structure of the credit spread.

When $b_1^B\ne 0$, $r_t$ follows (13); here, we assume that the jump’s sizes follow an exponential distribution with parameter $\omega >0$. Since jump process is involved in our model, Equation (32) is far more complex for computing the yield spread compared to that of Figure 1. Futhermore, the shape of a contemporaneous default-free term structure also affects the yield spread. However, we expect the patterns exhibited in Figure 1 to persist. Namely, the yield spread will widen (narrow) over time with the default risk from the long (short) position.

In Figure 2, this results come from both economy-wide state variables and counterparty risk. We find that jump diffusion risk and counterparty risk have caused significant changes in the effects of different $b_1^B$ on yield spread, while the CIR process dilutes the effect of $b_1^B$ on yield spread, so the impact of $b_1^B$ on yield spread is minimal. Besides these conjectures, in Figure 3, we could also get a way to extract information on the counterparty risk with empirical evidence. The effect of counterparty risk has caused the distortion of the term structure of the primary firms’ credit spreads (see Panel (d), (f) of Figure 4), which is basically the re-adjusted default-free term structure. In fact, during estimation, counterparty risk causes the derivation between the credit spread curve and the shape of the default-free term structure. This mainly comes from the simple one-factor term structure model as well as the default process, which only depends on the contemporaneous level of the spot rate. It is easy to extend our model to a multi-factor environment where other macro-economic factors can also affect default.

In Figure 5, we also get the way to extract information on the economy-wide risk with empirical evidence. The secondary firms’ possibility of default is affected by economy-wide risk factors, as is illustrated in Figure 4. Compared with Figure 4, interest rate is driven by the jump-diffusion Cox–Ingersoll–Ross (JCIR) process simultaneously in Figure 5. In addition, the default intensity is also correlated to the default states of counterparty firms. From Figure 5, we find that the larger the $b_1^B$, the larger the short-term yield spread; $b_1^B$ is very sensitive to yield spread, and this phenomenon is completely in line with the facts.

4. Default Swap Rates

In this section, based on the results in Section 3, we derive the swap rate in the reduced-form model. We assume that firm C holds bonds from reference firm A, and in the meantime, is a CDS buyer from firm B for a compensation of the possible loss induced by firm A’s default. The maturity dates of the bond and the CDS are assumed to be $T_1$ and $T_2$ ($T_2\le T_1$), respectively. Here, we only consider firm A and B as being the primary and secondary party, respectively. The recovery rate of the bond issued by firm A is assumed to be zero, with its face value being 1 dollar. The swap rate could be obtained by the following theorem.

Theorem 2.

Assume that $r_t$ follows the stochastic differential Equation (13), while ${\lambda }^A$ and ${\lambda }^B$ satisfy (11) and (12), respectively. Then, the swap rate

$$\begin{array}{c}\hfill c=\frac{V^B(0,T_2)-e^{-(b_0^B+b_0^A)T_2}g(0,1+b_1^B+b_1^A,0,T_2)}{{\int }_0^{T_2}{V}^C(0,s)ds},\end{array}$$

(39)

where

$g(\mu ,k,t,T)$ and $V^B(0,T_2)$, $V^C(0,s)$ are given by Lemma 1 and Theorem 1, respectively.

Proof. 

First, the time-0 market value of buyer C’s payment to B is

$$\begin{array}{c}\hfill \mathbb{E}[{\int }_0^{T_2}exp(-{\int }_0^s{r}_{u}du)c{1}_{\{{\tau }^C>s\}}ds]=c{\int }_0^{T_2}{V}^C(0,s)ds,\end{array}$$

(40)

while that of B’s promised compensation in the case of A’s default is

$$\begin{array}{c}\hfill \mathbb{E}[1_{\{{\tau }^A\le T_2\}}exp(-{\int }_0^{T_2}{r}_{u}du)1_{\{{\tau }^B>T_2\}}].\end{array}$$

(41)

Thus, using the principle of no-arbitrage, we obtain

$$\begin{array}{ccc}\hfill c& =& \frac{\mathbb{E}[exp(-{\int }_0^{T_2}(r_u+{\lambda }_u^B)du)]-\mathbb{E}[1_{\{{\tau }^A>T_2\}}exp(-{\int }_0^{T_2}(r_u+{\lambda }_u^B)du)]}{{\int }_0^{T_2}{V}^C(0,s)ds}.\hfill \end{array}$$

(42)

A brief inspection of the expression in (42) confirms two intuitions. First, c is equal to zero when the reference asset A is default-free. Second, the swap rate increases with the default probabilities of A and C, and decreases with that of B. For more details, one can refer to Appendix F of [7]. Note that ${\int }_0^{T_2}{V}^C(0,s)ds$ and the first term of the numerator of (42), which is equal to $V^B(0,T_2)$, can be derived by (31) and (32), respectively. Substituting (12) into the expectation term above, we obtain

$$\begin{array}{ccc}\hfill & & \mathbb{E}[1_{\{{\tau }^A>T_2\}}exp(-{\int }_0^{T_2}(r_u+{\lambda }_u^B)du)]\hfill \\ & =& \mathbb{E}[1_{\{{\tau }^A>T_2\}}exp(-{\int }_0^{T_2}(b_0^B+(1+b_1^B)r_u+b{1}_{\{{\tau }^A\le u\}})du)]\hfill \\ & =& \mathbb{E}[\mathbb{E}\left[1_{\{{\tau }^A>T_2\}}\right|{\mathcal{F}}_{T^{*}}]exp(-b_0^B{T}_2-(1+b_1^B)R_{T_2})]\hfill \\ & =& \mathbb{E}[exp(-b_0^B{T}_2-(1+b_1^B)R_{T_2}-{\int }_0^{T_2}{\lambda }_u^{A}du)],\hfill \end{array}$$

(43)

where the second equality involves the property of conditional expectation, the last one follows (2). Substituting (11) into (43), we obtain

$$\begin{array}{ccc}\hfill & & \mathbb{E}[exp(-b_0^B{T}_2-(1+b_1^B)R_{T_2}-{\int }_0^{T_2}{\lambda }_u^{A}du)]\hfill \\ & =& exp(-(b_0^B+b_0^A)T_2)g(0,1+b_1^A+b_1^B,0,T_2).\hfill \end{array}$$

(44)

Now, substituting (44) into (42), (39) holds. The proof of Theorem 2 is complete. □

In conjunction with the pricing results of defaultable bonds, we obtain the explicit formula of default swap rates, which is an important indicator in the risk management market. With given parameters, we can obtain the relevant prices of defaultable bonds and swap rates. However, the method for evaluating the parameters is beyond the scope of our article and is left for future discussion. For an insight into the improvement of the results in our model, the numerical illustrations for swap rate are provided.

Example 2.

We assume that the jump’s sizes follow an exponential distribution with parameter $\omega >0$, and firm C is not defaulted in the past with $V^C(0,s)=E\left[e^{-R_s}\right]=g(0,1,0,s)$. We analyze the dynamic relations between the default swap rate c and the maturity date T ($T_2$ in Theorem 2) for different forms of risk-free interest rate, different mean positive jumps ω, and different counterparty risk levels b. The swap rate decreases with the maturity increasing by intuition.

Firstly, in panel (a) of Figure 6, in terms of the influence of risk-free interest rate forms chosen, although the swap rate decreases with the same trends, consistent with the intuition, there is a clear difference between the results of our model and the others. The swap rate, compared with applying the JCIR process, is overestimated in the other cases. These results clarify the essential modification of the swap rate when applying JCIR process for the risk-free interest rate.

Secondly, in panel (b) of Figure 6, we find that the default swap rate is notably affected by ω. For larger ω, generally, there will be a higher jump probability in the interest rate process, leading to a more unstable interest rate, which increases the firms’ default probability. Meanwhile, the swap rate increases with the default probabilities of firm A, but decreases with that of firm B. Moreover, firm B’s default intensities, empirically, play a decisive role in pricing the swap rate. Consequently, as a function of the maturity date, the larger the ω, the slower c decreases, which agrees with the trend obtained in panel (b). This emphasizes the necessity of considering the jump factor in the stochastic interest rate process.

Thirdly, according to the results of different b in panel (c) of Figure 6, we find that the default swap rate is significantly overpriced when ignoring the default correlation ($b=0$). Therefore, it is vital to consider the contagion. A successively higher b indicates an increasing default correlation between the swap seller, B, and the reference asset A. As b becomes very large, we expect the fair swap rate to drop to zero since the default swap is ineffective.

Finally, according to the results of different $b_1^B$ in panel (d) of Figure 6, we discover that when the risk-free interest rate follows the same JCIR process, the default swap rate is affected by $b_1^B$ to a very small extent. From a numerical perspective, in a short period of time, the larger the $b_1^B$ value, the greater the rate of decline of the default swap rate.

5. Conclusions

In this paper, we derive the joint Laplace transform for the distribution of the vector process $(r_t,R_t)$, and using the joint Laplace transform, we obtain explicit pricing formulae of defaultable securities in the primary–secondary framework, where the counterparty relationship among these firms and economy-wide state variables (risk-free interest rate) follow the JCIR process, being able to influence their default probabilities. Such configuration is found to be vital for a better approach to the CDS market. We show that the interaction of market-wide risk factors with company-specific counterparty risks lead to various shapes of term structure for credit spreads. Within such a framework, the pricing of the CDS is shown. In the end, numerical graphics vividly illustrate the effect of exponential distributed jump sizes on the yield spread and CDS.

In addition, it is also of interest and is challenging to further explore other heavy-tailed distributions of the jump sizes, for instance, the Pareto distribution, the Gumbel distribution, and the Féchet distribution. However, the expression of the joint Laplace transform might be implicit.