A Perturbed Milne’s Quadrature Rule for n-Times Differentiable Functions with Lp-Error Estimates
Abstract
1. Introduction
2. Perturbed Milne’s Quadrature Formula
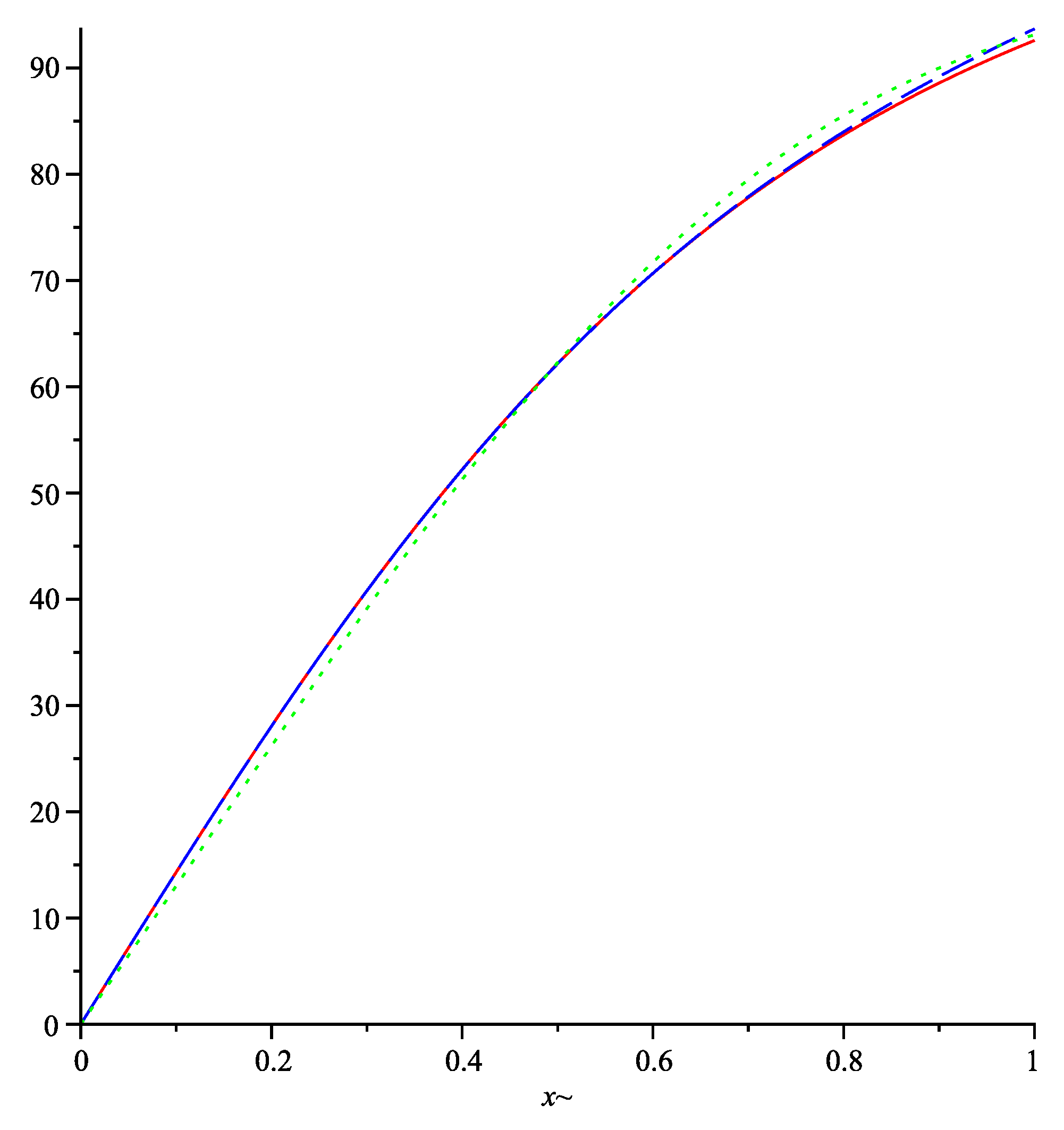
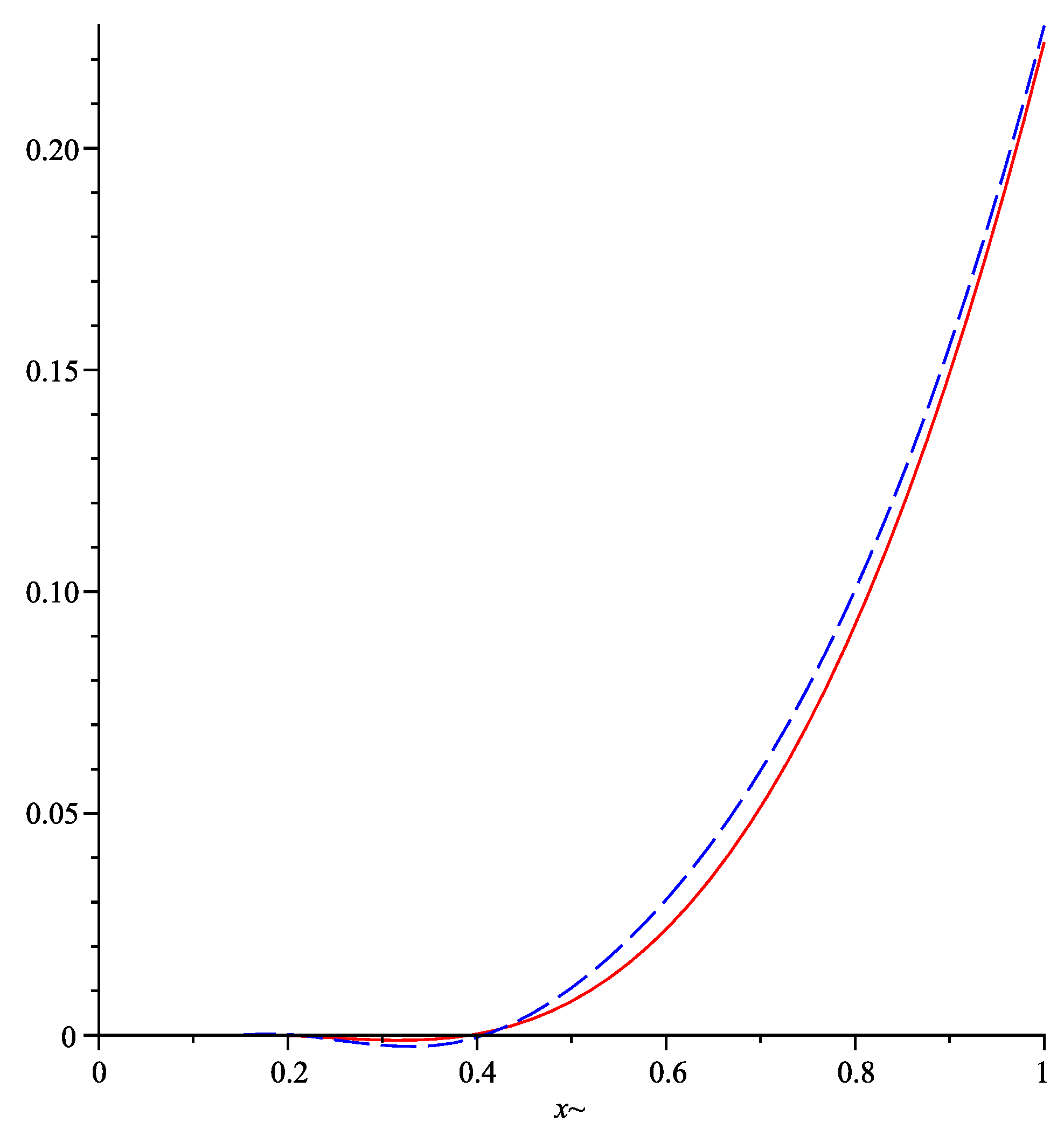
3. Error Estimation(s)
4. Other Estimations Involving Norms
5. More on –Bounds
5.1. Bounds in
5.2. Bounds in
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Booth, A.D. Numerical Methods, 3rd ed.; Butterworth & Co.: Berkeley, CA, USA, 1966. [Google Scholar]
- Dragomir, S.S. On Simpson’s quadrature formula for mappings of bounded variation and applications. Tamkang J. Math. 1999, 30, 53–58. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Agarwal, R.P.; Cerone, P. On Simpson’s inequality and applications. J. Inequal. Appl. 2000, 5, 533–579. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Set, E.; Ozdemir, M.E. On new inequalities of Simpson’s type for s-convex functions. Comput. Math. Appl. 2010, 60, 2191–2199. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Budak, H.; Erden, S. On new inequalities of Simpson’s type for generalized convex functions. Korean J. Math. 2019, 27, 279–295. [Google Scholar]
- Liu, Z. An inequality of Simpson type. Proc. R. Soc. Lond. Ser. A 2005, 461, 2155–2158. [Google Scholar] [CrossRef]
- Liu, Z. More on inequalities of Simpson type. Acta Math. Acad. Paedagog. Nyíregyházi. 2007, 23, 15–22. [Google Scholar]
- Shi, Y.; Liu, Z. Some sharp Simpson type inequalities and applications. Appl. Math. E-Notes 2009, 9, 205–215. [Google Scholar]
- Pečarić, J.; Varošanec, S. Simpson’s formula for functions whose derivatives belong to Lp spaces. Appl. Math. Lett. 2001, 14, 131–135. [Google Scholar] [CrossRef][Green Version]
- Ujević, N. Two sharp inequalities of Simpson type and applications. Georgian Math. J. 2004, 1, 187–194. [Google Scholar] [CrossRef]
- Ujević, N. Sharp inequalities of Simpson type and Ostrowski type. Comp. Math. Appl. 2004, 48, 145–151. [Google Scholar] [CrossRef]
- Ujević, N. A generalization of the modified Simpson’s rule and error bounds. ANZIAM J. 2005, 47, E1–E13. [Google Scholar] [CrossRef]
- Ujević, N. New error bounds for the Simpson’s quadrature rule and applications. Comp. Math. Appl. 2007, 53, 64–72. [Google Scholar] [CrossRef]
- Alomari, M.W.; Guessab, A. Lp–error bounds of two and three-point quadrature rules for Riemann–Stieltjes integrals. Moroccan J. Pure Appl. Anal. 2018, 4, 33–43. [Google Scholar] [CrossRef]
- Alomari, M.W. Two-point quadrature rules for Riemann–Stieltjes integrals with Lp–error estimates. Moroccan J. Pure Appl. Anal. 2018, 4, 94–110. [Google Scholar] [CrossRef]
- Alomari, M.W. Two-point Ostrowski’s inequality. Results Math. 2017, 72, 1499–1523. [Google Scholar] [CrossRef]
- Alomari, M.W. On Beesack–Wirtinger inequality. Results Math. 2017, 72, 1213–1225. [Google Scholar] [CrossRef]
- Alomari, M.W. Two–point Ostrowski and Ostrowski–Grüss type inequalities with applications. J. Anal. 2020, 28, 623–661. [Google Scholar] [CrossRef]
- Alomari, M.W. New sharp inequalities of Ostrowski and generalized trapezoid type for the Riemann–Stieltjes integrals and applications. Ukr. Math. J. 2013, 65, 895–916. [Google Scholar] [CrossRef][Green Version]
- Alomari, M.W.; Dragomir, S.S. A three-point quadrature rule for the Riemann-Stieltjes integral. Southeast Asian Bull. J. Math. 2018, 42, 1–14. [Google Scholar]
- Barnett, N.S.; Dragomir, S.S.; Gomma, I. A companion for the Ostrowski and the generalised trapezoid inequalities. Math. Comput. Model. 2009, 50, 179–187. [Google Scholar] [CrossRef]
- Barnett, N.S.; Cheung, W.-S.; Dragomir, S.S.; Sofo, A. Ostrowski and trapezoid type inequalities for the Stieltjes integral with Lipschitzian integrands or integrators. Comput. Math. Appl. 2009, 57, 195–201. [Google Scholar] [CrossRef][Green Version]
- Cerone, P.; Dragomir, S.S. New Bounds for the Three-Point Rule Involving the Riemann-Stieltjes Integrals. In Advances in Statistics Combinatorics and Related Areas; Gulati, C., Lin, Y., Mishra, S., Rayner, J., Eds.; World Science Publishing: Hackensack, NJ, USA, 2002; pp. 53–62. [Google Scholar]
- Cerone, P.; Dragomir, S.S. Approximating the Riemann–Stieltjes integral via some moments of the integrand. Math. Comput. Model. 2009, 49, 242–248. [Google Scholar] [CrossRef][Green Version]
- Alomari, M.W.; Liu, Z. New error estimations for the Milne’s quadrature formula in terms of at most first derivatives. Konuralp J. Math. 2013, 1, 17–23. [Google Scholar]
- Milovanović, G.V. Ostrowski type inequalities and some selected quadrature formulae. Appl. Anal. Discrete Math. 2021, 15, 151–178. [Google Scholar] [CrossRef]
- Qawasmeh, T.; Hatamleh, R. A new contraction based on H-simulation functions in the frame of extended b-metric spaces and application. Inter. J. Elec. Comp. Eng. 2023, 13, 4212–4221. [Google Scholar] [CrossRef]
- Qazza, A.; Hatamleh, R. The existence of a solution for semi-linear abstract differential equations with infinite B-chains of the characteristic. Inter. J. Appl. Math. 2018, 31, 611. [Google Scholar] [CrossRef]
- Salah, E.; Saadeh, R.; Qazza, A.; Hatamleh, R. Direct power series approach for solving nonlinear initial Value problems. Axioms 2023, 12, 111. [Google Scholar] [CrossRef]
- Cerone, P.; Dragomir, S.S. Midpoint–type rules from an inequalities point of view. In Handbook of Analytic Computational Methods in Applied Mathematics; Anastsssiou, G., Ed.; CRC Press: New York, NY, USA, 2000; pp. 135–200. [Google Scholar]
- Cerone, P.; Dragomir, S.S. Trapezoidal–type rules from an inequalities point of view. In Handbook of Analytic Computational Methods in Applied Mathematics; Anastsssiou, G., Ed.; CRC Press: New York, NY, USA, 2000; pp. 65–134. [Google Scholar]
- Cerone, P.; Dragomir, S.S.; Roumeliotis, J.; Šunde, J. A new generalization of the trapezoid formula for n-time differentiable mappings and applications. Demonstr. Math. 2000, 33, 719–736. [Google Scholar] [CrossRef]
- Guessab, A.; Schmeisser, G. Sharp integral inequalities of the Hermite-Hadamard type. J. Approx. Theory 2002, 115, 260–288. [Google Scholar] [CrossRef]
- Kovač, S.; Pečarić, J. Generalization of an integral formula of Guessab and Schmeisser. Banach J. Math. Anal. 2011, 5, 1–18. [Google Scholar] [CrossRef]
- Liu, Z. Some companions of an Ostrowski type inequality and applications. J. Ineq. Pure Appl. Math. 2009, 10, 52. [Google Scholar]
- Sofo, A. Integral Inequalities for n-Times Differentiable Mappings, Chapter II. In Ostrowski Type Inequalities and Applications in Numerical Integration; Dragomir, S.S., Rassias, T.M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Ujević, N. A generalization of Ostrowski’s inequality and applications in numerical integration. Appl. Math. Lett. 2004, 17, 133–137. [Google Scholar] [CrossRef]
- Davis, P.J. Interpolation and Approximation; Dover: Mineola, NY, USA, 1975. [Google Scholar]
- Dedić, L.; Matić, M.; Pečarić, J. On Euler–Maclaurin formulae. Math. Inequal. Appl. 2003, 6, 247–275. [Google Scholar] [CrossRef]
- Dedić, L.; Matić, M.; Pečarić, J. On dual Euler–Simpson formulae. Bull. Belg. Math. Soc. 2001, 8, 479–504. [Google Scholar] [CrossRef]
- Dedić, L.; Matić, M.; Pečarić, J. On Euler–Simpson formulae. Pan. Am. Math. J. 2001, 11, 47–64. [Google Scholar]
- Dedić, L.; Matić, M.; Pečarić, J. On generalizations of Ostrowski inequality via some Euler–type identities. Math. Inequal. Appl. 2000, 3, 337–353. [Google Scholar] [CrossRef]
- Hatamleh, R.; Zolotarev, V.A. Triangular Models of Commutative Systems of Linear Operators Close to Unitary Ones. Ukr. Math. J. 2016, 68, 791–811. [Google Scholar] [CrossRef]
- Franjić, I.; Pečarić, J.; Perić, I. General three–point quadrature formulas of Euler type. ANZIAM J. 2011, 52, 309–317. [Google Scholar] [CrossRef][Green Version]
- Franjić, I.; Perić, I.; Pečarić, J. Estimates for the Gauss four-point formula for functions with low degree of smoothness. Appl. Math. Lett. 2007, 20, 1–6. [Google Scholar] [CrossRef][Green Version]
- Franjić, I.; Pečarić, J. On corrected Bullen-Simpson’s 3/8 inequality. Tamkang J. Math. 2006, 37, 135–148. [Google Scholar] [CrossRef]
- Franjić, I.; Pečarić, J.; Perić, I. General Euler–Boole’s and dual Euler–Boole’s formulae. Math. Ineq. Appl. 2005, 8, 287–303. [Google Scholar]
- Franjić, I.; Pečarić, J. Corrected Euler–Maclaurin’s formulae. Rendi. Circolo Mate. Palermo 2005, 54, 259–272. [Google Scholar] [CrossRef]
- Kythe, P.K.; Schäferkotter, M.R. Handbook of Computational Methods for Integration; Chapman & HallL/CRC, A CRC Press Company: London, UK, 2005. [Google Scholar]
- Mastroianni, G.; Milovanović, G.V. Interpolation Processes–Basic Theory and Applications; Springer Monographs in Mathematics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
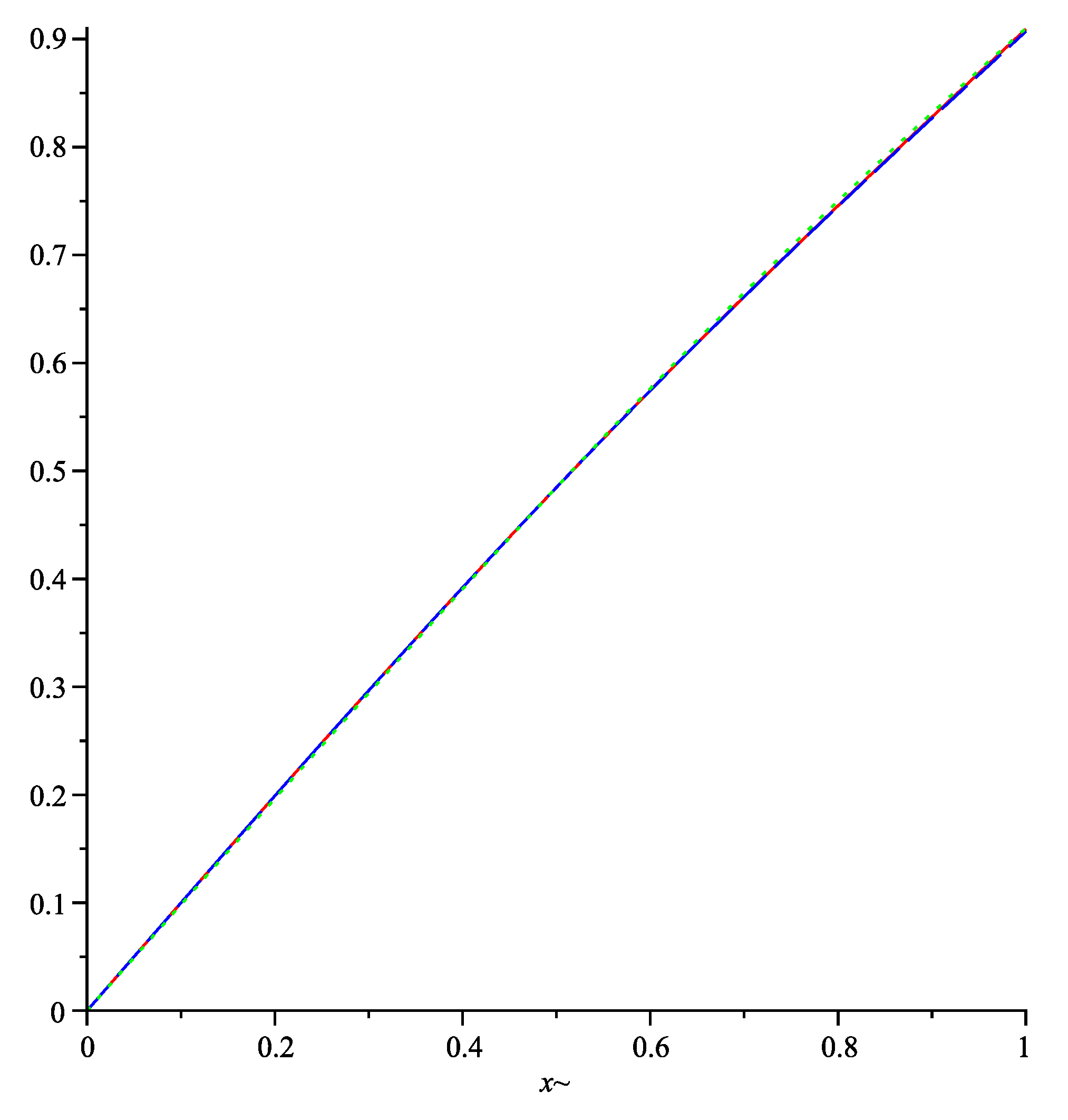

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hazaymeh, A.; Saadeh, R.; Hatamleh, R.; Alomari, M.W.; Qazza, A. A Perturbed Milne’s Quadrature Rule for n-Times Differentiable Functions with Lp-Error Estimates. Axioms 2023, 12, 803. https://doi.org/10.3390/axioms12090803
Hazaymeh A, Saadeh R, Hatamleh R, Alomari MW, Qazza A. A Perturbed Milne’s Quadrature Rule for n-Times Differentiable Functions with Lp-Error Estimates. Axioms. 2023; 12(9):803. https://doi.org/10.3390/axioms12090803
Chicago/Turabian StyleHazaymeh, Ayman, Rania Saadeh, Raed Hatamleh, Mohammad W. Alomari, and Ahmad Qazza. 2023. "A Perturbed Milne’s Quadrature Rule for n-Times Differentiable Functions with Lp-Error Estimates" Axioms 12, no. 9: 803. https://doi.org/10.3390/axioms12090803
APA StyleHazaymeh, A., Saadeh, R., Hatamleh, R., Alomari, M. W., & Qazza, A. (2023). A Perturbed Milne’s Quadrature Rule for n-Times Differentiable Functions with Lp-Error Estimates. Axioms, 12(9), 803. https://doi.org/10.3390/axioms12090803









