Boundary Controlling Synchronization and Passivity Analysis for Multi-Variable Discrete Stochastic Inertial Neural Networks
Abstract
:1. Introduction
- (1)
- (2)
2. Problem Formulation
2.1. SINNs in Discrete Form
- (F)
- and are n-order matrices ensuring
2.2. Some Important Inequalities
3. Stochastic Synchronization and Passivity-Based Control
3.1. Stochastic Synchronization
3.2. Passivity-Based Control
| Algorithm 1 Stochastic synchronization or passivity of INNs Equations (1) and (5) |
|
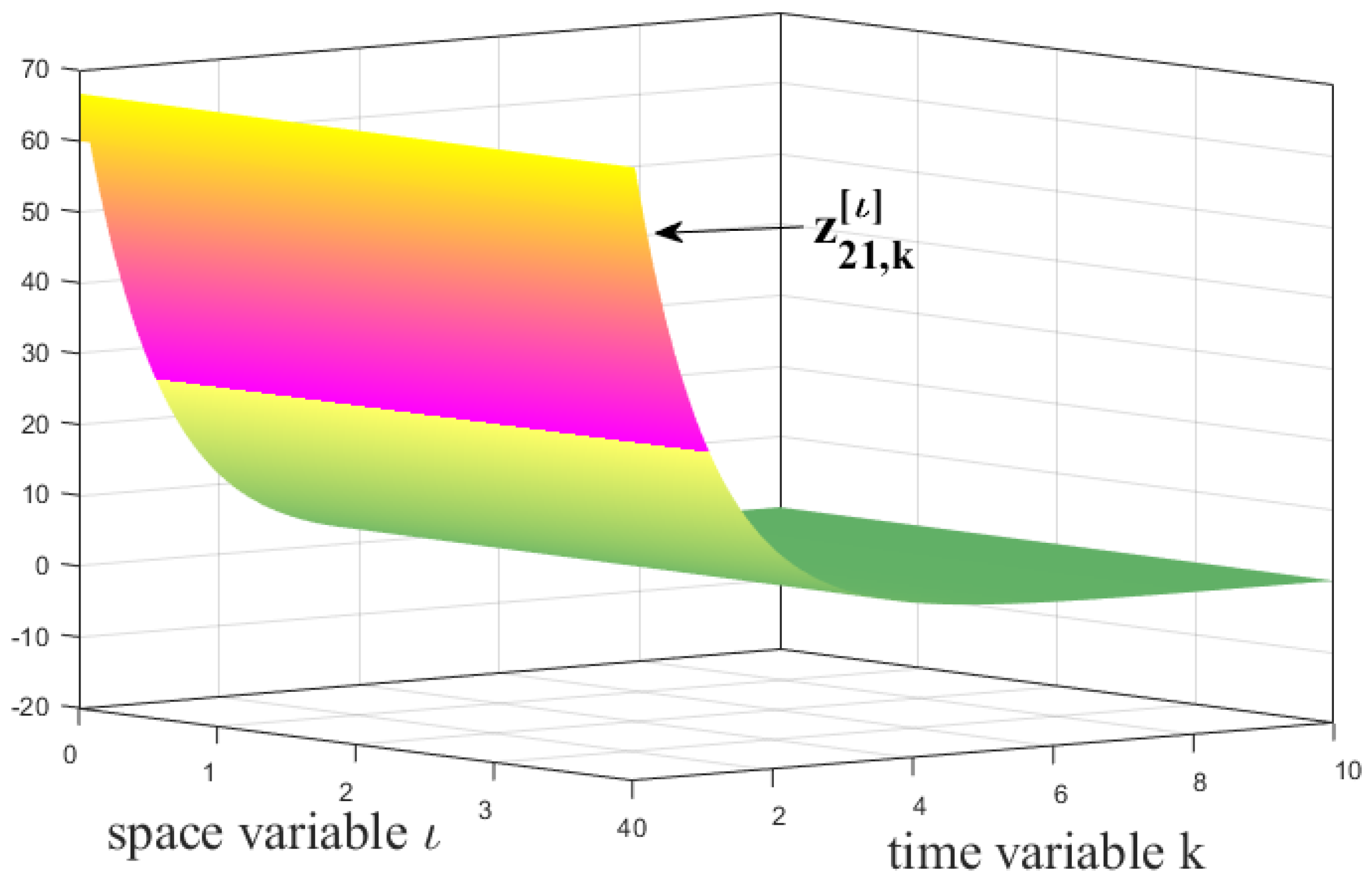
4. Numerical Example
5. Conclusions and Future Works
- Fractional dynamics has become a research hotspot in recent years, which could be discussed in the SINNs of this article.
- This paper only considers 1-dimensional space variables, which could be extended to higher dimensions.
- Exploration of alternative control techniques, such as impulsive controls and adaptive controls, holds promise for further investigation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ganesan, B.; Mani, P.; Shanmugam, L.; Annamalai, M. Synchronization of stochastic neural networks using looped-Lyapunov functional and its application to secure communication. IEEE Trans. Neural Netw. Learn. Syst. 2022; in press. [Google Scholar] [CrossRef]
- Alsaedi, A.; Cao, J.D.; Ahmad, B.; Alshehri, A.; Tan, X. Synchronization of master-slave memristive neural networks via fuzzy output-based adaptive strategy. Chaos Soliton Fractal 2022, 158, 112095. [Google Scholar] [CrossRef]
- Liu, F.; Meng, W.; Lu, R.Q. Anti-synchronization of discrete-time fuzzy memristive neural networks via impulse sampled-data communication. IEEE Trans. Cybern. 2022; in press. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, C.; Sun, Y.; Yao, W.; Lin, H. Cluster output synchronization for memristive neural networks. Inf. Sci. 2022, 589, 459–477. [Google Scholar] [CrossRef]
- Li, H.Y.; Fang, J.A.; Li, X.F.; Rutkowski, L.; Huang, T.W. Event-triggered synchronization of multiple discrete-time Markovian jump memristor-based neural networks with mixed mode-dependent delays. IEEE Trans. Circuits Syst. I-Regul. Pap. 2022, 69, 2095–2107. [Google Scholar] [CrossRef]
- Boonsatit, N.; Rajendran, S.; Lim, C.P.; Jirawattanapanit, A.; Mohandas, P. New adaptive finite-time cluster synchronization of neutral-type complex-valued coupled neural networks with mixed time delays. Fractal Fract. 2022, 6, 6090515. [Google Scholar] [CrossRef]
- Zaferani, E.J.; Teshnehlab, M.; Khodadadian, A.; Heitzinger, C.; Vali, M.; Noii, N.; Wick, T. Hyper-parameter optimization of stacked asymmetric auto-encoders for automatic personality traits perception. Sensors 2022, 22, 6206. [Google Scholar] [CrossRef]
- Alimi, A.M.; Aouiti, C.; Assali, E.A. Finite-time and fixed-time synchronization of a class of inertial neural networks with multiproportional delays and its application to secure communication. Neurocomputing 2019, 332, 29–43. [Google Scholar] [CrossRef]
- Song, X.N.; Man, J.; Park, J.H.; Song, S. Finite-time synchronization of reaction-diffusion inertial memristive neural networks via gain-scheduled pinning control. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5045–5056. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Huang, Z.; Wu, Z.; Cao, J.D.; Park, J.H. Nonfragile H∞ synchronization of BAM inertial neural networks subject to persistent dwell-time switching regularity. IEEE Trans. Cybern. 2022, 52, 6591–6602. [Google Scholar] [CrossRef]
- Shanmugasundaram, S.; Udhayakumar, K.; Gunasekaran, D.; Rakkiyappan, R. Event-triggered impulsive control design for synchronization of inertial neural networks with time delays. Neurocomputing 2022, 483, 322–332. [Google Scholar] [CrossRef]
- Liu, J.; Shu, L.; Chen, Q.; Zhong, S. Fixed-time synchronization criteria of fuzzy inertial neural networks via Lyapunov functions with indefinite derivatives and its application to image encryption. Fuzzy Sets Syst. 2022; in press. [Google Scholar] [CrossRef]
- Peng, Q.; Jian, J. Synchronization analysis of fractional-order inertial-type neural networks with time delays. Math. Comput. Simul. 2023, 205, 62–77. [Google Scholar] [CrossRef]
- Zhou, W.J.; Long, M.; Liu, X.Z.; Wu, K.N. Passivity-based boundary control for stochastic delay reaction-diffusion systems. Int. J. Syst. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Padmaja, N.; Balasubramaniam, P. Mixed H∞/passivity based stability analysis of fractional-order gene regulatory networks with variable delays. Math. And Computers Simul. 2022, 192, 167–181. [Google Scholar] [CrossRef]
- Shafiya, M.; Nagamani, G. New finite-time passivity criteria for delayed fractional-order neural networks based on Lyapunov function approach, Chaos. Solitons Fractals 2022, 158, 112005. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Hu, C.; Ma, T. Exponential passivity of discrete-time switched neural networks with transmission delays via an event-triggered sliding mode control. Neural Netw. 2021, 143, 271–282. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, F. Finite-time passivity and synchronization of coupled complex-valued memristive neural networks. Inf. Sci. 2021, 580, 775–800. [Google Scholar] [CrossRef]
- Han, X.X.; Wu, K.N.; Niu, Y. Asynchronous boundary control of Markov jump neural networks with diffusion terms. IEEE Trans. Cybern. 2022; in press. [Google Scholar] [CrossRef]
- Liu, X.Z.; Wu, K.N.; Ding, X.; Zhang, W. Boundary stabilization of stochastic delayed Cohen-Grossberg neural networks with diffusion terms. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3227–3237. [Google Scholar] [CrossRef]
- Wang, L.M.; He, H.B.; Zeng, Z.G. Intermittent stabilization of fuzzy competitive neural networks with reaction diffusions. IEEE Trans. Fuzzy Syst. 2021, 29, 2361–2372. [Google Scholar] [CrossRef]
- Song, X.N.; Man, J.T.; Ahn, C.K.; Song, S. Finite-time dissipative synchronization for markovian jump generalized inertial neural networks with reaction-diffusion terms. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3650–3661. [Google Scholar] [CrossRef]
- Sun, L.; Su, L.; Wang, J. Non-fragile dissipative state estimation for semi-Markov jump inertial neural networks with reaction-diffusion. Appl. Math. Comput. 2021, 411, 126404. [Google Scholar] [CrossRef]
- Song, X.N.; Man, J.T.; Song, S.; Wang, Z. An improved result on synchronization control for memristive neural networks with inertial terms and reaction-diffusion items. ISA Trans. 2020, 99, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekar, A.; Radhika, T.; Zhu, Q.X. Further results on input-to-state stability of stochastic Cohen-Grossberg BAM neural networks with probabilistic time-varying delays. Neural Process. Lett. 2022, 54, 613–635. [Google Scholar] [CrossRef]
- Sriraman, R.; Cao, Y.; Samidurai, R. Global asymptotic stability of stochastic complex-valued neural networks with probabilistic time-varying delays. Math. Comput. Simul. 2020, 171, 103–118. [Google Scholar] [CrossRef]
- Zhang, T.W.; Qu, H.Z.; Liu, Y.T.; Zhou, J.W. Weighted pseudo θ-almost periodic sequence solution and guaranteed cost control for discrete-time and discrete-space stochastic inertial neural networks. Chaos Solitons Fractals 2023, 173, 113658. [Google Scholar] [CrossRef]
- Zhang, T.W.; Li, Z.H. Switching clusters’ synchronization for discrete space-time complex dynamical networks via boundary feedback controls. Pattern Recognit. 2023, 143, 109763. [Google Scholar] [CrossRef]
- Zhang, T.W.; Liu, Y.T.; Qu, H.Z. Global mean-square exponential stability and random periodicity of discrete-time stochastic inertial neural networks with discrete spatial diffusions and Dirichlet boundary condition. Comput. Math. Appl. 2023, 141, 116–128. [Google Scholar] [CrossRef]
- Zhang, T.W.; Xiong, L.L. Periodic motion for impulsive fractional functional differential equations with piecewise Caputo derivative. Appl. Math. Lett. 2020, 101, 106072. [Google Scholar] [CrossRef]
- Adhira, B.; Nagamani, G.; Dafik, D. Non-fragile extended dissipative synchronization control of delayed uncertain discrete-time neural networks. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106820. [Google Scholar] [CrossRef]
- Zhang, T.W.; Li, Y.K. Global exponential stability of discrete-time almost automorphic Caputo-Fabrizio BAM fuzzy neural networks via exponential Euler technique. Knowl.-Based Syst. 2022, 246, 108675. [Google Scholar] [CrossRef]
- Huang, Z.K.; Mohamad, S.; Gao, F. Multi-almost periodicity in semi-discretizations of a general class of neural networks. Math. Comput. Simul. 2014, 101, 43–60. [Google Scholar] [CrossRef]
- Zhang, T.W.; Han, S.F.; Zhou, J.W. Dynamic behaviours for semi-discrete stochastic Cohen-Grossberg neural networks with time delays. J. Frankl. Inst. 2020, 357, 13006–13040. [Google Scholar] [CrossRef]
- Xiao, Q.; Huang, T.W.; Zeng, Z.G. On exponential stability of delayed discrete-time complex-valued inertial neural networks. IEEE Trans. Cybern. 2022, 52, 3483–3494. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; Huang, T.W. Quasisynchronization of discrete-time inertial neural networks with parameter mismatches and delays. IEEE Trans. Cybern. 2021, 51, 2290–2295. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lin, D.; Lan, W. Global dissipativity of delayed discrete-time inertial neural networks. Neurocomputing 2020, 390, 131–138. [Google Scholar] [CrossRef]
- Chen, X.; Lin, D. Passivity analysis of non-autonomous discrete-time inertial neural networks with time-varying delays. Neural Process. Lett. 2020, 51, 2929–2944. [Google Scholar] [CrossRef]
- Zhou, W.N.; Yang, J.; Zhou, L.W.; Tong, D.B. Stability and Synchronization Control of Stochastic Neural Networks; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Agarwal, R.P. Difference Equations and Inequalities; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Seuret, A.; Fridman, E. Wirtinger-like Lyapunov-Krasovskii functionals for discrete-time delay systems. IMA J. Math. Control. Inf. 2018, 35, 861–876. [Google Scholar] [CrossRef]
- Milovanović, G.V.; Milovanović, I.Ž. On discrete inequalities of Wirtinger’s type. J. Math. Anal. Appl. 1982, 88, 378–387. [Google Scholar] [CrossRef]
- Mollaiyan, K. Generalization of Discrete-Time Wirtinger Inequalities and a Preliminary Study of Their Application to SNR Analysis of Sinusoids Buried in Noise. Master’s Thesis, Concordia University, Montreal, QC, Canada, 2008. [Google Scholar]
- Zhong, X.; Ren, J.; Gao, Y. Passivity-based bipartite synchronization of coupled delayed inertial neural networks via non-reduced order method. Neural Process. Lett. 2022, 54, 4869–4892. [Google Scholar] [CrossRef]
- Fang, T.; Jiao, S.; Fu, D.; Su, L. Passivity-based synchronization for Markov switched neural networks with time delays and the inertial term. Appl. Math. Comput. 2021, 394, 125786. [Google Scholar] [CrossRef]
- Chen, W.; Ren, G.; Yu, Y.; Yuan, X. Quasi-synchronization of heterogeneous stochastic coupled reaction-diffusion neural networks with mixed time-varying delays via boundary control. J. Frankl. Inst. 2023, 360, 10080–10099. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, T.; Li, Z. Boundary Controlling Synchronization and Passivity Analysis for Multi-Variable Discrete Stochastic Inertial Neural Networks. Axioms 2023, 12, 820. https://doi.org/10.3390/axioms12090820
Yang Y, Zhang T, Li Z. Boundary Controlling Synchronization and Passivity Analysis for Multi-Variable Discrete Stochastic Inertial Neural Networks. Axioms. 2023; 12(9):820. https://doi.org/10.3390/axioms12090820
Chicago/Turabian StyleYang, Yongyan, Tianwei Zhang, and Zhouhong Li. 2023. "Boundary Controlling Synchronization and Passivity Analysis for Multi-Variable Discrete Stochastic Inertial Neural Networks" Axioms 12, no. 9: 820. https://doi.org/10.3390/axioms12090820
APA StyleYang, Y., Zhang, T., & Li, Z. (2023). Boundary Controlling Synchronization and Passivity Analysis for Multi-Variable Discrete Stochastic Inertial Neural Networks. Axioms, 12(9), 820. https://doi.org/10.3390/axioms12090820









