On the Structure of Quantum Markov Chains on Cayley Trees Associated with Open Quantum Random Walks

Abstract

Quantum Markov chains (QMCs) and open quantum random walks (OQRWs) represent different quantum extensions of the classical Markov chain framework. QMCs stand as a more profound layer within the realm of Markovian dynamics. The exploration of both QMCs and OQRWs has been a predominant focus over the past decade. Recently, a significant connection between QMCs and OQRWs has been forged, yielding valuable applications. This bridge is particularly impactful when studying QMCs on tree structures, where it intersects with the realm of phase transitions in models naturally arising from quantum statistical mechanics. Furthermore, it aids in elucidating statistical properties, such as recurrence and clustering. The objective of this paper centers around delving into the intricate structure of QMCs on Cayley trees in relation to OQRWs. The foundational elements of this class of QMCs are built upon using classical probability measures that encompass the hierarchical nature of Cayley trees. This exploration unveils the pivotal role that the dynamics of OQRWs play in shaping the behavior of the Markov chains under consideration. Moreover, the analysis extends to their classical counterparts. The findings are further underscored by the examination of notable examples, contributing to a comprehensive understanding of the outcomes.

1. Introduction

QMCs were introduced by L. Accardi in [1,2], and subsequently, they have been studied by many authors in the 1D case [3,4,5,6,7,8]. Important applications of QMCs have been investigated [7,9,10,11,12]. Namely, significant use cases of Markov chains in modeling collaborative interactions for detecting proteins within biological systems have been explored in prior studies, as evidenced by research, such as [13,14,15,16,17].

Motivated by the theory of Dobrushin’s Markov random fields [18], several extensions of QMCs to graphs and trees have been suggested [19,20]. Namely, a quantum phase transitions approach to QMCs on Cayley trees has been investigated [21,22]. Quantum Markov states (QMSs) [3] are particular QMCs. The tree extension of QMSs has been described in detail [23].

Over the past few decades, quantum random walks [24,25,26,27,28,29,30,31] have been extensively studied due to their usefulness as powerful tools for constructing quantum algorithms. From a probabilistic perspective, open quantum random walks (OQRWs) [32,33,34,35,36,37] represent a natural and direct extension of classical Markov chains, exhibiting many interesting statistical and physical properties.

Recently, a significant connection between QMCs and OQRWs has been established [38,39,40]. In [41], the study focused on investigating QMCs on trees associated with OQRWs in relation to phase transition phenomena. Moreover, a mean entropy formulae for the associated tree-indexed QMS has been calculated (see also [42,43]). In addition, the concept of stopping rules for QMCs on trees has been explored in [44,45]. Additionally, in [46], the recurrence problem for a specific class of QMCs on trees was studied with a connection to phase transitions in an Ising-type model. In [47], the notion of recurrence was associated with QMCs on trees in conjunction with OQRWs.

In this paper, we explore a new class of quantum Markov chains (QMCs) on the semi-infinite Cayley tree of order. We express their correlations using classical probability measures that are not Markovian. For each density matrix $\rho$, a probability measure ${\mathbb{P}}_{\rho }$ is naturally assigned to the space of trajectories ${\Lambda }^V$ as follows:

$${\mathbb{P}}_{\rho }(i_{u_1},i_{u_2},\cdots ,i_{u_m})=\frac{1}{\left({\rho }_{u_1}\right)}\left(B_{i_{u_{m-1}}}^{i_{u_m}}\cdots B_{i_{u_2}}^{i_{u_3}}{B}_{i_{u_1}}^{i_{u_2}}{\rho }_{u_1}{B}_{i_{u_1}}^{i_{u_2}*}{B}_{i_{u_2}}^{i_{u_3}*}\cdots B_{i_{u_{m-1}}}^{i_{u_m}*}\right)$$

(1)

for specific edge-paths $u_1\sim u_2\sim \cdots \sim u_m$ in the Cayley tree.

The obtained characterization of a QMC extends the results of previous works [41,47,48]. We point out that the hierarchical structure of the Cayley tree is essentially used in expressing the considered QMCs, as well as in defining the associated classical probability measure.

It should be emphasized that this work opens up possibilities for further investigations on OQRWs. Potential future research directions include exploring the action of symmetry groups on general QMCs on Cayley trees, studying phase transitions, investigating recurrence in the sense of [47], examining ergodic properties, and exploring entropy for the class of QMCs studied in this paper. These topics will be the focus of forthcoming studies.

The structure of this paper is outlined as follows. After the preliminary Section 2, we proceed to Section 3 where we introduce QMCs on trees. Section 4 presents a structure theorem for generalized QMCs associated with OQRWs. Finally, Section 5 is dedicated to expressing the classical probability measures associated with the QMCs under consideration. Section 6 is devoted to some illustrative examples.

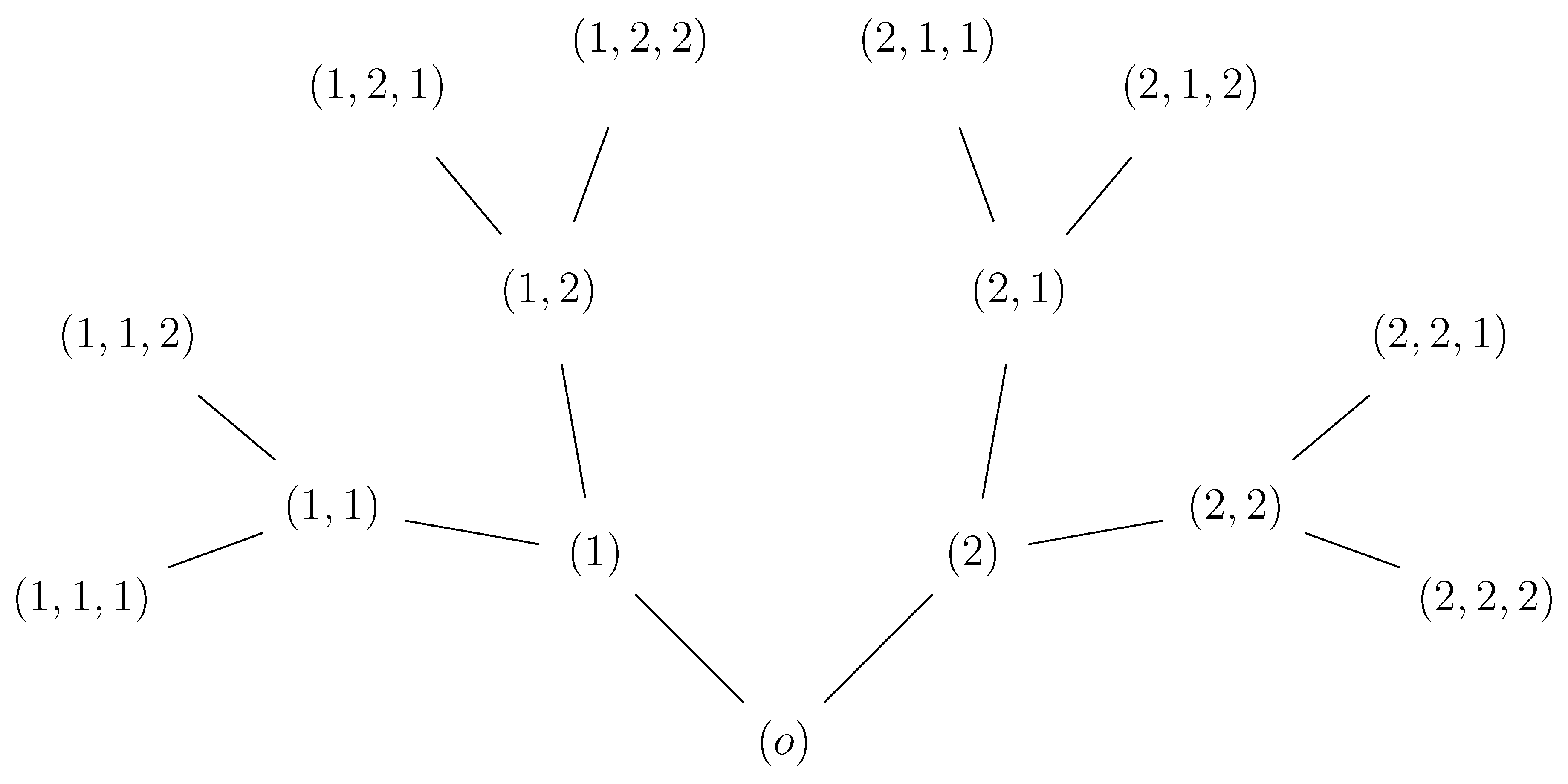
2. Preliminaries on Trees

By ${\mathsf{\Gamma }}_{+}^k=(V,E)$ ($k\in \mathbb{N}$), we denote the semi-infinite regular tree (Cayley tree) of order k. The vertex $o\in V$ represents its root. The nearest-neighbor nodes $u,v\in V$ are denoted as $u\sim v$ if and only if $<u,v>\in E$. A path on the tree is a finite list of pairwise distinct vertices $u_1\sim u_2\sim \cdots \sim u_m$, where m is referred to as the length of the path. The distance $d(u,v)$ between two vertices $u,v\in V$ is defined as the length of the unique path joining them.

A coordinate structure (see Figure 1) is naturally assigned to ${\mathsf{\Gamma }}_{+}^k$: each vertex $x\in W_m$ is identified with an n-tuple $x\equiv ({\ell }_1,\cdots ,{\ell }_m)$, where ${\ell }_j\in \{1,\cdots ,k\}$ for $1\le j\le n$. The root o is represented as $\left(o\right)$. The elements of the nth level $W_n$ can be listed as follows:

$$W_n=\{({\ell }_1,{\ell }_2,\cdots ,{\ell }_n);{\ell }_j=1,2,\cdots ,k\}$$

Put

$${\Lambda }_n=\bigcup _{j=1}^n{W}_j;{\Lambda }_{[m,n]}=\bigcup _{j=m}^n{W}_j$$

To each vertex $u=({\ell }_1,{\ell }_2,\cdots ,{\ell }_n)\in W_n$, we associate the unique path joining it to the root o as follows:

$$o\sim u_1=\left({\ell }_1\right)\sim u_2=({\ell }_1,{\ell }_2)\sim \cdots u_{n-1}=({\ell }_1,{\ell }_2,\cdots ,{\ell }_{n-1})\sim u$$

The direct successors set of u is defined by

$$S\left(u\right)=\left\{v\in W_{n+1}:u\sim v\right\}=\left\{(u,\ell ):\ell =1,2,\cdots ,k\right\}$$

(2)

For $u^{\prime }=({\ell }_1^{\prime },{\ell }_2^{\prime },\cdots ,{\ell }_m^{\prime })\in W_m$, we define

$$u\circ u^{\prime }=({\ell }_1,{\ell }_2,\cdots ,{\ell }_n,{\ell }_1^{\prime },{\ell }_2^{\prime },\cdots ,{\ell }_m^{\prime })\in W_{n+m}$$

In particular, $u\circ o=u$. Let $V_u$ be the set of vertices v whose unique path joining v to o contains $u=({\ell }_1,{\ell }_2,\cdots ,{\ell }_n)$. In other words,

$$V_u=\left\{v=u\circ u^{\prime }:u^{\prime }\in V\right\};$$

(3)

Let $V_{u;n}=V_u\cap {\Lambda }_n.$ The sub-tree ${\mathsf{\Gamma }}_{+;u}^k=(V_x,E_x)$, with vertex set $V_x$, is isomorphic to ${\mathsf{\Gamma }}_{+}^k$. Define

$${\alpha }_u\left(u^{\prime }\right):=u\circ u^{\prime }$$

(4)

The map ${\alpha }_u$ defines a graph isomorphism [49] from ${\mathsf{\Gamma }}_{+}^k$ into ${\mathsf{\Gamma }}_{+;u}^k$.

3. Quantum Markov Chains on Trees

For each $u\in V$, let ${\mathcal{A}}_u$ be a C${}^{*}$-algebra of observables on the site u with unit $\mathbf{1}{\mathrm{I}}_u$. Define ${\mathcal{A}}_{{\Lambda }_n}={⨂}_{u\in {\Lambda }_n}{\mathcal{A}}_u$ for each n. We then have the embedding

$${\mathcal{A}}_{{\Lambda }_n}\equiv {\mathcal{A}}_{{\Lambda }_n}\otimes \mathbf{1}{\mathrm{I}}_{W_{n+1}}\subset {\mathcal{A}}_{{\Lambda }_{n+1}}$$

where for each bounded region $F\subset V$, we have $\mathbf{1}{\mathrm{I}}_F={⨂}_{u\in F}\mathbf{1}{\mathrm{I}}_u$. The local algebra associated with the increasing net ${\left\{{\mathcal{A}}_{{\Lambda }_n}\right\}}_{n\ge 0}$ is denoted as

$${\mathcal{A}}_{V,\mathrm{loc}}=\uparrow \bigcup _{n\in \mathbb{N}}{\mathcal{A}}_{{\Lambda }_n}$$

and the associated quasi-local algebra is given by

$${\mathcal{A}}_V={\overline{{\mathcal{A}}_{V,\mathrm{loc}}}}^{C^{*}}$$

For further details about quasi-local algebras, we refer to [50].

The set of states of a C${}^{*}$-algebra $\mathcal{A}$ is denoted as $\mathcal{S}\left(\mathcal{A}\right)$. Consider unital C${}^{*}$-algebras $\mathcal{C}$ and $\mathcal{B}$, where $\mathcal{C}$ is a subset of $\mathcal{B}$, and $\mathcal{B}$ is a subset of $\mathcal{A}$. It is important to note the following definitions:

• A quasi-conditional expectation [51] is a linear map $E:\mathcal{A}\to \mathcal{B}$ that is completely positive and identity-preserving, satisfying the condition $E\left(ca\right)=cE\left(a\right)$ for all $a\in \mathcal{A}$ and $c\in \mathcal{C}$.
• A (Markov) transition expectation is a linear map between two unitary $C^{*}$-algebras that is completely positive and identity-preserving.

For a specific transition expectation denoted by ${\mathcal{E}}_{W_n}$ from ${\mathcal{A}}_{{\Lambda }_{[n,n+1]}}$ to ${\mathcal{A}}_{W_n}$, the map defined as

$$E_{{\Lambda }_n}={\mathrm{id}}_{{\mathcal{A}}_{{\Lambda }_{n-1}}}\otimes {\mathcal{E}}_{W_n}$$

(5)

is a transition expectation with respect to the triplet ${\mathcal{A}}_{{\Lambda }_{n-1}}\subset {\mathcal{A}}_{{\Lambda }_n}\subset {\mathcal{A}}_{{\Lambda }_{n+1}}$.

The hierarchical structure of the Cayley tree is evident from the following equation:

$$W_{n+1}=\underset{u\in W_n}{⨆}S\left(u\right)$$

(6)

This equation allows us to consider local transition expectations (see [23]), denoted by ${\mathcal{E}}_u$, from ${\mathcal{A}}_{\left\{u\right\}\cup S\left(u\right)}$ into ${\mathcal{A}}_u$. We then define the map

$${\mathcal{E}}_n:=\underset{u\in W_n}{⨂}{\mathcal{E}}_u$$

(7)

which provides a transition expectation from ${\mathcal{A}}_{{\Lambda }_{[n,n+1]}}$ into ${\mathcal{A}}_{W_n}$.

Definition 1.

A (backward) quantum Markov chain (QMC) on ${\mathcal{A}}_V$ is characterized by the triplet $({\varphi }_o,{\left({\mathcal{E}}_n\right)}_{n\ge 0},{\left(h_n\right)}_n)$, where we have the following:

• ${\varphi }_o\in \mathcal{S}\left({\mathcal{A}}_o\right)$ is the initial state;
• For each n, the map ${\mathcal{E}}_n$ is a transition expectation from ${\mathcal{A}}_{{\Lambda }_{[n,n+1]}}$ into ${\mathcal{A}}_{W_n}$;
• For each n, $h_n\in {\mathcal{A}}_{W_n,+}$ is a positive boundary condition.

The limit

$$\phi \left(a\right):=\underset{n\to \infty }{lim}{\varphi }_0\circ E_{{\Lambda }_0}\circ E_{{\Lambda }_1}\circ \cdots \circ E_{{\Lambda }_n}\left(h_{n+1}^{1/2}a{h}_{n+1}^{1/2}\right)$$

(8)

exists in the weak-*-topology for each $a\in {\mathcal{A}}_V$ and defines a state φ on ${\mathcal{A}}_V$, where $E_{{\Lambda }_k}$ is the quasi-conditional expectation given by (5) for every $k\in \mathbb{N}$. In this case, the state φ defined by (8) is also referred to as a quantum Markov chain (QMC). The triplet $({\varphi }_o,\mathcal{E},h)$ is called the tree-homogeneous QMC on ${\mathcal{A}}_V$.

Remark 1.

The definition above introduces quantum Markov chains on trees as a triplet that generalizes the definitions considered in [22] by incorporating boundary conditions. Additionally, it extends the recent unified definition of quantum Markov chains in the one-dimensional case [5] to trees.

Let $\mathcal{A}$ be a unital C${}^{*}$-algebra with identity $\mathbf{1}\mathrm{I}$. For each $u\in V$, we define ${\mathcal{A}}_u=\mathcal{A}$. The graph isomorphism $\widetilde{{\alpha }_u}$ given by (4) can be extended to an isomorphism from ${\mathcal{A}}_V$ to ${\mathcal{A}}_{V_u}$ as follows:

$$\widetilde{{\alpha }_u}\left(\underset{x\in {\Lambda }_n}{⨂}{a}_x\right)=\underset{x\in {\Lambda }_n}{⨂}{a}_x^{\left({\alpha }_u\left(x\right)\right)}=\underset{y\in {\Lambda }_{u;n}}{⨂}{a}_{{\alpha }_u^{-1}\left(y\right)}^{\left(y\right)}$$

(9)

Here, for each $a\in \mathcal{A}$, we define $\widetilde{{\alpha }_u}\left(a\right):=a^{\left(u\right)}=\left({⨂}_{v\in V\setminus \left\{u\right\}}\mathbf{1}{\mathrm{I}}_v\right)\otimes a$, which means that a appears as the u-th component of the infinite tensor product. The notation ${\alpha }_u^{-1}$ represents the inverse isomorphism of ${\alpha }_u$, mapping ${\Lambda }_{u;n}$ to ${\Lambda }_n$. Finally, let ${\widetilde{{\alpha }_u}}^{-1}$ be the inverse isomorphism from ${\mathcal{A}}_{V_u}$ to ${\mathcal{A}}_V$ [48].

4. Main Result

Consider a connected graph with a countable vertex set $\Lambda$. Let $\mathcal{H}$ and $\mathcal{K}$ be two separable Hilbert spaces. We define $\left\{\right|i\rangle ,i\in \Lambda \}$ as an orthonormal basis of $\mathcal{K}$ indexed by the graph $\Lambda$. Furthermore, let $\mathcal{A}=\mathcal{B}(\mathcal{H}\otimes \mathcal{K})$.

For each vertex $x\in V$, we associate the C${}^{*}$-algebra of observable ${\mathcal{A}}_x=\widetilde{{\alpha }_x}\left(\mathcal{A}\right)$. Additionally, for each pair $(i,j)\in {\Lambda }^2$, the transition from the state vector $|j\rangle$ to the state vector $|i\rangle$ is represented by an operator $B_j^i\in \mathcal{B}\left(\mathcal{H}\right)$, satisfying the following:

$$\sum _{i\in \Lambda }{B}_j^{i*}{B}_j^i=\mathbf{1}{\mathrm{I}}_{\mathcal{B}\left(\mathcal{H}\right)}.$$

(10)

Consider the density operator $\rho \in \mathcal{B}(\mathcal{H}\otimes \mathcal{K})$ of the form

$$\rho =\sum _{i\in \Lambda }{\rho }_i\otimes |i\rangle \langle i|;{\rho }_1\in \mathcal{B}{\left(\mathcal{H}\right)}^{+}.$$

In the sequel, for the sake of simplicity of the calculations, it is assumed that ${\rho }_i\ne 0$ for all $i\in \Lambda$ (see [39], Remark 4.5 for other kinds of initial states).

Let us consider the following:

$$M_j^i=B_j^i\otimes |i\rangle \langle j|\in \mathcal{B}(\mathcal{H}\otimes \mathcal{K})$$

(11)

Following [39,41], one defines

$$A_j^i:=\frac{1}{{\mathrm{Tr}\left({\rho }_j\right)}^{1/2}}{\rho }_j^{1/2}\otimes |i\rangle \langle j|,i,j\in \Lambda$$

(12)

For each $u\in V$, we set

$$K_j^i:=\widetilde{{\alpha }_o}\left(M_j^{i*}\right)\otimes \underset{v\in S\left(o\right)}{⨂}{A_j^i}^{\left(v\right)}\in {\mathcal{A}}_{\left\{o\right\}\cup S\left(o\right)}$$

(13)

Consider the symmetric group ${\mathfrak{S}}_{k+1}$, which consists of permutations on the set $\{0,1,\cdots ,k\}$. Each permutation $\sigma \in {\mathfrak{S}}_{k+1}$ defines an automorphism, denoted by $\sigma$, on ${\mathcal{A}}_{\left\{o\right\}\cup S\left(o\right)}$. This automorphism can be represented as a linear extension of the following mapping:

$$\sigma :a_{(o,0)}\otimes a_{(o,1)}\otimes \cdots \otimes a_{(o,k)}\mapsto a_{(o,\sigma (0\left)\right)}\otimes a_{(o,\sigma (1\left)\right)}\otimes \cdots \otimes a_{(o,\sigma (k\left)\right)}$$

(14)

Lemma 1.

Let $\sigma \in {\mathfrak{S}}_{k+1}$. The map defined by

$${\mathcal{E}}^{\sigma }\left(a\right)=\sum _{(i,j)\in {\Lambda }^2}{\mathrm{Tr}}_{o]}\left(K_j^i\sigma \left(a\right){K_j^i}^{*}\right),a\in {\mathcal{A}}_{\left\{o\right\}\cup S\left(o\right)}$$

(15)

is a Markov transition expectation from ${\mathcal{A}}_{\left\{o\right\}\cup S\left(o\right)}$ into ${\mathcal{A}}_o$. Moreover,

$${\mathcal{E}}^{\sigma }\left(a_{(o,0)}\otimes a_{(o,1)}\otimes \cdots \otimes a_{(o,k)}\right)=\sum _{(i,j)\in {\Lambda }^3}\left(\prod _{\ell =1}^k{\phi }_j\left(a_{(u,\sigma (\ell \left)\right)}\right)\right)M_j^{i*}{a}_{(o,\sigma (0\left)\right)}{M}_j^i$$

(16)

for every $a_{(o,i)}\in {\mathcal{A}}_{(o,i)},i=0,1,\cdots ,k.$ Here,

$${\phi }_j\left(b\right):=\frac{1}{\mathrm{Tr}\left({\rho }_j\right)}\mathrm{Tr}\left({\rho }_j\otimes |j\rangle \langle j|b\right);\forall b\in \mathcal{B}\left(\mathcal{H}\right)\otimes \mathcal{B}\left(\mathcal{K}\right)$$

(17)

Proof. 

The map $\sigma$ is completely positive from ${\mathcal{A}}_{\left\{o\right\}\cup S\left(o\right)}$ into itself. Moreover, the Kraus map $K:={\sum }_{i,j}{K}_j^i·{K_j^i}^{*}$ and the partial trace ${\mathrm{Tr}}_{o]}$ are completely positive. Then,

$${\mathcal{E}}^{\sigma }={\mathrm{Tr}}_{o]}\circ K\circ \sigma$$

is a composition of completely positive maps.

Let $a=a_{(o,0)}\otimes a_{(o,1)}\otimes \cdots \otimes a_{(o,k)}$; according to (13), (11), and (15), one has

$$\begin{array}{ccc}\hfill {\mathcal{E}}^{\sigma }\left(a\right)& =& \sum _{(i,j)\in {\Lambda }^2}{\mathrm{Tr}}_{u]}\left(K_j^i{a}_{(o,\sigma (0\left)\right)}\otimes a_{(o,\sigma (1\left)\right)}\cdots \otimes a_{(o,\sigma (k\left)\right)}{K_j^i}^{*}\right)\hfill \\ & =& {\mathrm{Tr}}_{u]}\left(\left(\sum _{(i,j)\in {\Lambda }^2}{K}_j^i\right)a{\left(\sum _{(i,j)\in {\Lambda }^2}{K}_j^i\right)}^{*}\right)\hfill \\ & =& \sum _{(i,j)\in {\Lambda }^2}{M}_j^{i*}{a}_{(o,\sigma (0\left)\right)}{M}_j^i\prod _{\ell =1}^k\mathrm{Tr}\left(A_j^i{a}_{(o,\sigma (\ell \left)\right)}{A}_j^{i*}\right).\hfill \end{array}$$

From (12) for each $\ell \in \{1,\cdots ,k\}$, one has

$$\mathrm{Tr}\left(A_j^i{a}_{(o,\ell )}{A}_j^{i*}\right)=\mathrm{Tr}\left(A_j^{i*}{A}_j^i{a}_{(o,\ell )}\right)=\frac{1}{\mathrm{Tr}\left({\rho }_j\right)}\mathrm{Tr}\left({\rho }_j\otimes |j\rangle \langle i|a_{\ell }^{(u,\ell )}\right)$$

This leads to (16). On the other hand, because ${\phi }_j\left(\mathbf{1}\mathrm{I}\right)=1$

$$\begin{array}{ccc}\hfill {\mathcal{E}}^{\sigma }\left(\mathbf{1}{\mathrm{I}}_{{\mathcal{A}}_{\left\{o\right\}\cup S\left(o\right)}}\right)& =& \sum _{(i,j)\in {\Lambda }^2}{M_j^i}^{*}{M}_j^i\hfill \\ & \stackrel{(11)}{=}& \sum _{(i,j)\in {\Lambda }^2}\left({B_j^i}^{*}\otimes |j\rangle \langle i|\right)\left(B_j^i\otimes |i\rangle \langle j|\right)\hfill \\ & =& \sum _{(i,j)\in {\Lambda }^2}\left({B_j^i}^{*}{B}_j^i\right)\otimes |j\rangle \langle j|\hfill \\ & =& \sum _{i\in \Lambda }\left({B_j^i}^{*}{B}_j^i\right)\otimes \mathbf{1}{\mathrm{I}}_{\mathcal{B}\left(\mathcal{K}\right)}\hfill \\ & \stackrel{(10)}{=}& \mathbf{1}{\mathrm{I}}_{{\mathcal{A}}_o}.\hfill \end{array}$$

Therefore, ${\mathcal{E}}^{\sigma }$ is a Markov transition expectation. This finishes the proof. □

For each $u\in V$, we consider the shifted transition expectation

$${\mathcal{E}}_u^{\sigma }=\widetilde{{\alpha }_u}\circ {\mathcal{E}}^{\sigma }\circ {\widetilde{{\alpha }_u}}^{-1}$$

(18)

from ${\mathcal{A}}_{\left\{u\right\}\cup S\left(u\right)}$ into ${\mathcal{A}}_u$. For $m\in \mathbb{N}$ and $(i_1,i_2,\cdots ,i_m)\in {\Lambda }^m$, one defines

$$B(i_1,i_2,\cdots ,i_m)=B_{i_{m-1}}^{i_m}{B}_{i_{m-2}}^{i_{m-1}}\cdots B_{i_2}^{i_3}{B}_{i_1}^{i_2}$$

(19)

The subsequent probability measure encompasses the open OQRW dynamics, taking into account the hierarchical structure of the Cayley trees via edge-paths.

$${\mathbb{P}}_{{\rho }_{i_1}}(i_1,i_2,\cdots ,i_m):=\frac{1}{\mathrm{Tr}\left({\rho }_{i_1}\right)}\mathrm{Tr}\left(B(i_1,i_2,\cdots ,i_m){\rho }_{i_1}{B}^{*}(i_1,i_2,\cdots ,i_m)\right)$$

(20)

For each $\ell \in \{1,2,\cdots ,k\}$, we introduce the following subsets of vertices:

$$W_{m;\ell }=\left\{x=({\ell }_1,\cdots ,{\ell }_m)\in W_m:{\ell }_1,\cdots ,{\ell }_{m-1}\in \{1,2,\cdots ,k\}\mathrm{and}{\ell }_m=\ell \right\}$$

$${\Lambda }_{n;\ell }:=\bigcup _{m=1}^n{W}_{m;\ell }$$

Denote

$$(x,{\ell }^{\left(m\right)}):=(x,\underset{m\mathrm{times}}{\underbrace{\ell ,\cdots ,\ell }})$$

In particular, for $x=o$, we denote $(o,{\ell }^{\left(m\right)})$ simply as $\left({\ell }^{\left(m\right)}\right)$. For each $x\in {\Lambda }_n$, we denote the largest integer $m_{x;n}$ such that $(x,{\ell }^{\left(m_{x;n}\right)})\in \Lambda$. Specifically, if $x\in W_j$ for some $j\le n$, then $m_{x;n}=n-j$. Please refer to Figure 2 for an illustration of the elements of ${\Lambda }_{n;2}$ in the case of the Cayley tree with order 3.

The set of vertices in which the coordinates do not incorporate ℓ as an element is defined by

$$N_{\ell }:=\left\{v=({\ell }_1,{\ell }_2,\cdots ,{\ell }_m):m\in \mathbb{N},{\ell }_i\ne \ell ,\forall i=1,2,\cdots ,m\right\}$$

(21)

In particular, for each $n\in \mathbb{N}$, we denote

$$N_{n;\ell }={\Lambda }_n\cap N_{\ell }$$

For every $u\in {\Lambda }_{\ell },$ we set

$$N_{u;\ell }:={\alpha }_u\left(N_{\ell }\right)=\{u\circ v:v\in N_{\ell }\};N_{u;n;\ell }:=N_{u;\ell }\cap {\Lambda }_n$$

Theorem 1.

Let $\sigma \in {\mathfrak{S}}_{k+1}$ such that $\ell :=\sigma \left(0\right)\ne 0$. In the notations of (12), (11), and Lemma 1, if ${\varphi }_o$ is a state on ${\mathcal{A}}_o$, the triple $({\varphi }_o,{\mathcal{E}}^{\sigma },h=\mathbf{1}{\mathrm{I}}_o)$ defines quantum Markov chains ${\phi }^{\sigma }$ on ${\mathcal{A}}_V$. Moreover, for each n and $a={⨂}_{u\in {\Lambda }_n}{a}_u:$

$${\phi }^{\sigma }\left(a\right)=\sum _{i_o\in \Lambda }\sum _{{\left(i_t\right)}_t\in {\Lambda }^{{\Lambda }_{n;\ell }}}\left[{\varphi }_o\left(M(i_o,i_{(\ell )},\cdots ,i_{{(\ell )}^{\left(n\right)}})\right){\phi }_{i_o}\left(a_o\right)\prod _{x\in N_{n;\ell }}{\phi }_{i_o}\left(a_x\right)\right]$$

(22)

$$\prod _{u\in {\Lambda }_{n,\ell }}\left[\prod _{v\in N_{u;n;\ell }}{\mathbb{P}}_{{\rho }_{i_u}}\left(i_u,i_{(v,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_u}}\left(i_u,i_{(v,\ell )},\cdots ,i_{(v,{\ell }^{\left(m_{v;n}\right)})}\right){\phi }_{i_u}\left(a_v\right)\right]{\phi }_{i_u}\left(a_u\right)$$

where

$$M(i,i_{(\ell )},\cdots ,i_{{(\ell )}^{\left(n\right)}})=B^{*}(i,i_{(\ell )},\cdots ,i_{{(\ell )}^{\left(n\right)}})B(i,i_{(\ell )},\cdots ,i_{{(\ell )}^{\left(n\right)}})\otimes |i\rangle \langle i|$$

(23)

Proof. 

Let us first prove the existence of the limit (8) for

$$E_{{\Lambda }_n}=i{d}_{{\mathcal{A}}_{{\Lambda }_{n-1}}}\otimes {\mathcal{E}}_n;{\mathcal{E}}_n=\underset{u\in W_n}{⨂}{\mathcal{E}}_u^{\sigma }$$

and $h_n=\mathbf{1}{\mathrm{I}}_{W_n}$. Let $n_0\in \mathbb{N}$. For $a=a_o\otimes a_{W_1}\otimes \cdots \otimes a_{W_n}\in {\mathcal{A}}_{{\Lambda }_n}$ and $m>n,$ one has

$$E_{{\Lambda }_m}^{\sigma }(a\otimes \mathbf{1}{\mathrm{I}}_{{\Lambda }_{m+1}\setminus {\Lambda }_m})=a\otimes {\mathcal{E}}_m(\mathbf{1}{\mathrm{I}}_{W_m}\otimes \mathbf{1}{\mathrm{I}}_{W_{m+1}})=a\otimes \mathbf{1}{\mathrm{I}}_{{\Lambda }_m\setminus {\Lambda }_n}$$

It follows that

$$\begin{array}{ccc}\hfill {\phi }_m^{\sigma }\left(a\right)& :=& {\phi }_o\circ E_{{\Lambda }_0}^{\sigma }\circ E_{{\Lambda }_1}^{\sigma }\circ \dots \circ E_{{\Lambda }_m}^{\sigma }\left(a\right)\hfill \\ & =& {\phi }_o\circ E_{{\Lambda }_0}^{\sigma }\circ E_{{\Lambda }_1}^{\sigma }\circ \dots \circ E_{{\Lambda }_{m-1}}^{\sigma }\left(a\right)\hfill \\ & & ⋮\hfill \\ & =& {\phi }_o\circ E_{{\Lambda }_0}^{\sigma }\circ E_{{\Lambda }_1}^{\sigma }\circ \dots \circ E_{{\Lambda }_n}^{\sigma }\left(a\right)\hfill \end{array}$$

Then, the strongly finite limit defined by (8) exists and gives rise to a positive functional ${\phi }^{\sigma }$. Based on Lemma 1, the map ${\mathcal{E}}_n$ is completely positive and implements a quantum channel with intermediate purification (CPIP). Therefore, ${\phi }^{\sigma }\equiv ({\varphi }_o,{\mathcal{E}}^{\sigma },\mathbf{1}{\mathrm{I}}_o)$ represents a quantum Markov chain (QMC) on ${\mathcal{A}}_V$. Furthermore, we obtain the following:

$${\phi }^{\sigma }\left(a\right)={\phi }_o\left({\mathcal{E}}_0\left(a_{W_0}\cdots \left({\mathcal{E}}_{n-1}\left(a_{W_{n-1}}\left({\mathcal{E}}_n\left(a_{W_n}\otimes \mathbf{1}{\mathrm{I}}_{Wn+1}\right)\right)\right)\right)\right)\right)$$

(24)

One has

$$\begin{array}{ccc}\hfill {\phi }_{j_u}\left(\sum _{i,j}{M_j^i}^{*}{a}_v{M}_j^i\right)& =& \frac{1}{\mathrm{Tr}\left({\rho }_{j_u}\right)}\mathrm{Tr}\left(\sum _{i,j}{\rho }_{j_u}\otimes |j_u\rangle \langle j_u|{M_j^i}^{*}{a}_v{M}_j^i\right)\hfill \\ & =& \frac{1}{\mathrm{Tr}\left({\rho }_{j_u}\right)}\mathrm{Tr}\left(\sum _{i,j}{M}_j^i{\rho }_{j_u}\otimes |j_u\rangle \langle j_u|{M_j^i}^{*}{a}_v\right)\hfill \\ & \stackrel{(11)}{=}& \frac{1}{\mathrm{Tr}\left({\rho }_{j_u}\right)}\mathrm{Tr}\left(\sum _i{B}_{j_u}^i{\rho }_{j_u}{B_{j_u}^i}^{*}\otimes |i\rangle \langle i|a_v\right)\hfill \end{array}$$

We are going to show by induction on p that

$$\begin{array}{ccc}& & {\mathcal{E}}_{n-p}\left(a_{W_{n-p}}\otimes {\mathcal{E}}_{n-p+1}\left(a_{W_{n-p+1}}\cdots {\mathcal{E}}_n\left(a_{W_n}\otimes \mathbf{1}\mathrm{I}\right)\cdots \right)\right)\hfill \\ & & =\underset{u\in W_{n-p}}{⨂}(\sum _{i_u\in \Lambda }\sum _{\left(i_v\right)\in {\Lambda }^{V_u\cap {\Lambda }_{n;\ell }}}M(i_u,i_{(u,\ell )},\cdots ,i_{(u,{(\ell )}^{\left(m_{u;n}\right)})}){\phi }_{i_u}\left(a_u\right)\prod _{x\in N_{u;n;\ell }}{\phi }_{i_u}\left(a_x\right)\hfill \\ & & \prod _{v\in V_u\cap {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right))\hfill \end{array}$$

(25)

Starting with the case $p=1$. For $u\in W_{n-1}$ and $v\in S\left(u\right)$. Let $u\in W_{n-1}$ and $v\in W_n$, and for each $b\in \mathcal{A}$, one has

$$\begin{array}{ccc}\hfill f_v\left(b\right):={\mathcal{E}}_v^{\sigma }\left(b\otimes \mathbf{1}{\mathrm{I}}_{(v,1)}\otimes \cdots \otimes \mathbf{1}{\mathrm{I}}_{(v,k)}\right)& \stackrel{(16)}{=}& \left(\sum _{i,j}{M_j^i}^{*}{M}_j^i\right){\phi }_j\left(b\right)\hfill \\ & \stackrel{(10)}{=}& \sum _j\mathbf{1}{\mathrm{I}}_{\mathcal{B}\left(\mathcal{H}\right)}\otimes |j\rangle \langle j|{\phi }_j\left(b\right).\hfill \end{array}$$

One can see that ${\phi }_j\left(f_v\left(a_v\right)\right)={\phi }_j\left(a_v\right)$. Then,

$$\begin{array}{ccc}\hfill {\mathcal{E}}_u^{\sigma }\left(a_u\otimes \underset{v\in S\left(u\right)}{⨂}{\mathcal{E}}_v^{\sigma }\left(a_v\otimes \mathbf{1}\mathrm{I}\right)\right)& \stackrel{(16)}{=}& {\mathcal{E}}_u^{\sigma }\left(a_u\otimes \underset{v\in S\left(u\right)}{⨂}{f}_v\left(a_v\right)\right)\hfill \end{array}$$

$$=\sum _{i_u,j_u}{M_{j_u}^{i_u}}^{*}f\left(a_{(u,{\ell }_0)}\right)M_{j_u}^{i_u}{\phi }_{j_u}\left(a_u\right)\prod _{v\in S\left(u\right)\setminus \left\{\right(u,\ell \left)\right\}}{\phi }_{j_u}\left(a_v\right).$$

One has

$$\begin{array}{ccc}\hfill {M_{j_u}^{i_u}}^{*}f\left(a_{(u,\ell )}\right)M_{j_u}^{i_u}& =& {M_{j_u}^{i_u}}^{*}\left(\sum _j\mathbf{1}{\mathrm{I}}_{\mathcal{B}\left(\mathcal{H}\right)}\otimes |j\rangle \langle j|\right)M_{j_u}^{i_u}\hfill \\ & =& \sum _j{B_{j_u}^{i_u}}^{*}{B}_{j_u}^{i_u}\otimes |j_u\rangle \langle j_u|{\delta }_{j,i_u}\hfill \\ & =& {B_{j_u}^{i_u}}^{*}{B}_{j_u}^{i_u}\otimes |j_u\rangle \langle j_u|.\hfill \end{array}$$

It follows that

$${\mathcal{E}}_u^{\sigma }\left(a_u\otimes \underset{v\in S\left(u\right)}{⨂}{\mathcal{E}}_v^{\sigma }\left(a_v\otimes \mathbf{1}\mathrm{I}\right)\right)=\sum _{i,j}{B}_j^{i*}{B}_j^i\otimes |j\rangle \langle j|{\phi }_j\left(a_u\right){\phi }_i\left(a_{(u,\ell )}\right)\prod _{v\in S\left(u\right)\setminus \left\{\right(u,\ell \left)\right\}}{\phi }_j\left(a_v\right).$$

It follows that

$${\mathcal{E}}_n\left(a_{n-1}\otimes {\mathcal{E}}_n(a_{W_n}\otimes \mathbf{1}\mathrm{I})\right)=\underset{u\in W_{n-1}}{⨂}{\mathcal{E}}_u^{\sigma }\left(a_u\otimes \underset{v\in S\left(u\right)}{⨂}{\mathcal{E}}_v^{\sigma }\left(a_v\otimes \mathbf{1}\mathrm{I}\right)\right)$$

$$=\underset{u\in W_{n-1}}{⨂}\left(\sum _{i,j}{B}_j^{i*}{B}_j^i\otimes |j\rangle \langle j|{\phi }_j\left(a_u\right){\phi }_i\left(a_{(u,\ell )}\right)\prod _{v\in S\left(u\right)\setminus \left\{\right(u,\ell \left)\right\}}{\phi }_j\left(a_v\right)\right).$$

Let us suppose that the induction hypothesis stated in (25) is valid for a specific value of p. In this case, it implies that

$${\mathcal{E}}_{n-p}\left(a_{W_{n-p}}\otimes {\mathcal{E}}_{n-p+1}\left(a_{W_{n-p+1}}\cdots {\mathcal{E}}_n\left(a_{W_n}\otimes \mathbf{1}\mathrm{I}\right)\cdots \right)\right)=\underset{u\in W_{n-p}}{⨂}{A}_u,$$

where

$$A_u:=\sum _{i_u\in \Lambda }\sum _{\left(i_v\right)\in {\Lambda }^{V_u\cap {\Lambda }_{n;\ell }}}M(i_u,i_{(u,\ell )},\cdots ,i_{(u,{(\ell )}^{\left(m_{u;n}\right)})}){\phi }_{i_u}\left(a_u\right)\prod _{x\in N_{u;n;\ell }}{\phi }_{i_u}\left(a_x\right)$$

$$\prod _{v\in V_u\cap {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right).$$

From the induction hypothesis (25), one finds

$$\begin{array}{ccc}& & {\mathcal{E}}_{n-p-1}\left(a_{W_{n-p-1}}\otimes {\mathcal{E}}_{n-p}\left(a_{W_{n-p}}\otimes {\mathcal{E}}_{n-p+1}\left(a_{W_{n-p+1}}\cdots {\mathcal{E}}_n\left(a_{W_n}\otimes \mathbf{1}\mathrm{I}\right)\cdots \right)\right)\right)\hfill \\ & & =\underset{t\in W_{n-p-1}}{⨂}{\mathcal{E}}_t^{\sigma }\left(a_t\otimes \underset{u\in S\left(t\right)}{⨂}{A}_u\right)\stackrel{(18)}{=}\sum _{i_t,j_t}{M}_{i_t}^{j_t*}{A}_{(t,\ell )}{M}_{i_t}^{j_t}{\phi }_{i_t}\left(a_t\right)\prod _{u\in S\left(\right(t,\ell )\setminus \{(t,\ell )\}}{\phi }_{i_t}\left(A_u\right).\hfill \end{array}$$

One has

$$\begin{array}{ccc}\hfill M_{i_t}^{j_t*}{A}_{(t,\ell )}{M}_{i_t}^{j_t}& =& \sum _{i_{(t,\ell )}}\sum _{\left(i_u\right)\in {\Lambda }^{V_{(t,\ell )}\cap {\Lambda }_n}}{B}_{i_t}^{j_t*}B{\left(i_{(t,\ell ),\cdots ,(t,{(\ell )}^{m_{t;n}})}\right)}^{*}B\left(i_{(t,\ell ),\cdots ,(t,{(\ell )}^{m_{t;n}})}\right)B_{i_t}^{j_t}\otimes |i_t\rangle \langle i_t|{\delta }_{j_t,i_{(t,\ell )}}\hfill \\ & & {\phi }_{i_{(t,\ell )}}\left(a_{(t,\ell )}\right)\prod _{x\in N_{(t,\ell );n;\ell }}{\phi }_{i_{(t,\ell )}}\left(a_x\right)\prod _{v\in V_u\cap {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots \hfill \\ & & {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right)\hfill \\ & \stackrel{(19)}{=}& \sum _{i_{(t,\ell )}}\sum _{\left(i_u\right)\in {\Lambda }^{V_{(t,\ell )}\cap {\Lambda }_n}}M(i_t,i_{(t,\ell ),\cdots ,(t,{(\ell )}^{m_{t;n}})}){\delta }_{j_t,i_{(t,\ell )}}{\phi }_{i_{(t,\ell )}}\left(a_{(t,\ell )}\right)\prod _{x\in N_{(t,\ell );n;\ell }}{\phi }_{i_{(t,\ell )}}\left(a_x\right)\hfill \\ & & \prod _{v\in V_u\cap {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right))\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\phi }_j\left(A_u\right)& =& \sum _{i_u\in \Lambda }\sum _{\left(i_v\right)\in {\Lambda }^{V_u\cap {\Lambda }_{n;\ell }}}{\phi }_{j_u}\left(M(i_u,i_{(u,\ell )},\cdots ,i_{(u,{(\ell )}^{\left(m_{u;n}\right)})})\right){\phi }_{i_u}\left(a_u\right)\prod _{x\in N_{u;n;\ell }}{\phi }_{i_u}\left(a_x\right)\hfill \\ & & \prod _{v\in V_u\cap {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right)\hfill \\ & \stackrel{(20)}{=}& \sum _{i_u\in \Lambda }\sum _{\left(i_v\right)\in {\Lambda }^{V_u\cap {\Lambda }_{n;\ell }}}{\mathbb{P}}_{{\rho }_{i_u}}(i_u,i_{(u,\ell )},\cdots ,i_{(u,{(\ell )}^{\left(m_{u;n}\right)})}){\delta }_{i_t,i_u}{\phi }_{i_u}\left(a_u\right)\prod _{x\in N_{u;n;\ell }}{\phi }_{i_u}\left(a_x\right)\hfill \\ & & \prod _{v\in V_u\cap {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right)\hfill \\ & \stackrel{(23)}{=}& \sum _{i_u\in \Lambda }\sum _{\left(i_v\right)\in {\Lambda }^{V_u\cap {\Lambda }_{n;\ell }}}{\mathbb{P}}_{{\rho }_{i_t}}(i_t,i_{(u,\ell )},\cdots ,i_{(u,{(\ell )}^{\left(m_{u;n}\right)})}){\phi }_{i_t}\left(a_u\right)\prod _{x\in N_{u;n;\ell }}{\phi }_{i_t}\left(a_x\right)\hfill \\ & & \prod _{v\in V_u\cap {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right).\hfill \end{array}$$

Summing up, one gets

$$\begin{array}{ccc}& & {\mathcal{E}}_{n-p-1}\left(a_{W_{n-p-1}}\otimes {\mathcal{E}}_{n-p}\left(a_{W_{n-p}}\otimes {\mathcal{E}}_{n-p+1}\left(a_{W_{n-p+1}}\cdots {\mathcal{E}}_n\left(a_{W_n}\otimes \mathbf{1}\mathrm{I}\right)\cdots \right)\right)\right)\hfill \\ & & =\underset{t\in W_{n-p-1}}{⨂}(\sum _{i_t\in \Lambda }\sum _{\left(i_v\right)\in {\Lambda }^{V_t\cap {\Lambda }_{n;\ell }}}M(i_t,i_{(t,\ell )},\cdots ,i_{(t,{(\ell )}^{\left(m_{t;n}\right)})}){\phi }_{i_t}\left(a_t\right)\prod _{x\in N_{t;n;\ell }}{\phi }_{i_t}\left(a_x\right)\hfill \\ & & \prod _{v\in V_t\cap {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right)).\hfill \end{array}$$

This proves that (25) holds for any integer $p\le n$. In particular, for $p=n$, one obtains the expression of

$$\begin{array}{ccc}& & {\mathcal{E}}_0\left(a_{W_0}\otimes {\mathcal{E}}_1\left(a_{W_1}\otimes \cdots {\mathcal{E}}_n\left(a_{W_n}\otimes \mathbf{1}\mathrm{I}\right)\cdots \right)\right)\hfill \\ & & =\sum _{i_o\in \Lambda }\sum _{\left(i_v\right)\in {\Lambda }^{{\Lambda }_{n;\ell }}}(M(i_o,i_{(o,\ell )},\cdots ,i_{(o,{(\ell )}^{\left(n\right)})}){\phi }_{i_o}\left(a_o\right)\prod _{x\in N_{n;\ell }}{\phi }_{i_o}\left(a_x\right)\hfill \\ & & \prod _{v\in {\Lambda }_{n,\ell }}{\phi }_{i_v}\left(a_v\right)\prod _{w\in N_{v,n,\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_v,i_{(w,\ell )},\cdots ,i_{(w,{\ell }^{\left(m_{w;n}\right)})}\right){\phi }_{i_v}\left(a_w\right)).\hfill \end{array}$$

By applying the initial state ${\varphi }_o$ to the expression above, we obtain (22). This step concludes the proof. □

Remark 2.

In the notation of Theorem 1, the case $\sigma \left(0\right)=0$ has been studied in [41]. In that situation, the QMC φ is represented by

$${\phi }^{\left(id\right)}\left(a\right)={\varphi }_0\left(\sum _{ij}{M_j^i}^{*}{a}_v{M}_j^i\right)\prod _{v\in S\left(u\right)}{\psi }_j\left(a_v\right).$$

(26)

For any localized element $a={⨂}_{u\in {\Lambda }_n}{a}_u$, here

$${\psi }_j\left(b\right)=\frac{1}{\mathrm{Tr}\left({\rho }_j\right)}\sum _{i\in \Lambda }\mathrm{Tr}\left(B_j^i{\rho }_j{B_j^i}^{*}\otimes |i\rangle \langle i|b\right).$$

(27)

Meanwhile, the case $\sigma \left(0\right)\ne 0$ leads to the QMC given by (22) which has a much more sophisticated structure.

Remark 3.

The equation (22) reveals that the essential constituents of the QMC ${\phi }^{\sigma }$ are formed by the probability measures (1). Consequently, the correlations of the QMC under study are governed by the OQRW dynamics. In the subsequent section, we will observe that this substantial reliance of the QMC on the OQRW dynamics is further demonstrated by focusing on a diagonal subalgebra.

5. Classical Probability Associated with OQRW

In this section, we examine the classical probability measures associated with the quantum Markov chains described in Theorem 1. Consider the set $\mathsf{\Omega }={\Lambda }^V$ equipped with the cylindrical $\sigma$-algebra $\mathcal{F}$. Let ${e=\left\{\right|i\rangle \}}_{i\in \Lambda }$ denote an orthonormal basis for $\mathcal{K}$. We define ${\mathcal{D}}_e$ as the diagonal subalgebra of $\mathcal{B}\left(\mathcal{K}\right)$ spanned by the projections $|i\rangle \langle i|$.

Given a state $\phi$ on ${\mathcal{A}}_V$, we associate a classical probability measure ${\mu }_{\phi }$ on $(\mathsf{\Omega },\mathcal{F})$, which operates on atomic events ${\left(i_x\right)}_{x\in {\Lambda }_n}$ as follows.

$${\mu }_{\phi }\left({\left(i_x\right)}_{x\in {\Lambda }_n})\right)=\phi \left(\underset{x\in {\Lambda }_n}{⨂}(\mathbf{1}{\mathrm{I}}_{\mathcal{H}}\otimes |i_x\rangle {\langle i_x\left|\right)}^{\left(x\right)}\right)$$

From (17) and (11), one finds

$${\phi }_j\left(\mathbf{1}{\mathrm{I}}_{\mathcal{H}}\otimes |i\rangle \langle i|\right)={\delta }_{i,j}.$$

The classical probability ${\mu }_{{\phi }^{\left(id\right)}}$ associated with the QMC ${\phi }^{\left(id\right)}$ given by (26) is the following:

$$\begin{array}{ccc}\hfill {\mu }_{{\phi }^{\left(id\right)}}\left({\left(i_x\right)}_{x\in {\Lambda }_n}\right)& =& {\varphi }_o\left({\mathcal{M}}_{i_o}(\mathbf{1}{\mathrm{I}}_{\mathcal{H}}\otimes |i_o\rangle \langle i_o|\right)\prod _{u\in {\Lambda }_{[1,n]}}{\phi }_{i_u}\left(\mathbf{1}{\mathrm{I}}_{\mathcal{H}}\otimes |i_u\rangle \langle i_u|\right){\delta }_{i_o,i_u}\hfill \\ \hfill & =& {\varphi }_o(\mathbf{1}{\mathrm{I}}_{\mathcal{H}}\otimes |i_o\rangle \langle i_o\left|\right)\prod _{u\in {\Lambda }_{[1,n]}}{\delta }_{i_o,i_u}.\hfill \end{array}$$

Let $\sigma \in {\mathfrak{S}}_{k+1}$ and let ${\phi }^{\left(\sigma \right)}$ be the QMC given by (22). The probability measure ${\mu }_{{\phi }^{\left(\sigma \right)}}$ associated with ${\phi }^{\left(\sigma \right)}$ is given by

$${\mu }_{{\phi }^{\left(\sigma \right)}}\left({\left(i_x\right)}_{x\in {\Lambda }_n}\right)={\varphi }_o\left(B^{*}(i_o,i_{(\ell )},\cdots ,i_{{(\ell )}^{\left(n\right)}})B(i_o,i_{(\ell )},\cdots ,i_{{(\ell )}^{\left(n\right)}})\otimes |i_o\rangle \langle i_o|\right)\prod _{x\in N_{n;\ell }}{\delta }_{i_x,i_o}$$

(28)

$$\prod _{u\in {\Lambda }_{n;\ell }}\prod _{v\in N_{u;n;\ell }}{\mathbb{P}}_{{\rho }_{i_v}}\left(i_u,i_{(v,\ell )}\right)\cdots {\mathbb{P}}_{{\rho }_{i_v}}\left(i_u,i_{(v,\ell )},\cdots ,i_{(v,{\ell }^{\left(m_{v;n}\right)})}\right){\delta }_{i_v,i_u}.$$

Remark 4.

The distinction between the two QMCs ${\phi }^{\left(id\right)}$ and ${\phi }^{\left(\sigma \right)}$ becomes evident in the expressions of their corresponding classical probability measures ${\mu }_{{\phi }^{\left(id\right)}}$ and ${\mu }_{{\phi }^{\left(\sigma \right)}}$. Specifically, when restricted to the cylinder ${\Lambda }^{{\Lambda }_n}$, the distribution ${\mu }_{{\phi }^{\left(id\right)}}$ focuses solely on the atomic events ${\left(i_x\right)}_{x\in {\Lambda }_n}$ where $i_x=i_o$ for every $x\in {\Lambda }_n$. On the other hand, the distribution ${\mu }_{{\phi }^{\left(\sigma \right)}}$ assigns probabilities to all atoms ${\left(i_x\right)}_{x\in {\Lambda }_n}$ that satisfy the condition

$$\forall x\in {\Lambda }_{n;\ell },\forall y\in N_{x;n;\ell },i_x=i_y$$

as depicted in Figure 2.

6. Application to OQRW on ${\mathbb{Z}}_{\mathbf{p}}$

In this section, we consider $\Lambda =\mathbb{Z}p:=\mathbb{Z}/p\mathbb{Z}=\overline{0},\overline{1},\cdots ,\overline{p-1}$, where $p>0$ is an integer. Let $\mathcal{H}={\mathbb{C}}^2$ and $\mathcal{K}$ be an infinite-dimensional Hilbert space with an orthonormal basis $\left(\right|i\rangle )i\in \Lambda$. We assume that $B,C\in \mathcal{B}\left(\mathcal{H}\right)$ satisfy $B^{*}B+C^{*}C=\mathbf{1}\mathrm{I}$. We define

$$B_{\overline{j}}^{\overline{i}}=\left\{\begin{array}{cc}B,\hfill & \mathrm{if}\overline{i}=\overline{j+1};\hfill \\ C,\hfill & \mathrm{if}\overline{i}=\overline{j-1};\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(29)

In the following, we will represent $\overline{i}$ as i for simplicity. We will maintain the same notations as in the previous sections and focus on the case where $k=2$, specifically the Cayley tree ${\mathsf{\Gamma }}_{+}^2$. Let $\ell =2$. The set ${\Lambda }_{n;2}$ consists of the vertices in the form $u=({\ell }_1,{\ell }_2,\cdots ,{\ell }_j,2)$, where $j\in \{1,\cdots ,n-1\}$ and ${\ell }_1,{\ell }_2,\cdots ,{\ell }_j\in \{1,2\}$. It can be observed that $|{\Lambda }_{n;2}|=2^{n-1}$. As a result, it divides the set ${\Lambda }_n$.

6.1. Example 1

Let us consider $\mathcal{H}$ as the complex vector space of dimension 2, denoted by ${\mathbb{C}}^2$. Let

$$B=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right],C=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$$

be the transition operators. By performing a straightforward computation, we can establish that B and C satisfy the equation $B^{*}B+C^{*}C=\mathbf{1}\mathrm{I}$. By utilizing the identities $B^2=B$, $BC=C$, and $C^2=CB=0$, it becomes evident that the only indices $(i_1,i_2,\cdots ,i_m)\in {\Lambda }^m$, where $m\in \mathbb{N}$, for which the quantity

$$B(i_1,i_2,\cdots ,i_m)=B_{i_{m-1}}^{i_m}{B}_{i_{m-2}}^{i_{m-1}}\cdots B_{i_2}^{i_3}{B}_{i_1}^{i_2}$$

is non-zero correspond to $i_{k+1}=i_k+1$ for all $k\in 2,\dots ,m-1$.

More specifically, for each $i\in \Lambda$, we have

$$\left\{\begin{array}{c}B(i,i+1,\cdots ,i+m)=B\hfill \\ B(i,i-1,i,i+1,\cdots ,i+m-2)=C\hfill \end{array}\right.$$

For $(i_1,i_2,\cdots ,i_m)\in {\Lambda }^m\setminus (i,i+1,\cdots ,i+m),(i,i-1,i,i+1,\cdots ,i+m-2);,i\in \Lambda$, we have $B(i_1,i_2,\cdots ,i_m)=0$.

Consider the density

$$\rho =\sum _{i\in \Lambda }{\rho }_i\otimes |i\rangle \langle i|$$

where ${\rho }_i=\left[\begin{array}{cc}{\rho }_{i,11}& {\rho }_{i,12}\\ {\rho }_{i,21}& {\rho }_{i,22}\end{array}\right]\in M_2\left(\mathbb{C}\right)\equiv \mathcal{B}\left(\mathcal{H}\right).$ It follows that the probability (20) satisfies

$${\mathbb{P}}_{{\rho }_{i_1}}(i_1,i_2,\cdots ,i_m)=\frac{1}{\mathrm{Tr}\left({\rho }_{i_1}\right)}\mathrm{Tr}\left(B(i_1,i_2,\cdots ,i_m){\rho }_{i_1}{B}^{*}(i_1,i_2,\cdots ,i_m)\right)$$

which is given by

$$\begin{array}{ccc}\hfill {\mathbb{P}}_{{\rho }_{i_1}}(i_1,i_2,\cdots ,i_m)& =& \left\{\begin{array}{cc}\frac{\mathrm{Tr}\left(B{\rho }_{i_1}B\right)}{\mathrm{Tr}\left({\rho }_{i_1}\right)},\hfill & \mathrm{if}{i}_{k+1}=i_k+1,\forall k\in \{1,\dots ,m-1\};\hfill \\ \\ \frac{\mathrm{Tr}\left(C{\rho }_{i_1}{C}^{*}\right)}{\mathrm{Tr}\left({\rho }_{i_1}\right)},\hfill & \mathrm{if}{i}_2=i_1-1\mathrm{and}{i}_{k+1}=i_k+1,\forall k\in \{2,\dots ,m-1\};\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \\ \\ & =& \left\{\begin{array}{cc}\frac{{\rho }_{i_1,11}}{{\rho }_{i_1,11}+{\rho }_{i_1,22}},\hfill & \mathrm{if}{i}_{k+1}=i_k+1,\forall k\in \{1,\dots ,m-1\};\hfill \\ \\ \frac{{\rho }_{i_1,22}}{{\rho }_{i_1,11}+{\rho }_{i_1,22}},\hfill & \mathrm{if}{i}_2=i_1-1\mathrm{and}{i}_{k+1}=i_k+1,\forall k\in \{2,\dots ,m-1\};\hfill \\ \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

6.2. Example 2

Take as above $\mathcal{H}={\mathbb{C}}^2$ and consider the transition operators

$$B=\left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right],C=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right].$$

A simple calculation shows that B and C satisfy the identity $B^{*}B+C^{*}C=\mathbf{1}\mathrm{I}$. Using the identities, $B^2=C^2=0$, and

$$BC=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right],CB=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right].$$

We can easily deduce that the only non-zero words formed by picking letters from the alphabet $\{B,C\}$ are of the form

$${\left(BC\right)}^{k}B=B,{\left(BC\right)}^k=BC,{\left(CB\right)}^k=CB\mathrm{and}{\left(CB\right)}^{k}C=C.$$

This leads us to consider two distinct cases, depending on whether m is even or odd. If m is odd, we have

$$B(i_1,i_2,\cdots ,i_m)=\left\{\begin{array}{cc}B,\hfill & i_1=i_3=\dots =i_m\mathrm{and}{i}_2=i_4=\dots =i_{m-1}=i_1+1\hfill \\ C,\hfill & i_1=i_3=\dots =i_m\mathrm{and}{i}_2=i_4=\dots =i_{m-1}=i_1-1\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Then, using $B^{*}=C$, we obtain

$${\mathbb{P}}_{\rho }(i_1,i_2,\cdots ,i_m)=\left\{\begin{array}{cc}\frac{\mathrm{Tr}\left(B\rho C\right)}{\mathrm{Tr}\left(\rho \right)},\hfill & i_1=i_3=\dots =i_m\mathrm{and}{i}_2=i_4=\dots =i_{m-1}=i_1+1\hfill \\ \frac{\mathrm{Tr}\left(C\rho B\right)}{\mathrm{Tr}\left(\rho \right)},\hfill & i_1=i_3=\dots =i_m\mathrm{and}{i}_2=i_4=\dots =i_{m-1}=i_1-1\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

If m is even, we have

$$B(i_1,i_2,\cdots ,i_m)=\left\{\begin{array}{cc}BC,\hfill & i_1=i_3=\dots =i_{m-1}\mathrm{and}{i}_2=i_4=\dots =i_m=i_1+1\hfill \\ CB,\hfill & i_1=i_3=\dots =i_{m-1}\mathrm{and}{i}_2=i_4=\dots =i_m=i_1-1\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

and

$${\mathbb{P}}_{\rho }(i_1,i_2,\cdots ,i_m)=\left\{\begin{array}{cc}\frac{\mathrm{Tr}\left(BC\rho CB\right)}{\mathrm{Tr}\left(\rho \right)},\hfill & i_1=i_3=\dots =i_{m-1}\mathrm{and}{i}_2=i_4=\dots =i_m=i_1+1\hfill \\ \frac{\mathrm{Tr}\left(CB\rho BC\right)}{\mathrm{Tr}\left(\rho \right)},\hfill & i_1=i_3=\dots =i_{m-1}\mathrm{and}{i}_2=i_4=\dots =i_m=i_1-1\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

7. Discussion

The complete understanding of the structure of general quantum Markov chain systems (QMCSs) associated with open quantum random walks (OQRWs) has been achieved. Contrary to the previous works, the correlation functions of the present QMCSs are heavily influenced by the dynamics of OQRWs. The probability measures defining these sequences establish potentially non-Markovian dynamics, which presents a significant avenue for future research. Exploring the entropy of this class of QMCSs and investigating their diagonalizability also pose intriguing questions for further exploration. Nevertheless, considering the recent advancements in this field, numerous other pertinent challenges are now approachable, including topics such as phase transitions, recurrence, clustering, and ergodic properties.