Minor and Major Strain: Equations of Equilibrium of a Plane Domain with an Angular Cutout in the Boundary
Abstract
:1. Introduction
- (A)
- Physically and geometrically linear;
- (B)
- Physically linear and geometrically nonlinear;
- (C)
- Physically nonlinear and geometrically linear;
- (D)
- Physically and geometrically nonlinear.
- (1)
- To formulate equilibrium equations for the deformed scheme and obtain equilibrium equations for cases of generalized stress and strain in the plane domain, taking into account geometric nonlinearity and physical linearity;
- (2)
- To formulate equilibrium equations for the deformed scheme in terms of possible relations of orders of linear strain, shear, and angles of rotation, and to analyze the effect of relations of strain orders on the form of equilibrium equations.
2. Materials and Methods
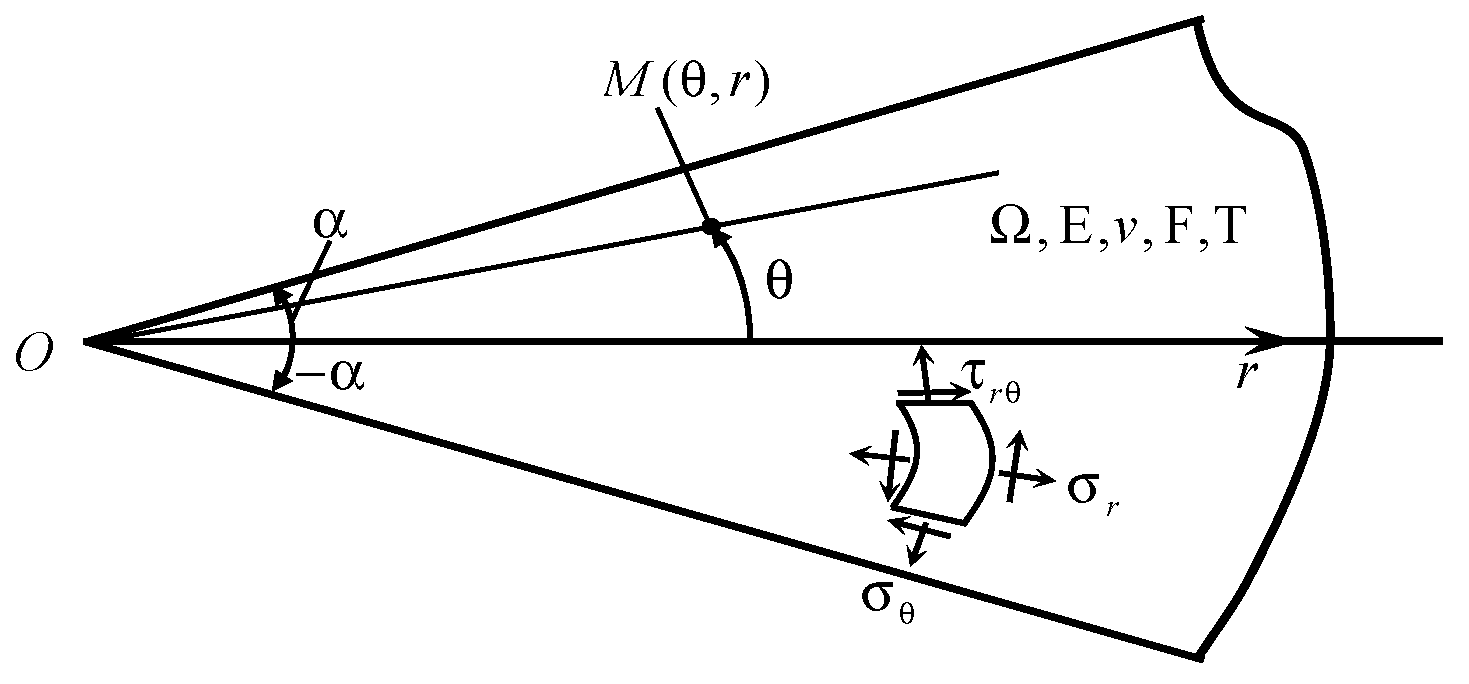
2.1. Problem Statement
2.2. Equilibrium Equations
2.3. Deformation Relations
2.4. Physical Relations
2.5. Relations of Strain Orders
- (1)
- Parameters are linear;
- (2)
- Products of parameters ;
- (3)
- Squared rotation parameter ;
- (4)
- Products of parameters , .
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cherepanov, G.P. Brittle Destruction Mechanics; Nauka: Moscow, Russia, 1974; 640p. [Google Scholar]
- Cherepanov, G.P. Singular Solutions in Theory of Elasticity; Shipbuilding: Leningrad, Russia, 1970; pp. 17–32. [Google Scholar]
- Timoshenko, S.P.; Goodyear, J. Elasticity Theory; Nauka: Moscow, Russia, 1975; 576p. [Google Scholar]
- Parton, V.Z.; Perlin, P.I. Methods of Mathematical Elasticity Theory; Nauka: Moscow, Russia, 1981; 688p. [Google Scholar]
- Kondratyev, V.A. Boundary problems for elliptical equations within the areas with conical and angular points. Work. Mosc. Math. Soc. 1967, 16, 209–292. [Google Scholar]
- Rabotnov, Y.N. Mechanics of Deformable Solids; Nauka: Moscow, Russia, 1979; 744p. [Google Scholar]
- Kuliev, V.D. Singular Boundary Problems; Nauka: Moscow, Russia, 2005; 719p. [Google Scholar]
- Xu, L.R.; Kuai, H.; Sengupta, S. Dissimilar material joints with and without free-edge stress singularities: Part I. A biologically inspired design. Exp. Mech. 2004, 44, 608–615. [Google Scholar] [CrossRef]
- Xu, L.R.; Kuai, H.; Sengupta, S. Dissimilar material joints with and without free-edge stress singularities: Part II. An integrated numerical analysis. Exp. Mech. 2004, 44, 616–621. [Google Scholar] [CrossRef]
- Yao, X.F.; Yeh, H.Y.; Xu, W. Fracture investigation at V-notch tip using coherent gradient sensing (CGS). Int. J. Solid Struct. 2006, 43, 1189–1200. [Google Scholar] [CrossRef]
- Matveenko, V.P.; Nakarjakova, T.O.; Sevodina, N.V.; Shardakov, I.N. Stress singularity at the top of homogeneous and composite cones with different boundary conditions. J. Math. Mech. 2008, 72, 477–484. [Google Scholar]
- Lourier, A.I. Elasticity Theory; Nauka: Moscow, Russia, 1970; 940p. [Google Scholar]
- Kogaev, V.P.; Makhutov, N.A.; Gusenkov, A.P. Calculations of Machine Parts and Structures for Strength and Durability: Handbook, Mechanical Engineering; Mashinostroenie: Moscow, Russia, 1985; 224p. [Google Scholar]
- Morozov, E.; Nikishkov, G. Finite Elements Method in Fracture Mechanics; Librokom: Moscow, Russia, 2017; 256p. [Google Scholar]
- Hesin, G.L.; Vardanyan, G.S.; Savost’yanov, V.N.; Shvej, E.M.; Musatov, L.G.; Pavlov, V.V.; Dolgopolov, V.V. The Photoelasticity Method; Stroyizdat: Moscow, Russia, 1975; Volume 3, 311p. [Google Scholar]
- Razumovskij, I.A. Interference-Optical Methods of Deformable Solid Mechanics; Bauman MSTU: Moscow, Russia, 2007; 240p. [Google Scholar]
- Kasatkin, B.S.; Kudrin, A.B.; Lobanov, L.M.; Pivtorak, V.A.; Polukhin, P.I.; Chikchenev, N.I. Experimental Methods for Studying Strain and Stress. Reference Manual; Kasatkin, B.S., Ed.; Naukova Dumka: Kiev, Ukraine, 1981; 584p. [Google Scholar]
- Frishter, L. Stress-strain state in structure angular zone taking into account differences between stress and deformation intensity factors. Adv. Intell. Syst. Comput. 2020, 982, 352–362. [Google Scholar] [CrossRef]
- Pestrenin, V.M.; Pestrenina, I.V.; Landik, L.V. Vestnik TGU. Math. Mech. 2013, 4, 80–87. [Google Scholar]
- Makhutov, N.A.; Moskvichev, V.V.; Morozov, E.V.; Goldstein, R.V. Unification of computation and experimental methods of testing for crack resistance: Development of the fracture mechanics and new goals. Indust. Lab. Diagn. Mater. 2017, 83, 55–64. [Google Scholar] [CrossRef]
- Novozhilov, V.V. Elasticity Theory; Sudpromgiz: Moscow, Russia, 1958; 370p. [Google Scholar]
- Novozhilov, V.V. Fundamentals of Nonlinear Theory of Elasticity; Gostekhizdat, OGIZ: Moscow, Russia, 1948; 211p. [Google Scholar]
- Lukash, P.A. Fundamentals of Nonlinear Structural Mechanics; Stroyizdat: Moscow, Russia, 1978; 204p. [Google Scholar]
- Lurie, A.I. Nonlinear Theory of Elasticity; Nauka: Moscow, Russia, 1980; 512p. [Google Scholar]
- Green, A.; Adkins, J. Large Elastic Deformations and Nonlinear Continuum Mechanics; World: Moscow, Russia, 1965; 456p. [Google Scholar]
- Sedov, L.I. Continuum Mechanics; Nauka: Moscow, Russia, 1994; Volume 1, 528p, Volume 2, 560p. [Google Scholar]
- Bakushev, S.V. Geometrically and Physically Nonlinear Continuum Mechanics: The Plane Problem; Book House LIBROKOM: Moscow, Russia, 2013; 321p. [Google Scholar]
- Bakushev, S.V. Resolving equations of plane deformation of geometrically nonlinear continuous medium in Cartesian coordinates. News Univ. Constr. 1998, 6, 31–35. [Google Scholar]
- Vardanyan, G.S.; Andreev, V.I.; Atarov, N.M.; Gorshkov, A.A. Resistance of Materials with the Bases of the Theory of Elasticity and Plasticity; ASV Publishers: Moscow, Russia, 1995; 568p. [Google Scholar]
- Frishter, L.Y. Infinitesimal and finite deformations in the polar coordinate system. Int. J. Comp. Civil Struct. Eng. 2023, 19, 204–211. [Google Scholar] [CrossRef]
- Bazhenov, V.A.; Perelmuter, A.V.; Shishov, O.V. SCAD SOFT Publisher; Publishing House ASV: Moscow, Russia, 2014; 911p. [Google Scholar]

| Options | Relations between Orders of Strain Parameters |
|---|---|
| Option I | Case (A). The value of rotation is small and of the same or a higher order of smallness than . |
| Case (A1). Temperature-induced strain is of the same order of smallness as or of a higher order of smallness than . | |
| Case (A2). The temperature in one domain is constant, and the other domain is stress free. | |
| Case (B). Values of strain parameters are small and of the same or a higher order of smallness than rotation squares . | |
| Case (B1). Temperature-induced strain has the same order of smallness as . | |
| Case (B2). Temperature-induced strain has a higher order of smallness than . | |
| Option II | Case (C). Strain is of a higher order of smallness than , rotations are of the same order as deformations . |
| Case (C1). Temperature-induced strain has the same order of change as , . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frishter, L. Minor and Major Strain: Equations of Equilibrium of a Plane Domain with an Angular Cutout in the Boundary. Axioms 2023, 12, 893. https://doi.org/10.3390/axioms12090893
Frishter L. Minor and Major Strain: Equations of Equilibrium of a Plane Domain with an Angular Cutout in the Boundary. Axioms. 2023; 12(9):893. https://doi.org/10.3390/axioms12090893
Chicago/Turabian StyleFrishter, Lyudmila. 2023. "Minor and Major Strain: Equations of Equilibrium of a Plane Domain with an Angular Cutout in the Boundary" Axioms 12, no. 9: 893. https://doi.org/10.3390/axioms12090893
APA StyleFrishter, L. (2023). Minor and Major Strain: Equations of Equilibrium of a Plane Domain with an Angular Cutout in the Boundary. Axioms, 12(9), 893. https://doi.org/10.3390/axioms12090893






