A Mixture Quantitative Randomized Response Model That Improves Trust in RRT Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Efficiency Metric
2.2. Privacy Metric
- is the number of ways is uniquely defined within the model.
- is a particular categorical way that is defined in the model.
- is the probability that category ‘j’ captures the respondent’s response.
- The superscript indicates that privacy is adjusted according to Gupta et al.’s (2018) [12] optionality adjustment ().
2.3. Unified Measure of Efficiency and Privacy
3. Proposed Mixture Optional Enhanced Trust Model (MOET)
3.1. MOET Model Introduction
3.2. MOET: Mean Estimator
3.3. MOET: Privacy Measure
3.4. MOET: Sensitivity Estimator
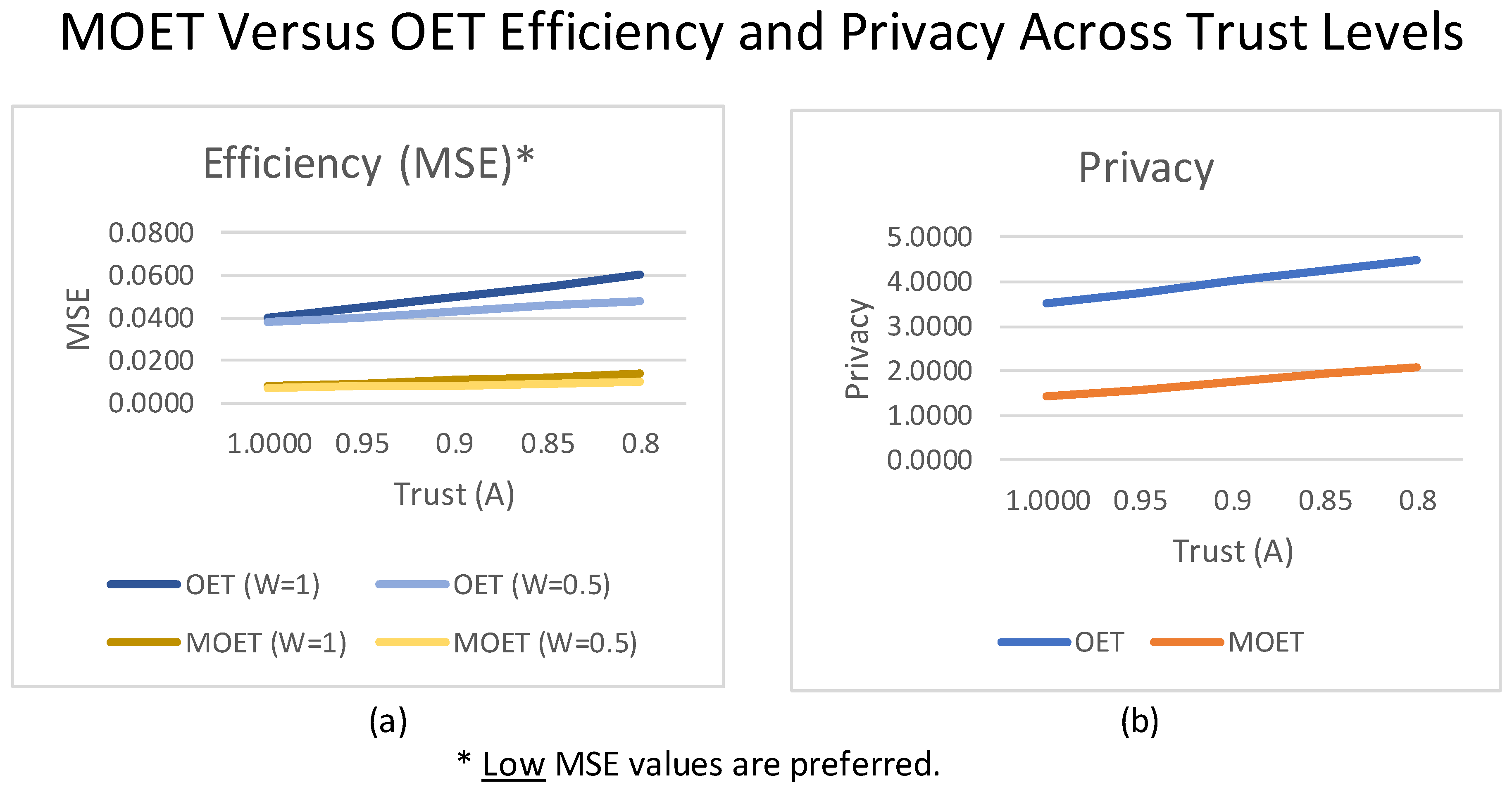
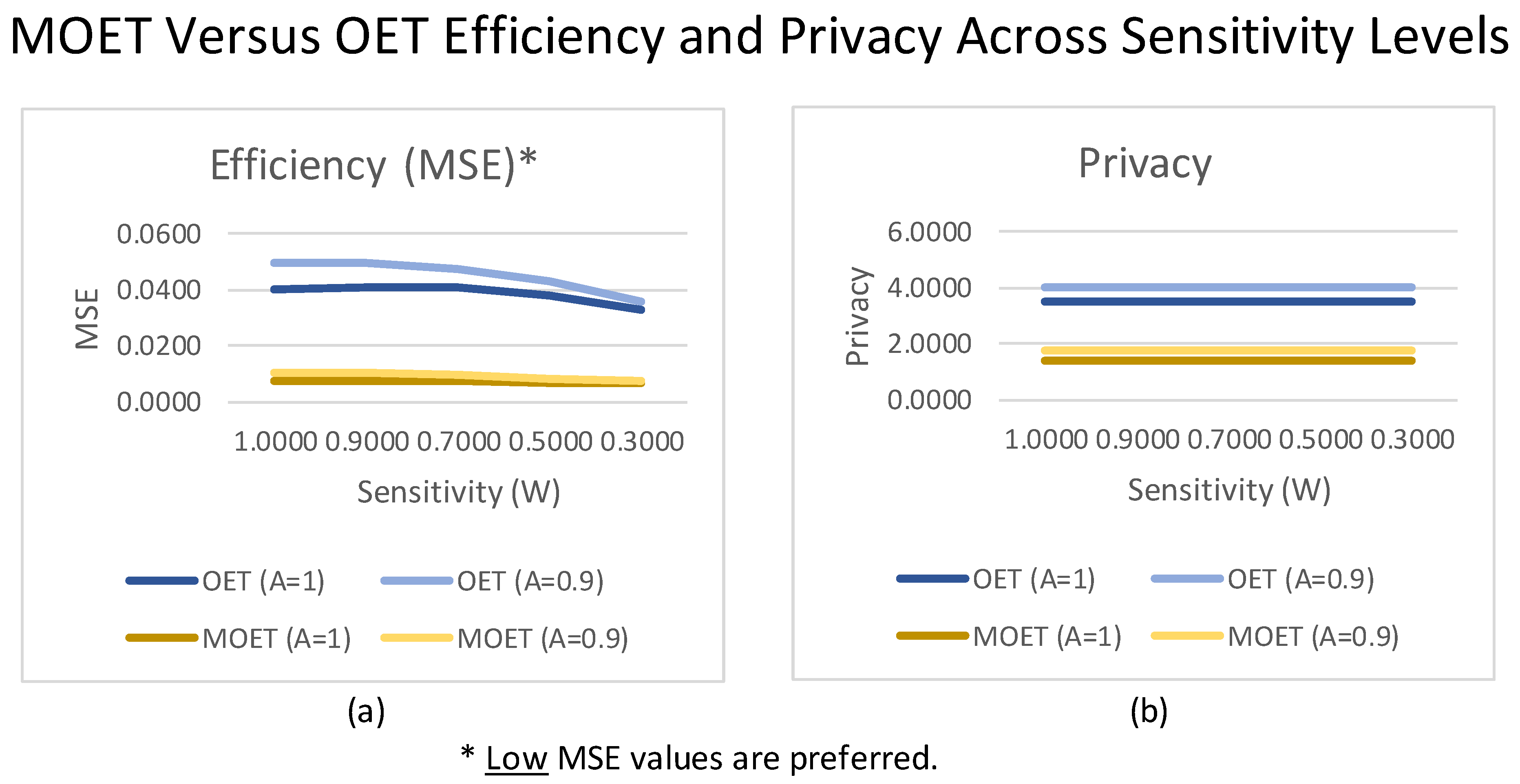
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MOET model | Mixture Optional Enhanced Trust model |
| OET model | Optional Enhanced Trust model |
| MSE | Mean Squared Error |
| RRT | Randomized Response Technique |
| SDB | Social Desirability Bias |
Appendix A. The Optional Enhanced Trust Model

References
- Raghavarao, D.; Federer, W.T. Block total response as an alternative to the randomized response method in surveys. J. R. Stat. Soc. Ser. B (Methodol.) 1979, 41, 40–45. [Google Scholar] [CrossRef]
- Reynolds, W. Development of a reliable and valid short form of the Marlowe-Crowne SDB scale. J. Clin. Psychol. 1982, 38, 119–125. [Google Scholar] [CrossRef]
- Jones, E.; Sigall, H. The Bogus Pipeline: A new paradigm for measuring effect and attitude. Psychol. Bull. 1971, 76, 349–364. [Google Scholar] [CrossRef]
- Warner, S. The Linear Randomized Response Model. J. Am. Stat. Assoc. 1971, 66, 884–888. [Google Scholar] [CrossRef]
- Greenberg, B.G.; Abul-Ela, A.L.A.; Simmons, W.R.; Horvitz, D.G. The unrelated question randomized response model: Theoretical framework. J. Am. Stat. Assoc. 1971, 666, 243–250. [Google Scholar] [CrossRef]
- Gupta, S.; Zhang, J.; Khalil, S.; Sapra, P. Mitigating Lack of Trust in Quantitative Randomized Response Techniques Models. Commun. Stat. Part B Simul. Comput. 2022, 51, 1–9. [Google Scholar] [CrossRef]
- Mehta, S.; Aggarwal, P. Bayesian estimation of sensitivity level and population proportion of a sensitive characteristic in a binary optional unrelated question rrt model. Commun. Stat.—Theory Methods 2018, 47, 4021–4028. [Google Scholar] [CrossRef]
- Diana, G.; Perri, P.F. A class of estimators for quantitative sensitive data. Stat. Pap. 2011, 52, 633–650. [Google Scholar] [CrossRef]
- Singh, G.N.; Kumar, A.; Vishwakarma, G.K. Some alternative additive randomized response models for estimation of population mean of quantitative sensitive variable in the presence of scramble variable. Commun. Stat.-Simul. Comput. 2018, 49, 2785–2807. [Google Scholar] [CrossRef]
- Priyanka, K.; Trisandhya, P. A composite class of estimators using scrambled response mechanism for sensitive population mean in successive sampling. Commun. Stat.—Theory Methods 2019, 48, 1009–1032. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, B.; Singh, S. Estimation of the sensitivity level of personal interview survey questions. J. Stat. Plan. Inference 2002, 100, 239–247. [Google Scholar] [CrossRef]
- Gupta, S.; Mehta, S.; Shabbir, J.; Khalil, S. A unified measure of respondent privacy and model efficiency in quantitative RRT models. J. Stat. Theory Pract. 2018, 12, 506–511. [Google Scholar] [CrossRef]
- Vishwakarma, G.K.; Kumar, A.; Kumar, N. Two-stage unrelated randomized response model to estimate the prevalence of a sensitive attribute. Comput. Stat. 2023, 52, 1–26. [Google Scholar] [CrossRef]
- Narjis, G.; Shabbir, J. An efficient partial randomized response model for estimating a rare sensitive attribute using poisson distribution. Commun. Stat.—Theory Methods 2021, 50, 1–17. [Google Scholar] [CrossRef]
- Lovig, M.; Khalil, S.; Rahman, S.; Sapra, P. A mixture binary RRT model with a unified measure of privacy and efficiency. Commun. Stat.—Simul. Comput. 2021, 52, 2727–2737. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, J.; Lai, J. An Efficiency and Protection Degree-Based Comparison Among the Quantitative Randomized Response Strategies. Theory Methods 2008, 38, 400–408. [Google Scholar] [CrossRef]

| A | W | α | * | * | * | * | * | * | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 2.0005 | 0.0122 | 0.0124 | 1.0000 | 1.0002 | 0.0122 | 0.0124 |
| 1 | 1 | 0.8 | 2.0017 | 0.0109 | 0.0111 | 1.0000 | 1.0003 | 0.0109 | 0.0111 |
| 1 | 1 | 0.6 | 2.0001 | 0.0097 | 0.0098 | 1.0000 | 0.9991 | 0.0097 | 0.0098 |
| 1 | 1 | 0.4 | 2.0021 | 0.0085 | 0.0083 | 1.0000 | 1.0012 | 0.0085 | 0.0083 |
| 1 | 1 | 0.2 | 1.9996 | 0.0073 | 0.0073 | 1.0000 | 1.0007 | 0.0073 | 0.0073 |
| 1 | 1 | 0 | 1.9999 | 0.0061 | 0.0061 | 1.0000 | 1.0016 | 0.0061 | 0.0061 |
| 1 | 0.6 | 1.0 | 2.0002 | 0.0097 | 0.0098 | 1.0000 | 1.0002 | 0.0097 | 0.0098 |
| 1 | 0.6 | 0.8 | 2.0005 | 0.0090 | 0.0092 | 1.0000 | 1.0003 | 0.0090 | 0.0092 |
| 1 | 0.6 | 0.6 | 2.0002 | 0.0083 | 0.0083 | 1.0000 | 0.9991 | 0.0083 | 0.0083 |
| 1 | 0.6 | 0.4 | 1.9999 | 0.0075 | 0.0075 | 1.0000 | 1.0012 | 0.0075 | 0.0075 |
| 1 | 0.6 | 0.2 | 1.9995 | 0.0068 | 0.0069 | 1.0000 | 1.0007 | 0.0068 | 0.0069 |
| 1 | 0.6 | 0 | 2.0006 | 0.0061 | 0.0062 | 1.0000 | 1.0016 | 0.0061 | 0.0062 |
| 1 | 0.2 | 1.0 | 1.9988 | 0.0073 | 0.0074 | 1.0000 | 1.0002 | 0.0073 | 0.0074 |
| 1 | 0.2 | 0.8 | 1.9988 | 0.0071 | 0.0069 | 1.0000 | 1.0003 | 0.0071 | 0.0069 |
| 1 | 0.2 | 0.6 | 2.0001 | 0.0068 | 0.0069 | 1.0000 | 0.9991 | 0.0068 | 0.0069 |
| 1 | 0.2 | 0.4 | 2.0006 | 0.0066 | 0.0066 | 1.0000 | 1.0012 | 0.0066 | 0.0066 |
| 1 | 0.2 | 0.2 | 2.0000 | 0.0063 | 0.0062 | 1.0000 | 1.0007 | 0.0063 | 0.0062 |
| 1 | 0.2 | 0 | 1.9996 | 0.0061 | 0.0062 | 1.0000 | 1.0016 | 0.0061 | 0.0062 |
| 0.9 | 1 | 1.0 | 2.0004 | 0.0152 | 0.0154 | 1.5000 | 1.5004 | 0.0101 | 0.0103 |
| 0.9 | 1 | 0.8 | 2.0002 | 0.0140 | 0.0137 | 1.4600 | 1.4585 | 0.0096 | 0.0094 |
| 0.9 | 1 | 0.6 | 1.9992 | 0.0128 | 0.0125 | 1.4200 | 1.4207 | 0.0090 | 0.0088 |
| 0.9 | 1 | 0.4 | 2.0016 | 0.0115 | 0.0116 | 1.3800 | 1.3798 | 0.0083 | 0.0084 |
| 0.9 | 1 | 0.2 | 1.9999 | 0.0103 | 0.0104 | 1.3400 | 1.3393 | 0.0077 | 0.0078 |
| 0.9 | 1 | 0 | 1.9992 | 0.0091 | 0.0089 | 1.3000 | 1.2982 | 0.0070 | 0.0069 |
| 0.9 | 0.6 | 1.0 | 2.0002 | 0.0116 | 0.0116 | 1.5000 | 1.5004 | 0.0077 | 0.0077 |
| 0.9 | 0.6 | 0.8 | 1.9992 | 0.0108 | 0.0109 | 1.4600 | 1.4585 | 0.0074 | 0.0075 |
| 0.9 | 0.6 | 0.6 | 1.9996 | 0.0101 | 0.0101 | 1.4200 | 1.4207 | 0.0071 | 0.0071 |
| 0.9 | 0.6 | 0.4 | 1.9988 | 0.0094 | 0.0092 | 1.3800 | 1.3798 | 0.0068 | 0.0067 |
| 0.9 | 0.6 | 0.2 | 2.0000 | 0.0086 | 0.0085 | 1.3400 | 1.3393 | 0.0064 | 0.0063 |
| 0.9 | 0.6 | 0 | 1.9995 | 0.0079 | 0.0080 | 1.3000 | 1.2982 | 0.0061 | 0.0062 |
| 0.9 | 0.2 | 1.0 | 2.0005 | 0.0079 | 0.0078 | 1.5000 | 1.5004 | 0.0053 | 0.0052 |
| 0.9 | 0.2 | 0.8 | 1.9989 | 0.0077 | 0.0076 | 1.4600 | 1.4585 | 0.0053 | 0.0052 |
| 0.9 | 0.2 | 0.6 | 2.0004 | 0.0074 | 0.0075 | 1.4200 | 1.4207 | 0.0052 | 0.0053 |
| 0.9 | 0.2 | 0.4 | 2.0001 | 0.0072 | 0.0072 | 1.3800 | 1.3798 | 0.0052 | 0.0052 |
| 0.9 | 0.2 | 0.2 | 2.0022 | 0.0069 | 0.0070 | 1.3400 | 1.3393 | 0.0051 | 0.0052 |
| 0.9 | 0.2 | 0 | 2.0007 | 0.0067 | 0.0069 | 1.3000 | 1.2982 | 0.0052 | 0.0053 |
| OET Model | MOET Model | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | W | * | |||||||||||
| 1 | 1 | 1.99899 | 0.0400 | 3.500 | 0.0114 | 1.0001 | 2.00122 | 0.0077 | 1.4250 | 0.0054 | 0.9956 | ||
| 1 | 0.9 | 2.0017 | 0.0409 | 3.500 | 0.0117 | 0.8989 | 1.9996 | 0.0075 | 1.4250 | 0.0053 | 0.8938 | ||
| 1 | 0.7 | 1.9975 | 0.0407 | 3.500 | 0.0116 | 0.7023 | 1.9993 | 0.0072 | 1.4250 | 0.0051 | 0.6938 | ||
| 1 | 0.5 | 1.9985 | 0.0380 | 3.500 | 0.0109 | 0.5013 | 2.0010 | 0.0069 | 1.4250 | 0.0048 | 0.4941 | ||
| 1 | 0.3 | 1.9999 | 0.0327 | 3.500 | 0.0093 | 0.3001 | 1.9997 | 0.0066 | 1.4250 | 0.0046 | 0.2914 | ||
| 0.95 | 1 | 2.0014 | 0.0450 | 3.750 | 0.0120 | 0.9989 | 1.9994 | 0.0092 | 1.5900 | 0.0058 | 0.9953 | ||
| 0.95 | 0.9 | 1.9991 | 0.0454 | 3.750 | 0.0121 | 0.9014 | 1.9990 | 0.0089 | 1.5900 | 0.0056 | 0.8933 | ||
| 0.95 | 0.7 | 2.0024 | 0.0442 | 3.750 | 0.0118 | 0.6980 | 2.0010 | 0.0083 | 1.5900 | 0.0052 | 0.6933 | ||
| 0.95 | 0.5 | 2.0006 | 0.0405 | 3.750 | 0.0108 | 0.4996 | 2.0005 | 0.0077 | 1.5900 | 0.0048 | 0.4925 | ||
| 0.95 | 0.3 | 1.9966 | 0.0342 | 3.750 | 0.0091 | 0.3030 | 1.9999 | 0.0071 | 1.5900 | 0.0045 | 0.2901 | ||
| 0.9 | 1 | 2.0010 | 0.0500 | 4.000 | 0.0125 | 0.9993 | 2.0007 | 0.0107 | 1.7550 | 0.0061 | 0.9960 | ||
| 0.9 | 0.9 | 1.9997 | 0.0499 | 4.000 | 0.0125 | 0.9000 | 1.9995 | 0.0103 | 1.7550 | 0.0059 | 0.8925 | ||
| 0.9 | 0.7 | 2.0010 | 0.0477 | 4.000 | 0.0119 | 0.6997 | 1.9996 | 0.0094 | 1.7550 | 0.0054 | 0.6916 | ||
| 0.9 | 0.5 | 1.9988 | 0.0430 | 4.000 | 0.0108 | 0.5013 | 1.9975 | 0.0084 | 1.7550 | 0.0048 | 0.4883 | ||
| 0.9 | 0.3 | 2.0000 | 0.0357 | 4.000 | 0.0089 | 0.3012 | 2.0002 | 0.0075 | 1.7550 | 0.0043 | 0.2889 | ||
| 0.85 | 1 | 2.0038 | 0.0550 | 4.250 | 0.0129 | 0.9980 | 2.0017 | 0.0122 | 1.9200 | 0.0064 | 0.9936 | ||
| 0.85 | 0.9 | 2.0024 | 0.0544 | 4.250 | 0.0128 | 0.8984 | 1.9996 | 0.0116 | 1.9200 | 0.0060 | 0.8910 | ||
| 0.85 | 0.7 | 2.0032 | 0.0512 | 4.250 | 0.0120 | 0.6988 | 1.9995 | 0.0104 | 1.9200 | 0.0054 | 0.6915 | ||
| 0.85 | 0.5 | 2.0002 | 0.0455 | 4.250 | 0.0107 | 0.4997 | 2.0000 | 0.0092 | 1.9200 | 0.0048 | 0.4882 | ||
| 0.85 | 0.3 | 1.9996 | 0.0372 | 4.250 | 0.0088 | 0.3000 | 2.0001 | 0.0080 | 1.9200 | 0.0042 | 0.2908 | ||
| 0.8 | 1 | 2.0028 | 0.0600 | 4.500 | 0.0133 | 0.9987 | 1.9974 | 0.0137 | 2.0850 | 0.0066 | 0.9917 | ||
| 0.8 | 0.9 | 2.0036 | 0.0589 | 4.500 | 0.0131 | 0.8982 | 2.0005 | 0.0130 | 2.0850 | 0.0062 | 0.8915 | ||
| 0.8 | 0.7 | 1.9997 | 0.0547 | 4.500 | 0.0122 | 0.7004 | 1.9996 | 0.0115 | 2.0850 | 0.0055 | 0.6895 | ||
| 0.8 | 0.5 | 2.0041 | 0.0480 | 4.500 | 0.0107 | 0.4971 | 2.0010 | 0.0100 | 2.0850 | 0.0048 | 0.4906 | ||
| 0.8 | 0.3 | 1.9990 | 0.0387 | 4.500 | 0.0086 | 0.3008 | 2.0000 | 0.0084 | 2.0850 | 0.0040 | 0.28888 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parker, M.; Gupta, S.; Khalil, S. A Mixture Quantitative Randomized Response Model That Improves Trust in RRT Methodology. Axioms 2024, 13, 11. https://doi.org/10.3390/axioms13010011
Parker M, Gupta S, Khalil S. A Mixture Quantitative Randomized Response Model That Improves Trust in RRT Methodology. Axioms. 2024; 13(1):11. https://doi.org/10.3390/axioms13010011
Chicago/Turabian StyleParker, Michael, Sat Gupta, and Sadia Khalil. 2024. "A Mixture Quantitative Randomized Response Model That Improves Trust in RRT Methodology" Axioms 13, no. 1: 11. https://doi.org/10.3390/axioms13010011
APA StyleParker, M., Gupta, S., & Khalil, S. (2024). A Mixture Quantitative Randomized Response Model That Improves Trust in RRT Methodology. Axioms, 13(1), 11. https://doi.org/10.3390/axioms13010011






