Stability Analysis of a New Fourth-Order Optimal Iterative Scheme for Nonlinear Equations

Abstract

In this paper, a new parametric class of optimal fourth-order iterative methods to estimate the solutions of nonlinear equations is presented. After the convergence analysis, a study of the stability of this class is made using the tools of complex discrete dynamics, allowing those elements of the class with lower dependence on initial estimations to be selected in order to find a very stable subfamily. Numerical tests indicate that the stable members perform better on quadratic polynomials than the unstable ones when applied to other non-polynomial functions. Moreover, the performance of the best elements of the family are compared with known methods, showing robust and stable behaviour.

1. Introduction and Preliminary Concepts

It is widely known that fixed-point iterative methods play a fundamental role in scientific disciplines such as Celestial Mechanics (see for example [1,2]), Electrical Power Systems [3], Chemistry [4], Hydraulic Engineering [5], and Civil Engineering [6]. These algorithms provide approximate solutions when exact solutions are challenging to obtain or when problems are ill-conditioned, while offering computational efficiency in terms of both time and computational resources.

In the field of numerical analysis, a current trend involves designing families of numerical methods that generalize existing approaches. Notable examples include King’s family [7] as well as the one developed by Hueso et al. in [8]. A number of these methods incorporate weight functions into their design process; see for example [9,10].

The efficiency index of an iterative method was defined by Ostrowski in [11] as $EI=p^{1/d}$, where p is the order of convergence and d is the number of functional evaluations per iteration. This concept is directly related to Kung and Traub’s conjecture [12], which states the order of convergence of any iterative scheme cannot be greater than $2^{d-1}$ (called the optimal order).

Several authors have generalized optimal iterative schemes according to the Kung–Traub conjecture. However, because there is no difference between the number of function evaluations and the order of the members within a class of iterative procedures, it is necessary to conduct a stability study on some simple nonlinear functions, such as quadratic polynomials. It has been observed that iterative schemes stable for such functions tend to perform better when applied to more complicated functions than methods exhibiting pathologies. To this end, the tools of complex discrete dynamics are employed to analyze stability in quadratic polynomials (see for example the work of Amat et al. in [13,14], Argyros et al. in [15], Behl et al. in [16], Chicharro et al. in [17], Rafiq et al. in [18], Kansal et al. in [19], Khirallah et al. in [20], and Moccari et al. in [21], among others).

A detailed description of the following concepts in complex dynamics appears in [22,23]. Let R be be a rational function on the Riemann sphere $\widehat{\mathbb{C}}=\mathbb{C}\cup$$\{\infty \}$, $R:\widehat{\mathbb{C}}\to \widehat{\mathbb{C}}$; then, we denote by $R\left(z\right)$ the operator $R\left(z\right)=\frac{P\left(z\right)}{Q\left(z\right)}$, with $P\left(z\right)$ and $Q\left(z\right)$ being complex polynomials. Usually, R is obtained by applying an iterative scheme on a quadratic polynomial $p\left(z\right)=(z-a)(z-b)$.

Given $z_0\in \widehat{\mathbb{C}}$, the orbit of $z_0$ under R is the sequence of points $\{z_0,z_1=R\left(z_0\right),z_2=R^2\left(z_0\right),\dots ,z_n=R^n\left(z_0\right),\dots \}$. Point $z_0$ is called the seed of the orbit. There are many different kind of orbits in a typical dynamical system. Undoubtedly, the most important kind of orbit is a fixed point, that is, a point $z_0$ that satisfies $R\left(z_0\right)=z_0$. Another important element is the periodic orbit or cycle. A point $z_0$ is n-periodic if $R^n\left(z_0\right)=z_0$ for some $n>0$, with $R^p\left(z_0\right)\ne z_0$ for any $p<n$. The smallest value of n for which the orbit becomes periodic is known as the period of the orbit.

Let us suppose that $z_0$ is a fixed point of R; then, $z_0$ is an attracting fixed point if $\left|R^{\prime }\left(z_0\right)\right|<1$. The point $z_0$ is a repelling fixed point if $\left|R^{\prime }\left(z_0\right)\right|>1$. Finally, if $\left|R^{\prime }\left(z_0\right)\right|=1$, then the fixed point is called neutral or indifferent.

Theorem 1

([23]). Attracting Fixed Point Theorem. Suppose that $z_0$ is an attracting fixed point for R. Then, there exists a domain D contained within the Riemann sphere such that $z_0\in D$ and in which the following conditions are satisfied: if $z\in D$, then $R^n\left(z\right)\in D$ for all n; moreover, $R^n\left(z\right)\to z_0$, as $n\to \infty$.

Theorem 2

([23]). Repelling Fixed Point Theorem. Suppose that $z_0$ is a repelling fixed point for R. Then, there exists a domain D contained within the Riemann sphere such that $z_0\in D$ and in which the following condition is satisfied: if $z\in D$ and $z\ne z_0$, then there is an integer $n>0$ such that $R^n\left(z\right)\notin D$.

Now, let us suppose that $z_0$ is an attracting fixed point for R. The basin of attraction of $z_0$ is the set of all points with orbits tending to $z_0$. The immediate basin of attraction of $z_0$ is the largest convex component containing $z_0$ that lies in the basin of attraction. The critical points of the operator R are those $z^C$ that meet $R^{\prime }\left(z^C\right)=0$. A critical point is called free if it does not match the roots of the polynomial. These two concepts are closely related to the next result.

Theorem 3

([24,25]). If R is a rational function, then the immediate basin of attraction of a periodic (or fixed) attracting point contains at least one critical point.

Fatou and Julia studied the iteration of rational maps $R:\widehat{\mathbb{C}}\to \widehat{\mathbb{C}}$ under the assumption that $deg\left(R\right)\ge 2$. They focused on a disjoint invariant decomposition of $\widehat{\mathbb{C}}$ into two sets. One of these sets is often called the Julia set. The other is referred as the Fatou set [22]. The Fatou set is the union of all basins of attraction, and the Julia set is its boundary.

Per Theorem 3, all of the attracting behaviours of a rational function can be found by iterating the free critical points and classifying them by their asymptotical performance in the Fatou set. This is accomplished by means of the parameter plane in the case where the rational function R depends on a complex parameter $\gamma$. This is the graphical representation that provides information about the choice of one or another value of a parameter $\gamma$ within a family of iterative methods. This graphical representation directly relates each point in the complex plane to the corresponding parameter value that specifies each member of the family. Given a free critical point of R used as the initial estimate, the parameter plane indicates which attracting periodic orbit or fixed point the orbit of the critical point converges to.

When all of the free critical points are known, we can calculate the parameter planes to determine which values of $\gamma$ relate the final state of all free critical points to any of the roots of $p\left(z\right)$. According to Theorem 3, this ensures the stability (on quadratic polynomials) of the associated elements of the class, as the only basins of attraction correspond with these roots.

Given a free critical point $cr\left(\gamma \right)$ as a seed of the rational function R, we define $D_{cr}$ as the set of values of $\gamma$ where the free critical point is in the basin of attraction of any of the roots of $p\left(z\right)$.

The characteristic function of the set $D_{cr}$ is defined as

$$F_{D_{cr}}\left(\gamma \right)=\left\{\begin{array}{ccc}1& \mathrm{if}& \gamma \in D_{cr},\\ 0& \mathrm{if}& \gamma \notin D_{cr}.\end{array}\right.$$

Therefore, we can consider the parameter plane by representing the characteristic function of $D_{cr}$, where a red color is assigned when $F_{D_{cr}}\left(\gamma \right)=1$ and black when $F_{D_{cr}}\left(\gamma \right)=0$.

Our interest is to determine the values of $\gamma$ for which the final state of the orbits of all free critical points is one of the polynomial roots. Because we construct a parameter plane for each free critical point, we proceed to construct the intersection of the parameter planes, which is called the unified parameter plane [26]. In this plane, we graph $F_{{\bigcap }_{i=1}^n{D}_{c{r}_i}}\left(\gamma \right)$, where n is the number of free critical points of the rational operator. Each red-colored point corresponds to values of $\gamma$ for which all members of the family of iterative schemes are stable on quadratic polynomials.

One way to validate the information obtained through parameter planes is to use dynamical planes, which graphically represent the basins of attraction of a set of initial values for a specific member of the family, that is, for a value of $\gamma$. In other words, given a parameter value for which the associated method is stable, its dynamical plane is composed only of the basins of the polynomial roots. This indicates that it will always be able to converge to one of the roots, regardless of the initial estimate of the method. On the other hand, if the parameter value is in the instability region on the parameter plane, other basins corresponding to attracting periodic or strange fixed points appear in addition to the basins of the roots. Through the dynamical planes, we can determine the attracting fixed point to which the orbit of any initial estimate $z_0$ converges for a specific value of $\gamma$.

The basin of attraction for the root $z=a$ is represented in orange color, while the basin for $z=b$ is represented in blue. Additionally, different colors such as green, red, etc. are assigned depending on the number of attracting strange fixed points associated with $\gamma$, and black is used to represent basins of periodic orbits. The decrease in brightness of each color is an indicator of the size of the orbit of each point, meaning that brighter colors represent points that require fewer iterations to reach the fixed or periodic point. The codes used to present the parameter and dynamical planes are defined by Chicharro et al. in [27].

Let us remark that all of the obtained information depends on the quadratic polynomial $p\left(z\right)$ used to define the rational function R by applying the class of iterative methods on it. A key tool to extend these results to any quadratic polynomial is the conjugation. Let f and g be two functions from the Riemann sphere to itself. An analytic conjugation between f and g is a diffeomorphism h of the Riemann sphere onto itself such that $h\circ f=g\circ h$, where h is called the conjugation. In [28], Blanchard introduced the conjugation map $\varphi \left(z\right)=\frac{z-a}{z-b}$, which is a Möbius transformation satisfying the following properties: $\varphi (\infty )=1$, $\varphi \left(a\right)=0$, and $\varphi \left(b\right)=\infty$, with a and b being the roots of the arbitrary quadratic polynomial $p\left(z\right)=(z-a)(z-b)$.

The next result was proven by [22,29] for Newton’s method. In Section 3, the Scaling Theorem is proven for the rational function related to the proposed class of iterative methods.

Theorem 4.

Scaling Theorem. Let $f\left(z\right)$ be an analytic function and let $A\left(z\right)=\eta z+\beta$, with $\eta \ne 0$ as an affine application. If $h\left(z\right)=\lambda (f\circ A)\left(z\right)$ with $\lambda \ne 0$, then $R_f$ is analytically conjugate with $R_h$ through A, i.e., $\left(A\circ R_h\circ A^{-1}\right)\left(z\right)=R_f\left(z\right).$

If a family of iterative methods satisfies the Scaling Theorem, then the Möbius transformation can be applied. As demonstrated by Blanchard in [22], the asymptotic behavior of the system is qualitatively equivalent under conjugation. This allows us to perform dynamical analysis on an associated operator that does not depend on the roots a and b. Instead, the dynamical study is conducted based on their corresponding values in the new operator, which are $\varphi \left(a\right)=0$ and $\varphi \left(b\right)=\infty$. Additionally, the strange fixed point $z=1$ is the divergence of the original scheme. This makes the analysis of its stability particularly important.

In the following Section 2 a one-parametric class of iterative procedures with fourth-order of convergence is designed using the weight function technique. In Section 3, the rational function resulting from the fixed point operator applied on a quadratic polynomial $p\left(z\right)$ is analyzed. More specifically, we study the dynamics of the fixed points of this rational operator R, allowing us to determine its stability. In Section 4, the numerical behavior of some of the most stable members on other non-polynomial functions is analyzed and compared with other known methods from the literature. Finally, in Section 5, conclusions highlighting the most significant findings of the research are presented.

2. Construction of a New Parametric Family of Iterative Methods

If $f\left(x\right)=0$ is a nonlinear equation, then an iterative method, under certain conditions, generates a sequence of real numbers that converges to a solution $\overline{x}$. However, the guarantee of convergence to a solution, the convergence rate, and the solution to which an iterative scheme converges all have a direct dependence on the initial estimate. The creation of a new class of iterative methods makes sense as long as there are members of the family that are competitive compared to existing schemes with good behavior. In our study, we present a new family of iterative methods using the weight function procedure, characterized by

$$\begin{array}{cc}\hfill y_k& =x_k-\beta \frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},\hfill \\ \hfill x_{k+1}& =x_k-H\left(\mu \right)\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},k=0,1,\dots ,\hfill \end{array}$$

(1)

where $\beta$ is an arbitrary parameter and H is a real function depending on $\mu \left(x\right)=\frac{f^{\prime }\left(x\right)}{f^{\prime }\left(y\right)}$. Now, we prove the convergence of this class, stating the conditions on $H\left(\mu \right(x\left)\right)$, to achieve fourth-order convergence.

Theorem 5.

Let $\overline{x}\in I$ be a simple zero of a sufficiently differentiable function $f:I\subset \mathbb{R}⟶\mathbb{R}$ and $\mu \left(x\right)=\frac{f^{\prime }\left(x\right)}{f^{\prime }\left(y\right)}$. Let us assume an initial estimation $x_0$ that is close enough to a zero $\overline{x}$ of f. If a weight function $H\left(\mu \left(x_k\right)\right)$, $\mu \left(x_k\right)=\frac{f^{\prime }\left(x_k\right)}{f^{\prime }\left(y_k\right)}$ is chosen that satisfies $H\left(1\right)=1$ in addition to $H^{\prime }\left(1\right)=\frac{3}{4}$, $H^{″}\left(1\right)=\frac{3}{4}$, and $\left|H^{‴}\left(1\right)\right|<+\infty$, then class (1) has an order of convergence of four if and only if $\beta =\frac{2}{3}$, with the following error equation:

$$e_{k+1}=\frac{1}{81}\left((117-32H^{‴}\left(1\right))c_2^3-81c_3{c}_2+9c_4\right)e_k^4+O\left(e_k^5\right),$$

where $c_j=\frac{1}{j!}\frac{f^{\left(j\right)}\left(\overline{x}\right)}{f^{\prime }\left(\overline{x}\right)}\mathrm{for}j=2,3,\dots$ and $e_k=x_k-\overline{x}.$

Proof. 

By applying Taylor expansion of $f\left(x_k\right)$ on $\overline{x}$,

$$f\left(x_k\right)=f^{\prime }\left(\overline{x}\right)\left[e_k+c_2{e}_k^2+c_3{e}_k^3+c_4{e}_k^4+O\left(e_k^5\right)\right]$$

(2)

and

$$f^{\prime }\left(x_k\right)=f^{\prime }\left(\overline{x}\right)\left[1+2c_2{e}_k+3c_3{e}_k^2+4c_4{e}_k^3+O\left(e_k^4\right)\right].$$

(3)

Dividing directly (2) by (3), we obtain

$$\begin{array}{c}\hfill \frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)}=e_k-c_2{e}_k^2+2\left(c_2^2-c_3\right)e_k^3+\left(-4c_2^3+7c_2{c}_3-3c_4\right)e_k^4+O\left(e_k^5\right).\end{array}$$

If, in the first step of (1), we subtract $\overline{x}$ on both sides, then we have its error expression

$$\begin{array}{cc}\hfill y_k-\overline{x}& =e_k-\beta \frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)}\hfill \\ & =(1-\beta )e_k+\beta c_2{e}_k^2+2\beta \left(c_3-c_2^2\right)e_k^3+\beta \left(4c_2^3-7c_2{c}_c+3c_4\right)e_k^4+O\left(e_k^5\right).\hfill \end{array}$$

Then,

$$\begin{array}{c}\hfill f^{\prime }\left(y_k\right)=1-2(\beta -1)c_2{e}_k+B_1{e}_k^2+B_2{e}_k^3+O\left(e_k^4\right),\end{array}$$

(4)

with

$$\begin{array}{cc}\hfill & B_1=3{(\beta -1)}^2{c}_3+2\beta c_2^2,\hfill \\ \hfill & B_2=-4{(\beta -1)}^3{c}_4-4\beta c_2^3+2(5-3\beta )\beta c_2{c}_3.\hfill \end{array}$$

Dividing (3) by (4),

$$\begin{array}{c}\hfill \mu \left(x_k\right)=\frac{f^{\prime }\left(x_k\right)}{f^{\prime }\left(y_k\right)}=1+2\beta c_2{e}_k+D_1{e}_k^2+D_2{e}_k^3+O\left(e_k^4\right),\end{array}$$

where

$$\begin{array}{cc}\hfill & D_1=\left((4\beta -6)c_2^2-3(\beta -2)c_1{c}_3\right)\beta ,\hfill \\ \hfill & D_2=\left(2\left({\beta }^2-3\beta +2\right)c_2^3+\left(-3{\beta }^2+9\beta -7\right)c_2{c}_3+\left({\beta }^2-3\beta +3\right)c_4\right)4\beta .\hfill \end{array}$$

We expand $H\left(\mu \left(x_k\right)\right)$ around one because the variable $\mu$ approaches unity as k tends to infinity:

$$\begin{array}{cc}\hfill H\left(\mu \left(x_k\right)\right)=& H\left(1\right)+H^{\prime }\left(1\right){\nu }_k+\frac{H^{″}\left(1\right)}{2!}{\nu }_k^2+\frac{H^{‴}\left(1\right)}{3!}{\nu }_k^3+O\left({\nu }_k^4\right)\hfill \\ \hfill =& H\left(1\right)+2\beta H^{\prime }\left(1\right)c_2{e}_k+F_1{e}_k^2+\frac{2\beta }{3}(F_2+F_3)e_k^3+O\left(e_k^4\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & {\nu }_k=\mu \left(x_k\right)-1,\hfill \\ \hfill & F_1=\left(2\left((2\beta -3)H^{\prime }\left(1\right)+\beta H^{″}\left(1\right)\right)c_2^2-3(\beta -2)H^{\prime }\left(1\right)\right)\beta c_3,\hfill \\ \hfill & F_2=6\left({\beta }^2-3\beta +3\right)c_4{H}^{\prime }\left(1\right)-3\left(2\left(3{\beta }^2-9\beta +7\right)H^{\prime }\left(1\right)+3(\beta -2)\beta H^{″}\left(1\right)\right)c_2{c}_3,\hfill \\ \hfill & F_3=2\left(6\left({\beta }^2-3\beta +2\right)H^{\prime }\left(1\right)+\beta \left((6\beta -9)H^{″}\left(1\right)+\beta H^{‴}\left(1\right)\right)\right)c_2^3.\hfill \end{array}$$

Subtracting $\overline{x}$ on both sides of the second step of (1),

$$\begin{array}{cc}\hfill e_{k+1}& =(x_k-\overline{x})-H\left(\frac{f^{\prime }\left(x_k\right)}{f^{\prime }\left(y_k\right)}\right)\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)}\hfill \\ \hfill & =(1-H\left(1\right))e_k+\left(H\left(1\right)-2\beta H^{\prime }\left(1\right)\right)c_2{e}_k^2+(2H\left(1\right)+3(\beta -2)\beta H^{\prime }\left(1\right))c_3\hfill \\ \hfill & -2\left(H\left(1\right)+\beta (2(\beta -2)H^{\prime }\left(1\right)+\beta H^{″}\left(1\right))c_2^2\right)e_k^3+O\left(e_k^4\right).\hfill \end{array}$$

(5)

Forcing the coefficients of $e_k$, $e_k^2$, and $e_k^3$ to be zero, we obtain $H\left(1\right)=1$, along with $H^{\prime }\left(1\right)=\frac{3}{4}$, $H^{″}\left(1\right)=\frac{3}{4}$, and $\beta =\frac{2}{3}$. By replacing them in (5), we have

$$\begin{array}{c}\hfill e_{k+1}=\frac{1}{81}\left((117-32H^{‴}\left(1\right))c_2^3-81c_2{c}_3+9c_4\right)e_k^4+O\left(e_k^5\right),\end{array}$$

and the optimal order of convergence of four is proven. □

Parametric Family

The proposed parametric family generalizes some existing classes of iterative methods. Let us recall the one-parameter families of fourth-order optimal iterative methods developed by Hueso et al. in [8]:

$$\begin{array}{cc}\hfill y_k& =x_k-\frac{2}{3}\frac{f\left(x_k\right)}{f\left(x_k\right)},k=0,1,\dots ,\hfill \\ \hfill x_{k+1}& =x_k-\left[\frac{5-8\alpha }{8}+\alpha \left(\frac{f^{\prime }\left(x_k\right)}{f^{\prime }\left(y_k\right)}\right)+\frac{\alpha }{3}{\left(\frac{f^{\prime }\left(x_k\right)}{f^{\prime }\left(y_k\right)}\right)}^{-1}+\frac{9-8\alpha }{24}{\left(\frac{f^{\prime }\left(x_k\right)}{f^{\prime }\left(y_k\right)}\right)}^2\right]\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)}\hfill \end{array}$$

(6)

and the parametric family defined by Cordero et al. in [10]:

$$\begin{array}{cc}\hfill y_k& =x_k-\frac{2}{3}\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},k=0,1,\dots ,\hfill \\ \hfill x_{k+1}& =x_k-\left[1-\frac{3}{4}\left(\frac{f^{\prime }\left(y_k\right)}{f^{\prime }\left(x_k\right)}-1\right)+\frac{9}{8}{\left(\frac{f^{\prime }\left(y_k\right)}{f^{\prime }\left(x_k\right)}-1\right)}^2+\frac{\alpha }{6}{\left(\frac{f^{\prime }\left(y_k\right)}{f^{\prime }\left(x_k\right)}-1\right)}^3\right]\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)}.\hfill \end{array}$$

(7)

Both families have the structure of the iterative function defined in Equation (1) for $\beta =\frac{2}{3}$, and their weight functions satisfy Theorem 5. It is evident that the weight functions of these families share similar structures, suggesting the possibility of constructing a generalized family that encompasses both.

The following result shows that, under certain conditions, the parametric weight function

$$\begin{array}{c}\hfill K\left(\mu \left(x\right)\right)=a_0{\mu }^{k_0}\left(x\right)+a_1{\mu }^{k_1}\left(x\right)+a_2{\mu }^{k_2}\left(x\right)+a_3{\mu }^{k_3}\left(x\right),\end{array}$$

(8)

where $a_i\in \mathbb{R}$ and $k_i\in \mathbb{N}$ for $i=0,1,2,3$, satisfies the conditions of Theorem 5.

Theorem 6.

The parametric weight function $K\left(\mu \left(x\right)\right)=a_0{\mu }^{k_0}\left(x\right)+a_1{\mu }^{k_1}\left(x\right)+a_2{\mu }^{k_2}\left(x\right)+a_3{\mu }^{k_3}\left(x\right)$ satisfies the conditions imposed on the weight function H of Theorem 5 if and only if

$$\begin{array}{cc}\hfill & k_i\ne k_j,\mathit{with}i\ne j,\hfill \\ & a_0=\frac{\left(k_1-k_2\right)\left(-3k_2+k_1\left(4k_2-3\right)+6\right)-\gamma {\varphi }_0}{4{\varphi }_3},\hfill \\ & a_1=\frac{\left(3\left(k_2-2\right)+k_0\left(3-4k_2\right)\right)\left(k_0-k_2\right)+\gamma {\varphi }_1}{4{\varphi }_3},\hfill \\ & a_2=\frac{\left(k_0-k_1\right)\left(-3k_1+k_0\left(4k_1-3\right)+6\right)-\gamma {\varphi }_2}{4{\varphi }_3},\hfill \\ & a_3=\gamma ,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & {\varphi }_n=\prod _{\begin{array}{c}i<j\\ i,j\ne n\end{array}}^{}(k_i-k_j),\mathit{with}i,j\mathit{and}n\in \{0,1,2,3\}.\hfill \end{array}$$

Proof. 

Considering that

$$\begin{array}{ccc}\hfill K\left(\mu \left(x\right)\right)& =& a_0{\mu }^{k_0}\left(x\right)+a_1{\mu }^{k_1}\left(x\right)+a_2{\mu }^{k_2}\left(x\right)+a_3{\mu }^{k_3}\left(x\right),\hfill \\ \hfill K^{\prime }\left(\mu \left(x\right)\right)& =& a_0{k}_0{\mu }^{k_0-1}\left(x\right)+a_1{k}_1{\mu }^{k_1-1}\left(x\right)+a_2{k}_2{\mu }^{k_2-1}\left(x\right)+a_3{k}_3{\mu }^{k_3-1}\left(x\right),\hfill \\ \hfill K^{″}\left(\mu \left(x\right)\right)& =& a_0\left(k_0-1\right)k_0{\mu }^{k_0-2}\left(x\right)+a_1\left(k_1-1\right)k_1{\mu }^{k_1-2}\left(x\right)+a_2\left(k_2-1\right)k_2{\mu }^{k_2-2}\left(x\right)\hfill \\ & & +a_3\left(k_3-1\right)k_3{\mu }^{k_3-2}\left(x\right),\hfill \end{array}$$

we have

$$\begin{array}{cc}\hfill & K\left(1\right)=a_0+a_1+a_2+a_3,\hfill \\ & K^{\prime }\left(1\right)=a_0{k}_0+a_1{k}_1+a_2{k}_2+a_3{k}_3,\hfill \\ & K^{″}\left(1\right)=a_0\left(k_0-1\right)k_0+a_1\left(k_1-1\right)k_1+a_2\left(k_2-1\right)k_2+a_3\left(k_3-1\right)k_3.\hfill \end{array}$$

If we equate these expressions to the conditions imposed in Theorem 5, then we have the following system:

$$\begin{array}{ccc}\hfill a_0+a_1+a_2+a_3& =& 1,\hfill \\ \\ \hfill a_0{k}_0+a_1{k}_1+a_2{k}_2+a_3{k}_3& =& \frac{3}{4},\hfill \\ \\ \hfill a_0\left(k_0-1\right)k_0+a_1\left(k_1-1\right)k_1+a_2\left(k_2-1\right)k_2+a_3\left(k_3-1\right)k_3& =& \frac{3}{4},\hfill \end{array}$$

for which the solution set for $a_3=\gamma$ and $k_i\ne k_j\mathrm{if}i\ne j$ is

$$\begin{array}{ccc}\hfill a_0& =& -\frac{4\gamma k_3^2-4\gamma k_1{k}_3-4\gamma k_2{k}_3+4\gamma k_1{k}_2+3k_1-4k_1{k}_2+3k_2-6}{4\left(k_0-k_1\right)\left(k_0-k_2\right)}=-\frac{3(k_2-2)+k_1\left(3-4k_2\right)}{4\left(k_0-k_1\right)\left(k_0-k_2\right)}+\frac{\gamma \left(k_1-k_3\right)\left(k_3-k_2\right)}{\left(k_0-k_1\right)\left(k_0-k_2\right)},\hfill \\ \\ \hfill a_1& =& -\frac{4\gamma k_3^2-4\gamma k_0{k}_3-4\gamma k_2{k}_3+4\gamma k_0{k}_2+3k_0-4k_0{k}_2+3k_2-6}{4\left(k_1-k_0\right)\left(k_1-k_2\right)}=\frac{3\left(k_2-2\right)+k_0\left(3-4k_2\right)}{4\left(k_0-k_1\right)\left(k_1-k_2\right)}+\frac{\gamma \left(k_0-k_3\right)\left(k_2-k_3\right)}{\left(k_0-k_1\right)\left(k_1-k_2\right)},\hfill \\ \\ \hfill a_2& =& -\frac{-4\gamma k_3^2+4\gamma k_0{k}_3+4\gamma k_1{k}_3-4\gamma k_0{k}_1-3k_0+4k_0{k}_1-3k_1+6}{4\left(k_1-k_2\right)\left(k_2-k_0\right)}=\frac{3\left(k_1-2\right)+k_0\left(3-4k_1\right)}{4\left(k_0-k_2\right)\left(k_2-k_1\right)}+\frac{\gamma \left(k_0-k_3\right)\left(k_1-k_3\right)}{\left(k_1-k_2\right)\left(k_2-k_0\right)},\hfill \\ \hfill a_3& =& \gamma .\hfill \end{array}$$

By defining

$$\begin{array}{cc}\hfill & {\varphi }_n=\prod _{\begin{array}{c}i<j\\ i,j\ne n\end{array}}^{}(k_i-k_j)\mathrm{with}i,j\mathrm{and}n\in \{0,\cdots ,3\},\hfill \end{array}$$

then multiplying and dividing by ${\varphi }_3$, we have

$$\begin{array}{ccc}\hfill a_0& =& \frac{\left(k_1-k_2\right)\left(-3k_2+k_1\left(4k_2-3\right)+6\right)-\gamma \left(k_1-k_2\right)\left(k_1-k_3\right)\left(k_2-k_3\right)}{4{\varphi }_3}=\frac{\left(k_1-k_2\right)\left(-3k_2+k_1\left(4k_2-3\right)+6\right)-\gamma {\varphi }_0}{4{\varphi }_3},\hfill \\ \\ \hfill a_1& =& \frac{\left(3\left(k_2-2\right)+k_0\left(3-4k_2\right)\right)\left(k_0-k_2\right)+\gamma \left(k_0-k_2\right)\left(k_0-k_3\right)\left(k_2-k_3\right)}{4{\varphi }_3}=\frac{\left(3\left(k_2-2\right)+k_0\left(3-4k_2\right)\right)\left(k_0-k_2\right)+\gamma {\varphi }_1}{4{\varphi }_3},\hfill \\ \\ \hfill a_2& =& \frac{\left(k_0-k_1\right)\left(-3k_1+k_0\left(4k_1-3\right)+6\right)-\gamma \left(k_0-k_1\right)\left(k_0-k_3\right)\left(k_1-k_3\right)}{4{\varphi }_3}=\frac{\left(k_0-k_1\right)\left(-3k_1+k_0\left(4k_1-3\right)+6\right)-\gamma {\varphi }_2}{4{\varphi }_3},\hfill \\ \\ \hfill a_3& =& \gamma ,\hfill \end{array}$$

and the proof is finished. □

In Theorem 6, it can be observed that the parametric weight function $K\left(\mu \right(x\left)\right)$ depends on the parameters $k_0,k_1,k_2,k_3,\mathrm{and}{a}_3$; thus, we denote it as $K_{(k_0,k_1,k_2,k_3,a_3)}\left(\mu \left(x\right)\right)$. It is easy to see that the families of iterative methods from the iterative expressions (6) and (7) are subfamilies of the family formed by the iterative scheme (1) when $H\left(\mu \right)=K_{(-1,0,1,2,\frac{9-8\alpha }{24})}\left(\mu \right)$ and $H\left(\mu \right)=K_{(-3,-2,-1,0,\frac{1}{6}\alpha )}\left(\mu \right)$, respectively.

3. Complex Stability Analysis

In Section 2, we have set the conditions for the following iterative scheme to be a fourth-order optimal class of iterative methods:

$$\begin{array}{ccc}\hfill y_k& =& x_k-\frac{2}{3}\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},k=0,1,\dots ,\hfill \\ \hfill x_{k+1}& =& x_k-\left[a_0\mu {\left(x_k\right)}^{k_0}+a_1\mu {\left(x_k\right)}^{k_1}+a_2\mu {\left(x_k\right)}^{k_2}+a_3\mu {\left(x_k\right)}^{k_3}\right]\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},\hfill \end{array}$$

(9)

where $\mu \left(x_k\right)={\displaystyle \frac{f^{\prime }\left(x_k\right)}{f^{\prime }\left(y_k\right)}}$.

If we assign integer values to $k_0$, $k_1$, $k_2$, and $k_3$, all distinct from each other, and define $a_i$ for $i\in \{0,1,2,3\}$ as in Theorem 6, then the following result demonstrates that the resulting one-parametric subfamily satisfies the Scaling Theorem. As a result, the Möbius transformation can be used as an analytical conjugation to analyze the stability of its members on quadratic polynomials by means of its associated rational operator.

Theorem 7.

Let $f\left(z\right)$ be an analytic function, let R be the rational operator associated with the iterative scheme (9), and let $A\left(z\right)={\eta }_{1}z+{\eta }_2$ with ${\eta }_1\ne 0$, an affine transformation. Let $h\left(z\right)=\lambda (f\circ A)\left(z\right)$; then, $R_f$ and $R_h$ are analytically conjugated by $A\left(z\right)$.

Proof. 

Let us consider $N_f\left(z\right)=z-\frac{2}{3}\frac{f\left(z\right)}{f^{\prime }\left(z\right)}$; taking into account that

$$\begin{array}{cc}\hfill A(x-y)& ={\eta }_1(x-y)+{\eta }_2=({\eta }_{1}x+{\eta }_2)-(\eta -1y+{\eta }_2)+{\eta }_2=A\left(x\right)-A\left(y\right)+{\eta }_2\hfill \end{array}$$

and $h\left(z\right)=\lambda (f\circ A)\left(z\right)=\lambda f\left(A\left(z\right)\right),\mathrm{then}{h}^{\prime }\left(z\right)=A^{\prime }\left(z\right)\lambda f^{\prime }\left(A\left(z\right)\right)={\eta }_1\lambda (f^{\prime }\circ A)\left(z\right)$, and it can be deduced that

$$\begin{array}{ccc}\hfill A\circ N_h\circ A^{-1}& =& A\left(A^{-1}\left(z\right)-\frac{2}{3}\frac{h\left(A^{-1}\left(z\right)\right)}{h^{\prime }\left(A^{-1}\left(z\right)\right)}\right)\hfill \\ & =& A\left(A^{-1}\left(z\right)-\frac{2}{3}\frac{f\left(z\right)}{{\eta }_1{f}^{\prime }\left(z\right)}\right)\hfill \\ & =& z-\frac{2}{3}\frac{f\left(z\right)}{f^{\prime }\left(z\right)}=N_f\left(z\right).\hfill \end{array}$$

Thus, $N_f$ and $N_h$ are analytically conjugated by $A\left(z\right)$. Then,

$$R_h=z-\left[\sum _{i=0}^3{a}_i{\left(\frac{h^{\prime }\left(z\right)}{h^{\prime }\left(N_h\right)}\right)}^{k_i}\right]\frac{h\left(z\right)}{h^{\prime }\left(z\right)}.$$

Because

$$\begin{array}{cc}\hfill h\left(z\right)& =\lambda (f\circ A)\left(z\right)=\lambda f\left(A\right(z\left)\right),\hfill \\ \hfill h^{\prime }\left(z\right)& ={\eta }_1\lambda (f^{\prime }\circ A)\left(z\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill h^{\prime }\left(N_h\right)& ={\eta }_1\lambda (f^{\prime }\circ A\circ N_h)\left(z\right),\hfill \end{array}$$

we have

$$R_h=z-\left[\sum _{i=0}^3{a}_i{\left(\frac{f^{\prime }\circ A}{f^{\prime }\circ A\circ N_h}\right)}^{k_i}\right]\frac{1}{{\eta }_1}\frac{f\circ A}{f^{\prime }\circ A}.$$

Using the fact that $A\circ N_h\circ A^{-1}=N_f$,

$$R_h\circ A^{-1}=A^{-1}\left(z\right)-\left[\sum _{i=0}^3{a}_i{\left(\frac{f^{\prime }\left(z\right)}{f^{\prime }\circ N_f}\right)}^{k_i}\right]\frac{1}{{\eta }_1}\frac{f\left(z\right)}{f^{\prime }\left(z\right)},$$

we obtain

$$A\circ R_h\circ A^{-1}=A\left[A^{-1}\left(z\right)-\left[\sum _{i=0}^3{a}_i{\left(\frac{f^{\prime }\left(z\right)}{f^{\prime }\circ N_f}\right)}^{k_i}\right]\frac{1}{{\eta }_1}\frac{f\left(z\right)}{f^{\prime }\left(z\right)}\right].$$

Because $A(x-y)=A\left(x\right)-A\left(y\right)+{\eta }_2$, we have

$$A\circ R_h\circ A^{-1}=z-\left[\sum _{i=0}^3{a}_i{\left(\frac{f^{\prime }\left(z\right)}{f^{\prime }\circ N_f}\right)}^{k_i}\right]\frac{f\left(z\right)}{f^{\prime }\left(z\right)}=R_f,$$

meaning that $R_f$ and $R_h$ are analytically conjugated by $A\left(z\right)$. □

3.1. Asymptotical Study of Fixed Points

As a consequence of Theorem 7 we know, under the conditions established for the parameters $k_i$ and $a_i$ for $i\in \{0,1,2,3\}$ in class (9), that the dynamical behavior of the associated rational operator remains invariant under the Möbius transformation through conjugation over quadratic polynomials.

Applying the family of iterative methods (9) on $p\left(z\right)=(z-a)(z-b)$, where $a,b\in \widehat{\mathbb{C}}$, we obtain the associated rational operator $R_K=\varphi \circ R_p\circ {\varphi }^{-1}$ after conjugation with the Möbius map $\varphi \left(z\right)={\displaystyle \frac{z-a}{z-b}}$.

Now, for the dynamical analysis, distinct integer values are assigned to $k_0,k_1,k_2$, and $k_3$ and the dynamics of the rational operator $R_K$ of the parametric family associated with these values is studied. We use the following criteria to select the class:

• As our aim is to construct a parameter plane for each independent free critical point, the polynomial with roots that are critical points depending on $\gamma$ should have a degree no higher than 4. This is because it becomes extremely laborious to construct parameter planes when the critical points that depend on $\gamma$ are the roots of a high-degree polynomial.
• It is necessary to find a radius disk where $|R_K^{\prime }(1,k_0,k_1,k_2,k_3,\gamma )|>1$ as much as is possible. By making $z=1$ in $R_K^{\prime }(z,k_0,k_1,k_2,k_3,\gamma )$, it is easy to see that $R_K^{\prime }(1,k_0,k_1,k_2,k_3,\gamma )$$=\frac{A(k_0,k_1,k_2,k_3)}{B(k_0,k_1,k_2,k_3)+C(k_0,k_1,k_2,k_3)\gamma }$, where $A(k_0,k_1,k_2,k_3)=8(k_0-k_1)(k_0-k_2)(k_1-k_2),$

  $$\begin{array}{cc}\hfill B(k_0,k_1,k_2,k_3)=& -{k_0}^2{k}_1{2}^{2-k_2}{3}^{k_2}+{k_0}^2{2}^{2-k_1}{3}^{k_1}{k}_2-{k_0}^2{2}^{-k_1}{3}^{k_1+1}+8{k_0}^2{k}_1\hfill \\ & +{k_0}^2{2}^{-k_2}{3}^{k_2+1}-8{k_0}^2{k}_2+k_0{k_1}^2{2}^{2-k_2}{3}^{k_2}-2^{2-k_0}{3}^{k_0}{k_1}^2{k}_2-8k_0{k_1}^2\hfill \\ & +2^{-k_0}{3}^{k_0+1}{k_1}^2-k_0{2}^{2-k_1}{3}^{k_1}{k_2}^2+2^{2-k_0}{3}^{k_0}{k}_1{k_2}^2\hfill \\ & +k_0{2}^{1-k_1}{3}^{k_1+1}{2}^{1-k_0}{3}^{k_0+1}{k}_1+8k_0{k_2}^2-2^{-k_0}{3}^{k_0+1}{k_2}^2-k_0{2}^{1-k_2}{3}^{k_2+1}\hfill \\ & +2^{1-k_0}{3}^{k_0+1}{k}_2-{k_1}^2{2}^{-k_2}{3}^{k_2+1}+8{k_1}^2{k}_2+2^{-k_1}{3}^{k_1+1}{k_2}^2-8k_1{k_2}^2\hfill \\ & +k_1{2}^{1-k_2}{3}^{k_2+1}-2^{1-k_1}{3}^{k_1+1}{k}_2,\hfill \end{array}$$

  and

  $$\begin{array}{cc}\hfill C(k_0,k_1,k_2,k_3)=& {k_0}^2{k}_1{2}^{2-k_2}{3}^{k_2}-{k_0}^2{2}^{2-k_1}{3}^{k_1}{k}_2-{k_0}^2{k}_1{2}^{2-k_3}{3}^{k_3}+{k_0}^2{2}^{2-k_1}{3}^{k_1}{k}_3+\hfill \\ \hfill & {k_0}^2{k}_2{2}^{2-k_3}{3}^{k_3}-{k_0}^2{2}^{2-k_2}{3}^{k_2}{k}_3-k_0{k_1}^2{2}^{2-k_2}{3}^{k_2}+2^{2-k_0}{3}^{k_0}{k_1}^2{k}_2+\hfill \\ & k_0{k_1}^2{2}^{2-k_3}{3}^{k_3}-2^{2-k_0}{3}^{k_0}{k_1}^2{k}_3+k_0{2}^{2-k_1}{3}^{k_1}{k_2}^2-2^{2-k_0}{3}^{k_0}{k}_1{k_2}^2-\hfill \\ & k_0{2}^{2-k_1}{3}^{k_1}{k_3}^2+2^{2-k_0}{3}^{k_0}{k}_1{k_3}^2-k_0{k_2}^2{2}^{2-k_3}{3}^{k_3}+2^{2-k_0}{3}^{k_0}{k_2}^2{k}_3+\hfill \\ & k_0{2}^{2-k_2}{3}^{k_2}{k_3}^2-2^{2-k_0}{3}^{k_0}{k}_2{k_3}^2-{k_1}^2{k}_2{2}^{2-k_3}{3}^{k_3}+{k_1}^2{2}^{2-k_2}{3}^{k_2}{k}_3+\hfill \\ & k_1{k_2}^2{2}^{2-k_3}{3}^{k_3}-2^{2-k_1}{3}^{k_1}{k_2}^2{k}_3-k_1{2}^{2-k_2}{3}^{k_2}{k_3}^2+2^{2-k_1}{3}^{k_1}{k}_2{k_3}^2.\hfill \end{array}$$

  Then, $|\frac{A(k_0,k_1,k_2,k_3)}{C(k_0,k_1,k_2,k_3)}|>|\frac{B(k_0,k_1,k_2,k_3)}{C(k_0,k_1,k_2,k_3)}+\gamma |$ when $|R^{\prime }(1,k_0,k_1,k_2,k_3,\gamma )|>1$, and now $G(k_0,k_1,k_2,k_3)=\frac{A(k_0,k_1,k_2,k_3)}{C(k_0,k_1,k_2,k_3)}$ is defined such that we choose values of $k_0,k_1,k_2$ and $k_3$ where $\left|G\right(k_0,k_1,k_2,k_3\left)\right|$ can be made as large as desired.
• The coefficients of the rational operator must be simple in the sense that they do not exceed three digits.

Table 1. Degrees of the polynomials with zeros that are free critical points of $R_K$.

Degree	Number of Families
18	36
16	56
14	63
12	60
10	50
8	30
6	26
4	8
2	1

presents the degrees of those polynomials with zeros that are free critical points of the rational operator associated with 330 one-parameter families constructed with values of $k_0$, $k_1$, $k_2$, and $k_3$ taken from the set of all unique permutations of integers from −5 to 5. Within this set, nine families can be identified that meet the criteria established in the first point. Of these, eight families have an associated polynomial of degree 4, while one family has a polynomial of degree 2.

Table 2. Values of $k_j$ related to parametric families where the degree (D) of the polynomial with zeros that are free critical points of the associated rational operator does not exceed 4 and their radius (r).

$\mathbf{(}{\mathit{k}}_{\mathbf{0}}\mathbf{,}{\mathit{k}}_{\mathbf{1}}\mathbf{,}{\mathit{k}}_{\mathbf{2}}\mathbf{,}{\mathit{k}}_{\mathbf{3}}\mathbf{)}$	r	D	${\mathit{R}}_{\mathit{K}}\mathbf{(}\mathit{z}\mathbf{,}\mathit{\gamma }\mathbf{)}$
$(1,2,3,4)$	$\frac{32}{3}$	4	$-\frac{z^4\left(-192\gamma +81z^5+135z^4+324z^3+204z^2-192\gamma z+187z-3\right)}{3(64\gamma +1)z^5+(192\gamma -187)z^4-204z^3-324z^2-135z-81}$
$(0,1,2,3)$	16	4	$-\frac{z^4\left(-64\gamma +27z^4+54z^3+90z^2+62z+39\right)}{(64\gamma -39)z^4-62z^3-90z^2-54z-27}$
$(-4,-3,-2,0)$	18	4	$-\frac{z^4\left(-256\gamma +27z^6+216z^5+729z^4+1296z^3+(1813-256\gamma )z^2-8(32\gamma -157)z+679\right)}{(256\gamma -679)z^6+8(32\gamma -157)z^5+(256\gamma -1813)z^4-1296z^3-729z^2-216z-27}$
$(-1,0,1,2)$	24	4	$-\frac{z^4\left(-64\gamma +27z^4+90z^3+138z^2+114z+63\right)}{(64\gamma -63)z^4-114z^3-138z^2-90z-27}$
$(-4,-3,-1,0)$	$\frac{162}{5}$	4	$-\frac{z^4\left(-384\gamma +81z^6+648z^5+2187z^4+3888z^3+(4839-384\gamma )z^2-8(64\gamma -421)z+1437\right)}{3(128\gamma -479)z^6+8(64\gamma -421)z^5+(384\gamma -4839)z^4-3888z^3-2187z^2-648z-81}$
$(-2,-1,0,1)$	36	4	$-\frac{z^4\left(-64\gamma +27z^4+126z^3+234z^2+198z+135\right)}{(64\gamma -135)z^4-198z^3-234z^2-126z-27}$
$(-4,-2,-1,0)$	$\frac{486}{11}$	4	$-\frac{z^4\left(-768\gamma +243z^6+1944z^5+6561z^4+11664z^3+(13629-768\gamma )z^2+(9512-1280\gamma )z+3423\right)}{(768\gamma -3423)z^6+8(160\gamma -1189)z^5+3(256\gamma -4543)z^4-11664z^3-6561z^2-1944z-243}$
$(-3,-2,-1,0)$	54	2	$-\frac{z^4\left(-64\gamma +27z^4+162z^3+378z^2+378z+319\right)}{(64\gamma -319)z^4-378z^3-378z^2-162z-27}$
$(-4,-3,-2,-1)$	81	4	$-\frac{z^4\left(-192\gamma +81z^6+648z^5+2187z^4+3888z^3+(5439-192\gamma )z^2-8(16\gamma -471)z+2037\right)}{3(64\gamma -679)z^6+8(16\gamma -471)z^5+3(64\gamma -1813)z^4-3888z^3-2187z^2-648z-81}$

presents the values of $k_j$ for $j=0,1,2,3$, radius $\left|G\right(k_0,k_1,k_2,k_3\left)\right|$, and rational function of those classes of iterative schemes such that the polynomials generating the free critical points have a degree lower than or equal to four. It can be observed that the families by Hueso et al. (6) and Cordero et al. (7) meet our selection criteria. In the case of the first family, the radius as a function of $\gamma$ of the disk where divergence is repelling is 24, and the polynomial that meets the first criterion is of degree 4. On the other hand, the second class has a radius as a function of $\gamma$ of 54, and possesses the only second-degree polynomial that satisfies the first criterion among all possible formed families. In both families, the coefficients of the rational operators do not exceed three digits.

The family associated with $K_{(-4,-3,-2,-1,\gamma )}$ has a divergence radius greater than that of the two families mentioned earlier, and the polynomial degree is 4. However, the coefficients of the rational operator are not simple. On the other hand, the family associated with $K_{(-2,-1,0,1,\gamma )}$ has simple coefficients and a radius of 36, which is greater than the radius of the family studied by Hueso et al. (6). Therefore, we focus our analysis on this family. It is worth mentioning that it would be interesting to study the dynamical behavior of the family associated with $K_{(0,1,2,3,\gamma )}$ or $K_{(1,2,3,4,\gamma )}$, as well as other families, without considering the simple coefficient criterion.

From Table 2, we denote the rational operator of the family associated with $K_{(-2,-1,0,1,\gamma )}$ by

$$R(z,\gamma )=\frac{z^4\left(27z^4+126z^3+234z^2+198z+135-64\gamma \right)}{\left(135-64\gamma \right)z^4+198z^3+234z^2+126z+27}.$$

Now, let us analyze some properties of the rational operator R.

Theorem 8.

The fixed points of the rational function $R(z,\gamma )$ are $z=0$, $z=\infty$, and the following strange fixed points:

• $e{x}_1\left(\gamma \right)=1$, which corresponds to divergence from the original method
• $e{x}_2\left(\gamma \right)=z_{1,1}=\frac{1}{2}\left(\frac{1}{9}S\left(\gamma \right)-\sqrt{{\left(-\frac{1}{9}S\left(\gamma \right)+\frac{17}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2-4}-\frac{17}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_3\left(\gamma \right)=z_{1,2}=\frac{1}{2}\left(\frac{1}{9}S\left(\gamma \right)+\sqrt{{\left(-\frac{1}{9}S\left(\gamma \right)+\frac{17}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2-4}-\frac{17}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_4\left(\gamma \right)=z_{2,1}=\frac{1}{2}\left(-\frac{1}{9}wS\left(\gamma \right)-\sqrt{-4+{\left(\frac{1}{9}wS\left(\gamma \right)-\frac{17\overline{w}}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2}+\frac{17\overline{w}}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_5\left(\gamma \right)=z_{2,2}=\frac{1}{2}\left(-\frac{1}{9}wS\left(\gamma \right)+\sqrt{-4+{\left(-\frac{1}{9}wS\left(\gamma \right)-\frac{17\overline{w}}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2}+\frac{17\overline{w}}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_6\left(\gamma \right)=z_{3,1}=\frac{1}{2}\left(-\frac{1}{9}\overline{w}S\left(\gamma \right)-\sqrt{-4+{\left(\frac{1}{9}\overline{w}S\left(\gamma \right)-\frac{17w}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2}+\frac{17w}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_7\left(\gamma \right)=z_{3,2}=\frac{1}{2}\left(-\frac{1}{9}\overline{w}S\left(\gamma \right)+\sqrt{-4+{\left(\frac{1}{9}\overline{w}S\left(\gamma \right)-\frac{17w}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2}+\frac{17w}{9S\left(\gamma \right)}-\frac{17}{9}\right)$

where $S\left(\gamma \right)=\sqrt[3]{3\sqrt{3}\sqrt{27648{\gamma }^2-60544\gamma +33327}-864\gamma +946}$ and $w=\frac{1}{2}\left(1-i\sqrt{3}\right).$

Proof. 

From the definition of a fixed point, we have $R(z,\gamma )=z$. Then,

$$\frac{z^4\left(27z^4+126z^3+234z^2+198z+135-64\gamma \right)}{\left(135-64\gamma \right)z^4+198z^3+234z^2+126z+27}=z.$$

Thus,

$$z\left[27\left(z^7-1\right)+126z\left(z^5-1\right)+234z^2\left(z^3-1\right)+\left(63+64\gamma \right)z^3\left(z-1\right)\right]=0$$

and

$$z\left(z-1\right)\left(27z^6+153z^5+387z^4+z^3(450+64\gamma )+387z^2+153z+27\right)=0.$$

Let $J(z,\gamma )$ denote the last factor of this equation. If we substitute $u=z+\frac{1}{z}$, then $u^2-2=z^2+\frac{1}{z^2}$ and $u^3-3u=z^3+\frac{1}{z^3}$. Thus, $J(z,\gamma )=z^3\left[27u^3+153u^2+306u+(144+64\gamma )\right]$. Therefore, the factor $27u^3+153u^2+306u+(144+64\gamma )$ must be zero. Consequently, we have

$$u_1\left(\gamma \right)=\frac{1}{9}S\left(\gamma \right)-\frac{17}{9S\left(\gamma \right)}-\frac{17}{9},$$

$$u_2\left(\gamma \right)=-\frac{1}{18}\left(1-i\sqrt{3}\right)S\left(\gamma \right)+\frac{17\left(1+i\sqrt{3}\right)}{18S\left(\gamma \right)}-\frac{17}{9},$$

$$u_3\left(\gamma \right)=-\frac{1}{18}\left(1+i\sqrt{3}\right)S\left(\gamma \right)+\frac{17\left(1-i\sqrt{3}\right)}{18S\left(\gamma \right)}-\frac{17}{9},$$

where

$$S\left(\gamma \right)=\sqrt[3]{3\sqrt{3}\sqrt{27648{\gamma }^2-60544\gamma +33327}-864\gamma +946}.$$

Therefore, $e{x}_{j+k}\left(\gamma \right)=\frac{u_i\left(\gamma \right)+{(-1)}^{j+k}\sqrt{u_i{\left(\gamma \right)}^2-4}}{2},$ for $i=1,2,3$, $j=1,3,5$ and $k=1,2.$ Note that the strange fixed points $e{x}_{i+1}\left(\gamma \right)=z_{i,2}=\frac{1}{z_{i,1}}=\frac{1}{e{x}_i\left(\gamma \right)}$, as $z^2-u_i\left(\gamma \right)z+1=0$ is a symmetric polynomial:

• $e{x}_2\left(\gamma \right)=z_{1,1}=\frac{1}{2}\left(\frac{1}{9}S\left(\gamma \right)-\sqrt{{\left(-\frac{1}{9}S\left(\gamma \right)+\frac{17}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2-4}-\frac{17}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_3\left(\gamma \right)=z_{1,2}=\frac{1}{2}\left(\frac{1}{9}S\left(\gamma \right)+\sqrt{{\left(-\frac{1}{9}S\left(\gamma \right)+\frac{17}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2-4}-\frac{17}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_4\left(\gamma \right)=z_{2,1}=\frac{1}{2}\left(-\frac{1}{9}wS\left(\gamma \right)-\sqrt{-4+{\left(\frac{1}{9}wS\left(\gamma \right)-\frac{17\overline{w}}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2}+\frac{17\overline{w}}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_5\left(\gamma \right)=z_{2,2}=\frac{1}{2}\left(-\frac{1}{9}wS\left(\gamma \right)+\sqrt{-4+{\left(-\frac{1}{9}wS\left(\gamma \right)-\frac{17\overline{w}}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2}+\frac{17\overline{w}}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_6\left(\gamma \right)=z_{3,1}=\frac{1}{2}\left(-\frac{1}{9}\overline{w}S\left(\gamma \right)-\sqrt{-4+{\left(\frac{1}{9}\overline{w}S\left(\gamma \right)-\frac{17w}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2}+\frac{17w}{9S\left(\gamma \right)}-\frac{17}{9}\right)$
• $e{x}_7\left(\gamma \right)=z_{3,2}=\frac{1}{2}\left(-\frac{1}{9}\overline{w}S\left(\gamma \right)+\sqrt{-4+{\left(\frac{1}{9}\overline{w}S\left(\gamma \right)-\frac{17w}{9S\left(\gamma \right)}+\frac{17}{9}\right)}^2}+\frac{17w}{9S\left(\gamma \right)}-\frac{17}{9}\right)$

where $w=\frac{1}{2}\left(1-i\sqrt{3}\right)$.

In a similar way, it can be easily checked that $z=0$ is a fixed point of $\frac{1}{R\left(\frac{1}{z},\gamma \right)}$; thus, $z=\infty$ is a fixed point of R. □

It is clear that the long-term behavior of fixed points is influenced by $\gamma$. This dependence can result in an attracting character of some strange fixed points, leading the corresponding numerical method to attract elements that are not solutions to the problem under investigation.

In order to perform a stability analysis of the fixed points, we can evaluate their derivative operator:

$$R^{\prime }(z,\gamma )=-\frac{36z^3{(z+1)}^{4}N(z,\gamma )}{{\left(64\gamma z^4-135z^4-198z^3-234z^2-126z-27\right)}^2},$$

where $N(z,\gamma )=(192\gamma -405)z^4-(96\gamma +540)z^3+(64\gamma -990)z^2-(96\gamma +540)z+(192\gamma -405)$.

Fixed points $z=0$ and $z=\infty$ have a superattracting character, as $|R^{\prime }(z,\gamma )|=0$ for those values. However, the stability of $z=1$ provides important numerical information, as it indicates divergence in the original procedure. Hence, we determine the stability of these fixed points in the forthcoming results.

Theorem 9.

For $\gamma \ne \frac{45}{4}$, the fixed point $e{x}_1\left(\gamma \right)=1$ has the following characteristics:

(i) 

It can not be superattracting;

(ii) 

When $\left|\frac{45}{4}-\gamma \right|<36$, it is repelling;

(iii) 

If $\left|\frac{45}{4}-\gamma \right|=36$, $e{x}_1\left(\gamma \right)=1$ is neutral;

(iv) 

When $\left|\frac{45}{4}-\gamma \right|>36$, then $e{x}_1\left(\gamma \right)=1$ is attracting.

Proof. 

(i)

The derivative $R_h^{\prime }(1,\gamma )=\frac{144}{45-4\gamma }$ is always different from zero; thus, $e{x}_1\left(\gamma \right)=1$ cannot be superattracting. Moreover, it is not defined for $\gamma =\frac{45}{4}$; thus, $z=1$ is not a fixed point for this value of $\gamma$.

(ii)

According to the definition, $e{x}_1\left(\gamma \right)=1$ is a repelling fixed point if $\left|R_h^{\prime }(1,\gamma ))\right|=\left|\frac{144}{45-4\gamma }\right|>1$. Therefore, $\left|\frac{144}{45-4\gamma }\right|>1$ is equivalent to $\left|\frac{45}{4}-\gamma \right|<\frac{144}{4}=36$.

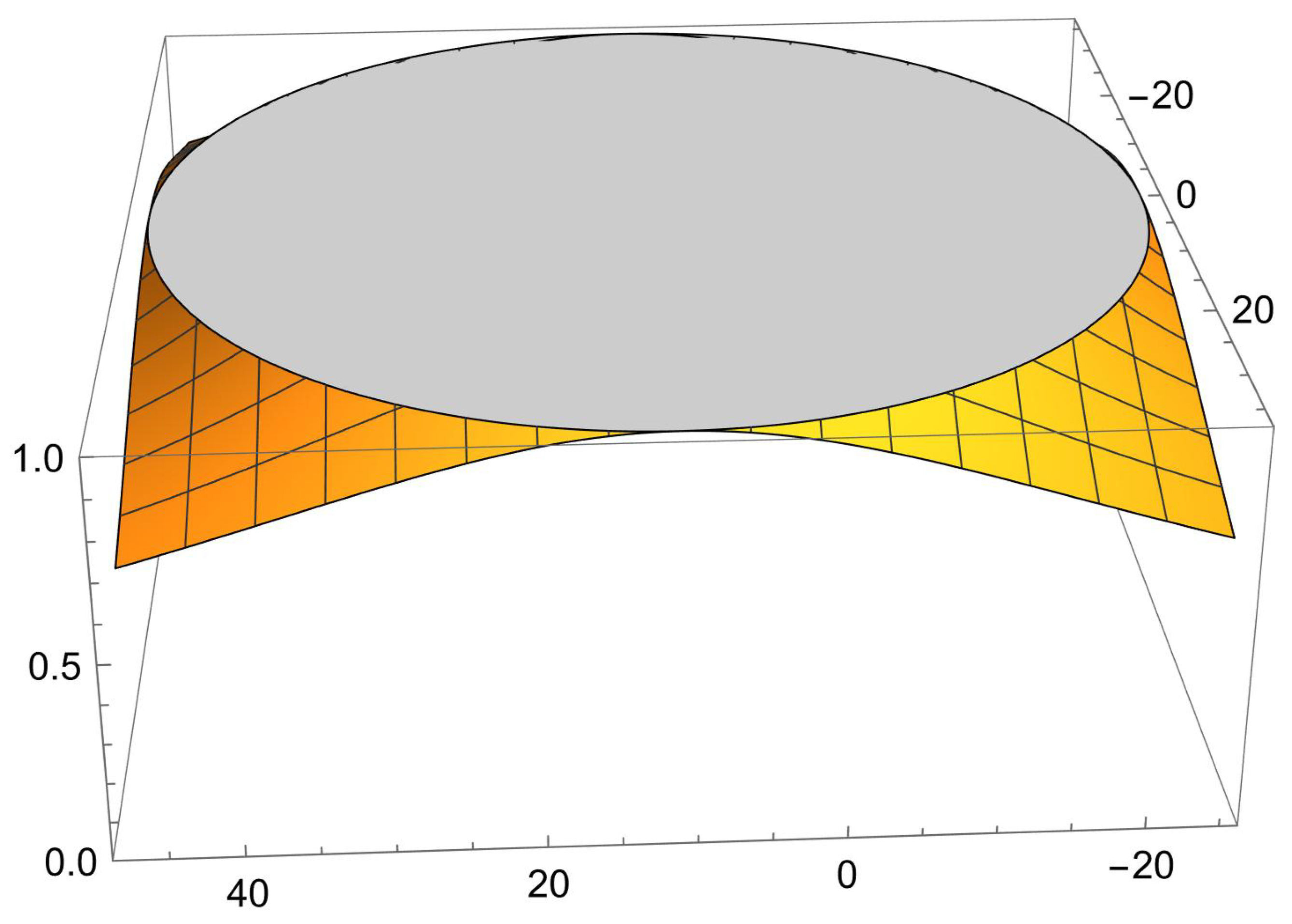
Let us consider an arbitrary complex number $\gamma =c+id$. Then, $\left|\frac{45}{4}-\gamma \right|<36$ is equivalent to ${(c-\frac{45}{4})}^2+d^2<{36}^2$, indicating that the divergence represents a repelling fixed point for values of $\gamma \ne \frac{45}{4}$ inside the disk $D_1$ centered at $C\left(\frac{45}{4},0\right)$ with a radius of 36. It is neutral at the circumference and attracting outside the disk; see Figure 1 for a visual representation.

The proofs for items (iii) and (iv) follow a similar approach to that for item (ii). □

We aim for the only attracting fixed points to be $z=0$ and $z=\infty$. Therefore, the stability function $\left|R^{\prime }(z,\gamma )\right|$ at the other fixed points should always be greater than one. Indeed, to prevent divergence, a stable method must be defined with a $\gamma$ value from within the disk $D_1$.

Figure 2 displays the stability function of $e{x}_2\left(\gamma \right)$ and $e{x}_3\left(\gamma \right)$, indicating that there are only attracting fixed points inside the orange cardioid contained within the rectangular region defined by

$$B\left(\gamma \right)=\left\{\gamma \in \mathbb{C}:\gamma =c+id,\frac{22}{5}<c<\frac{99}{8},-\frac{83}{20}<d<\frac{83}{20}\right\}.$$

Figure 3 displays the stability surfaces of the strange fixed points $e{x}_i\left(\gamma \right)$ for $i=4,5,6,7$, illustrating that they are always repelling for $\gamma$ values inside the disk $D_1$.

On the other hand, we know that $z=0$ and $z=\infty$ are critical points for all values of $\gamma$. The following result identifies the critical points of the rational operator, which allows us to determine the values of $\gamma$ for which the zeros of $p\left(z\right)$ are the only attracting elements.

Theorem 10.

The rational operator R has the following free critical points:

(i) 

$c{r}_1=-1,$

(ii) 

$c{r}_2\left(\gamma \right)=z_{1,1}=\frac{1}{2}\left(v_1\left(\gamma \right)-\sqrt{v_1^2\left(\gamma \right)-4}\right),$

(iii) 

$c{r}_3\left(\gamma \right)=z_{1,2}=\frac{1}{2}\left(v_1\left(\gamma \right)+\sqrt{v_1^2\left(\gamma \right)-4}\right),$

(iv) 

$c{r}_4\left(\gamma \right)=z_{2,1}=\frac{1}{2}\left(v_2\left(\gamma \right)-\sqrt{v_2^2\left(\gamma \right)-4}\right),$

(v) 

$c{r}_5\left(\gamma \right)=z_{2,2}=\frac{1}{2}\left(v_2\left(\gamma \right)+\sqrt{v_2^2\left(\gamma \right)-4}\right),$

where $v_1\left(\gamma \right)=\frac{2\left(-8\sqrt{3}\sqrt{83{\gamma }^2-90\gamma }+24\gamma +135\right)}{3(64\gamma -135)}$ and $v_2\left(\gamma \right)=\frac{2\left(8\sqrt{3}\sqrt{83{\gamma }^2-90\gamma }+24\gamma +135\right)}{3(64\gamma -135)}.$

Proof. 

It is straightforward that

$$R^{\prime }(z,\gamma )=-\frac{36z^3{(z+1)}^{4}M(z,\gamma )}{{\left(64\gamma z^4-135z^4-198z^3-234z^2-126z-27\right)}^2},$$

where $M(z,\gamma )=(192\gamma -405)z^4-(96\gamma +540)z^3+(64\gamma -990)z^2-(96\gamma +540)z+(192\gamma -405)$. Hence, the free critical points are $c{r}_1=-1$ and the solutions of the equation $M(z,\gamma )=0$. Thus, it can be expressed as

$$z^2\left[(192\gamma -405)z^2-(96\gamma +540)z+(64\gamma -990)-(96\gamma +540)\frac{1}{z}+(192\gamma -405)\frac{1}{z^2}\right]=0,$$

and we have

$$z^2\left[(192\gamma -405)(z^2+\frac{1}{z^2})-(96\gamma +540)(z+\frac{1}{z})+(64\gamma -990)\right]=0.$$

By making $v=z+\frac{1}{z}$, we have $v^2-2=z^2+\frac{1}{z^2}$. Then,

$$z^2\left[(192\gamma -405)(v^2-2)-(96\gamma +540)v+(64\gamma -990)\right]=0$$

and

$$z^2\left[(192\gamma -405)v^2-(96\gamma +540)v-(320\gamma +180)\right]=0.$$

Because $z\ne 0$,

$$(192\gamma -405)v^2-(96\gamma +540)v-(320\gamma +180)=0$$

and we have

$$v_1=\frac{2\left(-8\sqrt{3}\sqrt{83{\gamma }^2-90\gamma }+24\gamma +135\right)}{3(64\gamma -135)},$$

$$v_2=\frac{2\left(8\sqrt{3}\sqrt{83{\gamma }^2-90\gamma }+24\gamma +135\right)}{3(64\gamma -135)}.$$

Thus, the free critical points are $c{r}_{j+k}\left(\gamma \right)=\frac{v_i\left(\gamma \right)+{(-1)}^{j+k}\sqrt{v_i{\left(\gamma \right)}^2-4}}{2}$ for $i=1,2$, $j=1,3$, and $k=1,2.$

Note that $c{r}_{i+1}\left(\gamma \right)=\frac{1}{c{r}_i\left(\gamma \right)}$ for $i=1,2$. Therefore, $c{r}_i\left(\gamma \right)=\frac{v_i\left(\gamma \right)\pm \sqrt{v_i{\left(\gamma \right)}^2-4}}{2},$

$$c{r}_2\left(\gamma \right)=\frac{1}{2}\left(v_1\left(\gamma \right)-\sqrt{v_1^2\left(\gamma \right)-4}\right),$$

$$c{r}_3\left(\gamma \right)=\frac{1}{2}\left(v_1\left(\gamma \right)+\sqrt{v_1^2-4}\left(\gamma \right)\right),$$

$$c{r}_4\left(\gamma \right)=\frac{1}{2}\left(v_2\left(\gamma \right)-\sqrt{v_2^2-4}\left(\gamma \right)\right),$$

$$c{r}_5\left(\gamma \right)=\frac{1}{2}\left(v_2\left(\gamma \right)+\sqrt{v_2^2-4}\left(\gamma \right)\right).$$

 □

3.2. Parameter Plane

By means of Theorem 3, the critical points are employed to locate the basins of attraction of periodic or fixed attracting points. To achieve this, they are used as initial guesses, then the parameter planes are used to locate those values of $\gamma$ where the only attracting elements are the roots of polynomial $p\left(z\right)$.

The parameter plane is plotted for values of $\gamma$ in the rectangular region defined by

$$\{\gamma \in \mathbb{C}:\gamma =c+id,-\frac{99}{4}<c<\frac{198}{4},-36<d<36\},$$

as it contains $\left|\frac{45}{4}-\gamma \right|=36$. To generate the plot, we use a grid of $2000\times 2000$ points, a maximum of 200 iterations, and a tolerance of ${10}^{-3}$.

Given a free critical point as the initial estimate for our iterative scheme, we define $D_{c{r}_i}$ as the loci of the complex plane defined by the values of $\gamma$ for which the free critical point is in the basin of attraction of $z=0$ or $z=\infty$. The parameter plane is represented by the graph of the characteristic function of set $D_{c{r}_i}$, where the color red is assigned when $F_{D_{c{r}_i}}\left(\gamma \right)=1$ and black is assigned when $F_{D_{c{r}_i}}\left(\gamma \right)=0$. We plot the parameter plane for $\gamma$ values in the interior of the disk $D_1$ (defined in Theorem 9); this region guarantees the divergence, as $e{x}_1\left(\gamma \right)=1$ is repelling.

Figure 4 displays the parameter planes corresponding to the critical points $c{r}_i\left(\gamma \right)$, where $i=2,3,4,5$. Let us remark that because conjugate critical points have the same parameter plane, only two of them are independent.

On the other hand, Figure 5 represents the unified parameter plane corresponding to the characteristic function $F_{{\bigcap }_{i=2}^5{D}_{c{r}_i}}\left(\gamma \right)$, where each point colored in red corresponds to values of $\gamma$ for which all members of our family of iterative schemes are stable on quadratic polynomials.

3.3. Dynamical Planes of Some Stable and Unstable Members

In Figure 5, red represents the values of $\gamma$ associated with stable members. To obtain additional complementary information that allows us to verify the stability characterization obtained through the parameter planes and the stability functions of the strange fixed points, in Figure 6 we present the corresponding dynamical planes for some stable and unstable values, as per the information obtained from the intersection of parameter planes.

To construct the dynamical planes in Figure 6, we define a grid in the complex plane with $2000\times 2000$ points, where each one corresponds to a different value of the initial estimate $z_0$. Each dynamical plane shows the final state of the orbit of each point in the grid, considering a maximum of 200 iterations and a tolerance of ${10}^{-3}$. In each dynamical plane, we mark certain special points: repelling fixed points (RFP) are marked with circles (∘), critical points (CP) with squares (□), and attracting fixed points (AFP) with asterisks (∗).

Through the dynamical planes, we can determine the attracting elements that the orbit of any initial estimate $z_0$ converge to when using the rational operator R with a specific value of $\gamma$. The basin of attraction of $z=0$ is represented in orange, while the basin of $z=\infty$ is represented in blue. Additionally, different colors such as green, red, etc., are assigned to other attracting strange fixed points, while black is used to represent basins of periodic orbits.

We have confirmed that the values of $\gamma$ in the red region of Figure 5 have only two basins of attraction, namely, $z=0$ and $z=\infty$. This guarantees that the iterative scheme associated with these values of $\gamma$ always converges to a root of $p\left(z\right)$, regardless of the initial estimate $z_0$. Similarly, it is validated that there are always pathologies that depend on the initial estimate $z_0$ for the methods associated with values of $\gamma$ in the black region of the parameter plane.

In

Table 3. Stable and unstable values of $\gamma$.

$\mathit{\gamma }$	# RFP (∘)	# CP (□)	# AFP (∗)	Period	Stability
${\gamma }_{\left(a\right)}=\frac{9}{8}$	7	4	2	1	Stable
${\gamma }_{\left(b\right)}=\frac{45}{4}$	8	5	2	1	Stable
${\gamma }_{\left(c\right)}=1$	9	7	2	1	Stable
${\gamma }_{\left(d\right)}=0$	7	3	2	1	Stable
${\gamma }_{\left(e\right)}=-1$	9	7	2	1	Stable
${\gamma }_{\left(f\right)}=-\frac{1}{2}$	9	7	2	1	Stable
${\gamma }_{\left(g\right)}=\frac{1}{2}$	9	7	2	1	Stable
${\gamma }_{\left(h\right)}=-5$	9	7	2	1	Stable
${\gamma }_{\left(i\right)}=10-10i$	9	7	2	1	Stable
${\gamma }_{\left(j\right)}=-10-10i$	9	7	2	1	Stable
${\gamma }_{\left(k\right)}=-16-12i$	9	7	2	1	Stable
${\gamma }_{\left(l\right)}=-16$	9	7	4	1	Unstable
${\gamma }_{\left(m\right)}=20$	9	7	2	2	Unstable
${\gamma }_{\left(n\right)}=16$	9	7	2	2	Unstable
${\gamma }_{\left(o\right)}=-40$	9	7	3	1	Unstable
${\gamma }_{\left(p\right)}=10-30i$	9	7	2	4	Unstable
${\gamma }_{\left(q\right)}=-24$	9	7	4	1	Unstable
${\gamma }_{\left(r\right)}=-6+28i$	9	7	2	4	Unstable
${\gamma }_{\left(s\right)}=34$	9	7	2	2	Unstable
${\gamma }_{\left(t\right)}=-18$	9	7	4	1	Unstable

, we present a classification of the stability of the methods associated with the values of $\gamma$ presented in Figure 6, along with the number of special points and the period of the attracting orbits found for each $\gamma$.

4. Numerical Tests

In this section, numerical tests are conducted on some academical functions. Our goal is to determine whether methods that are stable in the previous analysis for quadratic polynomials perform better than unstable methods on non-polynomial functions. Subsequently, we compare the most effective methods on these functions with other well-known iterative methods in the field of numerical analysis, such as:

Newton’s method, the iterative expression of which is

$$\begin{array}{cc}\hfill x_{k+1}& =x_k-\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},k=0,1,\dots ,\hfill \end{array}$$

Chun’s method, defined in [9] as

$$\begin{array}{cc}\hfill y_k& =x_k-\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},\hfill \\ \hfill x_{k+1}& =y_k-\frac{f\left(x_k\right)+2f\left(y_k\right)}{f\left(x_k\right)}\frac{f\left(y_k\right)}{f^{\prime }\left(x_k\right)},k=0,1,\dots ,\hfill \end{array}$$

Ostrowski’s method, proposed in [11] and expressed as

$$\begin{array}{cc}\hfill y_k& =x_k-\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},\hfill \\ \hfill x_{k+1}& =y_k-\frac{f\left(x_k\right)}{f\left(x_k\right)-2f\left(y_k\right)}\frac{f\left(y_k\right)}{f^{\prime }\left(x_k\right)},k=0,1,\dots ,\hfill \end{array}$$

Kung-Traub’s method, defined in [12] with the iterative expression

$$\begin{array}{cc}\hfill y_k& =x_k-\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},\hfill \\ \hfill x_{k+1}& =y_k-\frac{f{\left(x_k\right)}^2}{{\left(f\left(x_k\right)-f\left(y_k\right)\right)}^2}\frac{f\left(y_k\right)}{f^{\prime }\left(x_k\right)},k=0,1,\dots ,\hfill \end{array}$$

and Jarratt’s method, constructed in [30] as

$$\begin{array}{cc}\hfill y_k& =x_k-\frac{2}{3}\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},\hfill \\ \hfill x_{k+1}& =x_k-\frac{1}{2}\left(\frac{3f^{\prime }\left(y_k\right)+f^{\prime }\left(x_k\right)}{3f^{\prime }\left(y_k\right)-f^{\prime }\left(x_k\right)}\right)\frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)},k=0,1,\dots .\hfill \end{array}$$

For our comparative analysis, we consider the best performing methods to be those iterative schemes that converge in the least number of iterations, where the estimation of the error is as small as possible, and where the theoretical order is closely approximated by the computational convergence order (ACOC) as defined by Cordero and Torregrosa in [31]:

$$ACOC=\frac{\frac{ln|x_{k+1}-x_k|}{|x_k-x_{k-1}|}}{\frac{ln|x_k-x_{k-1}|}{|x_{k-1}-x_{k-2}|}}.$$

The test functions and their zeros to be estimated are as follows:

$$\begin{array}{cc}{f}_1\left(x\right)=-2+\sqrt{x^2+2x+5}sin\left(x\right)-x^2+3,\hfill & \overline{x}\approx 2.33196765588396\hfill \\ f_2\left(x\right)=-1+{(x-1)}^3+e^x,\hfill & \overline{x}\approx 0.297570665698774\hfill \\ f_3\left(x\right)=arctan\left(x\right)+e^{x^3},\hfill & \overline{x}\approx -0.757044010769526\hfill \\ f_4\left(x\right)=x{e}^{x^2}-cos\left(x\right),\hfill & \overline{x}\approx 0.588401776500996\hfill \end{array}$$

We present numerical results obtained using a Thinkpad T480s laptop equipped with an eighth-generation Core i7 processor (Intel(R) Core(TM) i7-8650U CPU @ 1.90 GHz 2.11 GHz) and 16 GB of RAM. We used the academic version of MATLAB R2021b, employing variable-precision arithmetics with 200 digits.

Table 4. Number of iterations on test functions.

Parameter Values	${\mathit{f}}_{\mathbf{1}}$	${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$	${\mathit{f}}_{\mathbf{4}}$	Stability
${\gamma }_{\left(a\right)}=\frac{9}{8}$	4	5	4	7	Stable
${\gamma }_{\left(b\right)}=\frac{45}{4}$	4	100	4	100	Stable
${\gamma }_{\left(c\right)}=1$	4	5	4	6	Stable
${\gamma }_{\left(d\right)}=0$	4	5	4	6	Stable
${\gamma }_{\left(e\right)}=-1$	4	5	4	5	Stable
${\gamma }_{\left(f\right)}=-\frac{1}{2}$	4	4	4	5	Stable
${\gamma }_{\left(g\right)}=\frac{1}{2}$	4	5	4	6	Stable
${\gamma }_{\left(h\right)}=-5$	4	6	4	6	Stable
${\gamma }_{\left(i\right)}=10-10i$	4	100	4	100	Stable
${\gamma }_{\left(j\right)}=-10-10i$	4	64	4	100	Stable
${\gamma }_{\left(k\right)}=-16-12i$	4	37	4	100	Stable
${\gamma }_{\left(l\right)}=16$	4	100	4	100	Unstable
${\gamma }_{\left(m\right)}=20$	4	100	4	100	Unstable
${\gamma }_{\left(n\right)}=16$	4	100	4	100	Unstable
${\gamma }_{\left(o\right)}=-40$	4	59	5	100	Unstable
${\gamma }_{\left(p\right)}=10-30i$	4	100	4	100	Unstable
${\gamma }_{\left(q\right)}=-24$	4	100	4	31	Unstable
${\gamma }_{\left(r\right)}=-6+28i$	4	100	4	44	Unstable
${\gamma }_{\left(s\right)}=34$	4	100	4	100	Unstable
${\gamma }_{\left(t\right)}=-18$	4	100	4	11	Unstable

displays the number of iterations required for each proposed method to achieve the desired convergence for each of the functions when using the parameter values specified in Table 3. It can be observed that methods associated with values of $\gamma \ne \frac{45}{4}$, which are stable for real quadratic polynomials, demonstrate good performance on these test functions. However, methods associated with stable complex $\gamma$ values fail to converge in at least one of the test functions, as do methods associated with unstable $\gamma$ values. For $\gamma =\frac{45}{4}$, the associated method does not converge for either $f_2$ or $f_4$. It is worth noting that the color intensity in the dynamical plane associated with this value of $\gamma$ indicates the number of iterations required to ensure convergence. The latter is more intense than those associated with the other stable real values of $\gamma$, indicating that those converging in fewer iterations on quadratic polynomials are more reliable when applied to non-polynomial test functions (see Figure 6).

As shown in Table 4, seven of the methods associated with real values guarantee convergence within a maximum of nine iterations.

Table 5. Comparative analysis on $f_1\left(x\right)$.

Function			Method	Iter	Time	$\mathit{A}\mathit{C}\mathit{O}\mathit{C}$	$\mathbf{|}{\mathit{x}}_{\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{x}}_{\mathit{k}}\mathbf{|}$	$\mathbf{\left|}\mathit{f}\mathbf{\right(}{\mathit{x}}_{\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{\left)}\mathbf{\right|}$
			Newton	5	0.0713269	2	$8.68\times {10}^{-28}$	$2.11\times {10}^{-27}$
			Chun	5	0.0927903	2	$1.39\times {10}^{-27}$	$3.38\times {10}^{-27}$
			Ostrowski	5	0.0995647	2	$1.58\times {10}^{-27}$	$3.83\times {10}^{-27}$
$f_1\left(x\right)=\sqrt{x^2+2x+5}-2sin\left(x\right)-x^2+3$	$x_0=1.5$	$\overline{x}\approx 2.33196765588396$	Kung-Traub	5	0.1000585	2	$1.53\times {10}^{-27}$	$3.72\times {10}^{-27}$
			Jarratt	4	0.0862121	4	$1.44\times {10}^{-55}$	$3.50\times {10}^{-55}$
			${\gamma }_{\left(a\right)}$	4	0.0957585	4	$5.81\times {10}^{-57}$	$1.41\times {10}^{-56}$
			${\gamma }_{\left(c\right)}$	4	0.1063336	4	$2.11\times {10}^{-57}$	$5.11\times {10}^{-57}$
			${\gamma }_{\left(d\right)}$	4	0.0842142	4	$7.05\times {10}^{-58}$	$1.71\times {10}^{-57}$
			${\gamma }_{\left(e\right)}$	4	0.0909392	4	$2.56\times {10}^{-55}$	$6.21\times {10}^{-55}$
			${\gamma }_{\left(f\right)}$	4	0.0864402	4	$3.05\times {10}^{-56}$	$7.41\times {10}^{-56}$
			${\gamma }_{\left(g\right)}$	4	0.0856559	4	$1.99\times {10}^{-62}$	$4.82\times {10}^{-62}$
			${\gamma }_{\left(h\right)}$	4	0.0971327	4	$2.00\times {10}^{-52}$	$4.85\times {10}^{-52}$

,

Table 6. Comparative analysis on $f_2\left(x\right)$.

Function			Method	Iter	Time	$\mathit{A}\mathit{C}\mathit{O}\mathit{C}$	$\mathbf{|}{\mathit{x}}_{\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{x}}_{\mathit{k}}\mathbf{|}$	$\mathbf{\left|}\mathit{f}\mathbf{\right(}{\mathit{x}}_{\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{\left)}\mathbf{\right|}$
$f_2\left(x\right)={(x-1)}^3-1+e^x$	$x_0=1.5$	$\overline{x}\approx 0.297570665698774$	Newton	7	0.0590956	2	$1.03\times {10}^{-34}$	$2.93\times {10}^{-34}$
			Chun	6	0.0674999	2	$1.05\times {10}^{-27}$	$2.96\times {10}^{-27}$
			Ostrowski	8	0.1065735	2	$4.74\times {10}^{-30}$	$1.34\times {10}^{-29}$
			Kung-Traub	7	0.079534	2	$1.61\times {10}^{-24}$	$4.54\times {10}^{-24}$
			Jarratt	5	0.0657351	4	$2.29\times {10}^{-73}$	$6.48\times {10}^{-73}$
			${\gamma }_{\left(a\right)}$	5	0.0744865	4	$1.70\times {10}^{-53}$	$4.82\times {10}^{-53}$
			${\gamma }_{\left(c\right)}$	5	0.0720414	4	$2.82\times {10}^{-48}$	$7.98\times {10}^{-48}$
			${\gamma }_{\left(d\right)}$	5	0.071041	4	$2.10\times {10}^{-71}$	$5.93\times {10}^{-71}$
			${\gamma }_{\left(e\right)}$	5	0.069821	4	$1.66\times {10}^{-75}$	$4.68\times {10}^{-75}$
			${\gamma }_{\left(f\right)}$	4	0.0596417	4	$3.96\times {10}^{-38}$	$1.12\times {10}^{-37}$
			${\gamma }_{\left(g\right)}$	5	0.0698009	4	$6.62\times {10}^{-51}$	$1.87\times {10}^{-50}$
			${\gamma }_{\left(h\right)}$	6	0.1015708	4	$6.70\times {10}^{-33}$	$1.89\times {10}^{-32}$

,

Table 7. Comparative analysis on $f_3\left(x\right)$.

Function			Method	Iter	Time	$\mathit{A}\mathit{C}\mathit{O}\mathit{C}$	$\mathbf{|}{\mathit{x}}_{\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{x}}_{\mathit{k}}\mathbf{|}$	$\mathbf{\left|}\mathit{f}\mathbf{\right(}{\mathit{x}}_{\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{\left)}\mathbf{\right|}$
			Newton	5	0.0536364	2	$2.94\times {10}^{-20}$	$5.15\times {10}^{-20}$
			Chun	6	0.0789598	2	$3.14\times {10}^{-35}$	$5.49\times {10}^{-35}$
			Ostrowski	5	0.1089681	2	$3.26\times {10}^{-19}$	$5.70\times {10}^{-19}$
$f_3\left(x\right)=arctan\left(x\right)+e^{x^3}$	$x_0=-0.5$	$\overline{x}\approx -0.757044010769526$	Kung-Traub	6	0.0912986	2	$7.53\times {10}^{-38}$	$1.32\times {10}^{-37}$
			Jarratt	4	0.0626825	4	$2.81\times {10}^{-58}$	$4.92\times {10}^{-58}$
			${\gamma }_{\left(a\right)}$	4	0.0754623	4	$5.40\times {10}^{-44}$	$9.46\times {10}^{-44}$
			${\gamma }_{\left(c\right)}$	4	0.0704758	4	$2.02\times {10}^{-44}$	$3.53\times {10}^{-44}$
			${\gamma }_{\left(d\right)}$	4	0.0670903	4	$3.62\times {10}^{-49}$	$6.33\times {10}^{-49}$
			${\gamma }_{\left(e\right)}$	4	0.0725264	4	$1.51\times {10}^{-66}$	$2.64\times {10}^{-66}$
			${\gamma }_{\left(f\right)}$	4	0.0794614	4	$1.46\times {10}^{-53}$	$2.56\times {10}^{-53}$
			${\gamma }_{\left(g\right)}$	4	0.0924925	4	$2.00\times {10}^{-46}$	$3.50\times {10}^{-46}$
			${\gamma }_{\left(h\right)}$	4	0.0739391	4	$8.47\times {10}^{-49}$	$1.48\times {10}^{-48}$

and

Table 8. Comparative analysis on $f_4\left(x\right)$.

Function			Method	Iter	Time	$\mathit{A}\mathit{C}\mathit{O}\mathit{C}$	$\mathbf{|}{\mathit{x}}_{\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathit{x}}_{\mathit{k}}\mathbf{|}$	$\mathbf{\left|}\mathit{f}\mathbf{\right(}{\mathit{x}}_{\mathit{k}\mathbf{+}\mathbf{1}}\mathbf{\left)}\mathbf{\right|}$
$f_4\left(x\right)=x{e}^{x^2}-cos\left(x\right)$	$x_0=1.5$	$\overline{x}\approx 0.588401776500996$	Newton	9	0.0776262	2	$4.38\times {10}^{-26}$	$1.29\times {10}^{-25}$
			Chun	7	0.1032848	2	$1.02\times {10}^{-21}$	$3.01\times {10}^{-21}$
			Ostrowski	7	0.1054047	2	$1.49\times {10}^{-23}$	$4.39\times {10}^{-23}$
			Kung-Traub	7	0.1014812	2	$3.53\times {10}^{-22}$	$1.04\times {10}^{-21}$
			Jarratt	5	0.0895486	4	$1.04\times {10}^{-46}$	$3.05\times {10}^{-46}$
			${\gamma }_{\left(a\right)}$	7	0.1140201	4	$3.56\times {10}^{-65}$	$1.05\times {10}^{-64}$
			${\gamma }_{\left(c\right)}$	6	0.0925447	4	$1.16\times {10}^{-19}$	$3.43\times {10}^{-19}$
			${\gamma }_{\left(d\right)}$	6	0.1102584	4	$5.51\times {10}^{-51}$	$1.62\times {10}^{-50}$
			${\gamma }_{\left(e\right)}$	5	0.0844069	4	$1.33\times {10}^{-33}$	$3.92\times {10}^{-33}$
			${\gamma }_{\left(f\right)}$	5	0.0966304	4	$1.061\times {10}^{-20}$	$3.13\times {10}^{-20}$
			${\gamma }_{\left(g\right)}$	6	0.1174171	4	$1.94\times {10}^{-32}$	$5.72\times {10}^{-32}$
			${\gamma }_{\left(h\right)}$	6	0.1047413	4	$1.04\times {10}^{-46}$	$3.08\times {10}^{-46}$

present the results obtained when applying Newton, Chun, Ostrowski, Kung and Traub, Jarratt, and the seven proposed methods. These tables provide information about the function to which each iterative method is applied, the initial estimate used ($x_0$), the target root ($\overline{x}$) to which the methods are expected to converge within the stopping criterion $\left|x_{k+1}-x_k\right|+\left|f\left(x_{k+1}\right)\right|<{10}^{-18}$, the number of iterations (Iter) required for convergence, approximate order of computational convergence (ACOC), execution time (Time), estimation of the error in the last iteration ($\left|x_{k+1}-x_k\right|$ and $\left|f\left(x_{k+1}\right)\right|$), and the approximate solution $\overline{x}$.

The results suggest that the methods associated with $\gamma$ values demonstrate competitive performance compared to Kung and Traub, Newton, Chun, Ostrowski, and Jarratt based on our measurement parameters.

5. Conclusions

In this study, we have established a set of conditions that weight functions must satisfy in order to ensure that the resulting iterative scheme has a convergence order of at least 4. Furthermore, a generalization of known uniparametric families of fourth-order optimal iterative methods has been presented and criteria for selecting the best subfamilies of these uniparametric families have been established. A dynamical analysis allowed us to identify stable members within the subfamily that exhibit good performance on quadratic polynomials; however, elements with pathological behavior were observed as well, and these should be avoided in numerical applications.

Furthermore, the performance of stable members of the subfamily was evaluated in comparison to unstable members when applied to non-polynomial functions. The results highlight the importance of stability in quadratic polynomials and its positive influence on the overall performance of iterative methods in various contexts.

Finally, stable methods within the subfamily that compete favorably with widely used iterative schemes in the literature have been identified. Through academical examples and detailed comparisons, it is shown that the proposed methods represent viable and effective alternatives for solving nonlinear equations.