On the Interpolating Family of Distributions
Abstract
:1. Introduction
2. A Technical Lemma
3. Moments of the IF Random Variable
4. Entropies
5. Estimation
6. Simulation Study
- (a)
- Set , , , , and ;
- (b)
- (c)
- (d)
- Compute the biases asfor ;
- (e)
- Compute the mean squared errors asfor ;
- (f)
- Repeat steps (b) to (e) for .
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sinner, C.; Dominicy, Y.; Trufin, J.; Waterschoot, W.; Weber, P.; Ley, C. From Pareto to Weibull—A constructive review of distributions on R+. Int. Stat. Rev. 2023, 91, 35–54. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wright, E.M. The asymptotic expansion of the generalized hypergeometric function. J. Lond. Math. Soc. 1935, 10, 286–293. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Rényi, A. On measures of information and entropy. In Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability; Neyman, J., Ed.; University of California Press: Berkeley, CA, USA, 1960; Volume 1, pp. 547–561. [Google Scholar]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Ley, C.; Babic, S.; Craens, D. Flexible models for complex data with applications. Annu. Rev. Stat. Appl. 2021, 8, 369–391. [Google Scholar] [CrossRef]
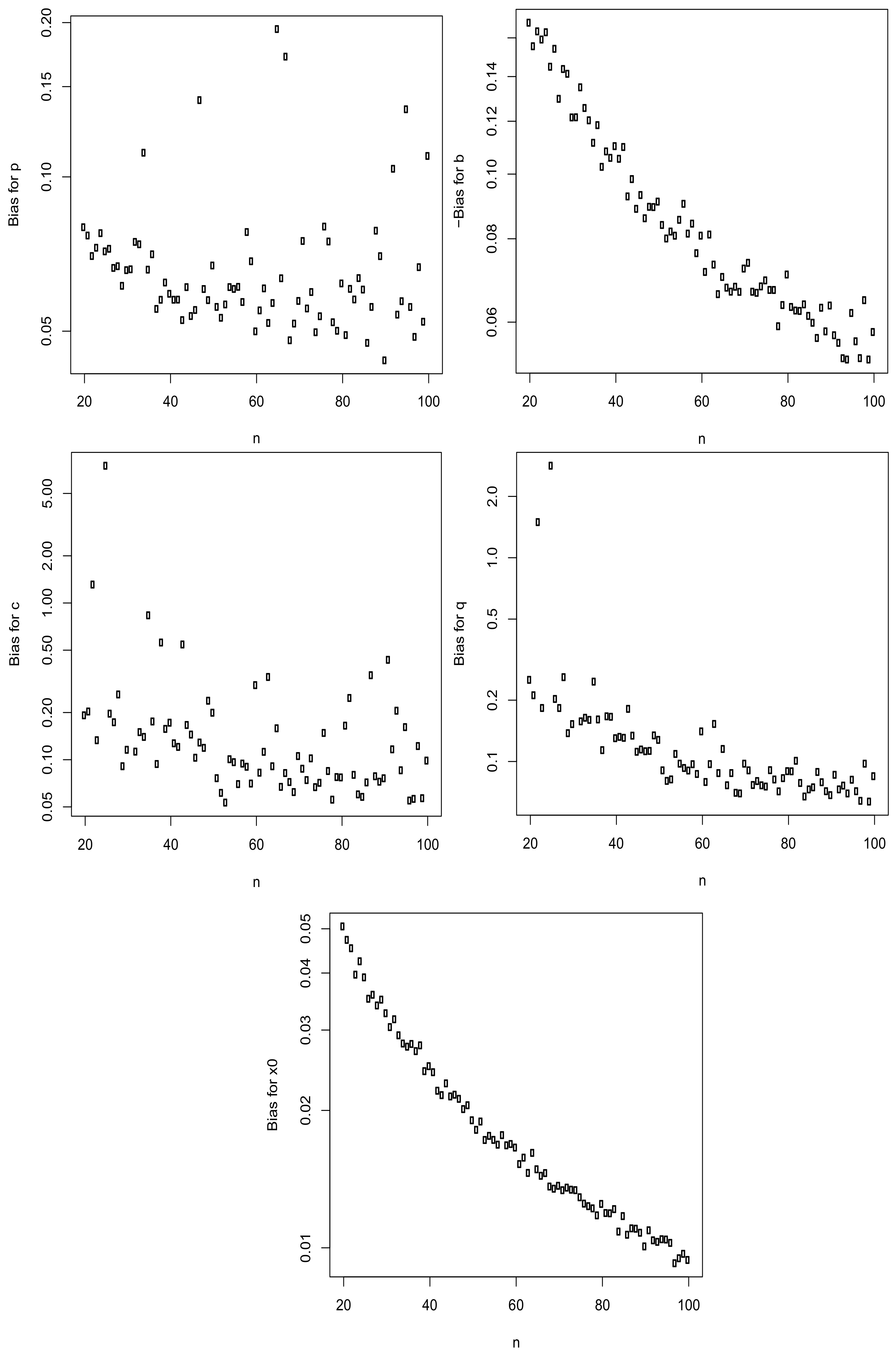

| n | Bias for | Bias for | Bias for | Bias for | Bias for |
|---|---|---|---|---|---|
| 20 | 0.080 | −0.169 | 0.192 | 0.251 | 0.051 |
| 21 | 0.077 | −0.155 | 0.203 | 0.211 | 0.047 |
| 22 | 0.070 | −0.164 | 1.308 | 1.494 | 0.045 |
| 23 | 0.073 | −0.159 | 0.133 | 0.183 | 0.040 |
| 24 | 0.078 | −0.163 | 2.497 | 4.725 | 0.042 |
| 25 | 0.072 | −0.145 | 7.497 | 2.826 | 0.039 |
| 26 | 0.072 | −0.154 | 0.196 | 0.202 | 0.035 |
| 27 | 0.066 | −0.130 | 0.173 | 0.183 | 0.036 |
| 28 | 0.067 | −0.144 | 0.260 | 0.259 | 0.034 |
| 29 | 0.061 | −0.141 | 0.091 | 0.137 | 0.035 |
| 30 | 0.066 | −0.122 | 0.115 | 0.152 | 0.033 |
| 31 | 0.066 | −0.122 | 4.587 | 3.811 | 0.030 |
| 32 | 0.075 | −0.135 | 0.112 | 0.157 | 0.032 |
| 33 | 0.074 | −0.126 | 0.150 | 0.164 | 0.029 |
| 34 | 0.111 | −0.120 | 0.140 | 0.160 | 0.028 |
| 35 | 0.066 | −0.111 | 0.833 | 0.246 | 0.028 |
| 36 | 0.071 | −0.118 | 0.175 | 0.161 | 0.028 |
| 37 | 0.055 | −0.102 | 0.094 | 0.114 | 0.027 |
| 38 | 0.058 | −0.108 | 0.558 | 0.166 | 0.028 |
| 39 | 0.062 | −0.106 | 0.157 | 0.166 | 0.024 |
| 40 | 0.059 | −0.110 | 0.172 | 0.130 | 0.025 |
| 41 | 0.058 | −0.105 | 0.127 | 0.132 | 0.024 |
| 42 | 0.058 | −0.110 | 0.120 | 0.130 | 0.022 |
| 43 | 0.053 | −0.093 | 0.543 | 0.181 | 0.022 |
| 44 | 0.061 | −0.098 | 0.166 | 0.134 | 0.023 |
| 45 | 0.053 | −0.089 | 0.144 | 0.111 | 0.021 |
| 46 | 0.055 | −0.093 | 0.103 | 0.114 | 0.022 |
| 47 | 0.141 | −0.086 | 0.128 | 0.112 | 0.021 |
| 48 | 0.060 | −0.089 | 0.119 | 0.113 | 0.020 |
| 49 | 0.057 | −0.089 | 0.237 | 0.134 | 0.021 |
| 50 | 0.067 | −0.091 | 0.199 | 0.127 | 0.019 |
| 51 | 0.056 | −0.084 | 0.076 | 0.090 | 0.018 |
| 52 | 0.053 | −0.080 | 0.061 | 0.080 | 0.019 |
| 53 | 0.056 | −0.082 | 0.053 | 0.082 | 0.017 |
| 54 | 0.061 | −0.081 | 0.101 | 0.109 | 0.018 |
| 55 | 0.060 | −0.085 | 0.096 | 0.097 | 0.017 |
| 56 | 0.061 | −0.090 | 0.070 | 0.093 | 0.017 |
| 57 | 0.057 | −0.081 | 0.094 | 0.090 | 0.018 |
| 58 | 0.078 | −0.084 | 0.090 | 0.097 | 0.017 |
| 59 | 0.068 | −0.076 | 0.070 | 0.087 | 0.017 |
| 60 | 0.050 | −0.081 | 0.299 | 0.140 | 0.017 |
| 61 | 0.055 | −0.071 | 0.083 | 0.079 | 0.015 |
| 62 | 0.061 | −0.081 | 0.112 | 0.097 | 0.016 |
| 63 | 0.052 | −0.073 | 0.337 | 0.153 | 0.015 |
| 64 | 0.057 | −0.066 | 0.091 | 0.088 | 0.016 |
| 65 | 0.194 | −0.070 | 0.158 | 0.115 | 0.015 |
| 66 | 0.063 | −0.068 | 0.067 | 0.076 | 0.014 |
| 67 | 0.172 | −0.067 | 0.082 | 0.088 | 0.015 |
| 68 | 0.048 | −0.068 | 0.072 | 0.070 | 0.014 |
| 69 | 0.052 | −0.067 | 0.062 | 0.070 | 0.013 |
| 70 | 0.057 | −0.072 | 0.105 | 0.097 | 0.014 |
| 71 | 0.075 | −0.074 | 0.087 | 0.090 | 0.013 |
| 72 | 0.055 | −0.067 | 0.074 | 0.077 | 0.014 |
| 73 | 0.060 | −0.066 | 0.102 | 0.080 | 0.013 |
| 74 | 0.050 | −0.068 | 0.067 | 0.076 | 0.013 |
| 75 | 0.053 | −0.069 | 0.071 | 0.075 | 0.013 |
| 76 | 0.080 | −0.067 | 0.148 | 0.091 | 0.012 |
| 77 | 0.075 | −0.067 | 0.085 | 0.081 | 0.012 |
| 78 | 0.052 | −0.059 | 0.055 | 0.071 | 0.012 |
| 79 | 0.050 | −0.064 | 0.077 | 0.083 | 0.012 |
| 80 | 0.062 | −0.071 | 0.077 | 0.090 | 0.012 |
| 81 | 0.049 | −0.063 | 0.165 | 0.089 | 0.012 |
| 82 | 0.060 | −0.062 | 0.247 | 0.101 | 0.012 |
| 83 | 0.058 | −0.062 | 0.080 | 0.078 | 0.012 |
| 84 | 0.063 | −0.064 | 0.060 | 0.067 | 0.011 |
| 85 | 0.060 | −0.061 | 0.058 | 0.073 | 0.012 |
| 86 | 0.047 | −0.060 | 0.071 | 0.075 | 0.011 |
| 87 | 0.056 | −0.057 | 0.345 | 0.089 | 0.011 |
| 88 | 0.078 | −0.063 | 0.078 | 0.079 | 0.011 |
| 89 | 0.070 | −0.058 | 0.072 | 0.071 | 0.011 |
| 90 | 0.044 | −0.064 | 0.076 | 0.068 | 0.010 |
| 91 | 0.940 | −0.057 | 0.433 | 0.086 | 0.011 |
| 92 | 0.104 | −0.056 | 0.116 | 0.073 | 0.010 |
| 93 | 0.054 | −0.053 | 0.205 | 0.076 | 0.010 |
| 94 | 0.057 | −0.053 | 0.085 | 0.070 | 0.010 |
| 95 | 0.135 | −0.062 | 0.161 | 0.081 | 0.010 |
| 96 | 0.056 | −0.056 | 0.055 | 0.071 | 0.010 |
| 97 | 0.049 | −0.053 | 0.056 | 0.064 | 0.009 |
| 98 | 0.067 | −0.065 | 0.122 | 0.097 | 0.009 |
| 99 | 0.052 | −0.053 | 0.057 | 0.063 | 0.010 |
| 100 | 0.110 | −0.058 | 0.099 | 0.085 | 0.009 |
| n | MSE for | MSE for | MSE for | MSE for | MSE for |
|---|---|---|---|---|---|
| 20 | 0.029 | 0.079 | 1.514 | 0.758 | 0.005 |
| 21 | 0.067 | 0.079 | 1.934 | 0.404 | 0.005 |
| 22 | 0.015 | 0.073 | 1223.421 | 1613.096 | 0.004 |
| 23 | 0.021 | 0.068 | 1.575 | 0.317 | 0.003 |
| 24 | 0.023 | 0.073 | 6.000 | 2.000 | 0.004 |
| 25 | 0.020 | 0.062 | 54,678.407 | 7090.633 | 0.003 |
| 26 | 0.017 | 0.065 | 2.425 | 0.647 | 0.003 |
| 27 | 0.021 | 0.066 | 8.314 | 1.291 | 0.003 |
| 28 | 0.018 | 0.062 | 12.663 | 5.791 | 0.002 |
| 29 | 0.012 | 0.058 | 0.309 | 0.129 | 0.003 |
| 30 | 0.019 | 0.053 | 0.596 | 0.276 | 0.002 |
| 31 | 0.018 | 0.051 | 2.000 | 2.000 | 0.002 |
| 32 | 0.102 | 0.053 | 0.321 | 0.160 | 0.002 |
| 33 | 0.094 | 0.055 | 0.849 | 0.198 | 0.002 |
| 34 | 1.597 | 0.050 | 1.045 | 0.240 | 0.002 |
| 35 | 0.081 | 0.050 | 470.452 | 8.305 | 0.002 |
| 36 | 0.119 | 0.046 | 4.209 | 0.510 | 0.002 |
| 37 | 0.012 | 0.043 | 0.225 | 0.095 | 0.002 |
| 38 | 0.016 | 0.037 | 188.949 | 0.990 | 0.002 |
| 39 | 0.016 | 0.046 | 1.936 | 0.674 | 0.001 |
| 40 | 0.014 | 0.038 | 5.865 | 0.366 | 0.001 |
| 41 | 0.012 | 0.040 | 1.112 | 0.253 | 0.001 |
| 42 | 0.029 | 0.034 | 0.406 | 0.147 | 0.001 |
| 43 | 0.011 | 0.035 | 89.766 | 1.348 | 0.001 |
| 44 | 0.021 | 0.033 | 4.228 | 0.207 | 0.001 |
| 45 | 0.011 | 0.037 | 3.408 | 0.173 | 0.001 |
| 46 | 0.013 | 0.033 | 0.814 | 0.133 | 0.001 |
| 47 | 7.915 | 0.036 | 2.364 | 0.156 | 0.001 |
| 48 | 0.023 | 0.031 | 0.600 | 0.146 | 0.001 |
| 49 | 0.021 | 0.031 | 19.995 | 0.978 | 0.001 |
| 50 | 0.187 | 0.032 | 4.219 | 0.315 | 0.001 |
| 51 | 0.022 | 0.027 | 0.199 | 0.081 | 0.001 |
| 52 | 0.012 | 0.027 | 0.115 | 0.057 | 0.001 |
| 53 | 0.015 | 0.029 | 0.079 | 0.045 | 0.001 |
| 54 | 0.092 | 0.022 | 0.337 | 0.097 | 0.001 |
| 55 | 0.031 | 0.027 | 0.402 | 0.106 | 0.001 |
| 56 | 0.026 | 0.028 | 0.151 | 0.064 | 0.001 |
| 57 | 0.019 | 0.025 | 0.518 | 0.147 | 0.001 |
| 58 | 0.301 | 0.024 | 0.334 | 0.107 | 0.001 |
| 59 | 0.175 | 0.025 | 0.186 | 0.069 | 0.001 |
| 60 | 0.015 | 0.021 | 54.090 | 2.589 | 0.001 |
| 61 | 0.029 | 0.022 | 0.322 | 0.066 | 0.000 |
| 62 | 0.122 | 0.025 | 1.277 | 0.121 | 0.001 |
| 63 | 0.026 | 0.022 | 65.419 | 3.676 | 0.000 |
| 64 | 0.165 | 0.024 | 0.226 | 0.085 | 0.001 |
| 65 | 7.539 | 0.022 | 3.725 | 0.178 | 0.000 |
| 66 | 0.156 | 0.021 | 0.123 | 0.052 | 0.000 |
| 67 | 11.188 | 0.022 | 0.399 | 0.097 | 0.000 |
| 68 | 0.013 | 0.021 | 0.120 | 0.043 | 0.000 |
| 69 | 0.016 | 0.022 | 0.143 | 0.047 | 0.000 |
| 70 | 0.058 | 0.021 | 0.371 | 0.109 | 0.000 |
| 71 | 0.437 | 0.018 | 0.228 | 0.079 | 0.000 |
| 72 | 0.041 | 0.018 | 0.119 | 0.045 | 0.000 |
| 73 | 0.213 | 0.019 | 0.587 | 0.114 | 0.000 |
| 74 | 0.016 | 0.017 | 0.139 | 0.053 | 0.000 |
| 75 | 0.024 | 0.018 | 0.169 | 0.049 | 0.000 |
| 76 | 0.637 | 0.017 | 3.585 | 0.189 | 0.000 |
| 77 | 0.264 | 0.018 | 0.299 | 0.085 | 0.000 |
| 78 | 0.039 | 0.019 | 0.138 | 0.054 | 0.000 |
| 79 | 0.020 | 0.015 | 0.233 | 0.070 | 0.000 |
| 80 | 0.058 | 0.017 | 0.153 | 0.062 | 0.000 |
| 81 | 0.014 | 0.018 | 8.413 | 0.316 | 0.000 |
| 82 | 0.105 | 0.017 | 19.012 | 0.214 | 0.000 |
| 83 | 0.038 | 0.015 | 0.389 | 0.072 | 0.000 |
| 84 | 0.176 | 0.016 | 0.062 | 0.040 | 0.000 |
| 85 | 0.176 | 0.015 | 0.104 | 0.048 | 0.000 |
| 86 | 0.013 | 0.015 | 0.165 | 0.050 | 0.000 |
| 87 | 0.029 | 0.016 | 74.413 | 0.456 | 0.000 |
| 88 | 0.446 | 0.016 | 0.144 | 0.061 | 0.000 |
| 89 | 0.547 | 0.014 | 0.126 | 0.058 | 0.000 |
| 90 | 0.012 | 0.014 | 0.297 | 0.052 | 0.000 |
| 91 | 759.774 | 0.015 | 0.402 | 0.213 | 0.000 |
| 92 | 1.339 | 0.016 | 2.688 | 0.100 | 0.000 |
| 93 | 0.064 | 0.014 | 2.236 | 0.226 | 0.000 |
| 94 | 0.053 | 0.016 | 0.179 | 0.066 | 0.000 |
| 95 | 3.862 | 0.015 | 7.381 | 0.173 | 0.000 |
| 96 | 0.077 | 0.014 | 0.083 | 0.043 | 0.000 |
| 97 | 0.020 | 0.013 | 0.102 | 0.034 | 0.000 |
| 98 | 0.216 | 0.014 | 0.542 | 0.089 | 0.000 |
| 99 | 0.029 | 0.013 | 0.119 | 0.044 | 0.000 |
| 100 | 1.882 | 0.014 | 0.331 | 0.099 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadarajah, S.; Okorie, I.E. On the Interpolating Family of Distributions. Axioms 2024, 13, 70. https://doi.org/10.3390/axioms13010070
Nadarajah S, Okorie IE. On the Interpolating Family of Distributions. Axioms. 2024; 13(1):70. https://doi.org/10.3390/axioms13010070
Chicago/Turabian StyleNadarajah, Saralees, and Idika E. Okorie. 2024. "On the Interpolating Family of Distributions" Axioms 13, no. 1: 70. https://doi.org/10.3390/axioms13010070





