Computational Study of Shocked V-Shaped N2/SF6 Interface across Varying Mach Numbers
Abstract
1. Introduction
2. Problem Setup and Governing Equations
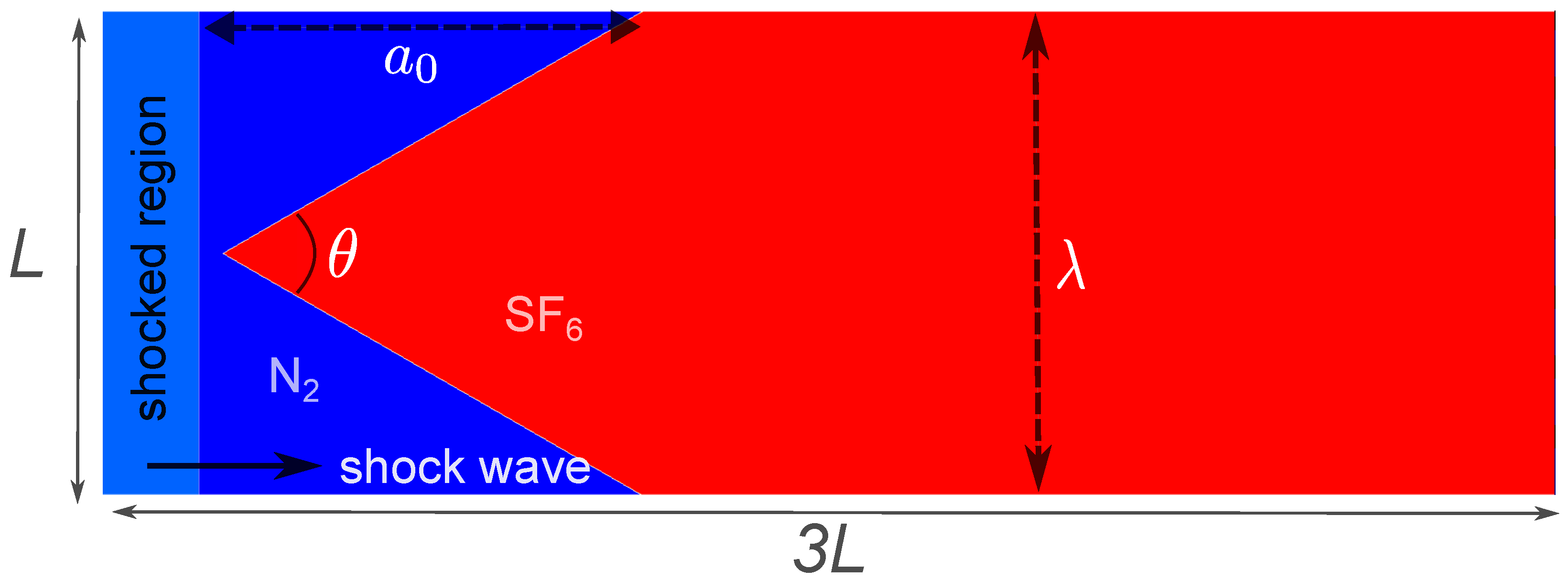
2.1. Problem Setup
2.2. Governing Equations
2.3. Initial Conditions
3. Numerical Method, Validation, and Mesh Convergence
3.1. Numerical Method
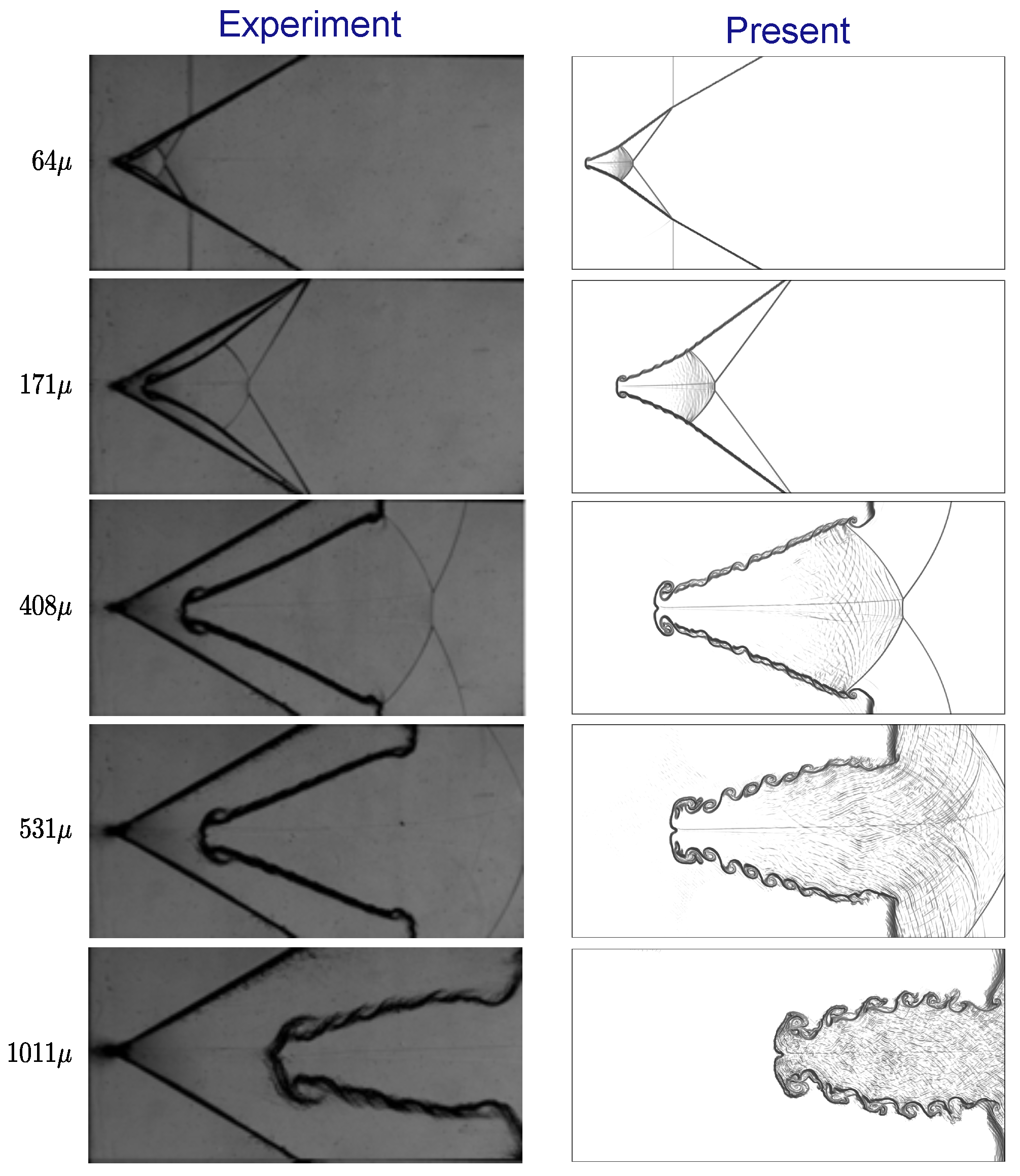
3.2. Validation
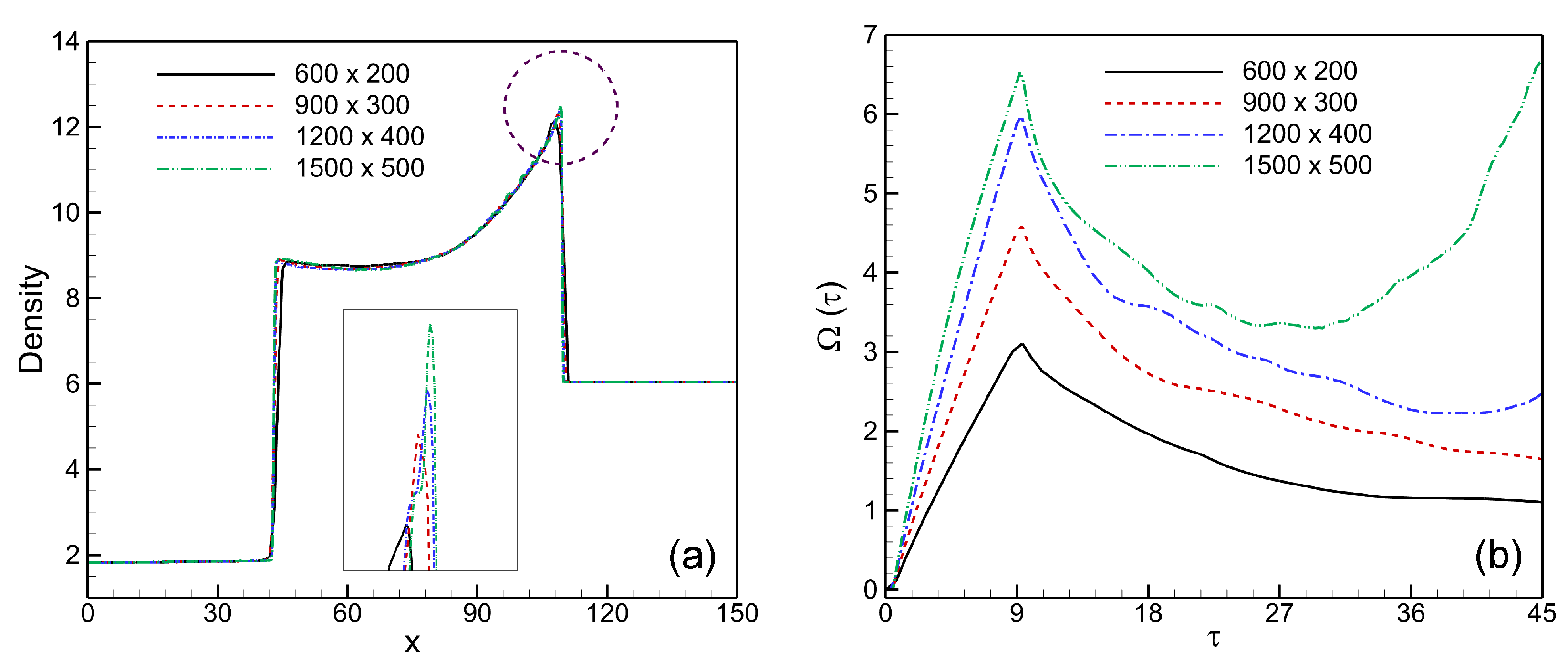
3.3. Mesh Convergence
3.4. Error Estimation
4. Results and Discussion: Mach Number Effects on V-Shaped / Interface
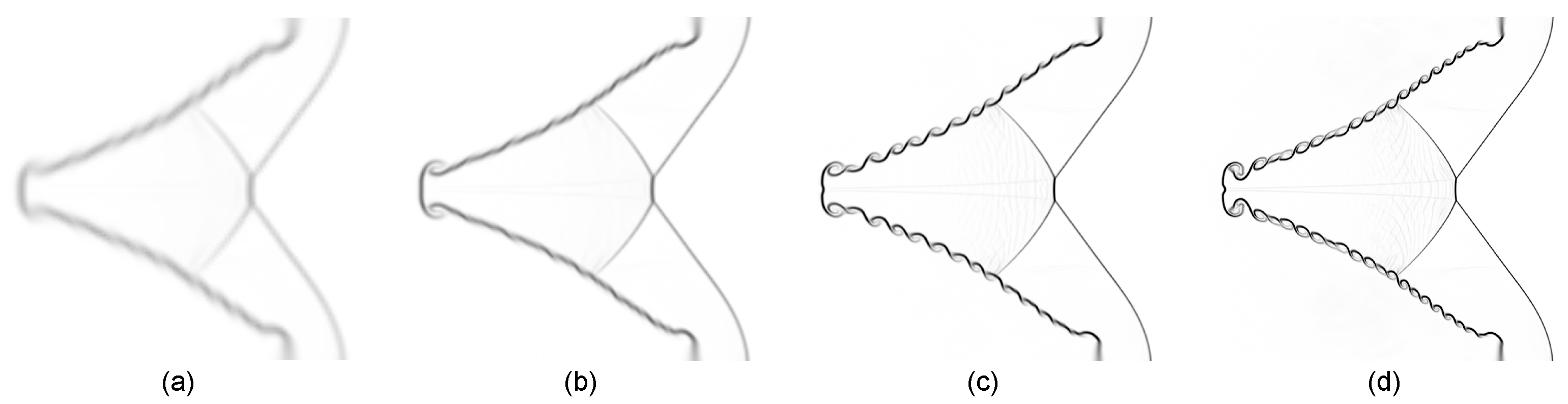
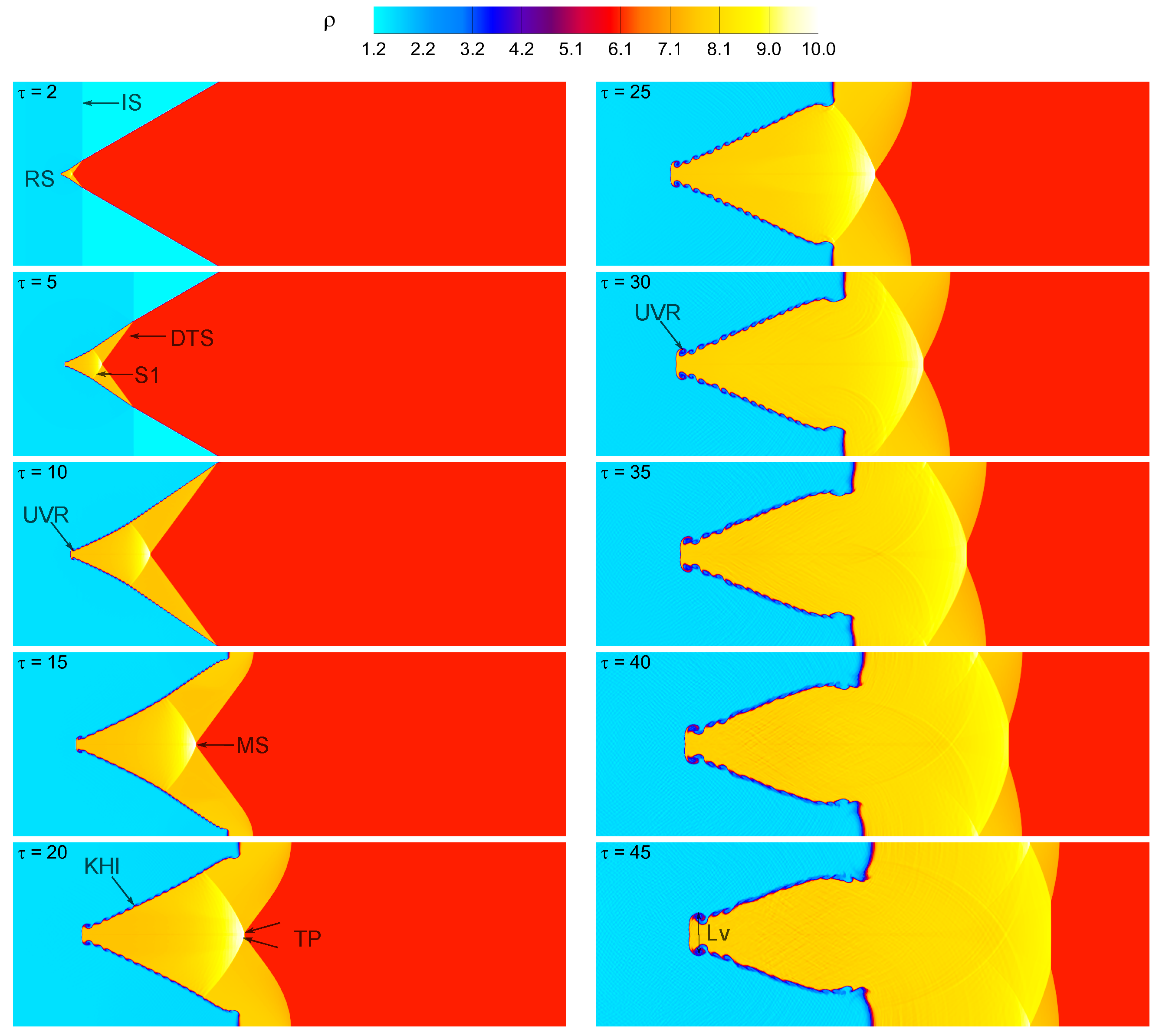
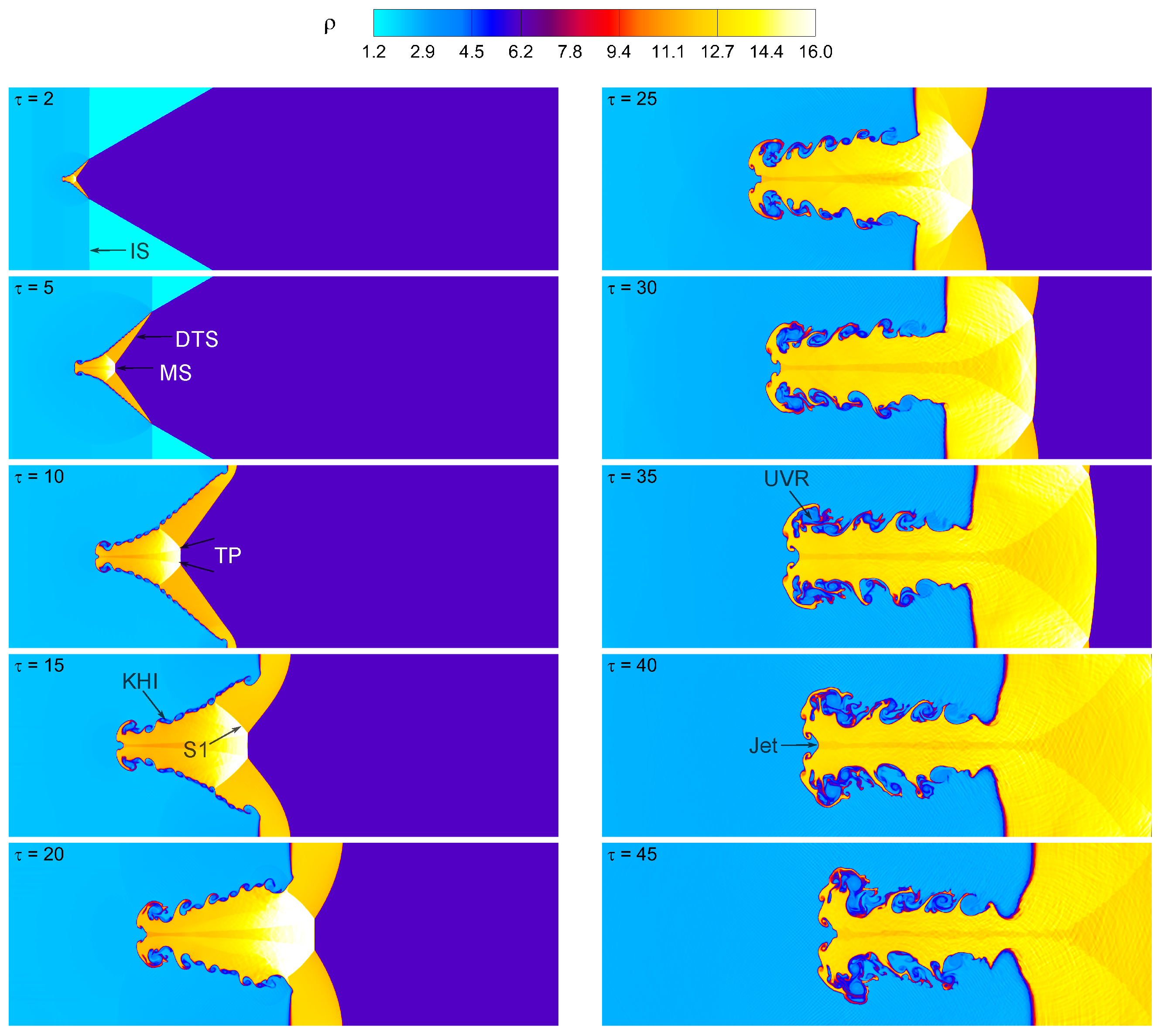
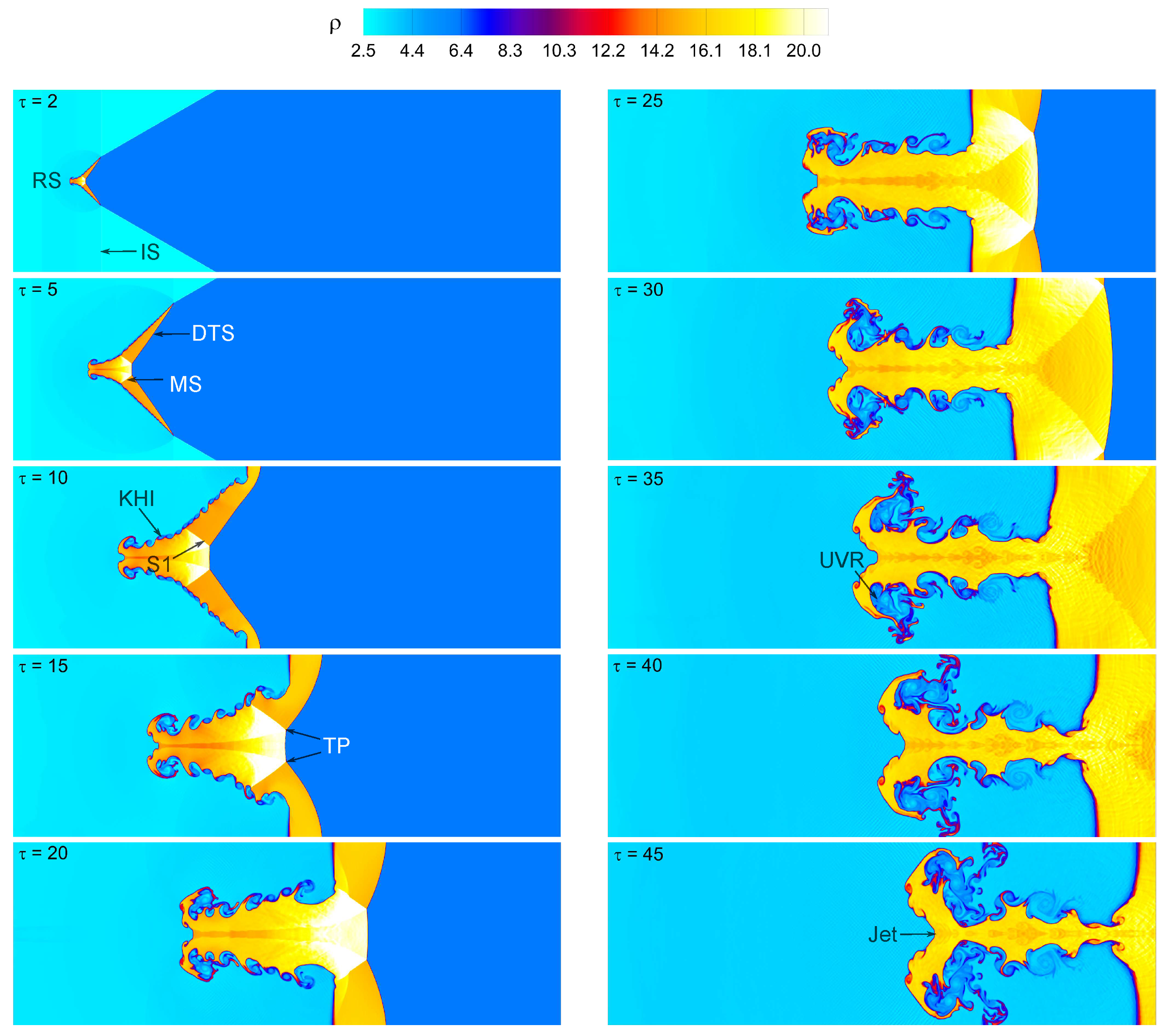
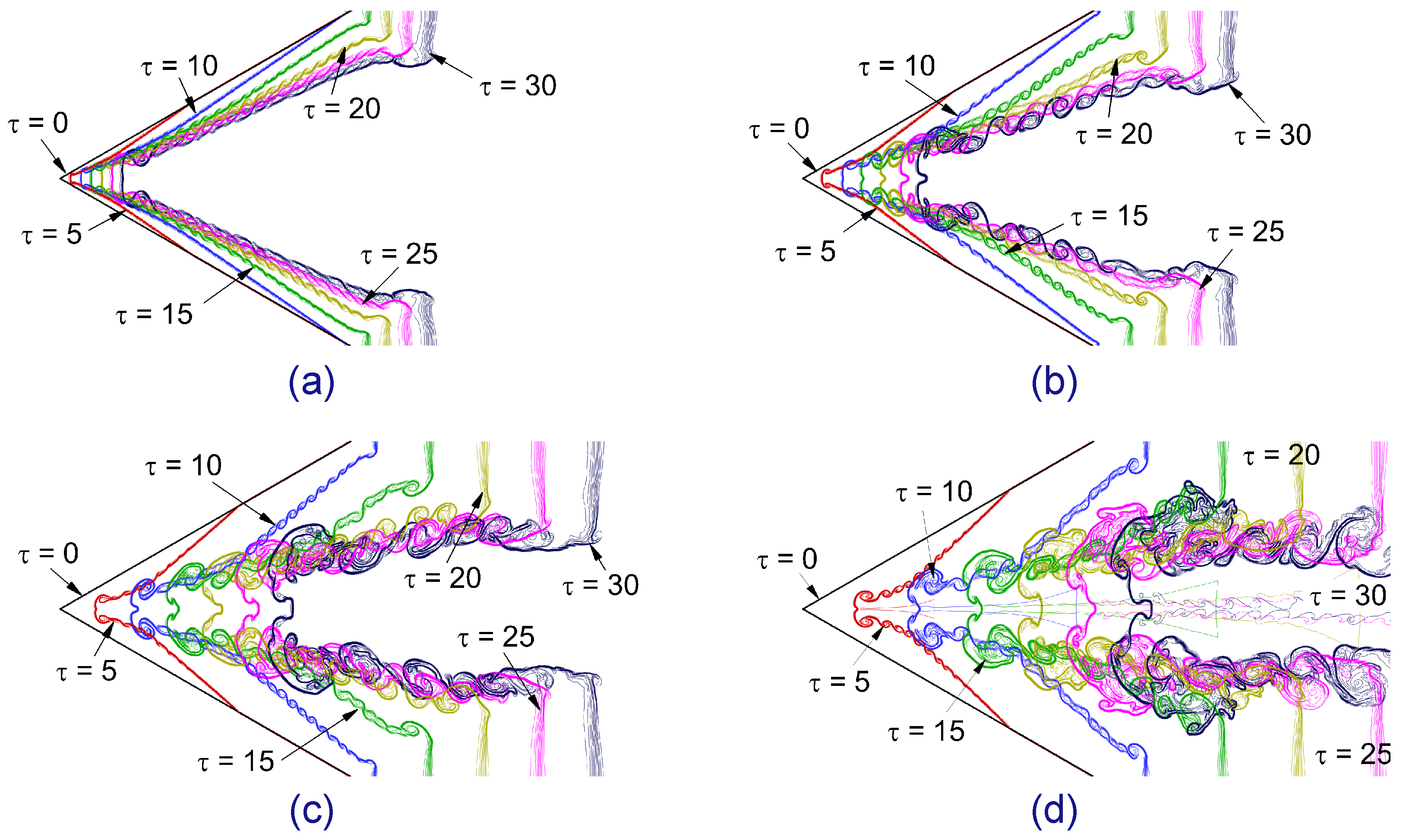
4.1. Visualization of Flow Fields and Wave Patterns
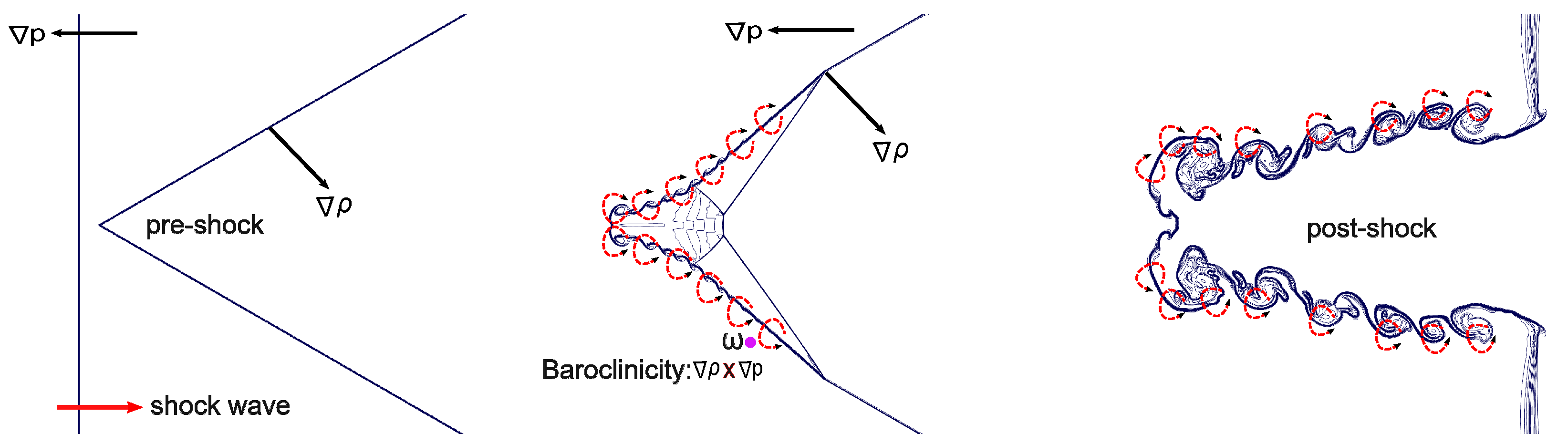
4.2. Vorticity Generation Mechanism
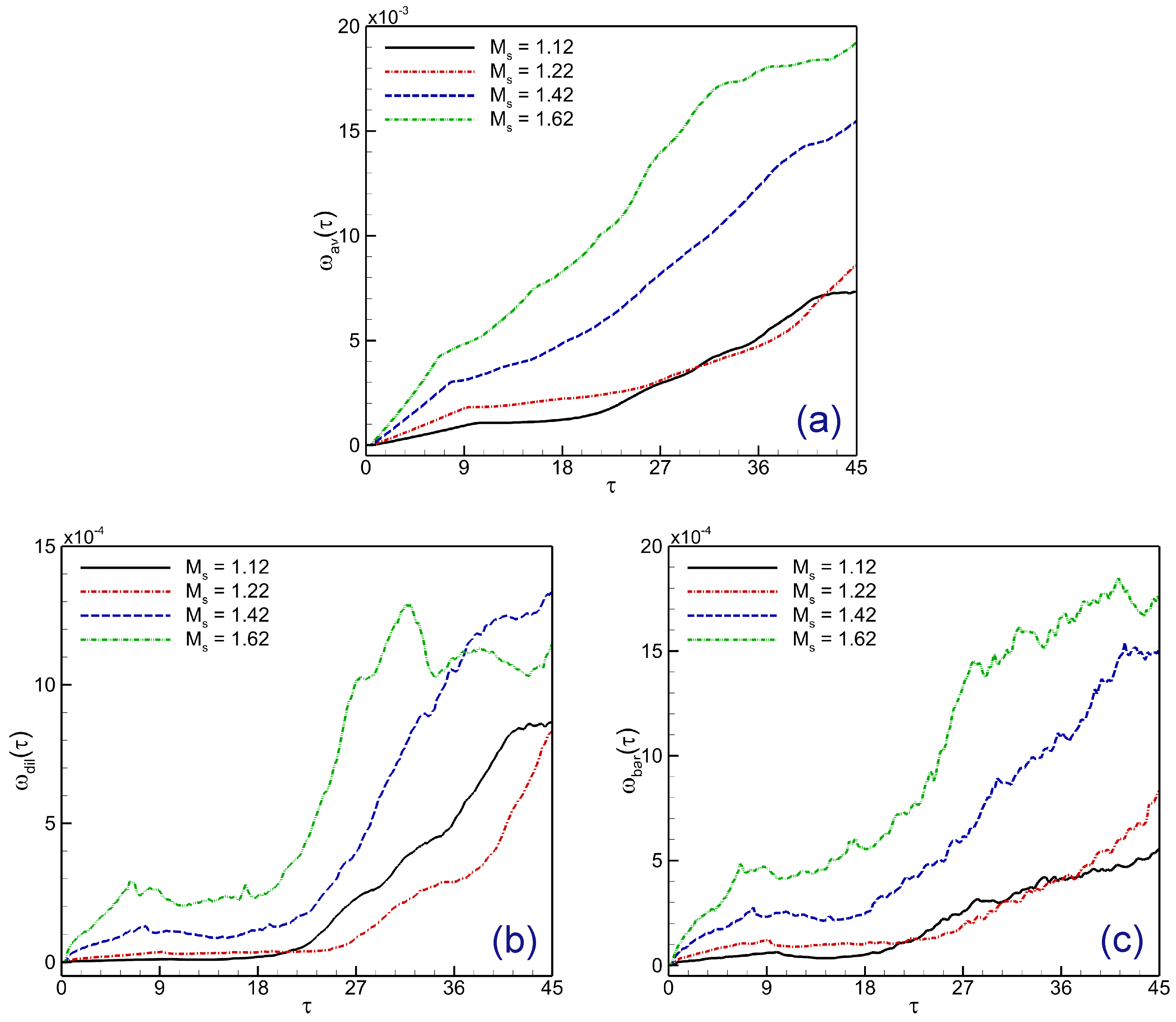
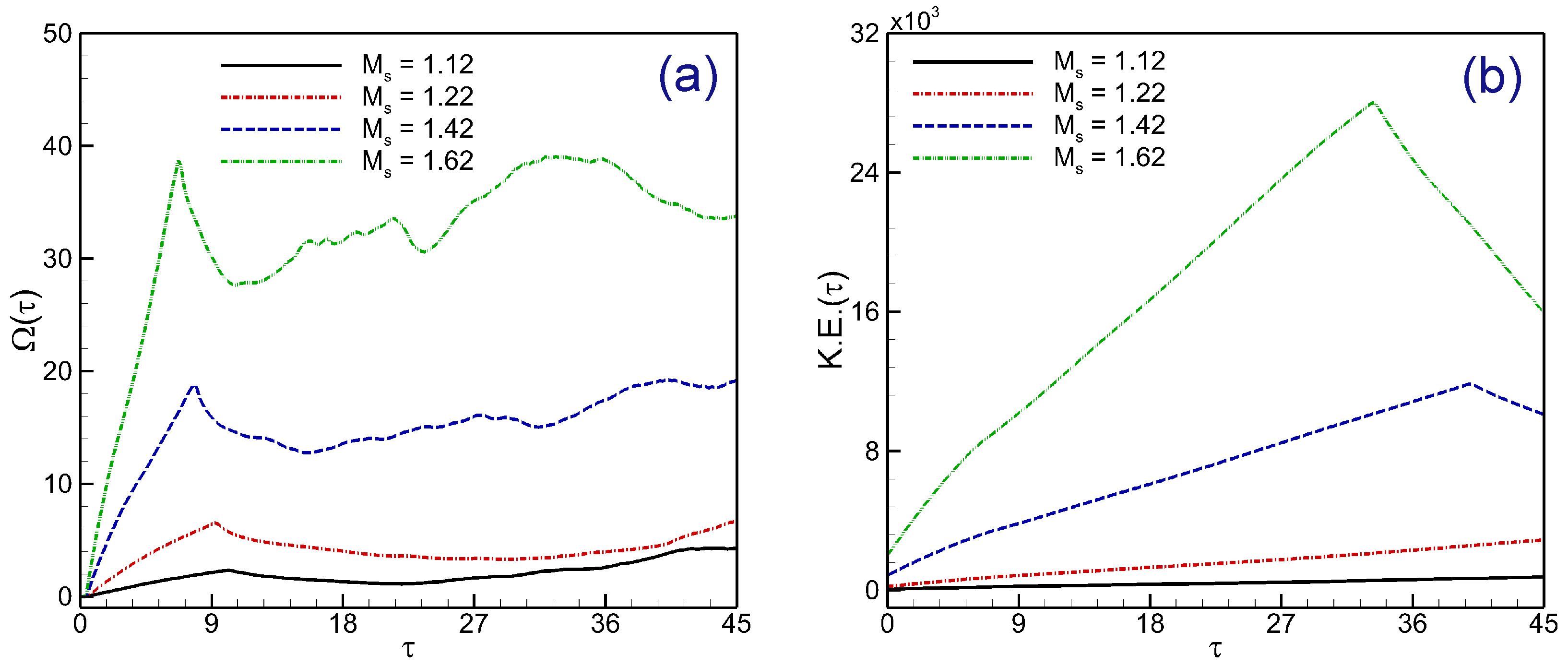
4.3. Mechanism of Enstrophy and Kinetic Energy Evolution
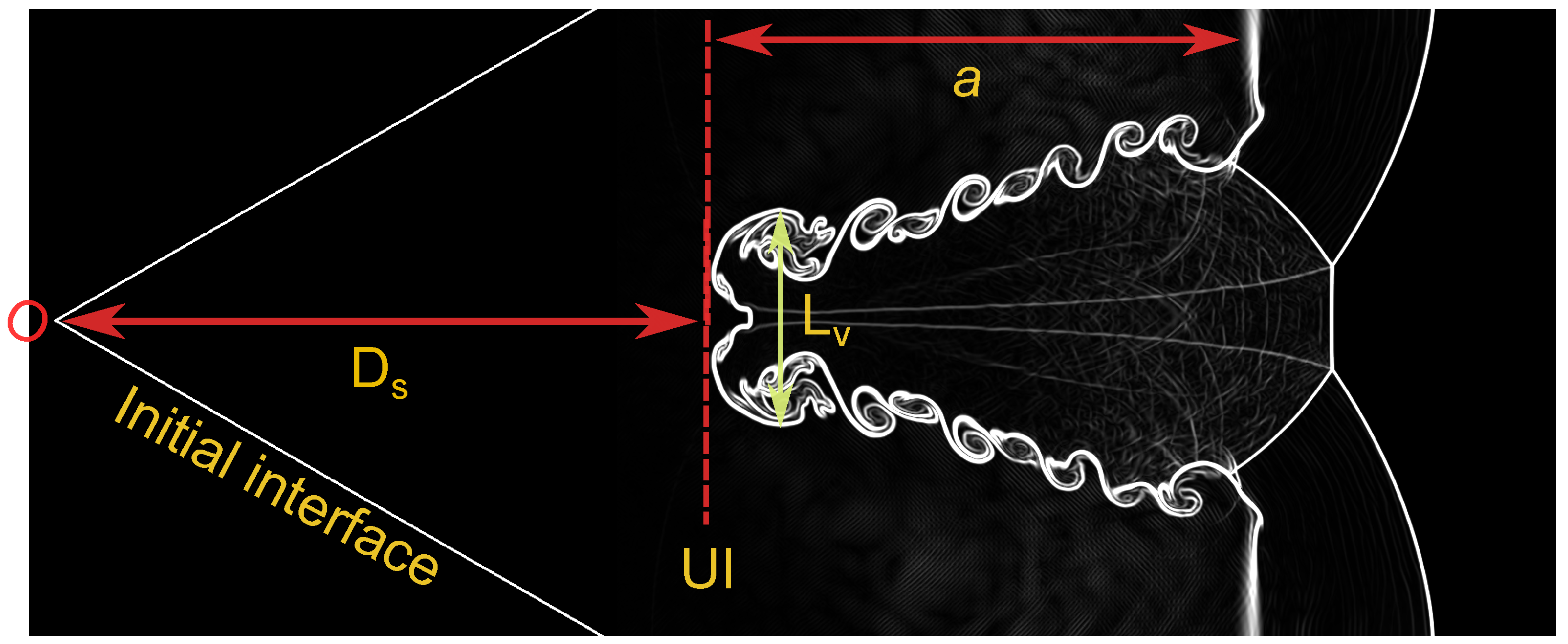
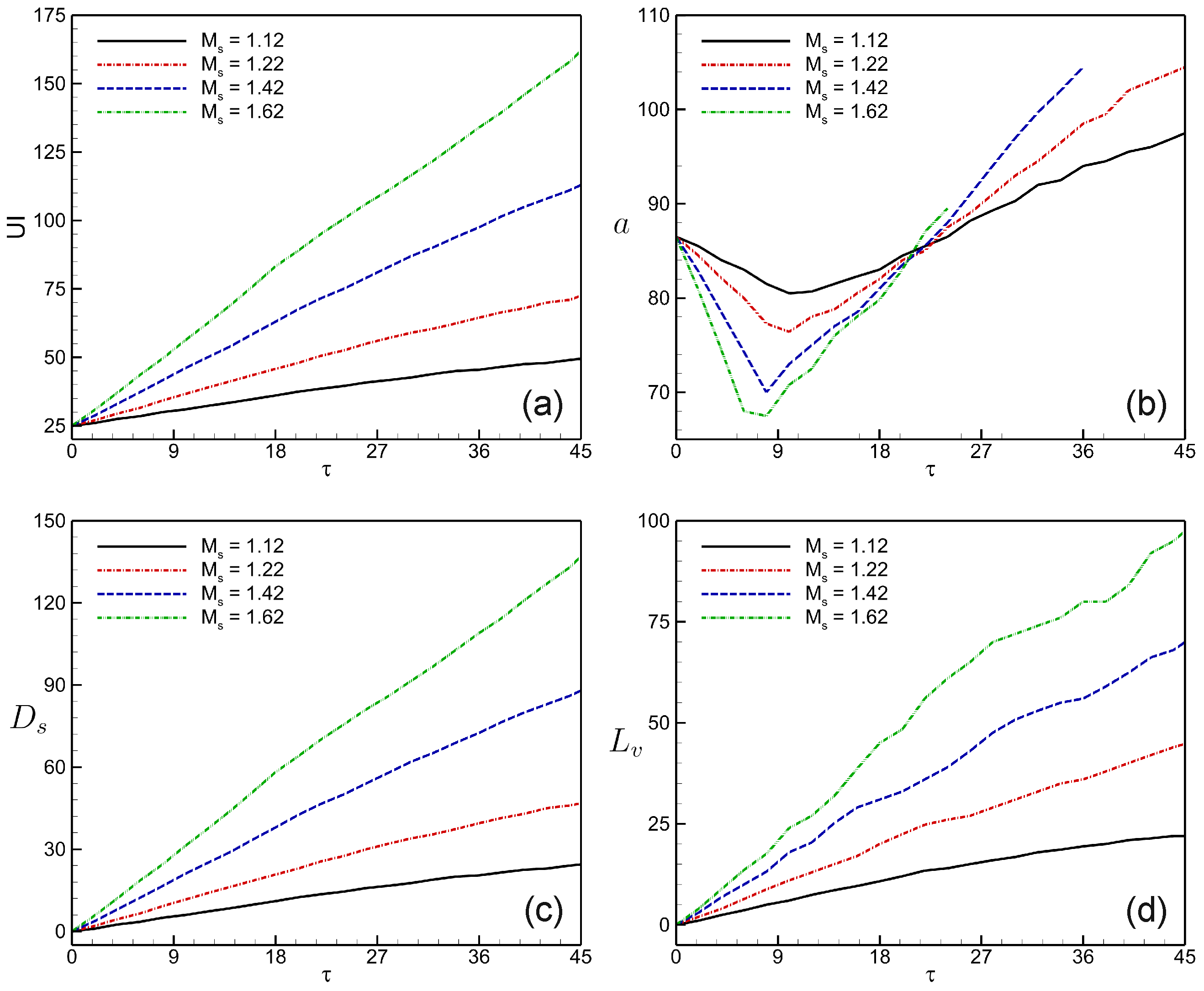
4.4. Interface Features
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
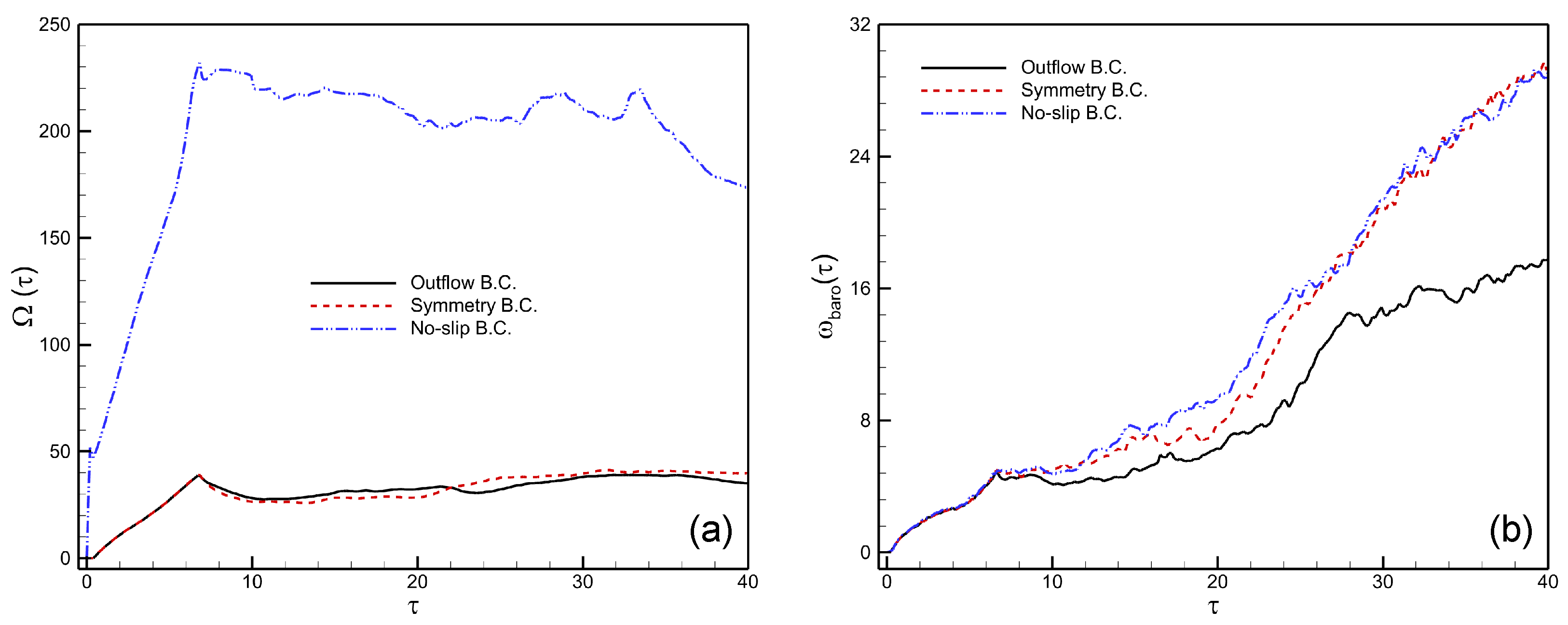
Appendix Effect of Boundary Conditions

References
- Richtmyer, R.D. Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Math. 1960, 13, 297–319. [Google Scholar] [CrossRef]
- Meshkov, E.E. Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 1969, 4, 101. [Google Scholar] [CrossRef]
- Livescu, D. Turbulence with large thermal and compositional density variations. Annu. Rev. Fluid Mech. 2020, 52, 309–341. [Google Scholar] [CrossRef]
- Zhou, Y.; Williams, R.J.; Ramaprabhu, P.; Groom, M.; Thornber, B.; Hillier, A.; Mostert, W.; Rollin, B.; Balachandar, S.; Powell, P.D.; et al. Rayleigh–Taylor and Richtmyer-Meshkov instabilities: A journey through scales. Physica D 2021, 423, 132838. [Google Scholar] [CrossRef]
- Rayleigh, L. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 1883, 14, 170–177. [Google Scholar] [CrossRef]
- Taylor, G. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 1950, 201, 192–196. [Google Scholar]
- Arnett, W.D.; Bahcall, J.N.; Kirshner, R.P.; Woosley, S.E. Supernova 1987A. Ann. Rev. Astron. Astrophys. 1989, 2, 629–700. [Google Scholar] [CrossRef]
- Lindl, J.; Landen, O.; Edwards, J.; Moses, E.; NIC Team. Review of the national ignition campaign 2009–2012. Phys. Plasmas 2014, 21, 020501. [Google Scholar] [CrossRef]
- Yang, J.; Kubota, T.; Zukoski, E.E. Applications of shock-induced mixing to supersonic combustion. AIAA J. 1993, 31, 854–862. [Google Scholar] [CrossRef]
- Zeng, W.G.; Pan, J.H.; Sun, Y.T.; Ren, Y.X. Turbulent mixing and energy transfer of reshocked heavy gas curtain. Phys. Fluids 2021, 30, 064106. [Google Scholar] [CrossRef]
- Brouillette, M. The Richtmyer-Meshkov instability. Annu. Rev. Fluid Mech. 2002, 34, 445. [Google Scholar] [CrossRef]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 2017, 720, 1–136. [Google Scholar]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 2017, 723, 1–160. [Google Scholar]
- Haas, J.F.; Sturtevant, B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities. J. Fluid Mech. 1987, 181, 41–76. [Google Scholar] [CrossRef]
- Ranjan, D.; Niederhaus, J.H.J.; Oakley, J.G.; Anderson, M.H.; Bonazza, R.; Greenough, J.A. Shock-bubble interactions: Features of divergent shock-refraction geometry observed in experiments and simulations. Phys. Fluids 2008, 20, 036101. [Google Scholar] [CrossRef]
- Quirk, J.J.; Karni, S. On the dynamics of a shock-bubble interaction. J. Fluid Mech. 1996, 318, 129–163. [Google Scholar] [CrossRef]
- Bagabir, A.; Drikakis, D. Mach number effects on shock-bubble interaction. Shock Waves 2001, 11, 209. [Google Scholar] [CrossRef]
- Shankar, S.K.; Kawai, S.; Lele, S.K. Two-dimensional viscous flow simulation of a shock accelerated heavy gas cylinder. Phys. Fluids 2011, 23, 024102. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M.; Myong, R.S. Impact of the bulk viscosity on flow morphology of shock-bubble interaction in diatomic and polyatomic gases. Phys. Fluids 2021, 33, 066103. [Google Scholar] [CrossRef]
- Singh, S.; Msmali, A.H.; Nelson, M.I. Unfolding of shocked hydrodynamic instability at SF6 elliptical interface: Physical insights from numerical simulations. Comput. Fluids 2024, 277, 106304. [Google Scholar] [CrossRef]
- Zhai, Z.; Wang, M.; Si, T.; Luo, X. On the interaction of a planar shock with a light polygonal interface. J. Fluid Mech. 2014, 757, 800. [Google Scholar] [CrossRef]
- Luo, X.; Wang, M.; Si, T.; Zhai, Z. On the interaction of a planar shock with an SF6 polygon. J. Fluid Mech. 2015, 773, 366. [Google Scholar] [CrossRef]
- Igra, D.; Igra, O. Shock wave interaction with a polygonal bubble containing two different gases, a numerical investigation. J. Fluid Mech. 2020, 889, A26. [Google Scholar] [CrossRef]
- Singh, S. Contribution of Mach number to the evolution of the Richtmyer-Meshkov instability induced by a shock-accelerated square light bubble. Phys. Rev. Fluids 2021, 6, 104001. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M. Numerical simulations of Richtmyer-Meshkov instability of SF6 square bubble in diatomic and polyatomic gases. Comput. Fluids 2022, 242, 105502. [Google Scholar] [CrossRef]
- Singh, S.; Torrilhon, M. On the shock-driven hydrodynamic instability in square and rectangular light gas bubbles: A comparative study from numerical simulations. Phys. Fluids 2023, 35, 012117. [Google Scholar] [CrossRef]
- Singh, S. Investigation of aspect ratio effects on flow characteristics and vorticity generation in shock-induced rectangular bubble. Eur. J. Mech. B/Fluids 2023, 101, 131. [Google Scholar] [CrossRef]
- Fraley, G. Rayleigh–Taylor stability for a normal shock wave–density discontinuity interaction. Phys. Fluids 1986, 29, 376–386. [Google Scholar] [CrossRef]
- Mikaelian, K.O. Growth rate of the Richtmyer-Meshkov instability at shocked interfaces. Phys. Rev. Lett. 1993, 71, 2903–2906. [Google Scholar] [CrossRef]
- Mikaelian, K.O. Richtmyer–Meshkov instability of arbitrary shapes. Phys. Fluids 2005, 17, 034101. [Google Scholar] [CrossRef]
- Luo, T.; Wang, J. Effects of Atwood number and stratification parameter on compressible multi-mode Rayleigh–Taylor instability. Phys. Fluids 2021, 33, 115111. [Google Scholar] [CrossRef]
- Thornber, B.; Drikakis, D.; Youngs, D.; Williams, R. Growth of a Richtmyer-Meshkov turbulent layer after reshock. Phys. Fluids 2011, 23, 095107. [Google Scholar] [CrossRef]
- Tritschler, V.K.; Olson, B.J.; Lele, S.K.; Hickel, S.; Hu, X.Y.; Adams, N.A. On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface. J. Fluid Mech. 2014, 755, 429–462. [Google Scholar] [CrossRef]
- Thornber, B.; Drikakis, D.; Youngs, D.L.; Williams, R.J.R. The influence of initial conditions on turbulent mixing due to Richtmyer–Meshkov instability. J. Fluid Mech. 2010, 654, 99–139. [Google Scholar] [CrossRef]
- Lombardini, M.; Pullin, D.I.; Meiron, D.I. Transition to turbulence in shock-driven mixing: A Mach number study. J. Fluid Mech. 2012, 690, 203–226. [Google Scholar] [CrossRef]
- Mohaghar, M.; Carter, J.; Pathikonda, G.; Ranjan, D. The transition to turbulence in shock-driven mixing: Effects of Mach number and initial conditions. J. Fluid Mech. 2016, 871, 595–635. [Google Scholar] [CrossRef]
- Probyn, M.G.; Williams, R.J.R.; Thornber, B.; Drikakis, D.; Youngs, D.L. 2D single-mode Richtmyer–Meshkov instability. Phys. D Nonlinear Phenom. 2021, 418, 132827. [Google Scholar] [CrossRef]
- Jahn, R.G. The refraction of shock waves at a gaseous interface. J. Fluid Mech. 1956, 1, 457–489. [Google Scholar] [CrossRef]
- Abd-El-Fattah, A.M.; Henderson, L.F. Shock waves at a fast-slow gas interface. J. Fluid Mech. 1978, 86, 15–32. [Google Scholar] [CrossRef]
- Abd-El-Fattah, A.M.; Henderson, L.F. The refraction of a plane shock wave at a gas interface. J. Fluid Mech. 1978, 86, 15. [Google Scholar] [CrossRef]
- Abd-El-Fattah, A.M.; Henderson, L.F. Shock waves at a slow-fast gas interface. J. Fluid Mech. 1978, 89, 79. [Google Scholar] [CrossRef]
- Abd-El-Fattah, A.M.; Henderson, L.F.; Lozzi, A. Precursor shock waves at a slow—Fast gas interface. J. Fluid Mech. 1976, 76, 157. [Google Scholar] [CrossRef]
- Henderson, L.F.; Colella, P.; Puckett, E.G. On the refraction of shock waves at a slow—Fast gas interface. J. Fluid Mech. 1991, 224, 1. [Google Scholar] [CrossRef]
- McFarland, J.A.; Greenough, J.A.; Ranjan, D. Computational parametric study of a Richtmyer-Meshkov instability for an inclined interface. Phys. Rev. E 2011, 84, 026303. [Google Scholar] [CrossRef]
- McFarland, J.A.; Greenough, J.A.; Ranjan, D. Investigation of the initial perturbation amplitude for the inclined interface Richtmyer–Meshkov instability. Phys. Scr. 2013, 155, 014014. [Google Scholar] [CrossRef]
- McFarland, J.A.; Greenough, J.A.; Ranjan, D. Simulations and analysis of the reshocked inclined interface Richtmyer–Meshkov instability for linear and nonlinear interface perturbations. J. Fluids Eng. 2014, 136, 071203. [Google Scholar] [CrossRef]
- McFarland, J.A.; Reilly, D.; Black, W.; Greenough, J.A.; Ranjan, D. Modal interactions between a large-wavelength inclined interface and small-wavelength multimode perturbations in a Richtmyer-Meshkov instability. Phys. Rev. E 2014, 92, 013023. [Google Scholar] [CrossRef]
- McFarland, J.A.; Reilly, D.; Creel, S.; McDonald, C.; Finn, T.; Ranjan, D. Experimental investigation of the inclined interface Richtmyer–Meshkov instability before and after reshock. Exp. Fluids 2014, 55, 1640–1653. [Google Scholar] [CrossRef]
- Reilly, D.; McFarland, J.A.; Mohaghar, M.; Ranjan, D. The effects of initial conditions and circulation deposition on the inclined-interface reshocked Richtmyer–Meshkov instability. Exp. Fluids 2015, 56, 168–183. [Google Scholar] [CrossRef]
- Luo, X.; Dong, P.; Si, T.; Zhai, Z. The Richtmyer–Meshkov instability of a ‘V’ shaped air/SF6 interface. J. Fluid Mech. 2016, 802, 186–202. [Google Scholar] [CrossRef]
- Zhai, Z.; Dong, P.; Si, T.; Luo, Z. The Richtmyer-Meshkov instability of a “V” shaped air/helium interface subjected to a weak shock. Phys. Fluids 2016, 28, 082104. [Google Scholar] [CrossRef]
- Wu-Wang, H.; Liu, C.; Xiao, Z. Parametric effects on Richtmyer–Meshkov instability of a V-shaped gaseous interface within linear stage. Phys. Fluids 2024, 36, 024114. [Google Scholar] [CrossRef]
- Alsaeed, S.S.; Singh, S. Numerical study of shock wave interaction with V-Shaped heavy/light interface. Mathematics 2024, 12, 3131. [Google Scholar] [CrossRef]
- Singh, S. Development of a 3D Discontinuous Galerkin Method for the Second-Order Boltzmann-Curtiss Based Hydrodynamic Models of Diatomic and Polyatomic Gases. Ph.D. Thesis, Gyeongsang National University, Jinju-si, Republic of Korea, 2018. [Google Scholar]
- Singh, S.; Karchani, A.; Chourushi, T.; Myong, R.S. A three-dimensional modal discontinuous Galerkin method for the second-order Boltzmann-Curtiss-based constitutive model of rarefied and microscale gas flows. J. Comput. Phys. 2022, 457, 111052. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Betelin, V.B.; Shagaliev, R.M.; Nikitin, V.F.; Belyakov, I.M.; Deryuguin, Y.N.; Aksenov, S.V.; Korchazhkin, D.A. Hydrogen fuel rocket engines simulation using LOGOS code. Int. J. Hydrogen Energy 2014, 39, 10748. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Betelin, V.B.; Nikitin, V.F.; Stamov, L.I.; Altoukhov, D.I. Accumulation of errors in numerical simulations of chemically reacting gas dynamics. Acta Astronaut. 2015, 117, 338. [Google Scholar] [CrossRef]
- Karchani, A. Discontinuous Galerkin Methods for the Second-Order Boltzmann-Based Hydrodynamic Models. Ph.D. Thesis, Gyeongsang National University, Jinju-si, Republic of Korea, 2017. [Google Scholar]
- Chan, J.; Lin, Y.; Warburton, T. Entropy stable modal discontinuous Galerkin schemes and wall boundary conditions for the compressible Navier-Stokes equations. J. Comput. Phys. 2022, 448, 110723. [Google Scholar] [CrossRef]




| Gas | Density | Heat Ratio () | Sound Speed |
|---|---|---|---|
| 1.25 | 1.40 | 352 | |
| 6.03 | 1.09 | 135 |
| Allowable Error (%) | Grid Resolution | Time Simulated | Number of Time Steps | Accumulated Error | Allowable Number of Time Steps | Reliability |
|---|---|---|---|---|---|---|
| 5 | 4 | 81 | 2868 | 33 | ||
| 5 | 4 | 177 | ||||
| 5 | 4 | 270 | ||||
| 5 | 4 | 369 | ||||
| 5 | 4 | 463 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaeed, S.S.; Singh, S. Computational Study of Shocked V-Shaped N2/SF6 Interface across Varying Mach Numbers. Axioms 2024, 13, 700. https://doi.org/10.3390/axioms13100700
Alsaeed SS, Singh S. Computational Study of Shocked V-Shaped N2/SF6 Interface across Varying Mach Numbers. Axioms. 2024; 13(10):700. https://doi.org/10.3390/axioms13100700
Chicago/Turabian StyleAlsaeed, Salman Saud, and Satyvir Singh. 2024. "Computational Study of Shocked V-Shaped N2/SF6 Interface across Varying Mach Numbers" Axioms 13, no. 10: 700. https://doi.org/10.3390/axioms13100700
APA StyleAlsaeed, S. S., & Singh, S. (2024). Computational Study of Shocked V-Shaped N2/SF6 Interface across Varying Mach Numbers. Axioms, 13(10), 700. https://doi.org/10.3390/axioms13100700







