Non-Fragile Sampled Control Design for an Interconnected Large-Scale System via Wirtinger Inequality

Abstract

A control design for a linear large-scale interconnected system composed of identical subsystems is presented in this paper. The control signal of all subsystems is sampled. For different subsystems, the sampling times are not identical. Nonetheless, it is assumed that a bound exists for the maximal sampling time. The control algorithm is designed using the Wirtinger inequality, and the non-fragile control law is proposed. The size of the linear matrix inequalities to be solved by the proposed control algorithm is independent of the number of subsystems composing the overall system. Hence, the algorithm is computationally effective. The results are illustrated by two examples. The first example graphically illustrates the function of the proposed algorithm while the second one compares with a method for stabilizing a large-scale system obtained earlier, thus illustrating the improved capabilities of the presented algorithm.

1. Introduction

To design control algorithms for large-scale interconnected systems, one usually divides the overall system into subsystems with not-too-strong interconnections. Then, one designs a control law so that the control input for a particular subsystem depends on the measurements from this subsystem only while, on the other hand, guaranteeing sufficient robustness to mitigate the effects of interconnections with the other subsystems. For more information (see, e.g., [1,2] or [3]). An important subclass of them is symmetrically interconnected systems (every subsystem is connected with every other one); see, e.g., [3], Chapter 12, for a thorough description.

A crucial step in the design of control of linear large-scale interconnected systems composed of identical subsystems is the definition of a certain transformation that converts the large-scale interconnected system into a set of (non-identical) disconnected systems. Stabilization of this set of autonomous systems implies stability of the original large-scale system as well (see, e.g., [4], among others). In [5], this approach to the stabilization of large-scale systems is applied to the control of large-scale nonlinear systems.

Control of large-scale systems is usually implemented via communication networks bringing flexibility and cost-effectiveness, but also introducing some undesired effects, such as sampling and quantization of the signals, the transmission of the measured data as well as the control signals is subject to time delays, packet dropouts are present, etc. (see, e.g., [6,7,8,9,10,11]).

As the state values are not always available for the controller, an observer must be designed. An observer-based decentralized control of large-scale systems was proposed in [12], and for systems with time delays in [13]. Event-triggered controller, allowing for reduction of the communication cost in the control loop, was designed for a nonlinear interconnected system in [14], and the stabilization of a large-scale system with quantized control signals was investigated in [11].

In many practical applications, the properties of the actuators are subject to changes in time due to various causes like material degradation, changing of properties depending on temperature, etc. However, their replacement can often be difficult or costly. Hence, there is a need to propose a control tolerating changes in the properties of the actuators (non-fragile control). This can be modeled as variations in the control gain. Here, additive perturbations of the control gain are considered (see, e.g., [15,16] or, for a related problem of multi-agent system synchronization, in [17] or [18]).

To find a stabilizing control for linear time-delay systems, the Lyapunov–Krasovskii (see, e.g., [5] or, for a multi-agent system, [19]) or Razumikhin functional-based methods (as in [6]) leading to linear matrix inequalities (LMI) are often applied. The Wirtinger inequality can be used in connection with the Lyapunov–Krasovskii-based methods (see, e.g., [20,21]), reducing the conservativeness of the involved estimates. The Lyapunov–Krasovskii functional sometimes requires the derivative of the time delay to be less than one. Hence, these methods are not suitable for systems with sampled controls. The so-called descriptor approach (see [22]) is a remedy [23], which uses this approach in connection with the Wirtinger inequality to stabilize a system with sampled controls. A large-scale system is stabilized by a Wirtinger inequality-based design in [24]. This paper extends these results.

• Purpose of this paper:
  • To present an improved algorithm for stabilization of an interconnected large-scale system with sampled controls under less restrictive conditions than required by the algorithm proposed by [6].
  • To provide a comparison of both approaches.
  • To present an algorithm that enables more general interconnections than the algorithm proposed by [6].
  • Based on existing results to propose the non-fragile control law extending the previous results to the case of fluctuating control gain.

The novel method is based on the Wirtinger inequality.

• Notation:
  • The LMI $P>0$ means matrix P is a square symmetric positive definite matrix.
  • For symmetric matrices, the elements below the diagonal are not written explicitly they are replaced by an asterisk: $\left(\begin{array}{cc}a& b\\ b^T& c\end{array}\right)=\left(\begin{array}{cc}a& b\\ \ast & c\end{array}\right).$
  • If no confusion can arise, the time argument t is omitted. The time delay is written using subscript: $x=x\left(t\right)$, $x(t-\tau )=x_{\tau }\left(t\right)=x_{\tau }$. However, if the time argument is different from t, it is written in full.
  • If A is a square matrix, then $I_A$ denotes the identity matrix with a dimension equal to the dimension of A; 0 denotes a zero block; its dimension will be clear from the context.
  • By $\mathrm{diag}(A,B)$ we denote the block-diagonal matrix $\mathrm{diag}(A,B)=\left(\begin{array}{cc}A& 0\\ 0& B\end{array}\right)$.
  • The symbol ⊗ denotes the Kronecker product. Its properties are summarized, e.g., in [25].

Outline of the paper: The problem is introduced in Section 2, and the necessary assumptions are presented here. Section 3 contains the design of the control algorithm based on the Wirtinger inequality. This section is divided into two subsections. The Wirtinger inequality-based control design algorithm is derived in the first subsection; however, the dimension of this problem is dependent on the number of subsystems. This issue is remedied in the second subsection, which contains a control algorithm design independent of the number of subsystems. Section 4 contains two illustrative examples; the first one graphically illustrates the capabilities of the algorithm, while the second one provides a comparison with a method derived earlier, thus highlighting the improvements achieved by the algorithm presented here. Then, the conclusions follow.

2. Problem Setting

Consider the following large-scale system, which is composed of N identical subsystems. For every $i=1,\dots ,N$, the ith subsystem is given by

$$\begin{array}{cc}\hfill {\dot{x}}_i=& A{x}_i+B{u}_i+\sum _{j=1}^N{e}_{ij}H{x}_j+G{w}_i,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill x_i\left(0\right)=& x_{i,0}.\hfill \end{array}$$

(2)

Here, $x_i\left(t\right)\in {\mathbb{R}}^n$, $u_i\left(t\right)\in {\mathbb{R}}^m$, $w_i\left(t\right)\in {\mathbb{R}}^q$ are the state, control, and disturbance, respectively. Moreover, $A,H\in {\mathbb{R}}^{n\times n}$, $B\in {\mathbb{R}}^{n\times m}$, and $G\in {\mathbb{R}}^{n\times q}$. We define also the interconnection matrix $E\in {\mathbb{R}}^{N\times N}$ as follows: let $i,j\in 1,\dots ,N$; if $i\ne j$ then $e_{ij}=1$ if the state of the jth subsystem influences the state of the ith subsystem, otherwise $e_{ij}=0$.

Assumption 1.

For every $i=1,\dots ,N$ holds $e_{ii}=0$ (the interconnection of the system has no loops).

Assumption 2.

Matrix E is symmetric.

The second assumption implies that there exists an orthogonal matrix $T^{\prime }$ and a real diagonal matrix $D^{\prime }$ such that

$$E=T^{\prime T}{D}^{\prime }{T}^{\prime }.$$

(3)

Without loss of generality, one can assume $d_1\le \cdots \le d_N$ and $D^{\prime }=\mathrm{diag}(d_1,\dots ,d_N)$.

Remark 1.

Due to the importance of symmetrically interconnected systems (every subsystem is connected to every other subsystem; in this case, $e_{ij}=1$ whenever $i\ne j$, $e_{ii}=0$), special methods for these systems were proposed. Papers [6,15] and Chapter 12 in [3], among others, are focused on the control of this class of interconnected systems. The most distinctive feature is that a different transformation can be defined for these systems: the transformation matrix is not necessarily constructed using eigenvectors; rather,

$$T^{″}={\displaystyle \frac{1}{N}}\left(\begin{array}{ccccc}(N-1)& -1& \dots & -1& -1\\ -1& (N-1)& \dots & -1& -1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ -1& -1& \dots & (N-1)& -1\\ 1& 1& \dots & 1& 1\end{array}\right)$$

can be used. This can be beneficial if N is large as construction of this transformation matrix does not require computation of eigenvectors and eigenstructures. Still, the method based on the computation of the eigenvalues is applicable for these systems if the computation of the eigenstructure of matrix E poses no difficulties. Although both methods lead to a stabilizing control, the results can be different in terms of conservativeness. This is why this case is treated separately in this paper.

Denote $D^{″}=\mathrm{diag}({\displaystyle \underset{N-1\mathrm{times}}{\overset{-1,\dots ,-1}{︸}}},N-1)$. As shown in [3] (Chapter 12), for an N-dimensional matrix E, the relation $E=T^{″-1}{D}^{″}{T}^{″}$ holds.

Let $x={(x_1^T,\dots ,x_N^T)}^T$, $\tilde{x}={(x_{1,{\tau }_1}^T,\dots ,x_{N,{\tau }_N}^T)}^T$, $w={(w_1^T,\dots ,w_N^T)}^T$, $u={(u_1^T,\dots ,u_N^T)}^T$. This allows us to rewrite the N-tuple of subsystems (1) and (2) in the compact form

$$\dot{x}=(I_E\otimes A+E\otimes H)x+(I_E\otimes B)u+(I_E\otimes G)w,x_0={(x_{1,0}^T,\dots ,x_{N,0}^T)}^T.$$

(4)

System (4) is referred to as the overall system.

Assumption 3.

The control is sampled; moreover, it is assumed the time interval of length ${\tau }^{\prime }$ elapses between the sampling time and the time instant when the measured value is available to the controller. The sequence of sampling times of the ith subsystem is denoted by $t_{i,k}$, $k\in \mathbb{N}$.

Assumption 4.

There exists $\overline{\tau }>0$ such that $t_{i,k}-t_{i,k-1}<\overline{\tau }$ for all $i=1,\dots ,N$ and all k.

We aim to find a matrix $K\in {\mathbb{R}}^{m\times n}$ so that the control law

$$u={(K{x}_1^T\left(t_{1,k_1}+{\tau }^{\prime }\right),\dots ,K{x}_N^T\left(t_{i,k_N}+{\tau }^{\prime }\right))}^T$$

(5)

stabilizes the overall system.

In (5), $t_{i,k_i}$ is defined as follows: $t_{i,k_i}=max\left(t_{i,k}\right|k\in \mathbb{N},t_{i,k}<t-{\tau }^{\prime })$. This is called the nominal case, as the control gain is not perturbed.

In some cases, the control gain matrix is subject to perturbations. We assume the perturbations are additive as in [15]; the matrix gain is time-dependent. Let there exist measurable functions $F_i:[0,\infty )\to {\mathbb{R}}^{\nu \times \nu }$ and matrices $D_K\in {\mathbb{R}}^{m\times \nu }$, $E_K\in {\mathbb{R}}^{\nu \times n}$ and $K\in {\mathbb{R}}^{m\times n}$. Then, we define functions $K_i$ by

$$K_i\left(t\right)=K+D_K{F}_i\left(t\right)E_K.$$

(6)

Assumption 5.

Functions $F_i:[0,\infty )\to {\mathbb{R}}^{\nu \times \nu }$ are measurable, and for all $i=1,\dots ,N$ and all $t\ge 0$, $\parallel F_i\left(t\right)\parallel \le 1$ holds.

Then, the control law is given as

$$u={(K_1\left(t\right)x_1^T\left(t_{1,k_1}+{\tau }^{\prime }\right),\dots ,K_N\left(t\right)x_N^T\left(t_{i,k_N}+{\tau }^{\prime }\right))}^T.$$

(7)

The goal is to find matrix K so that stabilization of the overall system is achieved under the control law (7). The delays satisfy the same conditions as in the nominal case. Matrix K is called the nominal control gain matrix.

Remark 2.

Matrices $D_K$ and $E_K$ are supposed to be known and available for the controller synthesis. On the other hand, functions $F_i$ are not known.

3. Control Design

3.1. Wirtinger Inequality and Its Application to the Control of a Large-Scale System

Lemma 1

([26], Lemma 3.1). (Wirtinger inequality) Let $a<b$ be real scalars, $z:[a,b)\to {\mathbb{R}}^n$ be an absolutely continuous function, $z\left(a\right)=0$; ${lim}_{t\to b-}z\left(t\right)$ exists and is finite, and ${\int }_a^b{\parallel \dot{z}\left(s\right)\parallel }^{2}ds$ exists and is finite. Let there also exist an $n\times n$-dimensional matrix $R>0$. Then, ${\int }_a^b{z}^T\left(s\right)Rz\left(s\right)ds\le {\displaystyle \frac{4{(b-a)}^2}{{\pi }^2}}{\int }_a^b{\dot{z}}^T\left(s\right)R\dot{z}\left(s\right)ds.$

This lemma was used to obtain the following result (Theorem 1 in [23]). For the sake of completeness of this paper, we repeat it here without proof.

Theorem 1.

Let $0<{\tau }^{\prime }<\overline{\tau }$. Consider system

$$\dot{x}={\mathcal{A}}^{\prime }x+{\mathcal{B}}^{\prime }u$$

(8)

where $x\left(t\right)\in {\mathbb{R}}^n$, $u\in {\mathbb{R}}^m$ and the control is sampled, so that Assumptions 3 and 4 hold. Let there exist a scalar $\epsilon >0$ and matrices ${\mathcal{U}}^{\prime }>0$, ${\mathcal{X}}^{\prime }>0$, ${\mathcal{M}}^{\prime }>0$, ${\mathcal{L}}^{\prime }>0$, ${\mathcal{Z}}^{\prime }$ nonsingular and ${\mathcal{K}}^{\prime }$ with compatible dimensions, so that, with matrix Σ defined as

$$\begin{array}{c}\hfill \Sigma ({\mathcal{A}}^{\prime },{\mathcal{B}}^{\prime },{\mathcal{X}}^{\prime },{\mathcal{Z}}^{\prime },{\mathcal{M}}^{\prime },{\mathcal{L}}^{\prime },{\mathcal{U}}^{\prime },{\mathcal{K}}^{\prime },\epsilon )=\left(\begin{array}{cccc}{\sigma }_{11}& {\sigma }_{12}& {\sigma }_{13}& {\sigma }_{14}\\ \ast & {\sigma }_{22}& {\sigma }_{23}& \epsilon {\sigma }_{14}\\ \ast & \ast & {\sigma }_{33}& 0\\ \ast & \ast & \ast & {\sigma }_{44}\end{array}\right),\end{array}$$

$$\begin{array}{cc}\hfill {\sigma }_{11}=& {\mathcal{A}}^{\prime T}{\mathcal{Z}}^{\prime }+{\mathcal{Z}}^{\prime T}{\mathcal{A}}^{\prime }+{\mathcal{M}}^{\prime }-{\mathcal{L}}^{\prime },{\sigma }_{12}={\mathcal{X}}^{\prime }-{\mathcal{Z}}^{\prime T}+\epsilon {\mathcal{A}}^{\prime T}{\mathcal{Z}}^{\prime },{\sigma }_{13}={\mathcal{L}}^{\prime }+{\mathcal{Z}}^{\prime T}{\mathcal{B}}^{\prime }{\mathcal{K}}^{\prime },\hfill \\ \hfill {\sigma }_{14}=& {\mathcal{Z}}^{\prime T}{\mathcal{B}}^{\prime }{\mathcal{K}}^{\prime },{\sigma }_{22}=-\epsilon ({\mathcal{Z}}^{\prime }+{\mathcal{Z}}^{\prime T})+{\tau }^{\prime 2}{\mathcal{M}}^{\prime }+{\overline{\tau }}^2{\mathcal{U}}^{\prime },{\sigma }_{23}=\epsilon {\mathcal{Z}}^{\prime T}{\mathcal{B}}^{\prime }{\mathcal{K}}^{\prime },\hfill \\ \hfill {\sigma }_{33}=& -{\mathcal{M}}^{\prime }-{\mathcal{L}}^{\prime },{\sigma }_{44}=-{\displaystyle \frac{{\pi }^2}{4}}{\mathcal{U}}^{\prime },\hfill \end{array}$$

the LMI

$$\Sigma ({\mathcal{A}}^{\prime },{\mathcal{B}}^{\prime },{\mathcal{X}}^{\prime },{\mathcal{Z}}^{\prime },{\mathcal{M}}^{\prime },{\mathcal{L}}^{\prime },{\mathcal{U}}^{\prime },{\mathcal{K}}^{\prime },\epsilon )<0$$

(9)

holds. Then, system (8) with sampled control $u={\mathcal{K}}^{\prime }x\left(t_k+{\tau }^{\prime }\right)$ is stable.

Remark 3.

Note that matrix inequality (9) is linear either in $\mathcal{Z}$ or in $\mathcal{K}$, but not simultaneously in both; hence, it is not applicable to the control synthesis problem. On the other hand, a standard procedure (applied in the subsequent text) yields a related matrix inequality that can be used to the control design.

Remark 4.

Parameter ε is not a decision variable; its value cannot be obtained from the solution of these LMI. Rather, its value must be determined before the above LMIs are solved. The presence of this parameter is characteristic for the control design using the descriptor approach (see [27]).

Remark 5.

Paper [23] presents a slightly more general version, with a general matrix instead of the multiple $\epsilon \mathcal{Z}$. However, for the control synthesis problem, this formulation is useful.

Remark 6.

Let $\tilde{\omega }=(x^T,{\dot{x}}^T,x-x_{{\tau }^{\prime }},x_{{\tau }^{\prime }}-x(t_k-{\tau }^{\prime }))$ (here, $t_k$ is the last sampling time before $t-{\tau }^{\prime }$). As shown in [23], if the Lyapunov–Krasovskii functional ${\mathcal{V}}^{\prime }$ is defined as

$$\begin{array}{cc}\hfill {\mathcal{V}}^{\prime }& =x^T{\mathcal{X}}^{\prime }x+{\int }_{t-{\tau }^{\prime }}^t{x}^T\left(s\right){\mathcal{M}}^{\prime }x\left(s\right)ds+{\tau }^{\prime }{\int }_{-{\tau }^{\prime }}^0{\int }_{t+\alpha }^t{\dot{x}}^T\left(s\right){\mathcal{L}}^{\prime }\dot{x}\left(s\right)dsd\alpha \hfill \\ \hfill & +{(\overline{\tau }-{\tau }^{\prime })}^2{\int }_{t_k-{\tau }^{\prime }}^{t-{\tau }^{\prime }}{\dot{x}}^T\left(s\right){\mathcal{U}}^{\prime }\dot{x}\left(s\right)ds\hfill \\ \hfill & -{\displaystyle \frac{{\pi }^2}{4}}{\int }_{t_k-{\tau }^{\prime }}^{t-{\tau }^{\prime }}{\left(x\left(s\right)-x(t_k-{\tau }^{\prime })\right)}^T{\mathcal{U}}^{\prime }\left(x\left(s\right)-x(t_k-{\tau }^{\prime })\right)ds\hfill \end{array}$$

then $\dot{\mathcal{V}}\le {\tilde{\omega }}^T\Sigma ({\mathcal{A}}^{\prime },{\mathcal{B}}^{\prime },{\mathcal{X}}^{\prime },{\mathcal{Z}}^{\prime },{\mathcal{M}}^{\prime },{\mathcal{L}}^{\prime },{\mathcal{U}}^{\prime },{\mathcal{K}}^{\prime },\epsilon )\tilde{\omega }<0$ for $\tilde{\omega }\ne 0$.

In the following, $n\times n$-dimensional matrices U, X, M, L, and Z, and also matrix $K\in {\mathbb{R}}^{m\times n}$ and constants $\gamma$ and $\epsilon$, will be used.

Notation: Let us define the following matrices:

$$\begin{array}{c}\mathcal{A}=I_E\otimes A+E\otimes H,\mathcal{B}=I_E\otimes B,\mathcal{G}=I_E\otimes G,\mathcal{U}=I_E\otimes U,\mathcal{X}=I_E\otimes X,\mathcal{M}=I_E\otimes M,\hfill \\ \mathcal{L}=I_E\otimes L,\mathcal{Z}=I_E\otimes Z,\mathcal{K}=I_E\otimes K,{\Sigma }_1=\Sigma (\mathcal{A},\mathcal{B},\mathcal{X},\mathcal{Z},\mathcal{M},\mathcal{L},\mathcal{U},\mathcal{K},\epsilon ),\hfill \\ {\Sigma }_2={\Sigma }_1+\mathrm{diag}(I_{\mathcal{A}}+{\displaystyle \frac{1}{\gamma }}{\mathcal{Z}}^T\mathcal{G}{\mathcal{G}}^T\mathcal{Z},{\displaystyle \frac{\epsilon }{\gamma }}{\mathcal{Z}}^T\mathcal{G}{\mathcal{G}}^T\mathcal{Z},0,0),\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \zeta =& \left(\begin{array}{ccc}{I}_{\mathcal{A}}& {\mathcal{Z}}^T\mathcal{G}& 0\\ 0& 0& \sqrt{\epsilon }{\mathcal{Z}}^T\mathcal{G}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\hfill \\ \hfill \Delta =& -\mathrm{diag}(I_{\mathcal{A}},\gamma I_{{\mathcal{G}}^T\mathcal{G}},\gamma I_{{\mathcal{G}}^T\mathcal{G}}),\Psi =\left(\begin{array}{cc}{\Sigma }_1& \zeta \\ \ast & \Delta \end{array}\right).\hfill \end{array}$$

(11)

Lemma 2.

Consider System (4), and let Assumptions 3 and 4 hold. Assume there exist $n\times n$-dimensional matrices $U>0$, $X>0$, $M>0$, $L>0$, Z nonsingular, an $m\times n$-dimensional matrix K, and scalars $\epsilon >0$ and $\gamma >0$, such that, using Notation (10), LMI

$$\Psi <0$$

(12)

holds. Let the control $u_i$ of the ith subsystem be given by (5). Then, if $w=0$, System (4) is asymptotically stabilized; otherwise, if $x\left(t\right)=0$ for all $t\in [-\overline{\tau },0]$, for every $t\ge 0$, ${\int }_0^t{x}^T\left(s\right)x\left(s\right)ds\le \gamma (1+\epsilon ){\int }_0^t{w}^T\left(s\right)w\left(s\right)ds$ holds.

Remark 7.

This is a direct counterpart of Theorem 7.1 in [27] for large-scale systems where the sampling times are different for different subsystems. Thus, the proof is sketched here.

Proof. 

First, observe that the Schur complement theorem yields $\Psi <0$, if and only if ${\Sigma }_2<0$. Moreover, for any scalar $\gamma >0$, one has

$$\begin{array}{cc}\hfill (x^T{\mathcal{Z}}^T+\epsilon {\dot{x}}^T{\mathcal{Z}}^T)\mathcal{G}w\le & {\displaystyle \frac{1}{\gamma }}{x}^T{\mathcal{Z}}^T\mathcal{G}{\mathcal{G}}^T\mathcal{Z}x+{\displaystyle \frac{1}{\gamma }}{\dot{x}}^T{\mathcal{Z}}^T\mathcal{G}{\mathcal{G}}^T\mathcal{Z}\dot{x}+(1+\epsilon )\gamma w^{T}w.\hfill \end{array}$$

Now, we are ready to prove that inequality ${\Sigma }_2<0$ implies the $H_{\infty }$-stability of the overall system. Let us introduce, for the $i=1,\dots ,N$ vector,

$$\begin{array}{cc}\hfill \omega =& (x_1^T,\dots ,x_N^T,{\dot{x}}_1^T,\dots ,{\dot{x}}_N^T,{(x_1-x_{1,{\tau }^{\prime }})}^T,\dots ,{(x_N-x_{N,{\tau }^{\prime }})}^T,\hfill \\ \hfill & x_{1,{\tau }^{\prime }}-x{(t_{1,k}-{\tau }^{\prime })}^T,\dots ,x_{N,{\tau }^{\prime }}-x{(t_{N,k}-{\tau }^{\prime })}^T{)}^T.\hfill \end{array}$$

Observe also that

$$\begin{array}{cc}\hfill \sum _{i=1}^N{x}_i^T{Z}^T\sum _{j=1}^N{e}_{ij}H{x}_j=& x^T(I_E\otimes Z^T)(E\otimes H)x,\hfill \\ \hfill \sum _{i=1}^N{\dot{x}}_i^T{Z}^T\sum _{j=1}^N{e}_{ij}H{x}_j=& {\dot{x}}^T(I_E\otimes Z^T)(E\otimes H)x.\hfill \end{array}$$

Define functional $\mathcal{V}$ by

$$\begin{array}{cc}\hfill \mathcal{V}& =x^T\mathcal{X}x+{\int }_{t-{\tau }^{\prime }}^t{x}^T\left(s\right)\mathcal{M}x\left(s\right)ds+{\tau }^{\prime }{\int }_{-{\tau }^{\prime }}^0{\int }_{t+\alpha }^t{\dot{x}}^T\left(s\right)\mathcal{L}\dot{x}\left(s\right)dsd\alpha \hfill \\ \hfill & +\sum _{i=1}^N{(\overline{\tau }-{\tau }^{\prime })}^2{\int }_{t_{i,k}-{\tau }^{\prime }}^{t-{\tau }^{\prime }}{\dot{x}}_i^T\left(s\right)U{\dot{x}}_i\left(s\right)ds\hfill \\ \hfill & -{\displaystyle \frac{{\pi }^2}{4}}{\int }_{t_{i,k}-{\tau }^{\prime }}^{t-{\tau }^{\prime }}{\left(x_i\left(s\right)-x(t_{i,k}-{\tau }^{\prime })\right)}^{T}U\left(x_i\left(s\right)-x(t_{i,k}-{\tau }^{\prime })\right)ds.\hfill \end{array}$$

The procedure described in the following is based on [23], where only one delay is considered. As multiple delays are present in our problem, we sketch a generalization of the results of that paper to systems with multiple delays. Thus, for the case without uncertainties in the control gain matrix, one obtains

$$\begin{array}{cc}\hfill \dot{\mathcal{V}}=& \sum _{i=1}^{N}2x_i^{T}X{\dot{x}}_i+x_i^{T}M{x}_i-x_{i,{\tau }^{\prime }}^{T}M{x}_{i,{\tau }^{\prime }}+{\dot{x}}_i^T({\tau }^{\prime 2}L+\overline{\tau }U){\dot{x}}_i\hfill \\ \hfill & -{\displaystyle \frac{{\pi }^2}{4}}(x_{i,{\tau }^{\prime }}-x{(t_{i,k}-{\tau }^{\prime })}^{T}U(x_{i,{\tau }^{\prime }}-x(t_{i,k}-{\tau }^{\prime })\hfill \\ \hfill & -{(x_i-x_{i,{\tau }^{\prime }})}^{T}L(x_i-x_{i,{\tau }^{\prime }})+(x_i^T{Z}^T+\epsilon {\dot{x}}_i^{T}Z)(-{\dot{x}}_i+A{x}_i\hfill \\ \hfill & +\sum _{j=1}^N{e}_{ij}H{x}_j+BK{x}_{i,{\tau }^{\prime }}+BK(x_{i,{\tau }^{\prime }}-x(t_{i,k}-{\tau }^{\prime })+G{w}_i)+x_i^T{x}_i-x_i^T{x}_i\hfill \\ \hfill \le & {\omega }^T{\Sigma }_2\omega .\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill \dot{\mathcal{V}}=& \dot{\mathcal{V}}+(x^T{\mathcal{Z}}^T+\epsilon {\dot{x}}^T{\mathcal{Z}}^T)\left(\stackrel{=0}{\overbrace{-\dot{x}+\mathcal{A}x+\mathcal{B}u+\mathcal{G}w}}\right)={\omega }^T{\Sigma }_1\omega +(x^T{\mathcal{Z}}^T+\epsilon {\dot{x}}^T{\mathcal{Z}}^T)\mathcal{G}w\hfill \\ \hfill \le & {\omega }^T{\Sigma }_2\omega +\gamma (1+\epsilon )w^{T}w-x^{T}x\le \gamma (1+\epsilon )w^{T}w-x^{T}x.\hfill \end{array}$$

As follows from the first part of the proof, Condition (12) implies ${\Sigma }_2<0$. Then, for $w=0$, the following holds: if $\parallel \omega \parallel \ne 0$, then $\dot{\mathcal{V}}<0$, which yields asymptotic stability. If $w\ne 0$ and $x\left(t\right)=0$ for $t\in [-\overline{\tau },0]$, then $\gamma (1+\epsilon ){\int }_0^t{w}^T\left(s\right)w\left(s\right)ds\ge {\int }_0^t{x}^T\left(s\right)x\left(s\right)ds$. □

Remark 8.

Finding the minimal γ satisfying assumption of Lemma 2 allows us to find the $H_{\infty }$-optimal control.

Consider now the case when the feedback gain is perturbed. The control gains are given by (6). Denote

$$\begin{array}{c}\hfill {\mathcal{D}}_K=I_E\otimes D_K,{\mathcal{E}}_K=I_E\otimes E_K,\mathcal{F}\left(t\right)=\mathrm{diag}(F_1\left(t\right),\dots ,F_N\left(t\right)).\end{array}$$

(13)

In this case, matrix ${\Sigma }_1$ is time dependent; time dependent terms appear in ${\sigma }_{13}$, ${\sigma }_{23}$, ${\sigma }_{14}$ and ${\sigma }_{24}=\epsilon {\sigma }_{14}$. They are estimated using the following proposition. Before it is formulated, let us choose a matrix $J\in {\mathbb{R}}^{\nu \times \nu }$, $J>0$, and also define

$$\mathcal{J}=I_E\otimes J.$$

(14)

With matrix $\mathcal{J}$, as well as the matrices defined in (13), we define auxiliary matrices ${\rm Y}\in {\mathbb{R}}^{Nn\times Nn}$, $\tilde{\Omega }\left(t\right),{\tilde{\Omega }}^{\prime }\in {\mathbb{R}}^{4Nn\times 4Nn}$ by

$$\begin{array}{cc}\hfill {\rm Y}=& {\mathcal{Z}}^T\mathcal{B}{\mathcal{D}}_K\mathcal{J}{\mathcal{D}}_K^T{\mathcal{B}}^T\mathcal{Z},\hfill \\ \hfill \tilde{\Omega }\left(t\right)=& \left(\begin{array}{cc}0& \left(\begin{array}{cc}{\mathcal{Z}}^T\mathcal{B}{\mathcal{D}}_K\mathcal{F}\left(t\right){\mathcal{E}}_K& {\mathcal{Z}}^T\mathcal{B}{\mathcal{D}}_K\mathcal{F}\left(t\right){\mathcal{E}}_K\\ \epsilon {\mathcal{Z}}^T\mathcal{B}{\mathcal{D}}_K\mathcal{F}\left(t\right){\mathcal{E}}_K& \epsilon {\mathcal{Z}}^T\mathcal{B}{\mathcal{D}}_K\mathcal{F}\left(t\right){\mathcal{E}}_K\end{array}\right)\\ \ast & 0\end{array}\right),\hfill \\ \hfill {\tilde{\Omega }}^{\prime }=& \left(\begin{array}{cccc}{\rm Y}& \epsilon {\rm Y}& 0& 0\\ \ast & {\epsilon }^2{\rm Y}& 0& 0\\ \ast & \ast & {\mathcal{E}}_K^T{\mathcal{J}}^{-1}{\mathcal{E}}_K& {\mathcal{E}}_K^T{\mathcal{J}}^{-1}{\mathcal{E}}_K\\ \ast & \ast & \ast & {\mathcal{E}}_K^T{\mathcal{J}}^{-1}{\mathcal{E}}_K\end{array}\right).\hfill \end{array}$$

Proposition 1.

With matrices $\tilde{\Omega }$ and ${\tilde{\Omega }}^{\prime }$ and with $\mathcal{J}>0$ one can see that inequality $\tilde{\Omega }\left(t\right)\le {\tilde{\Omega }}^{\prime }.$ holds for all $t\in [0,\infty )$.

Proof. 

The following holds for $\tilde{\Omega }$:

$$\begin{array}{cc}\hfill \tilde{\Omega }\left(t\right)=& \left(\begin{array}{cc}0& \left(\begin{array}{c}{\mathcal{Z}}^T\mathcal{B}{\mathcal{D}}_K\\ \epsilon {\mathcal{Z}}^T\mathcal{B}{\mathcal{D}}_K\end{array}\right)\mathcal{F}\left(t\right)\left({\mathcal{E}}_K{\mathcal{E}}_K\right)\\ \ast & 0\end{array}\right),\hfill \end{array}$$

The Young inequality then yields the result. □

For future purposes, we introduce matrix

$\Omega \in {\mathbb{R}}^{(5n+2q+\nu )N\times (5n+2q+\nu )N}$ as follows:

$$\begin{array}{cc}\hfill \Omega =& \left(\begin{array}{cccccccc}{\rm Y}& \epsilon {\rm Y}& 0& 0& 0& 0& 0& 0\\ \ast & {\epsilon }^2{\rm Y}& 0& 0& 0& 0& 0& 0\\ \ast & \ast & 0& 0& 0& 0& 0& {\mathcal{E}}_K^T\\ \ast & \ast & \ast & 0& 0& 0& 0& {\mathcal{E}}_K^T\\ \ast & \ast & \ast & \ast & 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -\mathcal{J}\end{array}\right).\hfill \end{array}$$

Moreover, let ${\overline{\Sigma }}_2$, $\overline{\Psi }$ be defined as

$$\begin{array}{cc}\hfill \overline{\Psi }=& \left(\begin{array}{cc}\Psi & 0\\ \ast & 0\end{array}\right)+\Omega .\hfill \end{array}$$

Lemma 3.

Consider System (4). Let Assumptions 3, 4, and 5 hold. Moreover, assume there exist $n\times n$-dimensional matrices $U>0$, $X>0$, $M>0$, $L>0$, Z nonsingular and $K\in {\mathbb{R}}^{m\times n}$, $J\in {\mathbb{R}}^{\nu \times \nu }$, such that $J>0$ and scalars $\epsilon >0$ and $\gamma >0$, so that, using notations (10), (11), (13), and (14), the LMI

$$\overline{\Psi }<0$$

(15)

holds. Assume System (4) with the control input (7). Then, if $w=0$, System (4) is asymptotically stabilized; otherwise, if $x\left(t\right)=0$ for every $t\in [-\overline{\tau },0]$, then for every $t\ge 0$, the following holds:

$${\int }_0^t{x}^T\left(s\right)x\left(s\right)ds\le \gamma (1+\epsilon ){\int }_0^t{w}^T\left(s\right)w\left(s\right)ds.$$

(16)

Proof. 

Proceeding as in the proof of Lemma 2, one can infer

$$\begin{array}{cc}\hfill \dot{\mathcal{V}}\le & {\tilde{\omega }}^T({\Sigma }_2+\tilde{\Omega }\left(t\right))\tilde{\omega }+\gamma (1+\epsilon )w^{T}w-x^{T}x.\hfill \end{array}$$

(17)

If one can prove the inequality

$${\Sigma }_2+\tilde{\Omega }\left(t\right)<0$$

(18)

for all $t\ge 0$, one then obtains that (17) implies $\dot{\mathcal{V}}<\gamma (1+\epsilon )w^{T}w-x^{T}x$.

Hence, it remains to prove the validity of (18) for all $t\ge 0$ if $\overline{\Psi }<0$. Taking the Schur complement of matrix $\Omega$, one obtains that $\overline{\Psi }<0$, if and only if

$$\Psi +\left(\begin{array}{cc}{\tilde{\Omega }}^{\prime }& 0\\ \ast & 0\end{array}\right)<0.$$

Proceeding as in the proof of Lemma 4, one has that the above inequality is equivalent to ${\Sigma }_2+{\tilde{\Omega }}^{\prime }<0$. Taking (1) into account, we arrive at (18).

To sum up, $\dot{\mathcal{V}}<\gamma (1+\epsilon )w^{T}w-x^{T}x$ if $x\left(t\right)=0$ in $[-\overline{\tau },0]$. As in the proof of Lemma 2, by integration from 0 to t, we arrive at ${\int }_0^t{x}^T\left(s\right)x\left(s\right)ds\le \gamma (1+\epsilon ){\int }_0^t{x}^T\left(s\right)x\left(s\right)ds$. On the other hand, if $w\left(t\right)=0$ for all $t\ge 0$, (17) implies $\dot{V}\le {\tilde{\omega }}^T({\Sigma }_2+\tilde{\Omega }\left(t\right))\tilde{\omega }<0$ if $\tilde{\omega }\ne 0$, and one has asymptotic stability of the closed loop. □

3.2. Reduction of the Size of the Problem and Controller Synthesis

The size of the optimization problem (12) is proportional to $nN$, hence it is too large for practical implementation. On the other hand, matrices $\Psi$ and $\overline{\Psi }$ can be transformed into a block-diagonal matrix, albeit with, in general, not equal terms on the diagonal. This procedure, as well as the subsequent procedure for the controller design, are rather standard; hence, their description is brief.

To proceed, let

$$\begin{array}{cc}\hfill {\zeta }^{\prime }=& \left(\begin{array}{ccc}{I}_A& Z^{T}G& 0\\ 0& 0& \sqrt{\epsilon }{Z}^{T}G\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\hfill \\ \hfill {\Delta }^{\prime }=& -\mathrm{diag}(I_A,\gamma I_{G^{T}G},\gamma I_{G^{T}G}).\hfill \end{array}$$

Define matrix-valued function ${\Psi }^{\prime }:{\mathbb{R}}^{n\times n}\to {\mathbb{R}}^{(5n+2q)\times (5n+2q)}$ as follows:

$$\begin{array}{cc}\hfill {\Psi }^{\prime }(\Lambda )=& \left(\begin{array}{cc}\left(\begin{array}{cccc}{\psi }_{11}^{\prime }(\Lambda )& {\psi }_{12}^{\prime }(\Lambda )& {\psi }_{13}^{\prime }& {\psi }_{14}^{\prime }\\ \ast & {\psi }_{22}^{\prime }& {\psi }_{23}^{\prime }& \epsilon {\psi }_{14}^{\prime }\\ \ast & \ast & {\psi }_{33}^{\prime }& 0\\ \ast & \ast & \ast & {\psi }_{44}^{\prime }\end{array}\right)& {\zeta }^{\prime }\\ \\ \ast & {\Delta }^{\prime }\end{array}\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\psi }_{11}^{\prime }(\Lambda )=& {\Lambda }^{T}Z+Z^T\Lambda +M-L+I_{\Lambda },\hfill \\ \hfill {\psi }_{12}^{\prime }(\Lambda )=& X-Z^T+\epsilon {\Lambda }^{T}Z,\hfill \\ \hfill {\psi }_{13}^{\prime }=& L+Z^{T}BK\hfill \\ \hfill {\psi }_{14}^{\prime }=& Z^{T}BK,\hfill \\ \hfill {\psi }_{16}^{\prime }=& Z^{T}G,\hfill \\ \hfill {\psi }_{22}^{\prime }=& -\epsilon (Z+Z^T)+{\tau }^{\prime 2}M+{\overline{\tau }}^{2}U,\hfill \\ \hfill {\psi }_{23}^{\prime }=& \epsilon Z^{T}BK,\hfill \\ \hfill {\psi }_{27}^{\prime }=& \sqrt{\epsilon }{Z}^{T}G,\hfill \\ \hfill {\psi }_{33}^{\prime }=& -M-L,\hfill \\ \hfill {\psi }_{44}^{\prime }=& -{\displaystyle \frac{{\pi }^2}{4}}U.\hfill \end{array}$$

Lemma 4

(No uncertainties in the control gain). Assume there exist $n\times n$-dimensional matrices $U>0$, $X>0$, $M>0$, $L>0$, Z nonsingular, and $K\in {\mathbb{R}}^{m\times n}$, and scalars $\epsilon >0$ and $\gamma >0$, so that at least one of the following conditions holds:

1. 

The eigenvalues of matrix E satisfy

$${\Psi }^{\prime }(A+d_{1}H)<0,{\Psi }^{\prime }(A+d_{N}H)<0.$$

(19)

2. 

The system is symmetrically connected, and

$$\begin{array}{c}\hfill {\Psi }^{\prime }(A-H)<0,{\Psi }^{\prime }(A+(N-1)H)<0.\end{array}$$

(20)

Then, $\Psi <0$.

Proof. 

In the first case, note that the matrix-valued $\Psi (A+dH)$ function is convex in d. Hence, conditions (19) imply $\Psi (A+d_{j}H)<0$ for all $j=1,\dots ,N$.

With help of relation (3), we introduce matrix ${\tilde{\Sigma }}_1$, defined by ${\tilde{\Sigma }}_1=\Sigma (I_E\otimes A+D^{\prime }\otimes H,\mathcal{B},\mathcal{X},\mathcal{Z},\mathcal{M},\mathcal{L},\mathcal{U},\mathcal{K},\epsilon )$,

$$\tilde{\Psi }=\left(\begin{array}{cc}{\tilde{\Sigma }}_1& \zeta \\ \ast & \Delta \end{array}\right).$$

If the first condition in the formulation of this lemma holds, observe that there exists a permutation matrix $\Pi$, such that

$$\tilde{\Psi }={\Pi }^T\mathrm{diag}({\Psi }^{\prime }(A+d_{1}H),\dots ,{\Psi }^{\prime }(A+d_{N}H))\Pi ,$$

hence, $\tilde{\Psi }<0$.

Define now $\mathcal{T}=\mathrm{diag}(T^{\prime }\otimes I_A,T^{\prime }\otimes I_A,T^{\prime }\otimes I_A,T^{\prime }\otimes I_A,T^{\prime }\otimes I_A,T^{\prime }\otimes I_{G^{T}G},T^{\prime }\otimes I_{G^{T}G})$. Properties of the Kronecker product imply $\Psi ={\mathcal{T}}^{-1}\tilde{\Psi }\mathcal{T}$, and one has $\Psi <0$.

If condition (20) holds, then define

${\mathcal{T}}^{″}=\mathrm{diag}(T^{″}\otimes I_A,T^{″}\otimes I_A,T^{″}\otimes I_A,T^{″}\otimes I_A,T^{″}\otimes I_A,T^{″}\otimes I_{G^{T}G},T^{″}\otimes I_{G^{T}G})$. Then, there is a permutation matrix ${\Pi }^{″}$, such that

$$\begin{array}{c}\hfill \Psi ={\left({\mathcal{T}}^{″}\right)}^{-1}{\Pi }^{″T}\mathrm{diag}\left({\Psi }^{\prime }(A+(N-1)H),\underset{N-1\mathrm{times}}{\underbrace{{\Psi }^{\prime }(A-H),\dots ,{\Psi }^{\prime }(A-H)}}\right){\Pi }^{″}{\mathcal{T}}^{″}\end{array}$$

which implies $\Psi <0$. This completes the proof of this case. □

To handle the case with uncertainties in the control gain, let us define matrices

$$\begin{array}{cc}\hfill {\overline{\psi }}_{11}^{\prime }(\Lambda )=& {\psi }_{11}^{\prime }(\Lambda )+Z^{T}B{D}_{K}J{D}_K^T{B}^{T}Z,\hfill \\ \hfill {\overline{\psi }}_{12}^{\prime }(\Lambda )=& {\psi }_{12}^{\prime }(\Lambda )+\epsilon Z^{T}B{D}_{K}J{D}_K^T{B}^{T}Z,\hfill \\ \hfill {\overline{\psi }}_{22}^{\prime }=& {\psi }_{22}^{\prime }+{\epsilon }^2{Z}^{T}B{D}_{K}J{D}_K^T{B}^{T}Z\hfill \end{array}$$

and a matrix-valued function ${\overline{\Psi }}^{\prime }:{\mathbb{R}}^{n\times n}\to {\mathbb{R}}^{(5n+2q)\times (5n+2q)}$ as follows:

$${\overline{\Psi }}^{\prime }(\Lambda )=\left(\begin{array}{ccc}\begin{array}{cccc}{\psi }_{11}^{\prime }(\Lambda )& {\psi }_{12}^{\prime }(\Lambda )& {\overline{\psi }}_{13}^{\prime }& {\overline{\psi }}_{14}^{\prime }\\ \ast & {\psi }_{22}^{\prime }& {\overline{\psi }}_{23}^{\prime }& \epsilon {\psi }_{14}^{\prime }\\ \ast & \ast & {\psi }_{33}^{\prime }& 0\\ \ast & \ast & \ast & {\psi }_{44}^{\prime }\end{array}& {\zeta }^{\prime }& \begin{array}{c}0\\ 0\\ E_K^T\\ E_K^T\end{array}\\ \ast & {\Delta }^{\prime }& 0\\ \ast & \ast & -J\end{array}\right).$$

Lemma 5

(Case with uncertainties in the control gain). Assume there exist $n\times n$-dimensional matrices $U>0$, $X>0$, $M>0$, $L>0$, Z nonsingular and $K\in {\mathbb{R}}^{m\times n}$, $J\in {\mathbb{R}}^{\nu \times \nu }$, such that $J>0$ and scalars $\epsilon >0$ and $\gamma >0$, so that at least one of the following conditions holds:

1. 

${\overline{\Psi }}^{\prime }(A+dH)$ for all $d\in \{d_1,d_N\}$.

2. 

The system is symmetrically connected and

${\overline{\Psi }}^{\prime }(A-H)<0$ as well as ${\overline{\Psi }}^{\prime }(A+(N-1)H)<0$.

Then, $\overline{\Psi }<0$.

The proof is analogous to the proof of Lemma 4; hence, it is omitted.

To derive the controller synthesis algorithm, the procedure is similar to that of [23]. Also let $Q=Z^{-1}$, $Y=K{Z}^{-1}$, $P=Z^{-T}X{Z}^{-1}$, $R=Z^{-T}M{Z}^{-1}$, $S=Z^{-T}L{Z}^{-1}$, and $W=Z^{-T}U{Z}^{-1}$. For $n\times n$-dimensional matrices $P>0$, $R>0$, $S>0$, $W>0$, Q nonsingular, a $m\times n$-dimensional matrix Y, and positive scalars $\gamma$, $\epsilon$, define matrices ${\xi }_{ij}$, $j=1,\dots ,4$ and a matrix-valued function $\Xi :{\mathbb{R}}^{n\times n}\to {\mathbb{R}}^{(5n+2q)\times (5n+2q)}$ by

$$\begin{array}{cc}\hfill {\xi }_{11}(\Lambda )=& Q^T{\Lambda }^T+\Lambda Q+R-S,\hfill \\ \hfill {\xi }_{12}(\Lambda )=& P-Q+\epsilon Q^T{\Lambda }^T,\hfill \\ \hfill {\xi }_{13}=& S+BY,\hfill \\ \hfill {\xi }_{14}=& BY,\hfill \\ \hfill {\xi }_{22}=& -\epsilon (Q+Q^T)+{\tau }^{\prime 2}R+{\overline{\tau }}^{2}W,\hfill \\ \hfill {\xi }_{23}=& \epsilon BY,\hfill \\ \hfill {\xi }_{33}=& -R-S,\hfill \\ \hfill {\xi }_{44}=& -{\displaystyle \frac{{\pi }^2}{4}}W,\hfill \end{array}$$

$$\Xi (\Lambda )=\left(\begin{array}{ccccccc}{\xi }_{11}(\Lambda )& {\xi }_{12}& {\xi }_{13}& {\xi }_{14}& Q^T& G& 0\\ \ast & {\xi }_{22}& {\xi }_{23}& \epsilon {\xi }_{14}& 0& 0& \sqrt{\epsilon }G\\ \ast & \ast & {\xi }_{33}& 0& 0& 0& 0\\ \ast & \ast & \ast & {\xi }_{44}& 0& 0& 0\\ \ast & \ast & \ast & \ast & -I_{\Lambda }& 0& 0\\ \ast & \ast & \ast & \ast & \ast & -\gamma I_{G{G}^T}& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -\gamma I_{G{G}^T}\end{array}\right).$$

Also define $\overline{\Xi }:{\mathbb{R}}^{n\times n}\to {\mathbb{R}}^{(5n+2q)\times (5n+2q)}$ as

$$\begin{array}{cc}\hfill {\overline{\xi }}_{11}(\Lambda )=& Q^T{\Lambda }^T+\Lambda Q+R-S+B{D}_{K}J{D}_K^T{B}^T,\hfill \\ \hfill {\overline{\xi }}_{12}(\Lambda )=& P-Q+\epsilon Q^T{\Lambda }^T+\epsilon B{D}_{K}J{D}_K^T{B}^T,\hfill \\ \hfill {\overline{\xi }}_{22}=& -\epsilon (Q+Q^T)+{\tau }^{\prime 2}R+{\overline{\tau }}^{2}W+{\epsilon }^{2}B{D}_{K}J{D}_K^T{B}^T,\hfill \end{array}$$

$$\overline{\Xi }(\Lambda )=\left(\begin{array}{cccccccc}{\overline{\xi }}_{11}(\Lambda )& {\overline{\xi }}_{12}(\Lambda )& {\xi }_{13}& {\xi }_{14}& Q^T& G& 0& 0\\ \ast & {\overline{\xi }}_{22}& {\xi }_{23}& \epsilon {\xi }_{14}& 0& 0& G& 0\\ \ast & \ast & {\xi }_{33}& 0& 0& 0& 0& Q^T{E}_K^T\\ \ast & \ast & \ast & {\xi }_{44}& 0& 0& 0& Q^T{E}_K^T\\ \ast & \ast & \ast & \ast & -I_{\Lambda }& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & -\gamma I_{G{G}^T}& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -\gamma I_{G{G}^T}& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -J\end{array}\right).$$

Lemma 6.

Consider System (4). Let there exist $n\times n$-dimensional matrices $P>0$, $R>0$, $S>0$, $W>0$, Q nonsingular, a $m\times n$-dimensional matrix Y, and positive scalars γ, ε. Then, for every matrix $\Lambda \in {\mathbb{R}}^{n\times n}$, $\Xi (\Lambda )<0$ holds if and only if $\Psi (\Lambda )<0$.

Proof. 

Let $\overline{\mathcal{Q}}=\mathrm{diag}(Q^{-1},Q^{-1},Q^{-1},Q^{-1},I_{\Lambda },I_{G^{T}G},I_{G^{T}G}).$ Then, ${\overline{\mathcal{Q}}}^T\Xi (\Lambda )\overline{\mathcal{Q}}=\Psi (\Lambda ).$ □

The following analogous result holds for the case with uncertainties in the control gain.

Lemma 7.

Let the assumptions of Lemma 6 hold; moreover, let there exist a $n\times n$-dimensional matrix $J>0$. Then, the condition $\overline{\Xi }(\Lambda )<0$ holds if and only if $\overline{\Psi }(\Lambda )<0$.

Proof. 

The proof is analogous to the proof of Lemma 6. The only difference is that matrix $\overline{\mathcal{Q}}$ is defined as $\overline{\mathcal{Q}}=\mathrm{diag}(Q^{-1},Q^{-1},Q^{-1},Q^{-1},I_A,I_{G^{T}G},I_{G^{T}G},I_{E_K^T{E}_K})$. □

The following theorem summarizes the results of the above lemmas.

Theorem 2.

1. Consider System (4). Let there exist $n\times n$-dimensional matrices $P>0$, $R>0$, $S>0$, $W>0$, Q nonsingular, a $m\times n$-dimensional matrix Y, and positive scalars γ, ε. Assume also the validity of at least one of the following conditions:

(a) 

$\Xi (A+d_{1}H)<0$ and $\Xi (A+d_{N}H)<0$.

(b) 

The overall system is symmetrically connected;

$\Xi (A-H)<0$ and $\Xi (A+(N-1\left)H\right)<0$.

Then, systems (1) for $i=1,\dots ,N$ are stabilized by the sampled control (5) where $K=Y{Q}^{-1}$.

2 

Assume moreover there exists a $n\times n$-dimensional matrix $J>0$, and assume at least one of the following conditions holds:

(a) 

$\overline{\Xi }(A+d_{1}H)<0$ and $\overline{\Xi }(A+d_{N}H)<0$.

(b) 

The overall system is symmetrically connected, and

$\overline{\Xi }(A-H)<0$ and $\overline{\Xi }(A+(N-1)H)<0$.

Then, System (1) for $i=1,\dots ,N$ is stabilized by the Control (7) with matrices $K_i$ given by (6), where $K=Y{Q}^{-1}$.

Proof of Theorem 2.

The first part is a consequence of Lemmas 6 and 4, the second part is the consequence of Lemmas 6 and 5. □

Remark 9.

Minimization of the parameter γ leads to the $H_{\infty }$-optimal control.

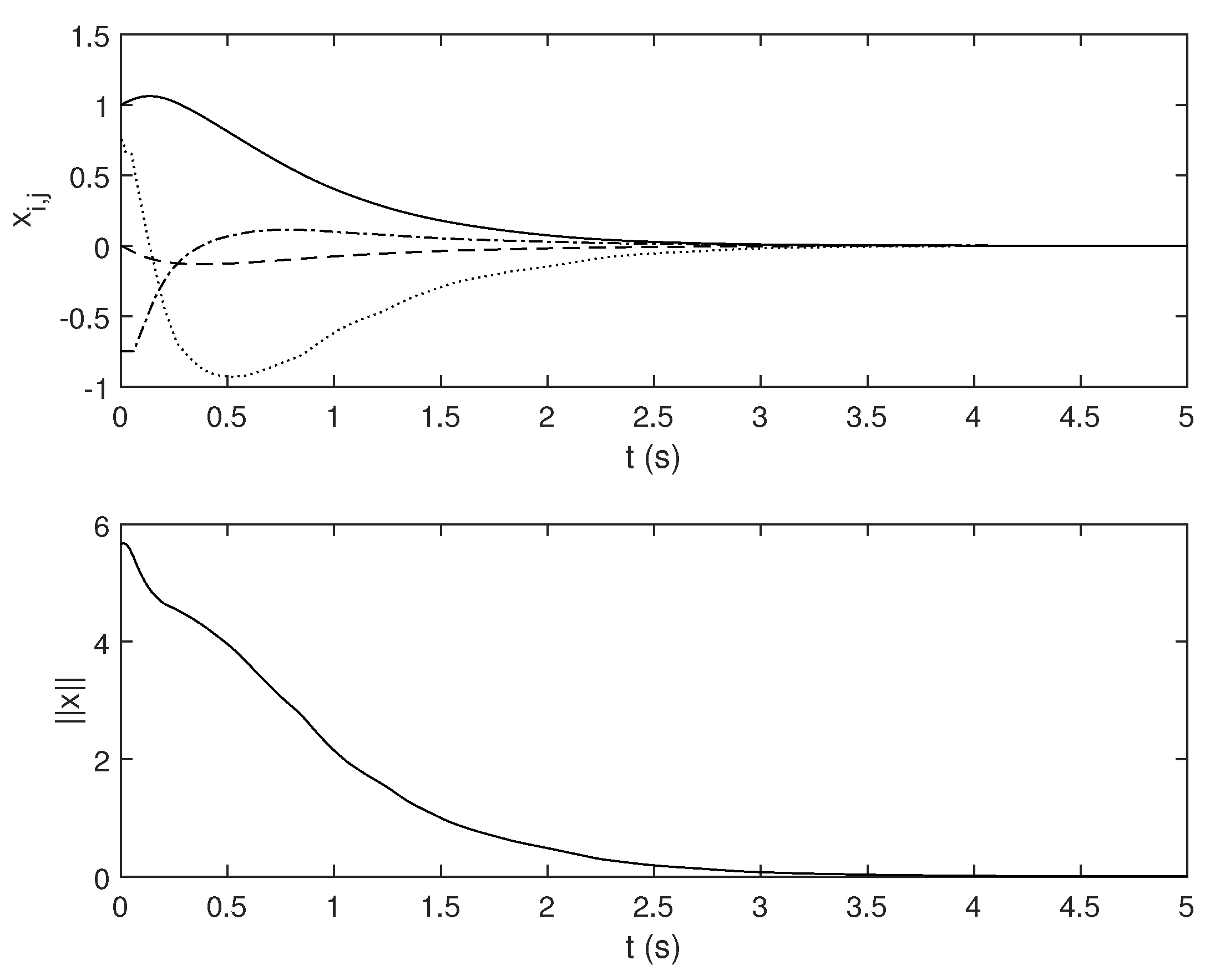
4. Examples

4.1. Example 1

System (4) is composed of 10 subsystems given as follows. The system matrices are given as $A=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$, $B=\left(\begin{array}{c}0\\ 1\end{array}\right)$, $H={\displaystyle \frac{1}{2}}\left(\begin{array}{cc}0& 0\\ 1& 1\end{array}\right)$, $D_K=1$, $E_K=(1,1),E=\left(e_{ij}\right),e_{i,i+1}=1,$ $e_{i+1,i}=1,i=1,\dots ,9,e_{ij}=0$ elsewhere; its eigenvalues are in the interval $[-1.92,1.92]$. Note that the overall system is unstable. Time delays are defined as ${\tau }^{\prime }=0.01s$, $\overline{\tau }=0.08s$. The sampling occurs at different time instants for different subsystems.

The LMI optimization problem obtained in this example is feasible. Computations from the previous section yield $K=(-3.70,-4.29),\gamma =9.36.$ The initial condition was chosen as $x\left(0\right)={(1,0.75,1,0,0,2,-1,2,0,-0.75,1,-2,1,0,2,0,-2,2,-1,-1)}^T.$

Figure 1 illustrates the results. The upper subplot shows the state $x_{1,1}$ (solid line), $x_{1,2}$ (dotted line), $x_{5,1}$ (dashed line) and $x_{5,2}$ (dash-dot line). The lower subplot illustrates the norm of the vector $x\left(t\right)$. There were no disturbances present in the simulated system. Therefore, the control algorithm achieved a full stabilization of the overall system, in spite of the presence of the interconnections. If some disturbances act upon the system, the state of the system would not, in general, achieve the zero value in the limit. However, the norm of the state would be, for a sufficiently large time, bounded by (16). The simulations were obtained using the Matlab R2021b software.

4.2. Example 2

The purpose of this example is to provide a fair comparison of the algorithm presented here with the algorithm derived in [6]. Both methods are applied to identical systems with equal parameters.

Matrices defining the ith subsystem are given as

$A=\left(\begin{array}{cc}0& 1\\ -0.1& -0.8\end{array}\right)$, $B=\left(\begin{array}{c}0\\ 0.1\end{array}\right)$, $H=\left(\begin{array}{cc}0.01& 0\\ 0& 0.012\end{array}\right)$, $G=\left(\begin{array}{c}1\\ 1\end{array}\right)$.

The system is symmetrically interconnected; matrix $T^{″}$, introduced in Remark 1, was applied in both cases.

The results are summarized in

Table 1. Comparison of results.

$\mathit{N}=\mathbf{20}$
$\overline{\tau }\left(s\right)$	${\gamma }_R$	$K_R$	${\gamma }_W$	$K_W$
0.001	48.55	(−5.683, −4.868)	3.86	(−20.183, −14.360)
0.01	49.27	(−5.740, −4.942)	3.87	(−20.17, −14.35)
0.1	infeasible		3.91	(−19.79 −13.99)
$\mathit{N}=\mathbf{30}$
$\overline{\tau }\left(s\right)$	${\gamma }_R$	$K_R$	${\gamma }_W$	$K_W$
0.001	55.38	(−6.34, −5.48)	4.31	(−21.39, −14.17)
0.01	56.42	(−6.40, −5.56)	4.32	(−21.39, −15.18)
0.1	infeasible		4.46	(−20.93 −14.77)

for various values of $\overline{\tau }$ and various numbers N of subsystems that were computed using the approach presented in this paper (values $K_W$ and ${\gamma }_W$, denoted by K and $\gamma$, respectively, in the above text) and a compared with results obtained by the method based on the Razumikhin functional as described in [6] (values $K_R$ and ${\gamma }_R$; these quantities are denoted by K and $\gamma$, respectively, in [6]).

In both cases, the value of the constant $\gamma$ computed by the LMIs based on the Wirtinger inequality is considerably smaller. Thus, the presented algorithm exhibits a better capability of disturbance attenuation. Also, it is capable of handling a larger set of parameters of the optimization problem.

5. Conclusions

An algorithm for the stabilization of large-scale interconnected systems with sampled controls was presented. The algorithm is based on the Wirtinger inequality. Results of the presented approach were compared with results previously obtained using an algorithm based on the Razumikhin functional. It is shown that the method presented here is less conservative. On the other hand, it is to point out that the method is applicable to linear systems; nonlinearities must be approximated using the Lipschitz property in combination with methods known from the robust control, hence leading to an overly conservative design.

In future research, we intend to focus on more nonlinear systems, systems with delays, and/or systems with fractional derivatives (see, e.g., [28]); the ultimate goal is to apply the proposed method in a practical setting.