Elliptic Quaternion Matrices: A MATLAB Toolbox and Applications for Image Processing
Abstract
1. Introduction
2. Mathematical Preliminaries
2.1. Elliptic Numbers
2.2. Elliptic Quaternions
3. MATLAB Toolbox for Elliptic Numbers and Elliptic Quaternions
| Listing 1. MATLAB console output of the function elliptic_number(). |
 |
| Listing 2. MATLAB console output of the functions elliptic_quaternion() and elliptic_q_product(). |
 |
| Listing 3. MATLAB console output of the functions elliptic_quaternion() and elliptic_q_svd(). |
  |
| Listing 4. MATLAB console output of the functions elliptic_quaternion() and elliptic_q_lss(). |
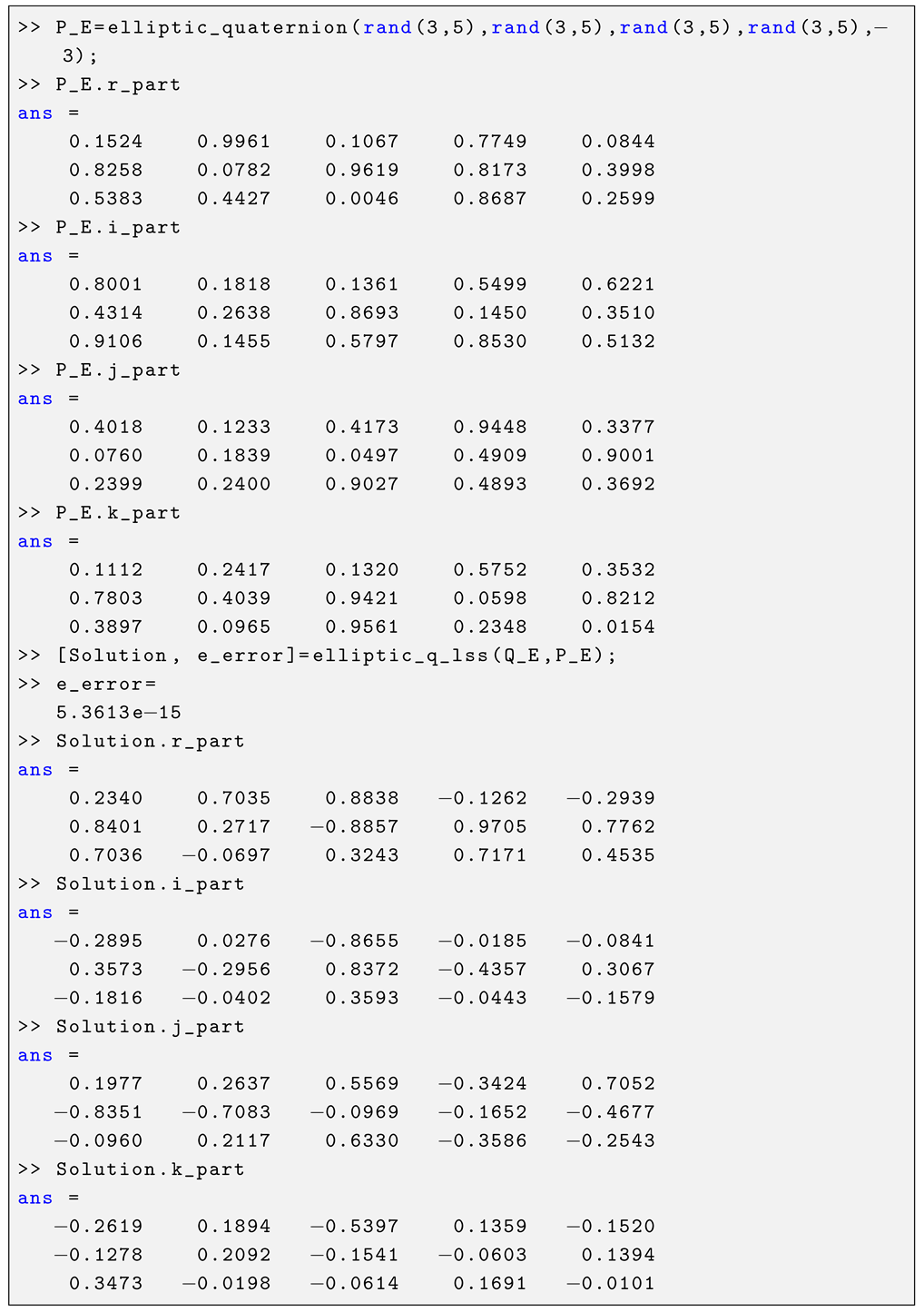 |
4. Color Image Processing Using Singular-Value Decomposition of Elliptic Quaternion Matrices
| Listing 5. MATLAB console output of the function image2elliptic(). |
 |
4.1. Eigenimages of Color Images
| Listing 6. MATLAB console output of the functions image2elliptic() and elliptic_q_eigenimage(). |
 |
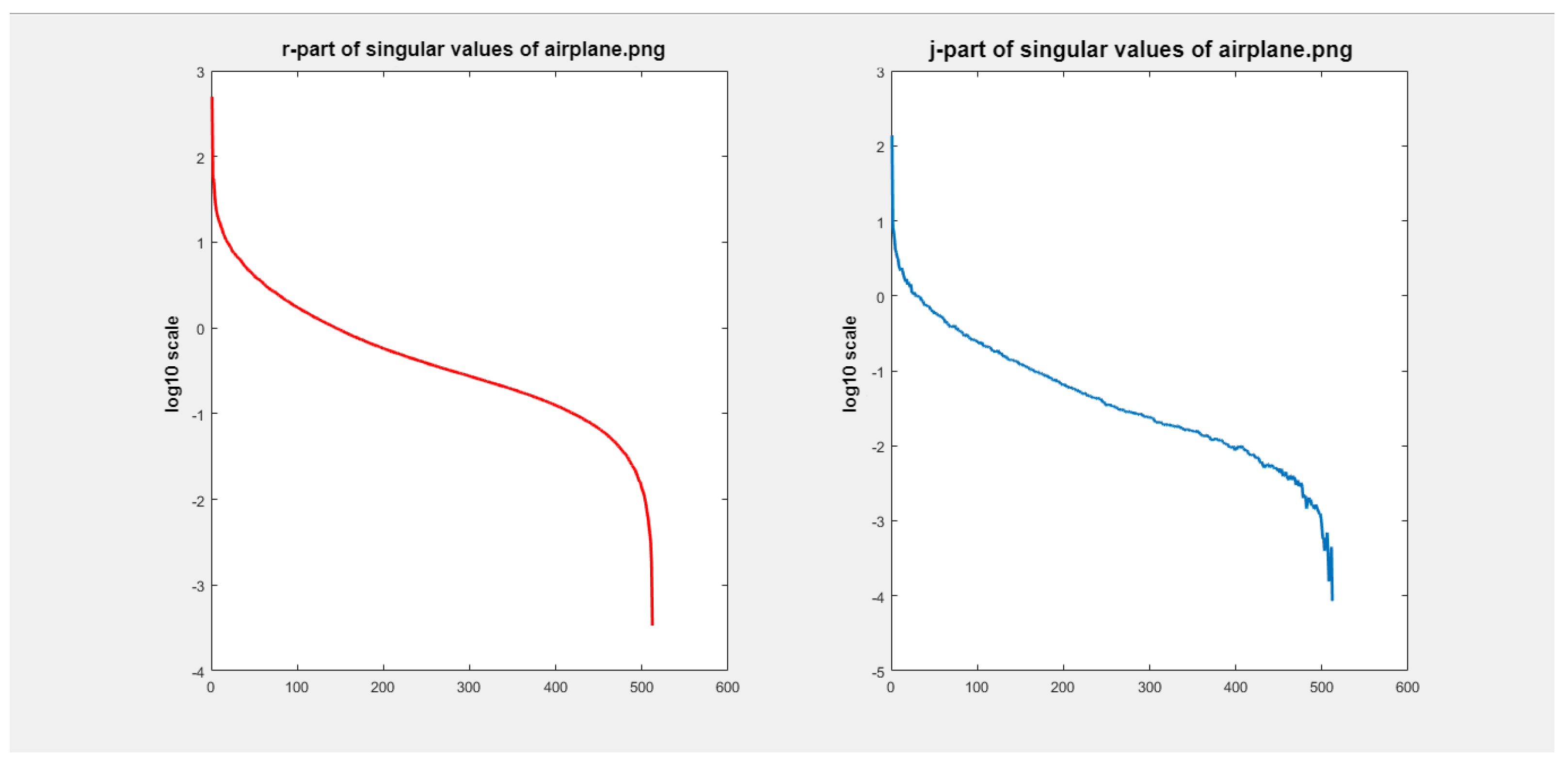
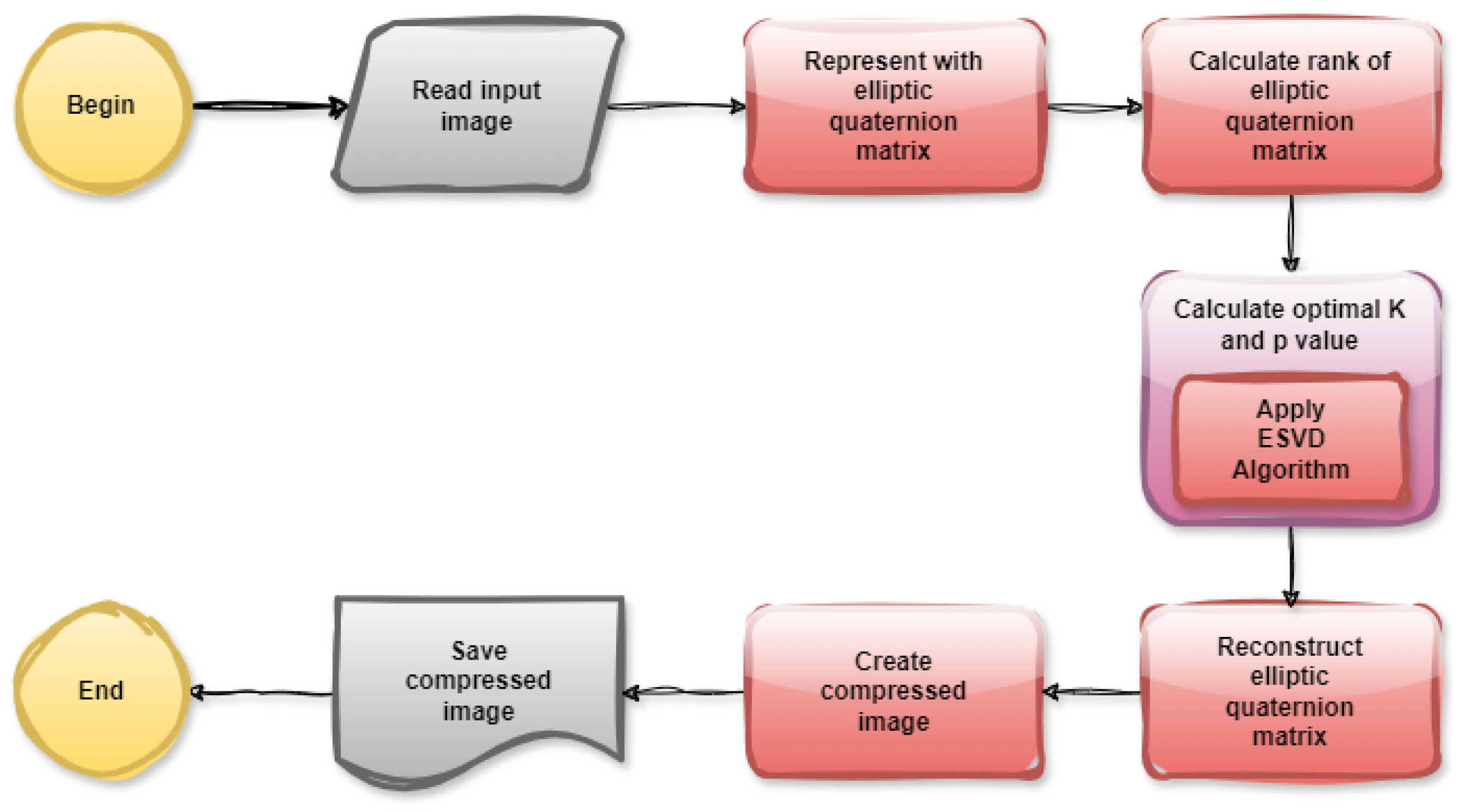
4.2. Color Image Compression with ESVD
| Listing 7. MATLAB console output of the functions image2elliptic() and elliptic_q_singularvalues(). |
 |
| Listing 8. MATLAB console output of the function elliptic_q_image_reconstruction(). |
 |
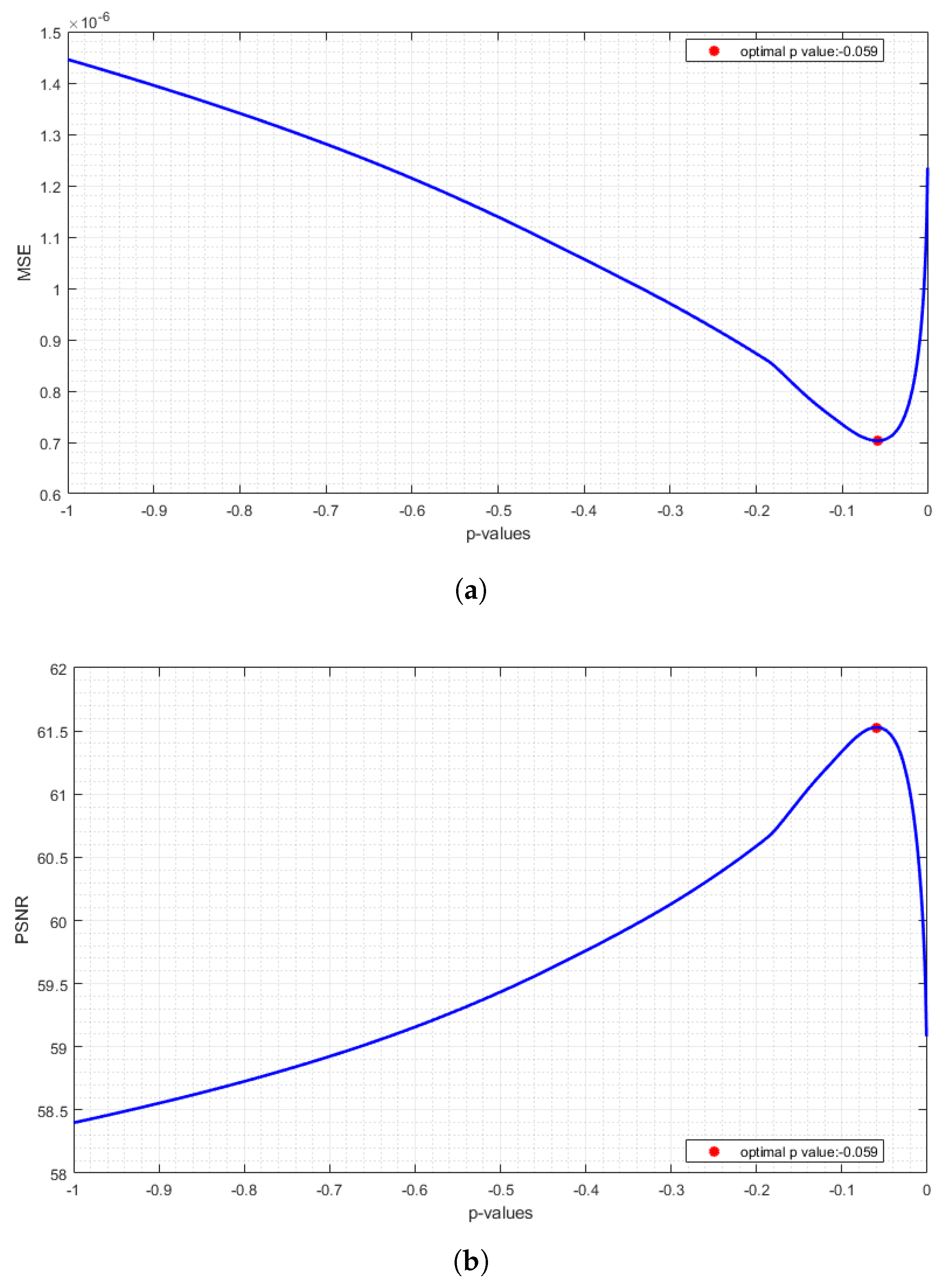
| Listing 9. MATLAB console output of the functions elliptic_q_optimal_p_for_psnr() and optimal_p_for_mse(). |
 |
4.3. Color Image Restoration with ESVD
- Step 1: An experimental test image is acquired for the ESVD-LSI image restoration method.
- Step 2: PSF is selected manually.
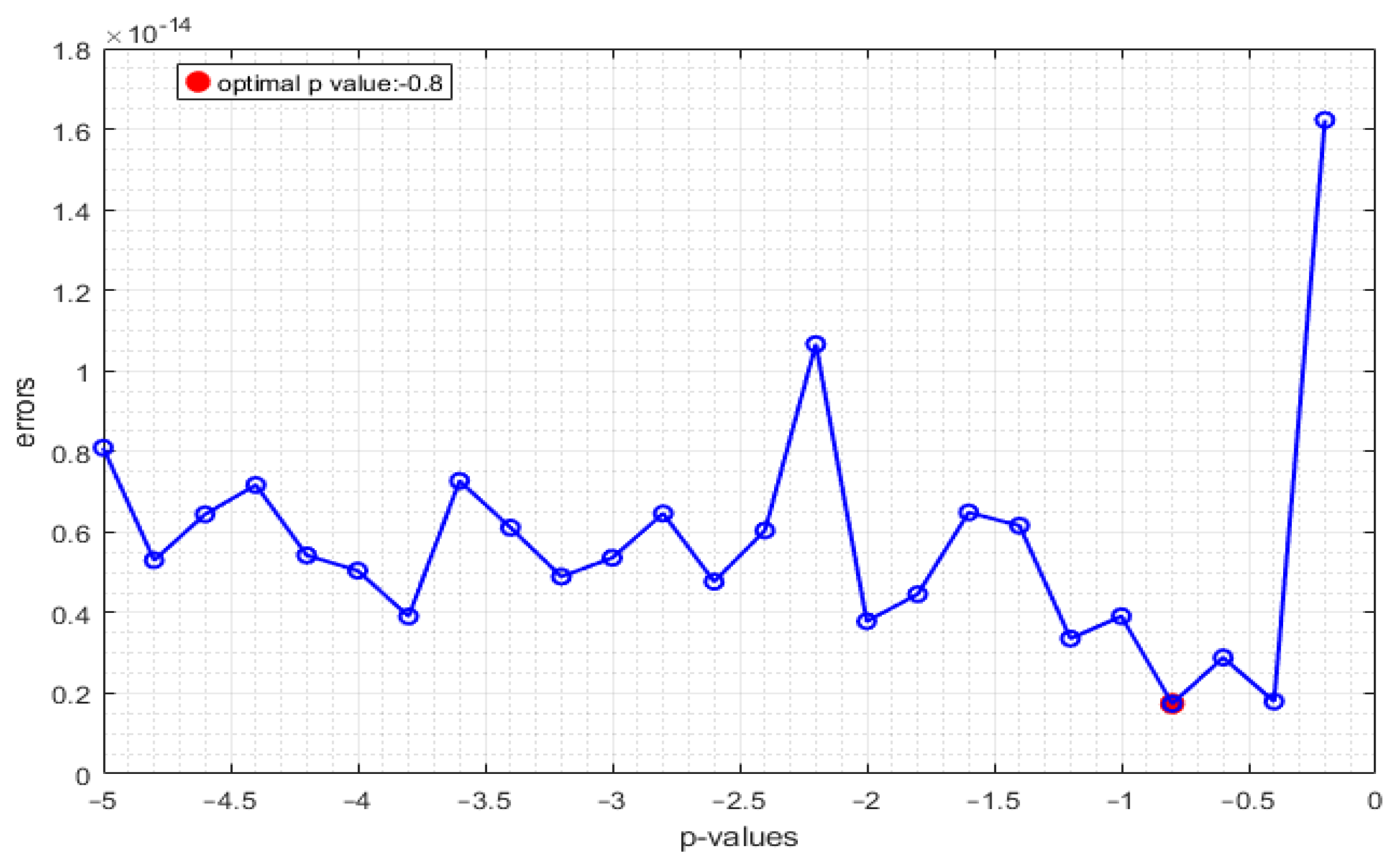
- Step 3: The range of p and step size are selected.
- Step 4: A degraded image is obtained.
- Step 5: According to Theorem 3, the least squares solution with the minimum norm of the elliptic quaternion matrix equation is
- Step 6: By using the step size and the range of p, the optimal p-value is obtained.
- Step 7: Finally, the enhanced image is obtained by reverse sampling from the elliptic quaternion matrices, which will be obtained by choosing the optimal p-value that makes the least squares error the smallest for .
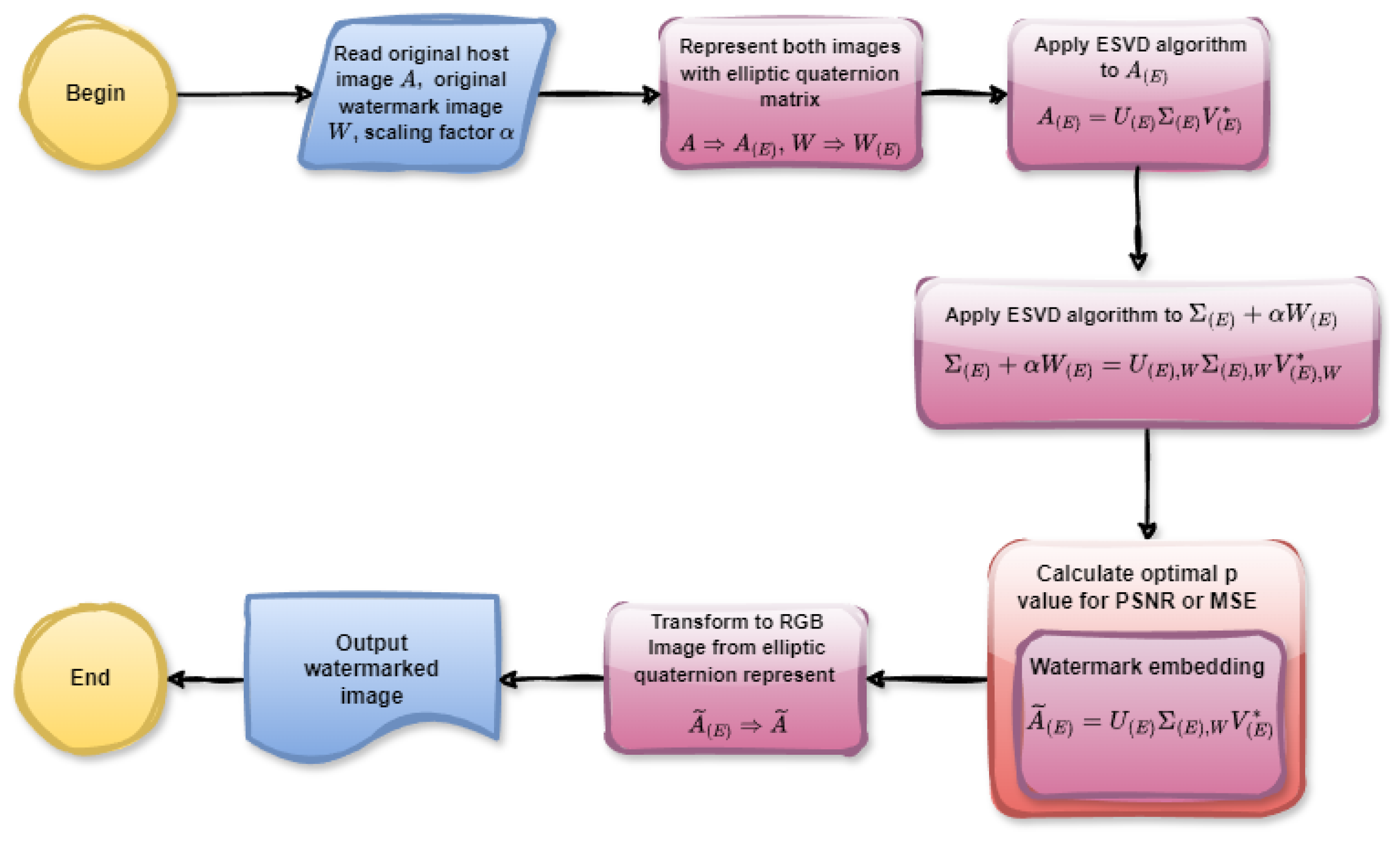
4.4. Color Image Watermarking with ESVD
| Listing 10. MATLAB console output of the functions image2elliptic() and elliptic_q_embedding_watermarking(). |
 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamilton, W.R. On a new species of imaginary quantities, connected with the theory of quaternions. Proc. R. Ir. Acad. 1840, 2, 424–434. [Google Scholar]
- Adler, S. Quaternionic Quantum Mechanics and Quantum Fields; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Mukundan, R. Quaternions. Advanced Methods in Computer Graphics: With Examples in OpenGL; Springer-Verlag London Limited: London, UK, 2012. [Google Scholar]
- Ell, T.A.; Bihan, N.L.; Sangwine, S.J. Quaternion Fourier Transforms for Signal and Image Processing; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Parcollet, T.; Morchid, M.; Linares, G. A survey of quaternion neural networks. Artif. Intell. Rev. 2020, 53, 2957–2982. [Google Scholar] [CrossRef]
- Sangwine, S.J.; Bihan, N.L. Quaternion Toolbox for Matlab. Available online: http://qtfm.sourceforge.net/ (accessed on 22 August 2024).
- Pei, S.C.; Chang, J.H.; Ding, J.J. Commutative Reduced Biquaternions and Their Fourier Transform for Signal and Image Processing Applications. IEEE Trans. Signal Process 2004, 52, 2012–2031. [Google Scholar] [CrossRef]
- Navarro-Moreno, J.; Fernández-Alcalá, R.M.; Ruiz-Molina, J.C. Proper ARMA Modeling and Forecasting in the Generalized Segre’s Quaternions Domain. Mathematics 2022, 10, 1083. [Google Scholar] [CrossRef]
- Catoni, F.; Cannata, R.; Zampetti, P. An introduction to commutative quaternions. Adv. Appl. Clifford Algebr. 2006, 16, 1–28. [Google Scholar] [CrossRef]
- Catoni, F.; Boccaletti, D.; Cannata, R.; Catoni, V.; Nichelatti, E.; Zampetti, P. The Mathematics of Minkowski Space–Time: With an Introduction to Commutative Hypercomplex Numbers; Birkhäuser: Basel, Switzerland, 2008. [Google Scholar]
- Yaglom, I.M. A Simple Non-Euclidean Geometry and Its Physical Basis; Springer: New York, NY, USA, 1979. [Google Scholar]
- Condurache, D.; Burlacu, A. Dual tensors based solutions for rigid body motion parameterization. Mech. Mach. Theory 2014, 74, 390–412. [Google Scholar] [CrossRef]
- Catoni, F.; Cannata, R.; Zampetti, P. An introduction to constant curvature spaces in the commutative (Segre) quaternion geometry. Adv. Appl. Clifford Algebr. 2006, 16, 85–101. [Google Scholar] [CrossRef]
- Gai, S. Theory of reduced biquaternion sparse representation and its applications. Expert Syst. Appl. 2023, 213, 119245. [Google Scholar] [CrossRef]
- Kosal, H.H.; Kisi, E.; Akyigit, M.; Celik, B. Elliptic Quaternion Matrices: Theory and Algorithms. Axioms 2024, 13, 656. [Google Scholar] [CrossRef]
- Gai, S.; Huang, X. Reduced biquaternion convolutional neural network for color image processing. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 1061–1075. [Google Scholar] [CrossRef]
- Kobayashi, M. Twin-multistate commutative quaternion Hopfield neural networks. Neurocomputing 2018, 320, 150–156. [Google Scholar] [CrossRef]
- Atali, G.; Kosal, H.H.; Pekyaman, M. A new image restoration model associated with special elliptic quaternionic least-squares solutions based on LabVIEW. J. Comput. Appl. Math. 2023, 425, 115071. [Google Scholar] [CrossRef]
- Harkin, A.A.; Harkin, J.B. Geometry of generalized complex numbers. Math. Mag. 2004, 77, 118–129. [Google Scholar] [CrossRef]
- Tosun, M.; Kösal, H.H. An Algorithm for Solving the Sylvester s-Conjugate Elliptic Quaternion Matrix Equations. In Algorithms as a Basis of Modern Applied Mathematics. Studies in Fuzziness and Soft Computing; Hošková-Mayerová, Š., Flaut, C., Maturo, F., Eds.; Springer: Cham, Switzerland, 2021; Volume 404. [Google Scholar]
- Chang, J.H.; Ding, J.J. Quaternion matrix singular value decomposition and its applications for color image processing. In Proceedings of the 2003 International Conference on Image Processing (Cat. No. 03CH37429), Barcelona, Spain, 14–17 September 2003; Volume 1, p. I-805. [Google Scholar]
- Pei, S.C.; Chang, J.H.; Ding, J.J.; Chen, M.Y. Eigenvalues and singular value decompositions of reduced biquaternion matrices. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 2673–2685. [Google Scholar]
- Gunturk, B.K. Fundamental of image restoration. In Image Restoration Fundamentals and Advances; Gunturk, B.K., Li, X., Eds.; CRC Press: New York, NY, USA, 2013; pp. 25–61. [Google Scholar]
- Abd El-Samie, F.E. An efficient singular value decomposition algorithm for digital audio watermarking. Int. J. Speech Technol. 2009, 12, 27–45. [Google Scholar] [CrossRef]
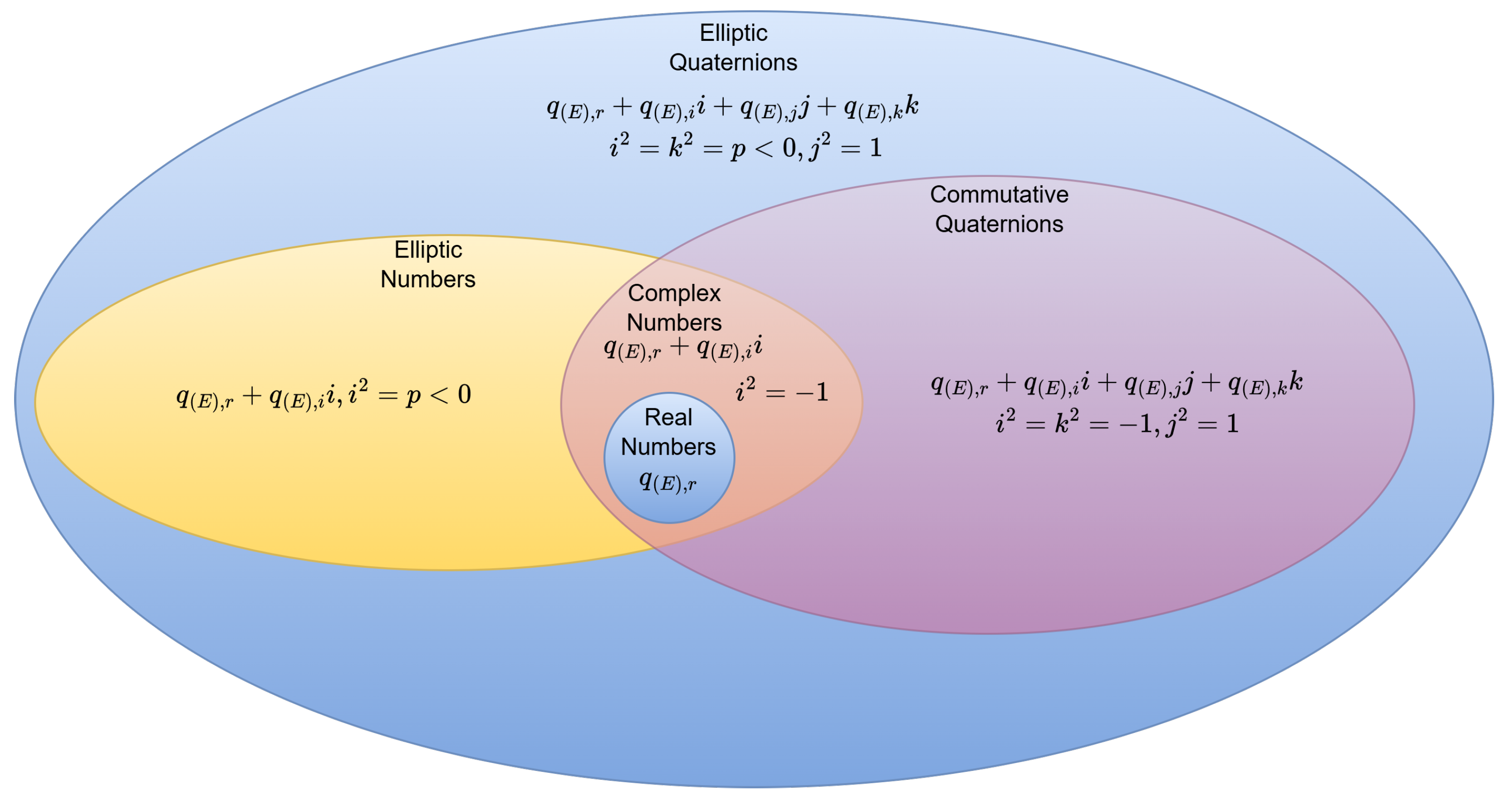













| Function Name | Description |
|---|---|
| ellipticcomplex2complexnumber() | Returns the complex number (or matrix) to which the elliptic number (or matrix) is isomorphic. |
| complexnumber2ellipticcomplex(-value, complex) | Returns the elliptic number (or matrix) to which the complex number (or matrix) is isomorphic. |
| elliptic_n_addition(,) | Returns the sum of two elliptic numbers (or matrices). |
| elliptic_n_subtraction(,) | Returns the difference of two elliptic numbers (or matrices). |
| elliptic_n_product(,) | Returns the product of two elliptic numbers (or matrices). |
| elliptic_n_transpose() | Returns the transpose of the elliptic matrix . |
| elliptic_n_conjugate() | Returns the conjugate of the elliptic matrix . |
| elliptic_n_hermitianconjugate() | Returns the Hermitian conjugate of the elliptic matrix . |
| elliptic_n_eig() | [,] = elliptic_n_eig() returns diagonal matrix of eigenvalues and matrix whose columns are the corresponding eigenvectors, so that . |
| elliptic_n_svd() | [,,] = elliptic_n_svd() performs a singular-value decomposition of elliptic matrix , such that . |
| elliptic_n_pinv() | Returns the pseudoinverse of the elliptic matrix . |
| elliptic_n_rank() | Returns the rank of the elliptic matrix . |
| elliptic_n_lss() | Returns the least squares solution of the elliptic matrix equation and the least squares error. |
| Function Name | Description |
|---|---|
| e1e2form() | Returns the elliptic quaternion (or elliptic quaternion matrix) given in ijk-form in - form. |
| ijkform(e1_part,e2_part) | Returns the elliptic quaternion (or elliptic quaternion matrix) given in - form in ijk form. |
| elliptic_q_conjugate_1() | Returns the 1st conjugate of the elliptic quaternion (or elliptic quaternion matrix). |
| elliptic_q_conjugate_2() | Returns the 2nd conjugate of the elliptic quaternion (or elliptic quaternion matrix). |
| elliptic_q_conjugate_3() | Returns the 3rd conjugate of the elliptic quaternion (or elliptic quaternion matrix). |
| elliptic_q_addition(,) | Returns the sum of two elliptic quaternions (or elliptic quaternion matrices). |
| elliptic_q_subtraction(,) | Returns the difference of two elliptic quaternions (or elliptic quaternion matrices). |
| elliptic_q_product(,) | Returns the product of two elliptic quaternions (or elliptic quaternion matrices). |
| elliptic_q_scalar(lamda,) | Returns the lambda scalar multiple of the elliptic quaternion (or elliptic quaternion matrix). |
| elliptic_q_norm() | Returns the norm of the elliptic quaternion (or elliptic quaternion matrix). |
| elliptic_q_transpose() | Returns the transpose of the elliptic quaternion matrix. |
| elliptic_q_hermitianconjugate() | Returns the conjugate transpose of the elliptic quaternion matrix. |
| elliptic_q_eig() | [,] = elliptic_q_eig() returns diagonal matrix of eigenvalues and matrix whose columns are the corresponding eigenvectors, so that . |
| elliptic_q_svd() | [,,] = elliptic_q_svd() performs a singular-value decomposition of elliptic quaternion matrix , such that . |
| elliptic_q_pseudoinverse() | Returns the pseudoinverse of the elliptic quaternion matrix. |
| elliptic_q_lss(,) | Returns the least squares solution of the elliptic quaternion matrix equation and the least squares error. |
| elliptic_q_qrank() | Returns the rank of the elliptic matrix. |
| Function Name | Description |
|---|---|
| image2elliptic_q(I,-value) | Returns the elliptic quaternion matrix representation of the image. |
| I (Type: uint8, array): The input image in RGB color space | |
| p-value (Type: negative double) | |
| elliptic_q2image() | Returns the RGB space representation of an image represented by an elliptical quaternion matrix. |
| (Type: Object): The elliptic quaternion matrix representation of the image. | |
| elliptic_q_eigenimage(,h) | Returns the desired eigenimages of the image in the elliptic quaternion matrix space. |
| h (Type: integer): Specifies the index of the eigenimage to be computed. | |
| elliptic_q_singularvalues() | It shows the change of singular values of the image in the elliptical quaternion matrix space. |
| elliptic_q_image_reconstruction(,k) | It compresses the image according to the desired k value in the elliptical quaternion matrix space. |
| k (Type: integer): The number of singular values to retain for the reconstruction. | |
| elliptic_q_optimal_p_for_psnr() | Returns the optimal p (for psnr) value for image compression performed in elliptic quaternion matrix space. |
| elliptic_q_optimal_p_for_mse() | Returns the optimal p (for mse) value for image compression performed in elliptic quaternion matrix space. |
| elliptic_q_embedding_watermarking(,,alpha) | The embedding_elliptic_watermarking function embeds a watermark into an object using elliptic quaternion matrix algebra. |
| (Type: Object): The primary object to be watermarked. | |
| (Type: Object): The watermark object to be embedded. | |
| alpha (Type: Double): The embedding strength parameter. | |
| elliptic_q_extraction_watermarking(,,U_w,V_w,alpha) | The extraction_elliptic_watermarking function extracts a watermark from a watermarked object using the elliptic quaternion matrix algebra. |
| (Type: Object): The watermarked object from which the watermark is to be extracted. | |
| (Type: Object): The original, unwatermarked object. | |
| U_w (Type: Object): The U component of the watermark’s singular-value decomposition. | |
| V_w (Type: Object): The V component of the watermark’s singular-value decomposition. | |
| elliptic_q_watermarking_optimal_p_for_psnr(,,alpha) | Finds the optimal p (for psnr) for watermarking using the elliptic quaternion matrix algebra |
| (Type: Object): The primary object to be watermarked. | |
| (Type: Object): The watermark object to be embedded. | |
| elliptic_q_watermarking_optimal_p_for_mse(,,alpha) | Finds the optimal p (for mse) for watermarking using the elliptic quaternion matrix algebra. |
| (Type: Object): The primary object to be watermarked. | |
| (Type: Object): The watermark object to be embedded. |
| Methods | K | airplane.png | baboon.png | baby.png | Barbara.png | monarch.png | peppers.png |
|---|---|---|---|---|---|---|---|
| Seperable | 10 | 22.47626 | 19.22365 | 23.97807 | 20.17889 | 19.47392 | 21.49341 |
| QSVD | 10 | 22.4593 | 19.2345 | 23.9613 | 20.1977 | 19.4925 | 21.4130 |
| RBSVD | 10 | 22.5009 | 19.3129 | 24.0043 | 20.2469 | 19.561 | 21.4875 |
| ESVD (Proposed Method) | 10 | 22.5705 () | 19.3139 () | 24.0406 () | 20.2534 () | 19.5665 () | 21.5484 () |
| Seperable | 50 | 30.53264 | 22.36072 | 32.18642 | 25.47954 | 27.17356 | 29.93859 |
| QSVD | 50 | 30.5012 | 22.3650 | 32.2036 | 25.5249 | 27.1818 | 29.9245 |
| RBSVD | 50 | 30.5456 | 22.504 | 32.2748 | 25.6348 | 27.2814 | 30.0184 |
| ESVD (Proposed Method) | 50 | 30.6426 () | 22.5321 () | 32.3295 () | 25.6730 () | 27.2899 () | 30.0510 () |
| Seperable | 90 | 35.29278 | 24.87109 | 36.67848 | 28.73954 | 31.59597 | 33.3296 |
| QSVD | 90 | 35.2712 | 24.8850 | 36.7164 | 28.7752 | 31.6127 | 33.3777 |
| RBSVD | 90 | 35.3386 | 25.0464 | 36.8034 | 28.9119 | 31.7219 | 33.4616 |
| ESVD (Proposed Method) | 90 | 35.4537 () | 25.0826 () | 36.8688 () | 28.9695 () | 31.7322 () | 33.4848 () |
| Seperable | 130 | 38.97289 | 27.25229 | 40.30344 | 31.8519 | 35.26918 | 35.70147 |
| QSVD | 130 | 38.9621 | 27.2877 | 40.3574 | 31.8910 | 35.3170 | 35.8012 |
| RBSVD | 130 | 39.0576 | 27.4817 | 40.4524 | 32.0467 | 35.4109 | 35.891 |
| ESVD (Proposed Method) | 130 | 39.1724 () | 27.5193 () | 40.5347 () | 32.1148 () | 35.4245 () | 35.9194 () |
| Methods | K | airplane.png | baboon.png | baby.png | Barbara.png | monarch.png | peppers.png |
|---|---|---|---|---|---|---|---|
| Seperable | 10 | 0.00565 | 0.01196 | 0.004 | 0.0096 | 0.01129 | 0.00709 |
| QSVD | 10 | 0.0057 | 0.0119 | 0.0040 | 0.0096 | 0.0112 | 0.0072 |
| RBSVD | 10 | 0.0056 | 0.011714 | 0.004 | 0.00944 | 0.0111 | 0.0071 |
| ESVD (Proposed Method) | 10 | 0.00553 () | 0.011711 () | 0.00394 () | 0.00943 () | 0.01104 () | 0.00700 () |
| Seperable | 50 | 0.00088 | 0.00581 | 0.0006 | 0.00283 | 0.00192 | 0.00101 |
| QSVD | 50 | 0.00089 | 0.0058 | 0.000602 | 0.0028 | 0.0019 | 0.0010 |
| RBSVD | 50 | 0.00088 | 0.0056 | 0.00059 | 0.00273 | 0.0019 | 0.00099 |
| ESVD (Proposed Method) | 50 | 0.00086 () | 0.0055 () | 0.00058 () | 0.00270 () | 0.00186 () | 0.00098 () |
| Seperable | 90 | 0.0003 | 0.00326 | 0.00021 | 0.00134 | 0.00069 | 0.00046 |
| QSVD | 90 | 0.000297 | 0.0032 | 0.000212 | 0.0013 | 0.00068 | 0.000459 |
| RBSVD | 90 | 0.00029 | 0.00312 | 0.000208 | 0.0013 | 0.000672 | 0.00045 |
| ESVD (Proposed Method) | 90 | 0.00028 () | 0.00310 () | 0.000205 () | 0.00126 () | 0.000671 () | 0.00044 () |
| Seperable | 130 | 0.00013 | 0.00188 | 0.00009 | 0.00065 | 0.0003 | 0.0003 |
| QSVD | 130 | 0.000127 | 0.0019 | 0.000092 | 0.00064 | 0.000293 | 0.00026 |
| RBSVD | 130 | 0.000124 | 0.0018 | 0.00009 | 0.00062 | 0.000287 | 0.000257 |
| ESVD (Proposed Method) | 130 | 0.00012 () | 0.0017 () | 0.00008 () | 0.00061 () | 0.000286 () | 0.000256 () |
| Methods | airplane.png | baboon.png | baby.png | Barbara.png | monarch.png | peppers.png |
|---|---|---|---|---|---|---|
| QSVD-LSI | ||||||
| RBSVD-LSI | ||||||
| ESVD-LSI (Proposed Method) |
| Methods | airplane.png | baboon.png | baby.png | Barbara.png | monarch.png | peppers.png | |
|---|---|---|---|---|---|---|---|
| Seperable | 0.05 | 56.9556 | 62.3572 | 56.5094 | 59.5572 | 58.6407 | 57.7683 |
| QSVD | 0.05 | 58.3759 | 65.2280 | 57.4869 | 60.8656 | 59.3973 | 59.7142 |
| RBSVD | 0.05 | 58.3989 | 64.8821 | 57.3881 | 60.6836 | 59.2756 | 59.7100 |
| ESVD (Proposed Method) | 0.05 | 61.5283 optimal | 66.2703 optimal | 58.9558 optimal | 61.5525 optimal | 60.9556 optimal | 61.8606 optimal |
| Methods | airplane.png | baboon.png | baby.png | Barbara.png | monarch.png | peppers.png | |
|---|---|---|---|---|---|---|---|
| Separable | 0.05 | ||||||
| QSVD | 0.05 | ||||||
| RBSVD | 0.05 | ||||||
| ESVD (Proposed Method) | 0.05 | optimal | optimal | optimal | optimal | optimal | optimal |
| Test Images | Noise 2% Gaussian | Cropping 25% | Noise + Cropping | Sharpening | Noise + Sharpening | Noise + Cropping + Sharpening | |
|---|---|---|---|---|---|---|---|
| airplane.png | 0.5 | 0.0142 | 0.0010 | 0.0086 | 0.0007 | 0.0396 | 0.0250 |
| baby.png | 0.5 | 0.0027 | 0.0017 | 0.0022 | 0.0018 | 0.0123 | 0.0071 |
| baboon.png | 0.5 | 0.0167 | 0.0005 | 0.0099 | 0.0006 | 0.0448 | 0.0281 |
| Barbara.png | 0.5 | 0.0104 | 0.0015 | 0.0072 | 0.0015 | 0.0313 | 0.0202 |
| monarch.png | 0.5 | 0.0131 | 0.0010 | 0.0077 | 0.0009 | 0.0354 | 0.0214 |
| peppers.png | 0.5 | 0.0088 | 0.0017 | 0.0066 | 0.0005 | 0.0256 | 0.0174 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kösal, H.H.; Kişi, E.; Akyiğit, M.; Çelik, B. Elliptic Quaternion Matrices: A MATLAB Toolbox and Applications for Image Processing. Axioms 2024, 13, 771. https://doi.org/10.3390/axioms13110771
Kösal HH, Kişi E, Akyiğit M, Çelik B. Elliptic Quaternion Matrices: A MATLAB Toolbox and Applications for Image Processing. Axioms. 2024; 13(11):771. https://doi.org/10.3390/axioms13110771
Chicago/Turabian StyleKösal, Hidayet Hüda, Emre Kişi, Mahmut Akyiğit, and Beyza Çelik. 2024. "Elliptic Quaternion Matrices: A MATLAB Toolbox and Applications for Image Processing" Axioms 13, no. 11: 771. https://doi.org/10.3390/axioms13110771
APA StyleKösal, H. H., Kişi, E., Akyiğit, M., & Çelik, B. (2024). Elliptic Quaternion Matrices: A MATLAB Toolbox and Applications for Image Processing. Axioms, 13(11), 771. https://doi.org/10.3390/axioms13110771






