A Unified Approach to Aitchison’s, Dually Affine, and Transport Geometries of the Probability Simplex
Abstract
1. Introduction
1.1. Probability Simplex
1.2. Compositions
1.3. Polytopes and Simplexes
1.4. Overview
2. Affine Geometry of the Probability Simplex
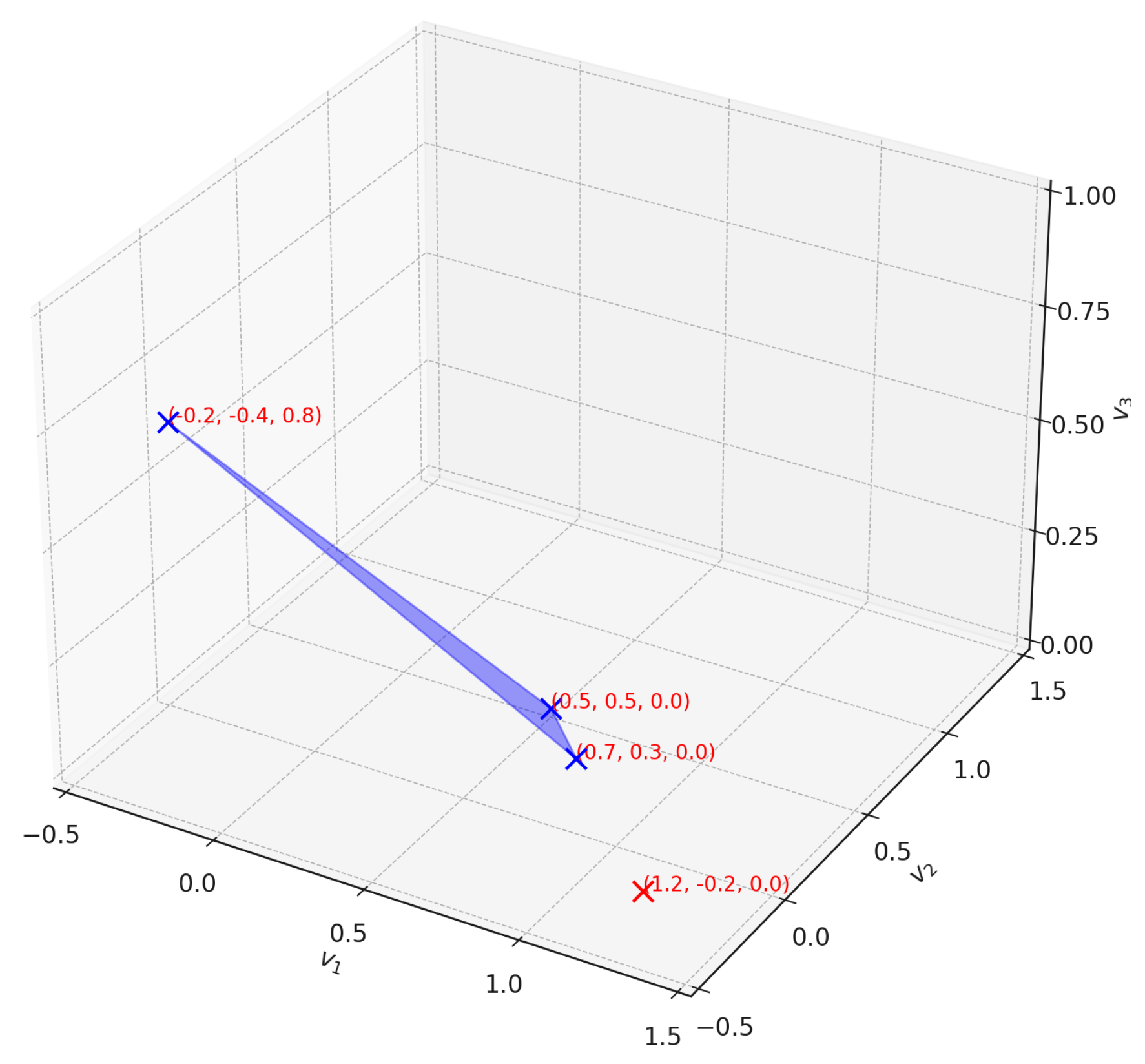
2.1. Affine Space
- 1.
- For each point , the partial mapping is injective (one-to-one) with the open image .
- 2.
- Given points p, q, and r, the displacement vectors satisfy the parallelogram law,
2.2. Affine Manifold
Aitchison’s Centered Log Ratio [5]
2.3. Tangent Bundle
3. Affine Statistical Bundle
3.1. Fisher’s Score
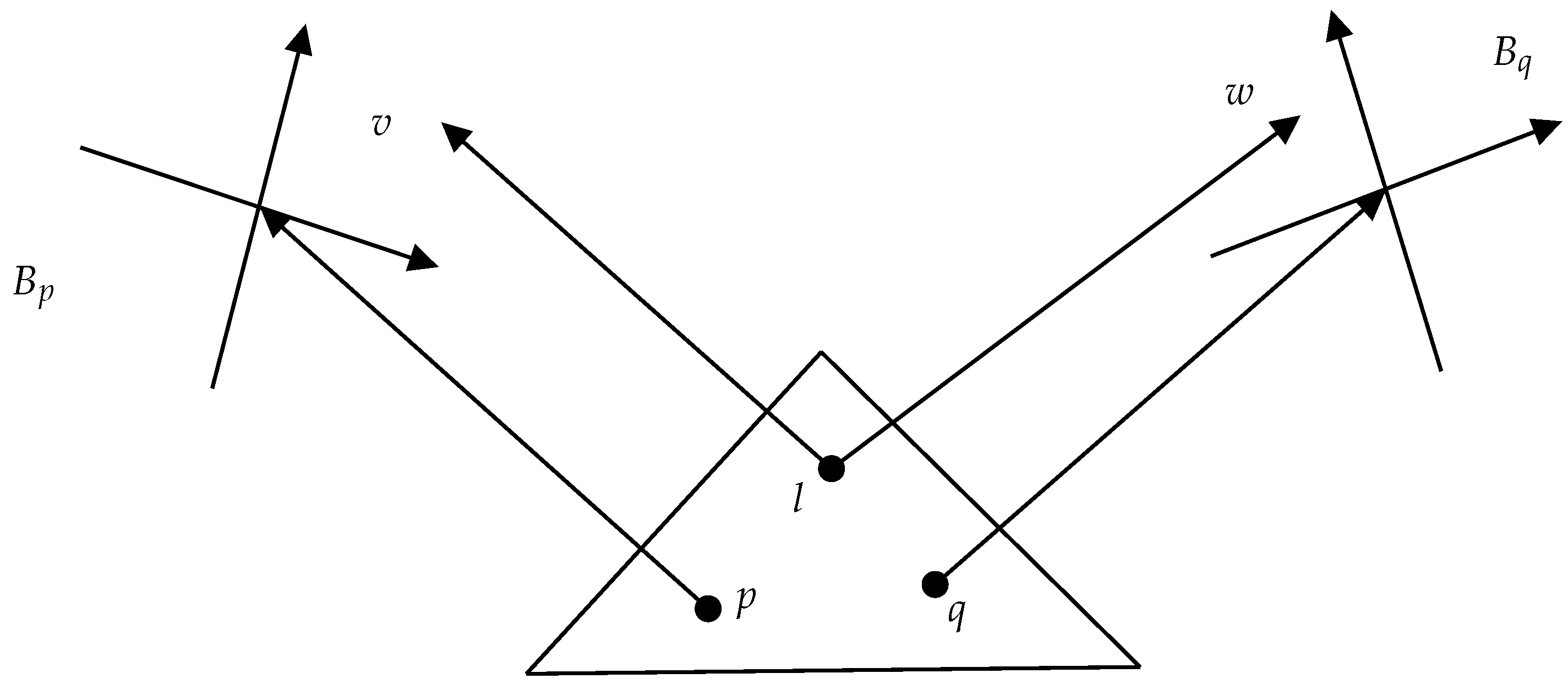
3.2. Statistical Bundle and Parallel Transports
3.3. Affine Bundle
- 1.
- For each fixed p, the mapping is 1-to-1, and it has an open image;
- 2.
- The parallelogram law holds,
3.4. Velocity and Natural Gradient
3.5. Dually Affine Atlases on the Open Probability Simplex
- 1.
- The equationdefines a cocycle of parallel transports. It is the exponential transport.
- 2.
- The equationdefines a cocycle of parallel transports. It is the mixture transport.
- 3.
- The exponential transport and the mixture transports are dual to each other in the covariance pairing. Namely, if and ,
- 1.
- The mappingis an affine displacement for the exponential parallel transport Theorem 1 item 1. The inverse of the exponential chart is the exponential model
- 2.
- The mappingis an affine displacement for the mixture displacement Theorem 1 item 2. The inverse of the mixture chart is the mixture model
- The generalized parallelogram law for the exponential displacement is
- The generalized parallelogram law for mixture displacement is
Kullback–Leibler Divergence
- 1.
- The derivative of at v in the direction h is
- 2.
- The second derivative of at v in the directions h and k is
- 3.
- The third derivative of at v in the directions and is
- 4.
- The cumulant functional is convex, and its gradient is the covariance at p given by . The inverse gradient mapping isand the convex conjugate is
- The convexity follows from items 1 and 2. The last statement is, in essence, a summary of the theorem itself.
3.6. Aitchison Geometry and Information Geometry
3.6.1. Mapping of n-Sequences
3.6.2. Mean, Variance, Velocity, and Velocity Curve
4. Product-Sample Spaces
4.1. Short Recap of Linear Programming
4.2. Product Sample Space
4.3. ANOVA Splitting of the Statistical Bundle
5. Second-Order Computations and Mechanical Models
- The exponential acceleration is
- The mixture acceleration is
5.1. Curves with Minimal Fisher’s Information
5.2. Lagrangian and Hamiltonian Formalism on the Probability Simplex
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amari, S. Dual connections on the Hilbert bundles of statistical models. In Geometrization of Statistical Theory; ULDM Publishing: Lancaster, PA, USA, 1987; pp. 123–151. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; Translated from the 1993 Japanese original by Daishi Harada; American Mathematical Society: Providence, RI, USA, 2000; Volume 191, 206p. [Google Scholar]
- Pistone, G.; Sempi, C. An infinite-dimensional geometric structure on the space of all the probability measures equivalent to a given one. Ann. Statist. 1995, 23, 1543–1561. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana-Delgado, R. Modelling and Analysis of Compositional Data; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Aitchison, J. The Statistical Analysis of Compositional Data; Monographs on Statistics and Applied Probability; Chapman & Hall: London, UK, 1986; 416p. [Google Scholar]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Tolosana-Delgado, R.; Ortego, M.I.; van den Boogaart, K.G. Bayes spaces: Use of improper distributions and exponential families. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. Mat. 2012, 107, 475–486. [Google Scholar] [CrossRef]
- Barvinok, A. A Course in Convexity; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2002; Volume 54, 366p. [Google Scholar]
- Lay, S.R. Convex Sets and Their Applications; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]
- Amari, S.I. Information Geometry and Its Applications; Applied Mathematical Sciences; Springer: Tokyo, Japan, 2016; 374p. [Google Scholar]
- Nomizu, K.; Sasaki, T. Affine Differential Geometry: Geometry of Affine Immersions; Cambridge Tracts in Mathematics; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Pistone, G. Information Geometry of the Probability Simplex: A Short Course. Nonlinear Phenom. Complex Syst. 2020, 23, 221–242. [Google Scholar] [CrossRef]
- Chirco, G.; Malagò, L.; Pistone, G. Lagrangian and Hamiltonian dynamics for probabilities on the statistical bundle. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250214. [Google Scholar] [CrossRef]
- Bourbaki, N. Variétés Differentielles et Analytiques. Fascicule de réSultats/Paragraphes 1 à 7; Springer Science and Business Media: New York, NY, USA, 1971. [Google Scholar]
- Lang, S. Differential and Riemannian Manifolds, 3rd ed.; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1995; 364p. [Google Scholar]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather. Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Weyl, H. Space—Time—Matter; Translation of the 1921 raum zeit materie; Dover: New York, NY, USA, 1952. [Google Scholar]
- Brown, L.D. Fundamentals of Statistical Exponential Families with Applications in Statistical Decision Theory; Institute of Mathematical Statistics: Beachwood, OH, USA, 1986; 283p. [Google Scholar]
- Efron, B.; Hastie, T. Computer Age Statistical Inference; IMS Monographs; Cambridge University Press: Cambridge, UK, 2016; Volume 19, 475p. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006; 748p. [Google Scholar]
- Ohara, A.; Amari, S. Differential geometric structures of stable state feedback systems with dual connections. Kybernetika 1994, 30, 369–386. [Google Scholar]
- Cafaro, C.; Alsing, P.M. Decrease of Fisher information and the information geometry of evolution equations for quantum mechanical probability amplitudes. Phys. Rev. E 2018, 97, 042110. [Google Scholar] [CrossRef] [PubMed]
- Ay, N.; Jost, J.; Lê, H.V.; Schwachhöfer, L. Information Geometry; Ergebnisse der Mathematik und ihrer Grenzgebiete; Springer: Cham, Switzerland, 2017; 407p. [Google Scholar] [CrossRef]
- Ohara, A. On Affine Immersions of the Probability Simplex and Their Conformal Flattening. In Proceedings of the Geometric Science of Information: Third International Conference, GSI 2017, Paris, France, 7–9 November 2017; Springer: Cham, Switzerland, 2017; pp. 247–254. [Google Scholar] [CrossRef]
- Duy, T.T.; Nguyen, L.V.; Nguyen, V.; Trung, N.; Abed-Meraim, K. Fisher information neural estimation. In Proceedings of the 30th European Signal Processing Conference (EUSIPCO), Belgrade, Serbia, 29 August–2 September 2022; pp. 2111–2115. [Google Scholar] [CrossRef]
- Ly, A.; Marsman, M.; Verhagen, J.; Grasman, R.; Wagenmakers, E. A Tutorial on Fisher Information. J. Math. Psychol. 2017, 80, 40–55. [Google Scholar] [CrossRef]
- Wei, X.X.; Stocker, A. Mutual Information, Fisher Information, and Efficient Coding. Neural Comput. 2016, 28, 305–326. [Google Scholar] [CrossRef] [PubMed]
- Gibilisco, P.; Pistone, G. Connections on non-parametric statistical manifolds by Orlicz space geometry. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 1998, 1, 325–347. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Csiszár, I. I-divergence geometry of probability distributions and minimization problems. Ann. Probability 1975, 3, 146–158. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Statistical Physics, 3rd ed.; Course of Theoretical Physics; Butterworth-Heinemann: Oxford, UK, 1980; Volume 5. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational Optimal Transport. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Fienberg, S.E. The Analysis of Cross-Classified Categorical Data; MIT Press: Cambridge, MA, USA, 1980; 198p. [Google Scholar]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Graduate Texts in Mathematics; Translated from the 1974 Russian original by K. Vogtmann and A. Weinstein; Springer: New York, NY, USA, 1989; 516p. [Google Scholar]
- Pistone, G. Lagrangian Function on the Finite State Space Statistical Bundle. Entropy 2018, 20, 139. [Google Scholar] [CrossRef] [PubMed]
- Do Carmo, M.P. Riemannian Geometry; Mathematics: Theory & Applications; Translated from the second Portuguese edition by Francis Flaherty; Birkhäuser Boston Inc.: Basel, Switzerland, 1992; 300p. [Google Scholar]
- Chirco, G.; Pistone, G. Dually affine Information Geometry modeled on a Banach space. arXiv 2022, arXiv:2204.00917. [Google Scholar]

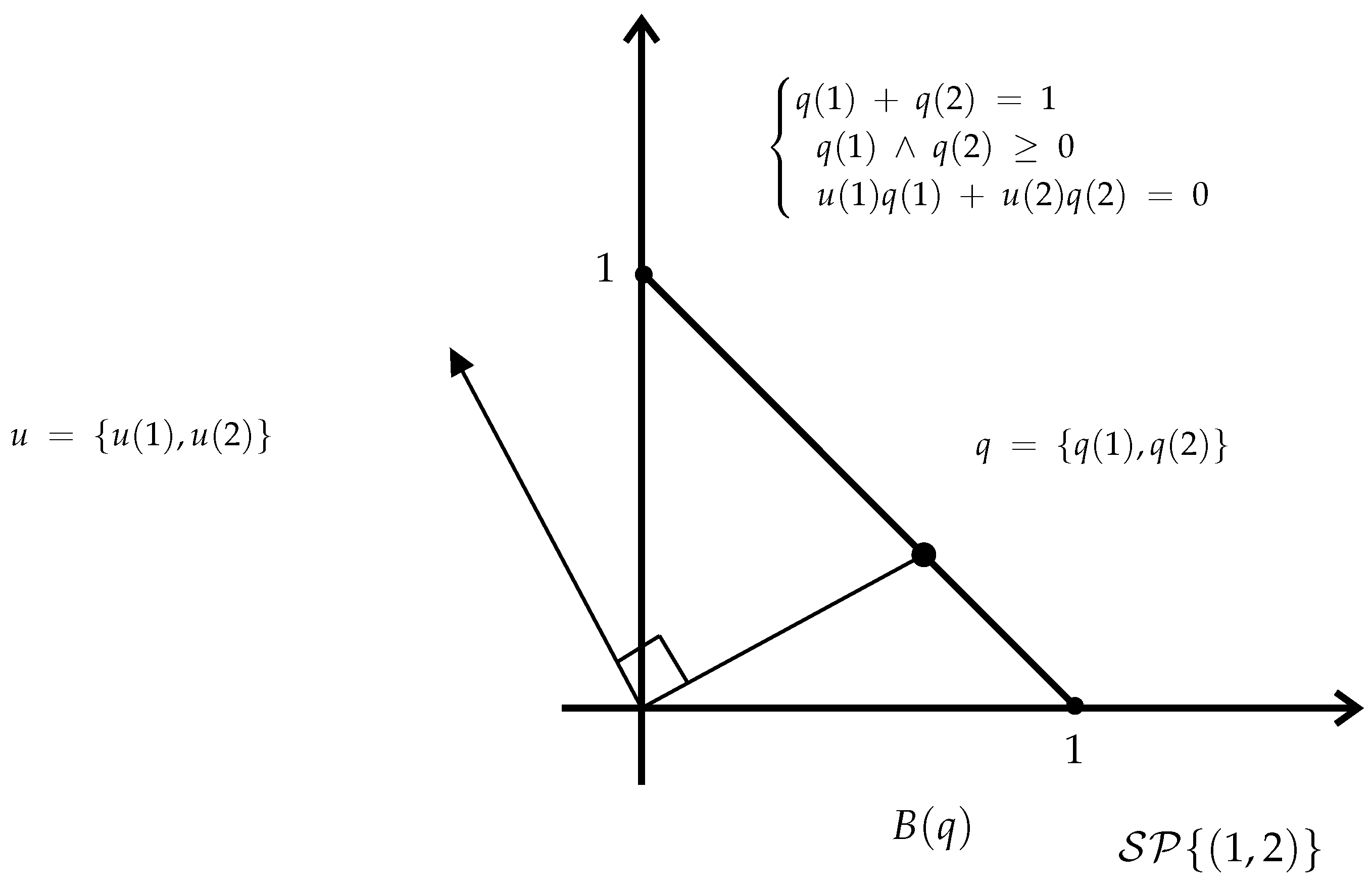
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pistone, G.; Shoaib, M. A Unified Approach to Aitchison’s, Dually Affine, and Transport Geometries of the Probability Simplex. Axioms 2024, 13, 823. https://doi.org/10.3390/axioms13120823
Pistone G, Shoaib M. A Unified Approach to Aitchison’s, Dually Affine, and Transport Geometries of the Probability Simplex. Axioms. 2024; 13(12):823. https://doi.org/10.3390/axioms13120823
Chicago/Turabian StylePistone, Giovanni, and Muhammad Shoaib. 2024. "A Unified Approach to Aitchison’s, Dually Affine, and Transport Geometries of the Probability Simplex" Axioms 13, no. 12: 823. https://doi.org/10.3390/axioms13120823
APA StylePistone, G., & Shoaib, M. (2024). A Unified Approach to Aitchison’s, Dually Affine, and Transport Geometries of the Probability Simplex. Axioms, 13(12), 823. https://doi.org/10.3390/axioms13120823






