Robustness Analysis for Sundry Disturbed Open Loop Dynamics Using Robust Right Coprime Factorization
Abstract
:1. Introduction
2. Problem Statement and Mathematical Preliminaries
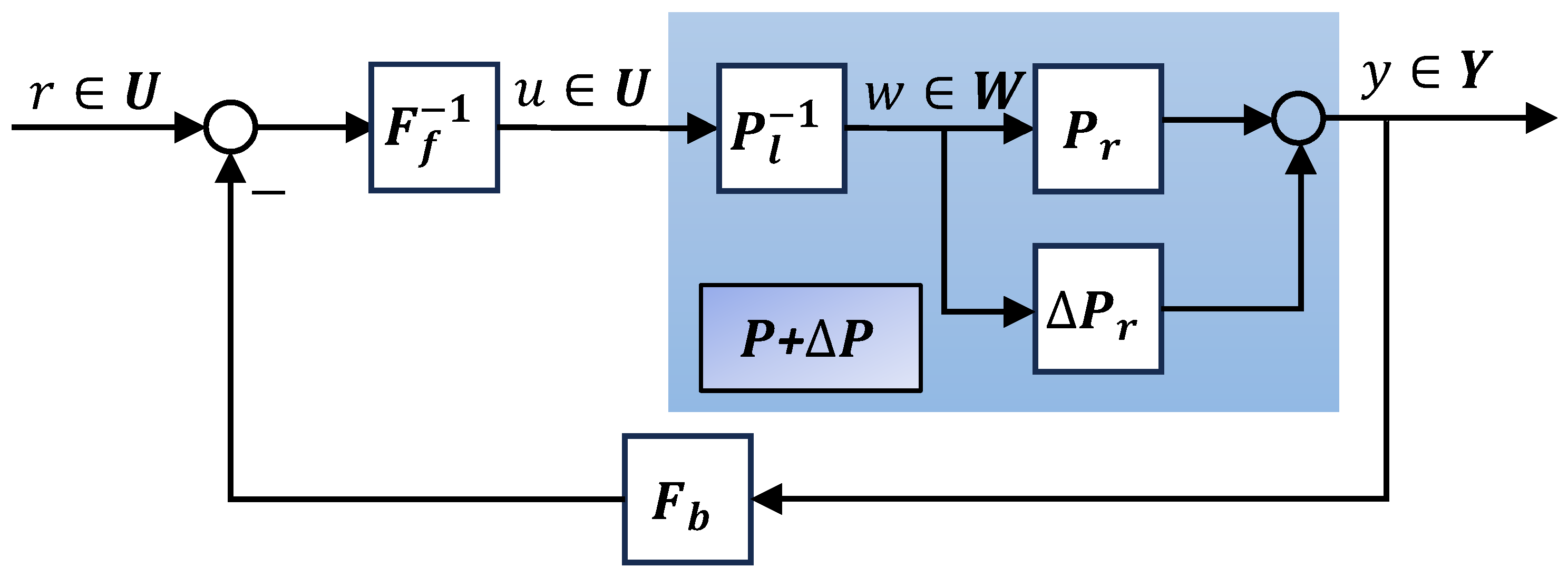
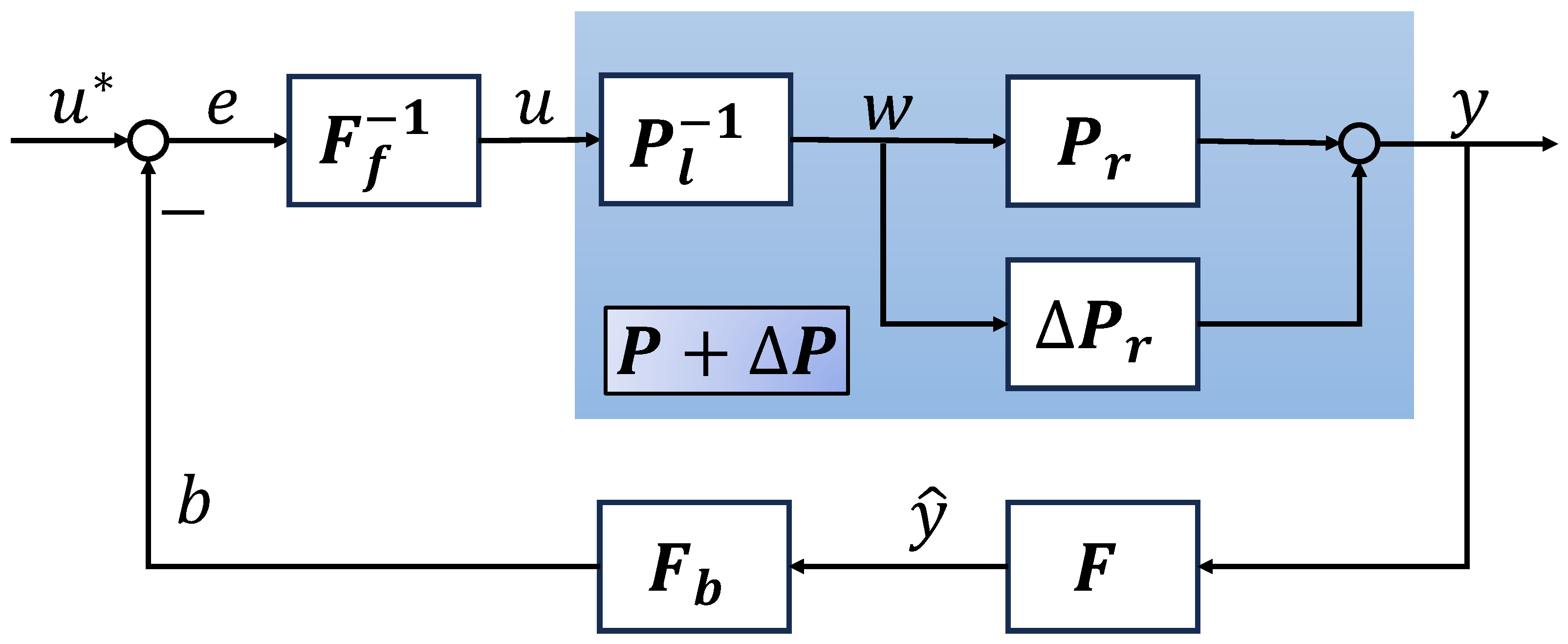
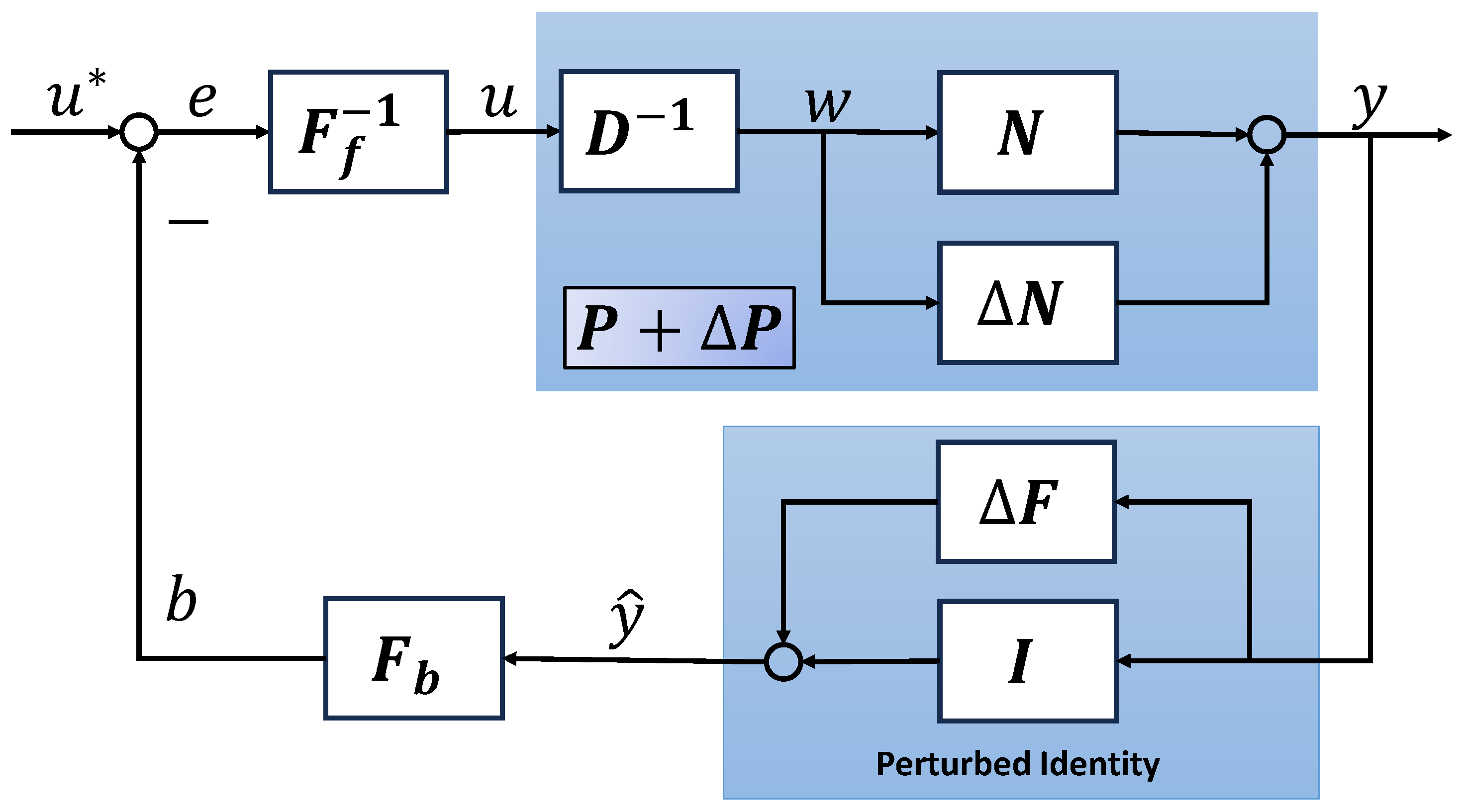
2.1. Problem Statement
2.2. Mathematical Preliminaries
3. Main Results
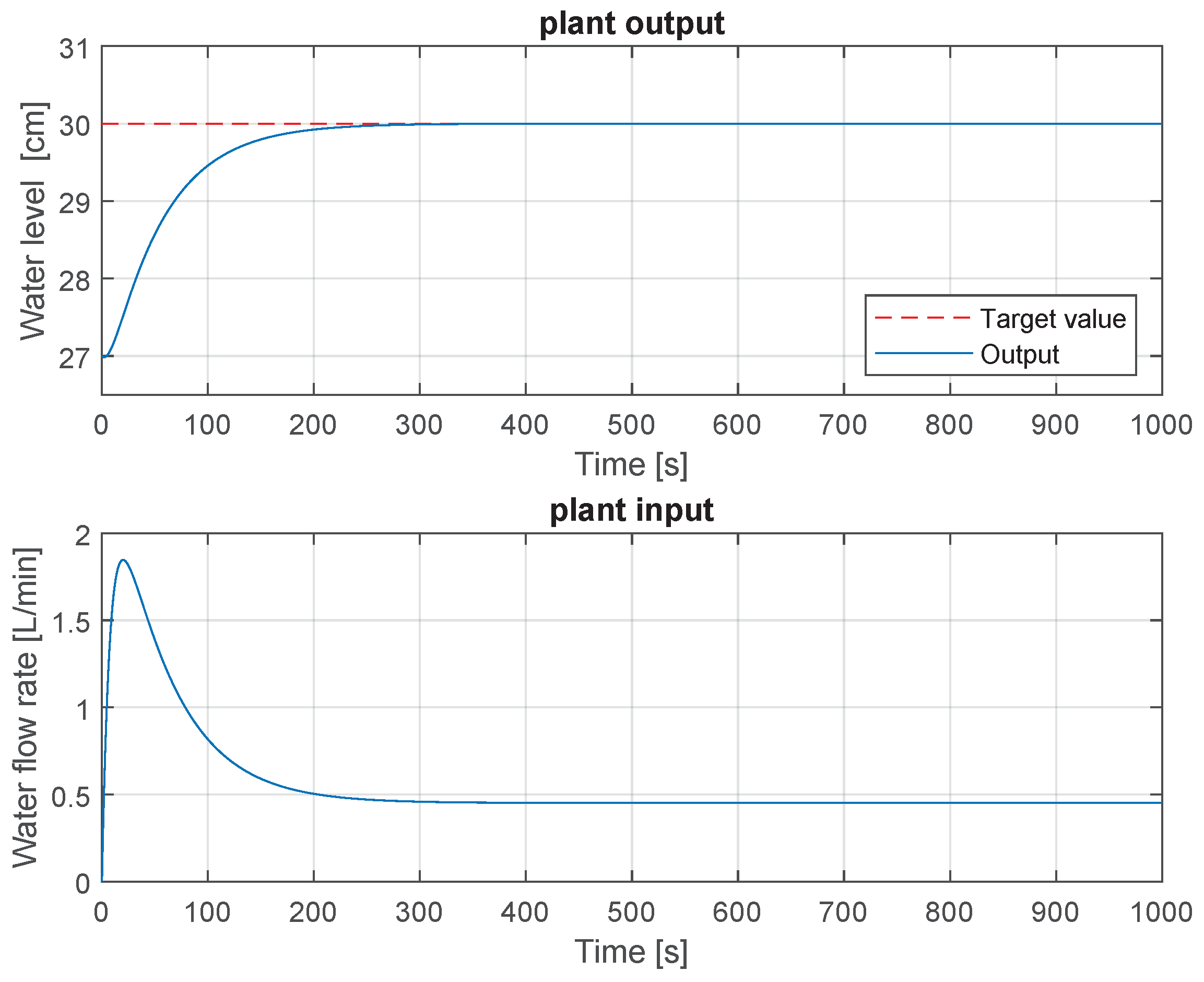
4. Numerical Examples
4.1. Case 1: Water Level Compensation System
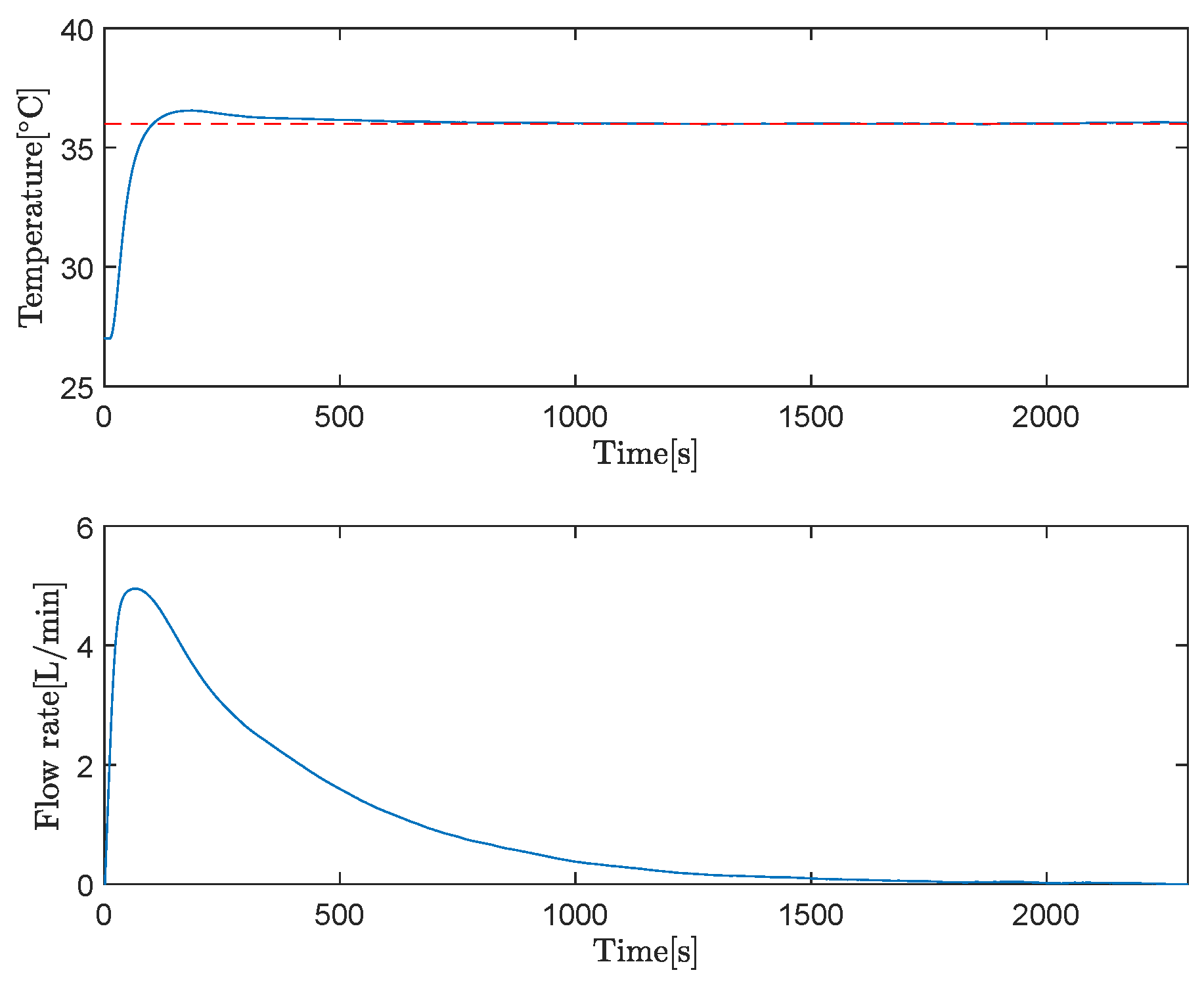
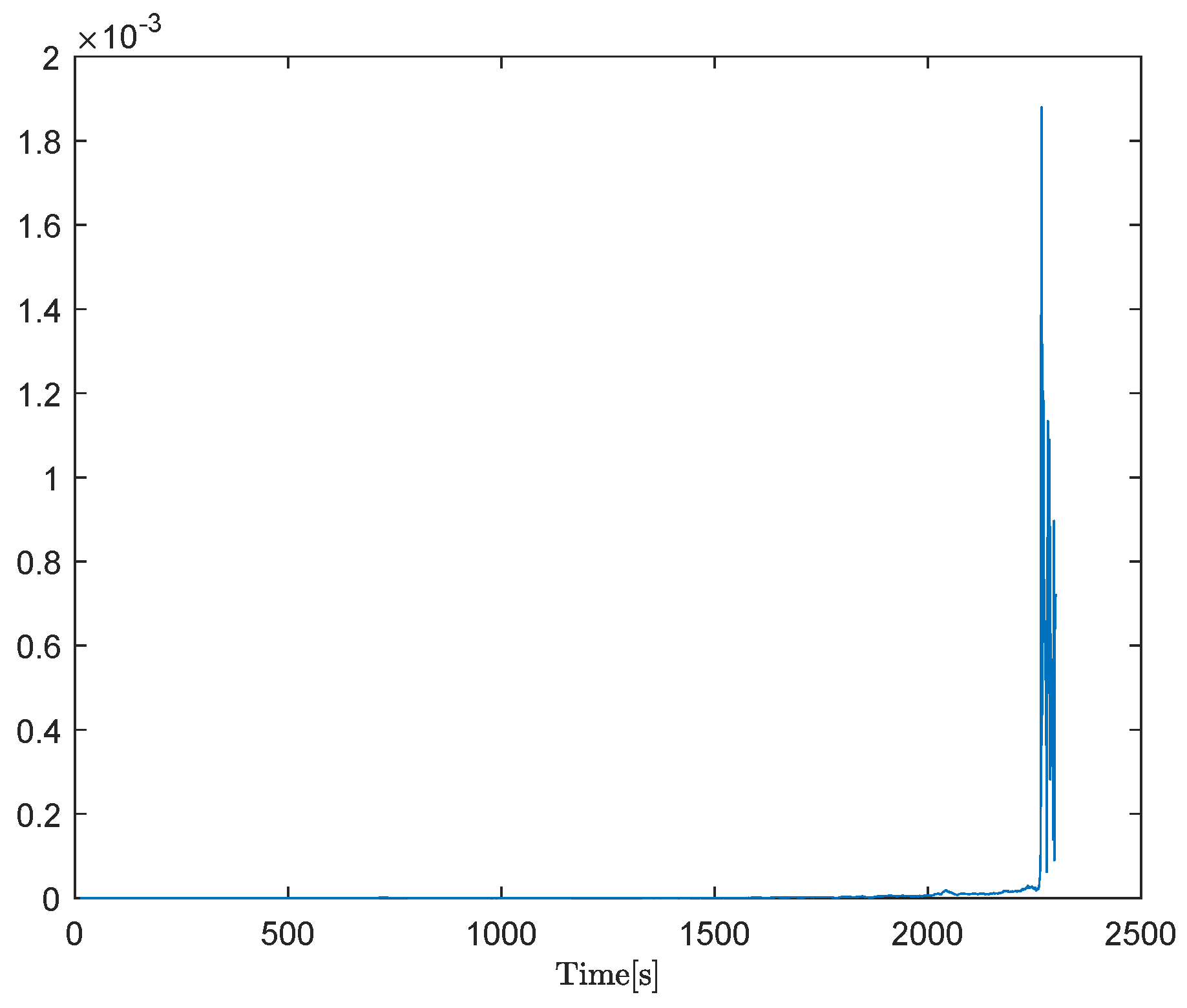
4.2. Case 2: Heat Exchange Process with a Spiral Heat Exchanger
5. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Water Level Compensation System
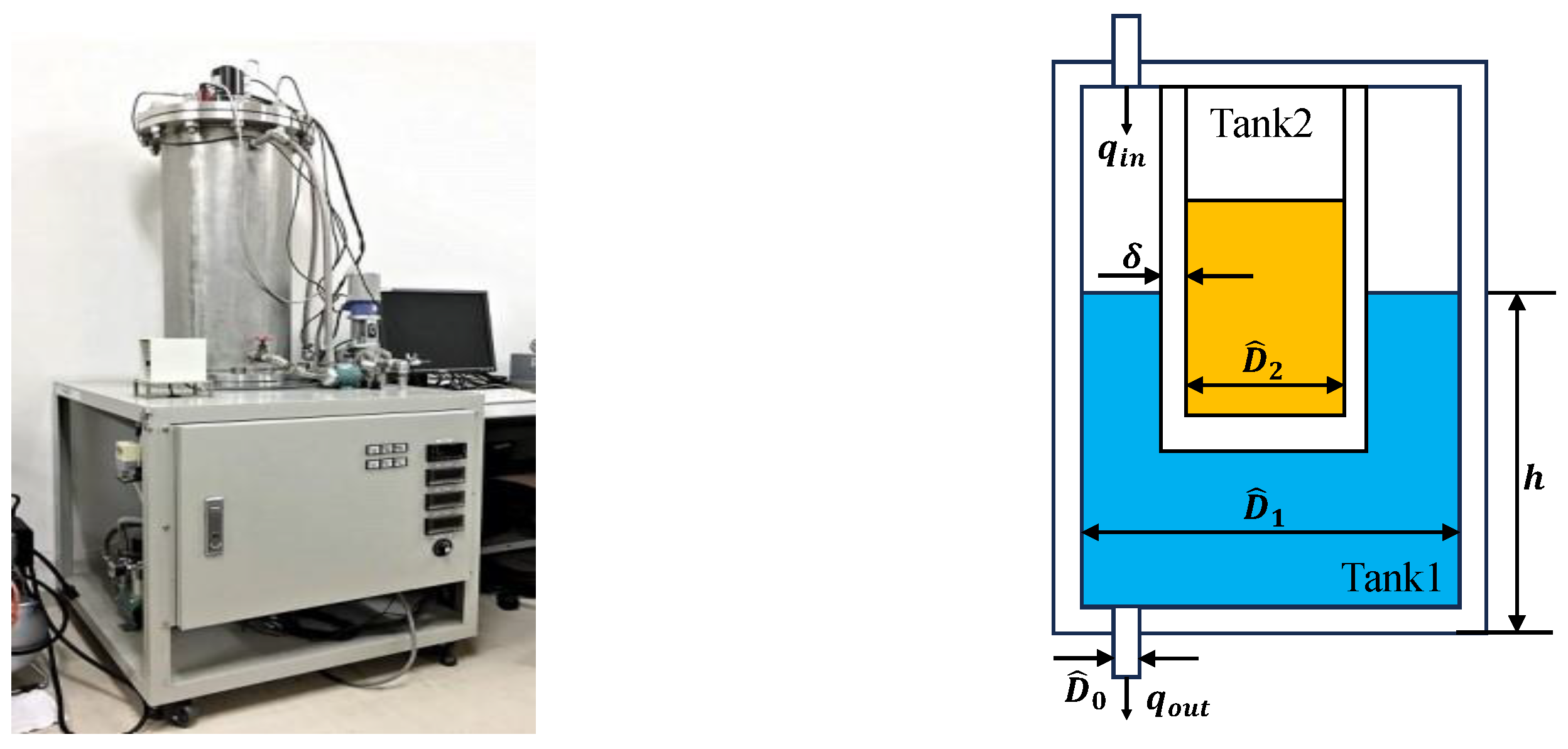
| T | simulation time | 1000 | [s] |
| sampling period | 1 | ||
| proportional gain | |||
| integral gain | |||
| K | designed parameter | ||
| thickness of sold wall | 2 | [cm] | |
| h | water level in Tank1 | [cm] | |
| v | outflow rate | [cm/s] | |
| water inflow of Tank1 | [L/min] | ||
| water outflow of Tank1 | [L/min] | ||
| Tank1 outlet inner diameter | [cm] | ||
| Tank1 inner diameter | [cm] | ||
| Tank2 inner diameter | [cm] | ||
| g | gravity acceleration | [cm/s2] |
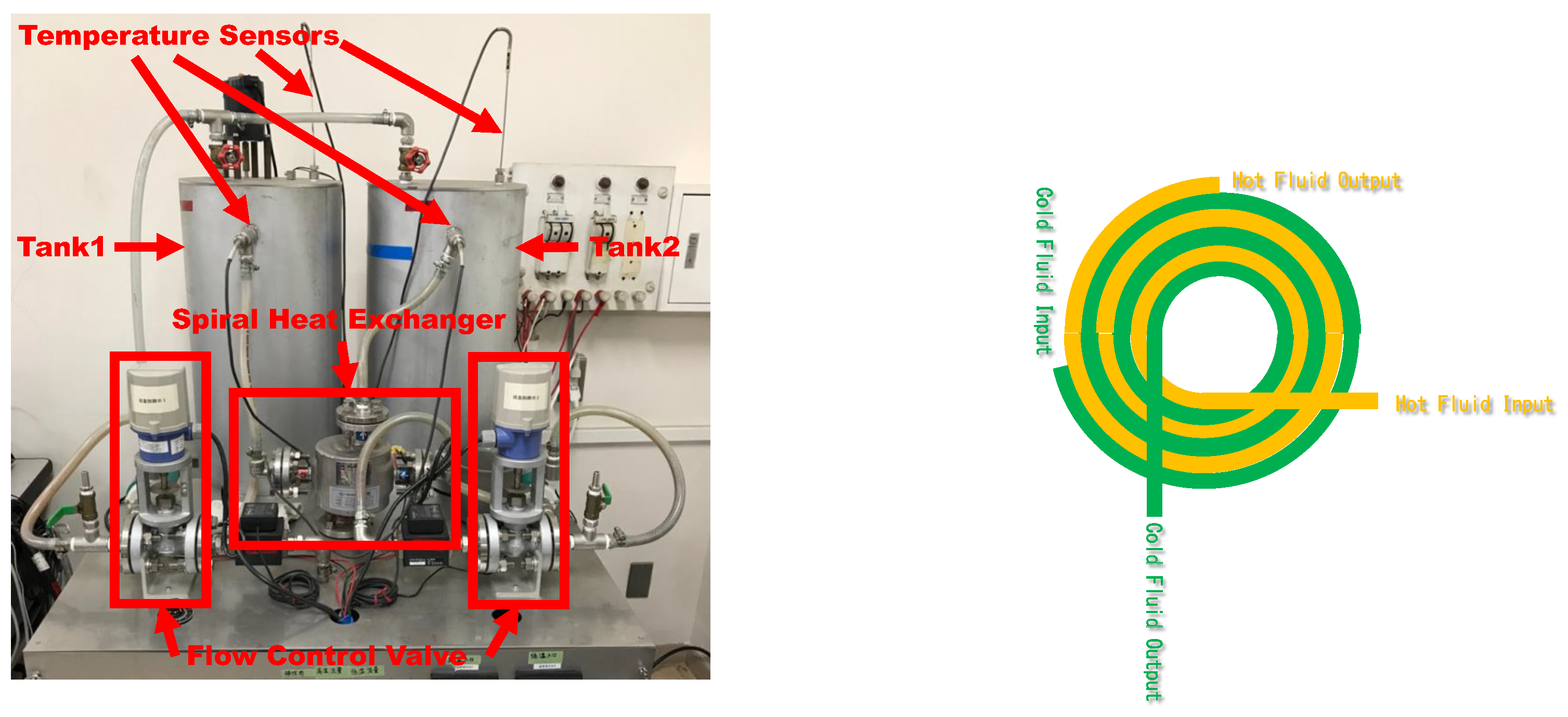
Appendix B. Heat Exchange Process with a Spiral Heat Exchanger
| r | Target temperature value | 36 °C |
| Hot fluid outlet temperature | 41 °C | |
| Initial cold fluid inlet temperature | 27 °C | |
| Initial cold fluid temperature | 27 °C | |
| a | Archimedes’ spiral equation constant | m/rad |
| Thermal conductivity of SUS304 | 16.7 W/(m · °C) | |
| Reynolds number | 22,000 | |
| Prandtl number | 7 | |
| B | Cross-section area of flow path | m2 |
| Specific heat of water | 4.2 kJ/(kg · °C) | |
| Density of water | 1000 kg/m3 | |
| Thickness of heat exchanger’s wall | m | |
| Width of flow path | m | |
| m | Mass of cold fluid flow rate | 0.0717 kg |
| M | Mass of cold fluid in Tank2 | 31.8 kg |
| - Design parameter | 0.3 L/min | |
| - Design parameter | 0.03 | |
| Design parameter for valve of hot fluid | 1.25 | |
| Design parameter for flow change of hot fluid | 0.026 | |
| K | Design parameter of | 0.7 |
| Proportional gain of C | 2000 | |
| Integral gain of C | 97 | |
| Sampling time | 1 s | |
| Simulation time | 2301 s | |
| Standard deviation of likelihood function | 0.01 °C |
Appendix C. Variant of Particle Filter Algorithm
References
- Åström, K.J. Introduction to Stochastic Control Theory; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Zheng, K.; Shi, D.; Hirche, S.; Shi, Y. Innovation-triggered Learning for Data-driven Predictive Control: Deterministic and Stochastic Formulations. arXiv 2024, arXiv:2401.15824. [Google Scholar]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998; Volume 104. [Google Scholar]
- Yan, Y.; Wang, X.F.; Marshall, B.J.; Liu, C.; Yang, J.; Chen, W.H. Surviving disturbances: A predictive control framework with guaranteed safety. Automatica 2023, 158, 111238. [Google Scholar] [CrossRef]
- Nikiforov, V.O. Nonlinear servocompensation of unknown external disturbances. Automatica 2001, 37, 1647–1653. [Google Scholar] [CrossRef]
- Bodson, M.; Jensen, J.S.; Douglas, S.C. Active noise control for periodic disturbances. IEEE Trans. Control Syst. Technol. 2001, 9, 200–205. [Google Scholar] [CrossRef]
- Back, J.; Shim, H. Adding robustness to nominal output-feedback controllers for uncertain nonlinear systems: A nonlinear version of disturbance observer. Automatica 2008, 44, 2528–2537. [Google Scholar] [CrossRef]
- Arias, G. Stabilization of a microbeam model with distributed disturbance. Syst. Control Lett. 2023, 173, 105466. [Google Scholar] [CrossRef]
- Modares, H. Data-driven Safe Control of Uncertain Linear Systems Under Aleatory Uncertainty. IEEE Trans. Autom. Control 2023, 69, 551–558. [Google Scholar] [CrossRef]
- Ahmadi, M.; Rosolia, U.; Ingham, M.D.; Murray, R.M.; Ames, A.D. Risk-Averse Decision Making Under Uncertainty. IEEE Trans. Autom. Control 2023, 69, 55–68. [Google Scholar] [CrossRef]
- Ebeigbe, D.; Nguyen, T. On Robust Control with Uncertainties in the Regressor Matrix and Parameter Vector. IEEE Trans. Autom. Control 2023, 69, 309–314. [Google Scholar] [CrossRef]
- Kwak, D.; Kim, J.H.; Hagiwara, T. Robust Stability Analysis of Sampled-Data Systems with Uncertainties Characterized by the L-infinity-induced Norm: Gridding Treatment with Convergence Rate Analysis. IEEE Trans. Autom. Control 2023, 68, 8119–8125. [Google Scholar] [CrossRef]
- Sibai, H.; Mitra, S. State Estimation of Continuous-time Dynamical Systems with Uncertain Inputs with Bounded Variation: Entropy, Bit Rates, and Relation with Switched Systems. IEEE Trans. Autom. Control 2023, 68, 7041–7056. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Sanjayan, J.; Shang, W.; Lam, W.Y. Robust trajectory tracking control for cable-driven parallel robots with model uncertainty. Control Eng. Pract. 2023, 140, 105662. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Han, Q.L.; Ra, T. Watermark-based Proactive Defense Strategy Design For Cyber-Physical Systems With Unknown-but-bounded Noises. IEEE Trans. Autom. Control 2022, 68, 3300–3315. [Google Scholar] [CrossRef]
- Rizvi, S.A.A.; Pertzborn, A.J.; Lin, Z. Reinforcement learning based optimal tracking control under unmeasurable disturbances with application to HVAC systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7523–7533. [Google Scholar] [CrossRef] [PubMed]
- Meng, T.; Xie, Y.; Lin, Z. Consensus of Linear Multi-Agent Systems in the Presence of Bounded Measurement Noises. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5128–5133. [Google Scholar]
- Rsetam, K.; Cao, Z.; Man, Z. Design of robust terminal sliding mode control for underactuated flexible joint robot. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 4272–4285. [Google Scholar] [CrossRef]
- Wang, H.; Man, Z.; Kong, H.; Zhao, Y.; Yu, M.; Cao, Z.; Zheng, J.; Do, M.T. Design and implementation of adaptive terminal sliding-mode control on a steer-by-wire equipped road vehicle. IEEE Trans. Ind. Electron. 2016, 63, 5774–5785. [Google Scholar] [CrossRef]
- Chen, J.; Qian, D. Three controllers via 2nd-order sliding mode for leader-following formation control of multi-robot systems. Int. J. Adv. Mechatron. Syst. 2021, 9, 85–101. [Google Scholar] [CrossRef]
- Guzmán, P.; Prieur, C. Rapid stabilization of a reaction-diffusion equation with distributed disturbance. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Republic of Korea, 14–18 December 2020; pp. 666–671. [Google Scholar]
- Pisano, A.; Orlov, Y. Boundary second-order sliding-mode control of an uncertain heat process with unbounded matched perturbation. Automatica 2012, 48, 1768–1775. [Google Scholar] [CrossRef]
- Ferrara, A.; Incremona, G.P.; Vecchio, C. Adaptive Multiple-Surface Sliding Mode Control of Nonholonomic Systems with Matched and Unmatched Uncertainties. IEEE Trans. Autom. Control 2023, 69, 614–621. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Goto, S. Operator based thermal control of an aluminum plate with a Peltier device. Int. J. Innov. Comput. Inf. Control 2008, 4, 3219–3229. [Google Scholar]
- Deng, M.; Inoue, A.; Ishikawa, K. Operator-based nonlinear feedback control design using robust right coprime factorization. IEEE Trans. Autom. Control 2006, 51, 645–648. [Google Scholar] [CrossRef]
- An, Z.; Bu, N. Modeling for a Bellow-Shaped Soft Actuator Based on Yeoh model and Operator-Based Nonlinear Control Design. In Proceedings of the 2023 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, Australia, 4–7 September 2023; pp. 1–5. [Google Scholar]
- Bu, N.; Liu, H.; Li, W. Robust passive tracking control for an uncertain soft actuator using robust right coprime factorization. Int. J. Robust Nonlinear Control 2021, 31, 6810–6825. [Google Scholar] [CrossRef]
- Deng, M.; Iwai, Z.; Mizumoto, I. Robust parallel compensator design for output feedback stabilization of plants with structured uncertainty. Syst. Control Lett. 1999, 36, 193–198. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Zhu, Q. An integrated study procedure on real-time estimation of time-varying multi-joint human arm viscoelasticity. Trans. Inst. Meas. Control 2011, 33, 919–941. [Google Scholar] [CrossRef]
- Bu, N.; Wang, X. Swing-up design of double inverted pendulum by using passive control method based on operator theory. Int. J. Adv. Mechatron. Syst. 2023, 10, 1–7. [Google Scholar] [CrossRef]
- Li, M.; Deng, M. Operator-based external disturbance rejection of perturbed nonlinear systems by using robust right coprime factorization. Trans. Inst. Meas. Control 2018, 40, 3169–3178. [Google Scholar] [CrossRef]
- Gao, X.; Yang, Q.; Zhang, J. Multi-objective optimisation for operator-based robust nonlinear control design for wireless power transfer systems. Int. J. Adv. Mechatron. Syst. 2022, 9, 203–210. [Google Scholar] [CrossRef]
- Xu, Y.; Deng, M. Particle filter design for robust nonlinear control system of uncertain heat exchange process with sensor noise and communication time delay. Appl. Sci. 2022, 12, 2495. [Google Scholar] [CrossRef]
- Kochi, R.; Deng, M. Multivariable Fractional-Order Controller Design of Nonlinear Dual Tank Device. Fractal Fract. 2024, 8, 27. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Deng, M. Robustness Analysis for Sundry Disturbed Open Loop Dynamics Using Robust Right Coprime Factorization. Axioms 2024, 13, 116. https://doi.org/10.3390/axioms13020116
Xu Y, Deng M. Robustness Analysis for Sundry Disturbed Open Loop Dynamics Using Robust Right Coprime Factorization. Axioms. 2024; 13(2):116. https://doi.org/10.3390/axioms13020116
Chicago/Turabian StyleXu, Yuanhong, and Mingcong Deng. 2024. "Robustness Analysis for Sundry Disturbed Open Loop Dynamics Using Robust Right Coprime Factorization" Axioms 13, no. 2: 116. https://doi.org/10.3390/axioms13020116
APA StyleXu, Y., & Deng, M. (2024). Robustness Analysis for Sundry Disturbed Open Loop Dynamics Using Robust Right Coprime Factorization. Axioms, 13(2), 116. https://doi.org/10.3390/axioms13020116








