Abstract
In the context of robust Bayesian analysis, studies mainly focus on computing the range of some quantities of interest when the prior distribution varies in a class. We use the concept of distorted bands to introduce a family of priors on the shape parameter of the Generalized Pareto distribution. We show how certain properties of the likelihood ratio order allow us to propose novel sensitivity measures for Value at Risk and Conditional Value at Risk, which are the most useful and reliable risk measures. Although we focus on the Generalized Pareto distribution, which is essential in Extreme Value Theory, the new sensitivity measures could be employed for all the distributions that verify certain conditions related to likelihood ratio order. A thorough simulation study was carried out to perform a sensitivity analysis, and two illustrative examples are also provided.
Keywords:
robust Bayesian; sensitivity analysis; class of priors; distortion functions; Generalized Pareto distribution; risk measures MSC:
49Q12; 62C12; 65C60
1. Introduction
In Bayesian analysis, the choice of a prior distribution is a crucial issue. Without the expert’s information, we can only implement the process at our own will (using Jeffreys’ prior and other uninformative priors). The considerations of classes of priors and loss functions is the starting point for many developments in Bayesian sensitivity analysis, also called robust Bayesian analysis. Bayesian sensitivity analysis aims to quantify and model the uncertainty induced by the choice of the prior, likelihood, or loss [1,2]. Excellent surveys of Bayesian sensitivity analysis with respect to the prior are found in [3,4], whereas sensitivity regarding the loss function was considered in [5,6,7,8,9], among others. Some interesting applications can be found in [10,11].
In order to model the uncertainty of the prior information, a class of prior distributions is generally employed. Therefore, parametric classes, -contaminated classes [1], band classes, or quantile classes have been defined (see [2,12] for a general revision).
Distorted band classes were defined in [13] and were employed to define a class of priors in [14], which was called distorted band priors. Later, Ref. [15] applied them to insurance problems and [16] employed them in a collective risk model for insurance claims. More recently, Ref. [17] extended the concept of distorted bands to the multivariate case.
In this work, we employ distorted bands for prior distribution in order to make a Bayesian sensitivity analysis for the most useful and reliable risk measures employed in Extreme Value Theory.
Extreme Value Theory (EVT) is the science that studies rare events and employs statistical tools to model and predict them. It has been widely developed in Finance and Insurance, when the interest is focused on observations that differ significantly from the majority of data [18,19,20,21]. EVT provides statistical models to compute extreme risk measures, such as Value at Risk (VaR), Conditional Value at Risk (CVaR), and Return Level. Some other ways of measuring extreme risk were proposed by [22]. They are used, for example, to study the behavior of extreme returns on investment portfolios [23,24] and involve extreme quantiles estimation. There are several reasons why it is important to compute accurate estimates for the most employed risk measures, VaR and CVaR. From an economic point of view, underestimation of risk could obviously cause immense problems for banks and other participants in financial markets. On the other hand, an overestimation of risk may cause one to allocate too much capital as a cushion for risk exposures, having a negative effect on profits. Therefore, precise estimates of risk measures are obviously desirable.
A distribution of probability that plays an essential role in EVT is the Generalized Pareto distribution (GPD). Loosely speaking, Refs. [25,26] showed that, when we consider the distribution of data above a certain threshold u, it can usually be approximated by a properly scaled GPD as u tends to the endpoint of the distribution. Several methods have been developed for inferring the parameters of the GPD [27,28]. From a Bayesian point of view, Refs. [29,30] employed Markov chain Monte Carlo methods, Ref. [31] employed Jeffrey’s prior and the Metropolis–Hastings algorithm, and ref. [32] employed GPD itself as prior distribution. Mixture models were first proposed by [33], and afterwards, Ref. [34] studied an additive mixture model, where one of the components is the GPD, to make Bayesian inference on extreme quantiles. In addition, Ref. [35] defined a combination of mixture of Gamma below the threshold and a GPD above it. Afterwards, Ref. [36] also used a mixture model and focused on estimating the threshold. More recently, Ref. [37] employed all the data available to make estimations, using relations between the parameters of the baseline distribution and the parameters of the limit GPD distribution, following a similar idea developed in [38] for the Gumbel distribution. For both works, considered priors were highly informative.
The main novelty of this work is the proposal of sensitivity and relative sensitivity measures for VaR and CVaR, by introducing distorted bands for prior distributions. We focus on GPD distribution, because of its importance in EVT, and make use of properties related to the likelihood ratio order to define the sensitivity measures. The distorted band prior is defined on the shape parameter of the GPD. The measures of sensitivity and relative sensitivity are valid for all the distributions that fulfill condition (10) from Proposition 1, like Gamma or Weibull distributions.
In Section 2, we introduce the concept of distorted bands and show how we can use them to define bands for priors on the shape parameter of a GPD and the properties associated with them. In Section 3, we provide the definitions of VaR and CVaR and an essential result that allows us to define the new sensitivity measures for VaR and CVaR.
In Section 4, we describe a thorough simulation study in which we performed a sensitivity analysis employing the new sensitivity measures.
Finally, in Section 5, we provide two illustrative examples with real-life applications in two different fields, in order to show the usefulness of the sensitivity measures.
2. Distorted Band Priors
We recall the definition of the likelihood ratio order for two random variables and the concept of distortion function.
Let X and Y be absolutely continuous random variables with probability density functions (pdfs) and , respectively. X is said to be smaller than Y in the likelihood ratio order, and we denote it by (or ), if the ratio
increases over the union of the supports of the two pdfs.
A distortion function is a non-decreasing continuous function such that and .
Definition 1.
Given a random variable X and a distortion function h, we call X distorted by h, and we denote it as ; the random variable has the distribution function
If is differentiable, then, taking the derivative in Equation (2), we obtain the distorted density function of
In a Bayesian framework, let denote a prior distribution over the set of states , with pdf , where represents the unknown parameter. After taking into account the observed data x, let denote the posterior distribution. Let and denote the distorted distributions and by h, respectively.
In addition, let denote the random variable of the posterior predictive distribution associated with , with the density function
and denote the random variable of the posterior predictive distribution associated with .
Although priors can be distorted according to different criteria, Ref. [14] were in favor of the use of convex and concave distortion functions because of their desirable properties when we compare the original prior with the distorted one. That is, if and are distortion functions, with being concave and convex, it follows from Lemma 1 in [14] that
Inspired by this last property, Ref. [14] defined the distorted band as follows:
Definition 2.
The distorted band associated with π based on and , a concave distortion function and a convex distortion function, respectively, is defined as
As an immediate consequence, it was shown by [14] that the distorted posterior distributions and are also lower and upper bounds for the class of all posteriors because they interit the likelihood ratio order, i.e., for all ; then,
Due to the fact that Definition 2 is based on and , we can provide many possible bands just considering different concave and convex distortion functions. Of course, the choice of those functions cannot be arbitrary and should represent the uncertainty about the prior belief in each problem. For example, a convex (concave) distortion function will give more (less) weight to larger values.
A typical way of measuring a distortion is given by the classical power functions
where it is well known that if we take in Equation (8), then and can be interpreted as the minimum and the maximum, respectively, of an independent and identically distributed sample of size n that comes from the basis prior distribution . Therefore, let be the distorted band associated with and and given by (8), for a fixed .
As we commented in the Introduction, the Generalized Pareto distribution (GPD) is essential in Extreme Value Theory. We will deduce some properties about the likelihood ratio order and distorted bands for the GPD.
Definition 3.
Given a random variable X, we say that it follows a GPD with parameters θ, σ, , if its distribution function is
with support , , where θ and σ are the shape and scale parameters, respectively.
An interesting property of the GPD that allows us to establish an order is the following.
Proposition 1.
Let be a random variable that follows a GPD with shape parameter θ. If follow GPD with the same scale σ, then
Proof.
If and , then
where . For all , it is easy to prove that this ratio increases over the support . Therefore, . □
Proposition 2.
Let be a random variable with uncertainty in the shape parameter θ (conditionally independent with x under θ), and let the scale parameter σ be fixed. Let π be a prior distribution and a distorted band associated with π based on and . For all sample x and for all
Proof.
Let and be two GPDs with shape parameters , such that . Then, by Proposition 1, .
For all , it is verified that ; then, for posterior predictive distributions,
due to Theorem 10 in [39]. □
It is clear that all the families of random variables verifying that when will also verify (11) from Proposition 2 for a distorted band prior . Examples of these distributions are Gamma on parameter and Weibull on both parameters. Therefore, the following results could also be developed for the cited distributions.
3. Bayesian Sensitivity Analysis for VaR and CVaR
As we mentioned in the Introduction, we are going to focus on two important risk measures that are widely employed: Value at Risk (VaR) and Conditional Value at Risk (CVaR).
Definition 4.
Let X be a random variable representing loss. Given a parameter , the Value-at-Risk () of X is the p-quantile of the distribution X
and the Conditional Value-at-Risk () of X is
is understood as the minimum loss that will not be exceeded with probability p, and we can understand it as the highest loss in the best cases. is the expected loss, conditioned on the fact that the loss exceeds the at the given confidence level . It is an alternate measure to , more sensitive to the shape of the tail of the loss distribution.
Proposition 3.
If , then
for all .
Proof.
Due to Proposition 2, if ,
for all sample x and . In addition, we have to apply the properties
They can be easily deduced taking into account that, if , then , for all x in the union of the supports. Therefore,
and
□
Corollary 1.
For all and for the prior distribution , which belong to a distorted band associated to π, , it is verified that
Proof.
It is a direct consequence of Proposition 3. □
The sensitivity analysis is essential in Bayesian analysis and decision theory. The main differences among works in Bayesian sensitivity are about the choice of the classes and the sensitivity measures. In most papers about Bayesian robustness, the range of the posterior expectation of a quantity of interest , with priors varying in a class ,
has been proposed as measure of sensitivity (global robustness).
The range is the most important sensitivity measure in global robustness. It has a simple interpretation: when reasonably reflects the uncertainty in the prior, a “small” range indicates robustness. On the other hand, a “large” range is an indication that there is lack of robustness, and we should obtain more information.
We have shown that considering the distorted band, both the VaR and CVaR for the posterior predictive distributions are ordered too. This means that the range of these measures can be computed determining only VaR and CVaR of the posterior predictive distortion distributions. If we compute this range with respect to the VaR and CVaR, we will have a relative sensitivity measure. Consequently, we can define two sensitivity measures for VaR and CVaR of posterior predictive distributions, when the prior distribution belongs to a class of prior distributions associated with , .
Definition 5.
Given a distorted band with , we define the following sensitivity measures for the VaR and CVaR of the posterior predictive distributions as
To provide more information on the sensitivity analysis, we will also define relative sensitivity measures over the VaR and CVaR, based on the relative measures proposed by [9].
Definition 6.
Relative Sensitivity measures are defined as
If these sensitivity measures are small, we will say the distorted band class is robust. Otherwise, a more precise distorted band class or another reference prior should be chosen.
4. Simulations
We considered a sample of size n of a random variable with fixed scale parameter and three prior distributions for the shape parameter , : an inverse gamma, , an inverse , and a Pareto distribution, . Let be the distorted prior band for .
For all the priors, the posterior distribution is an inverse gamma with hyperparameters and ,
where and .
Then, we fixed , and considered three representative values of , , and samples of size . For all the combinations of these hyperparameters, 100,000 values of the random variable were generated. We conducted 100 replications, in order to determine the sensitivity measures for VaR and CVaR, taking the mean of each measure.
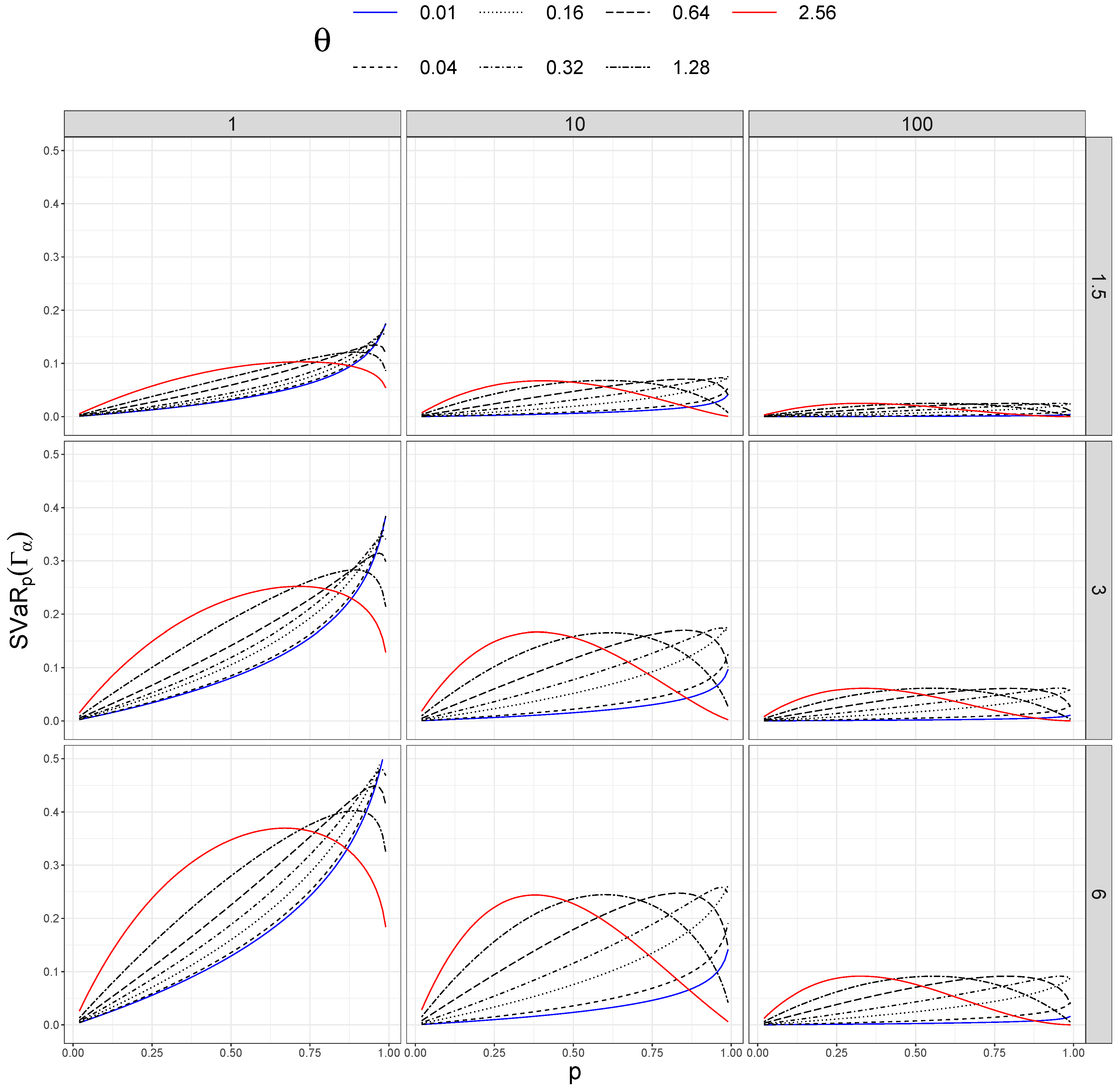
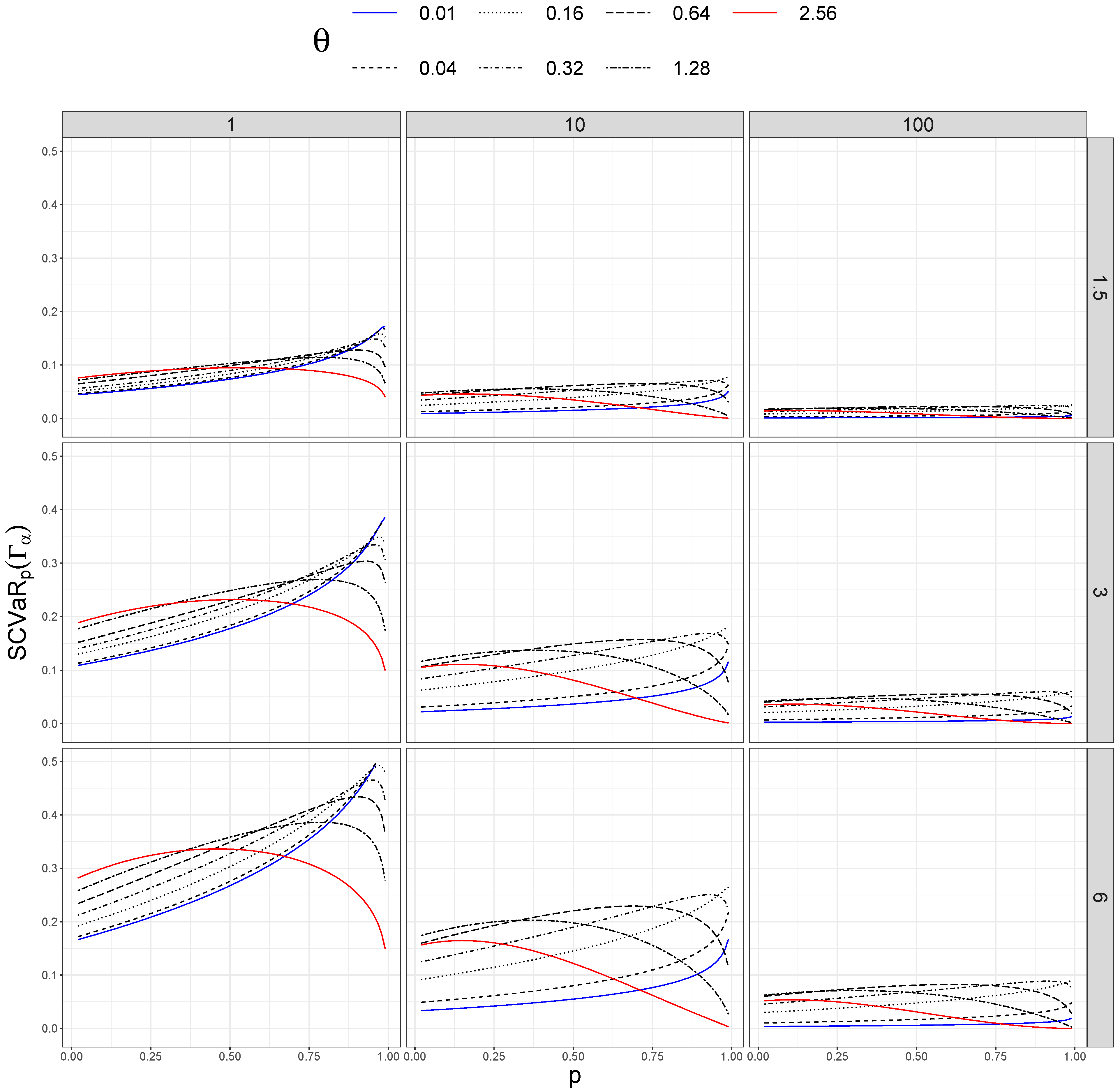
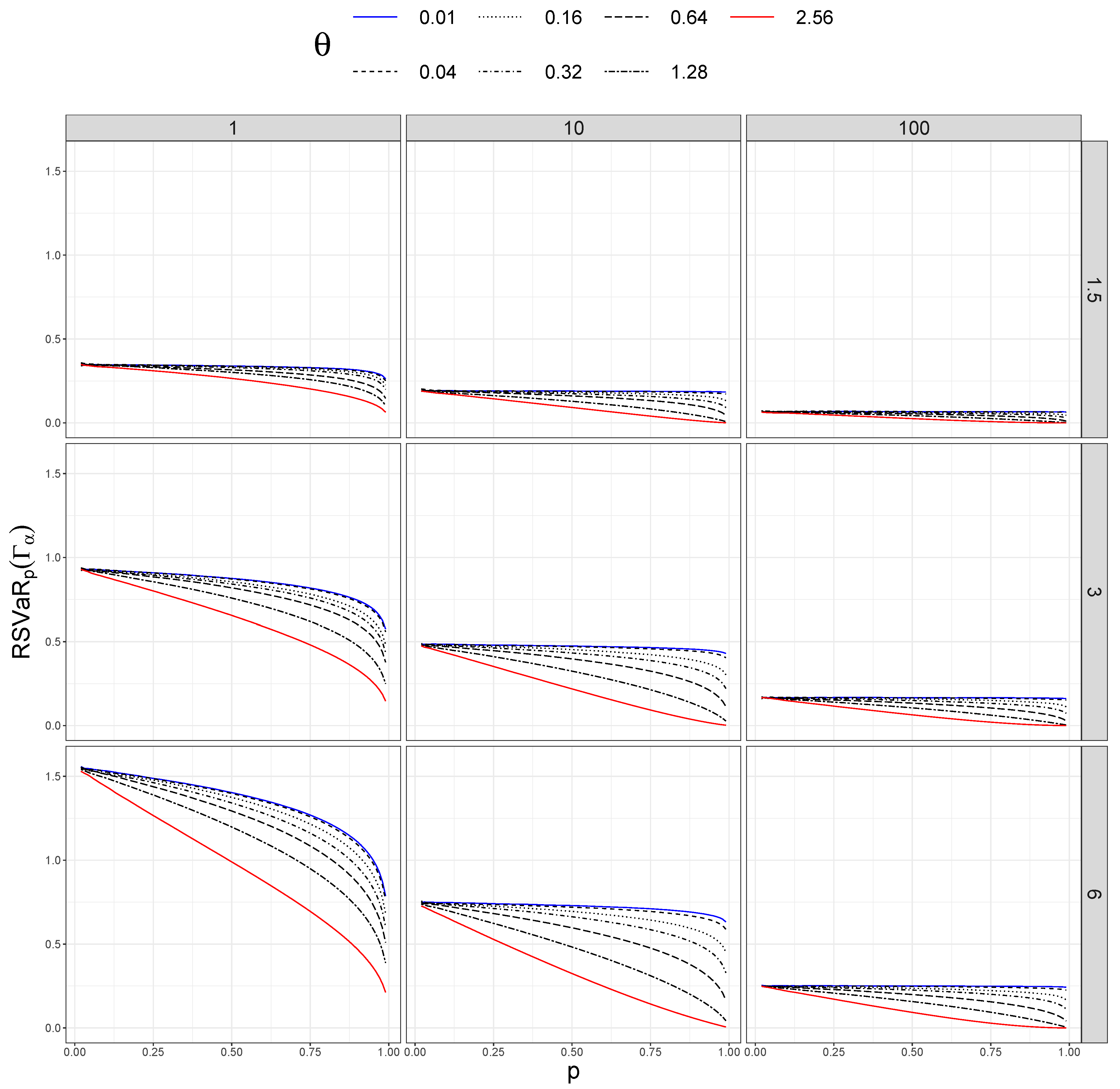
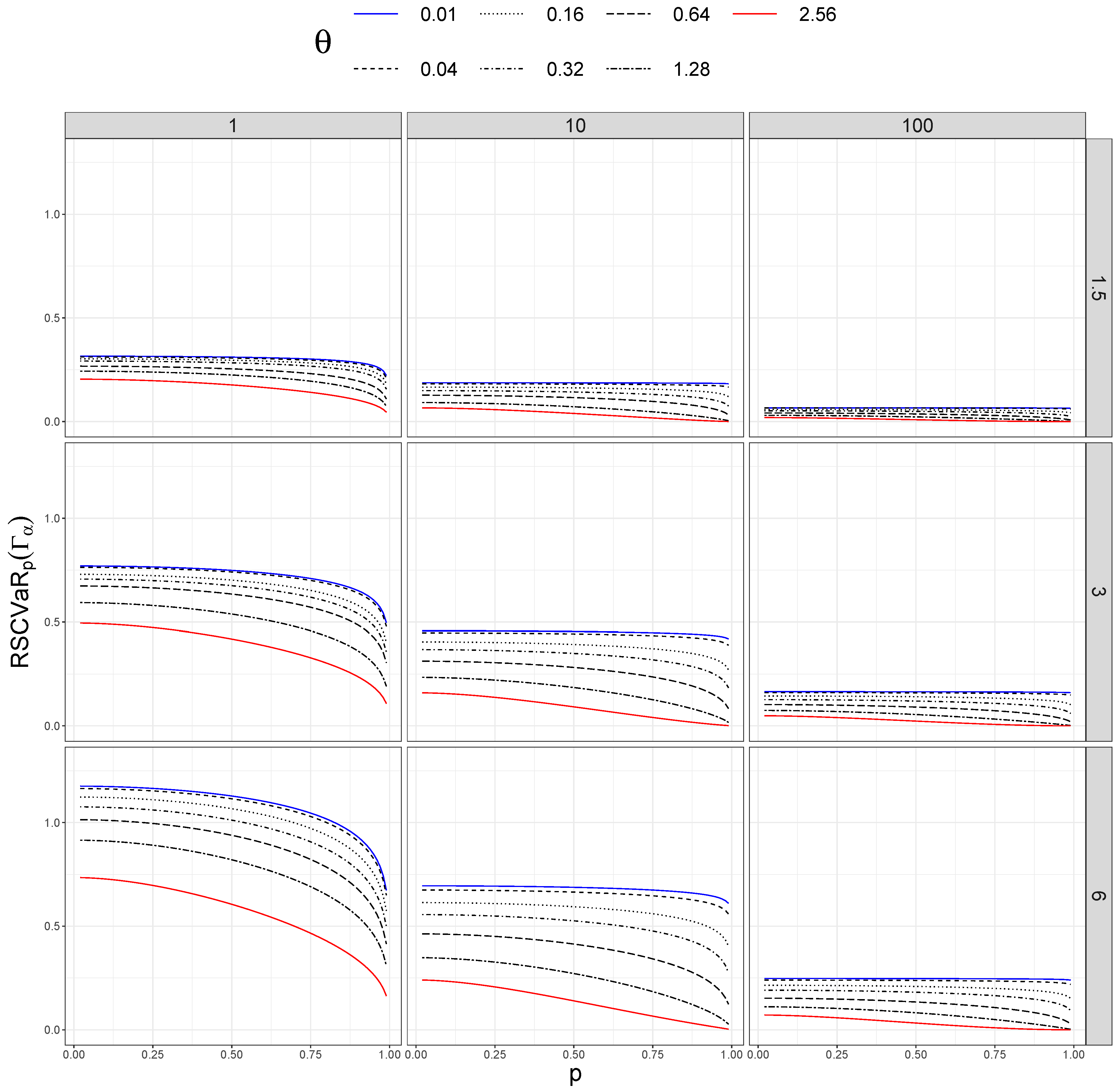
In addition, we took different values of . Figure 1, Figure 2, Figure 3 and Figure 4 show sensitivity measures for different values of p, taking different sizes of sample (columns) and distortion values (rows). In each figure, the blue lines correspond to , the red lines represent , and the dashed black lines between them are ordered by the values of .
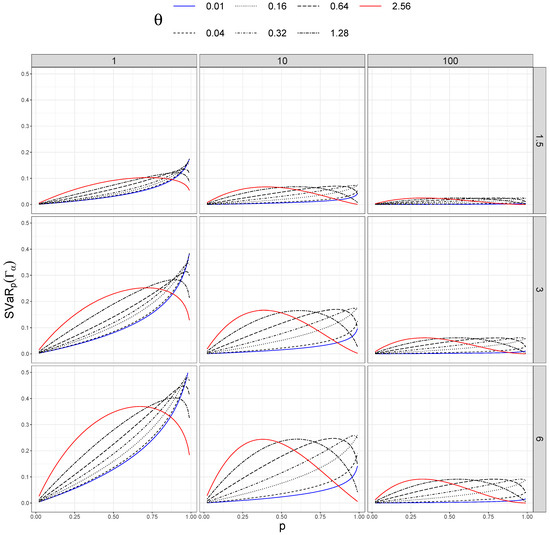
Figure 1.
Sensitivity of versus p for different values of (rows) and n (columns).
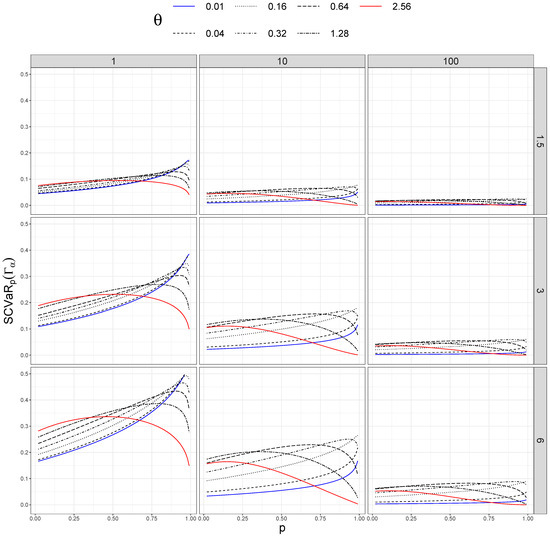
Figure 2.
Sensitivity of versus p for different values of (rows) and n (columns).
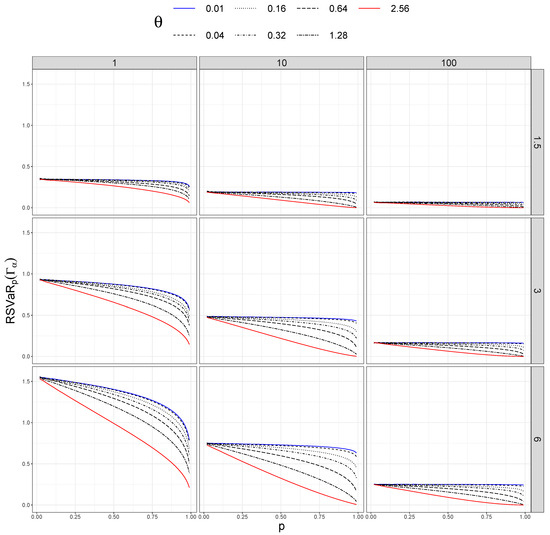
Figure 3.
Relative sensitivity of versus p for different values of (rows) and n (columns).
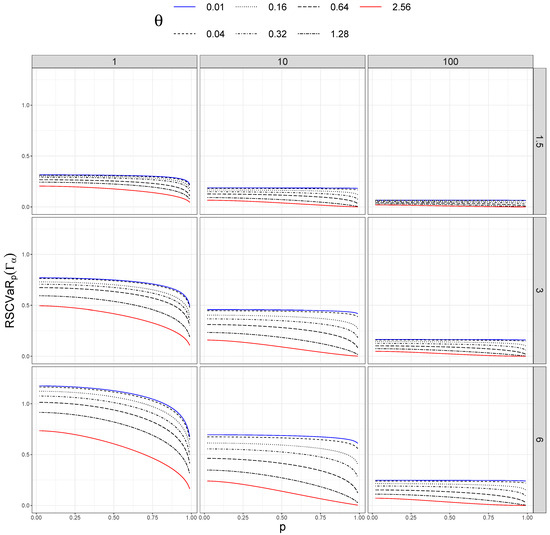
Figure 4.
Relative sensitivity of versus p for different values of (rows) and n (columns).
We can notice the interaction between the values of and p in Figure 2 and Figure 3. For the different values of the shape parameter , we can see the different behaviors of the variations in the sensitivity measures when the values of p change.
Differences in both measures are larger when the distortion (given by ) increases and also for large sizes of the dataset (n). Notice that for each size of the dataset n, the shape of the curves associated with is similar, and the maximum value of the sensitivity measure becomes smaller when n is larger.
However, the interaction between and p disappears when we plot the relative sensitivity measures (see Figure 3 and Figure 4). In this case, the measures are ordered by the values of ; they are larger for small datasets () and smaller if we have many data (). As in the previous measures, larger distortion also produces larger values of the measures.
5. Applications
In this Section, we show the usability of the new measures of sensitivity for VaR and CVaR for very different applications, with real-life data.
In the first one, we have a small dataset related to the stock index IBEX35, while for the second example, we have a larger dataset with air pollutants PM 2.5.
5.1. Iberia Index Dataset
In Spain, the most important stock index is the Iberia Index or IBEX35. This index is equivalent to the S&P500 index. For this study, the data of IBEX35’s daily closing for year 2022 were selected [40]. The dataset comprises a sample of 257 values.
Usually, the variable of interest to compute risk measures is the daily logarithmic return of stock index, defined by
where and indicate the stock index on days t and , respectively.
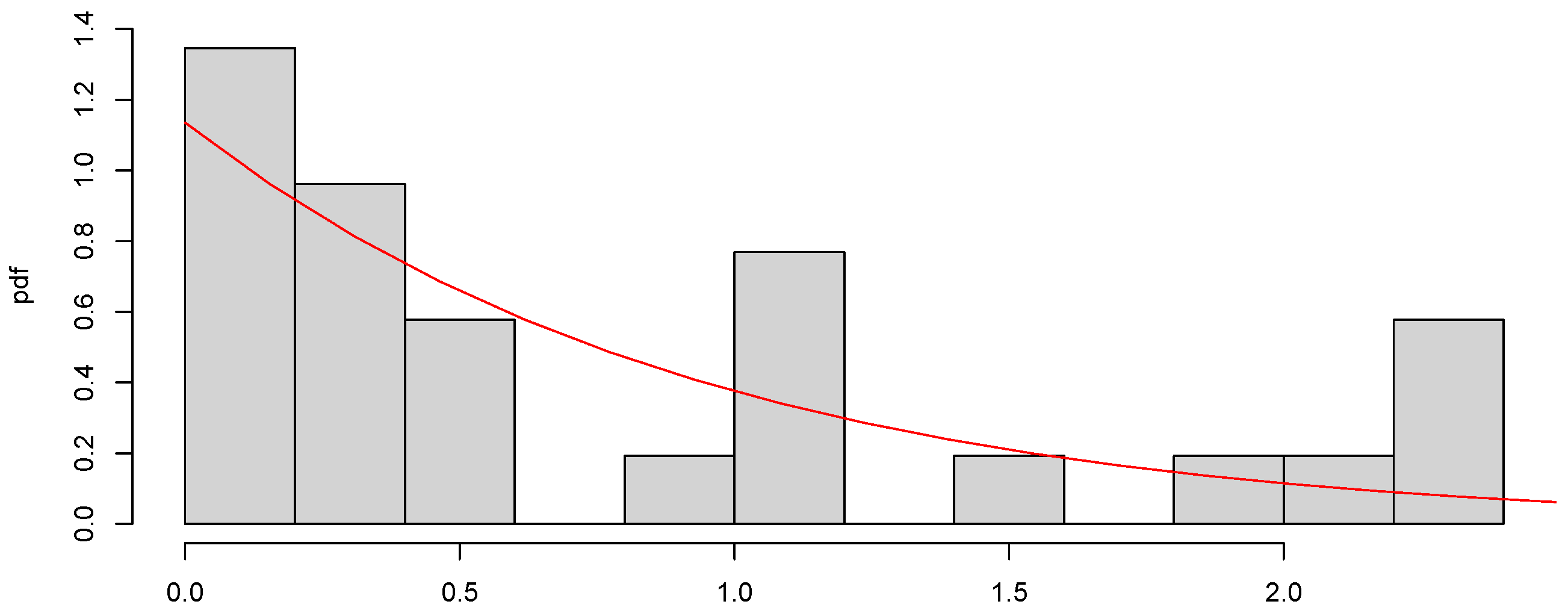
The values that exceed the 0.9 order quantile are considered extreme values and relocated. The resulting dataset is small, with 26 values. We can see the histogram of the dataset values on Figure 5, fitted to a GPD (0.06, 15.46). The estimations for and were computed using the function gpd from evir library [41] of R.
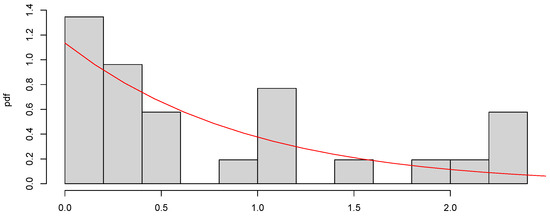
Figure 5.
Histogram of IBEX35 extreme values. The red curve represents the density of the GPD .
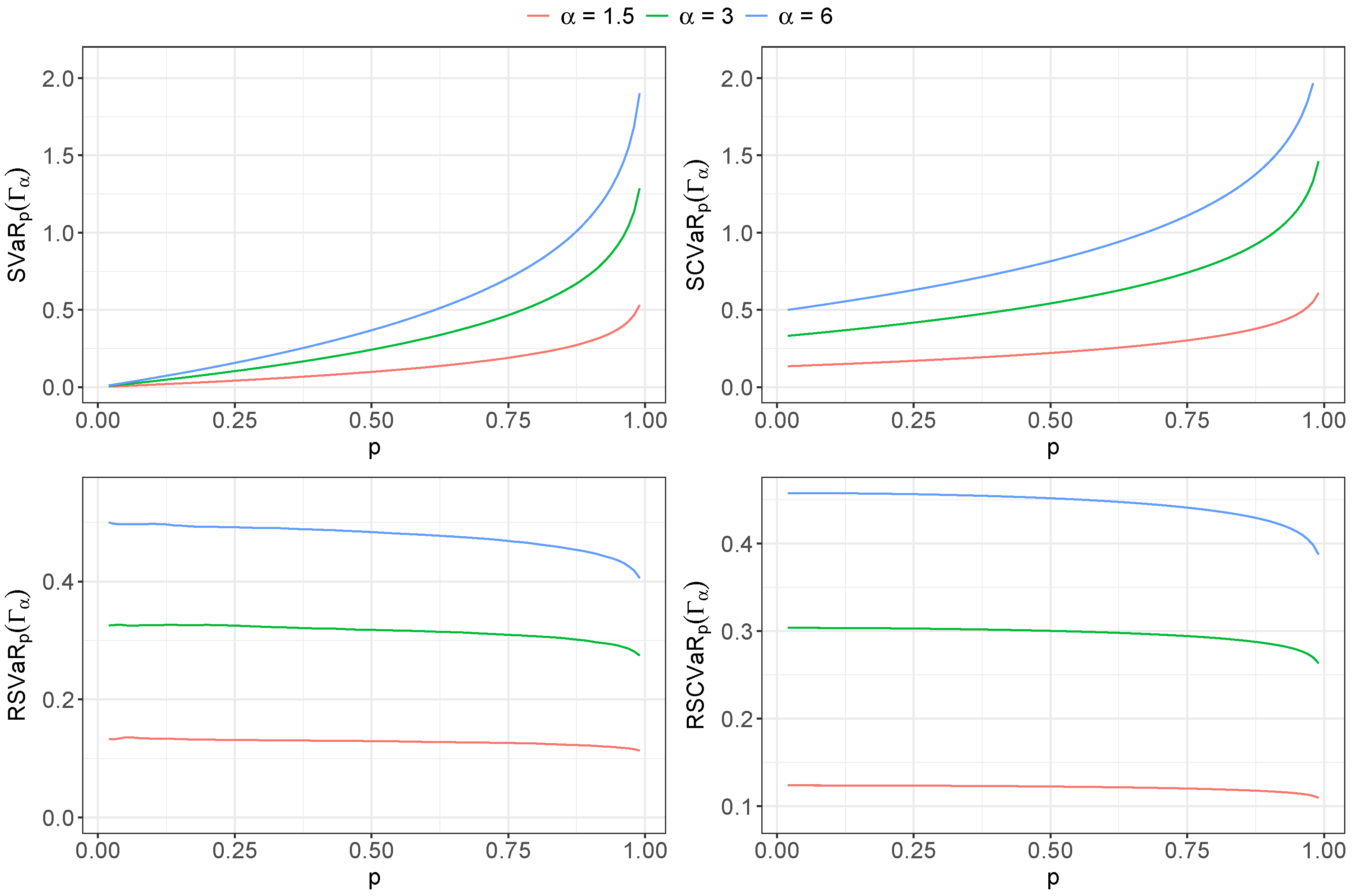
Then, we set , fixed , and took a prior distribution for the parameter . To determine the sensitivity measures for VaR and CVaR, we generated 100,000 values of the random variable , taking the mean of each measure. Figure 6 shows the sensitivity measures (upper charts) and relative sensitivity (lower charts) measures of VaR and CVaR for different values of p.
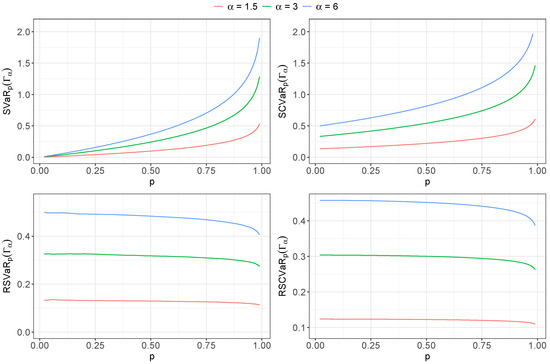
Figure 6.
Sensitivity (upper charts) and relative sensitivity (lower charts) of (left charts) and (right charts) versus p for different values of for Iberia index dataset.
As we expected, the values for all the sensitivity measures are larger for large values of . In addition, for each measure, the curves exhibit the same behavior for all the values of , reaching the maximum for the same value of p.
5.2. Particulate Matter 2.5 Dataset
Particulate matter (PM) is a mixture of solid particles and liquid droplets that can be inhaled and cause serious health problems. When particulate matter is less than 2.5 micrometers in diameter, it is known as PM 2.5, and it is considered to be especially dangerous for human health. In this context, studying the tail distribution of the levels of PM 2.5 and making a sensitivity analysis for VaR and CVaR can be undoubtedly useful.
We considered values of the levels of PM 2.5 measured in g/m3 for the Period 2011–2022 from Madrid (Spain), publicly available on the website [42]. The dataset comprises a sample of 10845 observations. As in the previous example, the values that exceed the threshold , relocated, were considered as extreme values.
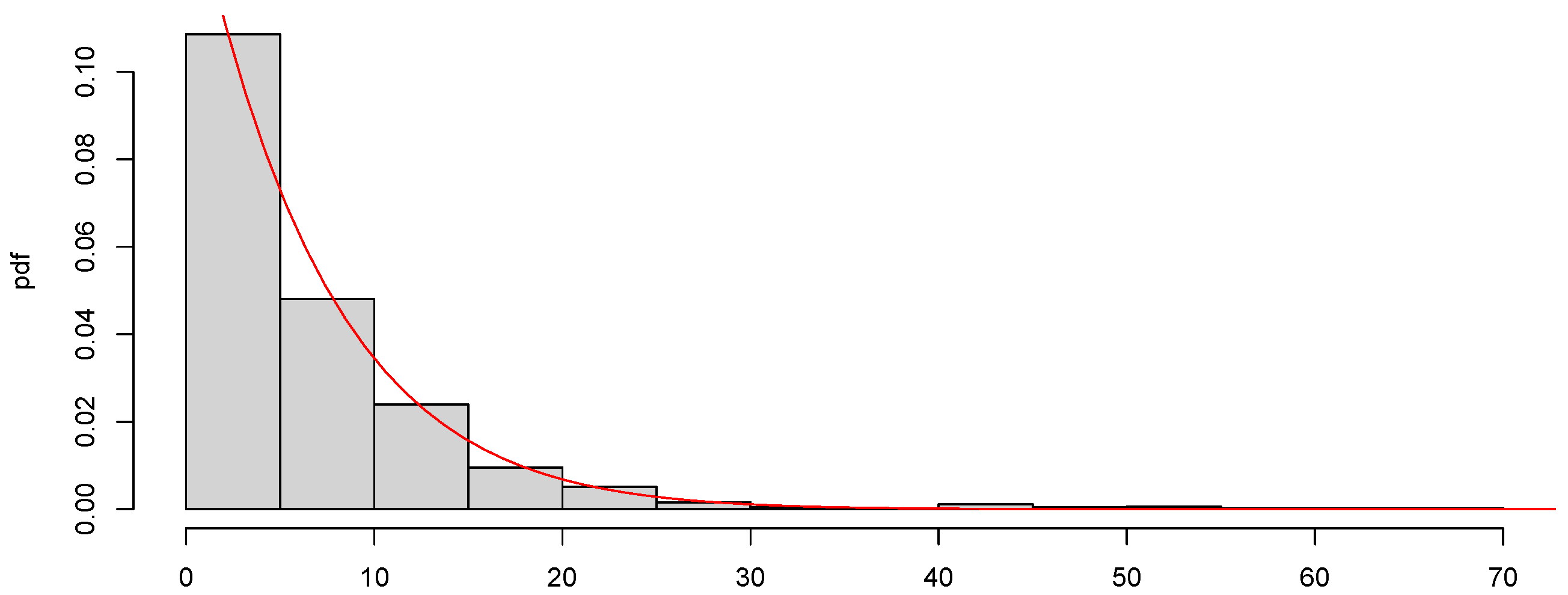
The resulting dataset consists of 1028 values. We adjusted a GPD distribution with the function gpd, obtaining values for and . Figure 7 shows the histogram of the extreme dataset, together with the GPD (0.06, 105.72) density function.
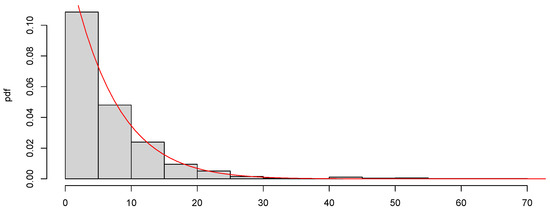
Figure 7.
Histogram of PM 2.5 extreme values. The red curve represents the density of the GPD .
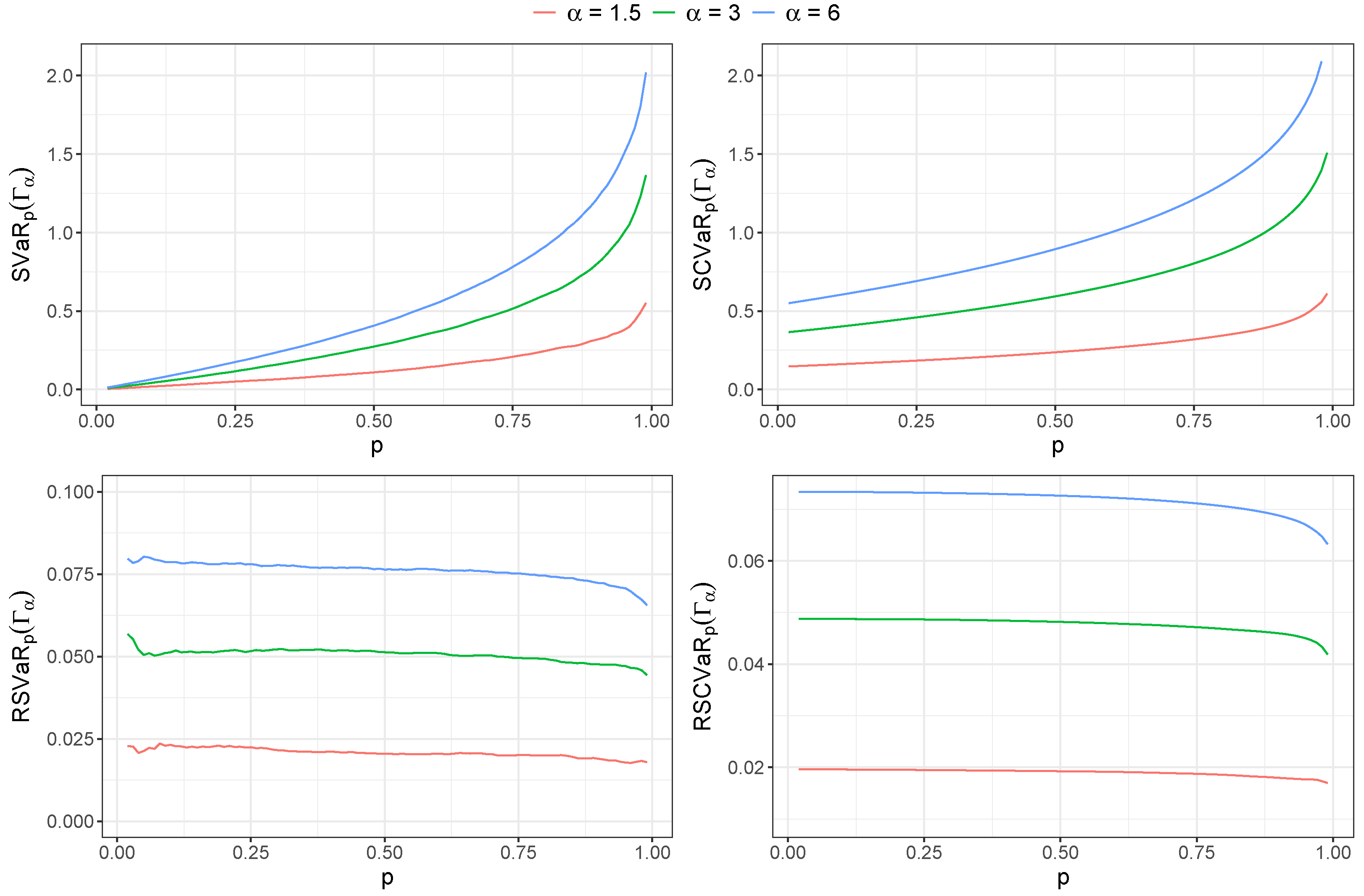
We set , fixed , and considered a prior distribution for the parameter . To determine the sensitivity measures for VaR and CVaR, we generated 100,000 values of the random variable , taking the mean of each measure. Figure 8 shows the sensitivity measures (upper charts) and relative sensitivity (lower charts) measures of VaR and CVaR for different values of p.
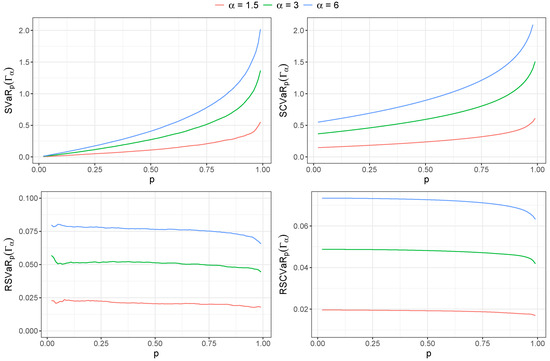
Figure 8.
Sensitivity (upper charts) and relative sensitivity (lower charts) of (left charts) and (right charts) versus p for different values of for PM 2.5 dataset.
6. Conclusions
- We provided sensitivity measures for the and of the GPD distribution when the prior distribution on the shape parameter varies on a class defined using the concept of distorted bands.
- The definitions of the sensitivity measures and and the relative sensitivity measures and were made using a property related to likelihood ratio order on the shape parameter of the GPD. Therefore, it could be extended to other distributions that fulfill that property for a parameter.
- An extensive simulation study was carried out in order to perform a sensitivity analysis, for different values of , sizes of the dataset n, and the distortion parameter , when . We concluded that there is interaction between the parameters and p for the sensitivity measures and . The relative sensitivity measures and are not affected by such interaction. For all four measures, the values are larger when the distortion () increases and when the size of the dataset is smaller. For each value of , the shape of the curves for the sensitivity measures versus p are similar.
- We illustrated the practical use of the sensitivity measures with two examples: for data from the IBEX35 index and PM2.5 air pollutants.
Author Contributions
Conceptualization, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Methodology, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Software, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Validation, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Formal analysis, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Investigation, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Resources, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Data curation, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Writing—original draft, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Writing—review & editing, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Visualization, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Supervision, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Project administration, J.P.A.-N., M.I.P., M.M.P. and E.L.S.; Funding acquisition, J.P.A.-N., M.I.P., M.M.P. and E.L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MCIN/AEI/10.13039/501100011033 and ERDF A way of making Europe as part of R&D&I Project PID2021-122209OB-C32.
Data Availability Statement
Iberia Index dataset is available on the website [40] and Particulate Matter 2.5 dataset is available on the website [42].
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Berger, J.; Berliner, L.M. Robust Bayes and empirical Bayes analysis with ε-contaminated priors. Ann. Stat. 1986, 14, 461–486. [Google Scholar] [CrossRef]
- Ríos Insua, D.; Ruggeri, F. Robust Bayesian Analysis; Springer: New York, NY, USA, 2000. [Google Scholar]
- Berger, J.O. Prior information and subjective probability. In Statistical Decision Theory and Bayesian Analysis; Springer: Berlin/Heidelberg, Germany, 1985; pp. 74–117. [Google Scholar]
- Moreno, E. Global Bayesian robustness for some classes of prior distributions. In Robust Bayesian Analysis; Springer: Berlin/Heidelberg, Germany, 2000; pp. 45–70. [Google Scholar]
- Makov, U.E. Some aspects of Bayesian loss-robustness. J. Stat. Plan. Inference 1994, 38, 359–370. [Google Scholar] [CrossRef]
- Martín, J.; Insua, D.R.; Ruggeri, F. Issues in Bayesian loss robustness. Sankhyā Indian J. Stat. Ser. A 1998, 60, 405–417. [Google Scholar]
- Dey, D.K.; Lou, K.R.; Bose, S. A Bayesian approach to loss robustness. Stat. Decis. 1998, 16, 65–87. [Google Scholar] [CrossRef]
- Arias-Nicolás, J.P.; Martín, J.; Suárez-Llorens, A. The non dominated set in Bayesian decision problems with convex loss functions. Commun. Stat.-Theory Methods 2006, 35, 593–607. [Google Scholar] [CrossRef]
- Arias-Nicolás, J.P.; Martín, J.; Ruggeri, F.; Suárez-Llorens, A. Optimal actions in problems with convex loss functions. Int. J. Approx. Reason. 2009, 50, 303–314. [Google Scholar] [CrossRef]
- Joshi, C.; Ruggeri, F.; Wilson, S.P. Prior robustness for bayesian implementation of the fault tree analysis. IEEE Trans. Reliab. 2017, 67, 170–183. [Google Scholar] [CrossRef]
- Barrera, M.; Lira, I.; Sánchez-Sánchez, M.; Suárez-Llorens, A. Bayesian treatment of results from radioanalytical measurements. Effect of prior information modification in the final value of the activity. Radiat. Phys. Chem. 2019, 156, 266–271. [Google Scholar] [CrossRef]
- Berger, J.O.; Moreno, E.; Pericchi, L.R.; Bayarri, M.J.; Bernardo, J.M.; Cano, J.A.; De la Horra, J.; Martín, J.; Ríos-Insúa, D.; Betrò, B.; et al. An overview of robust Bayesian analysis. Test 1994, 3, 5–124. [Google Scholar] [CrossRef]
- Basu, S.; DasGupta, A. Robust Bayesian analysis with distribution bands. Stat. Decis. 1995, 13, 333–349. [Google Scholar] [CrossRef]
- Arias-Nicolás, J.P.; Ruggeri, F.; Suárez-Llorens, A. New Classes of Priors Based on Stochastic Orders and Distortion Functions. Bayesian Anal. 2016, 11, 1107–1136. [Google Scholar] [CrossRef]
- Sánchez-Sánchez, M.; Sordo, M.A.; Suárez-Llorens, A.; Gómez-Déniz, E. Deriving robust Bayesian premiums under bands of prior distributions with applications. ASTIN Bull. 2019, 49, 147–168. [Google Scholar] [CrossRef]
- Boratyńska, A. Robust Bayesian insurance premium in a collective risk model with distorted priors under the generalised Bregman loss. Stat. Transit. New Ser. 2021, 22, 123–140. [Google Scholar] [CrossRef]
- Ruggeri, F.; Sánchez-Sánchez, M.; Sordo, M.Á.; Suárez-Llorens, A. On a new class of multivariate prior distributions: Theory and application in reliability. Bayesian Anal. 2021, 16, 31–60. [Google Scholar] [CrossRef]
- Bali, T.G. A generalized extreme value approach to financial risk measurement. J. Money Credit. Bank. 2007, 39, 1613–1649. [Google Scholar] [CrossRef]
- Trzpiot, G.; Majewska, J. Estimation of Value at Risk: Extreme value and robust approaches. Oper. Res. Decis. 2010, 20, 131–143. [Google Scholar]
- Singh, A.K.; Allen, D.E.; Powell, R.J. Value at risk estimation using extreme value theory. In Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011. [Google Scholar]
- Van der Merwe, S.; Steven, D.; Pretorius, M. Bayesian extreme value analysis of stock exchange data. arXiv 2018, arXiv:1804.01807. [Google Scholar]
- Miller, N.; Ruszczyński, A. Risk-adjusted probability measures in portfolio optimization with coherent measures of risk. Eur. J. Oper. Res. 2008, 191, 193–206. [Google Scholar] [CrossRef]
- Gilli, M.; Këllezi, E. An application of extreme value theory for measuring financial risk. Comput. Econ. 2006, 27, 207–228. [Google Scholar] [CrossRef]
- Magnou, G. An Application of Extreme Value Theory for Measuring Financial Risk in the Uruguayan Pension Fund. Compend. Cuad. Econ. Adm. 2017, 4, 1–19. [Google Scholar]
- Balkema, A.A.; De Haan, L. Residual life time at great age. Ann. Probab. 1974, 2, 792–804. [Google Scholar] [CrossRef]
- Pickands, J., III. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- de Zea Bermudez, P.; Kotz, S. Parameter estimation of the generalized Pareto distribution—Part I. J. Stat. Plan. Inference 2010, 140, 1353–1373. [Google Scholar] [CrossRef]
- de Zea Bermudez, P.; Kotz, S. Parameter estimation of the generalized Pareto distribution—Part II. J. Stat. Plan. Inference 2010, 140, 1374–1388. [Google Scholar] [CrossRef]
- de Zea Bermudez, P.; Turkman, M.A. Bayesian approach to parameter estimation of the generalized Pareto distribution. Test 2003, 12, 259–277. [Google Scholar] [CrossRef]
- Diebolt, J.; El-Aroui, M.A.; Garrido, M.; Girard, S. Quasi-conjugate Bayes estimates for GPD parameters and application to heavy tails modelling. Extremes 2005, 8, 57–78. [Google Scholar] [CrossRef]
- Castellanos, M.E.; Cabras, S. A default Bayesian procedure for the generalized Pareto distribution. J. Stat. Plan. Inference 2007, 137, 473–483. [Google Scholar] [CrossRef]
- Zhang, J.; Stephens, M.A. A new and efficient estimation method for the generalized Pareto distribution. Technometrics 2009, 51, 316–325. [Google Scholar] [CrossRef]
- Behrens, C.N.; Lopes, H.F.; Gamerman, D. Bayesian analysis of extreme events with threshold estimation. Stat. Model. 2004, 4, 227–244. [Google Scholar] [CrossRef]
- Cabras, S.; Castellanos, M.E. A Bayesian approach for estimating extreme quantiles under a semiparametric mixture model. ASTIN Bull. J. IAA 2011, 41, 87–106. [Google Scholar]
- do Nascimento, F.F.; Gamerman, D.; Lopes, H.F. A semiparametric Bayesian approach to extreme value estimation. Stat. Comput. 2012, 22, 661–675. [Google Scholar] [CrossRef]
- Villa, C. Bayesian estimation of the threshold of a generalised pareto distribution for heavy-tailed observations. Test 2017, 26, 95–118. [Google Scholar] [CrossRef]
- Martín, J.; Parra, M.I.; Pizarro, M.M.; Sanjuán, E.L. Baseline Methods for the Parameter Estimation of the Generalized Pareto Distribution. Entropy 2022, 24, 178. [Google Scholar] [CrossRef] [PubMed]
- Martín, J.; Parra, M.I.; Pizarro, M.M.; Sanjuán, E.L. Baseline Methods for Bayesian Inference in Gumbel distribution. Entropy 2020, 22, 1267. [Google Scholar] [CrossRef]
- Meczarski, M. Stochastic orders in the Bayesian framework. Ann. Coll. Econ. Anal. 2015, 37, 339–360. [Google Scholar]
- IBEX35. IBEX35 Historical Data. 2023. Available online: https://www.nasdaq.com/market-activity/stocks/ibex/historical (accessed on 1 October 2023).
- Hosking, J.R.M.; Wallis, J.R. Parameter and Quantile Estimation for the Generalized Pareto Distribution. Technometrics 1987, 29, 339–349. [Google Scholar] [CrossRef]
- PM25. Air Pollutants Historical Data, 2011–2022. Available online: https://www.miteco.gob.es/es/calidad-y-evaluacion-ambiental/temas/atmosfera-y-calidad-del-aire/calidad-del-aire/evaluacion-datos/datos/historico_calidad_aire.html (accessed on 12 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).