Study of the Six-Compartment Nonlinear COVID-19 Model with the Homotopy Perturbation Method
Abstract
1. Introduction
2. Homotopy Perturbation Method
- The second derivative of with respect to w must be small, because the parameter q may be relatively large, i.e., .
- The norm of must be smaller than one, in order for the series to converge.
Convergence of HPM
3. Application of HPM
3.1. Verification of Model and Numerical Results
3.2. Runge–Kutta Method and Error Analysis
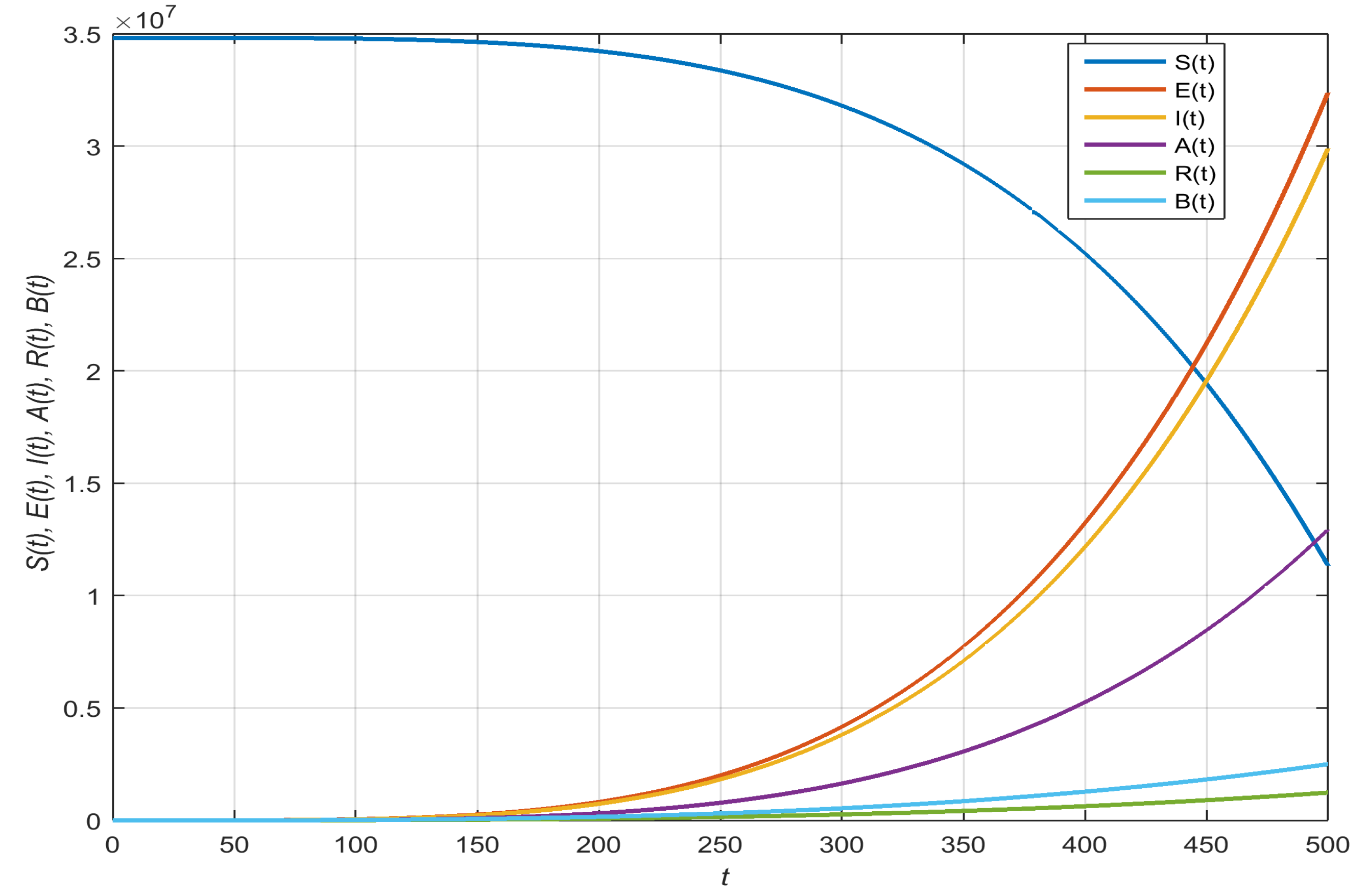
4. Numerical Simulation and Discussion
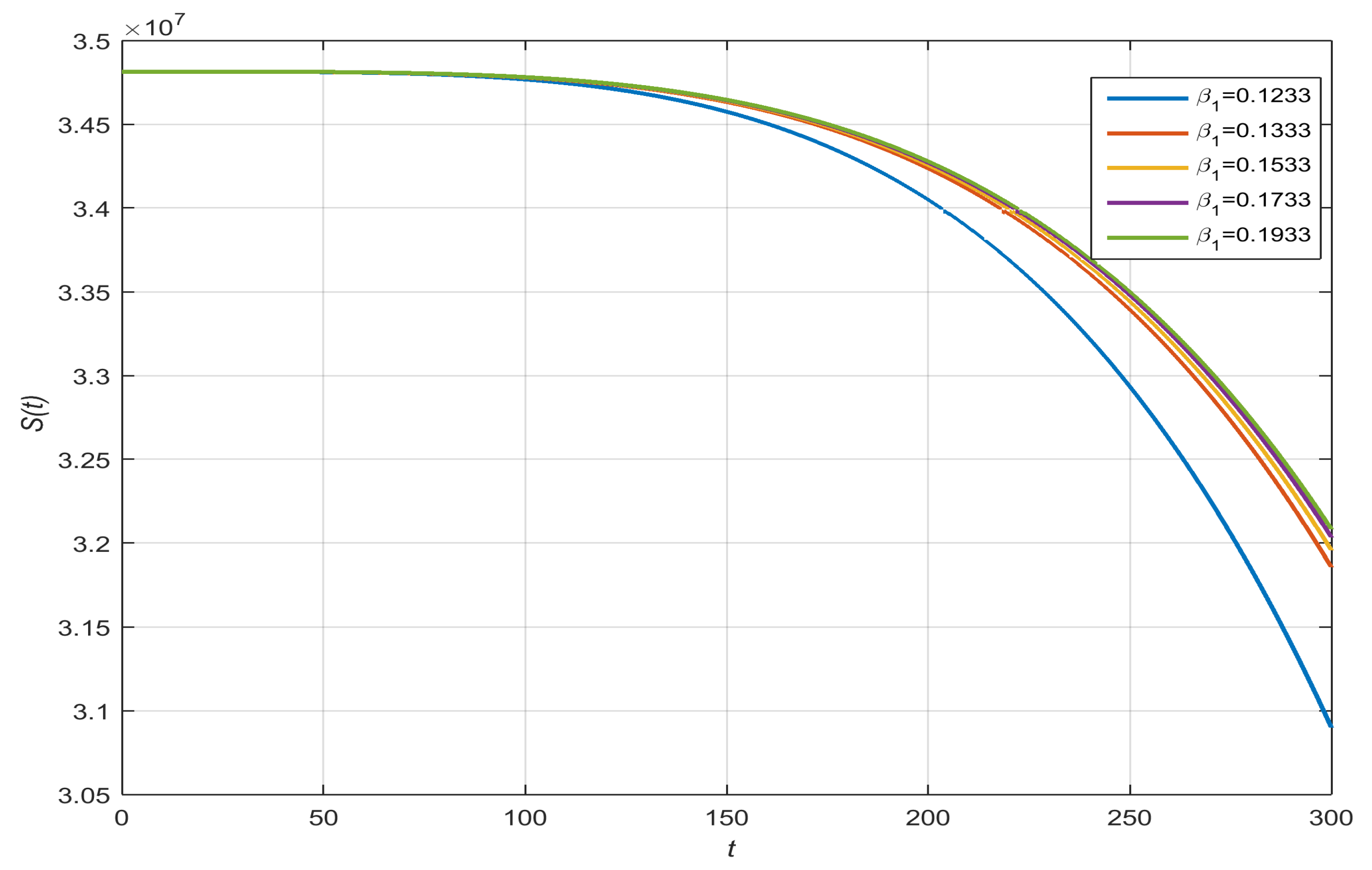
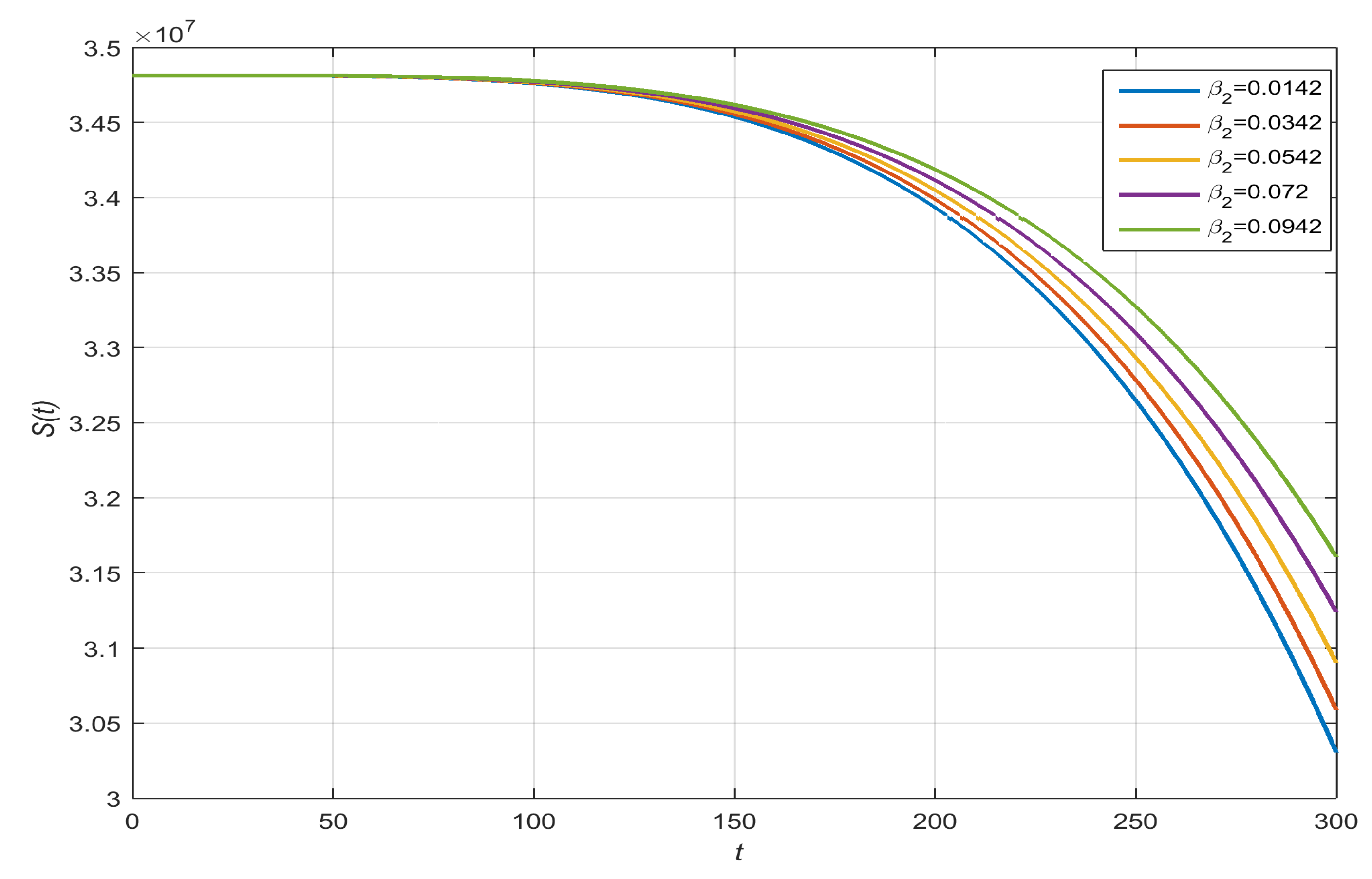
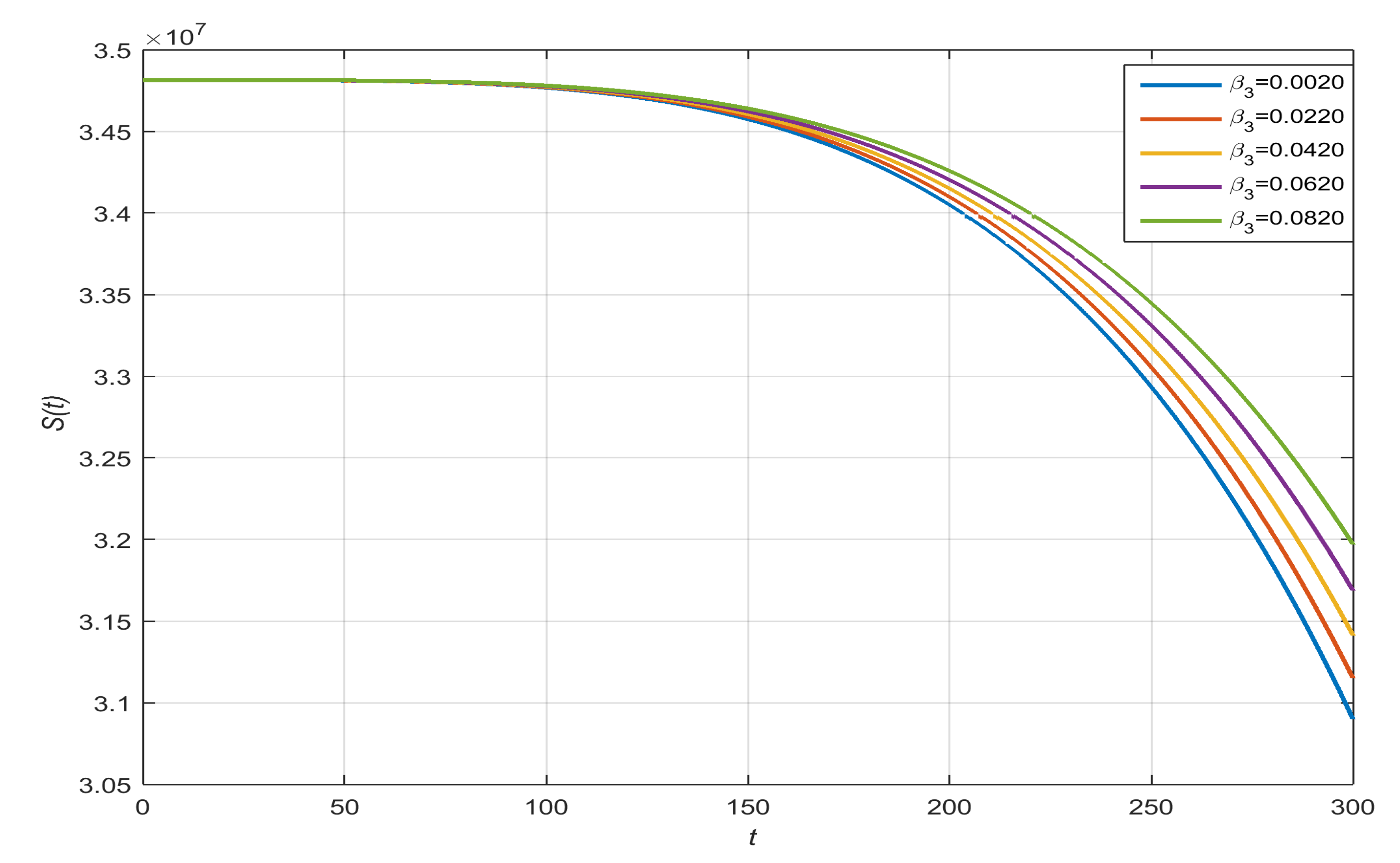
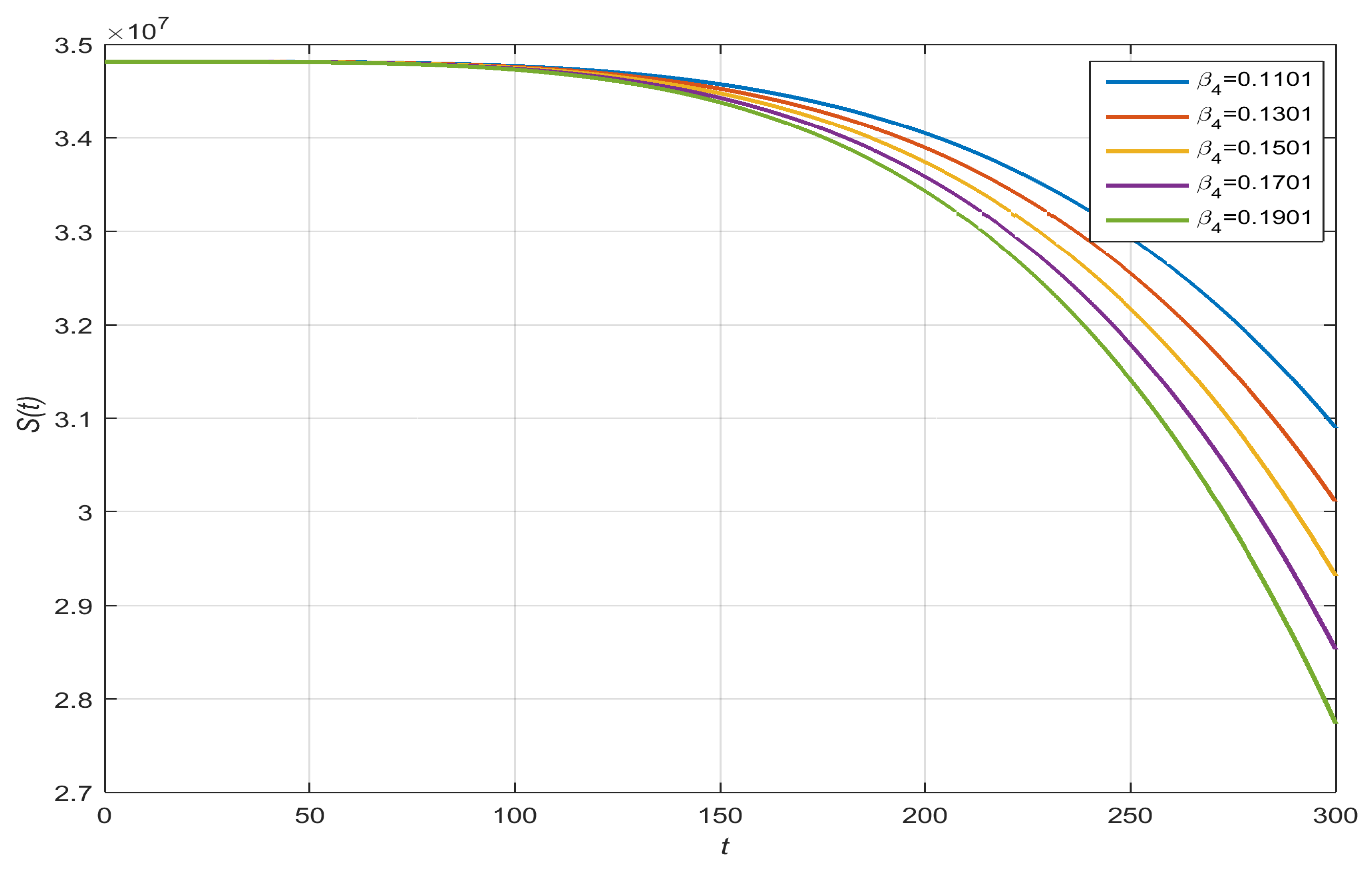
- Susceptible with , , , and :
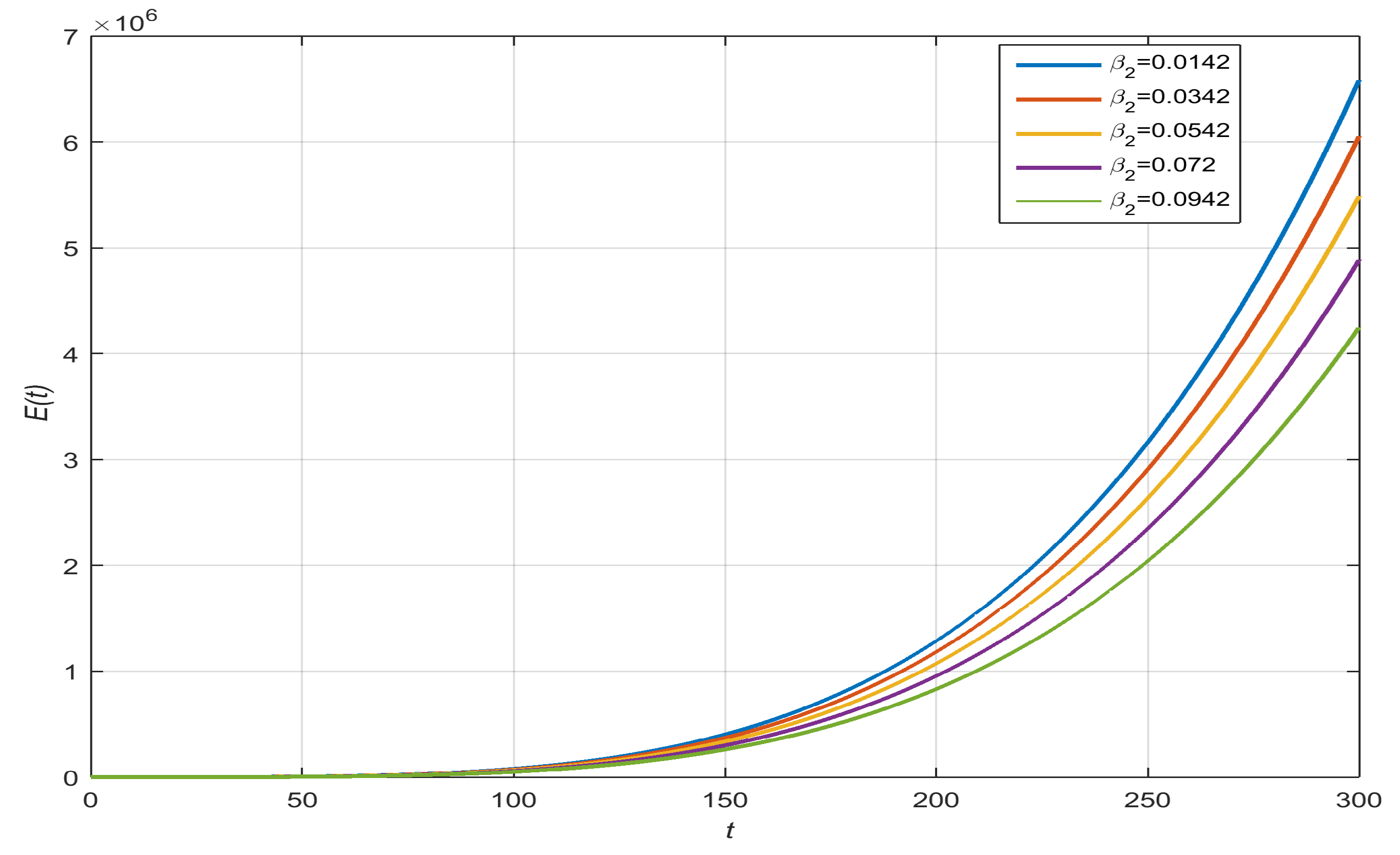
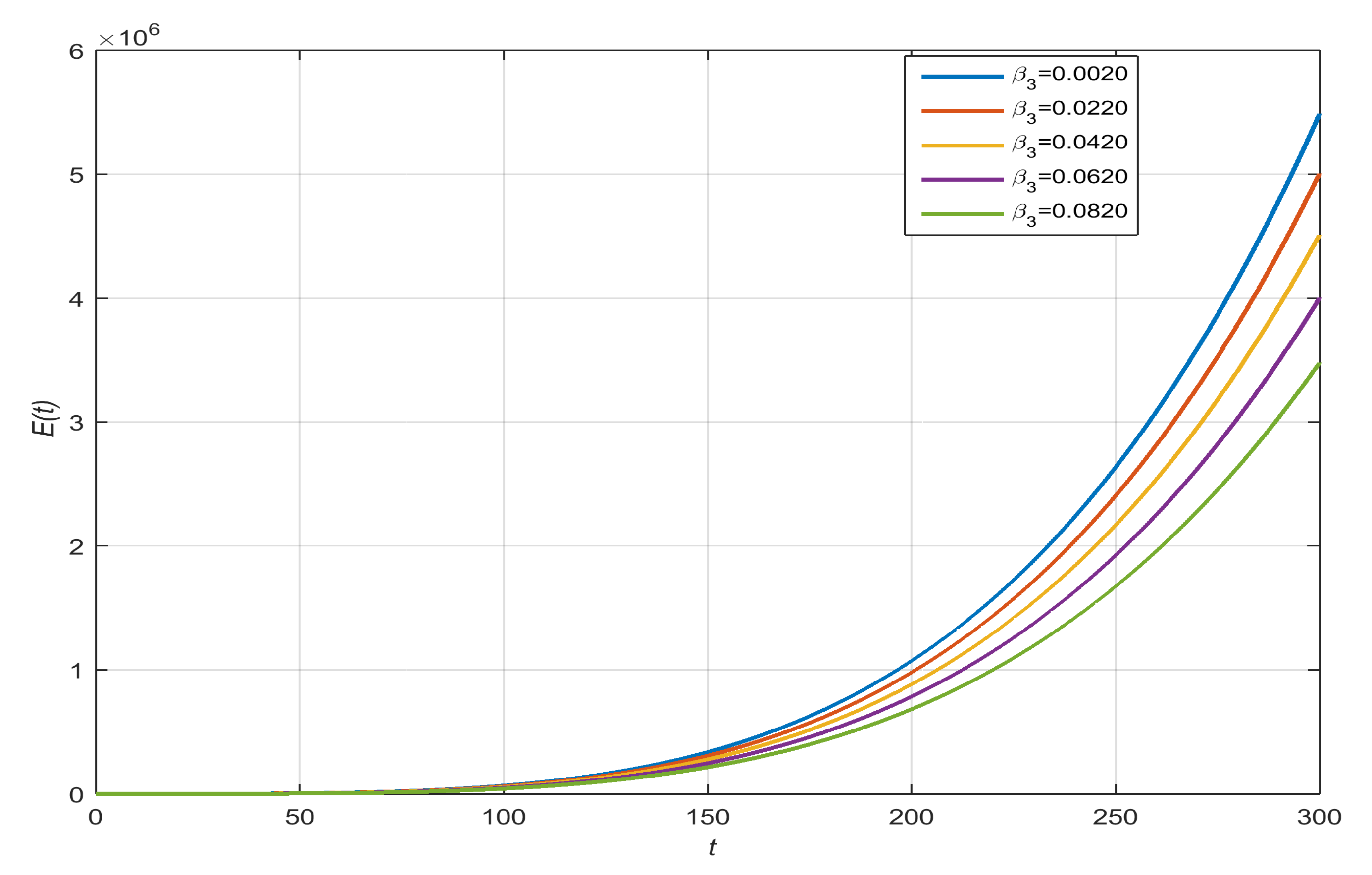
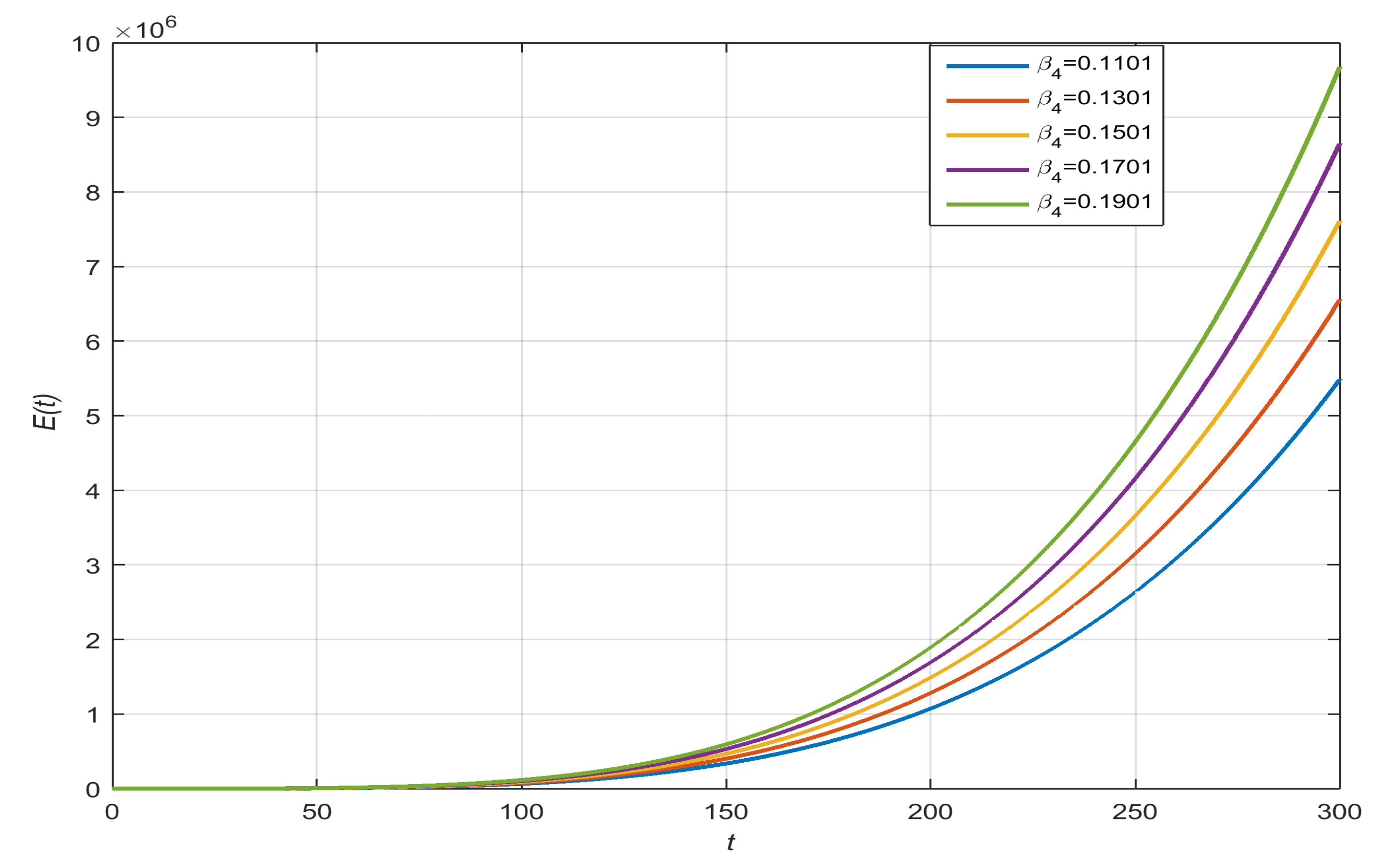
- Exposed People with , , , and :
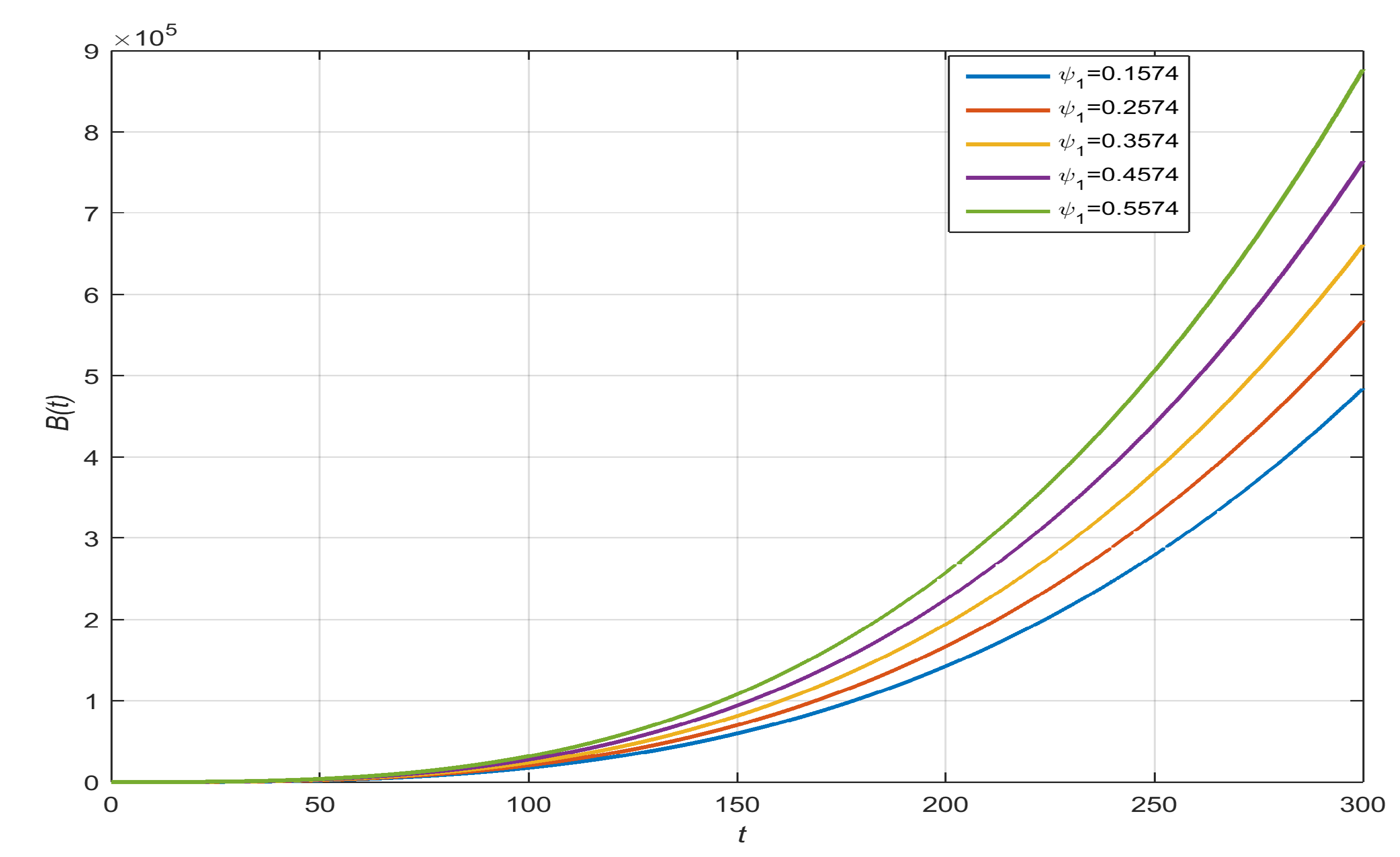
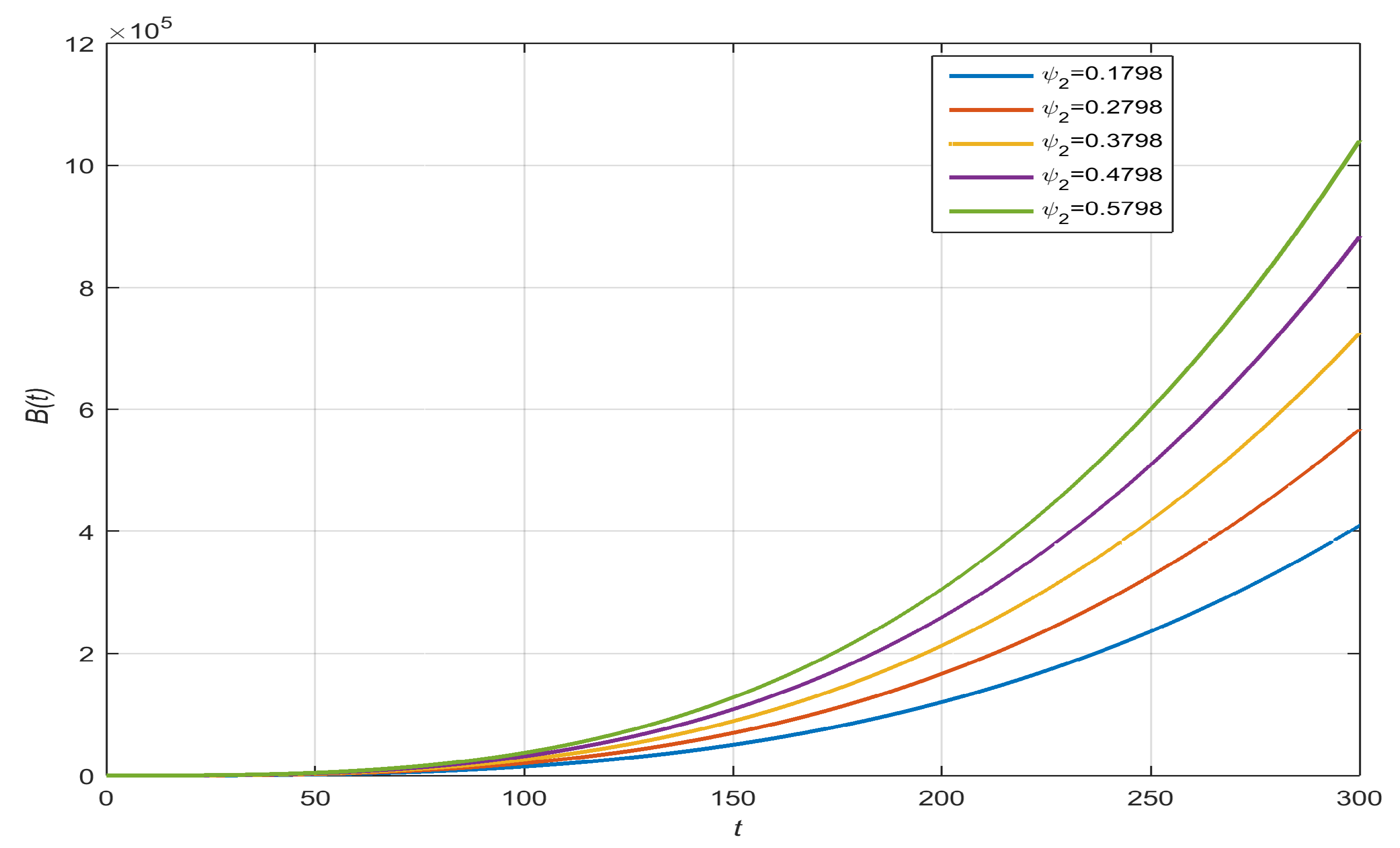
- Concentration of COVID-19 with , , , and :
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sarkar, K.; Mondal, J.; Khajanchi, S. How do the contaminated environment influence the transmission dynamics of COVID-19 pandemic? Eur. Phys. J. Spec. Top. 2022, 231, 3697–3716. [Google Scholar] [CrossRef]
- Hussain, S.; Madi, E.N.; Khan, H.; Gulzar, H.; Etemad, S.; Rezapour, S.; Kaabar, M.K. On the stochastic modeling of COVID-19 under the environmental white noise. J. Funct. Spaces 2022, 2022, 4320865. [Google Scholar] [CrossRef]
- Azoz, S.; Abdelhakiem, K.; Hussien, F. COVID-19 Mathematical Study with Environmental Reservoirs and Three General Functions for Transmissions. Authorea Prepr. 2022, 12, 951–968. [Google Scholar]
- Afzal, A.; Saleel, C.A.; Bhattacharyya, S.; Satish, N.; Samuel, O.D.; Badruddin, I.A. Merits and limitations of mathematical modeling and computational simulations in mitigation of COVID-19 pandemic: A comprehensive review. Arch. Comput. Methods Eng. 2022, 29, 1311–1337. [Google Scholar] [CrossRef] [PubMed]
- Saleem, F.; Al-Ghamdi, A.S.A.M.; Alassafi, M.O.; AlGhamdi, S.A. Machine learning, deep learning, and mathematical models to analyze forecasting and epidemiology of COVID-19: A systematic literature review. Int. J. Environ. Res. Public Health 2022, 19, 5099. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, I.; Chen, F.; Gandomi, A.H. A review on COVID-19 forecasting models. Neural Comput. Appl. 2023, 35, 23671–23681. [Google Scholar] [CrossRef]
- Pozo-Martin, F.; Beltran Sanchez, M.A.; Müller, S.A.; Diaconu, V.; Weil, K.; El Bcheraoui, C. Comparative effectiveness of contact tracing interventions in the context of the COVID-19 pandemic: A systematic review. Eur. J. Epidemiol. 2023, 38, 243–266. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Hashemi Doulabi, H. Robust modelling and prediction of the COVID-19 pandemic in Canada. Int. J. Prod. Res. 2023, 61, 8367–8383. [Google Scholar] [CrossRef]
- Moreau, J. Systematic Review of Mathematical Models for Viral Transmission Dynamics: Insights from COVID-19 Studies. Lett. Biomath. 2024, 11, 21–30. [Google Scholar]
- Naidoo, M.; Shephard, W.; Kambewe, I.; Mtshali, N.; Cope, S.; Rubio, F.A.; Rasella, D. Incorporating social vulnerability in infectious disease mathematical modelling: A scoping review. BMC Med. 2024, 22, 125. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, Y.; Ward, M.P.; Li, K.; Chen, Y.; Duan, M.; Zhang, Z. Optimization of Screening Strategies for COVID-19: Scoping Review. JMIR Public Health Surveill. 2024, 10, e44349. [Google Scholar] [CrossRef] [PubMed]
- Alqarni, M.S.; Alghamdi, M.; Muhammad, T.; Alshomrani, A.S.; Khan, M.A. Mathematical modeling for novel coronavirus (COVID-19) and control. Numer. Methods Partial. Differ. Equ. 2022, 38, 760–776. [Google Scholar] [CrossRef] [PubMed]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. Asymptotology by homotopy perturbation method. Appl. Math. Comput. 2004, 156, 591–596. [Google Scholar] [CrossRef]
- He, J.H. The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl. Math. Comput. 2004, 151, 287–292. [Google Scholar] [CrossRef]
- He, J.H. Limit cycle and bifurcation of nonlinear problems. Chaos Solitons Fractals 2005, 26, 827–833. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phys. Lett. A 2006, 350, 87–88. [Google Scholar] [CrossRef]
- Ganji, D.D. The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer. Phys. Lett. A 2006, 355, 337–341. [Google Scholar] [CrossRef]
- Singh, R.; Maurya, D.K.; Rajoria, Y.K. A mathematical model to solve the nonlinear Burger’s equation by homotopy perturbation method. Math. Eng. Sci. Aerosp. 2020, 11, 115–125. [Google Scholar]
- Wang, Q. Homotopy perturbation method for fractional KdV-Burgers equation. Chaos Solitons Fractals 2008, 35, 843–850. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Homotopy perturbation method with three expansions for Helmholtz-Fangzhu oscillator. Int. Mod. Phys. B 2021, 35, 2150244. [Google Scholar] [CrossRef]
- Aydın, D.; Sahin, S. Solutions of Linear Parabolic Equations with Homotopy Perturbation Method. Palest. J. Math. 2021, 10, 120–127. [Google Scholar]
- Saikia, R.; Phukan, P.; Sarma, J.K. An analytical solution of Balitsky-Kovchegov equation using homotopy perturbation method. arXiv 2022, arXiv:2204.10111. [Google Scholar] [CrossRef]
- Yadav, S.S.; Kumar, A. Solution of One-Dimensional Convection Diffusion Equation by Homotopy Perturbation Method. J. Algebr. Stat. 2022, 13, 3026–3031. [Google Scholar]
- Dubey, S.; Chakraverty, S. Solution of fractional wave equation by homotopy perturbation method. In Wave Dynamics; World Scientific: Singapore, 2022; pp. 263–277. [Google Scholar]
- Berberler, M.E.; Yildirim, A. He’s homotopy perturbation method for solving the shock wave equation. Appl. Anal. 2009, 88, 997–1004. [Google Scholar] [CrossRef]
- Jameel, A.F.; Amen, S.G.; Saaban, A.; Man, N.H.; Alipiah, F.M. Homotopy perturbation method for solving linear fuzzy delay differential equations using double parametric approach. Stat 2020, 8, 551–558. [Google Scholar] [CrossRef]
- Rekha, S.; Balaganesan, P.; Renuka, J. Homotopy Perturbation Method for Mathematical Modelling of Dengue Fever. J. Phys. Conf. Ser. 2021, 1724, 012056. [Google Scholar] [CrossRef]
- Praveen, J.P.; Rao, B.N.; Haranadh, Y.; Rao, B.A.; Narayana, C.; Mahaboob, B. Existence of solution of the nonlinear differential equation in the modeling of eardrum by using homotopy perturbation method. Adv. Math. Sci. J. 2020, 9, 4853–4862. [Google Scholar] [CrossRef]
- Ayoade, A.A.; Peter, O.J.; Abioye, A.I.; Aminu, T.F.; Uwaheren, O.A. Application of Homotopy Perturbation Method to an SIR Mumps Model. Adv. Math. Sci. J. 2020, 9, 1329–1340. [Google Scholar] [CrossRef]
- Rafiullah, M.; Rafiq, A. A new approach to solve systems of second order non-linear ordinary differential equations. Acta Univ. Apulensis Math. Inform. 2010, 24, 189–200. [Google Scholar]
- Saqib, M.; Iqbal, M. Some multi-step iterative methods for solving nonlinear equations. Open J. Math. Sci. 2017, 1, 25–33. [Google Scholar] [CrossRef]
- Buhe, E.; Rafiullah, M.; Jabeen, D.; Anjum, N. Application of homotopy perturbation method to solve a nonlinear mathematical model of depletion of forest resources. Front. Phys. 2023, 11, 1246884. [Google Scholar] [CrossRef]
- Agarwal, G.; Mohan Singh, M.; Suthar, D.L.; Purohit, S.D. Analysis and estimation of the COVID-19 pandemic by modified homotopy perturbation method. Appl. Math. Sci. Eng. 2023, 31, 2279170. [Google Scholar] [CrossRef]
- Nasution, H.; Mulyono, M.; Surbakti, N.M.; Sihaholo, R.S.B. Exploring of Homotopy Perturbation Method (HPM) for Solving Spread of COVID-19. Jambura J. Biomath. (JJBM) 2023, 4, 138–145. [Google Scholar] [CrossRef]
- Ayati, Z.; Biazar, J. On the convergence of Homotopy perturbation method. J. Egypt. Math. Soc. 2015, 23, 424–428. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Convergence of the homotopy perturbation method. Int. J. Nonlinear Sci. Numer. Simul. 2011, 12, 9–14. [Google Scholar] [CrossRef]



| Parameter | Description |
|---|---|
| Contact rate among exposed and susceptible | |
| Contact rate among infected (symptomatic) and susceptible | |
| Contact rate among infected (asymptomatic) and susceptible | |
| Contact rate among environment and susceptible | |
| Virus contribution due to E to B | |
| Virus contribution due to I to B | |
| Virus contribution due to A to B | |
| Natural death rate due to infection at I | |
| Recruitment rate | |
| d | Natural mortality rate |
| Incubation period | |
| Incubation period | |
| Recovery from I | |
| Recovery from A | |
| Virus removal from environment |
| t | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 1.616842099 | 1.92 × 10−7 | 3.10 × 10−6 | 2.35 × 10−6 | 4.99 × 10−6 | 1.06 × 10−5 |
| 1 | 3.233692616 | 4.23 × 10−5 | 5.34 × 10−5 | 5.41 × 10−6 | 6.64 × 10−5 | 0.000254454 |
| 1.5 | 4.850716822 | 0.000356877 | 0.000239544 | 6.51 × 10−5 | 0.00042068 | 0.00180683 |
| 2 | 6.468316101 | 0.001518456 | 0.000621071 | 0.000278623 | 0.001641022 | 0.007297106 |
| 2.5 | 8.087210111 | 0.004566927 | 0.001153262 | 0.000834699 | 0.004772735 | 0.021466895 |
| 3 | 9.708500035 | 0.011096696 | 0.001618225 | 0.002034279 | 0.011452179 | 0.051608136 |
| 3.5 | 11.33371698 | 0.023323999 | 0.001563129 | 0.004315138 | 0.02400971 | 0.107905772 |
| 4 | 12.96485896 | 0.044136898 | 0.000245444 | 0.00827457 | 0.045558465 | 0.203704952 |
| 4.5 | 14.60441884 | 0.07713207 | 0.003415046 | 0.014690223 | 0.080070501 | 0.355718662 |
| 5 | 16.25540547 | 0.126641564 | 0.01087792 | 0.024538976 | 0.132441761 | 0.584188452 |
| 5.5 | 17.92135941 | 0.197751982 | 0.024018022 | 0.039013869 | 0.208547273 | 0.913008351 |
| 6 | 19.60636462 | 0.296317974 | 0.045156182 | 0.059539181 | 0.315287878 | 1.369819985 |
| 6.5 | 21.3150571 | 0.428971505 | 0.077085337 | 0.087783756 | 0.46062964 | 1.9860852 |
| 7 | 23.052631 | 0.603128003 | 0.123092626 | 0.125672724 | 0.653636997 | 2.797141232 |
| 7.5 | 24.82484309 | 0.826990239 | 0.186977975 | 0.17539775 | 0.904500543 | 3.842242332 |
| 8 | 26.63801591 | 1.109550564 | 0.273069676 | 0.239425973 | 1.224560286 | 5.164590951 |
| 8.5 | 28.49903976 | 1.460592006 | 0.386237365 | 0.320507763 | 1.626325031 | 6.811360906 |
| 9 | 30.41537415 | 1.890688562 | 0.531902821 | 0.421683432 | 2.123488541 | 8.833714418 |
| 9.5 | 32.39504866 | 2.411204963 | 0.71604889 | 0.546289031 | 2.730942952 | 11.28681449 |
| t | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.05 | 0.161685288 | 1.60 × 10−7 | 1.94 × 10−8 | 3.17 × 10−7 | 1.81 × 10−7 | 2.25 × 10−8 |
| 0.1 | 0.323370315 | 2.98 × 10−7 | 2.76 × 10−8 | 6.21 × 10−7 | 3.80 × 10−7 | 9.60 × 10−8 |
| 0.15 | 0.485055074 | 4.21 × 10−7 | 3.41 × 10−8 | 9.12 × 10−7 | 6.02 × 10−7 | 2.37 × 10−7 |
| 0.2 | 0.64673958 | 5.33 × 10−7 | 6.00 × 10−8 | 1.19 × 10−6 | 8.63 × 10−7 | 4.81 × 10−7 |
| 0.25 | 0.808423825 | 6.33 × 10−7 | 1.38 × 10−7 | 1.45 × 10−6 | 1.18 × 10−6 | 8.90 × 10−7 |
| 0.3 | 0.970107831 | 7.10 × 10−7 | 3.10 × 10−7 | 1.70 × 10−6 | 1.58 × 10−6 | 1.56 × 10−6 |
| 0.35 | 1.131791621 | 7.44 × 10−7 | 6.28 × 10−7 | 1.92 × 10−6 | 2.11 × 10−6 | 2.64 × 10−6 |
| 0.4 | 1.29347524 | 7.03 × 10−7 | 1.15 × 10−6 | 2.11 × 10−6 | 2.81 × 10−6 | 4.33 × 10−6 |
| 0.45 | 1.45515871 | 5.39 × 10−7 | 1.95 × 10−6 | 2.26 × 10−6 | 3.74 × 10−6 | 6.89 × 10−6 |
| 0.5 | 1.616842091 | 1.89 × 10−7 | 3.10 × 10−6 | 2.35 × 10−6 | 4.99 × 10−6 | 1.06 × 10−5 |
| 0.55 | 1.778525457 | 4.26 × 10−7 | 4.68 × 10−6 | 2.36 × 10−6 | 6.66 × 10−6 | 1.60 × 10−5 |
| 0.6 | 1.940208867 | 1.41 × 10−6 | 6.77 × 10−6 | 2.29 × 10−6 | 8.84 × 10−6 | 2.35 × 10−5 |
| 0.65 | 2.101892419 | 2.88 × 10−6 | 9.47 × 10−6 | 2.10 × 10−6 | 1.17 × 10−5 | 3.37 × 10−5 |
| 0.7 | 2.263576232 | 4.98 × 10−6 | 1.29 × 10−5 | 1.76 × 10−6 | 1.54 × 10−5 | 4.73 × 10−5 |
| 0.75 | 2.42526041 | 7.89 × 10−6 | 1.71 × 10−5 | 1.24 × 10−6 | 2.00 × 10−5 | 6.51 × 10−5 |
| 0.8 | 2.586945102 | 1.18 × 10−5 | 2.22 × 10−5 | 5.18 × 10−7 | 2.59 × 10−5 | 8.81 × 10−5 |
| 0.85 | 2.748630479 | 1.69 × 10−5 | 2.82 × 10−5 | 4.62 × 10−7 | 3.32 × 10−5 | 0.000117264 |
| 0.9 | 2.910316721 | 2.35 × 10−5 | 3.54 × 10−5 | 1.74 × 10−6 | 4.21 × 10−5 | 0.000153809 |
| 0.95 | 3.07200402 | 3.19 × 10−5 | 4.38 × 10−5 | 3.37 × 10−6 | 5.31 × 10−5 | 0.000199056 |
| t | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.005 | 0.016168535 | 1.73 × 10−8 | 2.45 × 10−9 | 3.24 × 10−8 | 1.76 × 10−8 | 2.14 × 10−10 |
| 0.01 | 0.032337077 | 3.44 × 10−8 | 4.81 × 10−9 | 6.47 × 10−8 | 3.52 × 10−8 | 8.62 × 10−10 |
| 0.015 | 0.048505612 | 5.11 × 10−8 | 7.05 × 10−9 | 9.68 × 10−8 | 5.30 × 10−8 | 1.95 × 10−9 |
| 0.02 | 0.064674139 | 6.75 × 10−8 | 9.19 × 10−9 | 1.29 × 10−7 | 7.10 × 10−8 | 3.48 × 10−9 |
| 0.025 | 0.080842674 | 8.36 × 10−8 | 1.12 × 10−8 | 1.61 × 10−7 | 8.90 × 10−8 | 5.47 × 10−9 |
| 0.03 | 0.097011201 | 9.95 × 10−8 | 1.31 × 10−8 | 1.92 × 10−7 | 1.07 × 10−7 | 7.92 × 10−9 |
| 0.035 | 0.113179728 | 1.15 × 10−7 | 1.49 × 10−8 | 2.24 × 10−7 | 1.26 × 10−7 | 1.08 × 10−8 |
| 0.04 | 0.129348248 | 1.30 × 10−7 | 1.65 × 10−8 | 2.55 × 10−7 | 1.44 × 10−7 | 1.42 × 10−8 |
| 0.045 | 0.145516761 | 1.46 × 10−7 | 1.80 × 10−8 | 2.86 × 10−7 | 1.63 × 10−7 | 1.81 × 10−8 |
| 0.05 | 0.161685281 | 1.60 × 10−7 | 1.94 × 10−8 | 3.17 × 10−7 | 1.81 × 10−7 | 2.25 × 10−8 |
| 0.055 | 0.1778538 | 1.75 × 10−7 | 2.07 × 10−8 | 3.48 × 10−7 | 2.00 × 10−7 | 2.73 × 10−8 |
| 0.06 | 0.194022313 | 1.89 × 10−7 | 2.18 × 10−8 | 3.79 × 10−7 | 2.20 × 10−7 | 3.27 × 10−8 |
| 0.065 | 0.210190818 | 2.04 × 10−7 | 2.29 × 10−8 | 4.10 × 10−7 | 2.39 × 10−7 | 3.86 × 10−8 |
| 0.07 | 0.226359315 | 2.18 × 10−7 | 2.38 × 10−8 | 4.40 × 10−7 | 2.58 × 10−7 | 4.51 × 10−8 |
| 0.075 | 0.24252782 | 2.32 × 10−7 | 2.46 × 10−8 | 4.71 × 10−7 | 2.78 × 10−7 | 5.21 × 10−8 |
| 0.08 | 0.258696318 | 2.45 × 10−7 | 2.53 × 10−8 | 5.01 × 10−7 | 2.98 × 10−7 | 5.97 × 10−8 |
| 0.085 | 0.27486483 | 2.59 × 10−7 | 2.60 × 10−8 | 5.31 × 10−7 | 3.18 × 10−7 | 6.78 × 10−8 |
| 0.09 | 0.291033313 | 2.72 × 10−7 | 2.66 × 10−8 | 5.61 × 10−7 | 3.38 × 10−7 | 7.66 × 10−8 |
| 0.095 | 0.30720181 | 2.85 × 10−7 | 2.71 × 10−8 | 5.91 × 10−7 | 3.59 × 10−7 | 8.59 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafiullah, M.; Asif, M.; Jabeen, D.; Ibrahim, M.A. Study of the Six-Compartment Nonlinear COVID-19 Model with the Homotopy Perturbation Method. Axioms 2024, 13, 311. https://doi.org/10.3390/axioms13050311
Rafiullah M, Asif M, Jabeen D, Ibrahim MA. Study of the Six-Compartment Nonlinear COVID-19 Model with the Homotopy Perturbation Method. Axioms. 2024; 13(5):311. https://doi.org/10.3390/axioms13050311
Chicago/Turabian StyleRafiullah, Muhammad, Muhammad Asif, Dure Jabeen, and Mahmoud A. Ibrahim. 2024. "Study of the Six-Compartment Nonlinear COVID-19 Model with the Homotopy Perturbation Method" Axioms 13, no. 5: 311. https://doi.org/10.3390/axioms13050311
APA StyleRafiullah, M., Asif, M., Jabeen, D., & Ibrahim, M. A. (2024). Study of the Six-Compartment Nonlinear COVID-19 Model with the Homotopy Perturbation Method. Axioms, 13(5), 311. https://doi.org/10.3390/axioms13050311







