A Vector Representation of Multicomplex Numbers and Its Application to Radio Frequency Signals
Abstract
:1. Introduction
2. Multicomplex Numbers
- 1 real unit,
- imaginary units, which square to ,
- hyperbolic units, which square to 1.
- for ,
- for ,
- for ,
- in general,
2.1. Unit Representation and Multiplication
2.2. Multiplication by
2.3. Conjugation, Hyperbolic Real and Imaginary Parts
2.4. Multiplication of Multicomplex Numbers
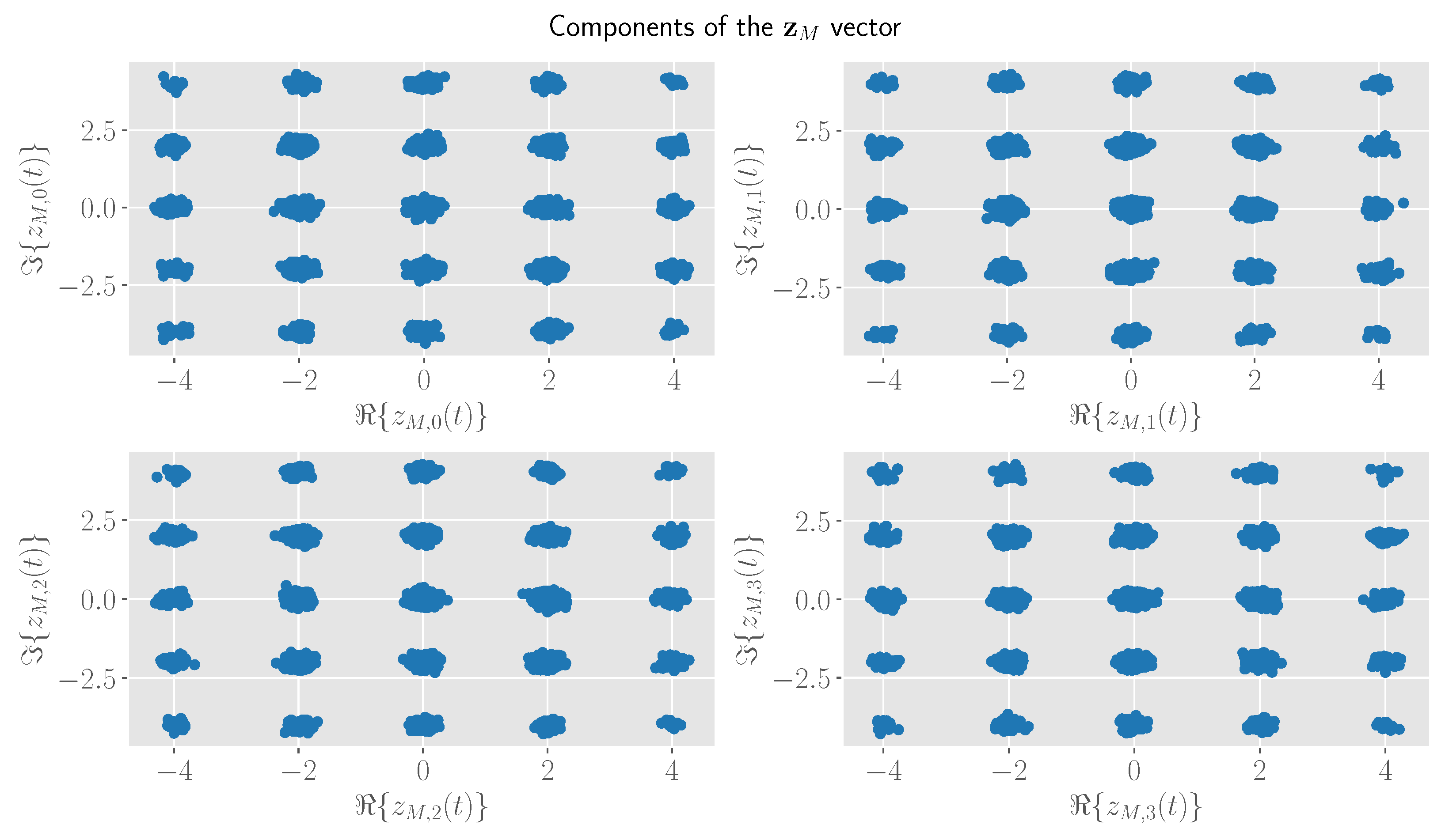
3. Orthogonal Decomposition
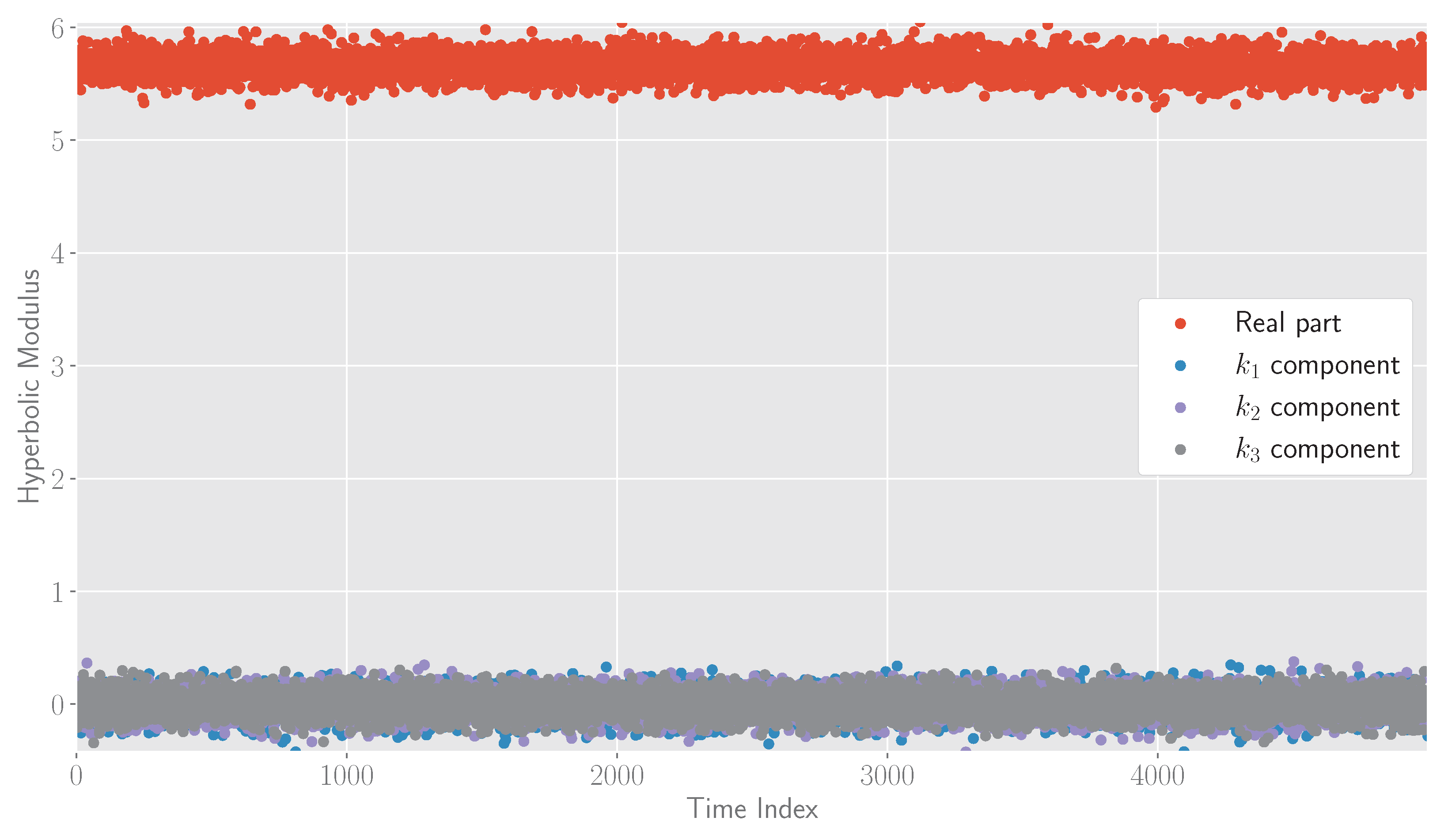
4. Polar Representation
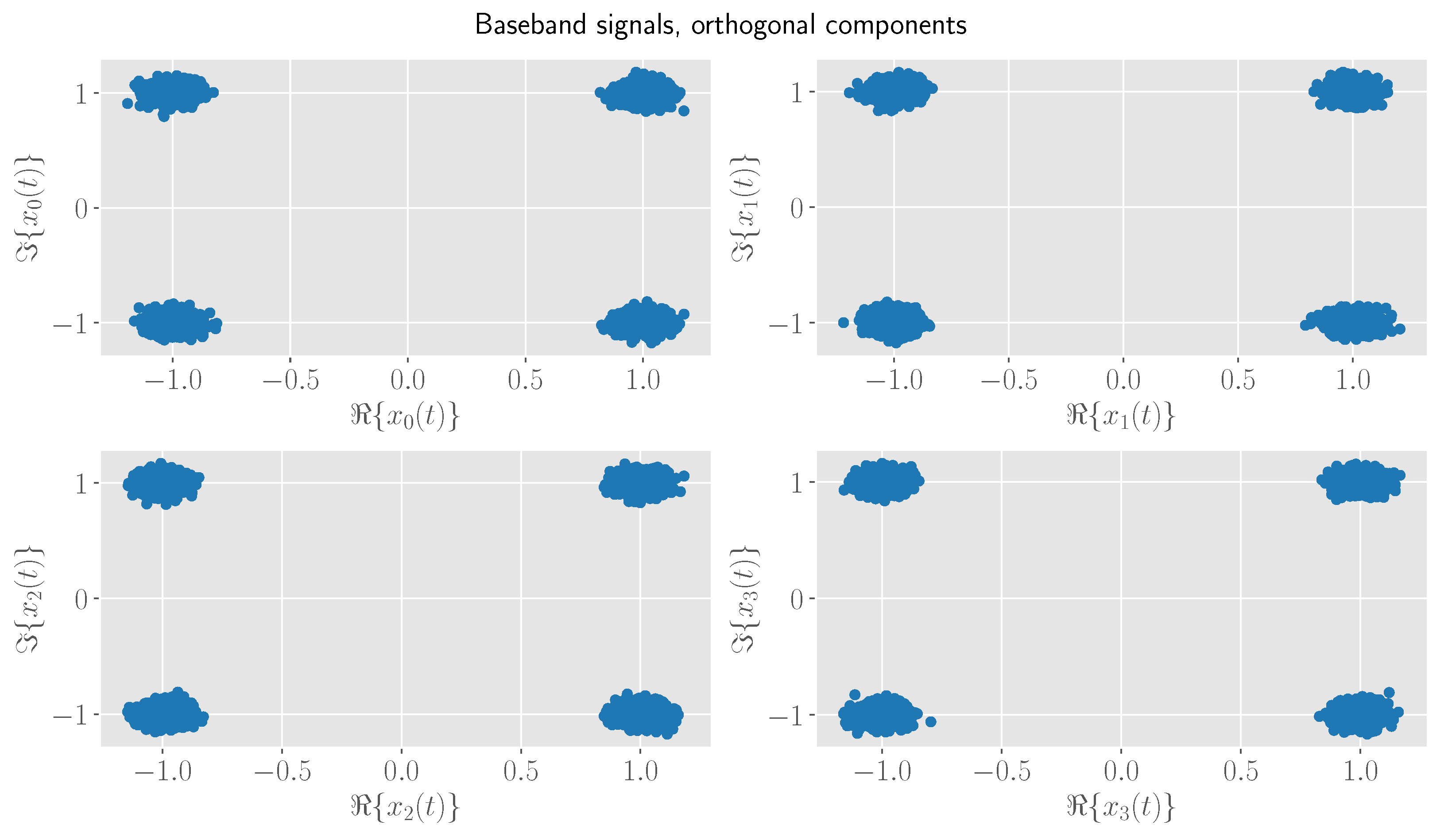
5. Baseband Representation of RF Signals
Orthogonal Decomposition
6. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ell, T.A.; Sangwine, S.J. Hypercomplex Fourier Transforms of Color Images. IEEE Trans. Image Process. 2007, 16, 22–35. [Google Scholar] [CrossRef]
- Snopek, K.M. The n-D analytic signals and Fourier spectra in complex and hypercomplex domains. In Proceedings of the International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 18–20 August 2011; pp. 423–427. [Google Scholar] [CrossRef]
- Alfsmann, D.; Göckler, H.G.; Sangwine, S.J.; Ell, T.A. Hypercomplex algebras in digital signal processing: Benefits and drawbacks. In Proceedings of the European Signal Processing Conference (EUSIPCO), Poznan, Poland, 3–7 September 2007; pp. 1322–1326. [Google Scholar]
- Valkova-Jarvis, Z.; Poulkov, V.; Stoynov, V.; Mihaylova, D.; Iliev, G. A Method for the Design of Bicomplex Orthogonal DSP Algorithms for Applications in Intelligent Radio Access Networks. Symmetry 2022, 14, 613. [Google Scholar] [CrossRef]
- Mengüç, E.C.; Acır, N.; Mandic, D.P. A Class of Online Censoring Based Quaternion-Valued Least Mean Square Algorithms. IEEE Signal Process. Lett. 2023, 30, 244–248. [Google Scholar] [CrossRef]
- Lin, D.; Zhang, Q.; Chen, S.; Wang, S. The Generalized HR q-Derivative and Its Application to Quaternion Least Mean Square Algorithm. IEEE Signal Process. Lett. 2022, 29, 857–861. [Google Scholar] [CrossRef]
- Took, C.C.; Mandic, D.P. Quaternion-Valued Stochastic Gradient-Based Adaptive IIR Filtering. IEEE Trans. Signal Process. 2010, 58, 3895–3901. [Google Scholar] [CrossRef]
- Alpay, D.; Diki, K.; Vajiac, M. Two Bicomplex and One Multicomplex Least Mean Square algorithms. arXiv 2023, arXiv:cs.LG/2209.11899. [Google Scholar]
- El-Melegy, M.T.; Kamal, A.T. Linear Regression Classification in the Quaternion and Reduced Biquaternion Domains. IEEE Signal Process. Lett. 2022, 29, 469–473. [Google Scholar] [CrossRef]
- Altmann, S.L. Rotations, Quaternions, and Double Groups; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Ell, T.A.; Le Bihan, N.; Sangwine, S.J. Quaternion Fourier Transforms for Signal and Image Processing; Digital Signal and Image, Processing; Wiley: Hoboken, NJ, USA; iSTE: London, UK, 2014. [Google Scholar]
- Alfsmann, D. On families of 2N-dimensional hypercomplex algebras suitable for digital signal processing. In Proceedings of the European Signal Processing Conference (EUSIPCO), Florence, Italy, 4–8 September 2006; pp. 1–4. [Google Scholar]
- Richter, W.D. On Complex Numbers in Higher Dimensions. Axioms 2022, 11, 22. [Google Scholar] [CrossRef]
- Catoni, F.; Cannata, R.; Zampetti, P. An Introduction to Commutative Quaternions. Adv. Appl. Clifford Algebr. 2006, 16, 1–28. [Google Scholar] [CrossRef]
- Pei, S.C.; Chang, J.H.; Ding, J.J. Commutative reduced biquaternions and their Fourier transform for signal and image processing applications. IEEE Trans. Signal Process. 2004, 52, 2012–2031. [Google Scholar] [CrossRef]
- Alpay, D.; Luna-Elizarrarás, M.E.; Shapiro, M.; Struppa, D.C. Basics of Functional Analysis with Bicomplex Scalars, and Bicomplex Schur Analysis; SpringerBriefs in Mathematics; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Price, G.B. An Introduction to Multicomplex Spaces and Functions, 1st ed.; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar] [CrossRef]
- Navarro-Moreno, J.; Fernández-Alcalá, R.M.; Jiménez-López, J.D.; Ruiz-Molina, J.C. Tessarine signal processing under the T-properness condition. J. Frankl. Inst. 2020, 357, 10100–10126. [Google Scholar] [CrossRef]
- Segre, C. Le rappresentazioni reali delle forme complesse e gli enti iperalgebrici. Math. Ann. 1891, 40, 413–467. [Google Scholar] [CrossRef]
- Alfsmann, D.; Göckler, H.G. On hyperbolic complex LTI digital systems. In Proceedings of the European Signal Processing Conference (EUSIPCO), Poznań, Poland, 3–7 September 2007; pp. 1332–1336. [Google Scholar]
- Borio, D. Bicomplex Representation and Processing of GNSS Signals. NAVIGATION J. Inst. Navig. 2023, 70, 1–33. [Google Scholar] [CrossRef]
- Fjelstad, P.; Gal, S.G. n-Dimensional hyperbolic complex numbers. Adv. Appl. Clifford Algebr. 1998, 8, 47–68. [Google Scholar] [CrossRef]
- Yarlagadda, R.K.R.; Hershey, J.E. Hadamard Matrix Analysis and Synthesis; The Springer International Series in Engineering and Computer Science; Springer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Proakis, J.G.; Salehi, M. Communication Systems Engineering, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Casado, J.M.V.; Hewson, R. Algorithm 1008: Multicomplex Number Class for Matlab, with a Focus on the Accurate Calculation of Small Imaginary Terms for Multicomplex Step Sensitivity Calculations. ACM Trans. Math. Softw. 2020, 46, 1–26. [Google Scholar] [CrossRef]
- Nasiruzzaman, M.; Mursaleen, M. The Multicomplex Numbers and Their Properties on Some Elementary Functions. Thai J. Math. 2023, 21, 77–100. [Google Scholar]
- European Union. Galileo Open Service Signal-In-Space Interface Control Document (OS SIS ICD). In Technical Report 2.1; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borio, D. A Vector Representation of Multicomplex Numbers and Its Application to Radio Frequency Signals. Axioms 2024, 13, 324. https://doi.org/10.3390/axioms13050324
Borio D. A Vector Representation of Multicomplex Numbers and Its Application to Radio Frequency Signals. Axioms. 2024; 13(5):324. https://doi.org/10.3390/axioms13050324
Chicago/Turabian StyleBorio, Daniele. 2024. "A Vector Representation of Multicomplex Numbers and Its Application to Radio Frequency Signals" Axioms 13, no. 5: 324. https://doi.org/10.3390/axioms13050324
APA StyleBorio, D. (2024). A Vector Representation of Multicomplex Numbers and Its Application to Radio Frequency Signals. Axioms, 13(5), 324. https://doi.org/10.3390/axioms13050324




