Regular, Beating and Dilogarithmic Breathers in Biased Photorefractive Crystals
Abstract
:1. Introduction
- (a).
- (b).
- (c).
- (d).
- unbiased photovoltaic photorefractive crystals affected by temperature variations (photovoltaic pyroelectric solitons) [5];
- (e).
- biased photovoltaic photorefractive crystals affected by temperature variations (screening photovoltaic pyroelectric solitons) [6];
- (f).
- photovoltaic crystals exhibiting a two-photon photorefractive effect [11].
2. The Fundamental Equation (GNLSE)
3. The Lagrangian Structure
4. Variational and Full Numerical Solutions
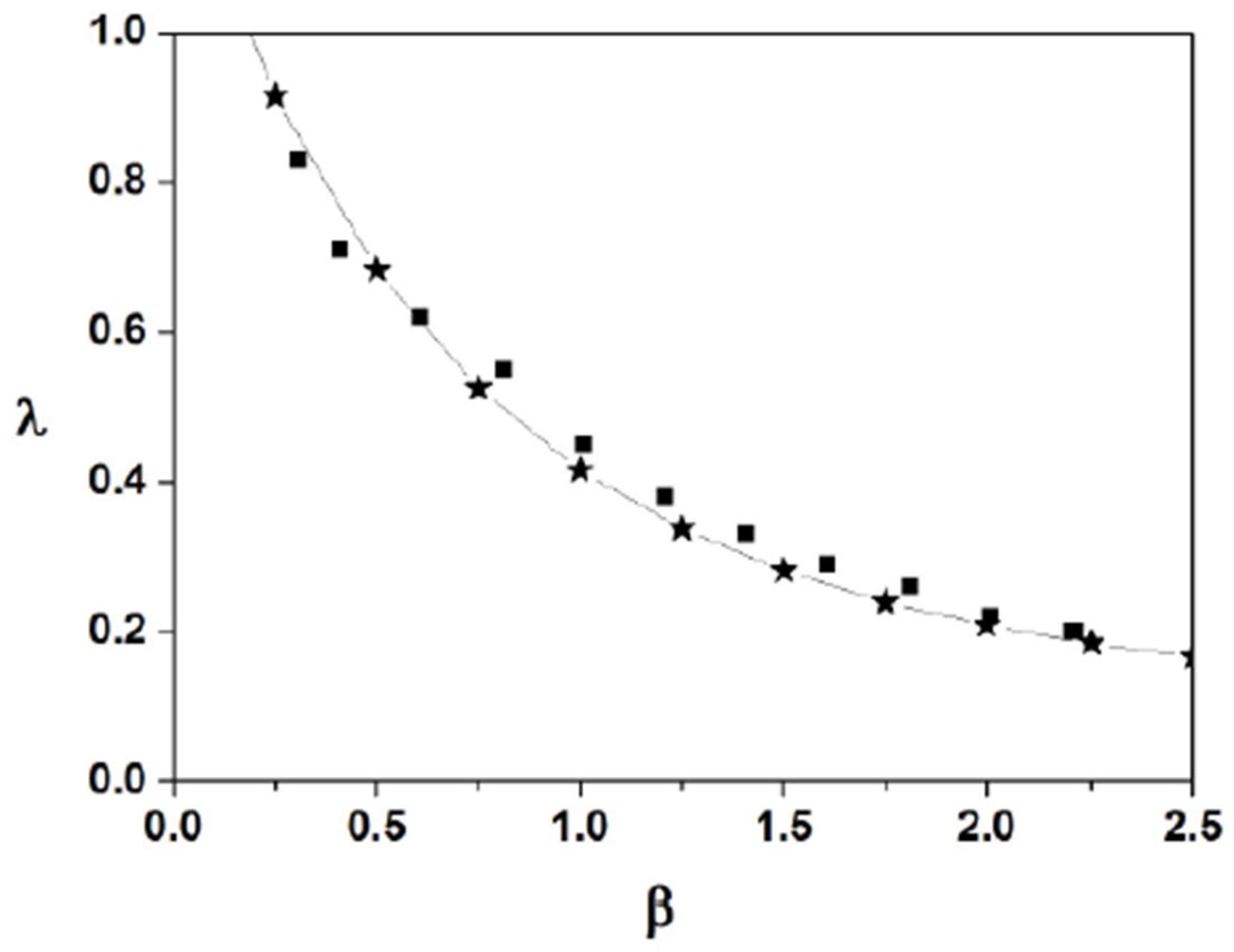
4.1. Variational Results Produced by the Sech Ansatz (16)
4.2. Variational Results Produced by the Ansatz (33)
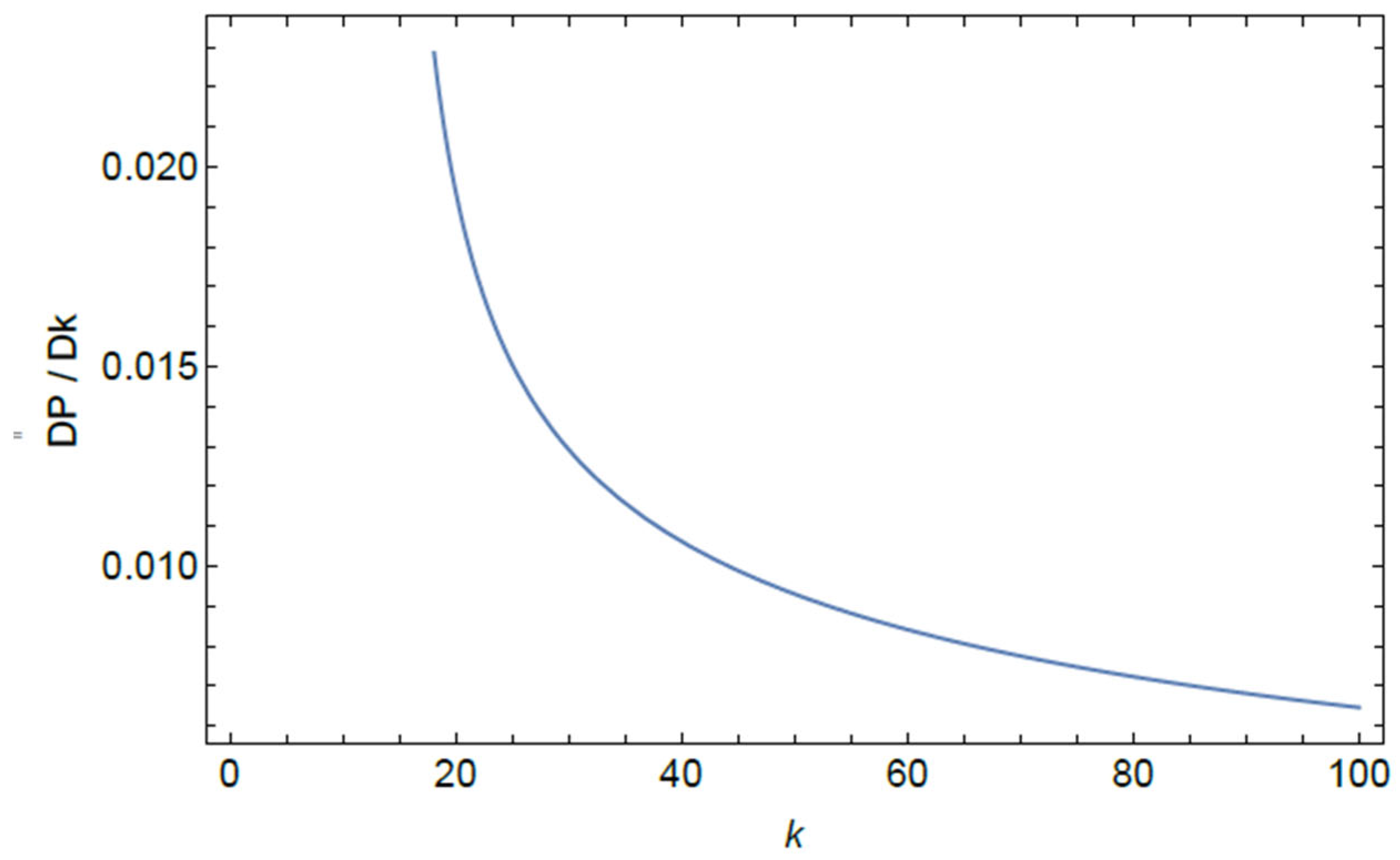
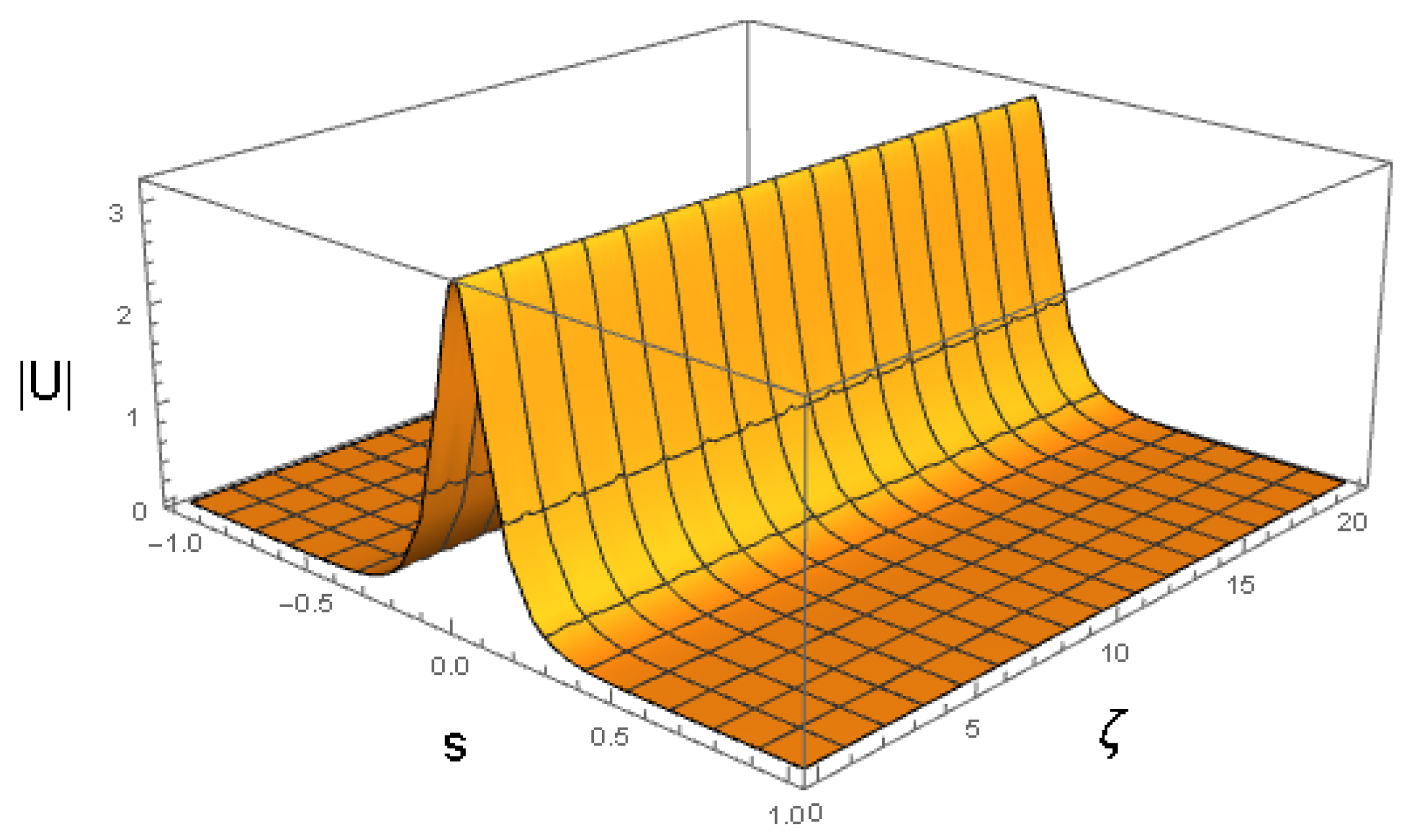
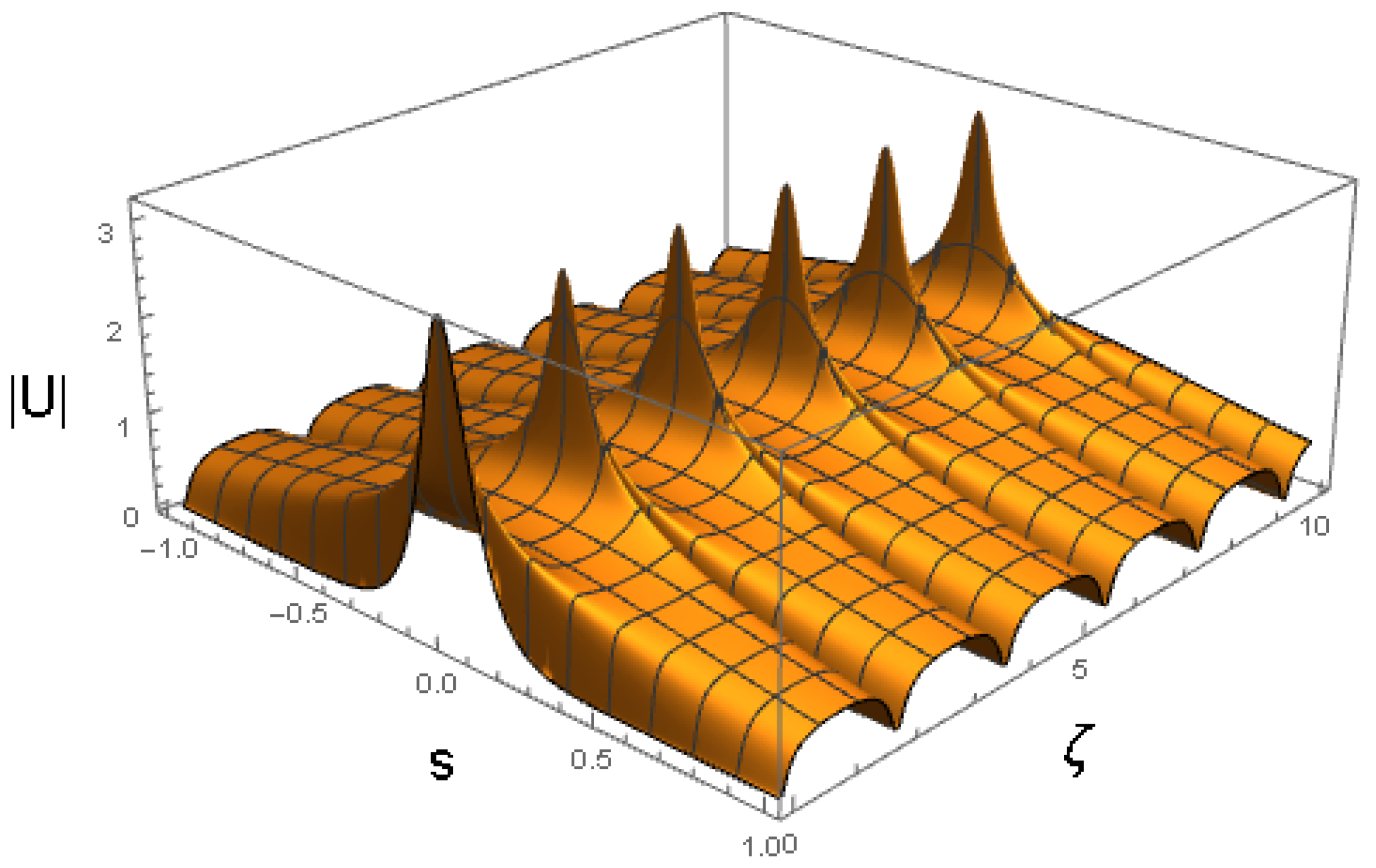
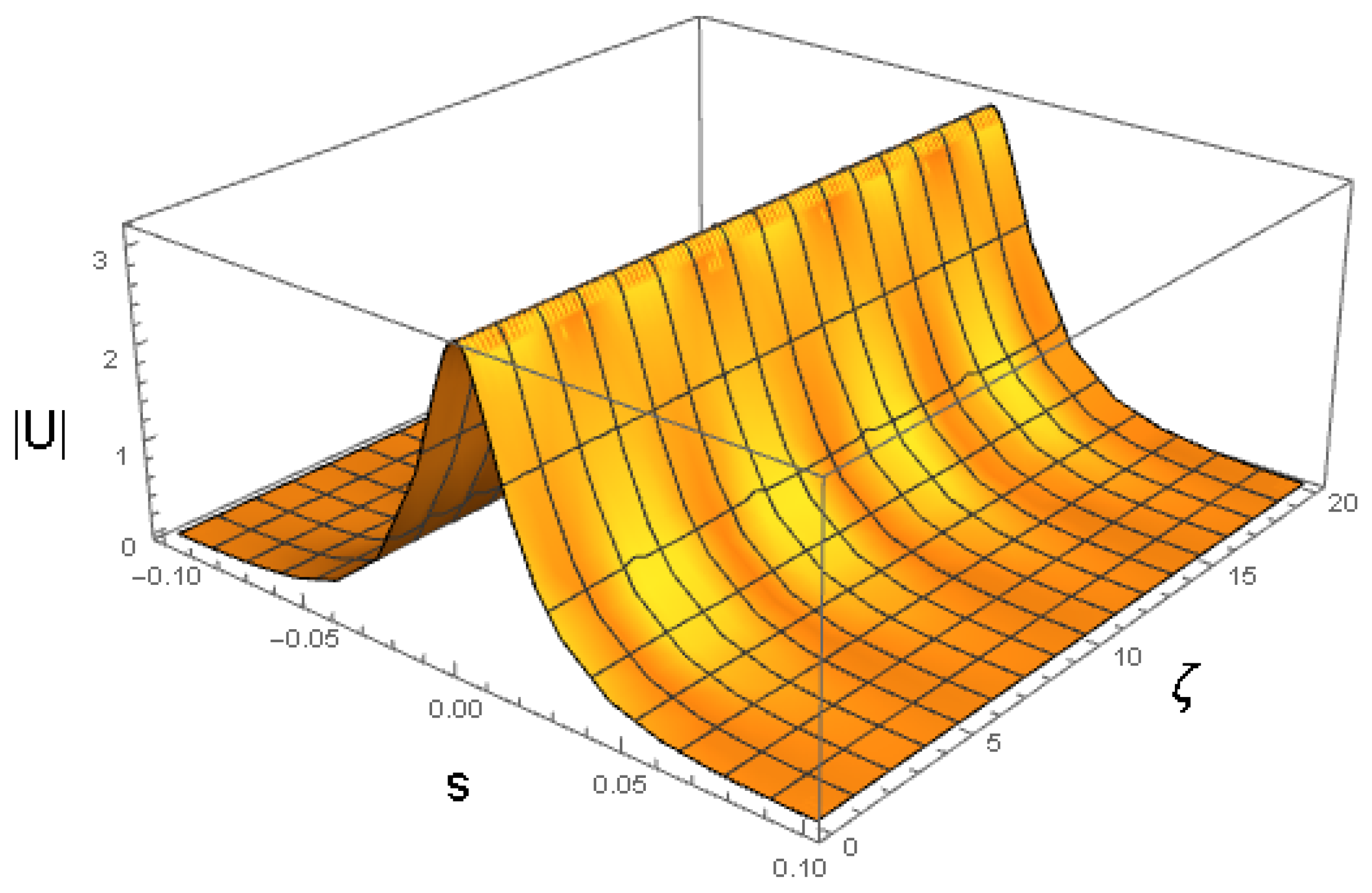
4.3. Direct Simulations of the Evolution of Solitons and Breathers
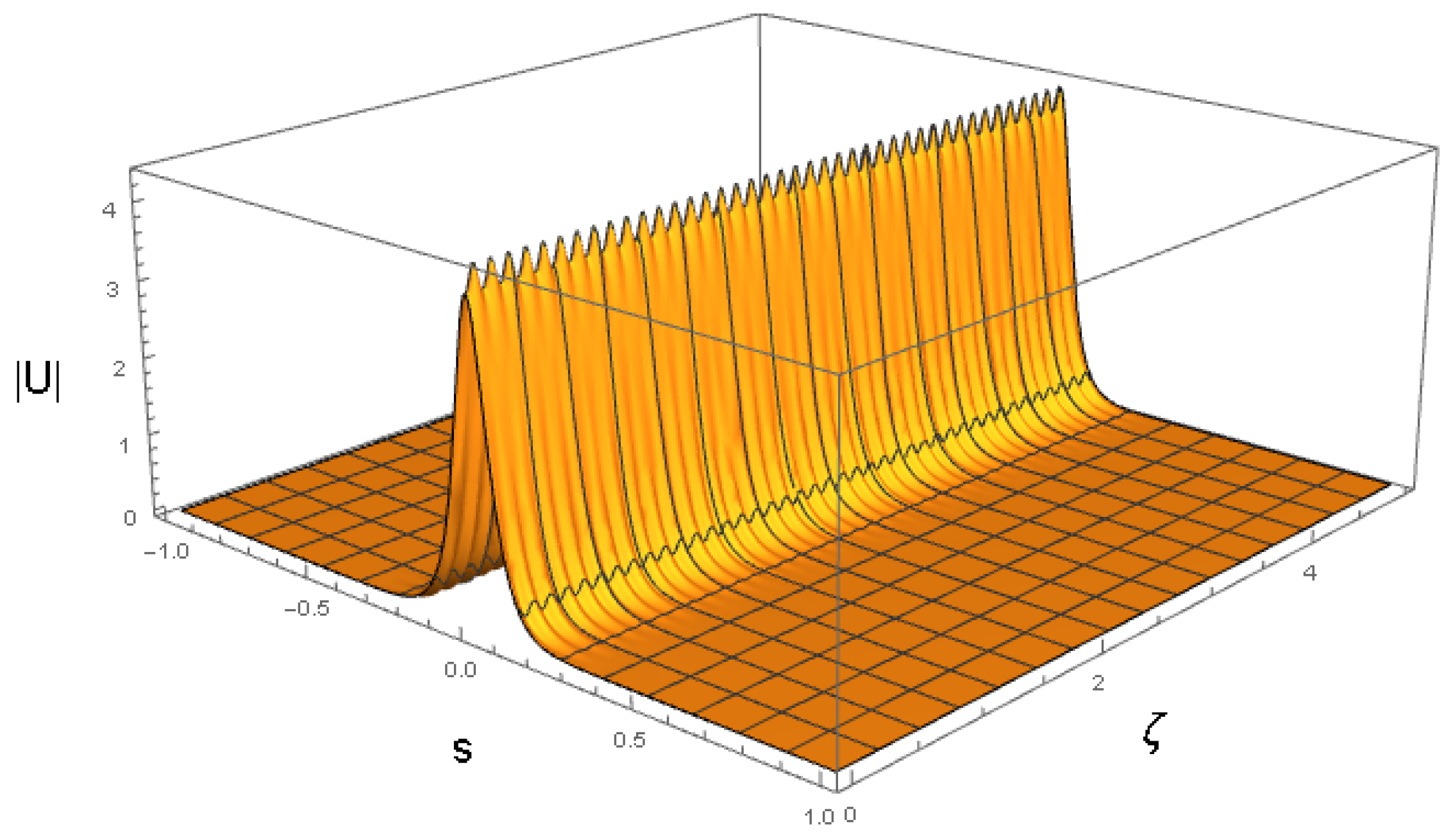
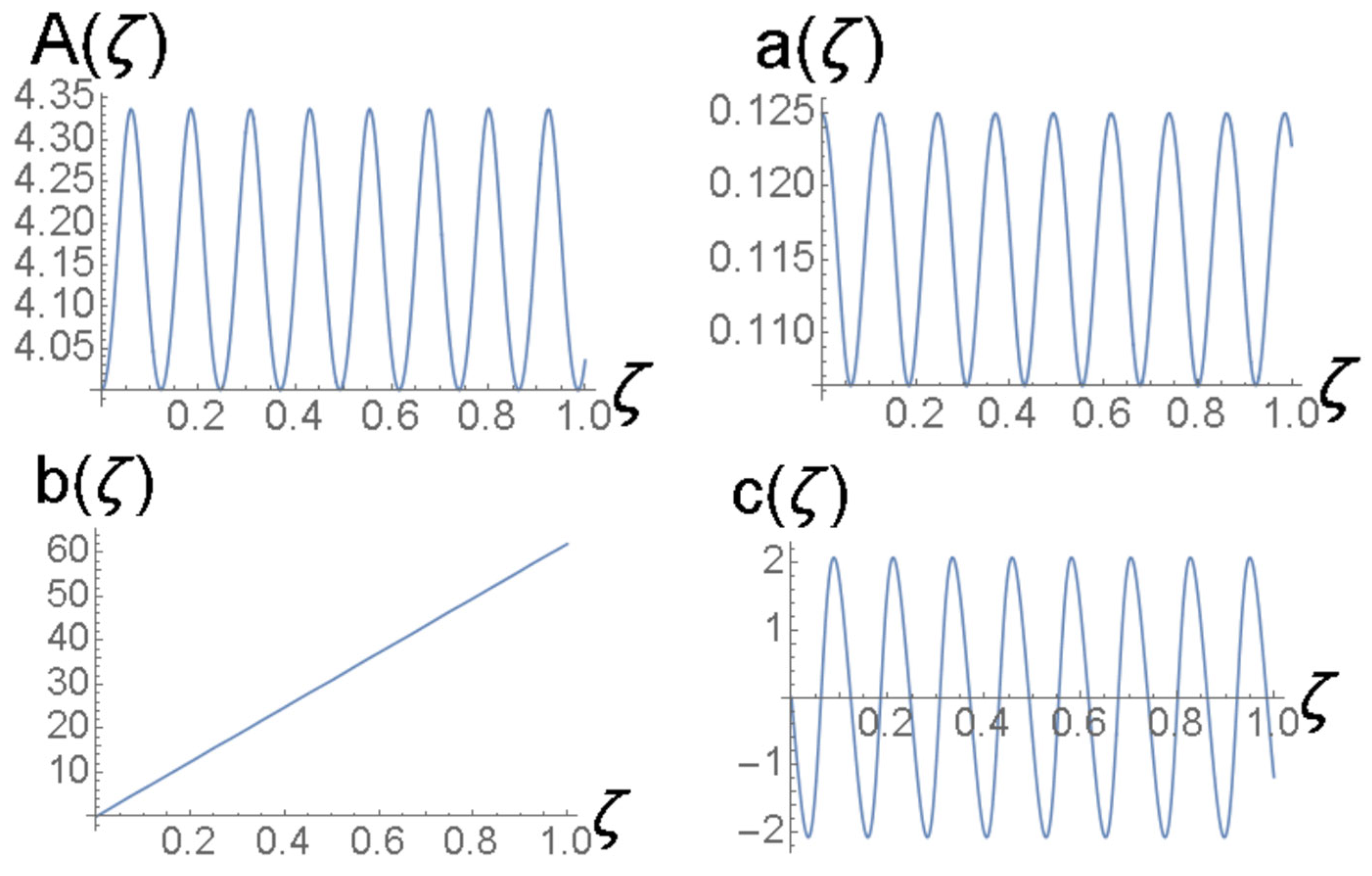
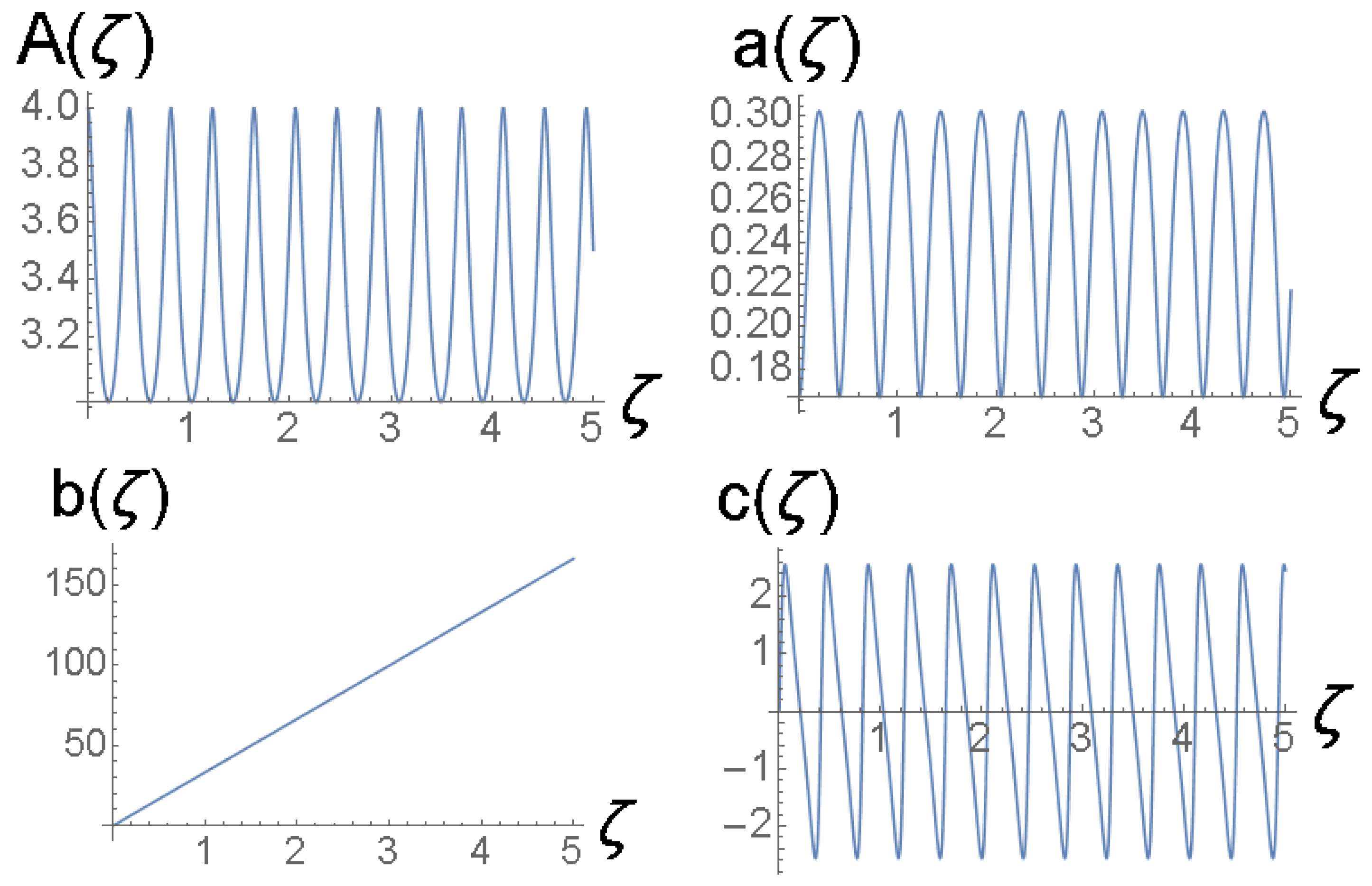
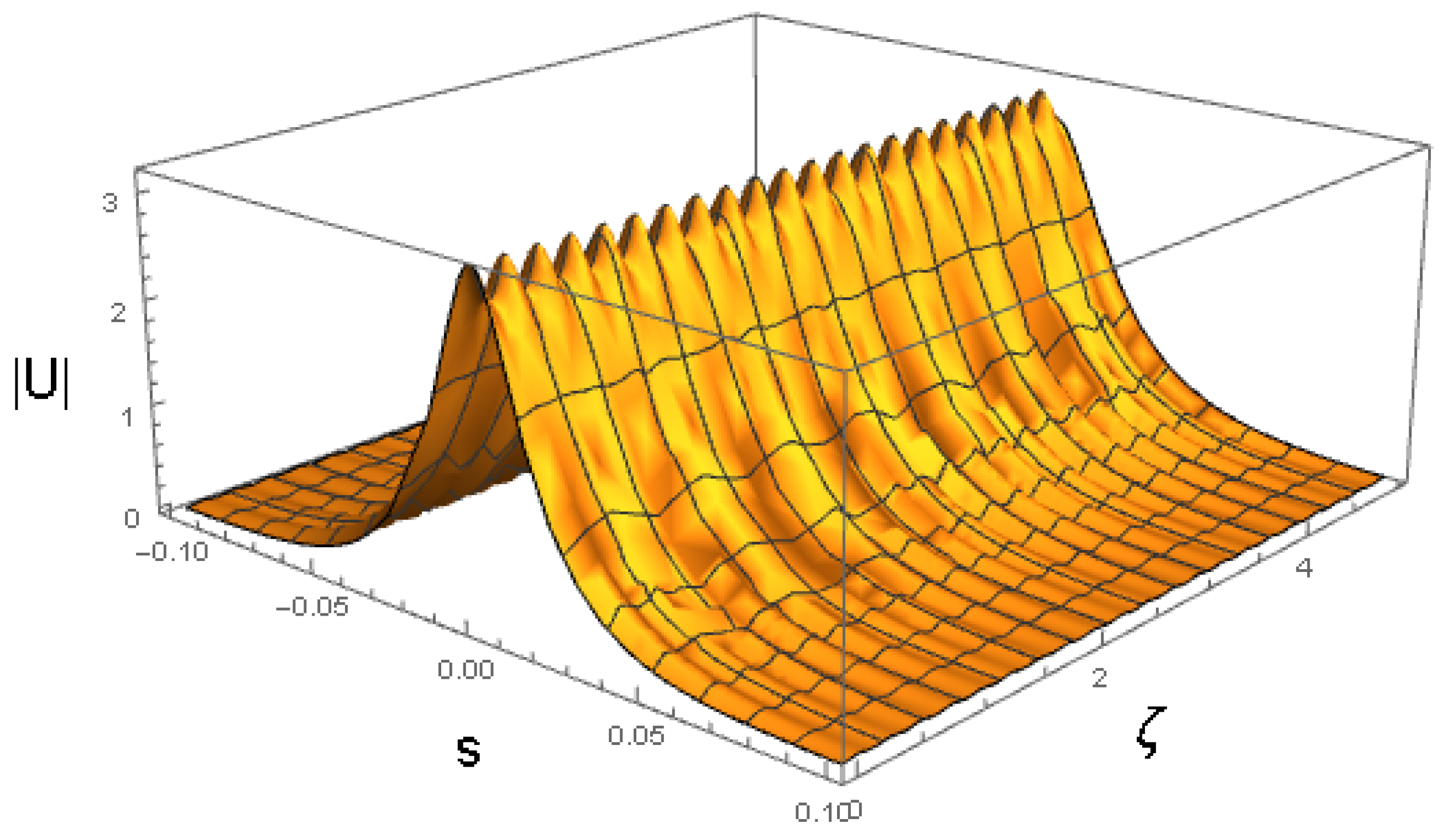
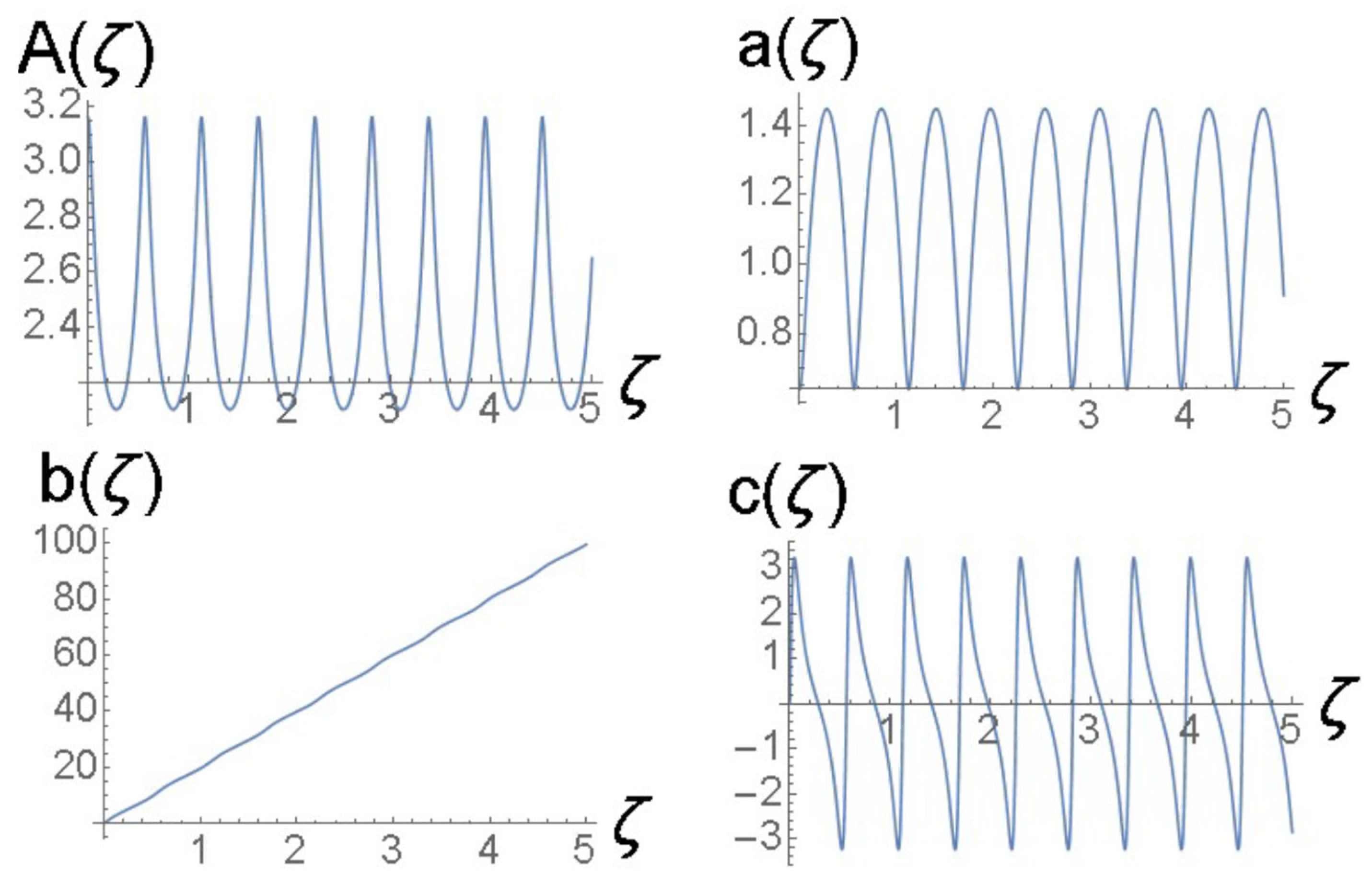
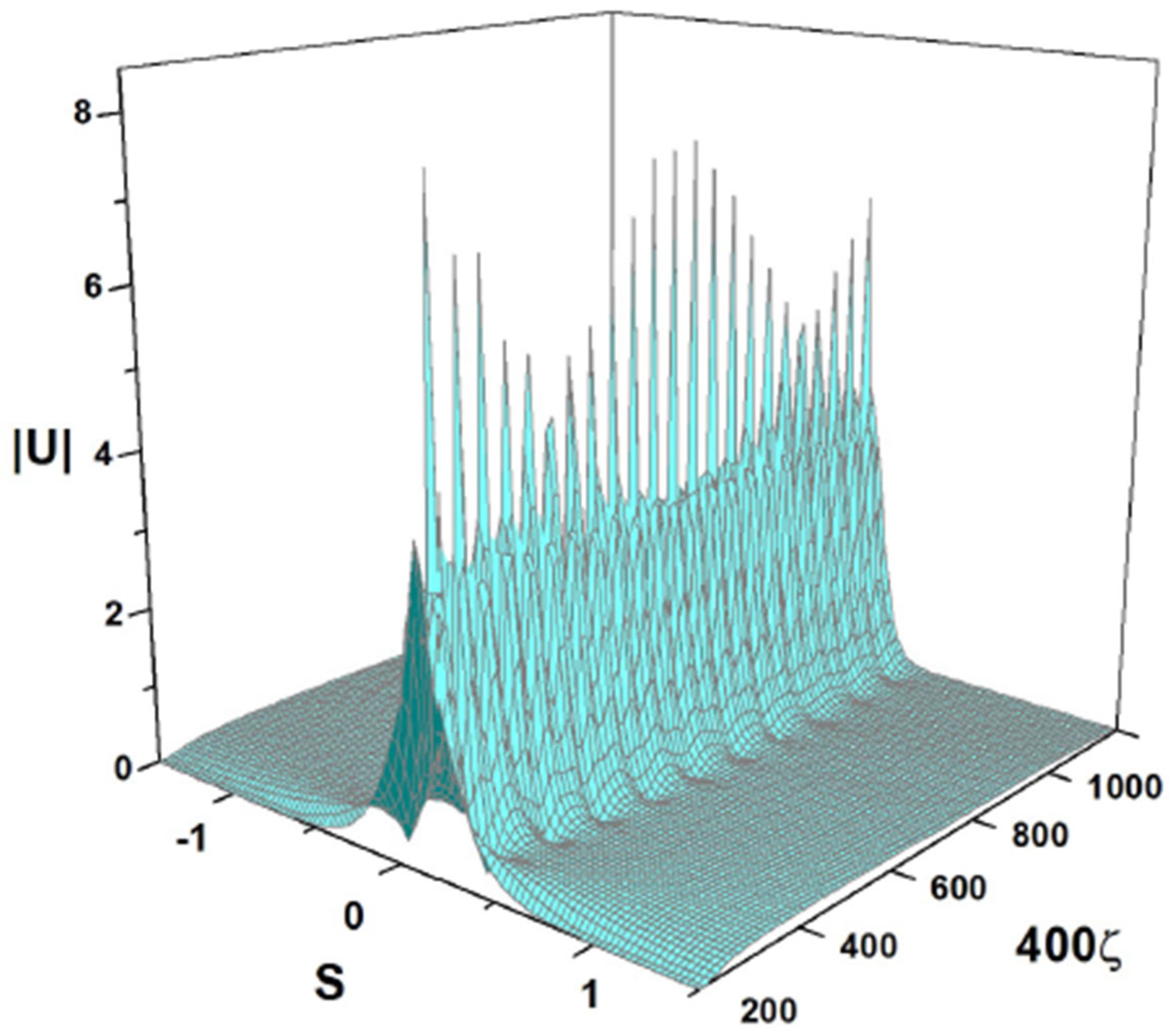
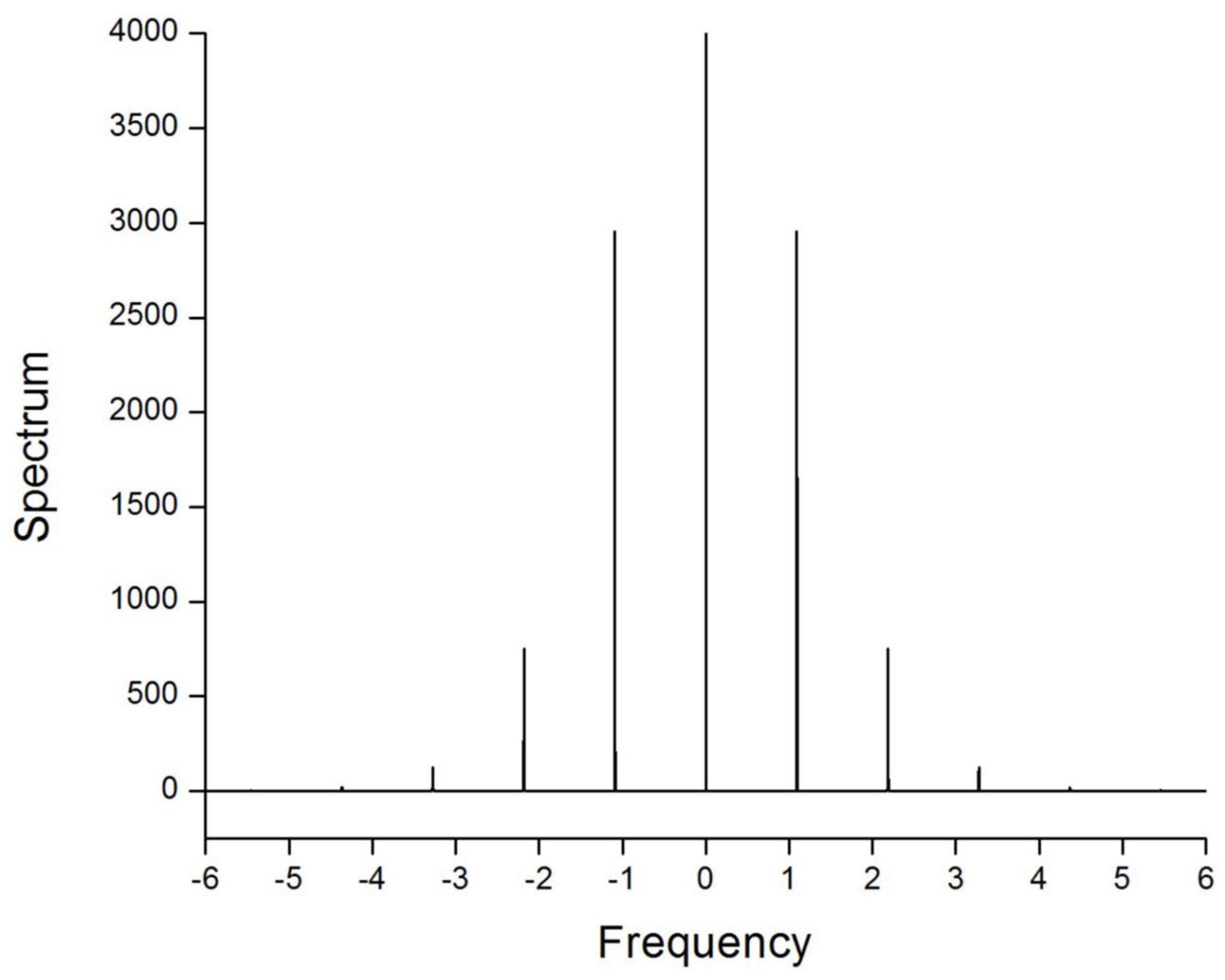
4.4. Breathers Modulated by Beats
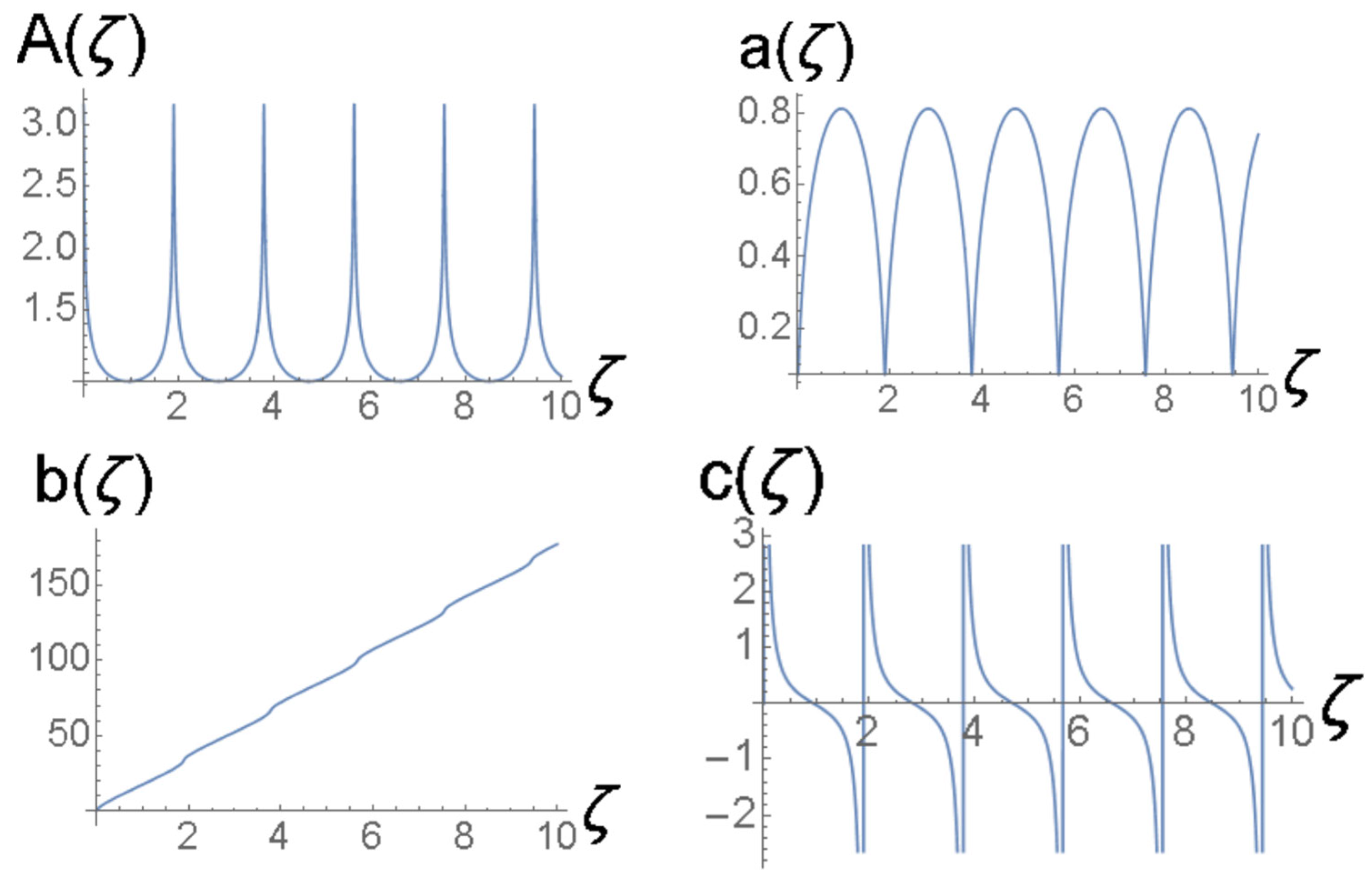
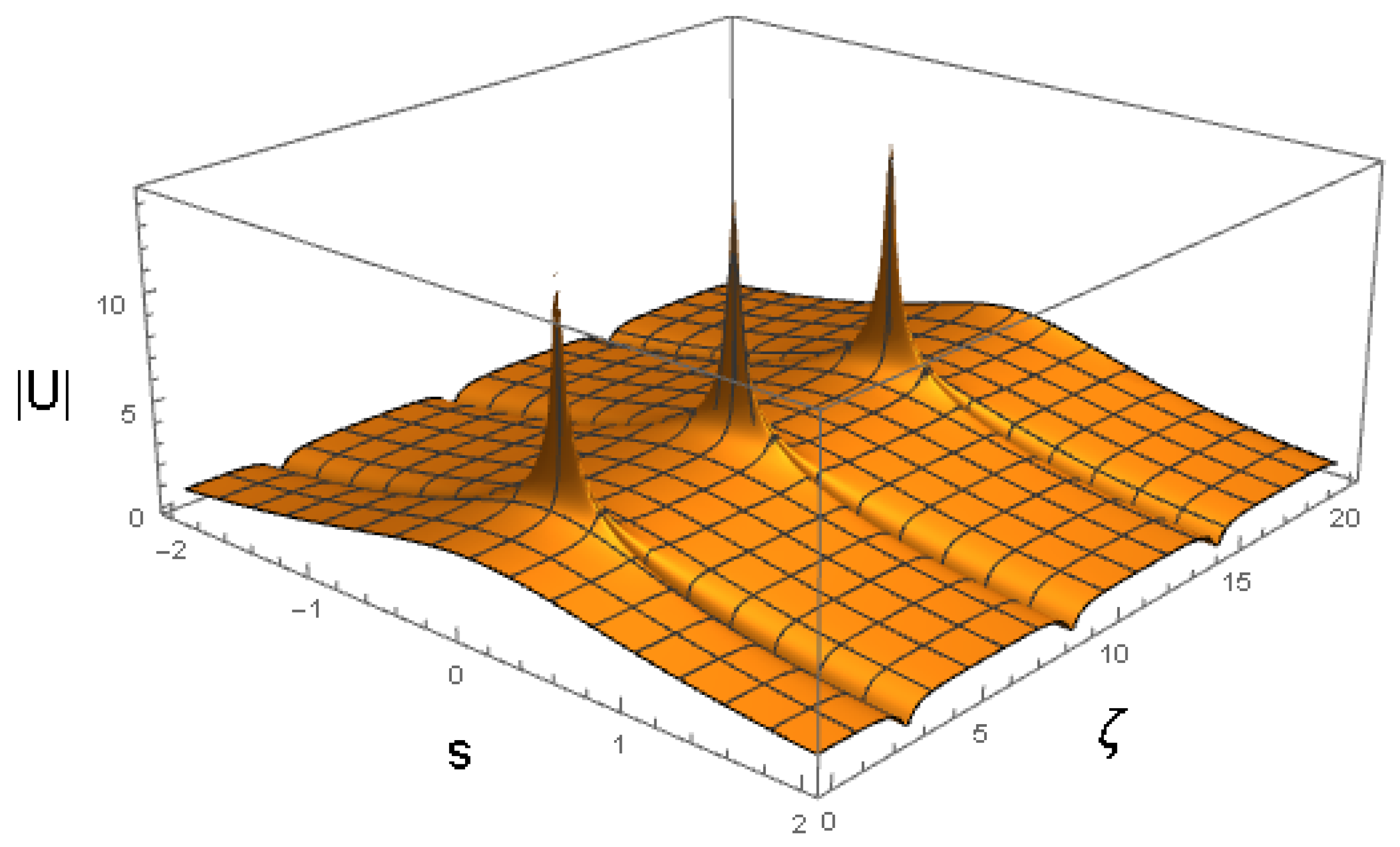
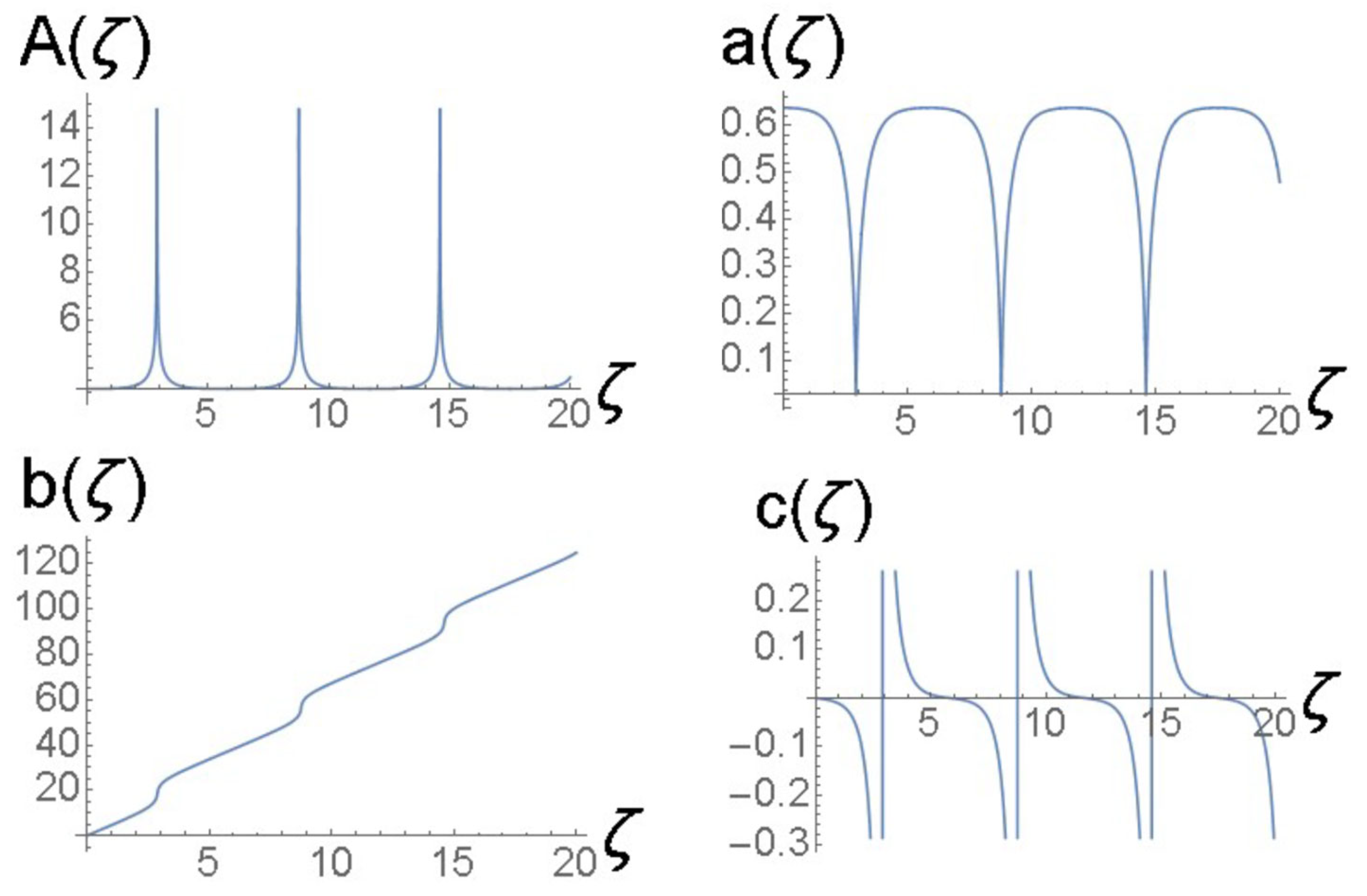
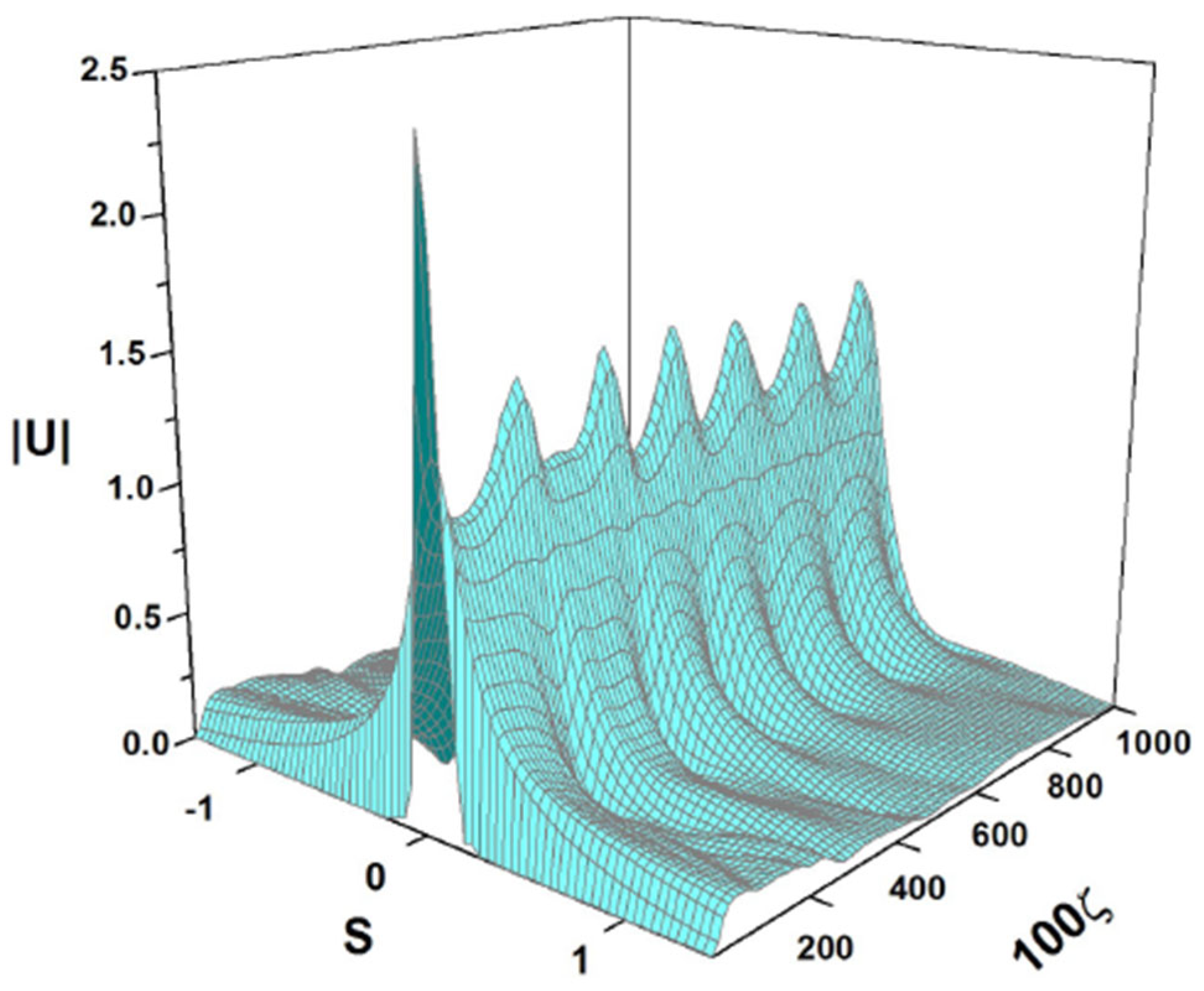
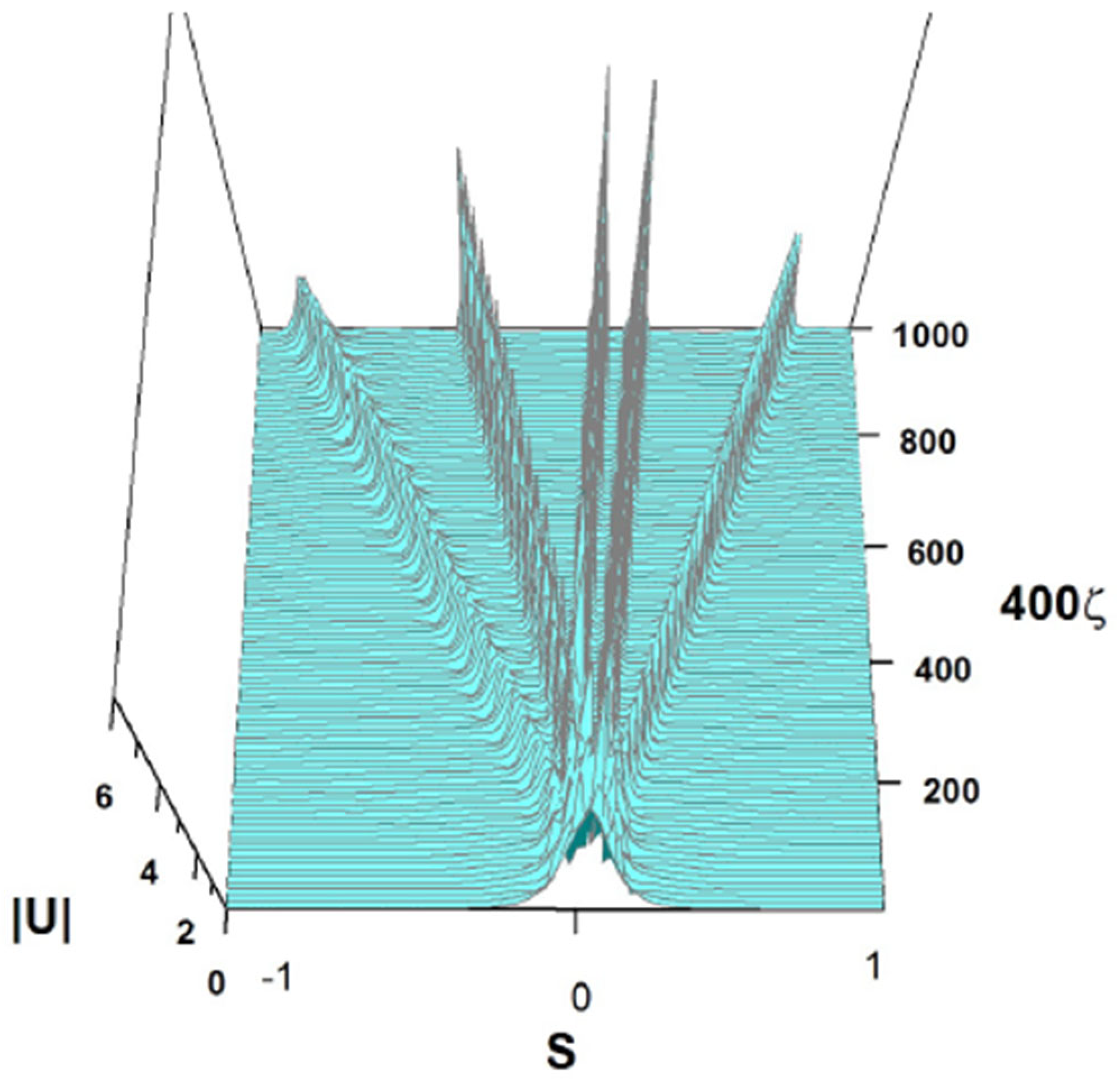
4.5. Splitting Breathers
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ashkin, A.; Boyd, C.D.; Dziedzic, J.M.; Smith, R.G.; Ballman, A.A.; Levinstein, J.J.; Nassau, K. Optically-induced refractive index inhomogeneities in LiNbO3 and LiTaO3. Appl. Phys. Lett. 1966, 9, 72. [Google Scholar] [CrossRef]
- Seguev, M.; Valley, G.C.; Crosignani, B.; Diporto, P.; Yariv, A. Steady-state spatial screening solitons in photorefractive materials with external applied field. Phys. Rev. Lett. 1994, 73, 3211. [Google Scholar] [CrossRef] [PubMed]
- Segev, M.; Valley, G.C.; Bashaw, M.C.; Taya, M.; Fejer, M.M. Photovoltaic spatial solitons. J. Opt. Soc. Am. B 1997, 14, 1772. [Google Scholar] [CrossRef]
- Liu, J.S.; Lu, K.Q. Screening-photovoltaic spatial solitons in biased photovoltaic–photorefractive crystals and their self-deflection. J. Opt. Soc. Am. B 1999, 16, 550. [Google Scholar] [CrossRef]
- Jiang, Q.; Su, Y.; Ji, X. Pyroelectric photovoltaic spatial solitons in unbiased photorefractive crystals. Phys. Lett. A 2012, 376, 3085. [Google Scholar] [CrossRef]
- Katti, A.; Yadav, R.A. Spatial solitons in biased photovoltaic photorefractive materials with the pyroelectric effect. Phys. Lett. A 2017, 381, 166. [Google Scholar] [CrossRef]
- Valley, G.C.; Segev, M.; Crosignani, B.; Yariv, A.; Fejer, M.M.; Bashaw, M.C. Dark and bright photovoltaic spatial solitons. Phys. Rev. A 1994, 50, R4457. [Google Scholar] [CrossRef] [PubMed]
- Taya, M.; Bashaw, M.C.; Fejer, M.M.; Segev, M.; Valley, G.C. Observation of dark photovoltaic spatial solitons. Phys. Rev. A 1995, 52, 3095. [Google Scholar] [CrossRef] [PubMed]
- She, W.L.; Xu, C.C.; Guo, B.; Lee, W.K. Formation of photovoltaic bright spatial soliton in photorefractive LiNbO3 crystal by a defocused laser beam induced by a background laser beam. J. Opt. Soc. Am. B 2006, 23, 2121. [Google Scholar] [CrossRef]
- Fazio, E.; Renzi, F.; Rinaldi, R.; Bertolotti, M.; Chauvet, M.; Ramadan, W.; Petris, A.; Vlad, V.I. Screening-photovoltaic bright solitons in lithium niobate and associated single-mode waveguides. App. Phys. Lett. 2004, 85, 2193. [Google Scholar] [CrossRef]
- Katti, A. Bright optical spatial solitons in a photovoltaic photorefractive waveguide exhibiting the two photon photorefractive effect. Rev. Mex. Física 2023, 69, 021301. [Google Scholar] [CrossRef]
- Carretero-González, R.; Promislow, K. Localized breathing oscillations of Bose-Einstein condensates in periodic traps. Phys. Rev. A 2002, 66, 033610. [Google Scholar] [CrossRef]
- Cuevas, J.; English, L.Q.; Kevrekidis, P.G.; Anderson, M. Discrete breathers in a forced-damped array of coupled pendula: Modeling, computation, and experiment. Phys. Rev. Lett. 2009, 102, 224101. [Google Scholar] [CrossRef] [PubMed]
- Nikolić, S.N.; Ashour, O.A.; Aleksić, N.B.; Belić, M.R.; Chin, S.A. Breathers, solitons and rogue waves of the quintic nonlinear Schrödinger equation on various backgrounds. Nonlinear Dyn. 2019, 95, 2855. [Google Scholar] [CrossRef]
- Flach, S.; Gorbach, A.V. Discrete breathers—Advances in theory and applications. Phys. Rep. 2008, 467, 1. [Google Scholar] [CrossRef]
- Burlak, G.; Chen, Z.; Malomed, B.A. Solitons in PT-symmetric systems with spin–orbit coupling and critical nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 2022, 109, 106282. [Google Scholar] [CrossRef]
- Konar, S.; Yacheslav, V.; Trofimov, A. Some aspects of optical spatial solitons in photorefractive media and their important applications. Pramana 2015, 85, 975. [Google Scholar] [CrossRef]
- Katti, A.; Yadav, R.A. Optical Spatial Solitons in Photorefractive Materiales; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar] [CrossRef]
- Anderson, D. Variational approach to nonlinear pulse propagation in optical fibers. Phys. Rev. A 1983, 27, 3135. [Google Scholar] [CrossRef]
- Anderson, D.; Lisak, M.; Reichel, T. Asymptotic propagation properties of pulses in a soliton-based optical-fiber communication system. J. Opt. Soc. Am. B 1988, 5, 207. [Google Scholar] [CrossRef]
- Malomed, B.A.; Parker, D.F.; Smyth, N.F. Resonant shape oscillations and decay of a soliton in a periodically inhomogeneous nonlinear optical fiber. Phys. Rev. E 1993, 48, 1418. [Google Scholar] [CrossRef] [PubMed]
- Kath, W.L.; Smyth, N.F. Soliton evolution and radiation loss for the nonlinear Schrödinger equation. Phys. Rev. E 1995, 51, 1484. [Google Scholar] [CrossRef] [PubMed]
- Doty, S.L.; Haus, J.W.; Oh, Y.; Fork, R.L. Soliton interactions on dual-core fibers. Phys. Rev. E 1995, 51, 709. [Google Scholar] [CrossRef] [PubMed]
- Paré, C.; Florjanczyk, M. Approximate model of soliton dynamics in all-optical couplers. Phys. Rev. A 1990, 41, 6287. [Google Scholar] [CrossRef] [PubMed]
- Rusin, R.; Kusdiantara, R.; Susanto, H. Variational approximations of soliton dynamics in the Ablowitz-Musslimani nonlinear Schrödinger equation. Phys. Lett. A 2019, 383, 2039. [Google Scholar] [CrossRef]
- Fujioka, J.; Espinosa, A. Stability of the bright-type algebraic solitary-wave solutions of two extended versions of the nonlinear Schrödinger equation. J. Phys. Soc. Jpn. 1996, 65, 2440. [Google Scholar] [CrossRef]
- Fujioka, J.; Espinosa, A. Soliton-like solution of an extended NLS equation existing in resonance with linear dispersive waves. J. Phys. Soc. Jpn. 1997, 66, 2601. [Google Scholar] [CrossRef]
- Fujioka, J.; Espinosa, A. Radiationless higher-order embedded solitons. J. Phys. Soc. Jpn. 2013, 82, 034007. [Google Scholar] [CrossRef]
- Velasco-Juan, M.; Fujioka, J. Lagrangian nonlocal nonlinear Schrödinger equations. Chaos Solitons Fractals 2022, 156, 111798. [Google Scholar] [CrossRef]
- Malomed, B.A. Variational methods in nonlinear fiber optics and related fields. Progr. Optics 2002, 43, 71–193. [Google Scholar] [CrossRef]
- Malomed, B.A. Multidimensional Solitons; American Institute of Physics Publishing: Melville, NY, USA, 2022. [Google Scholar] [CrossRef]
- Gunter, P.; Huignard, J.P. (Eds.) Photorefractive Materials and Their Applications I and II; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar] [CrossRef]
- Yeh, P. Photorefractive Nonlinear Optics; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Su, Y.; Jiang, Q.; Ji, X. Coherent interactions of multi bright spatial solitons in biased photorefractive crystals. Optik 2014, 125, 1231. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Amsterdam, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Petrović, M.S.; Strinić, A.I.; Aleksić, N.B.; Belić, M.R. Rotating solitons supported by a spiral waveguide. Phys. Rev. A 2018, 98, 063822. [Google Scholar] [CrossRef]
- Kalashnikov, V.L.; Apolonski, A. Energy scalability of mode-locked oscillators: A completely analytical approach to analysis. Opt. Express 2010, 18, 25757. [Google Scholar] [CrossRef] [PubMed]
- Vakhitov, N.G.; Kolokolov, A.A. Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quantum Electron. 1973, 16, 783. [Google Scholar] [CrossRef]
- Kolokolov, A.A. Stability of stationary solutions of nonlinear wave equations. Radiophys. Quantum Electron. 1974, 17, 1016. [Google Scholar] [CrossRef]
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; SIAM series on Mathematical Modeling and Computation; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Antar, N.; Bakirtaş, I.; Boaz, I. Band-gap boundaries and fundamental solitons in complex two-dimensional nonlinear lattices. Phys. Rev. A 2010, 81, 033834. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Gammal, A.; Tomio, L.; Frederico, T. Stability of Trpped Bose-Einstein condensates. Phys. Rev. A 2001, 63, 043604. [Google Scholar] [CrossRef]
- Kuznetsov, E.A.; Mikhailov, A.V.; Shimokhin, I.A. Nonlinear interaction of solitons and radiation. Physica D 1995, 87, 201–205. [Google Scholar] [CrossRef]
- Satsuma, J.; Yajima, N.B. Initial Value problems of one-dimensional self-modulation of nonlinear waves in dispersive media. Suppl. Prog. Theor. Phys. 1974, 55, 284. [Google Scholar] [CrossRef]
- Fazio, E.; Babin, V.; Bertolotti, M.; Vlad, V. Solitonlike propagation in photorefractive crystals with large optical activity and absorption. Phys. Rev. E 2002, 66, 016605. [Google Scholar] [CrossRef]
- Bland, T.; Parker, N.G.; Proukakis, N.P.; Malomed, B.A. Probing quasi-integrability of the Gross-Pitaevskii equation in a harmonic-oscillator potential. J. Phys. B 2018, 51, 205303. [Google Scholar] [CrossRef]
- Liu, Z.G.; Zhang, J.; Wang, Y.S.; Huang, G. Analytical solutions of solitary waves and their collision stability in a pre-compressed one-dimensional granular crystal. Nonlinear Dyn. 2021, 104, 4293–4309. [Google Scholar] [CrossRef]
- Boechler, N.; Theocharis, G.; Job, S.; Kevrekidis, P.G.; Porter, M.A.; Daraio, C. Discrete breathers in one-dimensional diatomic granular crystals. Phys. Rev. Lett. 2010, 104, 244302. [Google Scholar] [CrossRef] [PubMed]
- Chong, C.; Porter, M.A.; Kevrekidis, P.G.; Daraio, C. Nonlinear coherent structures in granular crystals. J. Phys. Condens. Matter 2017, 29, 413003. [Google Scholar] [CrossRef] [PubMed]
- Dimitriev, S.V.; Korznikova, E.A.; Baimova, Y.A.; Velarde, M.G. Discrete breathers in crystals. Phys.-Uspekhi 2016, 59, 446. [Google Scholar] [CrossRef]
- Duran, H.; Cuevas-Maraver, J.; Kevrekidis, P.G.; Vainchtein, A. Discrete breathers in a mechanical metamaterial. Phys. Rev. E 2023, 107, 014220. [Google Scholar] [CrossRef] [PubMed]
- Ovchinnikov, A.A.; Flach, S. Discrete Breathers in Systems with Homogeneous Potentials: Analytic Solutions. Phys. Rev. Lett. 1999, 83, 248. [Google Scholar] [CrossRef]
- Kaup, D.J.; El-Reedy, J.; Malomed, B.A. Effect of chirp on soliton production. Phys. Rev. E 1994, 50, 1635. [Google Scholar] [CrossRef] [PubMed]
- Erkintalo, M.; Hammani, M.K.; Kibler, B.; Finot, C.; Akhmediev, N.; Dudley, J.M.; Genty, G. Higher-order modulation instability in nonlinear fiber optics. Phys. Rev. Lett. 2011, 107, 253901. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Betancur-Silvera, C.A.; Espinosa-Cerón, A.; Malomed, B.A.; Fujioka, J. Regular, Beating and Dilogarithmic Breathers in Biased Photorefractive Crystals. Axioms 2024, 13, 338. https://doi.org/10.3390/axioms13050338
Betancur-Silvera CA, Espinosa-Cerón A, Malomed BA, Fujioka J. Regular, Beating and Dilogarithmic Breathers in Biased Photorefractive Crystals. Axioms. 2024; 13(5):338. https://doi.org/10.3390/axioms13050338
Chicago/Turabian StyleBetancur-Silvera, Carlos Alberto, Aurea Espinosa-Cerón, Boris A. Malomed, and Jorge Fujioka. 2024. "Regular, Beating and Dilogarithmic Breathers in Biased Photorefractive Crystals" Axioms 13, no. 5: 338. https://doi.org/10.3390/axioms13050338




