Analyzing Richtmyer–Meshkov Phenomena Triggered by Forward-Triangular Light Gas Bubbles: A Numerical Perspective
Abstract
1. Introduction
2. Computational Model
2.1. Governing Equations
2.2. Numerical Method
2.2.1. Modal DG Spatial Discretization
2.2.2. Numerical Flux Scheme
2.2.3. Temporal Discretization
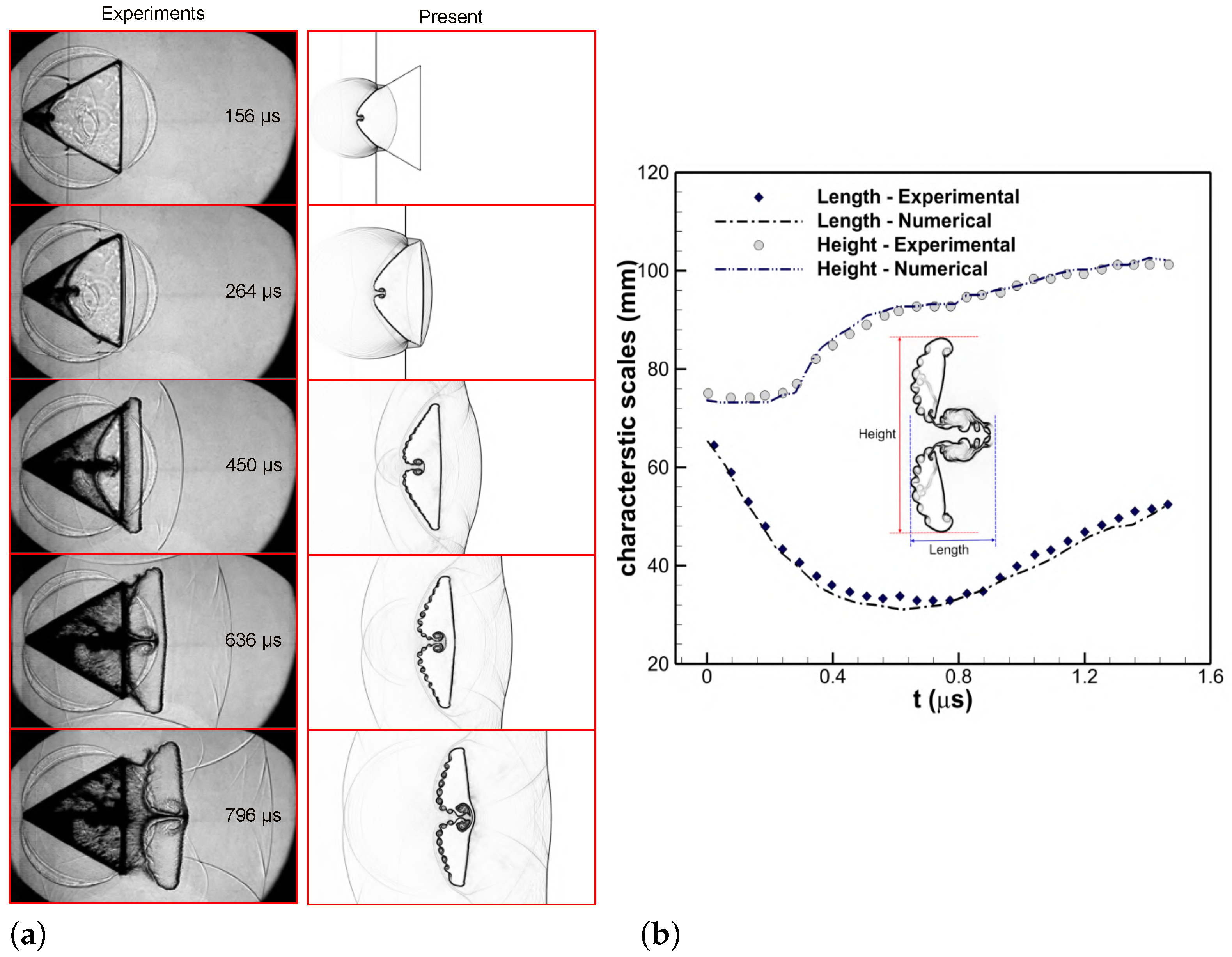
2.3. Validation of the Numerical Solver
2.4. Important Physical Quantities
2.4.1. Atwood Number
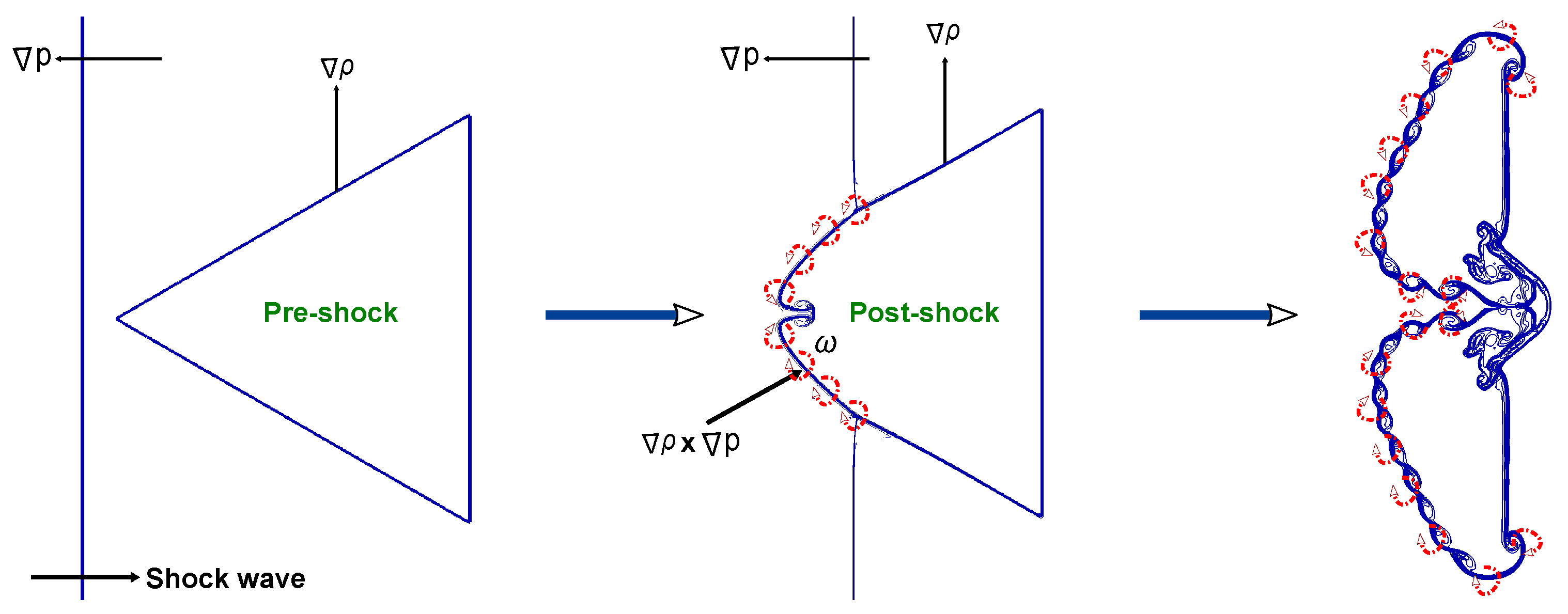
2.4.2. Vorticity
2.4.3. Vorticity Transport Equation
2.4.4. Spatial Integrated Field of Vorticity Production Terms
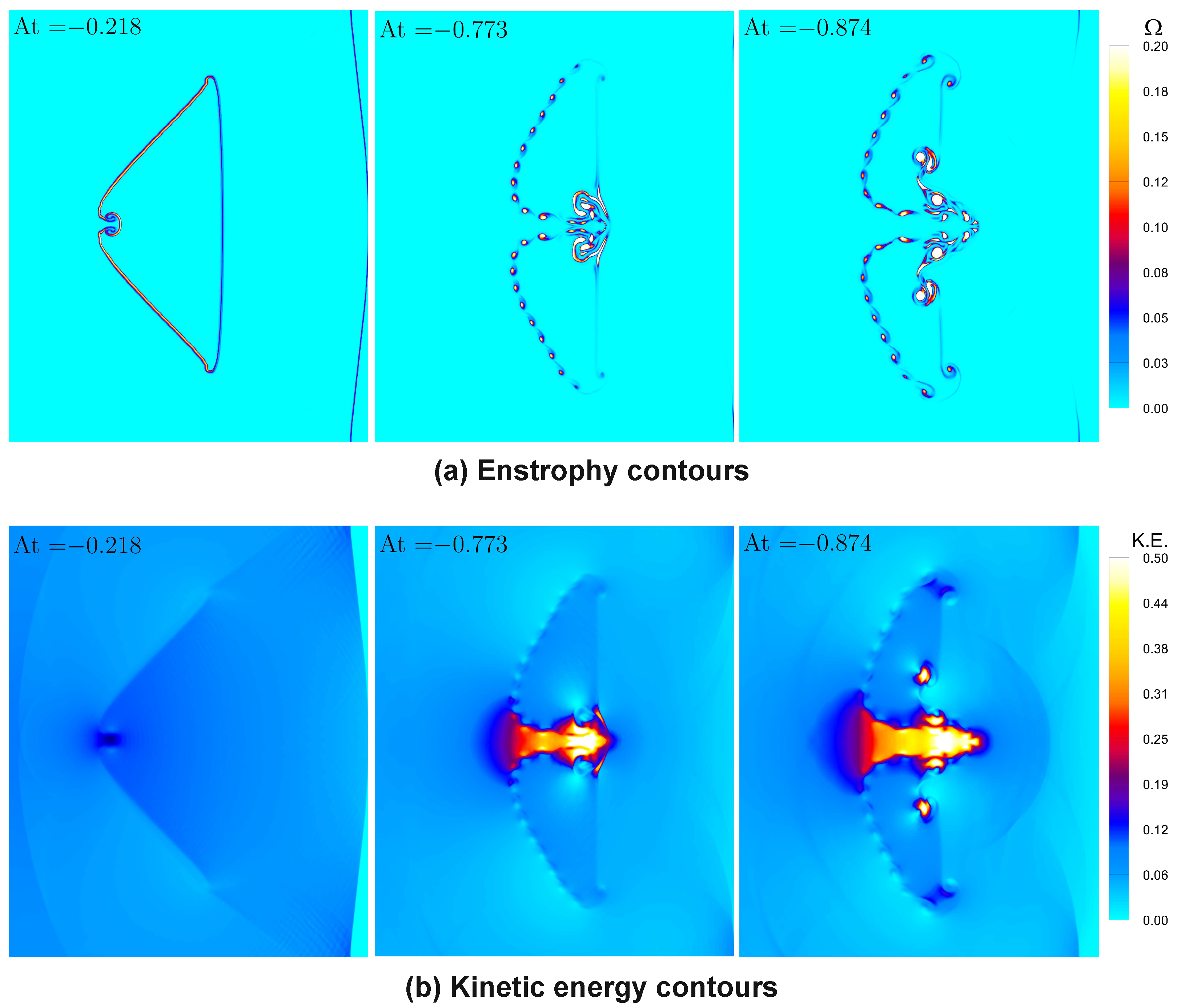
2.4.5. Enstrophy
2.4.6. Kinetic Energy
3. Problem Setup and Grid Refinement Study
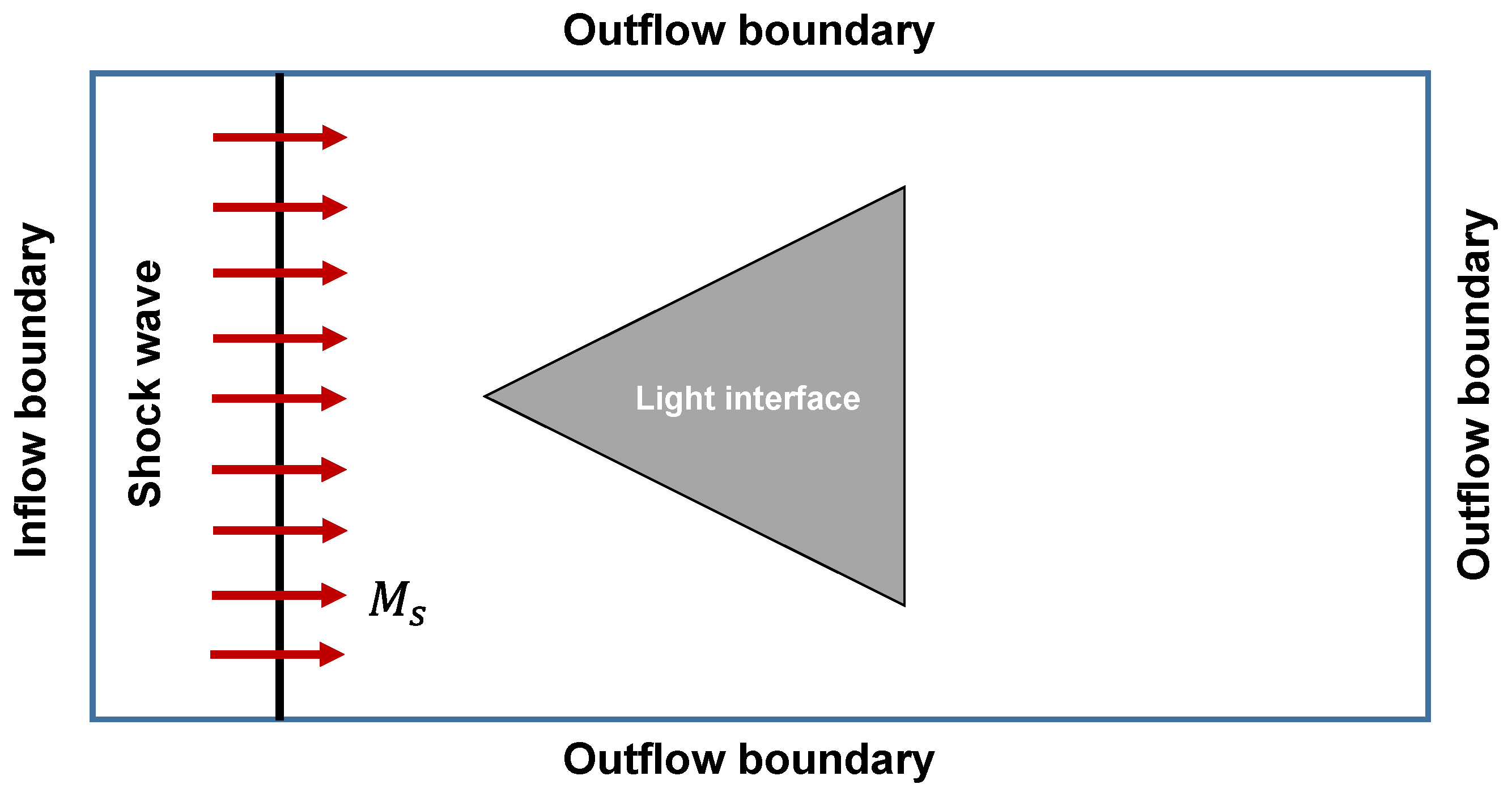
3.1. Problem Setup
3.2. Initialization of Numerical Simulations
3.3. Grid Refinement Study
4. Results and Discussion
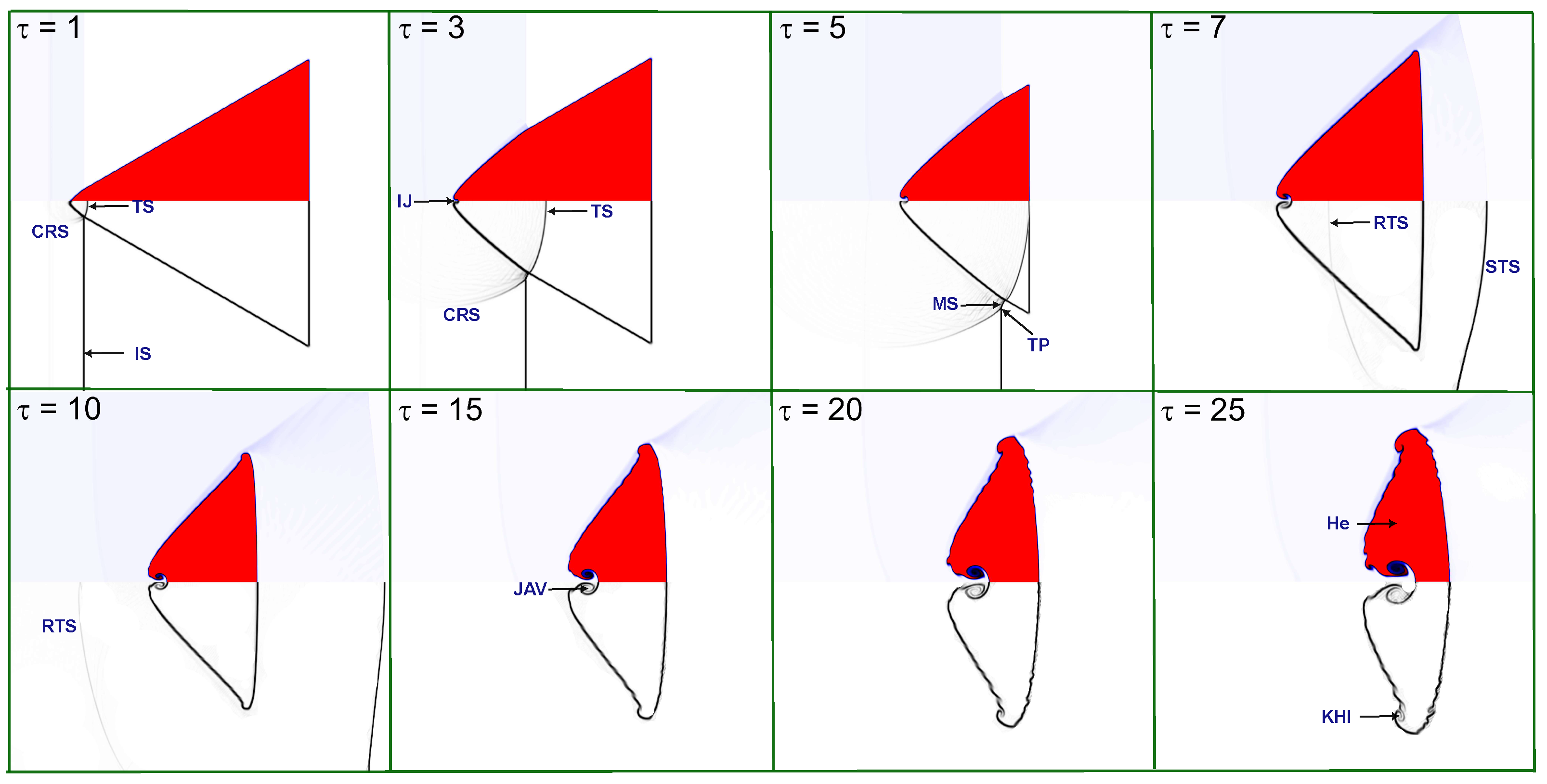
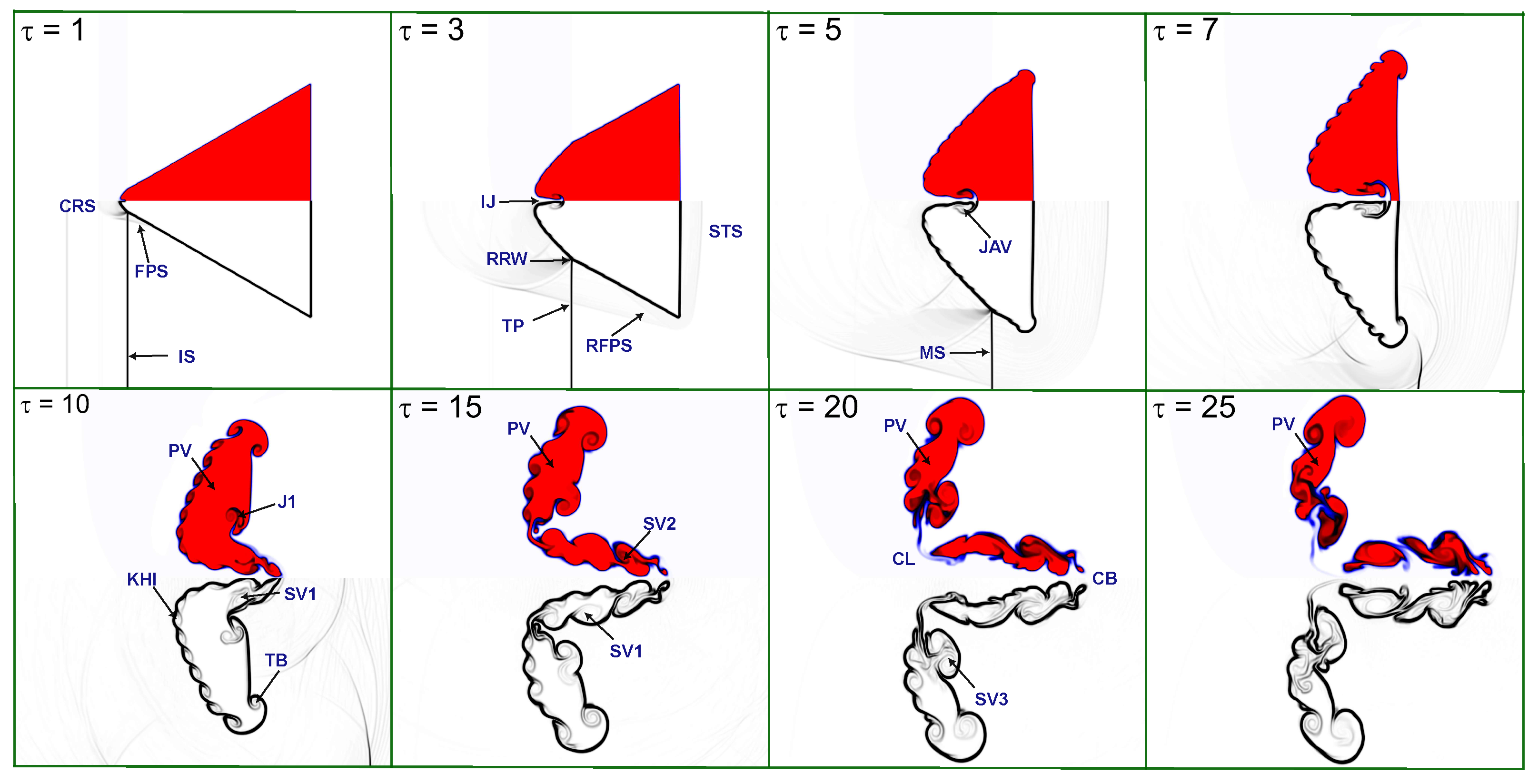
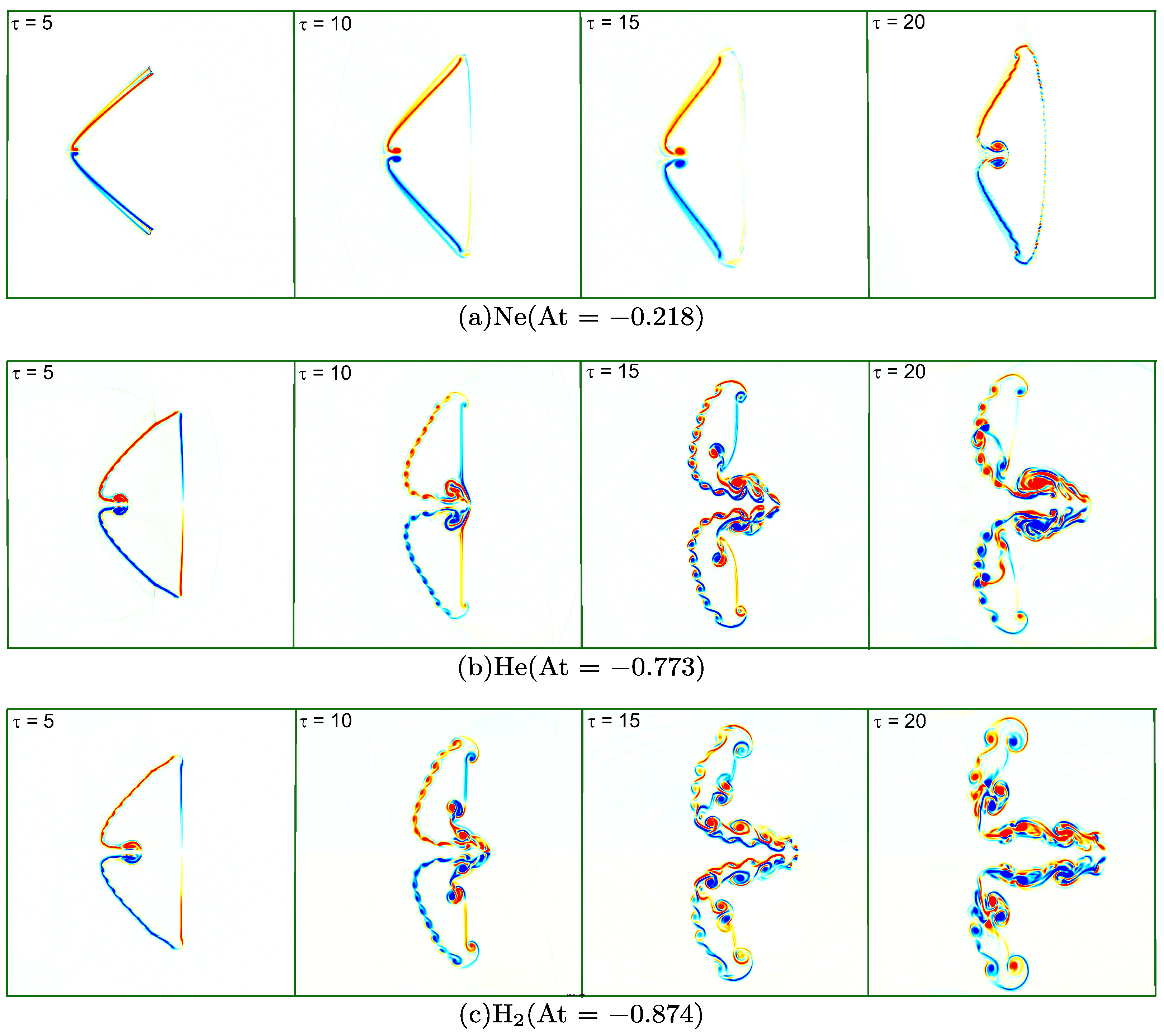
4.1. Evolution of Flow Morphology
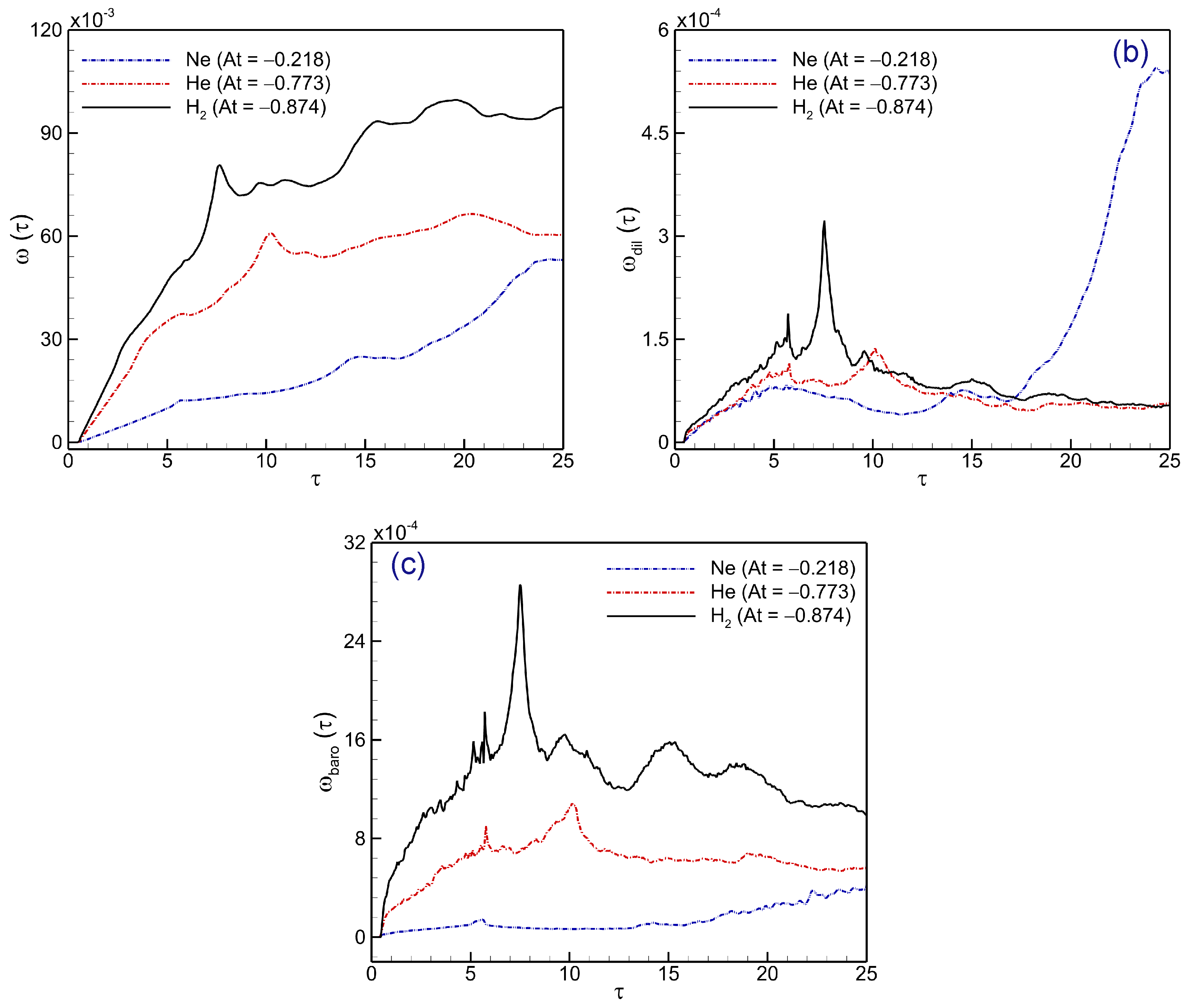
4.2. Vorticity Generation
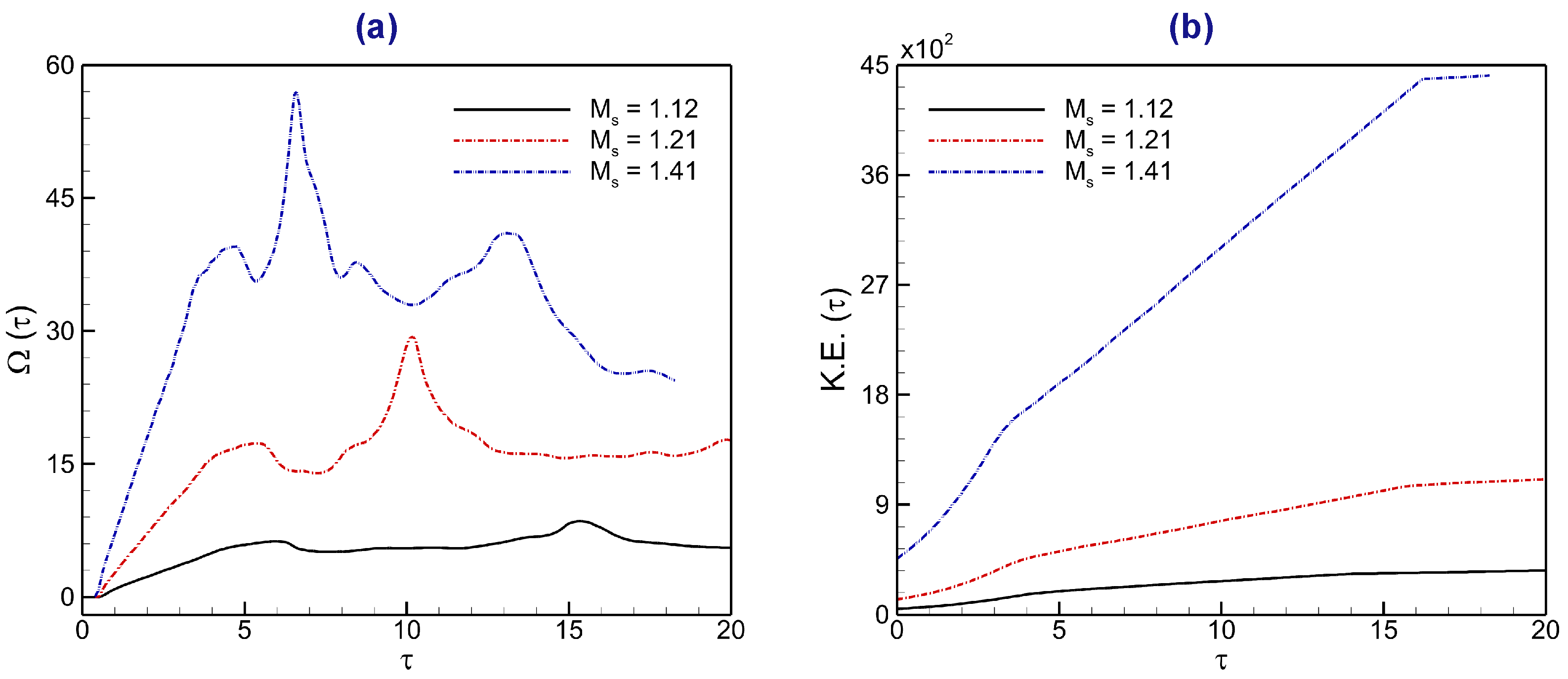
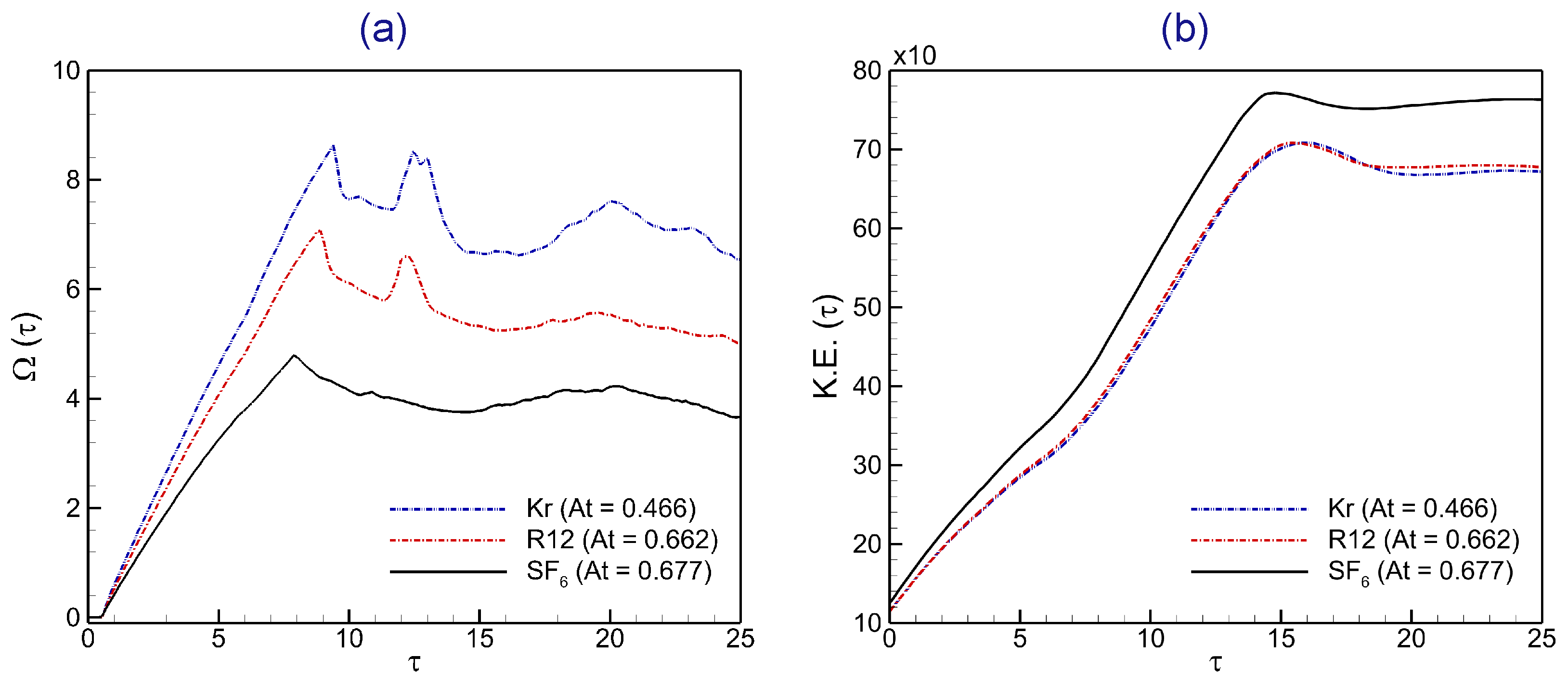
4.3. Evolution of Enstrophy and Kinetic Energy
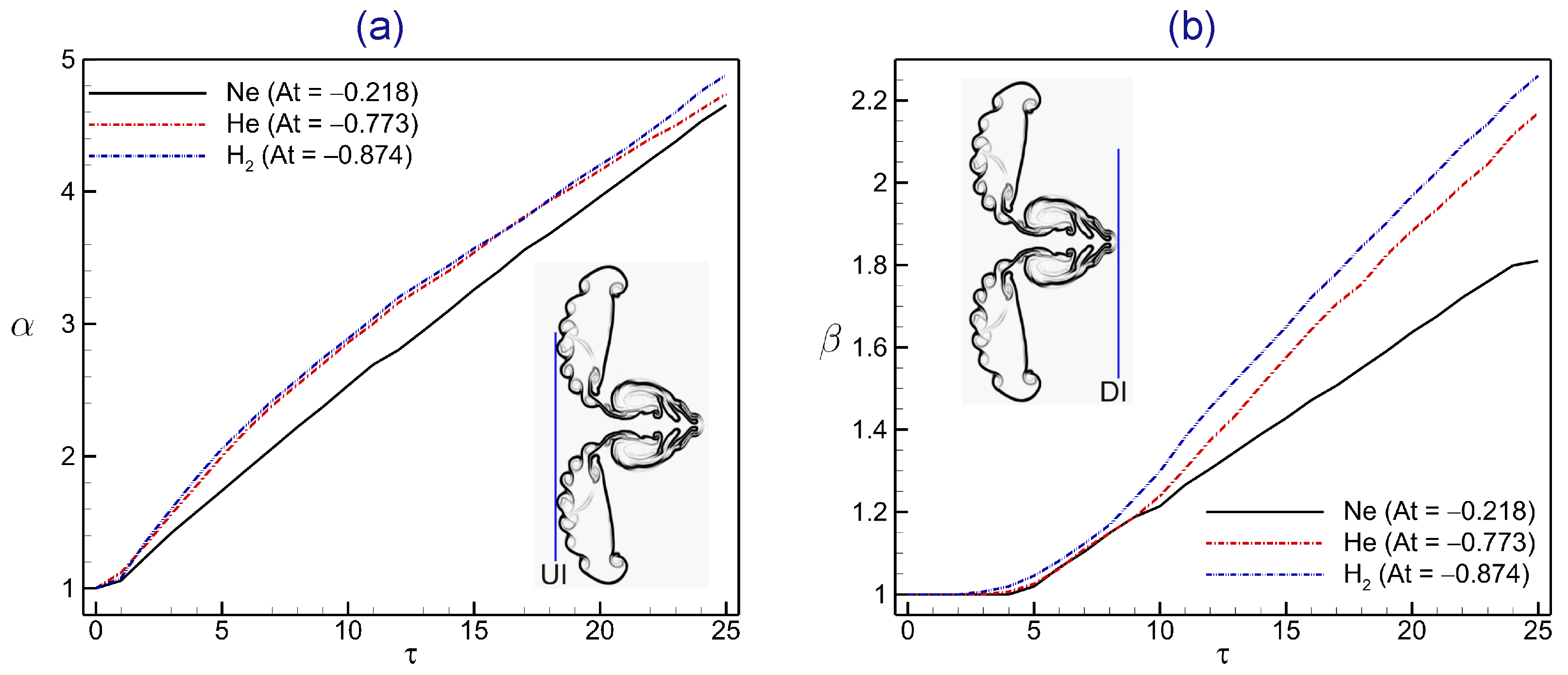
4.4. Interface Features
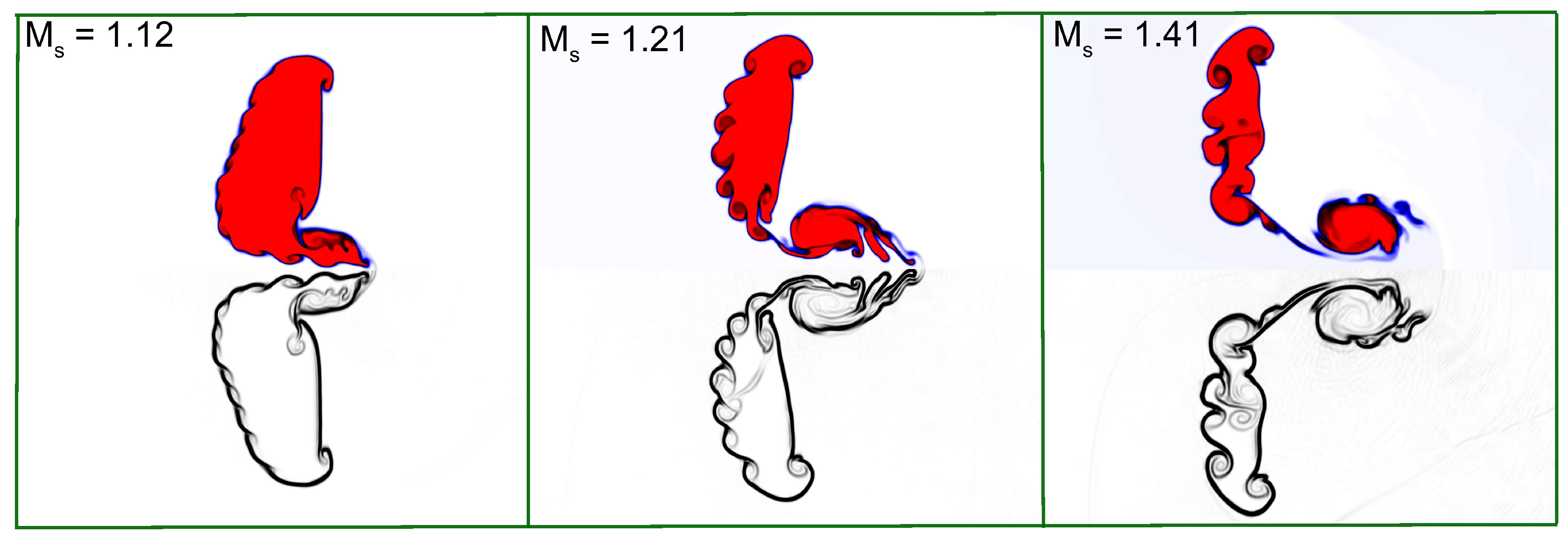
4.5. Impact of Shock Mach Number
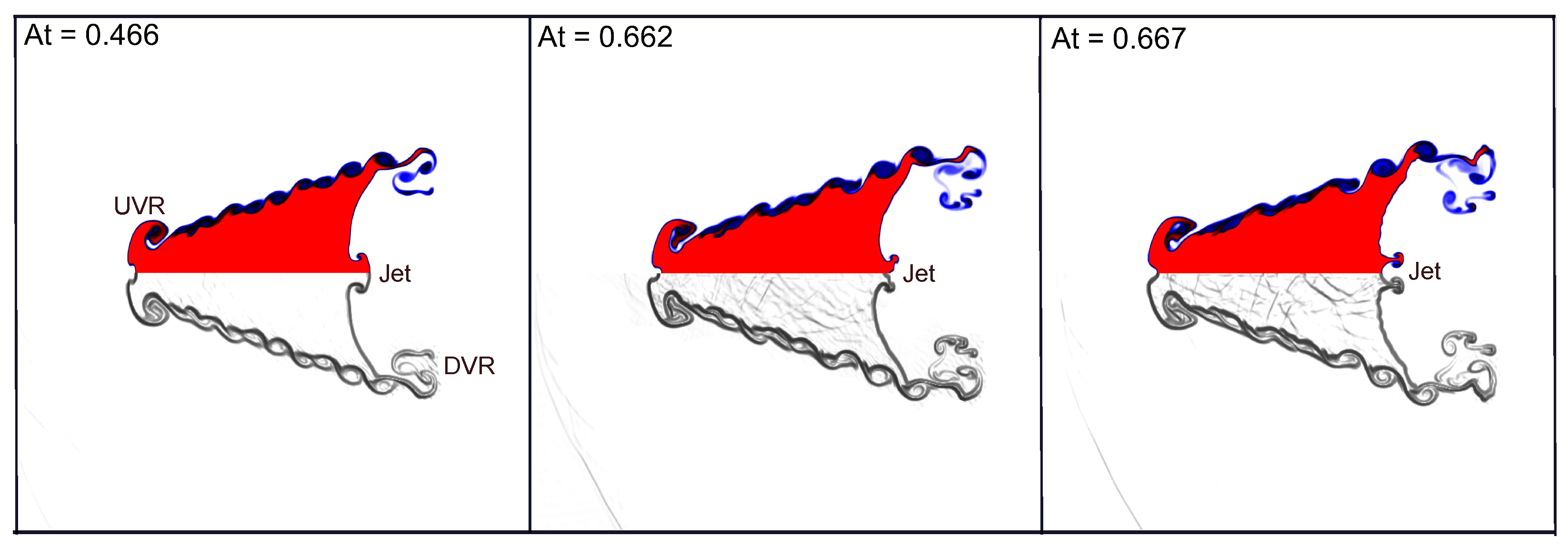
4.6. Impact of Positive Atwood Number
5. Concluding Remarks and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and Symbols
| RM | Richtmyer–Meshkov |
| DG | Discontinuous Galerkin |
| KHI | Kelvin–Helmholtz instability |
| Courant–Friedrichs–Lewy number | |
| KE | Kinetic energy |
| IS | Incident shock |
| TS | Transmitted shock |
| CRS | Curved reflected shock |
| IJ | Inward jet |
| TP | Triple point |
| MS | Mach stem |
| STS | Second transmitted shock |
| RTS | Reflected transmitted shock |
| JAV | Jet-associated vortex |
| RRW | Reflected rarefaction wave |
| FPS | Free precursor shock |
| DS | Detached shock |
| TB | Trailing bubbles |
| TNR | Twin von-Neumann refraction |
| PV | Primary vortex |
| SV1, SV2, SV3 | Secondary vortices |
| UVR, DVR | Upstream and downstream vortex rings |
| CB, CL | Connecting bridge and connecting line |
| UI, DI | Upstream and downstream interfaces |
| Atwood number | |
| Incoming shock Mach number | |
| D | Computational domain |
| Density | |
| Velocity components of velocity vector in x- and y-directions | |
| Conservative vector | |
| Inviscid flux vectors | |
| p | Total pressure |
| Mass fraction | |
| Specific heat ratio of mixture | |
| Specific heat ratios | |
| Specific heats at constant volume | |
| Specific heats at constant pressure | |
| Polynomials of degree at most k on element | |
| Normalized time | |
| Degree of freedom | |
| Total count of basis functions | |
| Basis function | |
| Element size lengths | |
| Time step | |
| Maximum wave speed of inviscid flux | |
| Densities of bubble gas and enclosing ambient gas | |
| Vorticity | |
| Enstrophy | |
| Average vorticity | |
| Dilatational and baroclinic vortcity production terms | |
| Block diagonal mass matrix | |
| Residual vector | |
| Speeds of the left and right waves | |
| Numerical fluxes | |
| HLLC Riemann numerical flux | |
| Intermediate fluxes | |
| Intermediate wave speed | |
| components of outward unit normal vector | |
| Legendre polynomials |
References
- Richtmyer, R.D. Taylor instability in shock acceleration of compressible fluids. Commun. Pure. Appl. Math. 1960, 13, 297–319. [Google Scholar] [CrossRef]
- Meshkov, E.E. Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 1969, 4, 101. [Google Scholar] [CrossRef]
- von Helmholtz, H. Über Discontinuirliche Flüssigkeits-Bewegungen; Akademie der Wissenschaften zu Berlin: Berlin, Germany, 1868. [Google Scholar]
- Kelvin, L. On the motion of free solids through a liquid. Phil. Mag. 1871, 42, 362–377. [Google Scholar]
- Arnett, W.D.; Bahcall, J.N.; Kirshner, R.P.; Woosley, S.E. Supernova 1987A. Ann. Rev. Astron. Astrophys. 1989, 2, 629–700. [Google Scholar] [CrossRef]
- Lindl, J.; Landen, O.; Edwards, J.; Moses, E.; Team, N. Review of the national ignition campaign 2009–2012. Phys. Plasmas 2014, 21, 020501. [Google Scholar] [CrossRef]
- Yang, J.; Kubota, T.; Zukoski, E.E. Applications of shock-induced mixing to supersonic combustion. AIAA J. 1993, 31, 854–862. [Google Scholar] [CrossRef]
- Zeng, W.G.; Pan, J.H.; Sun, Y.T.; Ren, Y.X. Turbulent mixing and energy transfer of reshocked heavy gas curtain. Phys. Fluids 2021, 30, 064106. [Google Scholar] [CrossRef]
- Brouillette, M. The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 2002, 34, 445. [Google Scholar] [CrossRef]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 2017, 720, 1–136. [Google Scholar]
- Zhou, Y. Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 2017, 723, 1–160. [Google Scholar]
- Zhou, Y.; Williams, R.J.; Ramaprabhu, P.; Groom, M.; Thornber, B.; Hillier, A.; Mostert, W.; Rollin, B.; Balachandar, S.; Powell, P.D.; et al. Rayleigh–Taylor and Richtmyer–Meshkov instabilities: A journey through scales. Physica D 2021, 423, 132838. [Google Scholar] [CrossRef]
- Jahn, R.G. The refraction of shock waves at a gaseous interface. J. Fluid Mech. 1956, 1, 457–489. [Google Scholar] [CrossRef]
- Abd-El-Fattah, A.M.; Henderson, L.F. Shock waves at a fast-slow gas interface. J. Fluid Mech. 1978, 86, 15–32. [Google Scholar] [CrossRef]
- Henderson, L.F. The refraction of a plane shock wave at a gas interface. J. Fluid Mech. 1966, 26, 607–637. [Google Scholar] [CrossRef]
- Abd-El-Fattah, A.M.; Henderson, L.F. Shock waves at a slow-fast gas interface. J. Fluid Mech. 1978, 89, 79–95. [Google Scholar] [CrossRef]
- Abd-El-Fattah, A.M.; Henderson, L.F.; Lozzi, A. Precursor shock waves at a slow—Fast gas interface. J. Fluid Mech. 1976, 76, 157. [Google Scholar] [CrossRef]
- Henderson, L.F.; Colella, P.; Puckett, E.G. On the refraction of shock waves at a slow—Fast gas interface. J. Fluid Mech. 1991, 224, 1. [Google Scholar] [CrossRef]
- Markstein, G.H. A Shock-Tube Study of Flame Front-Pressure Wave Interaction, 6th ed.; International Symposium on Combustion; Elsevier: Amsterdam, The Netherlands, 1957; Volume 6, p. 387. [Google Scholar]
- Haas, J.F.; Sturtevant, B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities. J. Fluid Mech. 1987, 181, 41. [Google Scholar] [CrossRef]
- Jacobs, J.W. Shock-induced mixing of a light-gas cylinder. J. Fluid Mech. 1992, 234, 629. [Google Scholar] [CrossRef]
- Jacobs, J.W. The dynamics of shock accelerated light and heavy gas cylinders. Phys. Fluids 1993, A5, 2239. [Google Scholar] [CrossRef]
- Layes, G.; Jourdan, G.; Houas, L. Distortion of a spherical gaseous interface accelerated by a plane shock wave. Phys. Rev. Lett. 2003, 91, 174502. [Google Scholar] [CrossRef] [PubMed]
- Ranjan, D.; Niederhaus, J.H.J.; Oakley, J.G.; Anderson, M.H.; Bonazza, R.; Greenough, J.A. Shock-bubble interactions: Features of divergent shock-refraction geometry observed in experiments and simulations. Phys. Fluids 2008, 20, 036101. [Google Scholar] [CrossRef]
- Zhai, Z.; Si, T.; Luo, X.; Yang, J. On the evolution of spherical gas interfaces accelerated by a planar shock wave. Phys. Fluids 2011, 23, 084104. [Google Scholar] [CrossRef]
- Si, T.; Zhai, Z.; Luo, X. Experimental study of Richtmyer–Meshkov instability in a cylindrical converging shock tube. Phys. Fluids 2014, 32, 343–351. [Google Scholar] [CrossRef]
- Ding, J.; Si, T.; Chen, M.; Zhai, Z.; Lu, X.; Luo, X. On the interaction of a planar shock with a three-dimensional light gas cylinder. J. Fluid Mech. 2017, 828, 289–317. [Google Scholar] [CrossRef]
- Quirk, J.J.; Karni, S. On the dynamics of a shock-bubble interaction. J. Fluid Mech. 1996, 318, 129. [Google Scholar] [CrossRef]
- Giordano, J.; Burtschell, Y. Richtmyer–Meshkov instability induced by shock-bubble interaction: Numerical and analytical studies with experimental validation. Phys. Fluids 2006, 18, 036102. [Google Scholar] [CrossRef]
- Bagabir, A.; Drikakis, D. Mach number effects on shock-bubble interaction. Shock Waves 2001, 11, 209. [Google Scholar] [CrossRef]
- Niederhaus, J.H.J.; Greenough, J.A.; Oakley, J.G.; Ranjan, D.; Anderson, M.H.; Bonazza, R.A. A computational parameter study for the three-dimensional shock-bubble interaction. J. Fluid Mech. 2008, 594, 85. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, B.; Chen, H.; Zhang, B.; Liu, H. Scaling vortex breakdown mechanism based on viscous effect in shock cylindrical bubble interaction. Phys. Fluids 2018, 30, 126103. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M. Behavior of a shock-accelerated heavy cylindrical bubble under nonequilibrium conditions of diatomic and polyatomic gases. Phys. Rev. Fluids 2021, 6, 044001. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M.; Myong, R.S. Impact of the bulk viscosity on flow morphology of shock-bubble interaction in diatomic and polyatomic gases. Phys. Fluids 2021, 33, 066103. [Google Scholar] [CrossRef]
- Bai, J.; Zou, L.; Wang, T.; Liu, K.; Huang, W.; Liu, J.; Li, P.; Tan, D.; Liu, C. Experimental and numerical study of shock-accelerated elliptic heavy gas cylinders. Phys. Rev. E 2010, 82, 056318. [Google Scholar] [CrossRef]
- Georgievskiy, P.Y.; Levin, V.A.; Sutyrin, O.G. Interaction of a shock with elliptical gas bubbles. Shock Waves 2015, 25, 357–369. [Google Scholar] [CrossRef]
- Zou, L.; Liao, S.; Liu, C.; Wang, Y.; Zhai, Z. Aspect ratio effect on shock-accelerated elliptic gas cylinders. Phys. Fluids 2016, 28, 036101. [Google Scholar] [CrossRef]
- Chen, J.; Qu, F.; Wu, X.; Wang, Z.; Bai, J. Numerical study of interactions between shock waves and a circular or elliptic bubble in air medium. Phys. Fluids 2021, 33, 043301. [Google Scholar] [CrossRef]
- Singh, S.; Sengupta, B.; Awasthi, M.K.; Vinesh, V. Insight on the flow physics of shock-driven elliptical gas inhomogeneity with different Atwood numbers. Int. J. Math. Eng. Manag. Sci. 2024, 33, 1–22. [Google Scholar] [CrossRef]
- Singh, S.; Msmali, A.H.; Nelson, M.I. Unfolding of shocked hydrodynamic instability at SF6 elliptical interface: Physical insights from numerical simulations. Comput. Fluids 2024, 277, 106304. [Google Scholar] [CrossRef]
- Zhai, Z.; Wang, M.; Si, T.; Luo, X. On the interaction of a planar shock with a light polygonal interface. J. Fluid Mech. 2014, 757, 800–816. [Google Scholar] [CrossRef]
- Luo, X.; Wang, M.; Si, T.; Zhai, Z. On the interaction of a planar shock with an SF6 polygon. J. Fluid Mech. 2015, 773, 366–394. [Google Scholar] [CrossRef]
- Igra, D.; Igra, O. Numerical investigation of the interaction between a planar shock wave with square and triangular bubbles containing different gases. Phys. Fluids 2018, 30, 056104. [Google Scholar] [CrossRef]
- Lindner, J.R. Microbubbles in medical imaging: Current applications and future directions. Nat. Rev. Drug Discov. 2004, 3, 527–533. [Google Scholar] [CrossRef]
- Sinibaldi, G.; Occhicone, A.; Alves, P.F.; Caprini, D.; Marino, L.; Michelotti, F.; Casciola, C.M. Laser induced cavitation: Plasma generation and breakdown shockwave. Phys. Fluids 2019, 31, 103302. [Google Scholar] [CrossRef]
- Reuter, F.; Mettin, R. Mechanisms of single bubble cleaning. Ultrason. Sonochem. 2016, 29, 550–562. [Google Scholar] [CrossRef] [PubMed]
- Qiu, N.; Zhou, W.; Che, B.; Wu, D.; Wang, L.; Zhu, H. Effects of microvortex generators on cavitation erosion by changing periodic shedding into new structures. Phys. Fluids 2020, 32, 104108. [Google Scholar] [CrossRef]
- Bates, K.R.; Nikiforakis, N.; Holder, D. Richtmyer–Meshkov instability induced by the interaction of a shock wave with a rectangular block of SF6. Phys. Fluids 2007, 19, 036101. [Google Scholar] [CrossRef]
- Singh, S. Role of Atwood number on flow morphology of a planar shock-accelerated square bubble: A numerical study. Phys. Fluids 2020, 32, 126112. [Google Scholar] [CrossRef]
- Singh, S. Contribution of Mach number to the evolution of the Richtmyer–Meshkov instability induced by a shock-accelerated square light bubble. Phys. Rev. Fluids 2021, 6, 104001. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M. Numerical investigation of shock Mach number effects on Richtmyer–Meshkov instability in a heavy square bubble. Phys. D Nonlinear Phenom. 2023, 453, 133844. [Google Scholar] [CrossRef]
- Singh, S.; Torrilhon, M. On the shock-driven hydrodynamic instability in square and rectangular light gas bubbles: A comparative study from numerical simulations. Phys. Fluids 2023, 35, 012117. [Google Scholar] [CrossRef]
- Singh, S. Investigation of aspect ratio effects on flow characteristics and vorticity generation in shock-induced rectangular bubble. Eur. J. Mech. B/Fluids 2023, 101, 131. [Google Scholar] [CrossRef]
- Singh, S.; Jalleli, D.T. Investigation of coupling effect on the evolution of Richtmyer–Meshkov instability at double heavy square bubbles. Sci. China-Phys. Mech. Astron. 2024, 67, 214711. [Google Scholar] [CrossRef]
- Singh, S.; Karchani, A.; Chourushi, T.; Myong, R.S. A three-dimensional modal discontinuous Galerkin method for the second-order Boltzmann-Curtiss-based constitutive model of rarefied and microscale gas flows. J. Comput. Phys. 2022, 457, 111052. [Google Scholar] [CrossRef]
- Krivodonova, L. Limiters for high-order discontinuous Galerkin methods. J. Comput. Phys. 2007, 226, 879–896. [Google Scholar] [CrossRef]
- Johnsen, E.; Colonius, T. Implementation of WENO schemes in compressible multicomponent flow problems. J. Comput. Phys. 2006, 219, 715–732. [Google Scholar] [CrossRef]
- Gottlieb, S.; Shu, C.-W.; Tadmor, E. Strong stability-preserving high-order time discretization methods. SIAM Rev. 2001, 43, 89–112. [Google Scholar] [CrossRef]





| Gas | Density | Heat Ratio | Sound Speed | Atwood Number |
|---|---|---|---|---|
| () | (At) | |||
| 1.25 | 1.40 | 352 | ambient | |
| Ne | 0.80 | 1.03 | 452 | −0.218 |
| He | 0.16 | 1.66 | 1007 | −0.773 |
| 0.084 | 1.41 | 1320 | −0.874 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Msmali, A.H. Analyzing Richtmyer–Meshkov Phenomena Triggered by Forward-Triangular Light Gas Bubbles: A Numerical Perspective. Axioms 2024, 13, 365. https://doi.org/10.3390/axioms13060365
Singh S, Msmali AH. Analyzing Richtmyer–Meshkov Phenomena Triggered by Forward-Triangular Light Gas Bubbles: A Numerical Perspective. Axioms. 2024; 13(6):365. https://doi.org/10.3390/axioms13060365
Chicago/Turabian StyleSingh, Satyvir, and Ahmed Hussein Msmali. 2024. "Analyzing Richtmyer–Meshkov Phenomena Triggered by Forward-Triangular Light Gas Bubbles: A Numerical Perspective" Axioms 13, no. 6: 365. https://doi.org/10.3390/axioms13060365
APA StyleSingh, S., & Msmali, A. H. (2024). Analyzing Richtmyer–Meshkov Phenomena Triggered by Forward-Triangular Light Gas Bubbles: A Numerical Perspective. Axioms, 13(6), 365. https://doi.org/10.3390/axioms13060365







