Analytical and Numerical Investigation for the Inhomogeneous Pantograph Equation
Abstract
:1. Introduction
2. Solution in Closed Series Form
3. Convergence Analysis
4. Exact Solutions at Special Cases
5. Results and Validations
5.1. Exact Solutions of Some Classes
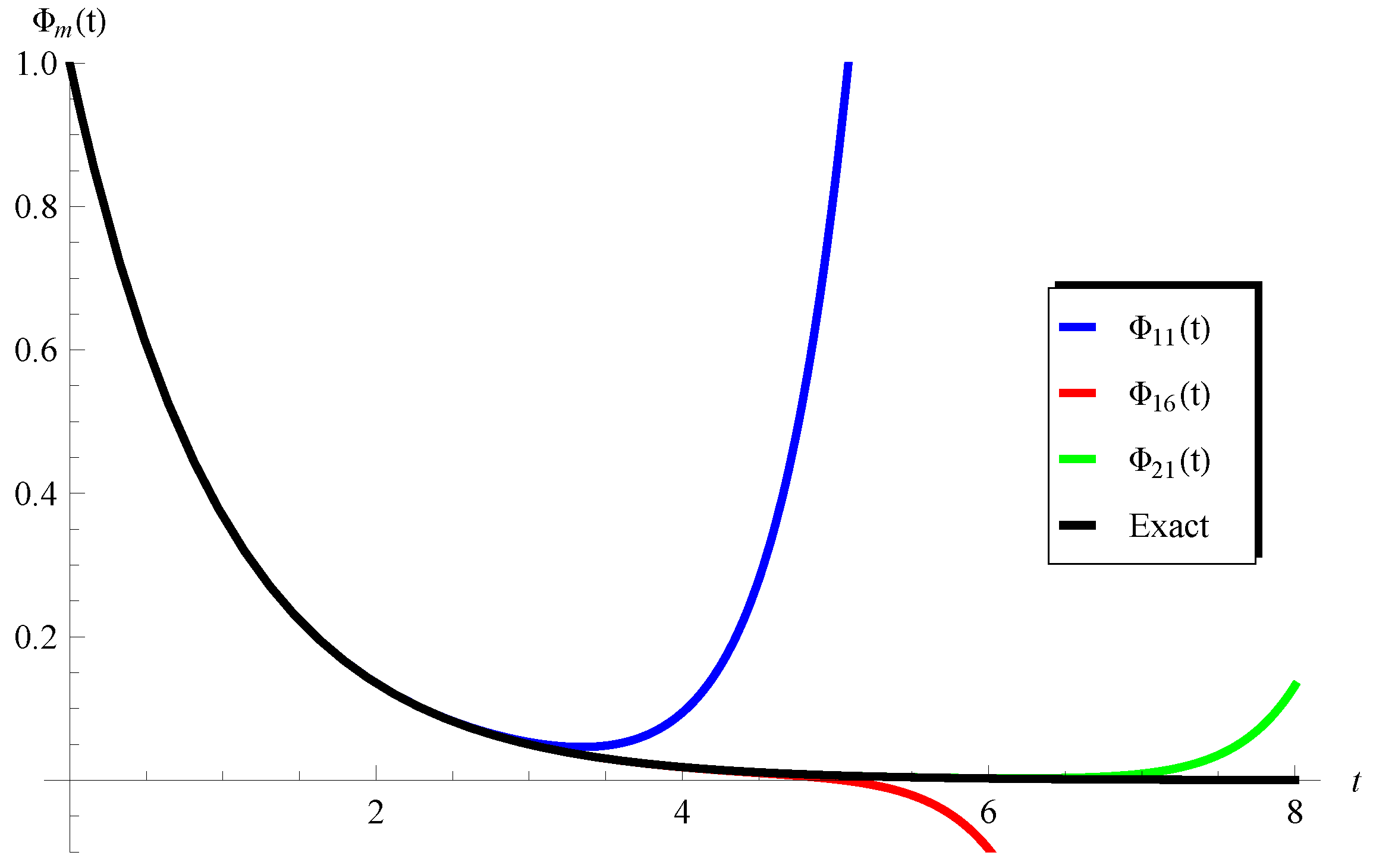
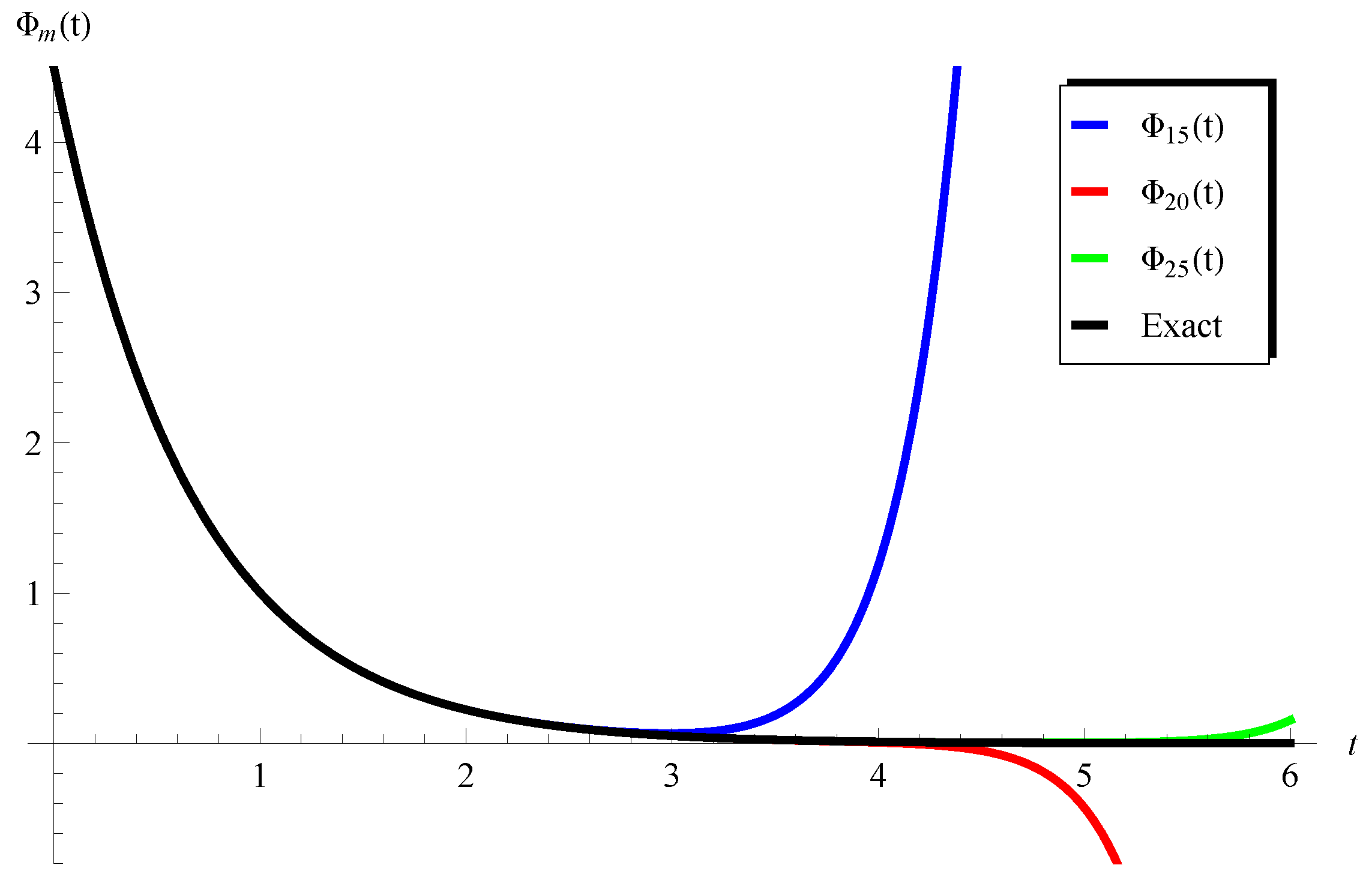
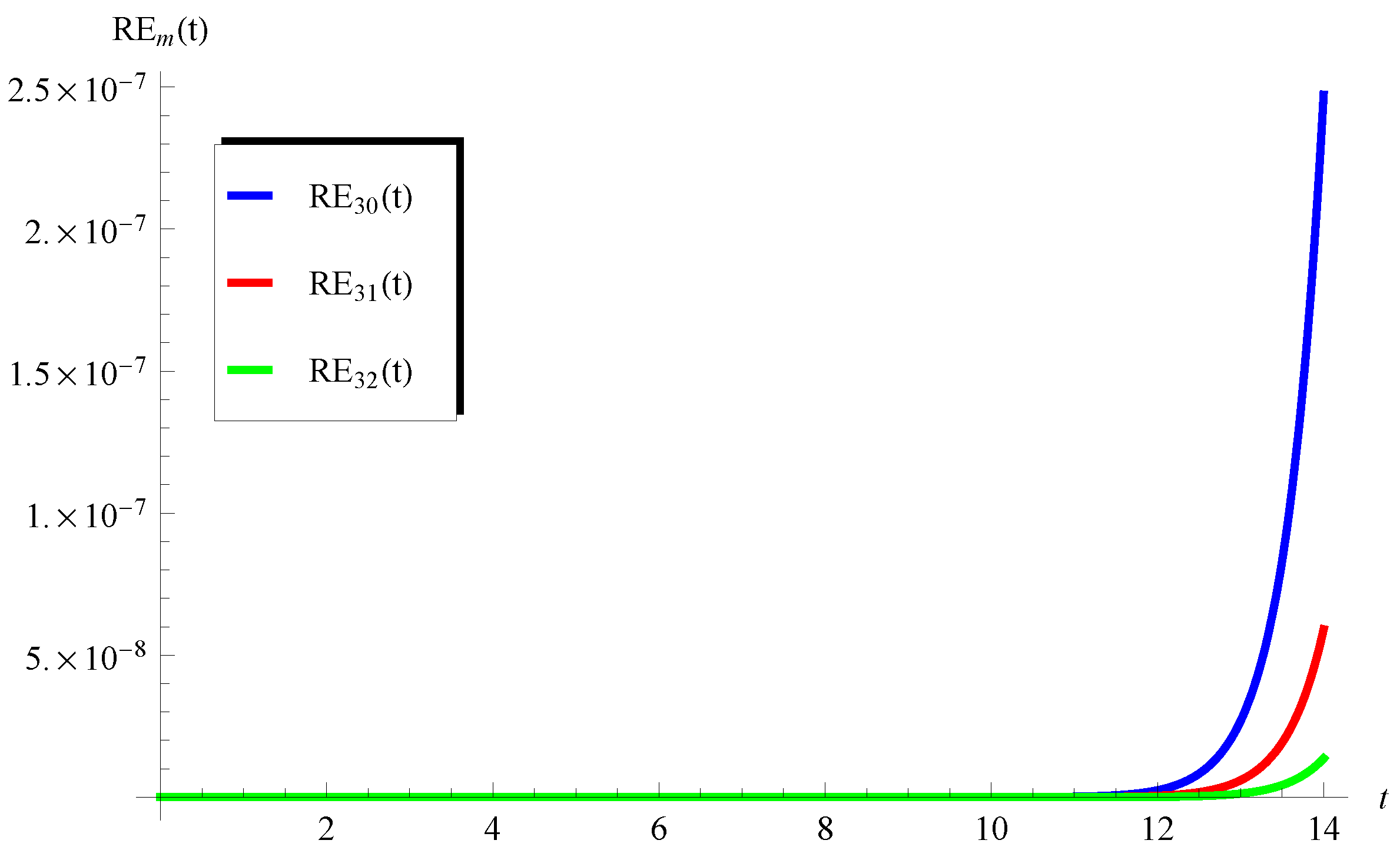
5.2. Validation of Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sezera, M.; Akyüz-Dascıoglub, A. A Taylor method for numerical solution of generalized pantograph equations with linear functional argument. J. Comput. Appl. Math. 2007, 200, 217–225. [Google Scholar] [CrossRef]
- Sedaghat, S.; Ordokhani, Y.; Dehghan, M. Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4815–4830. [Google Scholar] [CrossRef]
- Tohidi, E.; Bhrawy, A.H.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Javadi, S.; Babolian, E.; Taheri, Z. Solving generalized pantograph equations by shifted orthonormal Bernstein polynomials. J. Comput. Appl. Math. 2016, 303, 1–4. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2011; Volume 41. [Google Scholar]
- Jafari, H.; Mahmoudi, M.; Noori Skandari, M.H. A new numerical method to solve pantograph delay differential equations with convergence analysis. Adv. Differ. Equ. 2021, 2021, 129. [Google Scholar] [CrossRef]
- Ezz-Eldien, S.S. On solving systems of multi-pantograph equations via spectral tau method. Appl. Math. Comput. 2018, 321, 63–73. [Google Scholar] [CrossRef]
- Isik, O.R.; Turkoglu, T. A rational approximate solution for generalized pantograph-delay differential equations. Math. Methods Appl. Sci. 2016, 39, 2011–2024. [Google Scholar] [CrossRef]
- Andrews, H.I. Third paper: Calculating the behaviour of an overhead catenary system for railway electrification. Proc. Inst. Mech. Eng. 1964, 179, 809–846. [Google Scholar] [CrossRef]
- Gilbert, G.; Davtcs, H.E.H. Pantograph motion on a nearly uniform railway overhead line. Proc. Inst. Electr. Eng. 1966, 113, 485–492. [Google Scholar] [CrossRef]
- Caine, P.M.; Scott, P.R. Single-wire railway overhead system. Proc. Inst. Electr. Eng. 1969, 116, 1217–1221. [Google Scholar] [CrossRef]
- Abbott, M.R. Numerical method for calculating the dynamic behaviour of a trolley wire overhead contact system for electric railways. Comput. J. 1970, 13, 363–368. [Google Scholar] [CrossRef]
- Ockendon, J.; Tayler, A.B. The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1971, 322, 447–468. [Google Scholar]
- Al-Enazy, A.H.S.; Ebaid, A.; Algehyne, E.A.; Al-Jeaid, H.K. Advanced Study on the Delay Differential Equation y′(t) = ay(t) + by(ct). Mathematics 2022, 10, 4302. [Google Scholar] [CrossRef]
- Albidah, A.B.; Kanaan, N.E.; Ebaid, A.; Al-Jeaid, H.K. Exact and Numerical Analysis of the Pantograph Delay Differential Equation via the Homotopy Perturbation Method. Mathematics 2023, 11, 944. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; Ebaid, A. Analytical and Numerical Simulations of a Delay Model: The Pantograph Delay Equation. Axioms 2022, 11, 741. [Google Scholar] [CrossRef]
- Alrebdi, R.; Al-Jeaid, H.K. Accurate Solution for the Pantograph Delay Differential Equation via Laplace Transform. Mathematics 2023, 11, 2031. [Google Scholar] [CrossRef]
- Khaled, S.M. Applications of Standard Methods for Solving the Electric Train Mathematical Model with Proportional Delay. Int. J. Anal. Appl. 2022, 20, 27. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Jeaid, H.K. On the Exact Solution of the Functional Differential Equation y′(t) = ay(t) + by(−t). Adv. Differ. Equ. Control Processes 2022, 26, 39–49. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method. Mathematics 2018, 6, 331. [Google Scholar] [CrossRef]
- Ebaid, A.; Cattani, C.; Al Juhani, A.S.; El-Zahar, E.R. A novel exact solution for the fractional Ambartsumian equation. Adv. Differ. Equ. 2021, 2021, 88. [Google Scholar] [CrossRef]
- Dogan, N. Solution of the system of ordinary differential equations by combined Laplace transform-Adomian decomposition method. Math. Comput. Appl. 2012, 17, 203–211. [Google Scholar] [CrossRef]
- Atangana, A.; Alkaltani, B.S. A novel double integral transform and its applications. J. Nonlinear Sci. Appl. 2016, 9, 424–434. [Google Scholar] [CrossRef]
- Khaled, S.M. The exact effects of radiation and joule heating on Magnetohydrodynamic Marangoni convection over a flat surface. Therm. Sci. 2018, 22, 63–72. [Google Scholar] [CrossRef]
- Venkata Pavani, P.; Lakshmi Priya, U.; Amarnath Reddy, B. Solving differential equations by using Laplace transforms. Int. J. Res. Anal. Rev. 2018, 5, 1796–1799. [Google Scholar]
- Alrebdi, R.; Al-Jeaid, H.K. Two Different Analytical Approaches for Solving the Pantograph Delay Equation with Variable Coefficient of Exponential Order. Axioms 2024, 13, 229. [Google Scholar] [CrossRef]
- Kac, V.G.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2002. [Google Scholar]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Beijing and Springer-Verlag; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 9783642181009. [Google Scholar]


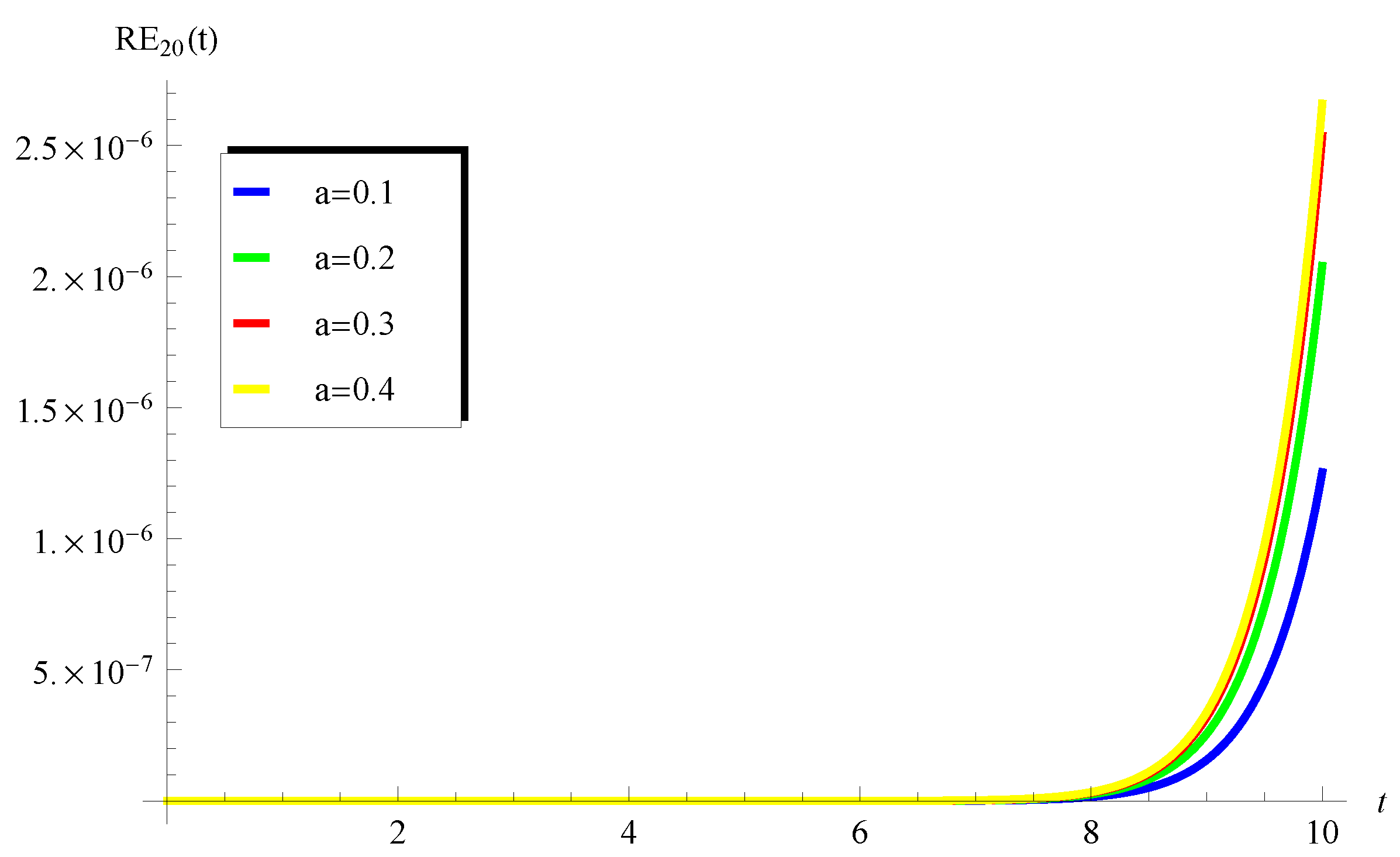

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldosari, F.; Ebaid, A. Analytical and Numerical Investigation for the Inhomogeneous Pantograph Equation. Axioms 2024, 13, 377. https://doi.org/10.3390/axioms13060377
Aldosari F, Ebaid A. Analytical and Numerical Investigation for the Inhomogeneous Pantograph Equation. Axioms. 2024; 13(6):377. https://doi.org/10.3390/axioms13060377
Chicago/Turabian StyleAldosari, Faten, and Abdelhalim Ebaid. 2024. "Analytical and Numerical Investigation for the Inhomogeneous Pantograph Equation" Axioms 13, no. 6: 377. https://doi.org/10.3390/axioms13060377






