Weighted Convolution for Quaternion Linear Canonical Cosine Transform and Its Application

Abstract

Convolution plays a pivotal role in the domains of signal processing and optics. This paper primarily focuses on studying the weighted convolution for quaternion linear canonical cosine transform (QLCcT) and its application in multiplicative filter analysis. Firstly, we propose QLCcT by combining quaternion algebra with linear canonical cosine transform (LCcT), which extends LCcT to Hamiltonian quaternion algebra. Secondly, we introduce weighted convolution and correlation operations for QLCcT, accompanied by their corresponding theorems. We also explore the properties of QLCcT. Thirdly, we utilize these proposed convolution structures to analyze multiplicative filter models that offer lower computational complexity compared to existing methods based on quaternion linear canonical transform (QLCT). Additionally, we discuss the rationale behind studying such transforms using quaternion functions as an illustrative example.

1. Introduction

The linear canonical transform (LCT) [1,2] is an important integral transform that enables the manipulation of signals through scaling, rotation, and reflection. It exhibits unique advantages, strong flexibility, and processing ability when dealing with non-stationary and non-Gaussian signals. Significant progress has been made in signal sampling and filtering [3,4], discrete algorithms [5,6], convolution theory [7,8,9], time-frequency analysis [10,11,12], parameter estimation [13,14], uncertainty principles [11,15,16], image encryption [17,18], etc. The linear canonical cosine transform (LCcT) is widely recognized for its excellent orthogonal properties that enable efficient compression of energy distribution. When processing signals, LCcT offers a significant advantage by requiring only half the number of real number multiplications compared to LCT [19], applicable to both even and odd signals. This feature makes LCcT highly valuable in digital signal processing applications. In recent years, researchers have increasingly focused on studying various properties of LCcT, such as duality, sampling, multiplication, convolution, and correlation [20,21,22,23,24]. These studies not only enhance our understanding of the working principles behind LCct but also broaden its range of applications in digital signal processing.

Quaternions are a crucial mathematical tool that play an important role in representing and handling complex mathematical operations, including rotations and transformations. They have wide applications in mathematics, physics, engineering, and computer graphics, providing an efficient mathematical method for solving various complex problems [25,26]. In recent years, with the continuous progress of mathematical theory, researchers have begun to extend the concept of integral transforms to the field of quaternion algebra. This extension has led to new theoretical frameworks, such as the quaternion Fourier transform (QFT) [27,28], the quaternion fractional Fourier transform (QFRFT) [29,30], the quaternion linear canonical transform (QLCT) [31,32,33,34], and the quaternion offset linear canonical transform (QOLCT) [7,35,36]. These theoretical frameworks provide new methods and tools for processing and analyzing quaternion signals. Despite remarkable progress in the study of quaternion integral transforms, the extension of the important LCcT transform to the quaternion domain remains an under-explored area. Therefore, the study of the quaternion linear canonical cosine transform (QLCcT) can provide us with more convenient, efficient, accurate, and stable methods for rotation representation and calculation, as well as important mathematical tools and solutions for complex problems in various fields.

Motivated by the significance of QLCcT in mathematics and signal processing, we will investigate its properties and applications. The central goal of this article is to define right-side QLCcT, establish an essential weighted convolution theorem, and design a multiplicative filter using the given convolution.

The main research findings of this article are reflected in the following three aspects: (1) The right-side QLCcT is defined. By exploring the relationship between the right-side and left-side QLCcT, we have discovered that the right-side QLCcT can be simply transformed into its left-side counterpart. This discovery implies that all research findings applicable to the right-side QLCcT are also applicable to its left-side counterpart. We also illustrate the relationships of right-side QLCcT with QFcT, and derive various fundamental properties, including linearity, shift, modulation, scale property, differential property, inversion formula, and Plancherel formula for right-side QLCcT. (2) We propose weighted convolution structures and establish a corresponding weighted convolution theorem for the QLCcT domain, which states that the convolution of two functions can be simplified to a multiplication operation in the QLCcT domain. These structures are particularly suitable and easily applied for constructing filter models. (3) We apply a novel convolution specifically designed for the analysis of multiplicative filter models. These models are particularly advantageous due to their reduced computational complexity when compared to traditional methods employed in the QLCT domain. Additionally, the quaternion function is utilized as an example to provide insights into the rationale and potential applications of such a transformation.

This paper is structured as follows: Section 2 presents a comprehensive overview of the basic concepts necessary for understanding the subsequent discussions. Section 3 considers the definition of right-side QLCcT, along with some properties, and the relationships between QLCcT and other transformations is studied. In Section 4, three types of weighted convolutions for QLCcT are presented, and corresponding convolution theorems are derived. The relationship between the proposed convolutions is also discussed. Section 5 provides an example and demonstrates application of QLCcT. Finally, this article concludes in Section 6.

2. Preliminaries

In this section, we present a review of fundamental concepts related to quaternion algebra and provide a concise overview of the QLCT.

2.1. Quaternion Algebra

Within the field of mathematics, there exist different types of numbers, each having unique properties and applications. One such fundamental construct is quaternions, an intricate mathematical entity comprising four distinct components, together forming a comprehensive mathematical structure. The invention of the quaternion is attributed to the renowned mathematician Hamilton in 1843 [25], and is denoted by the symbol $\mathbb{H}$. Within the framework of quaternion algebra, each element is represented by a specific form as follows:

$$\mathbb{H}=\left\{q\right|q=q_0+\mu q_1+\upsilon q_2+\eta q_3,q_0,q_1,q_2,q_3\in \mathbb{R}\},$$

(1)

and $\mu ,\upsilon ,\eta$ are imaginary units that follow the multiplication rules [25,26]

$$\mu \upsilon =-\upsilon \mu =\eta ,{\mu }^2={\upsilon }^2={\eta }^2=\mu \upsilon \eta =-1.$$

(2)

For $q=q_0+\mu q_1+\upsilon q_2+\eta q_3=q_0+\underline{q}\in \mathbb{H}$, where $q_0$ and $\underline{q}$ represent the scalar and the pure part of q, respectively. Let $\mathbb{U}=\left\{\underline{q}\right|{\underline{q}}^2=-1\}$ and $\mathbb{H}\left(\mu \right)=\left\{q\right|q=q_1+\mu q_2,\mu \in \mathbb{U},q_1,q_2\in \mathbb{R}\}$.

If $p=p_0+\underline{p}$ and $q=q_0+\underline{q}$, their product is defined as follows:

$$pq=p_0{q}_0+\underline{p}\underline{q}+p_0\underline{q}+q_0\underline{p}+\underline{p}\times \underline{q},$$

(3)

where “×” denote the cross-product.

The conjugate and modulus of q are defined, respectively, as follows:

$$\overline{q}=q_0-\mu q_1-\upsilon q_2-\eta q_3,\left|q\right|=\sqrt{q\overline{q}}=\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}.$$

The following identities can be easily verified:

$$\overline{pq}=\overline{q}\overline{p},\left|pq\right|=\left|p\right|\left|q\right|,\forall p,q\in \mathbb{H}.$$

(4)

Any $q\in \mathbb{H}$ can be represented by

$$q=q_0+\mu q_1+\upsilon q_2+\eta q_3=q_{\alpha }+q_{\beta }\upsilon =q_{\alpha }+\upsilon {\overline{q}}_{\beta },$$

where $q_{\alpha },q_{\beta }\in \mathbb{H}\left(\mu \right)$.

A quaternion function f defined on the real domain can be represented as

$$f=f_r+\mu f_{\mu }+\upsilon f_{\upsilon }+\eta f_{\eta }=f_{\alpha }+f_{\beta }\upsilon ,$$

(5)

where $f_r,f_{\mu },f_{\upsilon },f_{\eta }$ are all real functions, and $f_{\alpha }=f_r+\mu f_{\mu }$, $f_{\beta }=f_{\upsilon }+\mu f_{\eta }$.

The inner product of the f and g, belonging to the space $L^2(\mathbb{R}$, $\mathbb{H})$, is defined as follows:

$${\langle f,g\rangle }_{L^2(\mathbb{R},\mathbb{H})}={\int }_{\mathbb{R}}f\left(x\right)\overline{g\left(x\right)}dx.$$

The norm of $f\in L^2(\mathbb{R},\mathbb{H})$ is defined as:

$$\begin{array}{cc}\hfill {\parallel f\parallel }_{L^2(\mathbb{R},\mathbb{H})}^2& ={\langle f,f\rangle }_{L^2(\mathbb{R},\mathbb{H})}={\int }_{\mathbb{R}}{\left|f\right|}^{2}dx<\infty .\hfill \end{array}$$

(6)

The convolution operator ∗ and the correlation operator ⊙ for $f,g\in L^1(\mathbb{R},\mathbb{H})$ are defined according to [27]:

$$(f\ast g)\left(x\right)={\int }_{\mathbb{R}}f\left(t\right)g(x-t)\mathrm{d}t,$$

(7)

and

$$(f\odot g)\left(x\right)={\int }_{\mathbb{R}}f\left(t\right)g(t+x)\mathrm{d}t,$$

(8)

respectively.

2.2. Linear Canonical Integral Transform

We will review several integral transformations pertaining to LCT [1,2] and the QLCT [31,32].

Definition 1.

(Linear canonical transform) For $f\in L^2\left(\mathbb{R}\right)$, and $A=(a,b,c,d)$, Det $A=1$, then, the linear canonical transform (LCT) of f is defined as:

$$\left(L^{A}f\right)\left(u\right)=\left\{\begin{array}{cc}{\int }_{\mathbb{R}}f\left(x\right)K_A^i(u,x)\mathrm{d}x,\hfill & b\ne 0,\hfill \\ \sqrt{d}f\left(du\right)e^{i\frac{cd}{2}{u}^2},\hfill & b=0.\hfill \end{array}\right.$$

(9)

where the kernel is as follows:

$$K_A^i(u,x)=\sqrt{\frac{1}{i2\pi b}}{e}^{i\frac{d}{2b}{u}^2-i\frac{u}{b}x+i\frac{a}{2b}{x}^2},$$

(10)

when $A=(cos\alpha ,sin\alpha ,-sin\alpha ,cos\alpha )$, the LCT is equivalent to the fractional Fourier transform (FRFT) [37,38]. Additionally, when $A=(0,1,-1,0)$, the LCT is equivalent to the Fourier transform (FT).

The inverse formula with $A^{-1}=(d,-b,-c,a)$ is expressed as follows:

$$f\left(x\right)=\left\{\begin{array}{cc}{\int }_{\mathbb{R}}{\mathcal{L}}^A\left(u\right)K_{A^{-1}}^i(x,u)\mathrm{d}u,\hfill & b\ne 0,\hfill \\ \sqrt{a}f\left(ax\right)e^{-i\frac{ac}{2}{x}^2},\hfill & b=0.\hfill \end{array}\right.$$

(11)

Definition 2.

The linear canonical cosine transform (LCcT) and the linear canonical sine transform (LCsT) of $f\in L^2\left(\mathbb{R}\right)$ are given by:

$$\left(L_c^{A}f\right)\left(u\right)={\int }_{\mathbb{R}}f\left(x\right)K_{c,A}^i(x,u)\mathrm{d}x,$$

(12)

and

$$\left(L_s^{A}f\right)\left(u\right)={\int }_{\mathbb{R}}f\left(x\right)K_{s,A}^i(x,u)\mathrm{d}x,$$

(13)

respectively. The kernels $K_{c,A}^i(u,x)$ of LCcT and $K_{s,A}^i(u,x)$ of LCsT are defined as follows:

$$K_{c,A}^i(x,u)=\sqrt{\frac{1}{i2\pi b}}{e}^{i\frac{d}{2b}{u}^2+i\frac{a}{2b}{x}^2}(cos\frac{u}{b}x),$$

and

$$K_{s,A}^i(x,u)=\sqrt{\frac{1}{i2\pi b}}{e}^{i\frac{d}{2b}{u}^2+i\frac{a}{2b}{x}^2}(-isin\frac{u}{b}x),$$

when $A=(0,1,-1,0)$, the LCcT corresponds to the Fourier cosine transform (FCT) while the LCsT corresponds to the Fourier sine transform (FST), respectively. When $A=(cos\alpha ,sin\alpha ,-sin\alpha ,cos\alpha )$, the LCcT corresponds to the fractional cosine transform (FRCT) while the LCsT reduces to the fractional sine transform (FRST), respectively.

Definition 3.

(Quaternion linear canonical transform) For $f\in L^2(\mathbb{R},\mathbb{H})$, the right-side QLCT is defined as follows:

$$\left({\mathcal{QL}}_A^{\mu }f\right)\left(u\right)=\left\{\begin{array}{cc}{\int }_{\mathbb{R}}f\left(x\right)K_A^{\mu }(u,x)\mathrm{d}x,\hfill & b\ne 0,\hfill \\ \sqrt{d}f\left(du\right)e^{\mu \frac{cd}{2}{u}^2},\hfill & b=0,\hfill \end{array}\right.$$

(14)

the kernel of QLCT is as follows:

$$K_A^{\mu }(u,x)=\sqrt{\frac{1}{\mu 2\pi b}}{e}^{\mu \frac{d}{2b}{u}^2-\mu \frac{u}{b}x+\mu \frac{a}{2b}{x}^2},$$

(15)

where $\mu \in \mathbb{U}$. To obtain the left-side variant of QLCT, shift the kernel $K_A^{\mu }(u,x)$ to the left side of f in Equation (14). When parameter $A=(cos\alpha ,sin\alpha ,-sin\alpha ,cos\alpha )$ is used, the QLCT can be simplified to a quaternion fractional Fourier transform (QFRFT). Similarly, when $A=(0,1,-1,0)$ is chosen as a parameter value for QLCT in Equation (14), it simplifies to a quaternion Fourier transform (QFT).

The inverse for QLCT is given as,

$$f\left(x\right)=\left\{\begin{array}{cc}{\int }_{\mathbb{R}}{\mathcal{QL}}_A^{\mu }\left(u\right)K_{A^{-1}}^{\mu }(x,u)\mathrm{d}u,\hfill & b\ne 0,\hfill \\ \sqrt{a}f\left(ax\right)e^{-\mu \frac{ac}{2}{x}^2},\hfill & b=0.\hfill \end{array}\right.$$

(16)

3. Quaternion Linear Canonical Cosine and Sine Transform

In this section, the QLCcT and the QLCsT are introduced. Subsequently, a comprehensive investigation is conducted to explore the fundamental properties of the QLCcT and the QLCsT in depth. Additionally, precise definitions for the convolution and correlation operations of both the QLCcT and the QLCsT are provided, accompanied by the derivation of their respective convolution and correlation theorems.

3.1. Definition of QLCcT and QLCsT

In this subsection, QLCcT and QLCsT are proposed, along with the relationship between these two transforms and the quaternion Fourier cosine transform (QFcT) as well as the quaternion Fourier sine transform (QFsT).

Definition 4.

The definition of the right side of QLCcT and QLCsT for $f\in L^2(\mathbb{R},\mathbb{H})$ is as follows:

$${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)=\left\{\begin{array}{cc}{\int }_{\mathbb{R}}f\left(x\right)K_{c,A}^{\mu }(u,x)\mathrm{d}x,\hfill & b\ne 0,\hfill \\ \sqrt{d}f\left(du\right)e^{\mu \frac{cd}{2}{u}^2},\hfill & b=0,\hfill \end{array}\right.$$

(17)

and

$${\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)=\left\{\begin{array}{cc}{\int }_{\mathbb{R}}f\left(x\right)K_{s,A}^{\mu }(u,x)\mathrm{d}x,\hfill & b\ne 0,\hfill \\ \sqrt{d}f\left(du\right)e^{\mu \frac{cd}{2}{u}^2},\hfill & b=0,\hfill \end{array}\right.$$

(18)

kernels $K_{c,A}^{\mu }(u,x)$ of QLcCT and $K_{s,A}^{\mu }(x,u)$ of QLcST are defined as follows:

$$K_{c,A}^{\mu }(u,x)=\sqrt{\frac{1}{2\mu \pi b}}(cos\frac{u}{b}x)e^{\mu \frac{d}{2b}{u}^2+\mu \frac{a}{2b}{x}^2}$$

and

$$K_{s,A}^{\mu }(x,u)=\sqrt{\frac{1}{2\mu \pi b}}(-\mu sin\frac{u}{b}x)e^{\mu \frac{d}{2b}{u}^2+\mu \frac{a}{2b}{x}^2},$$

respectively. Where $A=(a,b,c,d)$, such that $a,b,c,d\in \mathbb{R}$ and Det $A=1$. The right side of QLCcT and QLCsT for the quaternion function f are denoted as ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$ and ${\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$, respectively. The left side of QLCcT and QLCsT are denoted as ${\mathcal{QL}}_{l,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$ and ${\mathcal{QL}}_{l,s,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$, which are defined by shifting the kernels $K_{c,A}^{\mu }(x,u)$ in Equation (17) and $K_{s,A}^{\mu }(x,u)$ in Equation (18) to the left side of $f\left(x\right)$.

Remark 1.

(1) When $A=(\cos \alpha ,\sin \alpha ,-\sin \alpha ,\cos \alpha )$, the QLCcT and QLCsT can be simplified to the new transforms called the fractional quaternion cosine transform (QFRcT) and the fractional quaternion sine transform (QFRsT),

$$\left({\mathcal{QF}}_{c,\alpha }^{\mathbb{H},\mu }f\right)\left(u\right)={\int }_{\mathbb{R}}f\left(x\right)K_{c,\alpha }^{\mu }(u,x)\mathrm{d}x,$$

(19)

and

$$\left({\mathcal{QF}}_{s,\alpha }^{\mathbb{H},\mu }f\right)\left(u\right)={\int }_{\mathbb{R}}f\left(x\right)K_{s,\alpha }^{\mu }(u,x)\mathrm{d}x,$$

(20)

respectively. Where $K_{c,\alpha }^{\mu }(x,u)$ and $K_{s,\alpha }^{\mu }(x,u)$ are defined as follows:

$$\begin{array}{c}{K}_{c,\alpha }^{\mu }(u,x)=\sqrt{\frac{1-\mu cot\varphi }{2\pi }}{e}^{\mu \frac{x^2+u^2}{2}cot\varphi }cos(xucsc\varphi ),\hfill \\ K_{s,\alpha }^{\mu }(u,x)=\sqrt{\frac{1-\mu cot\varphi }{2\pi }}{e}^{\mu \frac{x^2+u^2}{2}cot\varphi }{e}^{\varphi -\frac{\pi }{2}}sin(xucsc\varphi ).\hfill \end{array}$$

(21)

(2) If $A=(0,1,-1,0)$, then, the QLCcT and QLCsT can be simplified to the novel transform called the Fourier quaternion cosine transform (QFcT) and the Fourier quaternion sine transform (QFsT)

$$\left({\mathcal{QF}}_c^{\mathbb{H},\mu }f\right)\left(u\right)={\int }_{\mathbb{R}}f\left(x\right)cos\left(ux\right)\mathrm{d}x,$$

(22)

and

$$\left({\mathcal{QF}}_s^{\mathbb{H},\mu }f\right)\left(u\right)={\int }_{\mathbb{R}}f\left(x\right)sin\left(ux\right)\mathrm{d}x.$$

(23)

respectively.

In the following, we will investigate the relationship between QLCcT, QLCsT, QFcT, and QFsT.

Theorem 1.

Let $f\in L^2\left(\mathbb{R}\right)$ be any quaternion function; the relationship between the right side and left side of QLCcT is as follows:

$${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)=\overline{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},-\mu }\left\{f\right\}\left(u\right)}.$$

(24)

Proof. 

Applying the conjugate properties of a quaternion f, we have

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)& ={\int }_{\mathbb{R}}f\left(\tau \right)K_{c,A}^{\mu }(u,x)\mathrm{d}\tau ={\int }_{\mathbb{R}}\overline{K_{c,A}^{-\mu }(u,\tau )\overline{f\left(\tau \right)}\mathrm{d}\tau }\hfill \\ \hfill & =\overline{{\mathcal{QL}}_{l,c,A}^{\mathbb{H},-\mu }\left\{\overline{f}\right\}\left(u\right)}.\hfill \end{array}$$

(25)

Similar to Theorem 1, the similar results for QLCsT can be obtained as follows:

$$\begin{array}{c}\hfill {\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)=\overline{{\mathcal{QL}}_{l,s,A}^{\mathbb{H},-\mu }\left\{\overline{f}\right\}\left(u\right)}.\end{array}$$

(26)

□

Theorem 2.

The right-side QLCcT of $f\in L^2\left(\mathbb{R}\right)$ can be seen as the right-side QFcT given by Equation (22) as follows:

$${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)=\sqrt{\frac{1}{2\mu \pi b}}{e}^{\mu \frac{d}{2b}{u}^2}{\mathcal{QF}}_{r,c}^{\mathbb{H},\mu }\left\{f\left(x\right)e^{\mu \frac{a}{2b}{x}^2}\right\}\left(\frac{u}{b}\right).$$

(27)

Proof. 

From the definition of right-side QLCcT, we have

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)& =\sqrt{\frac{1}{2\mu \pi b}}{e}^{\mu \frac{d}{2b}{u}^2}{\int }_{\mathbb{R}}f\left(x\right)cos\left(\frac{u}{b}x\right)e^{\mu \frac{a}{2b}{x}^2}\mathrm{d}x\hfill \\ \hfill & =\sqrt{\frac{1}{2\mu \pi b}}{e}^{\mu \frac{d}{2b}{u}^2}{\mathcal{QF}}_{r,c}^{\mathbb{H},\mu }\left\{f\left(x\right)e^{\mu \frac{a}{2b}{x}^2}\right\}\left(\frac{u}{b}\right).\hfill \end{array}$$

(28)

□

Remark 2.

Similar to Theorem 2, we can obtain the relationship between the right-side QLCsT and the right-side QFsT as follows:

$${\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)=\sqrt{\frac{1}{2\mu \pi b}}{e}^{\mu \frac{d}{2b}{u}^2}{\mathcal{QF}}_{r,s}^{\mathbb{H},\mu }\left\{f\left(x\right)e^{\mu \frac{a}{2b}{x}^2}\right\}\left(\frac{u}{b}\right).$$

(29)

From the above discussion, by combining Equations (27) and (29), we can calculate the right-side QLCcT and QLCsT using the corresponding right-side QFcT and QFsT, respectively (see Figure 1 and Figure 2).

3.2. Properties for QLCcT

In the following subsection, the inverse and Plancherel theorem for the right-side QLCcT will be investigated. Other properties are shown in

Table 1. Some properties of the right-side QLCcT.

Order	Function	The Right-Side QLCcT
1	$ϵf\left(x\right)+\gamma f\left(x\right)$	$ϵ\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)\left(u\right)+\gamma \left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)\left(u\right),ϵ,\gamma$ are constants.
2	$f(x-k)$	$\left(\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)(u+ak)-\left({\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }f\right)(u+ak)\right)\frac{1}{2}{e}^{\mu \frac{1-ad}{2b}(a{k}^2+2uk)}$
		+$\left(\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)(u-ak)+\left({\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }f\right)(u-ak)\right)\frac{1}{2}{e}^{\mu \frac{1-ad}{2b}(a{k}^2-2uk)}.$
3	$f\left(\frac{x}{\lambda }\right)$	$\lambda \left({\mathcal{QL}}_{r,c,\tilde{A}}^{\mathbb{H},\mu }f\right)\left(u\lambda \right)$, where $\tilde{A}=(a{\lambda }^2,b,c,\frac{d}{{\lambda }^2})$.
4	$e^{\mu \lambda x}f\left(x\right)$	$\left(\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)(u+b\lambda )-\left({\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }f\right)(u+b\lambda )\right)\frac{1}{2}{e}^{-\mu \frac{2u\lambda +b{\lambda }^2}{2}}$
		+$\left(\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)(u-b\lambda )+\left({\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }f\right)(u-b\lambda )\right)\frac{1}{2}{e}^{\mu \frac{2u\lambda -b{\lambda }^2}{2}}.$
5	$cos\left(\lambda ux\right)f\left(x\right)$	$\frac{1}{2}{e}^{-\mu \frac{d\lambda }{2}(b\lambda +2)u^2}\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)(b\lambda +1)u$
		$-\frac{1}{2}{e}^{-\mu \frac{d\lambda }{2}(b\lambda -2)u^2}\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)(b\lambda -1)u.$
6	$sin\left(\lambda ux\right)f\left(x\right)$	$-\frac{1}{2}\mu e^{-\mu \frac{d\lambda }{2}(b\lambda +2)u^2}\left({\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }f\right)(b\lambda +1)u$
		$-\frac{1}{2}\mu e^{-\mu \frac{d\lambda }{2}(b\lambda -2)u^2}\left({\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }f\right)(b\lambda -1)u.$
7	$\frac{df\left(x\right)}{dx}$	$-\mu \frac{a}{b}\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }xf\right)\left(u\right)-\mu \frac{u}{b}\left({\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }f\right)\left(u\right).$
8	$f\left(x\right)$	$\frac{d}{dx}\left(\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)\left(u\right)\right)=-\mu \frac{d}{b}u\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }f\right)\left(u\right)-\mu \frac{1}{b}\left({\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }xf\right)\left(u\right).$

.

Theorem 3.

(Inversion theorem) The inverse of the right-side QLCcT of $f\in L^2(\mathbb{R},\mathbb{H})$ is provided

$$f\left(x\right)={\int }_{\mathbb{R}}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)K_{c,A^{-1}}^{\mu }(u,x)\mathrm{d}u.$$

(30)

Proof. 

Applying the right-side QLCcT of $\delta \left(\mathbf{x}\right)$, we have

$$\begin{array}{c}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{\delta (x-\tau )\right\}\left(u\right)=\sqrt{\frac{2}{\mu \pi b}}(cos\frac{u}{b}\tau )e^{\mu \frac{d}{2b}{u}^2+\mu \frac{a}{2b}{\tau }^2}.\end{array}$$

(31)

From the definition of the right-side QLCcT with the parameter $A^{-1}=(d,-b,-c,a)$, we have

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\left\{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)\right\}\left(x\right)& ={\int }_{(\mathbb{R}}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\})\left(u\right)K_{c,A^{-1}}^{\mu }(u,x)\mathrm{d}u\hfill \\ \hfill & ={\int }_{\mathbb{R}}f\left(t\right)\left({\int }_{\mathbb{R}}{K}_{c,A^{-1}}^{\mu }(u,x)K_{c,A}^{\mu }(t,u)du\right)\mathrm{d}t\hfill \\ \hfill & =f\left(x\right),\hfill \end{array}$$

(32)

the proof is thereby concluded. □

Remark 3.

Similar to Theorem 3, we can obtain the inverse of the right-side QLCsT for $f\in L^2(\mathbb{R},\mathbb{H})$ as follows:

$$f\left(x\right)={\int }_{\mathbb{R}}{\mathcal{QL}}_{r,s,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)K_{s,A^{-1}}^{\mu }(x,u)\mathrm{d}u.$$

(33)

Theorem 4.

(Plancherel theorem) Let ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$ and ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right)$ be the right-side QLCcT for $f,h\in L^2({\mathbb{R}}^2,\mathbb{H})$, respectively. Then, we obtain

$${\langle f,h\rangle }_{L^2(\mathbb{R},\mathbb{H})}=\langle {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right),{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right)\rangle }_{L^2(\mathbb{R},\mathbb{H})}.$$

(34)

Proof. 

From Equation (4), Equation (17), it follows that

$$\begin{array}{cc}\hfill {\langle f,h\rangle }_{L^2(\mathbb{R},\mathbb{H})}& ={\int }_{\mathbb{R}}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)\left[{\int }_{\mathbb{R}}{K}_{c,A^{-1}}^{\mu }(u,x)\overline{h\left(x\right)}dx\right]\mathrm{d}u\hfill \\ \hfill & ={\int }_{\mathbb{R}}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)\overline{\left[{\int }_{\mathbb{R}}h\left(x\right)K_{c,A}^{\mu }(u,x)dx\right]}\mathrm{d}u\hfill \\ \hfill & ={\int }_{\mathbb{R}}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)\overline{\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\right)\left(u\right)}\mathrm{d}u\hfill \\ \hfill & =\langle {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right),{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right)\rangle ,\hfill \end{array}$$

(35)

which completes the proof. □

4. Convolution and Correlation for QLCcT

Quaternion convolution is an operation based on the definition of quaternions, which are used to describe the interaction between quaternion signals. By utilizing quaternion convolution operations, signal filtering and feature extraction can be achieved, which is highly significant for processing multi-dimensional and rotating signals. Quaternion correlation operations are employed to depict the similarity and correlation between quaternion signals. Through these operations, signal matching and similarity comparison can be performed, providing essential tools and methods for signal processing and analysis. Quaternion convolution and correlation operations find wide applications in image processing, video processing, attitude estimation, and other fields as they assist in effectively handling complex signals, extracting valuable information, and accomplishing various signal processing tasks. Therefore, understanding and applying quaternion convolution and correlation operations play a crucial role in enhancing the performance and efficiency of signal processing algorithms.

4.1. Convolution for QLCcT

In this subsection, we introduce the quaternion weighted convolution for the right-side QLCcT, and establish its corresponding convolution theorem. For the purpose of discussion, we confine the right-side QLCcT to a half-interval.

Definition 5.

The weighted convolution operator ${\stackrel{A}{\otimes }}_{c,\gamma }$ of $f,h$ in $L^2$$(\mathbb{R},\mathbb{H}(\mu \left)\right)$ for the right-side QLCcT is defined as follows:

$$\begin{array}{cc}\hfill \left(f{\stackrel{A}{\otimes }}_{c,\gamma }h\right)\left(x\right)=\sqrt{\frac{1}{8\mu \pi b}}{e}^{-\mu \frac{a}{2b}{x}^2}{\int }_{{\mathbb{R}}_{+}}\tilde{f}\left(\tau \right)& \left[\tilde{h}(x+\tau +b)+\tilde{h}\left(\right|x-\tau -b\left|\right)\right.\hfill \\ \hfill +& \left.\tilde{h}\left(\right|x+\tau -b\left|\right)+\tilde{h}\left(\right|x-\tau +b\left|\right)\right]\mathrm{d}\tau ,\hfill \end{array}$$

(36)

where $\tilde{f}\left(x\right)=e^{\mu \frac{a}{2b}{x}^2}f\left(x\right),\tilde{h}\left(x\right)=e^{\mu \frac{a}{2b}{x}^2}h\left(x\right)$, $\gamma =e^{-u}cosu$. When $A=(0,1,-1,0)$, and $\mu =i$ (i denotes an imaginary unit), $\gamma =1$. Then, the weighted convolution ${\stackrel{A}{\otimes }}_{c,\gamma }$ can be simplified to the convolution for FCT [38].

Definition 6.

Let $f=f_{\alpha }+f_{\beta }\upsilon ,h=h_{\alpha }+h_{\beta }\upsilon$, $f_{\alpha },f_{\beta },h_{\alpha },h_{\beta }\in \mathbb{H}\left(\mu \right)$; the weighted convolution operator ${\stackrel{A}{\mathsf{\Theta }}}_{c,\gamma }$ of $f,h$∈$L^2$$(\mathbb{R},\mathbb{H})$ for the right-side QLCcT is defined as

$$\begin{array}{cc}\hfill \left(f{\stackrel{A}{\mathsf{\Theta }}}_{c,\gamma }h\right)\left(x\right)=& f_{\alpha }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }{h}_{\alpha }\left(x\right)+f_{\alpha }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }{h}_{\beta }\left(x\right)\upsilon \hfill \\ \hfill & +f_{\beta }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }\overline{h_{\alpha }\left(x\right)}\upsilon -f_{\beta }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }\overline{h_{\beta }\left(x\right)},\hfill \end{array}$$

(37)

where the weighted convolution operator ${\stackrel{A}{\otimes }}_{c,\gamma }$ is defined in Definition 5.

Definition 7.

Let $f\left(x\right)=f_{\alpha }+f_{\beta }\upsilon ,h=h_{\alpha }+h_{\beta }\upsilon$, $f_{\alpha },f_{\beta },h_{\alpha },h_{\beta }\in \mathbb{H}\left(\mu \right)$; the convolution operator ${\stackrel{A}{⊚}}_{c,\gamma }$ of $f,h$∈$L^2$$(\mathbb{R},\mathbb{H})$ for the right-side QLCcT is defined as

$$\begin{array}{cc}\hfill \left(f{\stackrel{A}{⊚}}_{c,\gamma }h\right)\left(x\right)=& \left({\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }\overline{f_{\alpha }\left(x\right)}{\stackrel{A}{\otimes }}_{c,\gamma }{h}_{\alpha }\left(x\right)+{\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }{\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }\overline{h_{\beta }\left(x\right)}\right)\hfill \\ \hfill & +\left({\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }\overline{f_{\alpha }\left(x\right)}{\stackrel{A}{\otimes }}_{c,\gamma }{h}_{\beta }\left(x\right)-{\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }{\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }\overline{h_{\alpha }\left(x\right)}\right)\upsilon ,\hfill \end{array}$$

(38)

where the weighted convolution operator ${\stackrel{A}{\otimes }}_{c,\gamma }$ is defined in Definition 5.

The subsequent step entails deriving the convolution theorem for the right-side QLCcT.

Theorem 5.

Let ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$ and ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right)$ be the right-side QLCcT of f and h∈$L^2$$(\mathbb{R},\mathbb{H}(\mu \left)\right)$, respectively. Then, we have

$$\begin{array}{cc}\hfill & {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f{\stackrel{A}{\otimes }}_{c,\gamma }h\right\}\left(u\right)=cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right).\hfill \end{array}$$

(39)

Proof. 

Using Equation (16), we obtain

$$\begin{array}{cc}\hfill cos\left(u\right)e^{-\mu \frac{a}{2b}{u}^2}& {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right)\hfill \\ \hfill =& \frac{2}{\mu \pi b}{e}^{\mu \frac{d}{2b}{u}^2}{\int }_{{\mathbb{R}}_{+}}{\int }_{{\mathbb{R}}_{+}}f\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(u\right)cos\left(\frac{u}{b}x\right)cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z,\hfill \end{array}$$

(40)

the utilization of the product and difference formulas of trigonometric functions, we have

$$\begin{array}{cc}\hfill & cos\left(\frac{u}{b}x\right)cos\left(\frac{u}{b}z\right)cos\left(u\right)\hfill \\ \hfill =& \frac{1}{4}\left\{cos\frac{(x+z+b)u}{b}+cos\frac{(x+z-b)u}{b}+cos\frac{(x-z+b)u}{b}+cos\frac{(x-z-b)u}{b}\right\}.\hfill \end{array}$$

(41)

From Equations (40) and (41), we have

$$\begin{array}{cc}\hfill cos\left(u\right)e^{-\mu \frac{a}{2b}{u}^2}& {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\left(x\right)\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\left(x\right)\right\}\left(u\right)\hfill \\ \hfill =& \frac{1}{2\mu \pi b}{e}^{\mu \frac{d}{2b}{u}^2}{\int }_{{\mathbb{R}}_{+}}{\int }_{{\mathbb{R}}_{+}}f\left(x\right)h\left(z\right)\left\{cos\left(\frac{x+z+b}{b}u\right)+cos\left(\frac{x+z-b}{b}u\right)\right.\hfill \\ \hfill & \left.+cos\left(\frac{x-z+b}{b}u\right)+cos\left(\frac{x-z-b}{b}u\right)\right\}{e}^{\mu \frac{a}{2b}(x^2+z^2)}\mathrm{d}x\mathrm{d}z.\hfill \end{array}$$

(42)

From the calculation of integration, we can obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{{\mathbb{R}}_{+}}f\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{x+z+b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}}{\int }_{b+x}^{\infty }f\left(x\right)h(z-x-b)e^{\mu \frac{a}{2b}(x^2+{(z-x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{{\mathbb{R}}_{+}}f\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{x+z-b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}}{\int }_{b-x}^{\infty }f\left(x\right)h(z-x+b)e^{\mu \frac{a}{2b}(x^2+{(z-x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{{\mathbb{R}}_{+}}f\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{x-z+b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}}{\int }_{-b-x}^{\infty }f\left(x\right)h(z+x+b)e^{\mu \frac{a}{2b}(x^2+{(z+x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z,\hfill \end{array}$$

(45)

and

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{{\mathbb{R}}_{+}}f\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{x-z-b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}}{\int }_{-b+x}^{\infty }f\left(x\right)h(z+x-b)e^{\mu \frac{a}{2b}(x^2+{(z+x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z.\hfill \end{array}$$

(46)

From Equations (43) and (45), we can obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}{\int }_{b+x}^{\infty }& f\left(x\right)h(h-x-b)e^{\mu \frac{a}{2b}(x^2+{(h-x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & +{\int }_{{\mathbb{R}}_{+}}{\int }_{-b-x}^{\infty }f\left(x\right)h(z+x+b)e^{\mu \frac{a}{2b}(x^2+{(z+x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}}{\int }_{b+x}^{\infty }f\left(x\right)h(z-x-b)e^{\mu \frac{a}{2b}(x^2+{(z-x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & +{\int }_{{\mathbb{R}}_{+}}{\int }_{{\mathbb{R}}_{+}}f\left(x\right)h(z+x+b)e^{\mu \frac{a}{2b}(x^2+{(z+x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & +{\int }_{{\mathbb{R}}_{+}}{\int }_0^{b+x}f\left(x\right)h(-z+x+b)e^{\mu \frac{a}{2b}(x^2+{(-z+x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}^2}\tilde{f}\left(x\right)\left(\tilde{h}(z+x+b)+\tilde{g}\left(\right|y-x-b\left|\right)\right)cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z.\hfill \end{array}$$

(47)

Similarly, from Equations (44) and (46), we can obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{-b-x}^{\infty }f\left(x\right)h(z+x+b)e^{\mu \frac{a}{2b}(x^2+{(z+x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & +{\int }_{{\mathbb{R}}_{+}}{\int }_{-b+x}^{\infty }f\left(x\right)h(z+x-b)e^{\mu \frac{a}{2b}(x^2+{(z+x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}^2}\tilde{f}\left(x\right)\left(\tilde{h}\left(\right|z+x-b\left|\right)+\tilde{h}\left(\right|z-x+b\left|\right)\right)cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z.\hfill \end{array}$$

(48)

Combined with Equations (40), (47) and (48), we can obtain

$$\begin{array}{cc}\hfill & cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\left(x\right)\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\left(x\right)\right\}\left(u\right)\hfill \\ \hfill =& \frac{1}{2\mu \pi b}{e}^{\mu \frac{d}{2b}{u}^2}{\int }_{{\mathbb{R}}_{+}^2}\tilde{f}\left(x\right)\left\{\tilde{h}(z+x+b)+\tilde{h}\left(\right|z-x-b\left|\right)\right.\hfill \\ \hfill & +\left.\tilde{h}(z+x-b)+\tilde{h}\left(\right|z-x+b\left|\right)\right)\mathrm{d}x\mathrm{d}z.\hfill \end{array}$$

(49)

From Definition 4 and Equation (49), we obtain

$$\begin{array}{cc}\hfill cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}& {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\left(x\right)\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\left(x\right)\right\}\left(u\right)\hfill \\ \hfill =& \sqrt{\frac{2}{\mu \pi b}}{\int }_{{\mathbb{R}}_{+}}\left(f\left(y\right){\stackrel{A}{\otimes }}_{c,\gamma }h\left(z\right)\right)e^{\mu (\frac{d}{2b}{u}^2+\frac{a}{2b}{z}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}z\hfill \\ \hfill =& {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }h\left(x\right)\right\}\left(u\right),\hfill \end{array}$$

(50)

the proof is thereby concluded. □

Theorem 6.

Let $f=f_{\alpha }+f_{\beta }\upsilon ,h=h_{\alpha }+h_{\beta }\upsilon$, $f_{\alpha },f_{\beta },h_{\alpha },h_{\beta }\in \mathbb{H}\left(\mu \right)$, ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$ and ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right)$ are the right-side QLCcT of f and h∈$L^2$$(\mathbb{R},\mathbb{H})$, respectively. Then, we have

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }& \left\{f{\stackrel{A}{\mathsf{\Theta }}}_{c,\gamma }h\right\}\left(u\right)\hfill \\ \hfill =& cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}\left\{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f_{\alpha }\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h_{\alpha }\right\}\left(u\right)\right.\hfill \\ \hfill & -\left.{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f_{\beta }\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{\overline{h_{\beta }}\right\}\left(u\right)\right\}\hfill \\ \hfill & +cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}\left\{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f_{\alpha }\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h_{\beta }\right\}\left(u\right)\right.\hfill \\ \hfill & +\left.{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f_{\beta }\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{\overline{h_{\alpha }}\right\}\left(u\right)\right\}\upsilon .\hfill \end{array}$$

(51)

Proof. 

By substituting $f=f_{\alpha }+f_{\beta }\upsilon ,h=h_{\alpha }+h_{\beta }\upsilon$ into the weighted convolution operation ${\stackrel{A}{\otimes }}_{c,\gamma }$ in Definition 5, we obtain

$$\begin{array}{cc}\hfill \left(f{\stackrel{A}{\mathsf{\Theta }}}_{c,\gamma }h\right)\left(x\right)=& f_{\alpha }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }{h}_{\alpha }\left(x\right)+f_{\alpha }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }{h}_{\beta }\left(x\right)\upsilon \hfill \\ \hfill & +f_{\beta }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }\overline{h_{\alpha }\left(x\right)}\upsilon -f_{\beta }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }\overline{h_{\beta }\left(x\right)}.\hfill \end{array}$$

(52)

By using Theorem 5 and the linear properties of the right-side QLCcT, we can derive Theorem 6, and the proof is complete. □

Theorem 7.

Let $f=f_{\alpha }+f_{\beta }\upsilon ,h=h_{\alpha }+h_{\beta }\upsilon$, $f_{\alpha },f_{\beta },h_{\alpha },h_{\beta }\in \mathbb{H}\left(\mu \right)$, ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$ and ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right)$ of $f,h$∈$L^2$$(\mathbb{R},\mathbb{H})$ are the right-side QLCcT of f and h, respectively. Then, we have

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }& \left\{f{\stackrel{A}{⊚}}_{c,\gamma }h\right\}\left(u\right)=cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{\overline{f\left(x\right)}\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\left(x\right)\right\}\left(u\right).\hfill \end{array}$$

(53)

Proof. 

From Definition 7 in Equation (38), we have

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }& \left\{f\left(x\right){\stackrel{A}{⊚}}_{c,\gamma }h\left(x\right)\right\}\left(u\right)\hfill \\ \hfill =& {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left({\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }\overline{f_{\alpha }\left(x\right)}{\stackrel{A}{\otimes }}_{c,\gamma }{h}_{\alpha }\left(x\right)+{\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }{\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }\overline{h_{\beta }\left(x\right)}\right)\hfill \\ \hfill & +{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left({\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }\overline{f_{\alpha }\left(x\right)}{\stackrel{A}{\otimes }}_{c,\gamma }{h}_{\beta }\left(x\right)-{\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right){\stackrel{A}{\otimes }}_{c,\gamma }{\mathcal{QL}}_{r,c,A^{-2}}^{\mathbb{H},\mu }\overline{h_{\alpha }\left(x\right)}\right)\upsilon \hfill \\ \hfill =& cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}\left({\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\overline{f_{\alpha }\left(x\right)}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }{h}_{\alpha }\left(x\right)+{\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right){\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\overline{h_{\beta }\left(x\right)}\right)\hfill \\ \hfill & +cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}\left({\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\overline{f_{\alpha }\left(x\right)}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }{h}_{\beta }\left(x\right)-{\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right){\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\overline{h_{\alpha }\left(x\right)}\right)\upsilon \hfill \\ \hfill =& cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}\left(\overline{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }{f}_{\alpha }\left(x\right)}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }{h}_{\alpha }\left(x\right)+{\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right)\overline{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }{h}_{\beta }\left(x\right)}\right)\hfill \\ \hfill & +cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}\left(\overline{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }{f}_{\alpha }\left(x\right)}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }{h}_{\beta }\left(x\right)-{\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right)\overline{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }{h}_{\alpha }\left(x\right)}\right)\upsilon .\hfill \end{array}$$

(54)

Using the conjugate property of the QLCcT:

$$\overline{{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }(f_{\alpha }\left(x\right)+f_{\beta }\left(x\right))\upsilon }={\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\overline{f_{\alpha }\left(x\right)}-{\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }{f}_{\beta }\left(x\right)\upsilon ,$$

(55)

combined with Equations (52) and (53), we can achieve Equation (51), which completes the proof. □

4.2. Correlation for QLCcT

The present subsection introduces a correlation for the QLCcT and explores the associated correlation theorem.

Definition 8.

Let $f,h$∈$L^2$$(\mathbb{R},\mathbb{H}(\mu \left)\right)$; the correlation ${\stackrel{A}{\oplus }}_{c,\gamma }$ for the QLCcT is defined as

$$\begin{array}{cc}\hfill \left(f{\stackrel{A}{\oplus }}_{c,\gamma }h\right)\left(x\right)=\sqrt{\frac{1}{8\mu \pi b}}{e}^{-\mu \frac{a}{2b}{x}^2}{\int }_{{\mathbb{R}}_{+}}\widetilde{\overline{f}\left(\tau \right)}& \left[\tilde{h}(x+\tau +b)+\tilde{h}\left(\right|x-\tau -b\left|\right)\right.\hfill \\ \hfill +& \left.\tilde{h}\left(\right|x+\tau -b\left|\right)+\tilde{h}\left(\right|x-\tau +b\left|\right)\right]\mathrm{d}\tau ,\hfill \end{array}$$

(56)

where $\overline{f}\left(x\right)$ is a conjugate of $f\left(x\right)$, $\widetilde{\overline{f}\left(x\right)}=e^{\mu \frac{a}{2b}{x}^2}\overline{f}\left(x\right)$, $\tilde{h}\left(x\right)=e^{\mu \frac{a}{2b}{x}^2}h\left(x\right)$, $\gamma =e^{-u}cosu$.

When $A=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$, and $\mu =i$ (i is an imaginary unit), $\gamma =1$, then the weighted correlation operator ${\stackrel{A}{\oplus }}_{c,\gamma }$ reduces to the classical correlation for FCT.

The correlation theorem for the QLCcT will be derived next.

Theorem 8.

Let $f,h$∈$L^2$$(\mathbb{R},\mathbb{H}(\mu \left)\right)$; ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)$ and ${\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\right\}\left(u\right)$ are the QLCcT of f, h, respectively. The QLCcT of the correlation for f, h is given by

$$\begin{array}{cc}\hfill & {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f{\stackrel{A}{\oplus }}_{c,\gamma }h\right\}\left(u\right)=cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{\overline{f}(-x)\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\left(x\right)\right\}\left(u\right).\hfill \end{array}$$

(57)

Proof. 

Based on Equations (36), (37), and (41), and Equation (56), we can conclude

$$\begin{array}{cc}\hfill cos\left(u\right)e^{-\mu \frac{a}{2b}{x}^2}& {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{\overline{f}(-x)\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\left(x\right)\right\}\left(u\right)\hfill \\ \hfill =& \frac{1}{2\mu \pi b}{e}^{\mu \frac{d}{2b}{u}^2}{\int }_{{\mathbb{R}}_{+}}{\int }_{{\mathbb{R}}_{+}}\overline{f}(-x)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}\left\{cos\left(\frac{x+z+b}{b}u\right)\right.\hfill \\ \hfill & \left.+cos\left(\frac{x+z-b}{b}u\right)+cos\left(\frac{x-z+b}{b}u\right)+cos\left(\frac{x-z-b}{b}u\right)\right\}\mathrm{d}x\mathrm{d}z,\hfill \end{array}$$

(58)

through direct calculation, we can obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{{\mathbb{R}}_{+}}\overline{f}(-x)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{x+z+b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}}{\int }_{{\mathbb{R}}_{+}}\overline{f}\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{z-x+b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}}{\int }_{b-x}^{\infty }\overline{f}\left(x\right)h(z+x-b)e^{\mu \frac{a}{2b}(x^2+{(z+x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z,\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{{\mathbb{R}}_{+}}\overline{f}(-x)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{x-z+b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}}{\int }_{{\mathbb{R}}_{+}}\overline{f}\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{z+x-b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}}{\int }_{-b+x}^{\infty }\overline{f}\left(x\right)h(z-x+b)e^{\mu \frac{a}{2b}(x^2+{(z-x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z,\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{{\mathbb{R}}_{+}}\overline{f}(-x)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{x+z-b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}}{\int }_{{\mathbb{R}}_{+}}\overline{f}\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{z-x-b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}}{\int }_{-b-x}^{\infty }\overline{f}\left(x\right)h(z+x+b)e^{\mu \frac{a}{2b}(x^2+{(z+x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z,\hfill \end{array}$$

(61)

and

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{{\mathbb{R}}_{+}}\overline{f}(-x)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{x-z-b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}}{\int }_{{\mathbb{R}}_{+}}\overline{f}\left(x\right)h\left(z\right)e^{\mu \frac{a}{2b}(x^2+z^2)}cos\left(\frac{z+x+b}{b}u\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}}{\int }_{b+x}^{\infty }\overline{f}\left(x\right)h(z-x-b)e^{\mu \frac{a}{2b}(x^2+{(z-x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z.\hfill \end{array}$$

(62)

From Equations (59) and (60), we can obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{b-x}^{\infty }\overline{f}\left(x\right)h(z+x-b)e^{\mu \frac{a}{2b}(x^2+{(z+x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & +{\int }_{{\mathbb{R}}_{+}}{\int }_{-b+x}^{\infty }\overline{f}\left(x\right)h(z-x+b)e^{\mu \frac{a}{2b}(x^2+{(z-x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}^2}\widetilde{\overline{f}\left(x\right)}\left(\tilde{h}\left(\right|z+x-b\left|\right)+\tilde{h}\left(\right|z-x+b\left|\right)\right)cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z.\hfill \end{array}$$

(63)

Similarly, from Equations (61) and (62), we can obtain

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}_{+}}& {\int }_{-b-x}^{\infty }\overline{f}\left(x\right)h(z+x+b)e^{\mu \frac{a}{2b}(x^2+{(z+x+b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill & +{\int }_{{\mathbb{R}}_{+}}{\int }_{b+x}^{\infty }\overline{f}\left(x\right)h(z-x-b)e^{\mu \frac{a}{2b}(x^2+{(z-x-b)}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& {\int }_{{\mathbb{R}}_{+}^2}\widetilde{\overline{f}\left(x\right)}\left(\tilde{h}(z+x+b)+\tilde{h}\left(\right|z-x-b\left|\right)\right)cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z.\hfill \end{array}$$

(64)

Combined with Equations (58), (63) and (64) and Definition 8, we can obtain

$$\begin{array}{cc}\hfill & cos\left(u\right)e^{-\mu \frac{d}{2b}{u}^2}{\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{\overline{f}(-x)\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{h\left(x\right)\right\}\left(u\right)\hfill \\ \hfill =& \frac{1}{2\mu \pi b}{e}^{\mu \frac{d}{2b}{u}^2}{\int }_{{\mathbb{R}}_{+}^2}\widetilde{\overline{f}\left(x\right)}\left\{\tilde{h}(z+x+b)+\tilde{h}\left(\right|z-x-b\left|\right)\right.\hfill \\ \hfill & +\left.\tilde{g}(z+x-b)+\tilde{h}\left(\right|z-x+b\left|\right)\right)cos\left(\frac{u}{b}z\right)\mathrm{d}x\mathrm{d}z\hfill \\ \hfill =& \sqrt{\frac{2}{\mu \pi b}}{\int }_{{\mathbb{R}}_{+}}\left(f\left(z\right){\stackrel{A}{\oplus }}_{c,\gamma }h\left(z\right)\right)e^{\mu (\frac{d}{2b}{u}^2+\frac{a}{2b}{z}^2)}cos\left(\frac{u}{b}z\right)\mathrm{d}z\hfill \\ \hfill =& {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f{\stackrel{A}{\oplus }}_{c,\gamma }h\right\}\left(u\right),\hfill \end{array}$$

(65)

this completes the proof. □

Remark 4.

(1) If $A=\left(\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right)$, Theorem 8 can be simplified to a version of the correlation theorem for QFRcT.

(2) If $A=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$, Theorem 8 can be simplified to a version of the correlation theorem for QFcT.

5. Example and Application for QLCcT

In this section, the proposed right-side QLCcT will be demonstrated through an illustrative example. Subsequently, the application of QLCcT to investigate multiplicative filters will be discussed.

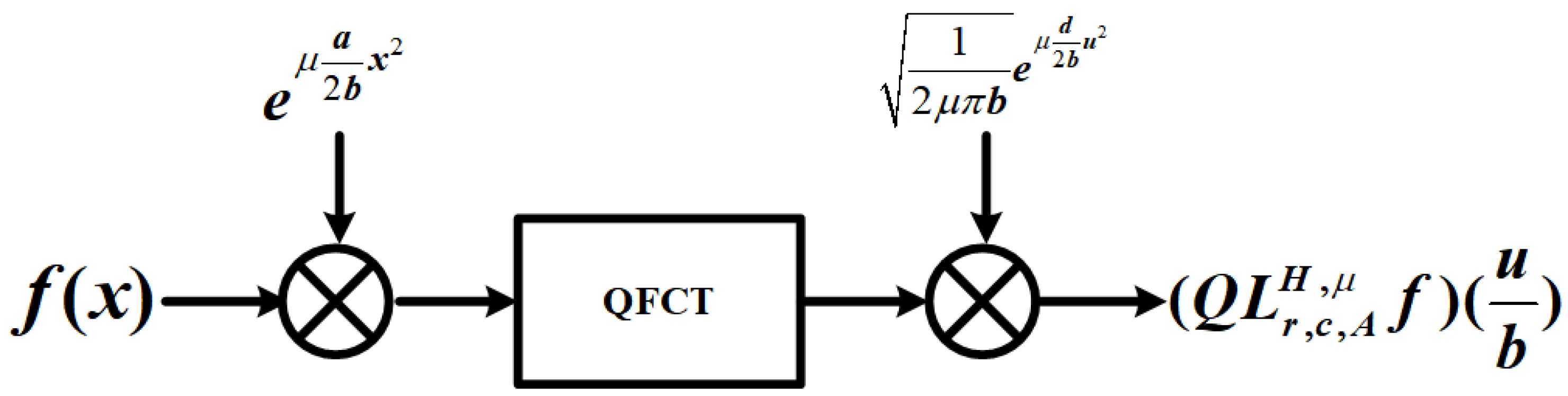
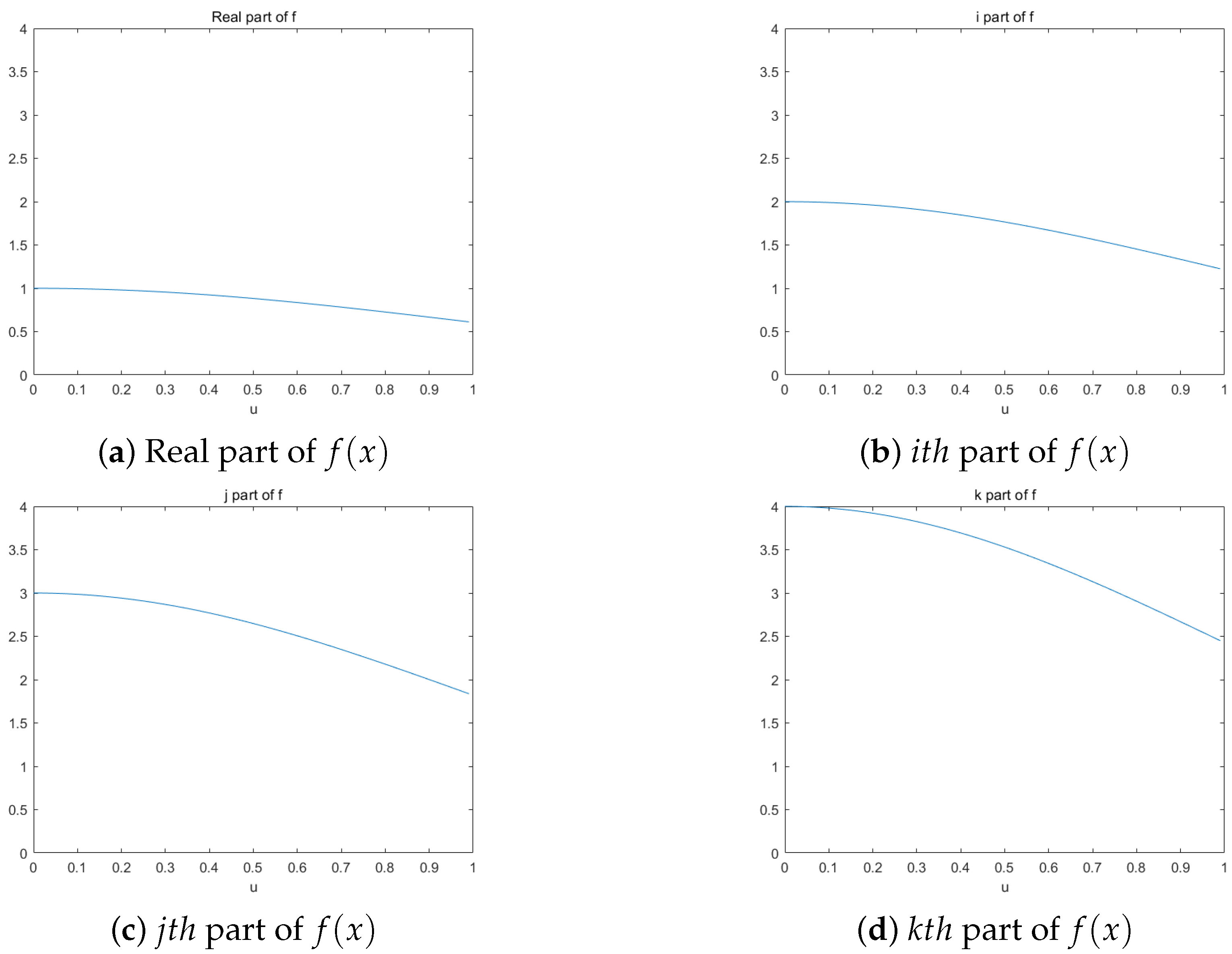
5.1. Example and Simulations for QLCcT

We consider the following quaternion-valued signal:

$$f\left(x\right)=({\sigma }_0+{\sigma }_1\mu +{\sigma }_2\upsilon +{\sigma }_3\eta )e^{-\frac{\lambda }{2}{x}^2},{\sigma }_0,{\sigma }_1,{\sigma }_2,{\sigma }_3\in \mathbb{R},\lambda \in {\mathbb{R}}_{+}.$$

The right-side QLCcT of $f\left(x\right)$ can be calculated as follows:

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\right\}\left(u\right)=& {\int }_{\mathbb{R}}({\sigma }_0+{\sigma }_1\mu +{\sigma }_2\upsilon +{\sigma }_3\eta )e^{-\frac{\lambda }{2}{x}^2}{K}_{c,A}^{\mu }(x,u)\mathrm{d}x\hfill \\ \hfill =& ({\sigma }_0+{\sigma }_1\mu +{\sigma }_2\upsilon +{\sigma }_3\eta )\sqrt{\frac{1}{2\mu \pi b}}{e}^{-\mu \frac{d}{2b}{u}^2}{\int }_{\mathbb{R}}{e}^{-\frac{b\lambda -\mu a}{2b}{x}^2}cos\left(\frac{u}{b}x\right)\mathrm{d}x\hfill \\ \hfill =& \frac{{\sigma }_0+{\sigma }_1\mu +{\sigma }_2\upsilon +{\sigma }_3\eta }{2}\sqrt{\frac{1}{2\mu \pi b}}{e}^{-\mu \frac{d}{2b}{u}^2}{\int }_{\mathbb{R}}{e}^{-x^2\frac{b\lambda -\mu a}{2b}+x\frac{\mu u}{b}}\mathrm{d}x\hfill \\ \hfill & +\frac{{\sigma }_0+{\sigma }_1\mu +{\sigma }_2\upsilon +{\sigma }_3\eta }{2}\sqrt{\frac{1}{2\mu \pi b}}{e}^{-\mu \frac{d}{2b}{u}^2}{\int }_{\mathbb{R}}{e}^{-x^2\frac{b\lambda -\mu a}{2b}-x\frac{\mu u}{b\mathrm{d}}}\mathrm{d}x\hfill \\ \hfill =& ({\sigma }_0+{\sigma }_1\mu +{\sigma }_2\upsilon +{\sigma }_3\eta )\sqrt{\frac{1}{b\lambda -\mu a}}{e}^{-\mu \frac{d}{2b}{u}^2}{e}^{-\frac{a^2}{2b(b\lambda -\mu a)}}.\hfill \end{array}$$

(66)

For the sake of computational convenience, we opt for $A=(1,1,0,1)$, ${\sigma }_0={\sigma }_1={\sigma }_2={\sigma }_3=1$, $\lambda =1$, and employ the imaginary unit $\mu =i$, $\upsilon =j$, and $\eta =k$. $i,j,$ and k represent imaginary units according to Hamilton’s multiplication rules. Hence, from Equation (66), we obtain

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\left(x\right)\right\}\left(u\right)=& \frac{1+i+j+k}{\sqrt{2}}\sqrt{1-i}{e}^{i\frac{u^2}{2}}{e}^{-\frac{1}{2(1-i)}}\hfill \\ \hfill =& \frac{1}{\sqrt{2}}{e}^{-\frac{1}{4}}(1+i+j+k)({\omega }_1-{\omega }_{2}i)(cos\psi +isin\psi ),\hfill \end{array}$$

(67)

where ${\omega }_1=\sqrt{\frac{\sqrt{2}+1}{2}}$, ${\omega }_2=\sqrt{\frac{\sqrt{2}-1}{2}}$, $\psi =\frac{u^2}{2}-\frac{1}{4}$.

$$\begin{array}{cc}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f\left(x\right)\right\}\left(u\right)=& \frac{1}{\sqrt{2}}{e}^{-\frac{1}{4}}\left(({\omega }_1+{\omega }_2)+({\omega }_1-{\omega }_2)i\right.\hfill \\ \hfill & \left.+({\omega }_1+{\omega }_2)j+({\omega }_1-{\omega }_2)k\right)(cos\psi +isin\psi )\hfill \\ \hfill =& \frac{1}{\sqrt{2}}{e}^{-\frac{1}{4}}\left(({\omega }_1+{\omega }_2)cos\psi -({\omega }_1-{\omega }_2)sin\psi \right)\hfill \\ \hfill & +\frac{1}{\sqrt{2}}{e}^{-\frac{1}{4}}\left(({\omega }_1-{\omega }_2)cos\psi +({\omega }_1+{\omega }_2)sin\psi \right)i\hfill \\ \hfill & +\frac{1}{\sqrt{2}}{e}^{-\frac{1}{4}}\left(({\omega }_1+{\omega }_2)cos\psi +({\omega }_1-{\omega }_2)sin\psi \right)j\hfill \\ \hfill & +\frac{1}{\sqrt{2}}{e}^{-\frac{1}{4}}\left(({\omega }_1-{\omega }_2)cos\psi -({\omega }_1+{\omega }_2)sin\psi \right)k.\hfill \end{array}$$

(68)

The visual representation of the provided quaternion signal $f\left(x\right)=({\sigma }_0+{\sigma }_1\mu +{\sigma }_2\upsilon +{\sigma }_3\eta )e^{-\frac{\lambda }{2}{x}^2}$ is plotted in Figure 3, where ${\sigma }_0={\sigma }_1={ϵ}_2={ϵ}_3=1$, $\lambda =1$. On the other hand, its QLCcT of a signal $f\left(x\right)$ is depicted in Figure 4 with $A=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$. From Figure 4, we can observe that the quaternion linear canonical cosine transform has better spectral resolution and energy concentration. It can effectively describe the frequency domain characteristics of signals.

5.2. Application of QLCcT

Multiplicative filtering is a signal processing method in the frequency domain that is used to denoise and enhance signals. It can modify the amplitude and spectrum of the signal while preserving its relative position, effectively improving signal quality and analysis accuracy. Therefore, it holds great significance in communication and image processing fields.

In this subsection, a multiplicative filter is designed in the QLCcT domain according to Theorem 7, and its model is depicted in Figure 5.

Therefore, the design expression can be formulated as follows:

$$\begin{array}{c}\hfill f_{out}\left(x\right)={\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f_{in}\left(x\right)\right\}\left(u\right){\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{g\left(x\right)\right\}\left(u\right)\right)\left(x\right).\end{array}$$

(69)

Let

$$\begin{array}{c}\hfill {\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{g\left(x\right)\right\}\left(u\right)=\left\{\begin{array}{cc}1,\hfill & u_1<u<u_2,\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.\end{array}$$

(70)

be the transformed function; we choose the function:

$$g\left(x\right)={\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{g\left(x\right)\right\}\left(u\right)\right)\left(x\right),$$

as the lowpass filter for QLCcT with passband over $[u_1,u_2]$. Combining Equation (69) and the reversibility property of the QLCcT, we can obtain the quaternion function $f_{out}\left(x\right)$ as follows:

$$\begin{array}{c}\hfill f_{out}\left(x\right)={\mathcal{QL}}_{r,c,A^{-1}}^{\mathbb{H},\mu }\left({\mathcal{QL}}_{r,c,A}^{\mathbb{H},\mu }\left\{f_{in}\left(x\right)\right\}\left(u\right)\right)\left(x\right)=f_{in}\left(x\right),u_1<u<u_2.\end{array}$$

(71)

In the next analysis, we explore the computational complexity of a specific method when applied to signals of varying sizes. For the purpose of discussion, let us consider a signal with a size denoted by N; the traditional complex FT requires $Nlo{g}_{2}N$ real-number multiplications [39]. According to Theorem 2, the QLCcT can be represented in terms of the QFcT, with the added benefit of the QFcT’s complexity being merely half that of the QFT. The computational complexity of the QFT is equivalent to that of the traditional complex FT, which is $O\left(N{log}_{2}N\right)$. Therefore, based on Definition 1 and Equations (69)–(71), we can deduce that the computational complexity of the multiplicative filter is $O\left(4N{log}_{2}N\right)$.

6. Conclusions

This paper introduces QLCcT, which can be regarded as a generalization of classical QFRcT and QFcT. It also presents the key properties associated with it. Additionally, novel convolution operators for QLCcT are proposed, along with an accompanying correlation operator. Moreover, by utilizing the newly introduced convolution operators, we derive the corresponding weighted convolution and correlation theorems. Finally, an illustrative example is provided to demonstrate the application of right-side QLCcT. As an application for QLCcT, we deal with multiplicative filter design to show that this QLCcT and its properties allow signal reconstruction.