Intuitionistic Fuzzy Granular Matrix: Novel Calculation Approaches for Intuitionistic Fuzzy Covering-Based Rough Sets

Abstract

Intuitionistic fuzzy (IF) $\beta$-minimal description operators can deal with noise data in the IF covering-based rough set theory. That is to say, they can be used to find data that we need in IF environments. For an IF $\beta$-covering approximation space (i.e., an IF environment) with a high cardinality, it would be tedious and complicated to use IF set representations to calculate them. Therefore, it is necessary to find a quick method to obtain them. In this paper, we present the notion of IF $\beta$-maximal description based on the definition of IF $\beta$-minimal description, along with the concepts of IF granular matrix and IF reduction. Moreover, we propose matrix calculation methods for IF covering-based rough sets, such as IF $\beta$-minimal descriptions, IF $\beta$-maximal descriptions, and IF reductions. Firstly, the notion of an IF granular matrix is presented, which is used to calculate IF $\beta$-minimal description. Secondly, inspired by IF $\beta$-minimal description, we give the notion of IF $\beta$-maximal description. Furthermore, the matrix representations of IF $\beta$-maximal descriptions are presented. Next, two types of reductions for IF $\beta$-covering approximation spaces via IF $\beta$-minimal and fuzzy $\beta$-minimal descriptions are presented, along with their matrix representations. Finally, the new calculation methods are compared with corresponding set representations by carrying out several experiments.

1. Introduction

Covering-based rough set theory [1] was proposed to deal with the type of covering data, which enriched classical rough set theory [2]. Nearly forty covering rough set models [3,4,5] have been developed in covering approximation space. These models popularized their application to practical problems such as decision rule synthesis [6,7,8], knowledge reduction [9,10,11] and other fields [12,13,14]. Using set representations to investigate issues in real-life problems would be complicated and tedious in a covering approximation space with a high cardinality. As computer-implemented methods, matrix approaches are the ideal tools for managing this problem; these include matrices for axiomatizing three types of covering approximation operators [15], matrices for studying knowledge reduction in dynamic covering decision information systems [16], matrices for representing 32 pairs of neighborhood-based upper and lower approximation operators [17], and matrices for minimal and maximal descriptions in covering-based rough sets [18].

Fuzzy set theory [19] addresses the issue of how to understand and manipulate imperfect knowledge. It and rough set theory are related, but distinct and complementary [20]. The first type of fuzzy rough set model based on an fuzzy similarity relation was established in [21]. Then, some essential research on fuzzy rough set models was finished by different fuzzy logical connectives [22,23] and fuzzy relations [24,25]. Recently, some fuzzy rough set models were constructed under a fuzzy covering approximation space [26,27]. In particular, Ma [28] presented the concept of a fuzzy $\beta$-covering approximation space by replacing “1” with a parameter $\beta$, where “1” is a condition for the definition of fuzzy covering. Inspired by Ma’s work, many fuzzy covering-based rough set models were established. For example, several newly important notions and other types of fuzzy $\beta$-covering rough set models are presented in [29]. Multigranulation fuzzy rough covering models based on fuzzy $\beta$-neighborhoods were used to solve the problem of multi-criteria group decision making in [30]. At the same time, the matrix approaches are the most used in these studies. For example, Ma [28] proposed the matrix representations of two pairs of fuzzy $\beta$-covering approximation operators. Yang and Hu [31] used matrices to represent three pairs of L-fuzzy covering-based approximation operators, as well as other fuzzy covering approximation operators in [32]. Wang et al. [33] used matrices to calculate fuzzy $\beta$-minimal descriptions, $\beta$-maximal descriptions and fuzzy $\beta$-neighborhoods.

As a generalization of fuzzy set theory, intuitionistic fuzzy (IF) set theory [34] expresses stronger information uncertainty. Therefore, IF $\beta$-covering rough set models [35] were first presented in IF $\beta$-covering approximation spaces. They were extended to other models [36,37], which were used in decision making and feature selection. Since an IF set explains the degrees of membership and non-membership of an element, it is difficult to use matrices to study these IF $\beta$-covering rough sets. To solve this problem, we use matrix approaches in IF $\beta$-covering approximation spaces, providing a new viewpoint to investigate IF $\beta$-covering rough set models and optimize complex computations expressed by IF sets. The motivations and contents of this paper are listed as follows:

• Huang et al. [35] presented the notion of IF $\beta$-minimal description. But the dual notion of IF $\beta$-maximal description is not proposed. Therefore, this new notion will be given in this paper, which reflects a different method of information screening.
• In [33], matrix methods are used for calculating minimal and maximal descriptions in covering approximation spaces. In [33,38], fuzzy matrix methods are used for calculating fuzzy $\beta$-minimal and fuzzy $\beta$-maximal descriptions in fuzzy $\beta$-covering approximation spaces. Therefore, we can also present IF matrix methods for calculating IF $\beta$-minimal and IF $\beta$-maximal descriptions in IF $\beta$-covering approximation spaces.
• There are many different notions of reductions in covering and fuzzy $\beta$-covering approximation spaces, respectively. It is interesting to define reductions in IF $\beta$-covering approximation spaces by IF $\beta$-minimal and IF $\beta$-maximal descriptions in this paper, respectively. Based on the matrix representations of IF $\beta$-minimal and $\beta$-maximal descriptions, these new notions of IF reductions can be represented by matrices.

The rest of this article is arranged as follows: Section 2 reviews some basic definitions about coverings, IF sets and IF $\beta$-covering approximation space. In Section 3, the notion of an IF granular matrix is presented in an IF $\beta$-covering approximation space. Then, IF matrix approaches are used to calculate the IF $\beta$-minimal and $\beta$-maximal descriptions. In Section 4, two types of reductions in an IF $\beta$-covering approximation space are presented through IF $\beta$-minimal and $\beta$-maximal descriptions, respectively. Moreover, these two types of reductions are represented in the IF granular matrix. Section 5 compares the existing set representation method with the new IF matrix method through a number of experiments. The advantages and efficiency of the new method are explained from different viewpoints. Section 6 provides the conclusion and prospects.

2. Basic Definitions

This section recalls some fundamental definitions related to coverings, IF sets and IF covering-based rough sets. Suppose U is a nonempty and finite set called a “universe” unless stated to the contrary.

Definition 1

([39,40]). Let U be a universe and $\mathit{C}$ be a family of subsets of U. If no element in $\mathbf{C}$ is empty and $\bigcup \mathit{C}=U$, then $\mathit{C}$ is called a covering of U. We call $(U,\mathit{C})$ a covering approximation space.

We show the notions of minimal and maximal descriptions in the covering approximation space as follows:

Let $\mathbf{C}$ be a covering of U. For any $x\in U$, we call

$$M{d}_{\mathbf{C}}\left(x\right)=\{K\in \mathbf{C}:x\in K\wedge (\forall S\in \mathbf{C})(x\in S\wedge S\subseteq K\Rightarrow K=S)\}$$

the minimal description of x [1,41], and call

$$M{D}_{\mathbf{C}}\left(x\right)=\{K\in \mathbf{C}:x\in K\wedge (\forall S\in \mathbf{C})(x\in S\wedge K\subseteq S\Rightarrow K=S)\}$$

the maximal description of x [42].

In [18], we showed the advantages of matrix approaches for obtaining the minimal description and the maximal description in covering rough sets. Moreover, in [33], we showed the advantages of fuzzy minimal description and fuzzy maximal description in fuzzy covering rough sets. For example, they can be used in granular reductions (see Example 17 in [33]), and can also be used to obtain fuzzy neighborhoods (see Figure 4 in [33]).

In the following, we introduce some basic notions of IF set theory.

Definition 2

([34]). Let U be a universe. An intuitionistic fuzzy set (IFS) A in U is defined as follows:

$$A=\{\langle x,{\mu }_A\left(x\right),{\nu }_A\left(x\right)\rangle :x\in U\},$$

where ${\mu }_A:U\to [0,1]$ is called the degree of membership of the element $x\in U$ to A, ${\nu }_A:U\to [0,1]$ is called the degree of non-membership. They satisfy ${\mu }_A\left(x\right)+{\nu }_A\left(x\right)\le 1$ for all $x\in U$. The family of all intuitionistic fuzzy sets in U is denoted by $IF\left(U\right)$.

We call $\langle a,b\rangle$ with $0<a,b\le 1$ and $a+b\le 1$ an IF value. As is well known, for two IF values $\alpha =\langle a,b\rangle$ and $\beta =\langle c,d\rangle$ , $\alpha \le \beta \iff a\le c$ and $b\ge d$.

For any family ${\gamma }_i\in [0,1],i\in I$, $I\subseteq {\mathbb{N}}^{+}$ (${\mathbb{N}}^{+}$ is the set of all positive integers), we write ${\vee }_{i\in I}{\gamma }_i$ for the supremum of $\{{\gamma }_i:i\in I\}$, and ${\wedge }_{i\in I}{\gamma }_i$ for the infimum of $\{{\gamma }_i:i\in I\}$. Some basic operations on $IF\left(U\right)$ are listed as follows [34]: $A,B\in IF\left(U\right)$,

(1)

$A\subseteq B$ iff ${\mu }_A\left(x\right)\le {\mu }_B\left(x\right)$ and ${\nu }_B\left(x\right)\le {\nu }_A\left(x\right)$ for all $x\in U$;

(2)

$A=B$ iff $A\subseteq B$ and $B\subseteq A$;

(3)

$A\cup B=\{\langle x,{\mu }_A\left(x\right)\vee {\mu }_B\left(x\right),{\nu }_A\left(x\right)\wedge {\nu }_B\left(x\right)\rangle :x\in U\}$;

(4)

$A\cap B=\{\langle x,{\mu }_A\left(x\right)\wedge {\mu }_B\left(x\right),{\nu }_A\left(x\right)\vee {\nu }_B\left(x\right)\rangle :x\in U\}$;

(5)

$A^{\prime }=\{\langle x,{\nu }_A\left(x\right),{\mu }_A\left(x\right)\rangle :x\in U\}$.

Definition 3

([35]). Let U be a universe and $\beta =\langle a,b\rangle$ be an IF value. Then, we call $\widehat{\mathit{C}}=\{C_1,C_2,\dots ,C_m\}$, with $C_i\in IF\left(U\right)(i=1,2,\dots ,m)$, an IF β-covering of U, if for any $x\in U$ there exists $C_i\in \widehat{\mathit{C}}$ such that $C_i\left(x\right)\ge \beta$. We also call $(U,\widehat{\mathit{C}})$ an IF β-covering approximation space.

Finally, we introduce some notions in the IF $\beta$-covering approximation space.

Definition 4

([35]). Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space. For each $x\in U$, the IF β-neighborhood ${\tilde{N}}_{\widehat{\mathit{C}}\left(x\right)}^{\beta }$ of x induced by $\widehat{\mathit{C}}$ can be defined as follows:

$${\tilde{N}}_{\widehat{\mathit{C}}\left(x\right)}^{\beta }=\bigcap \{C\in \widehat{\mathbf{C}}:C\left(x\right)\ge \beta \}.$$

Definition 5

([35]). Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space. For any $x\in U$, its IF β-minimal description ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)$ is defined as follows:

$${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)=\{C\in \widehat{\mathit{C}}:C\left(x\right)\ge \beta \wedge (\forall D\in \widehat{\mathit{C}})(D\left(x\right)\ge \beta \wedge D\subseteq C\Rightarrow C=D)\}.$$

For better reading and understanding, we explain relevant symbols in

Table 1. Relevant symbols in this paper.

	Full Name	Relevant Symbol
Original Symbols	Covering approximation space	$(U,\mathbf{C})$
	Minimal description of x	$M{d}_{\mathbf{C}}\left(x\right)$
	Maximal description of x	$M{D}_{\mathbf{C}}\left(x\right)$
	IF $\beta$-covering approximation space	$(U,\widehat{\mathbf{C}})$
	IF $\beta$-neighborhood	${\tilde{N}}_{\widehat{\mathbf{C}}\left(x\right)}^{\beta }$
	IF $\beta$-minimal description of x	${\widetilde{Md}}^{\beta }(\widehat{\mathbf{C}},x)$
New Symbols	IF $\beta$-maximal description of x	${\widetilde{MD}}^{\beta }(\widehat{\mathbf{C}},x)$
	IF granular matrix representation of $\widehat{\mathbf{C}}$	$M_{\widehat{\mathbf{C}}}$
	IF eigenmatrix of x	$M_{\widehat{\mathbf{C}}}\left(x\right)$
	IF $\beta$-covering number matrix of $\widehat{\mathbf{C}}$	$\overline{M_{\widehat{\mathbf{C}}}}$

.

3. Matrix Representations of IF β-Minimal and β-Maximal Descriptions

In this section, IF $\beta$-minimal and $\beta$-maximal descriptions are computed by matrices. First, some new matrices and corresponding operations are proposed in an IF $\beta$-covering approximation space. Then, several properties of these new matrices are presented. Finally, we give the matrix representations of IF $\beta$-minimal and $\beta$-maximal descriptions based on the results above.

3.1. Matrix Representations of IF $\beta$-Minimal Descriptions

In this subsection, we present some new matrices and matrix operations in the IF $\beta$-covering approximation space. Moreover, the matrix representations of IF $\beta$-minimal and $\beta$-maximal descriptions are presented.

Definition 6.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space, where $U=\{x_1,\cdots ,x_n\}$ and $\widehat{\mathit{C}}=\{C_1,C_2,\dots ,C_m\}$. We call $M_{\widehat{\mathit{C}}}={\left(C_j\left(x_i\right)\right)}_{n\times m}$ an IF granular matrix representation of $\widehat{\mathit{C}}$.

Example 1.

Let $U=\{x_1,x_2,x_3,x_4,x_5,x_6\}$ and $\widehat{\mathit{C}}=\{C_1,C_2,C_3,C_4,C_5\}$, where

$$\begin{array}{cc} & C_1=\frac{\langle 0.6,0.3\rangle }{x_1}+\frac{\langle 0.5,0.2\rangle }{x_2}+\frac{\langle 0.7,0.3\rangle }{x_3}+\frac{\langle 0.6,0.4\rangle }{x_4}+\frac{\langle 0.7,0.3\rangle }{x_5}+\frac{\langle 0.6,0.2\rangle }{x_6},\hfill \\ & C_2=\frac{\langle 0.7,0.3\rangle }{x_1}+\frac{\langle 0.2,0.6\rangle }{x_2}+\frac{\langle 0.1,0.7\rangle }{x_3}+\frac{\langle 0.6,0.2\rangle }{x_4}+\frac{\langle 0.5,0.2\rangle }{x_5}+\frac{\langle 0.5,0.3\rangle }{x_6},\hfill \\ & C_3=\frac{\langle 0.7,0.2\rangle }{x_1}+\frac{\langle 0.6,0.1\rangle }{x_2}+\frac{\langle 0.8,0.1\rangle }{x_3}+\frac{\langle 0.6,0.3\rangle }{x_4}+\frac{\langle 0.8,0.1\rangle }{x_5}+\frac{\langle 0.6,0.1\rangle }{x_6},\hfill \\ & C_4=\frac{\langle 0.3,0.5\rangle }{x_1}+\frac{\langle 0.5,0.5\rangle }{x_2}+\frac{\langle 0.5,0.3\rangle }{x_3}+\frac{\langle 0.4,0.5\rangle }{x_4}+\frac{\langle 0.6,0.2\rangle }{x_5}+\frac{\langle 0.5,0.3\rangle }{x_6},\hfill \\ & C_5=\frac{\langle 0.5,0.1\rangle }{x_1}+\frac{\langle 0.6,0.4\rangle }{x_2}+\frac{\langle 0.7,0.2\rangle }{x_3}+\frac{\langle 0.6,0.3\rangle }{x_4}+\frac{\langle 0.7,0.2\rangle }{x_5}+\frac{\langle 0.6,0.2\rangle }{x_6}.\hfill \end{array}$$

Suppose $\beta =\langle 0.6,0.3\rangle$. By Definition 3, we know $\widehat{\mathit{C}}$ is an IF β-covering of U. By Definition 6, we have

Based on Definition 6, another two matrices about $M_{\widehat{\mathit{C}}}$ are proposed in the following definition.

Definition 7.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $M_{\widehat{\mathit{C}}}={(C_j(x_i))}_{n\times m}$ be a matrix representation of $\widehat{\mathit{C}}$, where $U=\{x_1,\cdots ,x_n\}$ and $\widehat{\mathit{C}}=\{C_1,C_2,\dots ,C_m\}$.

(1)

For any $1\le j\le m$, $M_{\widehat{\mathit{C}}}\left(x_i\right)={\left({\alpha }_{kj}\right)}_{n\times m}$ is called an IF eigenmatrix of $x_i$, where $1\le k\le n$,

$${\alpha }_{kj}=\left\{\begin{array}{cc}{C}_j\left(x_k\right),\hfill & C_j\left(x_i\right)\ge \beta ;\hfill \\ \langle 0,0\rangle ,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

(2)

$\overline{M_{\widehat{\mathit{C}}}}={\left(n\right)}_{m\times m}$ is called the IF β-covering number matrix of $\widehat{\mathit{C}}$.

Remark 1.

In Definition 7, for $M_{\widehat{\mathit{C}}}\left(x_i\right)$, if $C_j\left(x_i\right)\ge \beta$, then the $jth$ column of $M_{\widehat{\mathit{C}}}\left(x_i\right)$ is the $jth$ of $M_{\widehat{\mathit{C}}}$; otherwise, all elements in the $jth$ column of $M_{\widehat{\mathit{C}}}\left(x_i\right)$ are $\langle 0,0\rangle$.

Example 2 (Continued from Example 1).

By Definition 7, we have

$$\begin{array}{c}{M}_{\widehat{\mathit{C}}}\left(x_1\right)=\left(\begin{array}{ccccc}\langle 0.6,0.3\rangle & \langle 0.7,0.3\rangle & \langle 0.7,0.2\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.5,0.2\rangle & \langle 0.2,0.6\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.7,0.3\rangle & \langle 0.1,0.7\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.6,0.4\rangle & \langle 0.6,0.2\rangle & \langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.7,0.3\rangle & \langle 0.5,0.2\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.6,0.2\rangle & \langle 0.5,0.3\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \end{array}\right),\hfill \\ M_{\widehat{\mathit{C}}}\left(x_2\right)=\left(\begin{array}{ccccc}\langle 0,0\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0,0\rangle & \langle 0,0\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0,0\rangle & \langle 0,0\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0,0\rangle & \langle 0,0\rangle & \langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0,0\rangle & \langle 0,0\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0,0\rangle & \langle 0,0\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \end{array}\right),\hfill \\ M_{\widehat{\mathit{C}}}\left(x_3\right)=\left(\begin{array}{ccccc}\langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle & \langle 0,0\rangle & \langle 0.5,0.1\rangle \\ \langle 0.5,0.2\rangle & \langle 0,0\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0.6,0.4\rangle \\ \langle 0.7,0.3\rangle & \langle 0,0\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle \\ \langle 0.6,0.4\rangle & \langle 0,0\rangle & \langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0.6,0.3\rangle \\ \langle 0.7,0.3\rangle & \langle 0,0\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle \\ \langle 0.6,0.2\rangle & \langle 0,0\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0.6,0.2\rangle \end{array}\right),\hfill \\ M_{\widehat{\mathit{C}}}\left(x_4\right)=\left(\begin{array}{ccccc}\langle 0,0\rangle & \langle 0.7,0.3\rangle & \langle 0.7,0.2\rangle & \langle 0,0\rangle & \langle 0.5,0.1\rangle \\ \langle 0,0\rangle & \langle 0.2,0.6\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0.6,0.4\rangle \\ \langle 0,0\rangle & \langle 0.1,0.7\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle \\ \langle 0,0\rangle & \langle 0.6,0.2\rangle & \langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0.6,0.3\rangle \\ \langle 0,0\rangle & \langle 0.5,0.2\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle \\ \langle 0,0\rangle & \langle 0.5,0.3\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0.6,0.2\rangle \end{array}\right),\hfill \\ M_{\widehat{\mathit{C}}}\left(x_5\right)=\left(\begin{array}{ccccc}\langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle & \langle 0.3,0.5\rangle & \langle 0.5,0.1\rangle \\ \langle 0.5,0.2\rangle & \langle 0,0\rangle & \langle 0.6,0.1\rangle & \langle 0.5,0.5\rangle & \langle 0.6,0.4\rangle \\ \langle 0.7,0.3\rangle & \langle 0,0\rangle & \langle 0.8,0.1\rangle & \langle 0.5,0.3\rangle & \langle 0.7,0.2\rangle \\ \langle 0.6,0.4\rangle & \langle 0,0\rangle & \langle 0.6,0.3\rangle & \langle 0.4,0.5\rangle & \langle 0.6,0.3\rangle \\ \langle 0.7,0.3\rangle & \langle 0,0\rangle & \langle 0.8,0.1\rangle & \langle 0.6,0.2\rangle & \langle 0.7,0.2\rangle \\ \langle 0.6,0.2\rangle & \langle 0,0\rangle & \langle 0.6,0.1\rangle & \langle 0.5,0.3\rangle & \langle 0.6,0.2\rangle \end{array}\right),\hfill \\ M_{\widehat{\mathit{C}}}\left(x_6\right)=\left(\begin{array}{ccccc}\langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle & \langle 0,0\rangle & \langle 0.5,0.1\rangle \\ \langle 0.5,0.2\rangle & \langle 0,0\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0.6,0.4\rangle \\ \langle 0.7,0.3\rangle & \langle 0,0\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle \\ \langle 0.6,0.4\rangle & \langle 0,0\rangle & \langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0.6,0.3\rangle \\ \langle 0.7,0.3\rangle & \langle 0,0\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0.7,0.2\rangle \\ \langle 0.6,0.2\rangle & \langle 0,0\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0.6,0.2\rangle \end{array}\right),\hfill \\ \overline{M_{\widehat{\mathit{C}}}}=\left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right).\hfill \end{array}$$

Then, a new matrix operation is presented in the following definition.

Definition 8.

Let $A={\left({\alpha }_{ik}\right)}_{n\times m}$ and $B={\left({\gamma }_{kj}\right)}_{m\times s}$ be two matrices, where ${\alpha }_{ik}=\langle a_{ik}^{+},a_{ik}^{-}\rangle$ and ${\gamma }_{kj}=\langle b_{kj}^{+},b_{kj}^{-}\rangle$. We define $C=A⊵B={\left(c_{ij}\right)}_{n\times s}$, where

$$\begin{gathered} c_{ij}=\left\{\begin{array}{cc}{\displaystyle \sum _{k=1}^m}({\alpha }_{ik}⊵{\gamma }_{kj}),\hfill & \mathit{row}i\mathit{of}A\mathit{and}\mathit{column}j\mathit{of}B\mathit{are}\mathit{not}\mathit{0};\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.\mathit{and} \\ {\alpha }_{ik}⊵{\gamma }_{kj}=\left\{\begin{array}{cc}1,\hfill & a_{ik}^{+}\ge b_{kj}^{+}\wedge a_{ik}^{-}\le b_{kj}^{-};\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right. \end{gathered}$$

In Definition 8, $\mathbf{0}$ denotes the vector with any element $\langle 0,0\rangle$. Then, two characteristics of $M_{\widehat{\mathit{C}}}^T\left(x\right)⊵M_{\widehat{\mathit{C}}}\left(x\right)$$(\forall x\in U)$ are presented in the following two propositions, respectively.

Proposition 1.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $M_{\widehat{\mathit{C}}}^T\left(x_k\right)⊵M_{\widehat{\mathit{C}}}\left(x_k\right)={\left(a_{ij}\right)}_{m\times m}$, where $x_k\in U$ ($k=1,2,\cdots ,n$) and $\widehat{\mathit{C}}=\{C_1,C_2,\dots ,C_m\}$. Then, $a_{ij}=\left|\{x\in U:(C_i\cap C_j)\left(x_k\right)\ge \beta \wedge C_i\left(x\right)\ge C_j\left(x\right)\}\right|$.

Proof. 

$$\begin{array}{cc}{a}_{ij}\hfill & =\left\{\begin{array}{cc}{\displaystyle \sum _{x\in U}}(C_i\left(x\right)⊵C_j\left(x\right)),\hfill & C_i\left(x_k\right)\ge \beta \mathrm{and}{C}_j\left(x_k\right)\ge \beta ;\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \\ & =\left\{\begin{array}{cc}\left|\right\{x\in U:C_i\left(x\right)\ge C_j\left(x\right)\left\}\right|,\hfill & (C_i\cap C_j)\left(x_k\right)\ge \beta ;\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \\ & =\left|\right\{x\in U:(C_i\cap C_j)\left(x_k\right)\ge \beta \wedge C_i\left(x\right)\ge C_j\left(x\right)\left\}\right|.\hfill \end{array}$$

□

Proposition 2.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space, $x_k\in U$, $M_{\widehat{\mathit{C}}}^T\left(x_k\right)⊵M_{\widehat{\mathit{C}}}\left(x_k\right)={\left(a_{ij}\right)}_{m\times m}$ and $\overline{M_{\widehat{\mathit{C}}}}={\left(b_{ij}\right)}_{m\times m}$. For any $(t\in \{1,2,\cdots ,m\left\}\right)$, $a_{tt}=b_{tt}$ if and only if $a_{tt}>0$.

Proof. 

Suppose $U=\{x_1,\cdots ,x_n\}$ and $\widehat{\mathbf{C}}=\{C_1,C_2,\dots ,C_m\}$. Then,

$$a_{tt}=|\{x\in U:C_t\left(x_k\right)\ge \beta \}|=b_{tt}=n=\left|\{x:x\in U\}\right|\iff C_t\left(x_k\right)\ge \beta \iff a_{tt}>0.$$

□

Finally, the matrix representation of the IF $\beta$-minimal description is presented in Theorem 1. Let $A={\left(a_{ij}\right)}_{n\times n}$ and $B={\left(b_{ij}\right)}_{n\times n}$ be two matrices. We define $C=A\oplus$$B={\left(c_i\right)}_{n\times 1}$, where

$$c_i=\left\{\begin{array}{cc}1,\hfill & a_{ij}=b_{ij}\iff i=j;\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

Let $\widehat{\mathbf{C}}=\{C_1,C_2,\dots ,C_m\}$ be an IF $\beta$-covering of U and ${\widehat{\mathbf{C}}}_1\subseteq \widehat{\mathbf{C}}$. We call $f\left({\widehat{\mathbf{C}}}_1\right)={\left(y_i\right)}_{m\times 1}$ the membership function of ${\widehat{\mathbf{C}}}_1$ in $\widehat{\mathbf{C}}$, where

$$y_i=\left\{\begin{array}{cc}1,\hfill & C_i\in {\widehat{\mathbf{C}}}_1;\hfill \\ 0,\hfill & C_i\notin {\widehat{\mathbf{C}}}_1.\hfill \end{array}\right.$$

Note that “⊵” is before “⊕” in operations.

Theorem 1.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space, where $U=\{x_1,\cdots ,x_n\}$ and $\widehat{\mathit{C}}=\{C_1,C_2,\dots ,C_m\}$. Then,

$$f({\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_k\right))=M_{\widehat{\mathit{C}}}^T\left(x_k\right)⊵M_{\widehat{\mathit{C}}}\left(x_k\right)\oplus \overline{M_{\widehat{\mathit{C}}}}, k=1,2,\cdots ,n.$$

Proof. 

Suppose $M_{\widehat{\mathbf{C}}}^T\left(x_k\right)⊵M_{\widehat{\mathbf{C}}}\left(x_k\right)={\left(a_{ij}\right)}_{m\times m}$, $\overline{M_{\widehat{\mathbf{C}}}}={\left(b_{ij}\right)}_{m\times m}$ and $f({\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x_k\right))={\left(y_j\right)}_{m\times 1}$. For any $C_t\in \mathbf{C}$,

$$\begin{array}{cc}{C}_t\in {\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x_k\right)\hfill & \iff (C_t\left(x_k\right)\ge \beta )\wedge (\forall C_j\in \widehat{\mathbf{C}}\wedge (C_j\left(x_k\right)\ge \beta )\wedge (C_j\subseteq C_t\Rightarrow C_t=C_j))\hfill \\ & \iff (C_t\left(x_k\right)\ge \beta )\wedge (\forall j\in \{1,2,\cdots ,m\}\wedge (C_j\left(x_k\right)\ge \beta )\wedge (C_j\subseteq C_t\Rightarrow C_t=C_j))\hfill \\ & \iff (C_t\left(x_k\right)\ge \beta )\wedge (\forall j\in \{1,2,\cdots ,m\}\wedge (C_j\left(x_k\right)\ge \beta )\wedge \hfill \\ & \left(\right|\{x\in U:C_t\left(x\right)\ge C_j\left(x\right)\}|=n\Rightarrow C_t=C_j))\hfill \\ & \iff (C_t\left(x_k\right)\ge \beta )\wedge (\forall j\in \{1,2,\cdots ,m\}\wedge (a_{tj}=b_{tj}\Rightarrow t=j))\hfill \\ & \iff (a_{tt}>0)\wedge (a_{tj}=b_{tj}\Rightarrow t=j)\hfill \\ & \iff (a_{tt}=b_{tt})\wedge (a_{tj}=b_{tj}\Rightarrow t=j)\hfill \\ & \iff y_t=1.\hfill \end{array}$$

Hence, $f({\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x_k\right))=M_{\widehat{\mathbf{C}}}^T\left(x_k\right)⊵M_{\widehat{\mathbf{C}}}\left(x_k\right)\oplus \overline{M_{\widehat{\mathbf{C}}}}$. □

Example 3 Continued from Example 1).

(All $M_{\widehat{\mathit{C}}}\left(x_k\right)$ ($k=1,2,\cdots ,6$) and $\overline{M_{\widehat{\mathit{C}}}}$ are calculated in Examples 1 and 2. Hence,

$$\begin{array}{cc}f({\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_1\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_1\right)⊵M_{\widehat{\mathit{C}}}\left(x_1\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{cccccc}\langle 0.6,0.3\rangle & \langle 0.5,0.2\rangle & \langle 0.7,0.3\rangle & \langle 0.6,0.4\rangle & \langle 0.7,0.3\rangle & \langle 0.6,0.2\rangle \\ \langle 0.7,0.3\rangle & \langle 0.2,0.6\rangle & \langle 0.1,0.7\rangle & \langle 0.6,0.2\rangle & \langle 0.5,0.2\rangle & \langle 0.5,0.3\rangle \\ \langle 0.7,0.2\rangle & \langle 0.6,0.1\rangle & \langle 0.8,0.1\rangle & \langle 0.6,0.3\rangle & \langle 0.8,0.1\rangle & \langle 0.6,0.1\rangle \\ \langle 0,0\rangle & \langle 0,0\rangle & \langle 0,0\rangle & \langle 0,0\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0,0\rangle & \langle 0,0\rangle & \langle 0,0\rangle & \langle 0,0\rangle & \langle 0,0\rangle & \langle 0,0\rangle \end{array}\right)⊵\hfill \\ & \left(\begin{array}{ccccc}\langle 0.6,0.3\rangle & \langle 0.7,0.3\rangle & \langle 0.7,0.2\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.5,0.2\rangle & \langle 0.2,0.6\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.7,0.3\rangle & \langle 0.1,0.7\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.6,0.4\rangle & \langle 0.6,0.2\rangle & \langle 0.6,0.3\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.7,0.3\rangle & \langle 0.5,0.2\rangle & \langle 0.8,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \\ \langle 0.6,0.2\rangle & \langle 0.5,0.3\rangle & \langle 0.6,0.1\rangle & \langle 0,0\rangle & \langle 0,0\rangle \end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)\hfill \\ & =\left(\begin{array}{ccccc}6& 3& 0& 0& 0\\ 2& 6& 1& 0& 0\\ 6& 5& 6& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}1\\ 1\\ 0\\ 0\\ 0\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_1\right)=\{C_1,C_2\}$.

$$\begin{array}{cc}f({\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_2\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_2\right)⊵M_{\widehat{\mathit{C}}}\left(x_2\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 6& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_2\right)=\left\{C_3\right\}$.

$$\begin{array}{cc}f({\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_3\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_3\right)⊵M_{\widehat{\mathit{C}}}\left(x_3\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}6& 0& 0& 0& 1\\ 0& 0& 0& 0& 0\\ 6& 0& 6& 0& 5\\ 0& 0& 0& 0& 0\\ 4& 0& 1& 0& 6\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_3\right)=\{C_1,C_5\}$.

$$\begin{array}{cc}f({\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_4\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_4\right)⊵M_{\widehat{\mathit{C}}}\left(x_4\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 6& 1& 0& 1\\ 0& 5& 6& 0& 5\\ 0& 0& 0& 0& 0\\ 0& 4& 1& 0& 6\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_4\right)=\{C_2,C_3,C_5\}$.

$$\begin{array}{cc}f({\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_5\right)⊵M_{\widehat{\mathit{C}}}\left(x_5\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}6& 0& 0& 5& 1\\ 0& 0& 0& 0& 0\\ 6& 0& 6& 6& 5\\ 0& 0& 0& 6& 0\\ 4& 0& 1& 6& 6\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\\ 1\\ 0\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right)=\{C_1,C_4\}$.

$$\begin{array}{cc}f({\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_6\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_6\right)⊵M_{\widehat{\mathit{C}}}\left(x_6\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}6& 0& 0& 0& 1\\ 0& 0& 0& 0& 0\\ 6& 0& 6& 0& 5\\ 0& 0& 0& 0& 0\\ 4& 0& 1& 0& 6\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_6\right)=\{C_1,C_5\}$.

3.2. Matrix Representations of IF $\beta$-Maximal Descriptions

Based on Section 3.1, we present the matrix representation of the IF $\beta$-maximal description in this subsection. Firstly, the concept of IF $\beta$-maximal description is given in the following definition.

Definition 9.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space. For any $x\in U$, its IF β-maximal description ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)$ is defined as follows:

$${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)=\{C\in \widehat{\mathit{C}}:C\left(x\right)\ge \beta \wedge (\forall D\in \widehat{\mathit{C}})(D\left(x\right)\ge \beta \wedge C\subseteq D\Rightarrow C=D)\}.$$

To investigate the matrix representation of the IF $\beta$-maximal description, another new matrix operation is presented in the following definition.

Definition 10.

Let $A={\left({\alpha }_{ik}\right)}_{n\times m}$ and $B={\left({\gamma }_{kj}\right)}_{m\times s}$ be two matrices, where ${\alpha }_{ik}=\langle a_{ik}^{+},a_{ik}^{-}\rangle$ and ${\gamma }_{kj}=\langle b_{kj}^{+},b_{kj}^{-}\rangle$. We define $C=A⊴B={\left(c_{ij}\right)}_{n\times s}$, where

$$\begin{gathered} c_{ij}=\left\{\begin{array}{cc}{\displaystyle \sum _{k=1}^m}({\alpha }_{ik}⊴{\gamma }_{kj}),\hfill & \mathit{row}i\mathit{of}A\mathit{and}\mathit{column}j\mathit{of}B\mathit{are}\mathit{not}\mathit{0};\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right. \mathit{and} \\ {\alpha }_{ik}⊴{\gamma }_{kj}=\left\{\begin{array}{cc}1,\hfill & a_{ik}^{+}\le b_{kj}^{+}\wedge a_{ik}^{-}\ge b_{kj}^{-};\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right. \end{gathered}$$

By Definition 10, two characteristics of $M_{\widehat{\mathbf{C}}}^T\left(x\right)⊴M_{\widehat{\mathbf{C}}}\left(x\right)$$(\forall x\in U)$ are presented in the following two propositions.

Proposition 3.

Let $\widehat{\mathit{C}}=\{C_1,C_2,\dots ,C_m\}$ be an IF β-covering of $U=\{x_1,\cdots ,x_n\}$, $x_k\in U$ and $M_{\widehat{\mathit{C}}}^T\left(x_k\right)⊴M_{\widehat{\mathit{C}}}\left(x_k\right)={\left(a_{ij}\right)}_{m\times m}$. Then, $a_{ij}=\left|\{x\in U:(C_i\cap C_j)\left(x_k\right)\ge \beta \wedge C_i\left(x\right)\le C_j\left(x\right)\}\right|.$

Proof. 

$$\begin{array}{cc}{a}_{ij}\hfill & =\left\{\begin{array}{cc}{\displaystyle \sum _{x\in U}}(C_i\left(x\right)⊴C_j\left(x\right)),\hfill & C_i\left(x_k\right)\ge \beta \mathrm{and}{C}_j\left(x_k\right)\ge \beta ;\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \\ & =\left\{\begin{array}{cc}\left|\right\{x\in U:C_i\left(x\right)\le C_j\left(x\right)\left\}\right|,\hfill & (C_i\cap C_j)\left(x_k\right)\ge \beta ;\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \\ & =\left|\right\{x\in U:(C_i\cap C_j)\left(x_k\right)\ge \beta \wedge C_i\left(x\right)\le C_j\left(x\right)\left\}\right|.\hfill \end{array}$$

□

Proposition 4.

Let $\widehat{\mathit{C}}=\{C_1,C_2,\dots ,C_m\}$ be an IF β-covering of $U=\{x_1,\cdots ,x_n\}$, $x_k\in U$, $M_{\widehat{\mathit{C}}}^T\left(x_k\right)⊴M_{\widehat{\mathit{C}}}\left(x_k\right)={\left(a_{ij}\right)}_{m\times m}$ and $\overline{M_{\widehat{\mathit{C}}}}={\left(b_{ij}\right)}_{m\times m}$. $a_{tt}=b_{tt}$ if and only if $a_{tt}>0$$(t\in \{1,2,\cdots ,m\left\}\right)$.

Proof. 

$a_{tt}=|\{x\in U:C_t\left(x_k\right)\ge \beta \}|=b_{tt}=n=\left|\{x:x\in U\}\right|\iff C_t\left(x_k\right)\ge \beta \iff a_{tt}>0.$    □

Finally, the matrix representation of the IF $\beta$-maximal description is presented in the following theorem. Note that “⊴” is before “⊕” in operations.

Theorem 2.

Let $\widehat{\mathbf{C}}=\{C_1,C_2,\dots ,C_m\}$ be an IF β-covering of $U=\{x_1,\cdots ,x_n\}$. Then,

$$f({\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_k\right))=M_{\widehat{\mathit{C}}}^T\left(x_k\right)⊴M_{\widehat{\mathit{C}}}\left(x_k\right)\oplus \overline{M_{\widehat{\mathit{C}}}}, k=1,2,\cdots ,n.$$

Proof. 

Suppose $M_{\widehat{\mathbf{C}}}^T\left(x_k\right)⊴M_{\widehat{\mathbf{C}}}\left(x_k\right)={\left(a_{ij}\right)}_{m\times m}$, $\overline{M_{\widehat{\mathbf{C}}}}={\left(b_{ij}\right)}_{m\times m}$ and $f({\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x_k\right))={\left(y_j\right)}_{m\times 1}$. For any $C_t\in \mathbf{C}$,

$$\begin{array}{cc}{C}_t\in {\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x_k\right)\hfill & \iff (C_t\left(x_k\right)\ge \beta )\wedge (\forall C_j\in \widehat{\mathbf{C}}\wedge (C_j\left(x_k\right)\ge \beta )\wedge (C_j\supseteq C_t\Rightarrow C_t=C_j))\hfill \\ & \iff (C_t\left(x_k\right)\ge \beta )\wedge (\forall j\in \{1,2,\cdots ,m\}\wedge (C_j\left(x_k\right)\ge \beta )\wedge (C_j\supseteq C_t\Rightarrow C_t=C_j))\hfill \\ & \iff (C_t\left(x_k\right)\ge \beta )\wedge (\forall j\in \{1,2,\cdots ,m\}\wedge (C_j\left(x_k\right)\ge \beta )\wedge \hfill \\ & \left(\right|\{x\in U:C_t\left(x\right)\le C_j\left(x\right)\}|=n\Rightarrow C_t=C_j))\hfill \\ & \iff (C_t\left(x_k\right)\ge \beta )\wedge (\forall j\in \{1,2,\cdots ,m\}\wedge (a_{tj}=b_{tj}\Rightarrow t=j))\hfill \\ & \iff (a_{tt}=b_{tt})\wedge (a_{tj}=b_{tj}\Rightarrow t=j)\hfill \\ & \iff y_t=1.\hfill \end{array}$$

Hence, $f({\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x_k\right))=M_{\widehat{\mathbf{C}}}^T\left(x_k\right)⊴M_{\widehat{\mathbf{C}}}\left(x_k\right)\oplus \overline{M_{\widehat{\mathbf{C}}}}$. □

Example 4 (Continued from Example 1).

All $M_{\widehat{\mathit{C}}}\left(x_k\right)$ ($k=1,2,\cdots ,6$) and $\overline{M_{\widehat{\mathit{C}}}}$ are calculated in Example 2. Then,

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_1\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_1\right)⊴M_{\widehat{\mathit{C}}}\left(x_1\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}6& 2& 6& 0& 0\\ 3& 6& 5& 0& 0\\ 0& 1& 6& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 1\\ 0\\ 0\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_1\right)=\{C_2,C_3\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_2\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_2\right)⊴M_{\widehat{\mathit{C}}}\left(x_2\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 6& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_2\right)=\left\{C_3\right\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_3\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_3\right)⊴M_{\widehat{\mathit{C}}}\left(x_3\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}6& 0& 6& 0& 4\\ 0& 0& 0& 0& 0\\ 0& 0& 6& 0& 1\\ 0& 0& 0& 0& 0\\ 1& 0& 5& 0& 6\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_3\right)=\{C_3,C_5\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_4\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_4\right)⊴M_{\widehat{\mathit{C}}}\left(x_4\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 6& 5& 0& 4\\ 0& 1& 6& 0& 1\\ 0& 0& 0& 0& 0\\ 0& 1& 5& 0& 6\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_4\right)=\{C_2,C_3,C_5\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_5\right)⊴M_{\widehat{\mathit{C}}}\left(x_5\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}6& 0& 6& 0& 4\\ 0& 0& 0& 0& 0\\ 0& 0& 6& 0& 1\\ 5& 0& 6& 6& 6\\ 1& 0& 5& 0& 6\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right)=\{C_3,C_5\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_6\right))\hfill & =M_{\widehat{\mathit{C}}}^T\left(x_6\right)⊴M_{\widehat{\mathit{C}}}\left(x_6\right)\oplus \overline{M_{\widehat{\mathit{C}}}}\hfill \\ & =\left(\begin{array}{ccccc}6& 0& 6& 0& 4\\ 0& 0& 0& 0& 0\\ 0& 0& 6& 0& 1\\ 0& 0& 0& 0& 0\\ 1& 0& 5& 0& 6\end{array}\right)\oplus \left(\begin{array}{ccccc}6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\\ 6& 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_6\right)=\{C_3,C_5\}$.

4. Matrix Approaches for Reductions in IF $\mathit{\beta }$-Covering Approximation Spaces

In this section, we present two kinds of reductions in IF $\beta$-covering approximation spaces based on IF $\beta$-minimal and $\beta$-maximal descriptions, respectively. Moreover, they are calculated by matrices.

4.1. Reductions of IF $\beta$-Covering Approximation Spaces via IF $\beta$-Minimal Descriptions

The definitions of IF $\beta$-minimal reduction and corresponding matrix approaches are mainly presented in this subsection. Firstly, the notion of the subspace of the original IF $\beta$-covering approximation space is presented in the following definition.

Definition 11.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $\widehat{\mathit{D}}\subseteq \widehat{\mathit{C}}$. We call $(U,\widehat{\mathit{D}})$ an IF sub-β-covering approximation space of $(U,\widehat{\mathit{C}})$ if $\widehat{\mathit{D}}$ is also an IF β-covering of U. The family of all IF sub-β-covering approximation spaces of $(U,\widehat{\mathit{C}})$ is denoted by $\mathcal{S}(\widehat{\mathit{C}})$.

By Definition 11, $\widehat{\mathbf{C}}\in \mathcal{S}(\widehat{\mathbf{C}})$ for any IF $\beta$-covering approximation space $(U,\widehat{\mathbf{C}})$. We denote ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)=\{C\in \widehat{\mathbf{C}}:C\left(x\right)\ge \beta \}.$ Then, Propositions 5 and 6 show two properties of IF $\beta$-minimal descriptions in the IF sub-$\beta$-covering approximation space.

Proposition 5.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$. For any $x\in U$, if $|{\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)|=1$, then ${\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$.

Proof. 

If $|{\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)|=1$, then we suppose ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)=\left\{C^{\prime }\right\}$, where $C^{\prime }\in \widehat{\mathbf{C}}$ and $C^{\prime }\left(x\right)\ge \beta$. Since $\widehat{\mathbf{D}}\in \mathcal{S}(\widehat{\mathbf{C}})$, $C^{\prime }\in \widehat{\mathbf{D}}$. Hence, ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)=\left\{C^{\prime }\right\}$. By Definition 5, ${\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)=\{C\in \widehat{\mathbf{C}}:C\left(x\right)\ge \beta \wedge (\forall D\in \widehat{\mathbf{C}})(D\left(x\right)\ge \beta \wedge D\subseteq C\Rightarrow C=D)\}=\{C\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right):\forall D\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)\wedge D\subseteq C\Rightarrow C=D\}=\left\{C^{\prime }\right\}$ and ${\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)=\{C\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right):\forall D\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)\wedge D\subseteq C\Rightarrow C=D\}=\left\{C^{\prime }\right\}$. Therefore, ${\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$. □

Proposition 6.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$. For any $x\in U$, if ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$, then ${\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$.

Proof. 

Since ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$, ${\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)=\{C\in \widehat{\mathbf{C}}:C\left(x\right)\ge \beta \wedge (\forall D\in \widehat{\mathbf{C}})(D\left(x\right)\ge \beta \wedge D\subseteq C\Rightarrow C=D)\}=\{C\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right):\forall D\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)\wedge D\subseteq C\Rightarrow C=D\}=\{C\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right):\forall D\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)\wedge D\subseteq C\Rightarrow C=D\}={\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$. □

The converse of Proposition 3 is incorrect. That is to say, “for any $x\in U$, if ${\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$, then ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$” is not true. We use the following example to explain this.

Example 5 (Continued from Example 1).

In Example 1, $\widehat{\mathit{C}}=\{C_1,\cdots ,C_5\}$ is an IF β-covering of U. In Example 3, we have $f({\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right))={(1,0,0,1,0)}^T$, i.e., ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right)=\{C_1,C_4\}$. Suppose $\widehat{\mathit{D}}=\{C_1,\cdots ,C_4\}$. Then, $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$.

$$\begin{array}{cc}f({\widetilde{Md}}_{\widehat{\mathit{D}}}^{\beta }\left(x_5\right))\hfill & =M_{\widehat{\mathit{D}}}^T\left(x_5\right)⊵M_{\widehat{\mathit{D}}}\left(x_5\right)\oplus \overline{M_{\widehat{\mathit{D}}}}=\left(\begin{array}{cccc}6& 0& 0& 5\\ 0& 0& 0& 0\\ 6& 0& 6& 6\\ 0& 0& 0& 6\end{array}\right)\oplus \left(\begin{array}{cccc}6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{Md}}_{\widehat{\mathit{D}}}^{\beta }\left(x_5\right)=\{C_1,C_4\}$. Hence, ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right)={\widetilde{Md}}_{\widehat{\mathit{D}}}^{\beta }\left(x_5\right)=\{C_1,C_4\}$. But ${\tilde{\mathcal{N}}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right)=\{C_1,C_3,C_4,C_5\}$ and ${\tilde{\mathcal{N}}}_{\widehat{\mathit{D}}}^{\beta }\left(x_5\right)=\{C_1,C_3,C_4\}$, i.e., ${\tilde{\mathcal{N}}}_{\widehat{\mathit{C}}}^{\beta }\left(x_5\right)\ne {\tilde{\mathcal{N}}}_{\widehat{\mathit{D}}}^{\beta }\left(x_5\right)$.

Definition 12.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$. $\widehat{\mathit{D}}$ is called the IF β-minimal reduction of $\widehat{\mathit{C}}$ if $\widehat{\mathit{D}}$ satisfies the following conditions:

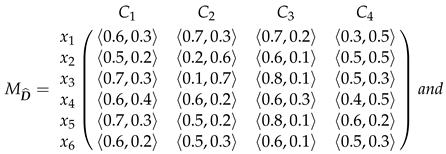
(1)

For any $x\in U$, ${\widetilde{Md}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)={\widetilde{Md}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)$;

(2)

For any $\widehat{\mathit{E}}\in \mathcal{S}(\widehat{\mathit{D}})-\{\widehat{\mathit{D}}\}$, there exists $x\in U$ such that ${\widetilde{Md}}_{\widehat{\mathit{E}}}^{\beta }\left(x\right)\ne {\widetilde{Md}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)$.

Let $\mathbf{A}$ be a family of subsets of $IF\left(U\right)$. We denote $Min\left(\mathbf{A}\right)=\{X\in \mathbf{A}:\forall Y\in \mathbf{A},Y\subseteq X\Rightarrow X=Y\}$.

Proposition 7.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space. $\widehat{\mathit{D}}$ is the IF β-minimal reduction of $\widehat{\mathit{C}}$ if and only if $\widehat{\mathit{D}}\in Min(\{\widehat{\mathbf{E}}\in \mathcal{S}(\widehat{\mathit{C}}):\forall x\in U,{\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{Md}}_{\widehat{\mathbf{E}}}^{\beta }\left(x\right)\})$.

Proof. 

By Definition 12, it is immediate. □

Theorem 3.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space. The IF β-minimal reduction of $\widehat{\mathit{C}}$ is unique.

Proof. 

By Definition 12, the existence of the IF $\beta$-minimal reduction is true. Then, we use proof by contradiction to prove uniqueness. Suppose ${\widehat{\mathbf{D}}}_1$ is an IF $\beta$-minimal reduction of $\widehat{\mathbf{C}}$ and ${\widehat{\mathbf{D}}}_2$ is the other one. Then, ${\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{Md}}_{{\widehat{\mathbf{D}}}_1}^{\beta }\left(x\right)={\widetilde{Md}}_{{\widehat{\mathbf{D}}}_2}^{\beta }\left(x\right)$ for any $x\in U$. Hence, there exists $K\in {\widehat{\mathbf{D}}}_2-{\widehat{\mathbf{D}}}_1$ such that $K\notin {\widetilde{Md}}_{{\widehat{\mathbf{D}}}_1}^{\beta }\left(x\right)$ for any $x\in U$. That is to say, $K\notin {\widetilde{Md}}_{{\widehat{\mathbf{D}}}_2}^{\beta }\left(x\right)$ for any $x\in U$. ${\widehat{\mathbf{D}}}_2-\left\{K\right\}$ is also an IF $\beta$-covering, since for any $x\in U$ there exists $C\in {\widetilde{Md}}_{{\widehat{\mathbf{D}}}_2}^{\beta }\left(x\right)$ such that $C\left(x\right)\ge \beta$. Therefore, ${\widetilde{Md}}_{{\widehat{\mathbf{D}}}_2-\left\{K\right\}}^{\beta }\left(x\right)={\widetilde{Md}}_{{\widehat{\mathbf{D}}}_2}^{\beta }\left(x\right)$ for any $x\in U$. So, ${\widehat{\mathbf{D}}}_2$ is not an IF $\beta$-minimal reduction of $\widehat{\mathbf{C}}$, which is contradictory with ${\widehat{\mathbf{D}}}_2$ being an IF $\beta$-minimal reduction of $\widehat{\mathbf{C}}$. Thus, the IF $\beta$-minimal reduction of $\widehat{\mathbf{C}}$ is unique. □

By Proposition 7 and Theorem 3, the steps of calculating all IF $\beta$-minimal reductions in the IF $\beta$-covering approximation space $(U,\widehat{\mathbf{C}})$ are presented as follows:

Step 1: Compute the family of all IF sub-$\beta$-covering approximation spaces of $(U,\widehat{\mathbf{C}})$ according to Definition 11, i.e., $\mathcal{S}(\widehat{\mathbf{C}})$.

Step 2: For any $x\in U$ and $\widehat{\mathbf{D}}\in \mathcal{S}(\widehat{\mathbf{C}})$, compute ${\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$ according to Theorem 1, i.e., $f({\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right))=M_{\widehat{\mathbf{D}}}^T\left(x\right)⊵M_{\widehat{\mathbf{D}}}\left(x\right)\oplus \overline{M_{\widehat{\mathbf{D}}}}$.

Step 3: Compute $F=Min(\{\widehat{\mathbf{D}}\in \mathcal{S}(\widehat{\mathbf{C}}):\forall x\in U,{\widetilde{Md}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)\})$. The element of F is the IF $\beta$-minimal reduction of $\widehat{\mathbf{C}}$ according to Proposition 7 and Theorem 3.

Hence, the IF $\beta$-minimal reduction of $\widehat{\mathbf{C}}$ belongs to F.

4.2. Reductions of IF $\beta$-Covering Approximation Spaces via IF $\beta$-Maximal Descriptions

Based on Section 4.1, we present the definition of IF $\beta$-maximal reduction and corresponding matrix approaches in this subsection. Firstly, we present two properties of IF $\beta$-minimal descriptions in the IF sub-$\beta$-covering approximation space in the following two propositions, respectively.

Proposition 8.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$. For any $x\in U$, if $|{\tilde{\mathcal{N}}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)|=1$, then ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)$.

Proof. 

If $|{\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)|=1$, then we suppose ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)=\left\{C^{\prime }\right\}$, where $C^{\prime }\in \widehat{\mathbf{C}}$ and $C^{\prime }\left(x\right)\ge \beta$. Since $\widehat{\mathbf{D}}\in \mathcal{S}(\widehat{\mathbf{C}})$, $C^{\prime }\in \widehat{\mathbf{D}}$. Hence, ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)=\left\{C^{\prime }\right\}$. By Definition 9, ${\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)=\{C\in \widehat{\mathbf{C}}:C\left(x\right)\ge \beta \wedge (\forall D\in \widehat{\mathbf{C}})(D\left(x\right)\ge \beta \wedge C\subseteq D\Rightarrow C=D)\}=\{C\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right):\forall D\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)\wedge C\subseteq D\Rightarrow C=D\}=\{C^{\prime }\}$ and ${\widetilde{Md}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)=\{C\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right):\forall D\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)\wedge C\subseteq D\Rightarrow C=D\}=\left\{C^{\prime }\right\}$. Therefore, ${\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$. □

Proposition 9.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$. For any $x\in U$, if ${\tilde{\mathcal{N}}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)={\tilde{\mathcal{N}}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)$, then ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)$.

Proof. 

Since ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$, ${\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)=\{C\in \widehat{\mathbf{C}}:C\left(x\right)\ge \beta \wedge (\forall D\in \widehat{\mathbf{C}})(D\left(x\right)\ge \beta \wedge C\subseteq D\Rightarrow C=D)\}=\{C\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right):\forall D\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)\wedge C\subseteq D\Rightarrow C=D\}=\{C\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right):\forall D\in {\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)\wedge C\subseteq D\Rightarrow C=D\}={\widetilde{MD}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$. □

The converse of Proposition 9 is incorrect. That is to say, “for any $x\in U$, if ${\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$, then ${\tilde{\mathcal{N}}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\tilde{\mathcal{N}}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$” is not true. We use the following example to explain this.

Example 6 (Continued from Example 1).

In Example 1, $\widehat{\mathit{C}}=\{C_1,\cdots ,C_5\}$ is an IF β-covering of U. In Example 4, we have $f({\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x_1\right))={(0,1,1,0,0)}^T$, i.e., ${\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x_1\right)=\{C_2,C_3\}$. Suppose $\widehat{\mathit{D}}=\{C_1^{\prime },C_2^{\prime },C_3^{\prime }\}$, where $C_1^{\prime }=C_2$, $C_2^{\prime }=C_3$, $C_3^{\prime }=C_5\}$. Then, $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_1\right))\hfill & =M_{\widehat{\mathit{D}}}^T\left(x_1\right)⊴M_{\widehat{\mathit{D}}}\left(x_1\right)\oplus \overline{M_{\widehat{\mathit{D}}}}=\left(\begin{array}{ccc}6& 5& 0\\ 1& 6& 0\\ 0& 0& 0\end{array}\right)\oplus \left(\begin{array}{ccc}6& 6& 6\\ 6& 6& 6\\ 6& 6& 6\end{array}\right)=\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_1\right)=\{C_1^{\prime },C_2^{\prime }\}=\{C_2,C_3\}$. Hence, ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x_1\right)={\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_1\right)=\{C_2,C_3\}$. But ${\tilde{\mathcal{N}}}_{\widehat{\mathit{C}}}^{\beta }\left(x_1\right)=\{C_1,C_2,C_3\}$ and ${\tilde{\mathcal{N}}}_{\widehat{\mathit{D}}}^{\beta }\left(x_1\right)=\{C_2,C_3\}$, i.e., ${\tilde{\mathcal{N}}}_{\widehat{\mathit{C}}}^{\beta }\left(x_1\right)\ne {\tilde{\mathcal{N}}}_{\widehat{\mathit{D}}}^{\beta }\left(x_1\right)$.

Definition 13.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$. $\widehat{\mathit{D}}$ is called an IF β-maximal reduction of $\widehat{\mathit{C}}$ if $\widehat{\mathit{D}}$ satisfies the following conditions:

(1)

For any $x\in U$, ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)$;

(2)

For any $\widehat{\mathit{E}}\in \mathcal{S}(\widehat{\mathit{D}})-\{\widehat{\mathit{D}}\}$, there exists $x\in U$ such that ${\widetilde{MD}}_{\widehat{\mathit{E}}}^{\beta }\left(x\right)\ne {\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)$.

Proposition 10.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space. $\widehat{\mathit{D}}$ is an IF β-maximal reduction of $\widehat{\mathit{C}}$ if and only if $\widehat{\mathit{D}}\in Min(\{\widehat{\mathit{E}}\in \mathcal{S}(\widehat{\mathit{C}}):\forall x\in U,{\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{\widehat{\mathit{E}}}^{\beta }\left(x\right)\})$.

Proof. 

By Definition 13, it is immediate. □

Theorem 4.

Let $(U,\widehat{\mathit{C}})$ be an IF β-covering approximation space and $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$. The IF β-maximal reduction of $\widehat{\mathit{C}}$ is unique.

Proof. 

By Definition 13, the existence of the IF $\beta$-maximal reduction is true. Then, we use proof by contradiction to prove the uniqueness. Suppose ${\widehat{\mathbf{D}}}_1$ is an IF $\beta$-maximal reduction of $\widehat{\mathbf{C}}$ and ${\widehat{\mathbf{D}}}_2$ is the other one. Then, ${\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{{\widehat{\mathbf{D}}}_1}^{\beta }\left(x\right)={\widetilde{MD}}_{{\widehat{\mathbf{D}}}_2}^{\beta }\left(x\right)$ for any $x\in U$. Hence, there exists $K\in {\widehat{\mathbf{D}}}_2-{\widehat{\mathbf{D}}}_1$ such that $K\notin {\widetilde{MD}}_{{\widehat{\mathbf{D}}}_1}^{\beta }\left(x\right)$ for any $x\in U$. That is to say, $K\notin {\widetilde{MD}}_{{\widehat{\mathbf{D}}}_2}^{\beta }\left(x\right)$ for any $x\in U$. ${\widehat{\mathbf{D}}}_2-\left\{K\right\}$ is also an IF $\beta$-covering, since for any $x\in U$, there exists $C\in {\widetilde{MD}}_{{\widehat{\mathbf{D}}}_2}^{\beta }\left(x\right)$ such that $C\left(x\right)\ge \beta$. Therefore, ${\widetilde{MD}}_{{\widehat{\mathbf{D}}}_2-\left\{K\right\}}^{\beta }\left(x\right)={\widetilde{MD}}_{{\widehat{\mathbf{D}}}_2}^{\beta }\left(x\right)$ for any $x\in U$. So, ${\widehat{\mathbf{D}}}_2$ is not an IF $\beta$-maximal reduction of $\widehat{\mathbf{C}}$, which is contradictory with ${\widehat{\mathbf{D}}}_2$ is an IF $\beta$-maximal reduction. Thus, the IF $\beta$-maximal reduction of $\widehat{\mathbf{C}}$ is unique. □

By Proposition 10 and Theorem 4, the steps of calculating the IF $\beta$-maximal reduction in the IF $\beta$-covering approximation space $(U,\widehat{\mathbf{C}})$ are presented as follows:

Step 1: Compute the family of all IF sub-$\beta$-covering approximation spaces of $(U,\widehat{\mathbf{C}})$ according to Definition 11, i.e., $\mathcal{S}(\widehat{\mathbf{C}})$.

Step 2: For any $x\in U$ and $\widehat{\mathbf{D}}\in \mathcal{S}(\widehat{\mathbf{C}})$, compute ${\widetilde{MD}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)$ according to Theorem 2, i.e., $f({\widetilde{MD}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right))=M_{\widehat{\mathbf{D}}}^T\left(x\right)⊴M_{\widehat{\mathbf{D}}}\left(x\right)\oplus \overline{M_{\widehat{\mathbf{D}}}}$.

Step 3: Compute $F=Min(\{\widehat{\mathbf{D}}\in \mathcal{S}(\widehat{\mathbf{C}}):\forall x\in U,{\widetilde{MD}}_{\widehat{\mathbf{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{\widehat{\mathbf{D}}}^{\beta }\left(x\right)\})$. The element of F is the IF $\beta$-maximal reduction of $\widehat{\mathit{C}}$ according to Proposition 10 and Theorem 4.

Example 7.

A customer wants to choose suitable attributes to evaluate a house. Let $U=\{x_1,x_2,\cdots ,x_6\}$ be a set of houses and $\widehat{\mathit{C}}=\{C_1,C_2,\cdots ,C_5\}$ be five attributes given by merchants, where $C_1,C_2,\cdots ,C_5$ represent expensive, beautiful, large, convenient traffic and green surroundings, respectively. Suppose $C_j\left(x_i\right)=\langle {\mu }_{C_j\left(x_i\right)},{\nu }_{C_j\left(x_i\right)}\rangle$, $(i=1,2,\cdots ,6;j=1,2,\cdots ,5)$, where ${\mu }_{C_j\left(x_i\right)}$ and ${\nu }_{C_j\left(x_i\right)}$ are the degrees of membership and non-membership of the alternative $x_i$ to the attribute $C_j$, respectively. Let $\beta =\langle 0.6,0.3\rangle$ be the critical value. Suppose that for each alternative $x_i$ there exists the attribute $C_j$ such that $C_j\left(x_i\right)\ge \beta$. It is obvious that $\widehat{\mathit{C}}$ is an IF β-covering presented in Example 1.

Step 1: $\mathcal{S}(\widehat{\mathit{C}})=\{\{C_1,C_2,C_3,C_4,C_5\},\{C_1,C_3,C_4,C_5\},\{C_1,C_2,C_3,C_5\},\{C_2,C_3,C_4,C_5\}, \{C_1,C_2,C_3,C_4\},\{C_3,C_4,C_5\},$$\{C_1,C_2,C_3\},\{C_1,C_3,C_4\},\{C_1,C_3,C_5\},\{C_2,C_3,C_5\},\{C_2,C_3, C_4\},\{C_3,C_4,C_5\},\{C_1,C_3\},$$\{C_2,C_3\},\{C_2,C_5\},\{C_3,C_4\},\{C_3,C_5\},\left\{C_3\right\}\}$.

Step 2: For any $x\in U$ and $\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}})$, we compute ${\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)$ by matrices. All ${\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)$ for any $x\in U$ were calculated in Example 4. Here, we show the process about $\widehat{\mathit{D}}=\{C_2,C_3,C_4,C_5\}$ only.

Suppose $\widehat{\mathit{D}}=\{C_1^{\prime },C_2^{\prime },C_3^{\prime },C_4^{\prime }\}$, where $C_1^{\prime }=C_2,C_2^{\prime }=C_3,C_3^{\prime }=C_4,C_4^{\prime }=C_5$. Then,

Hence,

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_1\right))\hfill & =M_{\widehat{\mathit{D}}}^T\left(x_1\right)⊴M_{\widehat{\mathit{D}}}\left(x_1\right)\oplus \overline{M_{\widehat{\mathit{D}}}}=\left(\begin{array}{cccc}6& 5& 0& 0\\ 1& 6& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)\oplus \left(\begin{array}{cccc}6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}1\\ 1\\ 0\\ 0\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_1\right)=\{C_1^{\prime },C_2^{\prime }\}=\{C_2,C_3\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_2\right))\hfill & =M_{\widehat{\mathit{D}}}^T\left(x_2\right)⊴M_{\widehat{\mathit{D}}}\left(x_2\right)\oplus \overline{M_{\widehat{\mathit{D}}}}=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 6& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)\oplus \left(\begin{array}{cccc}6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_2\right)=\left\{C_2^{\prime }\right\}=\left\{C_3\right\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_3\right))\hfill & =M_{\widehat{\mathit{D}}}^T\left(x_3\right)⊴M_{\widehat{\mathit{D}}}\left(x_3\right)\oplus \overline{M_{\widehat{\mathit{D}}}}=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 6& 0& 1\\ 0& 0& 0& 0\\ 0& 5& 0& 6\end{array}\right)\oplus \left(\begin{array}{cccc}6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_3\right)=\{C_2^{\prime },C_4^{\prime }\}=\{C_3,C_5\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_4\right))\hfill & =M_{\widehat{\mathit{D}}}^T\left(x_4\right)⊴M_{\widehat{\mathit{D}}}\left(x_4\right)\oplus \overline{M_{\widehat{\mathit{D}}}}=\left(\begin{array}{cccc}6& 5& 0& 4\\ 1& 6& 0& 1\\ 0& 0& 0& 0\\ 1& 5& 0& 6\end{array}\right)\oplus \left(\begin{array}{cccc}6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}1\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_4\right)=\{C_1^{\prime },C_2^{\prime },C_4^{\prime }\}=\{C_2,C_3,C_5\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_5\right))\hfill & =M_{\widehat{\mathit{D}}}^T\left(x_5\right)⊴M_{\widehat{\mathit{D}}}\left(x_5\right)\oplus \overline{M_{\widehat{\mathit{D}}}}=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 6& 0& 1\\ 0& 6& 6& 6\\ 0& 5& 0& 6\end{array}\right)\oplus \left(\begin{array}{cccc}6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_5\right)=\{C_2^{\prime },C_4^{\prime }\}=\{C_3,C_5\}$.

$$\begin{array}{cc}f({\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_6\right))\hfill & =M_{\widehat{\mathit{D}}}^T\left(x_6\right)⊴M_{\widehat{\mathit{D}}}\left(x_6\right)\oplus \overline{M_{\widehat{\mathit{D}}}}=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 6& 0& 1\\ 0& 0& 0& 0\\ 0& 5& 0& 6\end{array}\right)\oplus \left(\begin{array}{cccc}6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\\ 6& 6& 6& 6\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 1\end{array}\right),\hfill \end{array}$$

i.e., ${\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x_6\right)=\{C_2^{\prime },C_4^{\prime }\}=\{C_3,C_5\}$.

Step 3: $Min(\{\widehat{\mathit{D}}\in \mathcal{S}(\widehat{\mathit{C}}):\forall x\in U,{\widetilde{MD}}_{\widehat{\mathit{C}}}^{\beta }\left(x\right)={\widetilde{MD}}_{\widehat{\mathit{D}}}^{\beta }\left(x\right)\})=Min\left(\{\{C_1,C_2,C_3,C_5\}, \{C_2,C_3,C_4,C_5\},\{C_2,C_3,C_5\}\}\right)=$$\left\{\{C_2,C_3,C_5\}\right\}$. Therefore, $\{C_2,C_3,C_5\}$ is the IF β-maximal reduction of $\widehat{\mathit{C}}$.

5. Experimental Evaluations

Compared with the set representations, it is necessary to show the advantage of matrix representations of IF $\beta$-minimal and $\beta$-maximal descriptions. In this section, we call the presented matrix methods of IF $\beta$-minimal and $\beta$-maximal descriptions as “M-IFMin” and “M-IFMax”, respectively. Hence, we compare them with the set-based algorithms of IF $\beta$-minimal and $\beta$-maximal descriptions (which are named “S-IFMin” and “S-IFMax”, respectively) through several experiments.

5.1. The Process of Experiments

We construct some IF $\beta$-covering approximation spaces to run M-IFMin, M-IFMax, S-IFMin and S-IFMax on them. In Definition 6, we know that any IF $\beta$-covering approximation space can be seen as an IF granular matrix. The procedure of constructing the IF $\beta$-matrix is as follows: (1) The elements of the matrix are IF numbers, which are randomly chosen from $\{0,0.1,0.2,\cdots ,0.9,1\}$. (2) For any row of the matrix, if the maximal number of the row is less than $\beta$, then we denote $\beta$ as its maximal number. Hence, the matrix is the IF $\beta$-matrix, i.e., an IF $\beta$-covering approximation space.

Finally, we compare the computational time of M-IFMin, M-IFMax, S-IFMin and S-IFMax with different values of $\beta$, sizes of a universe and sizes of an IF $\beta$-covering. All of the experiments were carried out on a personal computer with 64-bit Windows 10, Intel(R) Core(TM) i7-8565U CPU @1.80 GHz 1.99 GHz, and 8 GB memory. The programming language was Matlab r2016a.

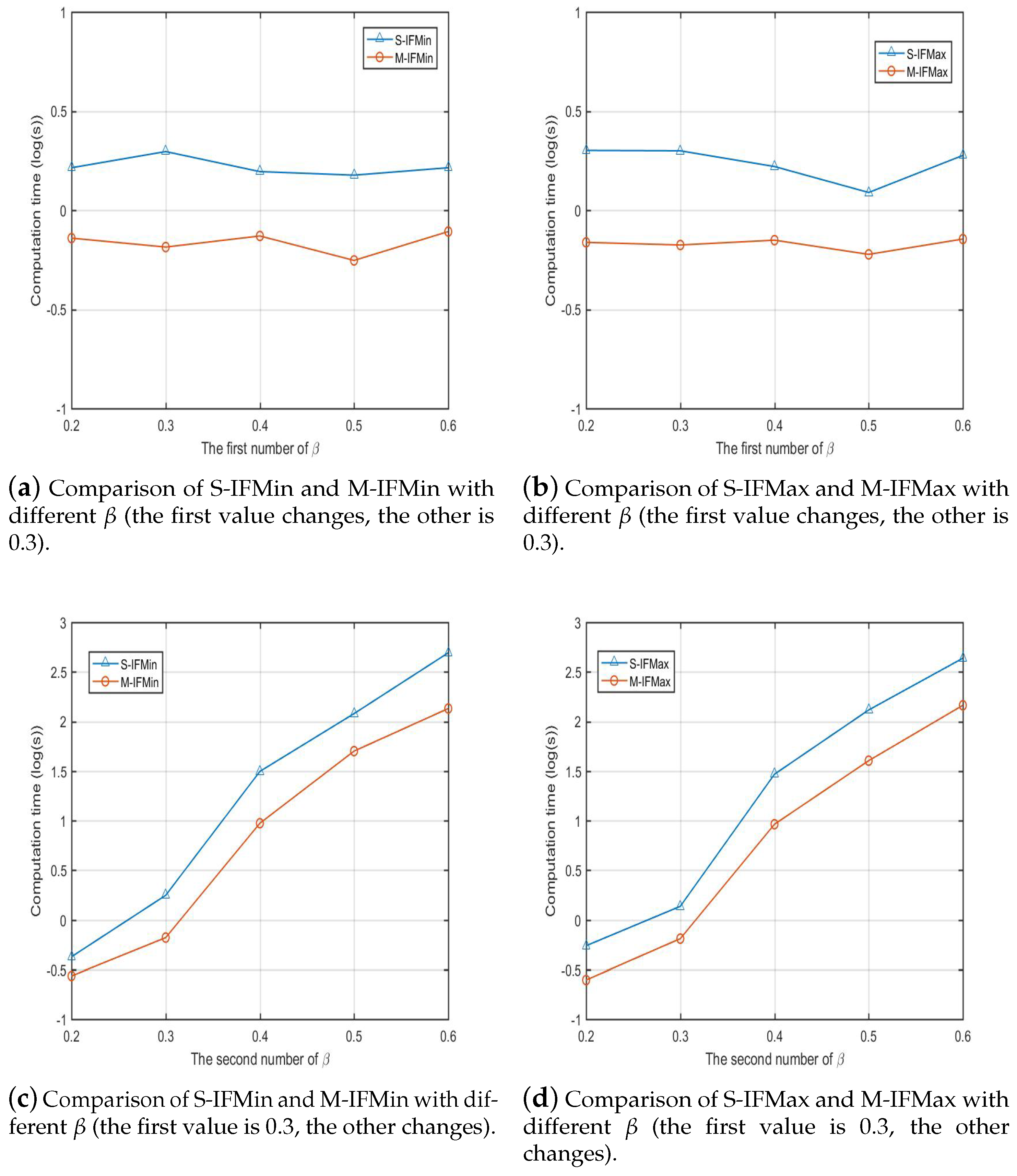
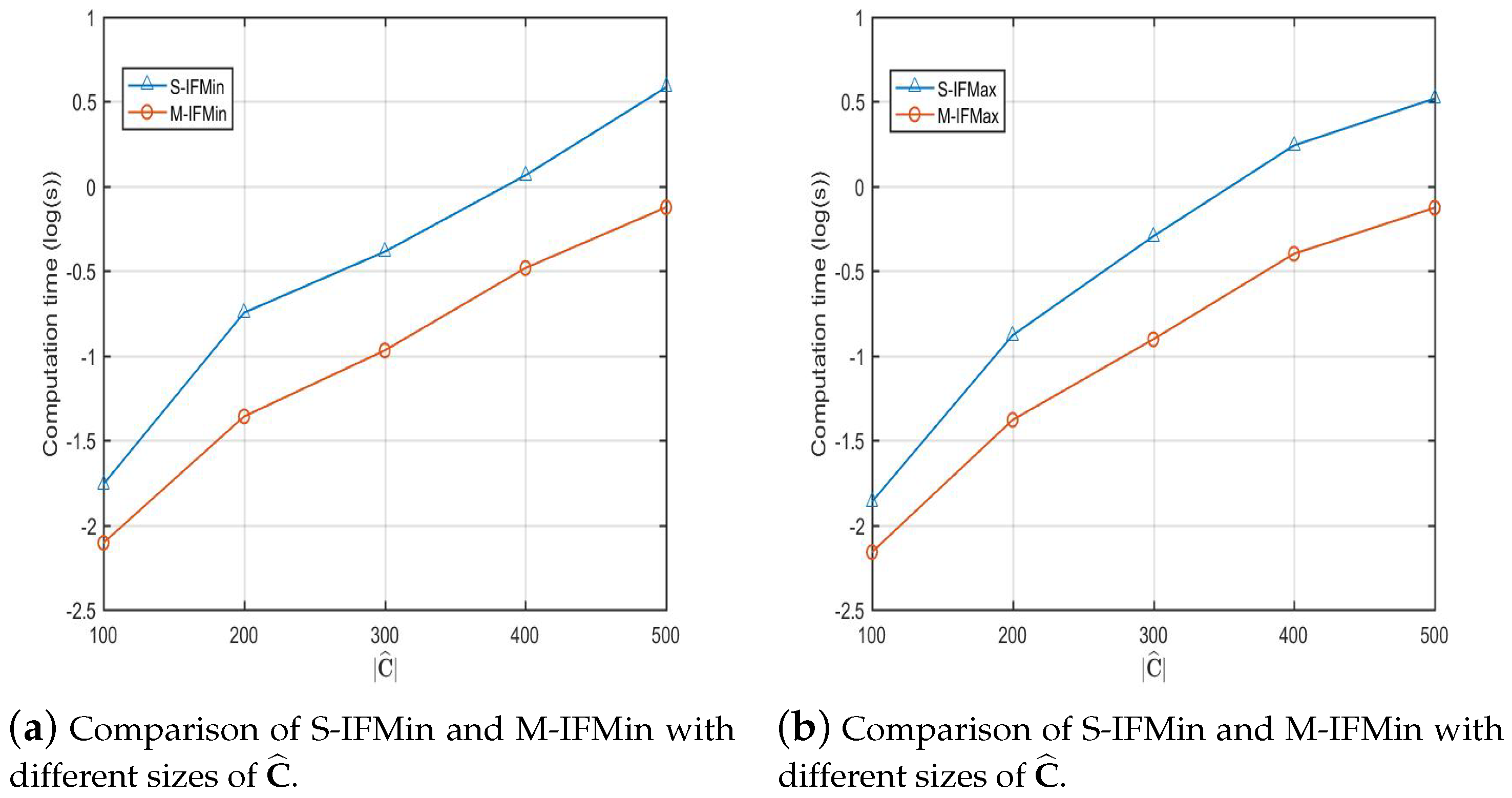
5.2. Results and Analysis

To compare the computational time of M-IFMin, M-IFMax, S-IFMin and S-IFMax with different values of $\beta$ in Figure 1, we set the size of U to 200 and the size of $\widehat{\mathbf{C}}$ to 600. The one value of $\beta$ ranges from $0.2$ to $0.6$, gradually increasing by a step of $0.1$, and the other value is $0.3$. Figure 1a,c show the computational time of M-IFMin and S-IFMin. In Figure 1a, the first value of $\beta$ ranges from $0.2$ to $0.6$, gradually increasing by a step of $0.1$, and the second value is $0.3$. In Figure 1c, the first value is $0.3$ and the second value of $\beta$ ranges from $0.2$ to $0.6$, gradually increasing by a step of $0.1$. Figure 1b,d show the computational time of M-IFMax and S-IFMax. In Figure 1b, the first value of $\beta$ ranges from $0.2$ to $0.6$, gradually increasing by a step of $0.1$, and the second value is $0.3$. In Figure 1d, the first value is $0.3$ and the second value of $\beta$ ranges from $0.2$ to $0.6$, gradually increasing by a step of $0.1$. In Figure 1, we can see that the computational time of M-IFMin, M-IFMax, S-IFMin and S-IFMax decreases with the gradual increase in the value of $\beta$. M-IFMin (or M-IFMax) is more efficient than S-IFMin (or S-IFMax) with different values of $\beta$, especially with small values of $\beta$.

To compare the computational time of M-IFMin, M-IFMax, S-IFMin and S-IFMax with different sizes of U in Figure 2, we set the value of $\beta$ to $\langle 0.6,0.3\rangle$ and the size of $\widehat{\mathbf{C}}$ to 200. The size of U ranges from 200 to 600, gradually increasing by a step of 100. In Figure 2, we can see that the computational time of M-IFMin, M-IFMax, S-IFMin and S-IFMax increases with the gradual increase in the size of U. M-IFMin (or M-IFMax) is more efficient than S-IFMin (or S-IFMax) with different sizes of U. Hence, for large universe sizes, M-IFMin (or M-IFMax) is feasible.

To compare the computational time of M-IFMin, M-IFMax, S-IFMin and S-IFMax with different sizes of $\widehat{\mathbf{C}}$ in Figure 3, we set the value of $\beta$ to $\langle 0.6,0.3\rangle$ and the size of U to 200. The size of $\widehat{\mathbf{C}}$ ranges from 100 to 500, gradually increasing by a step of 100. In Figure 3, we can see that the computational time of M-IFMin, M-IFMax, S-IFMin and S-IFMax increases with the gradual increase in the size of U. M-IFMin (or M-IFMax) is more efficient than S-IFMin (or S-IFMax) with different sizes of $\widehat{\mathbf{C}}$, especially with large $\widehat{\mathbf{C}}$.

By Figure 2 and Figure 3, we can see that M-IFMin and M-IFMax are feasible for large U and $\widehat{\mathbf{C}}$, respectively. That is to say, they are scalable on big data sets.

6. Conclusions

In this paper, we mainly use matrix approaches to study IF $\beta$-covering rough sets by IF $\beta$-minimal and $\beta$-maximal descriptions. Moreover, the feasibility of the proposed matrix approaches is studied by several experiments. The main conclusions of this paper are as follows:

• The matrix representations of IF $\beta$-minimal and $\beta$-maximal descriptions are proposed. Moreover, the comparative analysis illustrates that the proposed calculus based on matrices is feasible for large IF $\beta$-coverings as well as big data sets.
• Two new types of reductions of IF $\beta$-covering approximation spaces are proposed via IF $\beta$-minimal and $\beta$-maximal descriptions, respectively. They are calculated based on the matrix representations of IF $\beta$-minimal and $\beta$-maximal descriptions. It is a new viewpoint to study IF $\beta$-covering rough sets using IF $\beta$-minimal and $\beta$-maximal descriptions.

Although the matrix method proposed by us is faster than the existing set method in IF set theory, it is still somewhat time-consuming in the environment of big data, and further faster calculation methods need to be proposed. In the future, the following research topics are deserving of attention. These matrix approaches can be used in fuzzy soft covering-based multi-granulation fuzzy rough sets [43]. Moreover, Choquet-like integrals [44,45] were recently combined with fuzzy rough sets, which can connected with the content of this paper in further research.