Strong Consistency of Incomplete Functional Percentile Regression
Abstract
:1. Introduction
2. The Quantile with Regressor and Its Estimators
3. Main Results
- Theorem
- Proof of Theorem
4. Computational Aspects
4.1. Simulation Result
- Step 1.
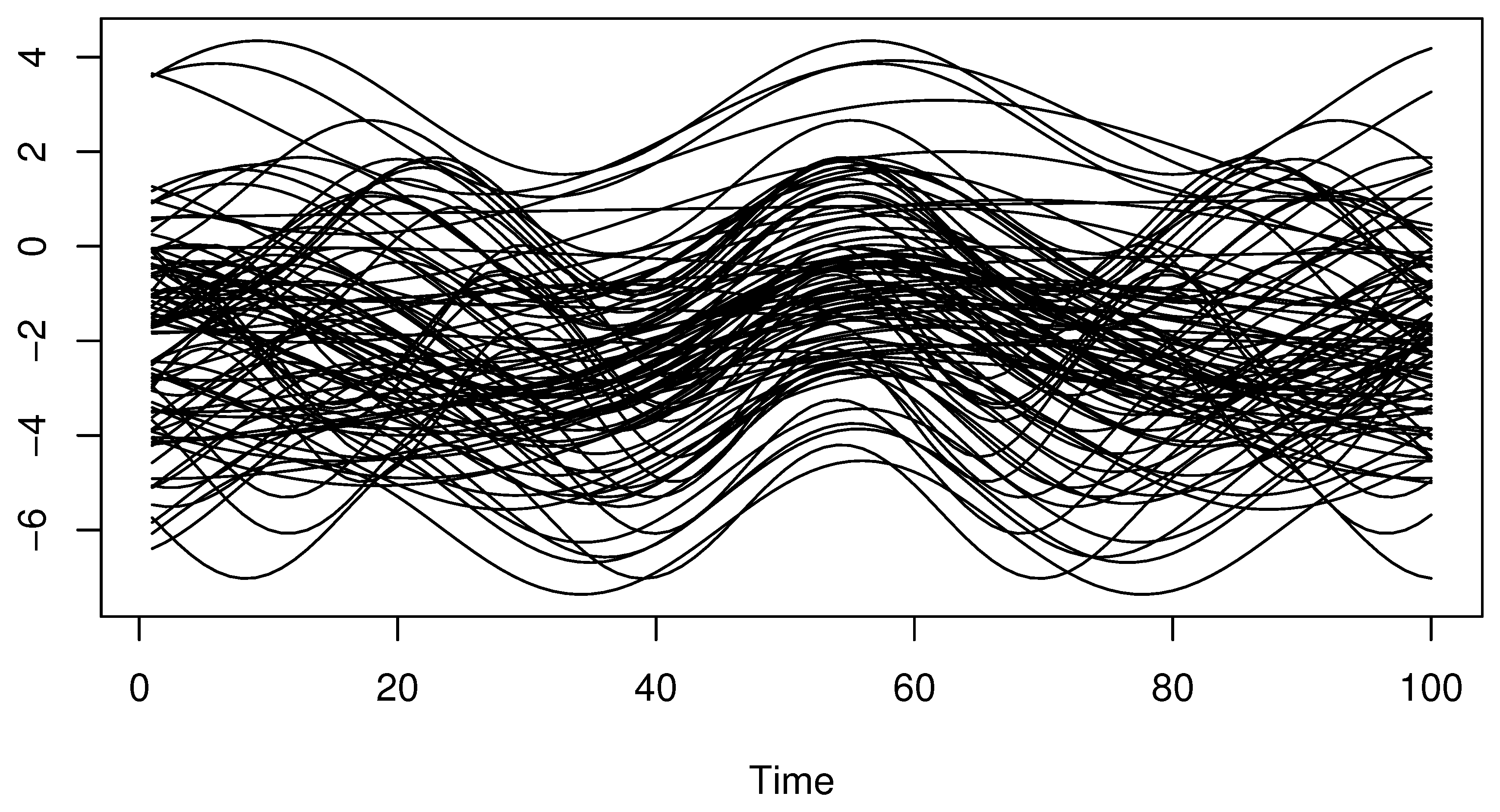
- We generate a sequence of functional exploratory variables fromwhere follows and follows . Such a sample of curves s is discretized in 100 equi-spaced grids in . The functional curves are presented in Figure 1.
- Step 2.
- We generate the output variable Y using a functional regression modelwhere is independent of X and has a Laplace distribution. This sampling algorithm shows that the law of is defined by shifting the distribution of .Next, to incorporate the theoretical part of this work, we pay attention in this comparative study to analyzing the behavior of the estimator using various missing levels. Specifically, we compare the resistance of the estimators , , and using different missing rates. Furthermore, the missing phenomena are modeled aswhere . This consideration allows us to control the missing rate through the parameter . Typically, we examine three levels of censoring levels, which are strong, medium, and weak, which correspond to , , and , respectively. Empirically, the missing level is evaluated byFor the above values of , we observe that there are 5% missed observations when ; 30% missed observations for ; and more than 57% missing observations when .
- Step 3.
- We calculate the three estimators , , and . For the practical computation of these estimators, we consider a kernel as a quadratic kerneland we choose the locating functions δ and ℓ defined bywhere denotes the ith derivative of x, and denotes the eigenfunction associated with the greatest eigenvalue of the covariance matrix
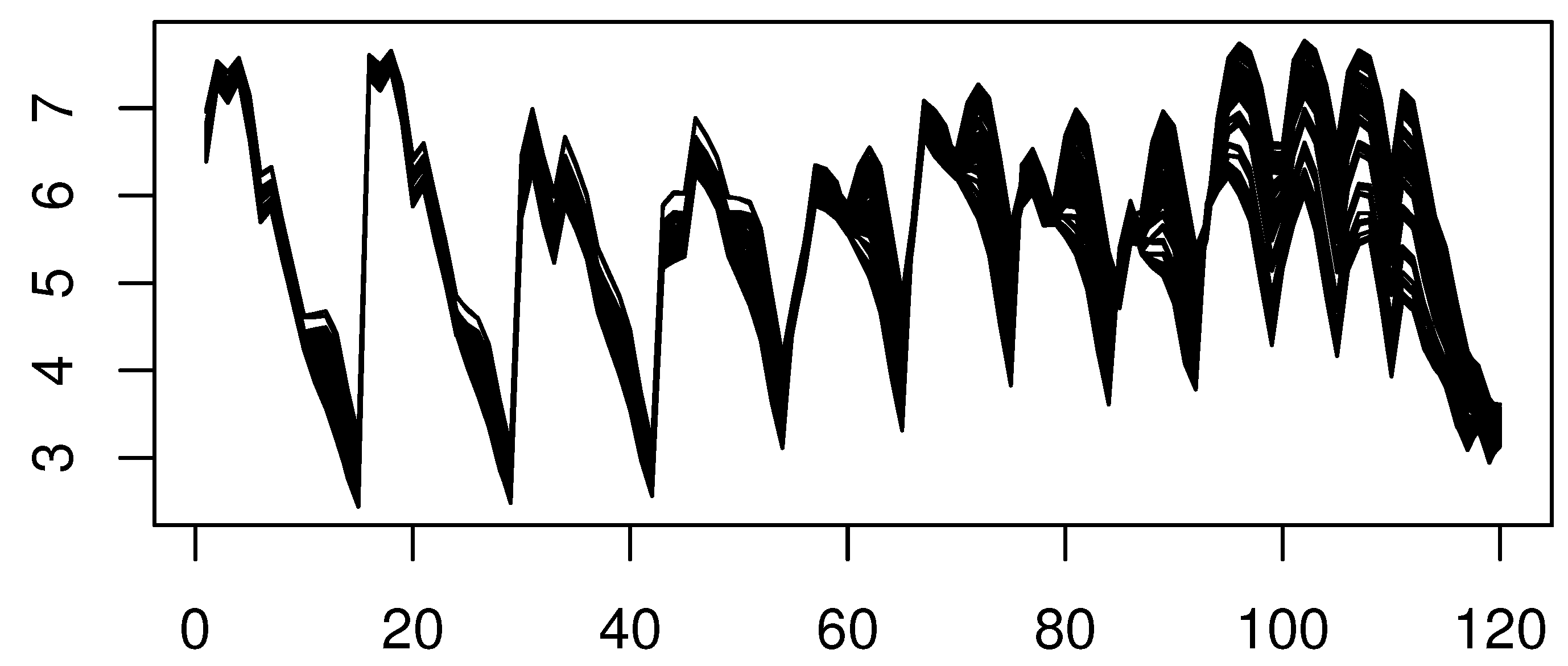
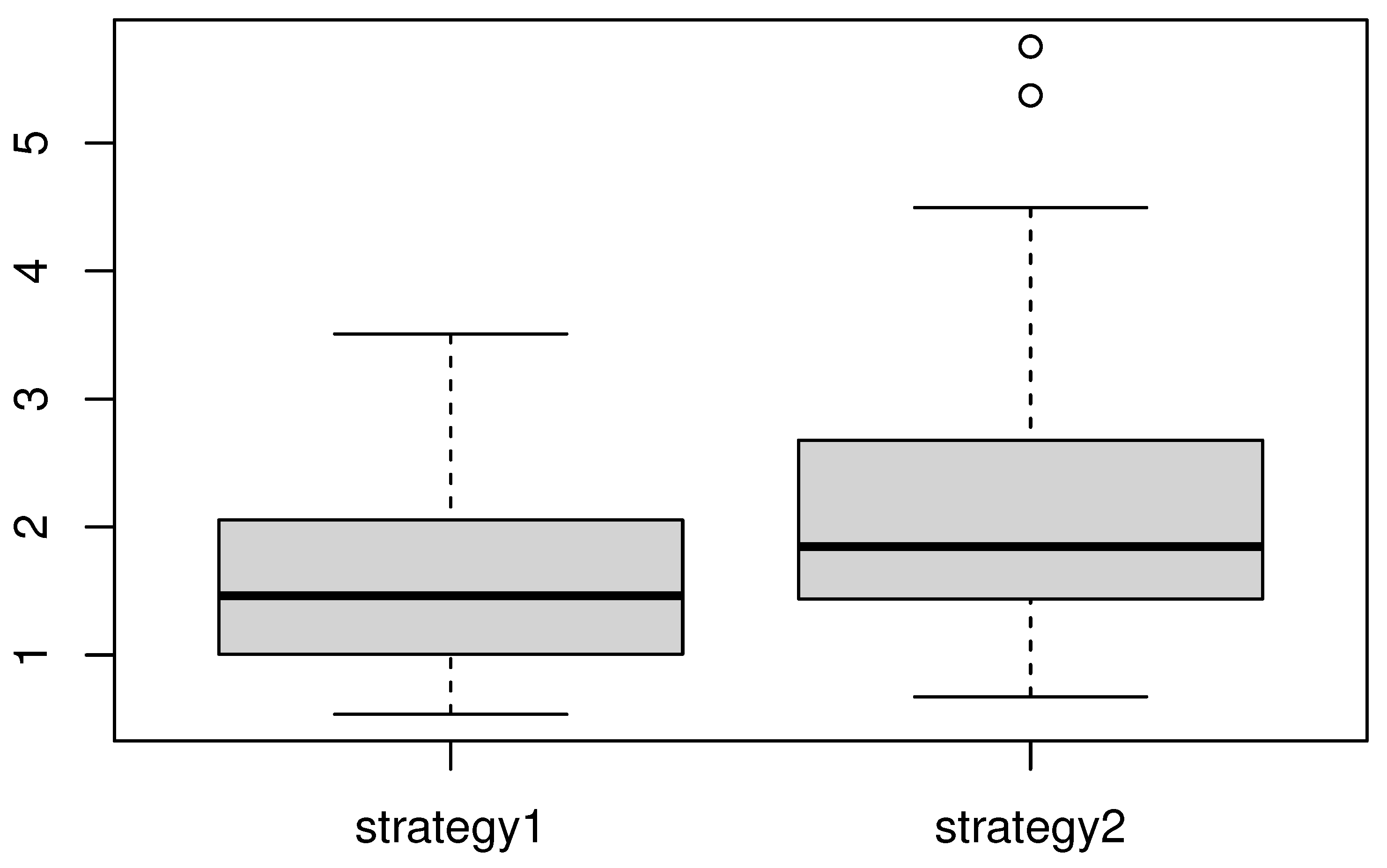
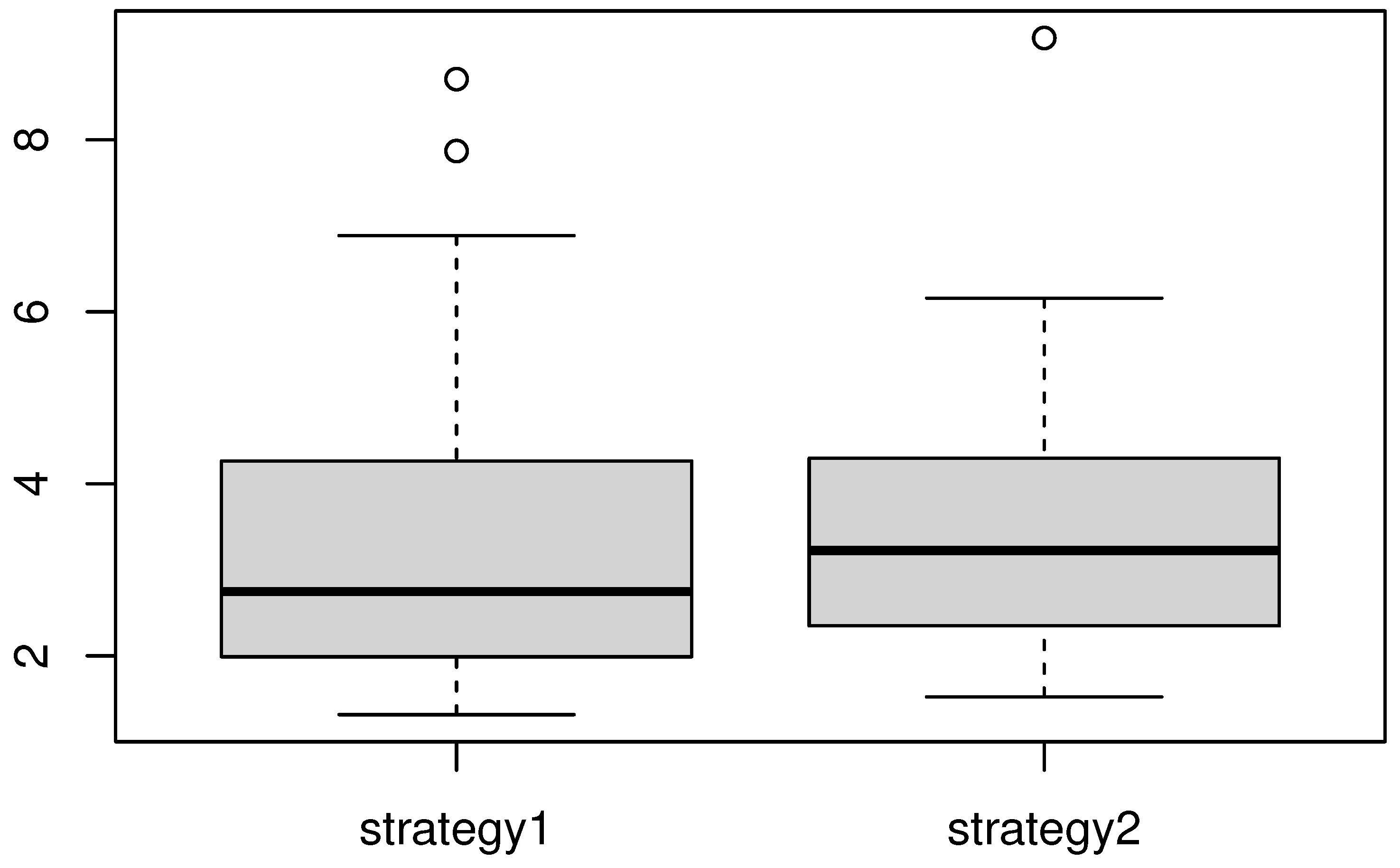
4.2. A Real Data Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Samanta, M. Nonparametric estimation of conditional quantiles. Statist. Probab. Lett. 1989, 7, 407–412. [Google Scholar] [CrossRef]
- Gannoun, A.; Saracco, J.; Yu, K. Nonparametric prediction by conditional median and quantiles. J. Statist. Plann. Inference 2003, 117, 207–223. [Google Scholar] [CrossRef]
- Zhou, Y.; Liang, H. Asymptotic normality for L1 norm Kernel estimator of conditional median under K-mixing dependence. J. Multivar. Anal. 2000, 73, 136–154. [Google Scholar] [CrossRef]
- Cardot, H.; Crambes, C.; Sarda, P. Estimation spline de quantiles conditionnels pour variables explicatives fonctionnelles. C. R. Math. Acad. Sci. Paris 2004, 339, 141–144. [Google Scholar] [CrossRef]
- Ferraty, F.; Laksaci, A.; Vieu, P. Estimating some characteristics of the conditional distribution in nonparametric functional models. Stat. Inference Stoch. Process. 2006, 9, 47–76. [Google Scholar] [CrossRef]
- Dabo-Niang, S.; Laksaci, A. Estimation non paramétrique de mode conditionnel pour variable explicative fonctionnelle. C. R. Math. Acad. Sci. Paris 2007, 344, 49–52. [Google Scholar] [CrossRef]
- He, F.Y.; Cheng, Y.B.; Tong, T.J. Nonparametric estimation of extreme conditional quantiles with functional covariate. Acta Math. Sin. (Engl. Ser.) 2018, 34, 1589–1610. [Google Scholar] [CrossRef]
- Laksaci, A.; Lemdani, M.; Ould Saïd, E. A generalized l1-approach for a Kernel estimator of conditional quantile with functional regressors: Consistency and asymptotic normality. Stat. Probab. Lett. 2009, 79, 1065–1073. [Google Scholar] [CrossRef]
- Laksaci, A.; Maref, F. Estimation non paramétrique de quantiles conditionnels pour des variables fonctionnelles spatialement dépendantes. Comptes Rendus Math. 2009, 347, 1075–1080. [Google Scholar] [CrossRef]
- Al-Awadhi, F.A.; Kaid, Z.; Laksaci, A.; Ouassou, I.; Rachdi, M. Functional data analysis: Local linear estimation of the L 1-conditional quantiles. Stat. Methods Appl. 2019, 28, 217–240. [Google Scholar] [CrossRef]
- Baìllo, A.; Grané, A. Local linear regression for functional predictor and scalar response. J. Multivar. Anal. 2009, 100, 102–111. [Google Scholar] [CrossRef]
- Berlinet, A.; Elamine, A.; Mas, A. Local linear regression for functional data. Ann. Inst. Stat. Math. 2011, 63, 1047–1075. [Google Scholar] [CrossRef]
- Barrientos, J.; Ferraty, F.; Vieu, P. Locally Modelled Regression and Functional Data. J. Nonparametr. Statist. 2010, 22, 617–632. [Google Scholar] [CrossRef]
- Demongeot, J.; Laksaci, A.; Madani, F.; Rachdi, M. Functional data: Local linear estimation of the conditional density and its application. Statistics 2013, 47, 26–44. [Google Scholar] [CrossRef]
- Demongeot, J.; Laksaci, A.; Rachdi, M.; Rahmani, S. On the local linear modelization of the conditional distribution for functional data. Sankhya A 2014, 76, 328–355. [Google Scholar] [CrossRef]
- Chouaf, A.; Laksaci, A. On the functional local linear estimate for spatial regression. Stat. Risk Model. 2012, 29, 189–214. [Google Scholar] [CrossRef]
- Xiong, X.; Zhou, P.; Ailian, C. Asymptotic normality of the local linear estimation of the conditional density for functional time-series data. Commun. -Stat.-Theory Methods. 2018, 47, 3418–3440. [Google Scholar] [CrossRef]
- Demongeot, J.; Naceri, A.; Laksaci, A.; Rachdi, M. Local linear regression modelization when all variables are curves. Stat. Probab. Lett. 2017, 121, 37–44. [Google Scholar] [CrossRef]
- Chahad, A.; Ait-Hennani, L.; Laksaci, A. Functional local linear estimate for functional relative-error regression. J. Stat. Theory Pract. 2017, 11, 771–789. [Google Scholar] [CrossRef]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Josse, J.; Reiter, J.P. Introduction to the special section on missing data. Stat. Sci. 2018, 33, 139–141. [Google Scholar] [CrossRef]
- Little, R.; Rublin, D. Statistical Analysis with Missing Data, 2nd ed.; John Wiley: New York, NY, USA, 2002. [Google Scholar]
- Efromovich, S. Nonparametric Regression with Predictors Missing at Random. J. Am. Stat. Assoc. 2011, 106, 306–319. [Google Scholar] [CrossRef]
- Ferraty, F.; Sued, F.; Vieu, P. Mean estimation with data missing at random for functional covariables. Statistics 2013, 47, 688–706. [Google Scholar] [CrossRef]
- Ling, N.; Liang, L.; Vieu, P. Nonparametric regression estimation for functional stationary ergodic data with missing at random. J. Statist. Plann. Inference 2015, 162, 75–87. [Google Scholar] [CrossRef]
- Ling, N.; Liu, Y.; Vieu, P. Conditional mode estimation for functional stationary ergodic data with responses missing at random. Statistics 2016, 50, 991–1013. [Google Scholar] [CrossRef]
- Bachir Bouiadjra, H. Conditional hazard function estimate for functional data with missing at random. Int. J. Stat. Econ. 2017, 18, 45–58. [Google Scholar]
- Almanjahie, I.M.; Mesfer, W.; Laksaci, A. The K nearest neighbors local linear estimator of functional conditional density when there are missing data. Hacet. J. Math. Stat. 2022, 51, 914–931. [Google Scholar] [CrossRef]
- Yu, K.; Jones, M. Local linear quantile regression. J. Am. Stat. Assoc. 1998, 93, 228–237. [Google Scholar] [CrossRef]
- Hallin, M.; Lu, Z.; Yu, K. Local linear spatial quantile regression. Bernoulli 2009, 15, 659–686. [Google Scholar] [CrossRef]
- Bhattacharya, P.K.; Gangopadhyay, A.K. Kernel and nearest-neighbor estimation of a conditional quantile. Ann. Stat. 1990, 18, 1400–1415. [Google Scholar] [CrossRef]
- Ma, X.; He, X.; Shi, X. A variant of K nearest neighbor quantile regression. J. Appl. Stat. 2016, 43, 526–537. [Google Scholar] [CrossRef]
- Cheng, P.E.; Chu, C.K. Kernel estimation of distribution functions and quantiles with missing data. Stat. Sin. 1996, 6, 63–78. [Google Scholar]
- Xu, D.; Du, J. Nonparametric quantile regression estimation for functional data with responses missing at random. Metrika 2020, 83, 977–990. [Google Scholar] [CrossRef]
- Kara-Zaitri, L.; Laksaci, A.; Rachdi, M.; Vieu, P. Data-driven kNN estimation for various problems involving functional data. J. Multivar. Anal. 2017, 153, 176–188. [Google Scholar] [CrossRef]
- Becker, E.M.; Christensen, J.; Frederiksen, C.S.; Haugaard, V.K. Front-face fluorescence spectroscopy and chemometrics in analysis of yogurt: Rapid analysis of riboflavin. J. Dairy Sci. 2003, 86, 2508–2515. [Google Scholar] [CrossRef]
| Estimator | Quartile | Rule | n | |||
|---|---|---|---|---|---|---|
| Estimator | Q1 | 1 | 50 | 0.2358 | 0.3997 | 0.4672 |
| 2 | 50 | 0.2067 | 0.2676 | 0.3879 | ||
| 1 | 250 | 0.1407 | 0.2340 | 0.3717 | ||
| 2 | 250 | 0.1835 | 0.1980 | 0.2140 | ||
| Estimator | Q1 | 1 | 50 | 0.3672 | 0.4426 | 1.0578 |
| 2 | 50 | 0.7697 | 1.1725 | 1.7811 | ||
| 1 | 250 | 0.3086 | 0.3508 | 0.682 | ||
| 2 | 250 | 0.4162 | 0.5117 | 0.8106 | ||
| Estimator | Q1 | 1 | 50 | 1.3672 | 1.6426 | 1.0578 |
| 2 | 50 | 1.7697 | 1.9725 | 2.7811 | ||
| 1 | 250 | 0.9086 | 1.3508 | 1.4282 | ||
| 2 | 250 | 1.0462 | 1.5117 | 1.9106 | ||
| Estimator | Q2 | 1 | 50 | 0.1840 | 0.2253 | 0.4102 |
| 2 | 50 | 0.2005 | 0.2339 | 0.3650 | ||
| 1 | 250 | 0.0912 | 0.1873 | 0.1494 | ||
| 2 | 250 | 0.1101 | 0.1991 | 0.1616 | ||
| Estimator | Q2 | 1 | 50 | 0.0657 | 0.1650 | 0.2107 |
| 2 | 50 | 0.0984 | 0.1922 | 0.188 | ||
| 1 | 250 | 0.0677 | 0.0971 | 0.1478 | ||
| 2 | 250 | 0.0327 | 0.0303 | 0.0643 | ||
| Estimator | Q2 | 1 | 50 | 0.6967 | 0.9824 | 1.0788 |
| 2 | 50 | 0.4176 | 0.4521 | 0.6588 | ||
| 1 | 250 | 0.2952 | 0.3880 | 0.4950 | ||
| 2 | 250 | 0.2965 | 0.3718 | 0.4301 | ||
| Estimator | Q3 | 1 | 50 | 1.851 | 2.5103 | 3.2202 |
| 2 | 50 | 1.2035 | 3.3339 | 3.5650 | ||
| 1 | 250 | 1.7182 | 1.4723 | 2.5494 | ||
| 2 | 250 | 1.3111 | 1.3991 | 2.18616 | ||
| Estimator | Q3 | 1 | 50 | 0.9257 | 1.0350 | 1.1317 |
| 2 | 50 | 1.0804 | 1.1232 | 1.188 | ||
| 1 | 250 | 0.7017 | 0.9751 | 1.0278 | ||
| 2 | 250 | 0.6127 | 0.8303 | 0.9613 | ||
| Estimator | Q3 | 1 | 50 | 2.6907 | 2.7824 | 4.8898 |
| 2 | 50 | 1.8176 | 1.8251 | 1.9688 | ||
| 1 | 250 | 1.1479 | 1.1780 | 1.18950 | ||
| 2 | 250 | 1.0985 | 2.0898 | 2.1201 |
| Constant C | Median Regression | Classical Regression |
|---|---|---|
| C = 1 | 1.37 | 1.72 |
| C = 2 | 1.66 | 4.79 |
| C = 5 | 2.24 | 10.17 |
| C = 10 | 4.18 | 45.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamari, M.B.; Almulhim, F.A.; Litimein, O.; Mechab, B. Strong Consistency of Incomplete Functional Percentile Regression. Axioms 2024, 13, 444. https://doi.org/10.3390/axioms13070444
Alamari MB, Almulhim FA, Litimein O, Mechab B. Strong Consistency of Incomplete Functional Percentile Regression. Axioms. 2024; 13(7):444. https://doi.org/10.3390/axioms13070444
Chicago/Turabian StyleAlamari, Mohammed B., Fatimah A. Almulhim, Ouahiba Litimein, and Boubaker Mechab. 2024. "Strong Consistency of Incomplete Functional Percentile Regression" Axioms 13, no. 7: 444. https://doi.org/10.3390/axioms13070444





