Mathematical Modeling of Immune Dynamics in Chronic Myeloid Leukemia Therapy: Unraveling Allergic Reactions and T Cell Subset Modulation by Imatinib
Abstract
:1. Introduction
2. The Mathematical Model
- —it balances the effect of the immune system on the leukemic cells and it depends on the total number of leukemic cells (naive and mature);
- —it controls the activation of APCs depending on the number of mature leukemic cells;
- —it regulates the immune response through the number of mature leukemic cells;
- —it regulates the population CD8+ mature cells through T-reg cells.
3. Positivity of Solutions
4. Stability of Some Equilibria
4.1. The Equilibrium Point
4.2. The Equilibrium Point
- The roots of have negative real parts.
4.3. Equilibrium Point
- The roots of have negative real parts
- The roots of have negative real parts
- and have no common imaginary zero.
- , for real y (the upper bar denotes complex conjugate).
- .
- There are at most a finite number of roots of in the right half-plane when .
- , for real y, has at most a finite number of real zeroes.
- (a)
- Suppose that the equation has no positive roots. Then, if is stable at , it remains stable for all , and if it is unstable at , it remains unstable for all .
- (b)
- Suppose that the equation has at least one positive root and that each positive root is simple. As increases, stability switches may occur. There exists a positive number such that the equation is unstable for all . As varies from 0 to , at most, a finite number of stability switches may occur.
4.4. Equilibrium Point
- The following equation has negative rootsi.e.,
- The roots ofhave negative real parts.
5. Parameters Values, Numerical Calculations, and Simulations
| The production rate of naive CD4+ cells [19] | 0.1 | |
| The strength of suppression rate of Th1 by Th2 [14] | 0.1 | |
| The strength of suppression of Th2 by Th1 [14] | 0.2 | |
| The strength of suppression rate by Treg [14] | 0.5 | |
| The differences in the autocrine action of the three subsets [14] | p | 0.05 |
| The differences in the autocrine action of the three subsets [14] | 0.1 | |
| The death rate of cells [27] | ||
| The death rate of cells [27] | ||
| The death rate of cells [27] | ||
| The proliferation rate of stimulated T cells [14] | 0.2 | |
| Time delay [22] | ||
| Initial number of immune cells [28] | = 0.1 in microliter |
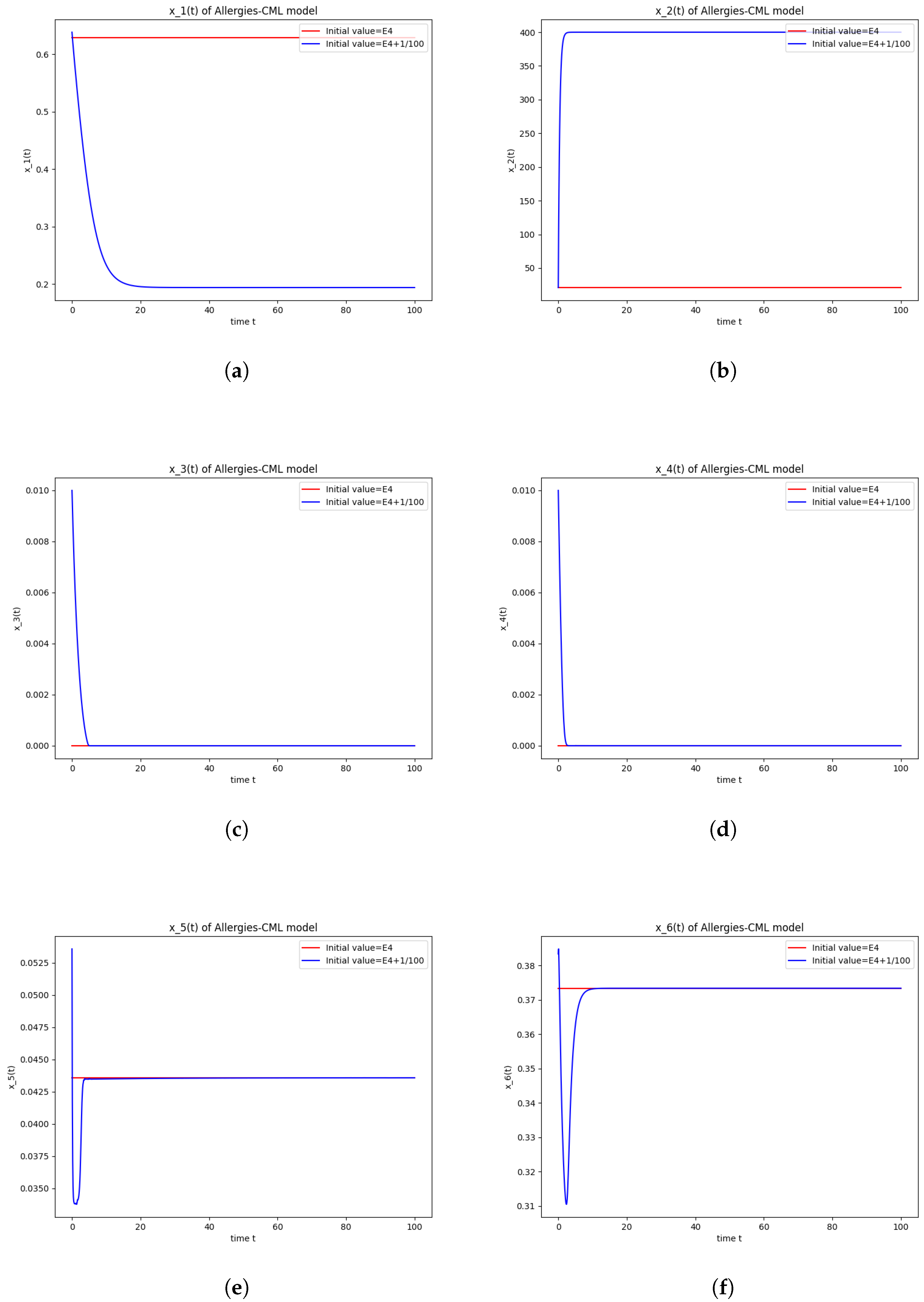
5.1. Numerical Simulations and Computations for
| Parameter for the function for healthy cells | 1.77 | |
| Parameter for the function for leukemia cells | 2 | |
| Parameter for the function k for healthy cells | 0.1 | |
| Parameter for the function k for leukemia cells | 0.4 | |
| The maximum value of the function for leukemic cells | 0.5 | |
| The maximum value of the function for healthy cells | 0.5 | |
| The maximum value of the function k for leukemic cells | 36 | |
| The maximum value of the function k for healthy cells | 36 | |
| Parameter of the Hill function | 2 | |
| Parameter of the Hill function | 2 | |
| Parameter of the Hill function | 2 | |
| Parameter of the Hill function | 2 | |
| Loss of stem cells due to mortality and differentiation in other lines for leukemic cells | 0.04 | |
| Loss of stem cells due to mortality and differentiation in other lines for healthy cells [2] | 0.1 | |
| Rate of asymmetric division for leukemic cells | 0.1 | |
| Rate of asymmetric division for healthy cells | 0.7 | |
| Rate of symmetric division for leukemic cells | 0.7 | |
| Rate of symmetric division for healthy cells | 0.1 | |
| Loss of stem cells due to cytotoxic T cells | 0.03 | |
| Instant mortality of mature leukemic leukocytes | 1.2, 0.15 | |
| Instant mortality of mature normal leukocytes | 2.4 | |
| Amplification factor for leukemic leukocytes | 1400 | |
| Amplification factor for normal leukocytes [2] | 1200 | |
| Loss of mature leukocytes due to cytotoxic T cells | 0.6 | |
| Standard half-saturation in a Michaelis–Menten low | 6 | |
| Supply rate of immature APCs | 0.3/day | |
| Death/turnover rate of immature APCs | 0.03/day | |
| Coefficient of the activation due to imatinib | 1 | |
| Coefficient of the activation due to leukemia cells | 2 | |
| Death/turnover rate of mature APCs | 0.8/day | |
| Supply rate of naive T cells CD4+ phenotype | 2 | |
| Death/turnover rate of naive CD4+ cells | 0.03/day | |
| Death/turnover rate of effector CD4+ T helper cells | 0.23/day | |
| Supply rate of naive T cells CD8+ phenotype | 2 | |
| Death/turnover rate of naive CD8+ cells | 0.23/day | |
| Kinetic coefficient | 0.2 | |
| Coefficient of the positive growth signal [19] | 20 | |
| The number of antigen depending divisions | 6 | |
| Coefficient of inhibition due to Treg cells | 1 | |
| Coefficient of inhibition due to leukemic cells | 1.2 or 50 | |
| Number of divisions in minimal CD8+ developmental program | m | 4 |
| First-order absorbtion rate | 0.61 | |
| Dose of administrated drug | K | 0.2824 |
| Clearance rate | 0.0412 | |
| Duration of cell cycle for leukemia stem-like cells | 5.5 | |
| Duration of cell cycle for normal stem-like cells | 2.8 | |
| Duration of leukocyte cycle for leukemic cells | 5.4 | |
| Duration of leukocyte cycle for normal cells | 3.5 | |
| Duration of one CD4+ T cell division (bifurcation parameter) | 2.4 days | |
| Duration of one CD8+ T cell division | 1.4 days | |
| Duration of minimal developmental program, | 5.6 | |
| Duration of minimal developmental program, | 8.4 |
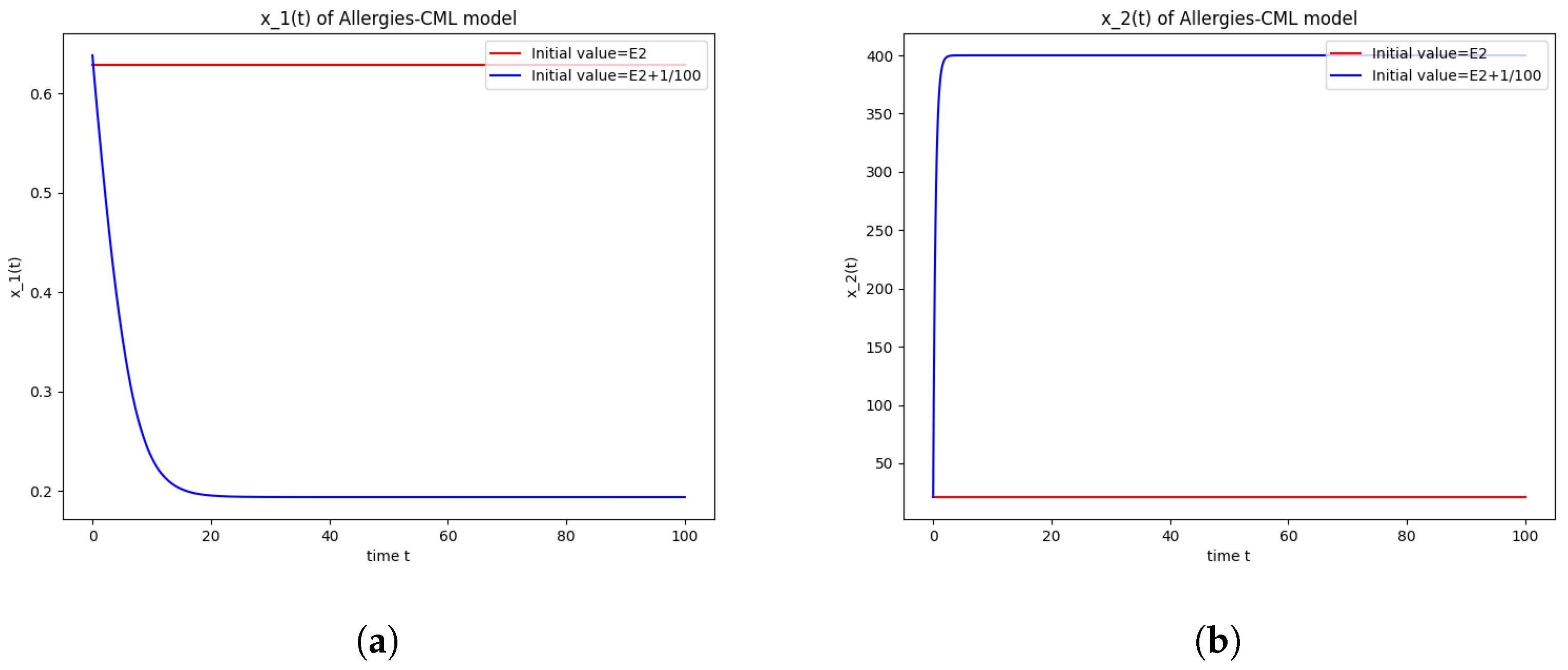
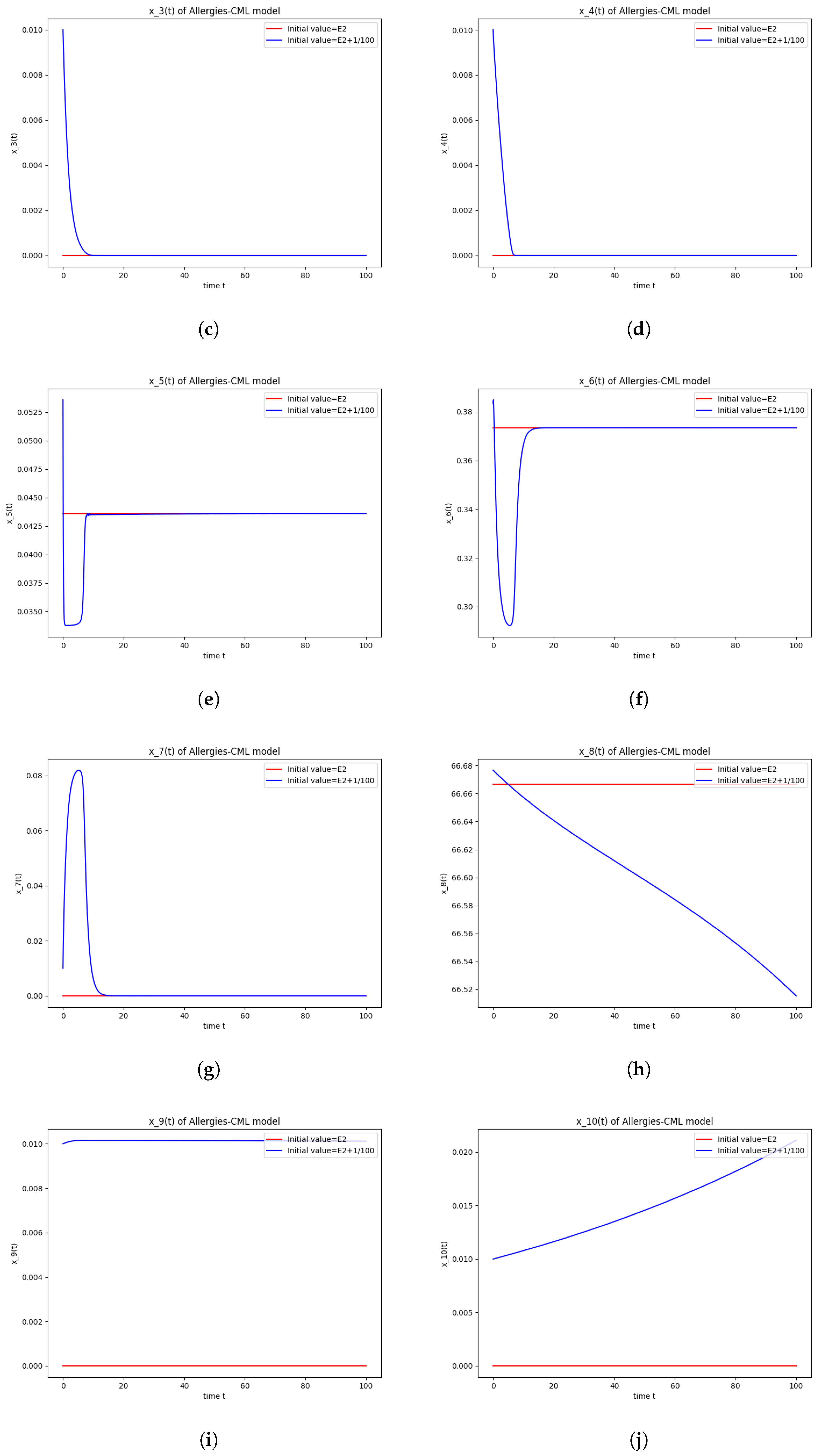
5.2. Numerical Simulations and Computations for
- The roots of have negative real parts.
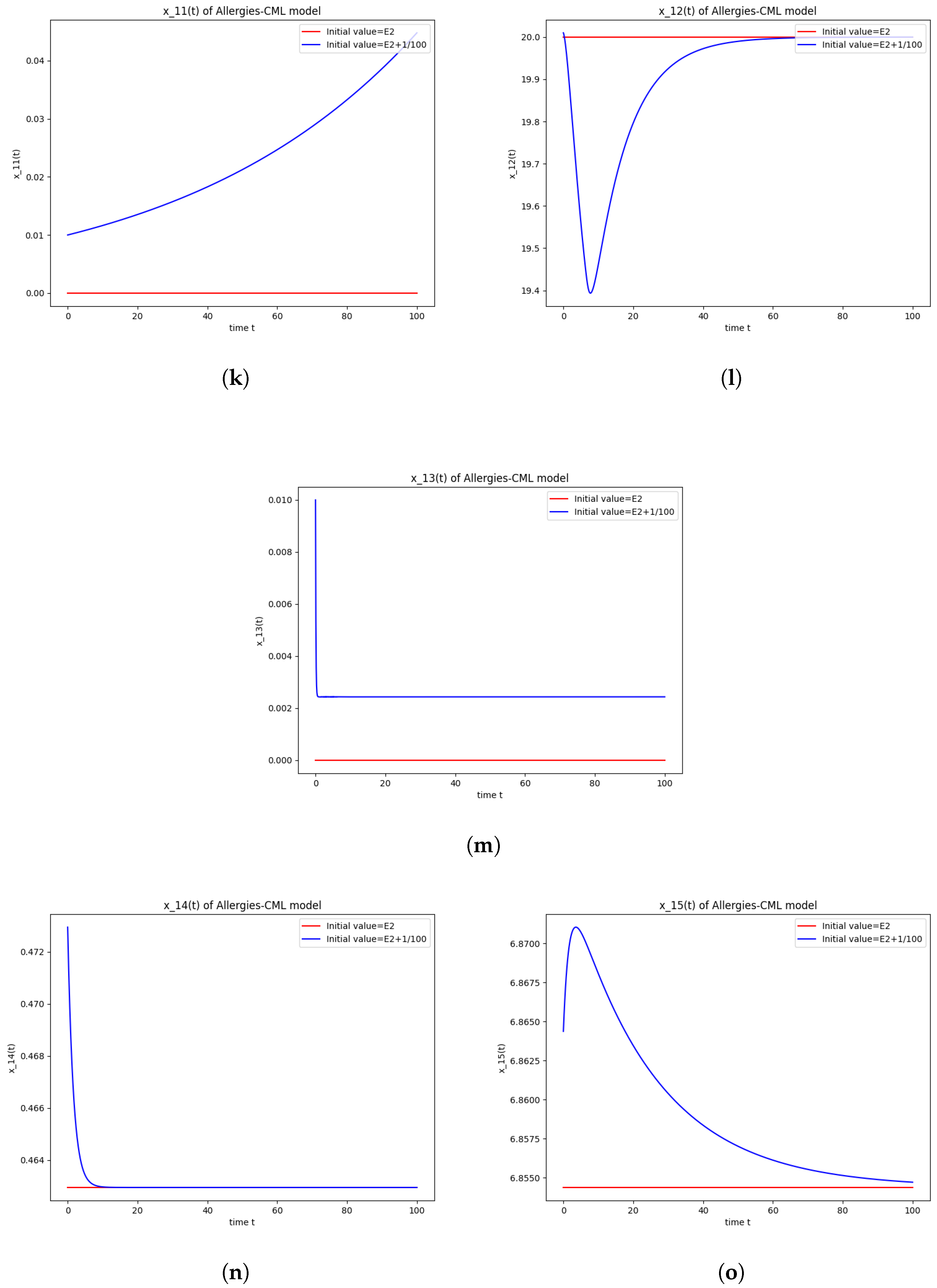
5.3. Numerical Simulations and Computations for
- The roots of have negative real parts
- The roots of have negative real parts
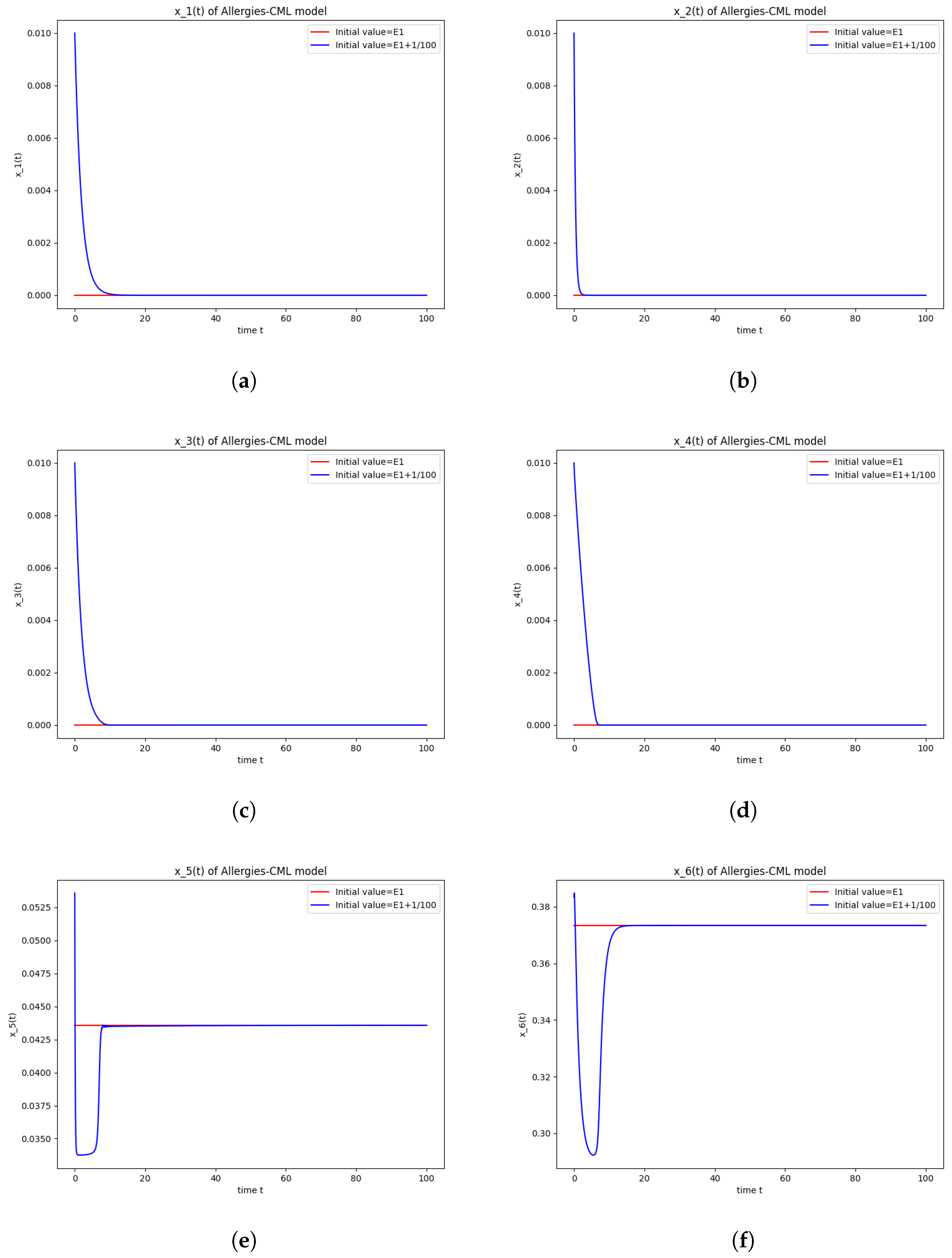
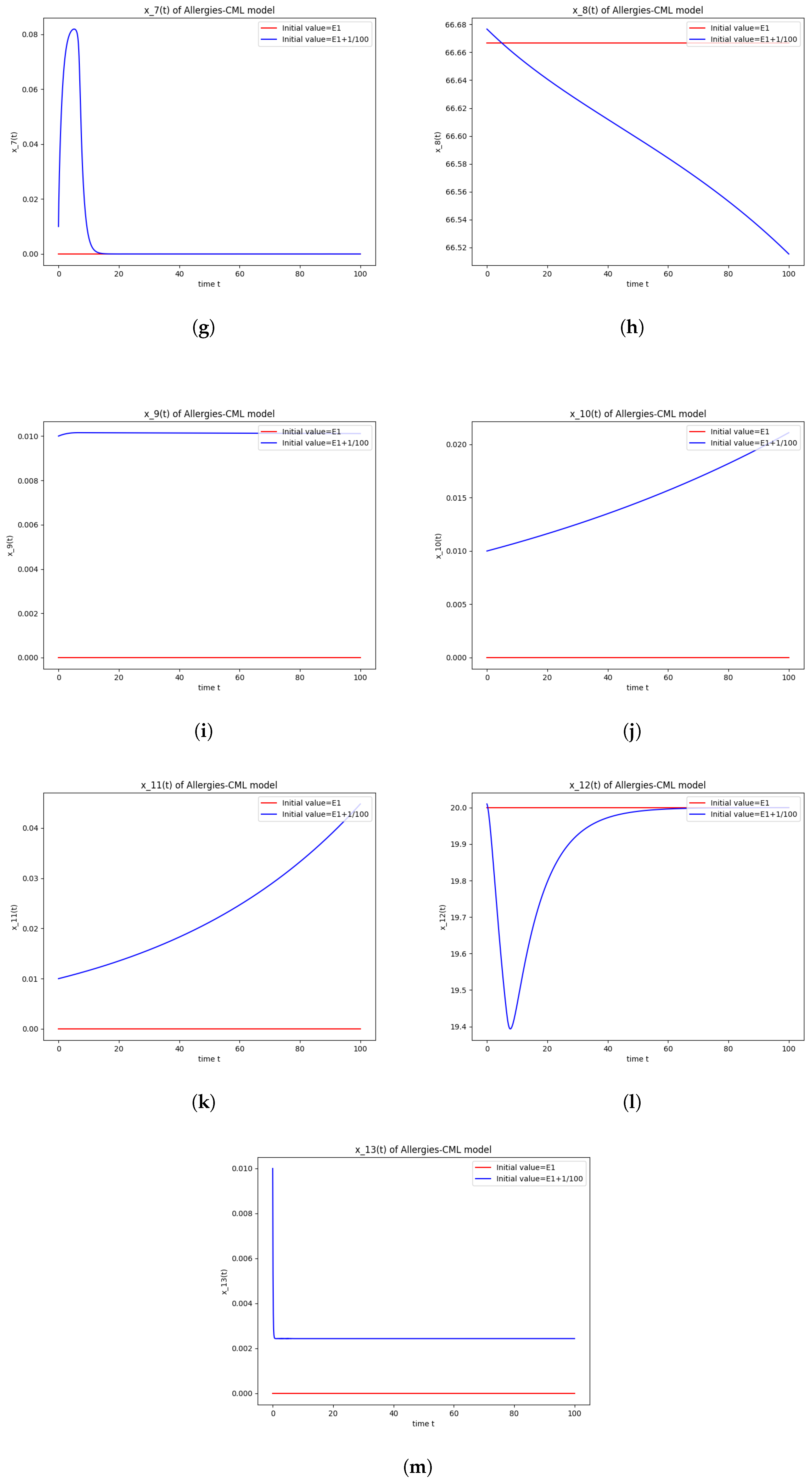
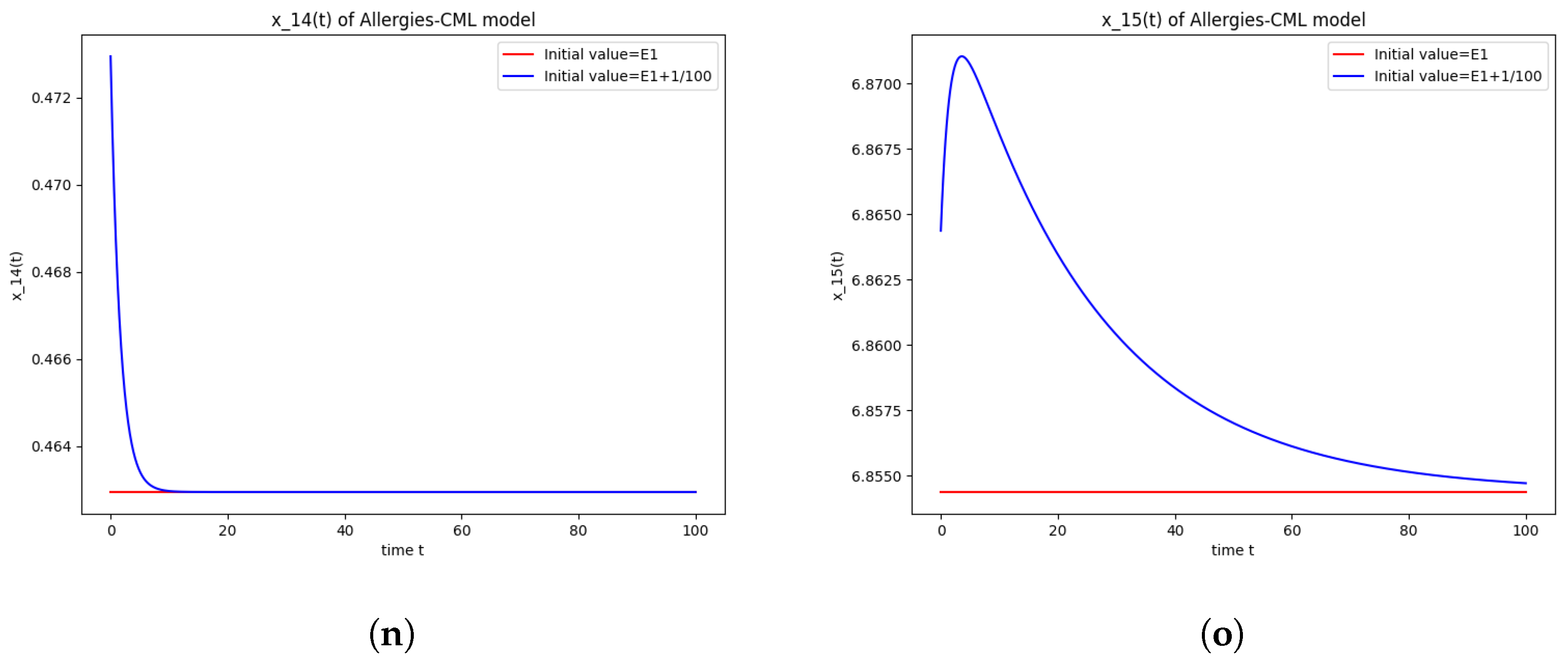
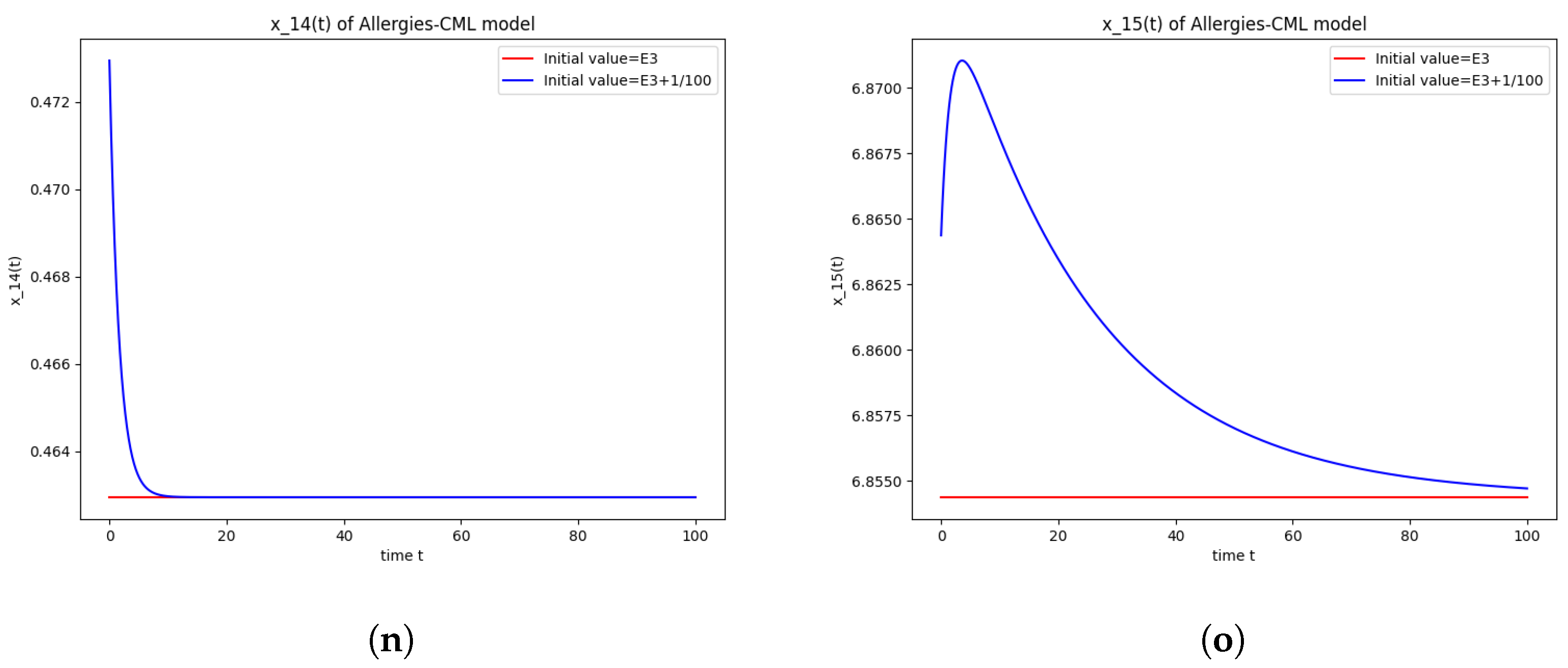
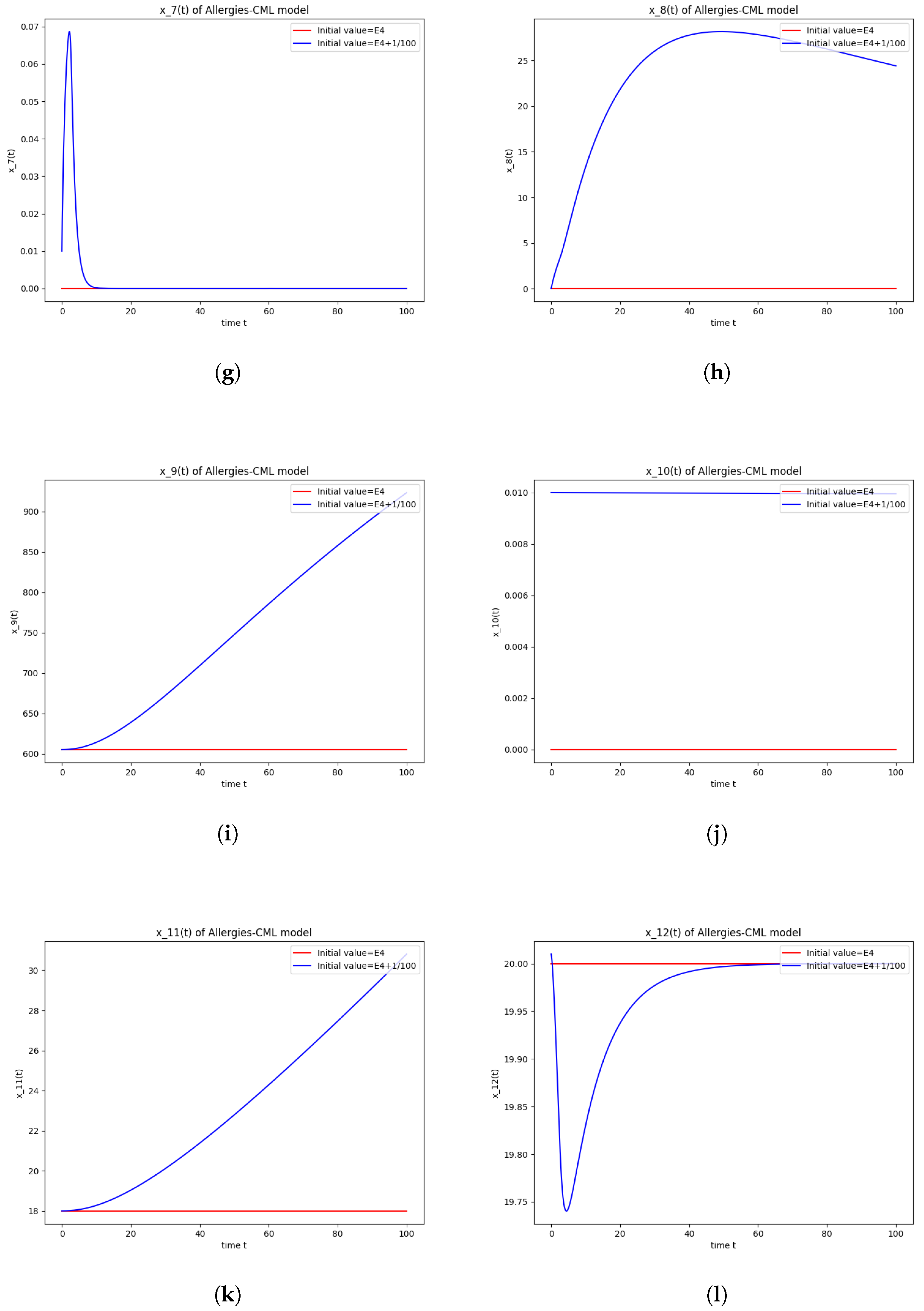
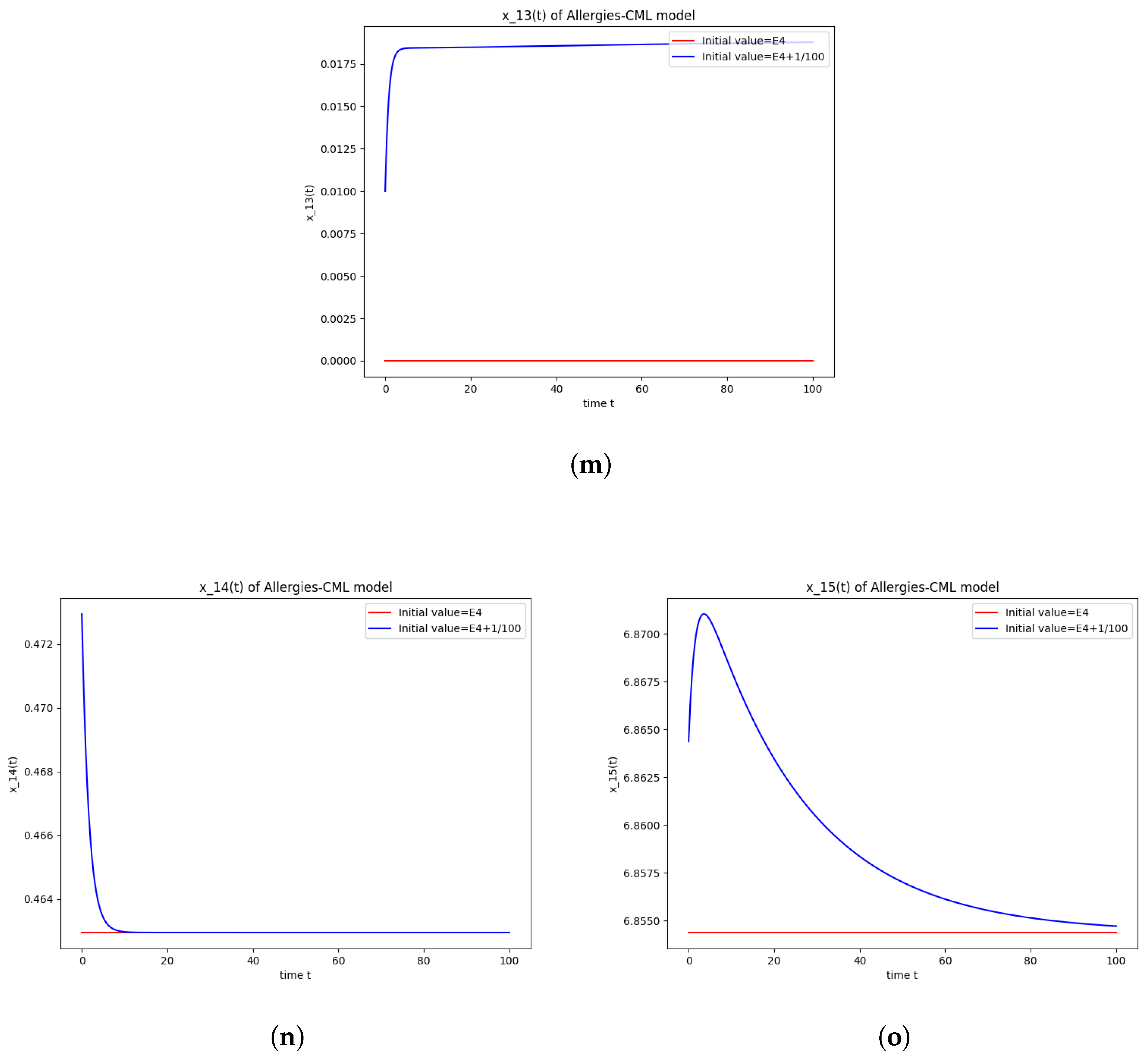
5.4. Numerical Simulations and Computations for
- The following equation has negative rootsi.e.,
- The roots ofhave negative real parts.
- Simulations indicate that in some scenarios, the concentration of Th2 cells exceeds that of Th1 cells, leading to allergic reactions. In these cases, both healthy and leukemic cell populations diminish to zero.
- In other scenarios, while leukemic cells reduce to undetectable levels, healthy cells stabilize at positive values. However, an imbalance favoring Th2 cells still results in allergic reactions.
- Some simulations show a positive evolution with leukemic cells dying out and a rapid increase in Th1 cell concentration. Yet, high Th2 cell concentrations indicate persistent allergic reactions.
- Importantly, there are scenarios where leukemic cells are eliminated without triggering allergic reactions. In these cases, the concentration of Th1 cells greatly outnumbers Th2 cells, providing a more favorable therapeutic outcome.
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Adimy, M.; Crauste, F.; Ruan, S. A mathematical study of the hematopoiesis process with application to chronic myelogenous leukemia. SIAM J. Appl. Math. 2005, 65, 1328–1352. [Google Scholar] [CrossRef]
- Colijn, C.; Mackey, M.C. A mathematical model of hematopoiesis I-Periodic chronic myelogenous leukemia. J. Theor. Biol. 2005, 237, 117–132. [Google Scholar] [CrossRef] [PubMed]
- Badralexi, I.; Halanay, A. A Complex Model for Blood Cells’ Evolution in Chronic Myelogenous Leukemia. In Proceedings of the 20th International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 27–29 May 2015; pp. 611–617. [Google Scholar]
- Radulescu, R.; Candea, D.; Halanay, A. Stability and bifurcation in a model for the dynamics of stem-like cells in leukemia under treatment. Am. Inst. Phys. Proc. 2012, 1493, 758–763. [Google Scholar]
- Halanay, A.; Cândea, D.; Rădulescu, I.R. Existence and Stability of Limit Cycles in a Two Delays Model of Hematopoietis Including Asymmetric Division. Math. Model. Nat. Phen. 2014, 9, 58–78. [Google Scholar] [CrossRef]
- Badralexi, I.; Candea, D.; Halanay, A.; Radulescu, I.R. A model for cell evolution in CML under treatment including pharmakodynamics. Bull. Math. Soc. Sci. Math. Roum. 2018, 61, 383–398. [Google Scholar]
- Badralexi, I.; Halanay, A. Stability and oscillations in a CML model. AIP Conf. Proc. 2017, 1798, 020011. [Google Scholar]
- Balea, S.; Halanay, A.; Neamtu, M. A feedback model for leukemia including cell competition and the action of the immune system. AIP Conf. Proc. 2014, 1637, 1316–1324. [Google Scholar]
- Kim, P.; Lee, P.; Levy, D. Dynamics and Potential Impact of the Immune Response to Chronic Myelogenous Leukemia. PLoS Comput. Biol. 2008, 4, e1000095. [Google Scholar] [CrossRef] [PubMed]
- Michor, F.; Hughes, T.; Iwasa, Y.; Branford, S.; Shah, N.P.; Sawyers, C.; Novak, M. Dynamics of chronic myeloid leukemia. Nature 2005, 435, 1267–1270. [Google Scholar] [CrossRef]
- Moore, H.; Li, N.K. A mathematical model for chronic myelogenous leukemia (CML) and T-cell interaction. J. Theor. Biol. 2004, 227, 513–523. [Google Scholar] [CrossRef]
- Peet, M.M.; Kim, P.S.; Niculescu, S.I.; Levy, D. New Computational Tools for Modeling Chronic Myelogenous Leukemia. Math. Model. Nat. Phenom. 2009, 4, 48–68. [Google Scholar] [CrossRef]
- Pujo-Menjouet, L.; Mackey, M.C. Contribution to the study of periodic chronic myelogenous leukemia. Comptes Rendus Biol. 2004, 327, 235–244. [Google Scholar] [CrossRef] [PubMed]
- Gross, F.; Metzner, G.; Behn, U. Mathematical modeling of allergy and specific immunotherapy: Th1, Th2 and Treg interactions. J. Theor. Biol. 2011, 269, 70–78. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, R.; Amin, K.; Halanay, A.; Mghames, R. Partial stability in a model for allergic reactions induced by chemotherapy of acute lymphoblastic leukemia. Ann. Ser. Math. Its Appl. 2023, 15, 443. [Google Scholar] [CrossRef]
- Behn, U.; Dambeck, H.; Metzner, G. Modeling th1-th2 regulation, allergy, and hyposensitization. In Dynamical Modeling in Biotechnology: Lectures Presented at the EU Advanced Workshop; World Scientic: Singapore, 2001; pp. 227–243. [Google Scholar]
- Segel, L.A.; Fishman, M.A. Modeling immunotherapy for allergy. Bull. Math. Biol. 1996, 58, 1099–1121. [Google Scholar]
- Klaewsongkram, J.; Thantiworasit, M.P.; Sodsai, P.; Buranapraditkun, S.; Mongkolpathumrat, P. Slow desensitization of imatinib-induced nonimmediate reactions and dynamic changes of drug-specific CD4+ CD25+ CD134+ lymphocytes. Ann. Allergy Asthma Immunol. 2016, 117, 514–519. [Google Scholar] [CrossRef] [PubMed]
- Kim, P.; Lee, P.; Levy, D. A theory of immunodominance and adaptive regulation. Bull. Math. Biol. 2011, 73, 1645–1665. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.Y.; Yang, X.; Wei, Q.; I, H.L.; Huang, X.B.; Wang, X.B. Effects of Tyrosine Kinase Inhibitors on the Th1 and Treg Cells of CML Patients. J. Exp. Hematol. 2019, 27, 25–32. [Google Scholar]
- Widmer, N.; Decosterd, L.A.; Csajka, C.; Leyvraz, S.; Duchosal, M.A.; Rosselet, A.; Rochat, B.; Eap, C.B.; Henry, H.; Biollaz, J.; et al. Population pharmacokinetics of imatinib and the role of pm 1-acid glycoprotein. Br. J. Clin. Pharmacol. 2006, 62, 97–112. [Google Scholar] [CrossRef] [PubMed]
- Wu, G. Calculation of steady-state distribution delay between central and peripheral compartments in two-compartment models with infusion regimen. Eur. J. Drug Metab. Pharmacokinet. 2002, 27, 259–264. [Google Scholar] [CrossRef]
- Bellman, R.; Cooke, K.L. Differential-Difference Equations; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Cooke, K.; Grossman, Z. Discrete Delay, Distribution Delay and Stability Switches. J. Math. Anal. Appl. 1982, 86, 592–627. [Google Scholar] [CrossRef]
- Wang, X.; Kottegoda, C.; Shan, C.; Huang, Q. Oscillations and coexistence generated by discrete delays in a two-species competition model. Discret. Contin. Dyn. Syst. B 2024, 29, 1798–1814. [Google Scholar] [CrossRef]
- Cooke, K.; van den Driessche, P. On zeros of some transcendental equations. Funkc. Ekvacioj 1986, 29, 77–90. [Google Scholar]
- Kogan, Y.; Agur, Z.; Elishmereni, M. A mathematical model for the immunotherapeutic control of the TH1/TH2 imbalance in melanoma. Discret. Contin. Dyn. Syst. B 2013, 18, 1017–1030. [Google Scholar] [CrossRef]
- Gil, W.; Carvalho, T.; Mancera, P.; Rodrigues, D.S. A Mathematical Model on the Immune System Role in Achieving Better Outcomes of Cancer Chemotherapy. Trends Comput. Appl. Math. 2019, 20, 343–357. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, R.; Badralexi, I.; Fakih, L.; Halanay, A. Mathematical Modeling of Immune Dynamics in Chronic Myeloid Leukemia Therapy: Unraveling Allergic Reactions and T Cell Subset Modulation by Imatinib. Axioms 2024, 13, 464. https://doi.org/10.3390/axioms13070464
Abdullah R, Badralexi I, Fakih L, Halanay A. Mathematical Modeling of Immune Dynamics in Chronic Myeloid Leukemia Therapy: Unraveling Allergic Reactions and T Cell Subset Modulation by Imatinib. Axioms. 2024; 13(7):464. https://doi.org/10.3390/axioms13070464
Chicago/Turabian StyleAbdullah, Rawan, Irina Badralexi, Laurance Fakih, and Andrei Halanay. 2024. "Mathematical Modeling of Immune Dynamics in Chronic Myeloid Leukemia Therapy: Unraveling Allergic Reactions and T Cell Subset Modulation by Imatinib" Axioms 13, no. 7: 464. https://doi.org/10.3390/axioms13070464
APA StyleAbdullah, R., Badralexi, I., Fakih, L., & Halanay, A. (2024). Mathematical Modeling of Immune Dynamics in Chronic Myeloid Leukemia Therapy: Unraveling Allergic Reactions and T Cell Subset Modulation by Imatinib. Axioms, 13(7), 464. https://doi.org/10.3390/axioms13070464





