Pole Analysis of the Inter-Replica Correlation Function in a Two-Replica System as a Binary Mixture: Mean Overlap in the Cluster Glass Phase
Abstract
:1. Introduction
2. Two-Replica System: Basic Formulation
2.1. Mean Overlap
2.2. Two Replicas as a Binary Mixture: Density–Density Correlations
2.3. The Ornstein–Zernike Equations in Symmetric Binary Mixtures
3. Pole Analysis: General Results
3.1. Pole Equations
- Combining Equations (23), (24), (27) and (31), it becomes apparent that a sign reversal occurs in glassy states: the pole equation for becomes that for .
- Equations (30)–(32) imply that there are two kinds of poles for TCFs, and , in glassy states: one type is constituted by some of the same poles as those in the liquid state, and the other by the poles satisfying Equation (31).
- Opposite phenomena: the enhancement of p-density fluctuations at leads to the suppression of n-density fluctuations and vice versa, which creates the inter-replica correlations.
- Exclusive poles: the above reverse trend in density fluctuations indicates that there are unique poles that and do not share with each other.
3.2. Two Requirements
4. Inter-Replica Total Correlation Function
4.1. General Form
4.2. Two-Mode Selection as a Minimal Model
5. Insights from the Free-Energy Landscape
5.1. The FEL for the Two-Replica System
5.2. Mixed State in Terms of the Bi-Axial FEL
5.3. Characteristic Lengths in the Two-Mode Model
6. Mean Field Analysis of the GCM: Assessing the Two-Mode Model
6.1. Intra-Replica TCF of the GCM in the Liquid State
6.2. Two Mode Numbers Selected
6.3. Comparison with Previous Results
- is secured for all curves.
- (or ) holds for when adopting in Equation (2), according to the previous results [22].
- We can find a location or region of where either or is satisfied.
7. Concluding Remarks
- (i)
- The flow to obtain Equation (44) is summarized in Figure 1, illustrating that two approaches lead to the same form, Equation (44). While the validity of Equation (44) is ensured by two physical requirements ([RR] and [FR]), we can derive Equation (44) from combining the OZ equations (Equations (19) and (20)) and the pole equation (Equation (27)). It is also important to note that spatial isotropy is assumed for TCFs, and , in the OZ equations. Applying this supposition to cluster glasses is equivalent to assuming the isotropic shape of each cluster. In other words, the morphological diversity of clusters is beyond the scope of this study, taking no account of the surface energy of clusters.
- (ii)
- Figure 2 illustrates the shift from ON to OFF state associated with switching off the attractive field (i.e., ) when considering the FEL for the two-replica system (i.e., ). The applied attractive field allows for two replicas to select the same basin in the y-axis direction of Figure 2b. After switching off the attractive field, two replicas in the cluster glass phase remain trapped in the same basin but are no longer confined within the same sub-basin in the x-axis direction of Figure 2b, which causes the blurring of cage-hopping dynamics.
- (iii)
- For assessing the analytical theory, we focus on discrete increases in due to lowering the normalized temperature in cluster glasses of the GCM. We can ascribe the discontinuous change to the second term on the RHS of Equation (71) that arises from the th mode of defined in Equation (22). Surprisingly, Table 2 supports the validity of our theory by demonstrating that the novel -dependencies of can be explained from the mode number that increases by one.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| GEM | generalized exponential model |
| GCM | Gaussian core model |
| FEL | free-energy landscape |
| TCF | total correlation function |
| DCF | direct correlation function |
| OZ equation | Ornstein–Zernike equation |
| interaction potential in units of | |
| r | interparticle distance in units of a characteristic length d |
| dimensionless interaction strength at zero separation | |
| microscopic density in replica of N-particle system | |
| mean overlap between configurations of replica and replica | |
| volume fraction defined using a uniform density | |
| p-density defined in Equation (7) | |
| n-density defined in Equation (8) | |
| TCF of p-p density fluctuations defined in Equation (10) | |
| TCF of n-n density fluctuations defined in Equation (11) | |
| intra-replica TCF | |
| inter-replica TCF | |
| intra-replica DCF | |
| inter-replica DCF | |
| structure factor of p-p density fluctuations defined in Equation (37) | |
| structure factor of n-n density fluctuations defined in Equation (37) |
References
- Likos, C.N. Effective interactions in soft condensed matter physics. Phys. Rep. 2001, 348, 267–439. [Google Scholar] [CrossRef]
- Likos, C.N. Soft matter with soft particles. Soft Matter 2006, 2, 478–498. [Google Scholar] [CrossRef] [PubMed]
- van Hecke, M. Jamming of soft particles: Geometry, mechanics, scaling and isostaticity. J. Phys. Condens. Matter 2009, 22, 033101. [Google Scholar] [CrossRef]
- Cinti, F.; Macrí, T.; Lechner, W.; Pupillo, G.; Pohl, T. Defect-induced supersolidity with soft-core bosons. Nat. Commun. 2014, 5, 3235. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Méndez, R.; Mezzacapo, F.; Lechner, W.; Cinti, F.; Babaev, E.; Pupillo, G. Glass transitions in monodisperse cluster-forming ensembles: Vortex matter in type-1.5 superconductors. Phys. Rev. Lett. 2017, 118, 067001. [Google Scholar] [CrossRef]
- Ikeda, A. Miyazaki, K. Glass transition of the monodisperse Gaussian core model. Phys. Rev. Lett. 2011, 106, 015701. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, A.; Miyazaki, K. Thermodynamic and structural properties of the high density Gaussian core model. J. Chem. Phys. 2011, 135, 024901. [Google Scholar] [CrossRef]
- Ikeda, A. Miyazaki, K. Slow dynamics of the high density gaussian core model. J. Chem. Phys. 2011, 135, 054901. [Google Scholar] [CrossRef] [PubMed]
- Coslovich, D. Bernabei, M. Moreno, A.J. Cluster glasses of ultrasoft particles. J. Chem. Phys. 2012, 137, 184904. [Google Scholar] [CrossRef]
- Coslovich, D. Ikeda, A. Cluster and reentrant anomalies of nearly Gaussian core particles. Soft Matter 2013, 9, 6786–6795. [Google Scholar] [CrossRef]
- Coslovich, D. Ikeda, A. Miyazaki, K. Mean-field dynamic criticality and geometric transition in the Gaussian core model. Phys. Rev. E 2016, 93, 042602. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, R.; Kawasaki, T.; Miyazaki, K. Cluster glass transition of ultrasoft-potential fluids at high density. Phys. Rev. Lett. 2016, 117, 165701. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, R.; Kawasaki, T.; Miyazaki, K. Slow dynamics coupled with cluster formation in ultrasoft-potential glasses. J. Chem. Phys. 2019, 150, 074503. [Google Scholar] [CrossRef] [PubMed]
- Louis, A.A.; Bolhuis, P.G.; Hansen, J.P. Mean-field fluid behavior of the Gaussian core model. Phys. Rev. E 2000, 62, 7961. [Google Scholar] [CrossRef]
- Lang, A.; Likos, C.N.; Watzlawek, M.; Löwen, H. Fluid and solid phases of the Gaussian core model. J. Phys. Condens. Matter 2000, 12, 5087. [Google Scholar] [CrossRef]
- Likos, C.N.; Lang, A.; Watzlawek, M.; Löwen, H. Criterion for determining clustering versus reentrant melting behavior for bounded interaction potentials. Phys. Rev. E 2001, 63, 031206. [Google Scholar] [CrossRef]
- Mladek, B.M.; Gottwald, D.; Kahl, G.; Neumann, M.; Likos, C.N. Formation of polymorphic cluster phases for a class of models of purely repulsive soft spheres. Phys. Rev. Lett. 2006, 96, 045701. [Google Scholar] [CrossRef]
- Mladek, B.M.; Gottwald, D.; Kahl, G.; Neumann, M.; Likos, C.N. Clustering in the absence of attractions: Density functional theory and computer simulations. J. Phys. Chem. B 2007, 111, 12799–12808. [Google Scholar] [CrossRef]
- Likos, C.N.; Mladek, B.M.; Gottwald, D.; Kahl, G. Why do ultrasoft repulsive particles cluster and crystallize? Analytical results from density-functional theory. J. Chem. Phys. 2007, 126, 224502. [Google Scholar] [CrossRef]
- Pini, D.; Parola, A.; Reatto, L. An unconstrained DFT approach to microphase formation and application to binary Gaussian mixtures. J. Chem. Phys. 2015, 143, 034902. [Google Scholar] [CrossRef]
- Nikiteas, I.; Heyes, D.M. Reentrant melting and multiple occupancy crystals of bounded potentials: Simple theory and direct observation by molecular dynamics simulations. Phys. Rev. E 2020, 102, 042102. [Google Scholar] [CrossRef]
- Bomont, J.M.; Likos, C.N.; Hansen, J.P. Glass quantization of the Gaussian core model. Phys. Rev. E 2022, 105, 024607. [Google Scholar] [CrossRef] [PubMed]
- Sposini, V.; Likos, C.N.; Camargo, M. Glassy phases of the Gaussian core model. Soft Matter 2023, 19, 9531–9540. [Google Scholar] [CrossRef] [PubMed]
- Montes-Saralegui, M.; Nikoubashman, A.; Kahl, G. Merging and hopping processes in systems of ultrasoft, cluster forming particles under compression. J. Chem. Phys. 2014, 141, 124908. [Google Scholar] [CrossRef]
- Schwanzer, D.F.; Coslovich, D.; Kahl, G. Two-dimensional systems with competing interactions: Dynamic properties of single particles, and of clusters. J. Phys. Condens. Matter 2016, 28, 414015. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, G.; Zhang, W.; Du, C.; Wesdemiotis, C.; Cheng, S.Z. Cooperative soft-cluster glass in giant molecular clusters. Macromolecules 2019, 52, 4341–4348. [Google Scholar] [CrossRef]
- Cho, J.H.; Cerbino, R.; Bischofberger, I. Emergence of multiscale dynamics in colloidal gels. Phys. Rev. Lett. 2020, 124, 088005. [Google Scholar] [CrossRef] [PubMed]
- Liebetreu, M.; Likos, C.N. Shear-induced stack orientation, and breakup in cluster glasses of ring polymers. ACS Appl. Polym. Mater. 2020, 2, 3505–3517. [Google Scholar] [CrossRef]
- Charbonneau, P.; Kurchan, J.; Parisi, G.; Urbani, P.; Zamponi, F. Fractal free energy landscapes in structural glasses. Nat. Commun. 2014, 5, 3725. [Google Scholar] [CrossRef]
- Müller, M.; Wyart, M. Marginal stability in structural, spin, and electron glasses. Annu. Rev. Condens. Matter Phys. 2015, 6, 177–200. [Google Scholar] [CrossRef]
- Berthier, L.; Biroli, G.; Charbonneau, P.; Corwin, E.I.; Franz, S.; Zamponi, F. Gardner physics in amorphous solids and beyond. J. Chem. Phys. 2019, 151, 010901. [Google Scholar] [CrossRef] [PubMed]
- Dennis, R.C.; Corwin, E.I. Jamming energy landscape is hierarchical and ultrametric. Phys. Rev. Lett. 2020, 124, 078002. [Google Scholar] [CrossRef] [PubMed]
- Hammond, A.P.; Corwin, E.I. Experimental observation of the marginal glass phase in a colloidal glass. Proc. Natl. Acad. Sci. USA 2020, 117, 5714–5718. [Google Scholar] [CrossRef]
- Ikeda, H.; Miyazaki, K.; Yoshino, H.; Ikeda, A. Multiple glass transitions and higher-order replica symmetry breaking of binary mixtures. Phys. Rev. E 2021, 103, 022613. [Google Scholar] [CrossRef] [PubMed]
- Arceri, F.; Corwin, E.I.; O’Hern, C.S. The jamming transition and the marginally stable solid. In Spin Glass Theory and Far Beyond: Replica Symmetry Breaking after 40 Years; Marinari, E., Mézard, M., Parisi, G., Ricci-Tersenghi, F., Sicuro, G., Zamponi, F., Eds.; World Scientific: Singapore, 2023; pp. 239–254. [Google Scholar]
- Franz, S.; Parisi, G. Phase diagram of coupled glassy systems: A mean-field study. Phys. Rev. Lett. 1997, 79, 2486–2489. [Google Scholar] [CrossRef]
- Franz, S.; Parisi, G. Effective potential in glassy systems: Theory and simulations. Phys. A Stat. Mech. 1998, 261, 317–339. [Google Scholar] [CrossRef]
- Cardenas, M.; Franz, S.; Parisi, G. Constrained Boltzmann-Gibbs measures and effective potential for glasses in hypernetted chain approximation and numerical simulations. J. Chem. Phys. 1999, 110, 1726–1734. [Google Scholar] [CrossRef]
- Franz, S.; Parisi, G. On non-linear susceptibility in supercooled liquids. J. Phys. Condens. Matter 2000, 12, 6335. [Google Scholar] [CrossRef]
- Jack, R.L.; Berthier, L. The melting of stable glasses is governed by nucleation-and-growth dynamics. J. Chem. Phys. 2016, 144, 244506. [Google Scholar] [CrossRef]
- Guiselin, B.; Berthier, L. Tarjus, G. Statistical mechanics of coupled supercooled liquids in finite dimensions. SciPost Phys. 2022, 12, 091. [Google Scholar] [CrossRef]
- Frusawa, H. Replica Field Theory for a Generalized Franz–Parisi Potential of Inhomogeneous Glassy Systems: New Closure and the Associated Self-Consistent Equation. Entropy 2024, 26, 241. [Google Scholar] [CrossRef] [PubMed]
- Berthier, L. Overlap fluctuations in glass-forming liquids. Phys. Rev. E 2013, 88, 022313. [Google Scholar] [CrossRef]
- Parisi, G.; Seoane, B. Liquid-glass transition in equilibrium. Phys. Rev. E 2014, 89, 022309. [Google Scholar] [CrossRef]
- Bomont, J.M.; Hansen, J.P.; Pastore, G. An investigation of the liquid to glass transition using integral equations for the pair structure of coupled replicae. J. Chem. Phys. 2014, 141, 174505. [Google Scholar] [CrossRef] [PubMed]
- Bomont, J.M.; Hansen, J.P.; Pastore, G. Hypernetted-chain investigation of the random first-order transition of a Lennard-Jones liquid to an ideal glass. Phys. Rev. E 2015, 92, 042316. [Google Scholar] [CrossRef] [PubMed]
- Bomont, J.M.; Pastore, G. An alternative scheme to find glass state solutions using integral equation theory for the pair structure. Mol. Phys. 2015, 113, 2770–2775. [Google Scholar] [CrossRef]
- Bomont, J.M.; Hansen, J.P.; Pastore, G. Revisiting the replica theory of the liquid to ideal glass transition. J. Chem. Phys. 2019, 150, 154504. [Google Scholar] [CrossRef] [PubMed]
- Bomont, J.M.; Pastore, G.; Hansen, J.P. Coexistence of low and high overlap phases in a supercooled liquid: An integral equation investigation. J.Chem. Phys. 2019, 146, 114504. [Google Scholar] [CrossRef] [PubMed]
- Evans, R.; Leote de Carvalho, R.J.F.; Henderson, J.R.; Hoyle, D.C. Asymptotic decay of correlations in liquids and their mixtures. J. Chem. Phys. 1994, 100, 591–603. [Google Scholar] [CrossRef]
- Dijkstra, M.; Evans, R. A simulation study of the decay of the pair correlation function in simple fluids. J. Chem. Phys. 2000, 112, 1449–1456. [Google Scholar] [CrossRef]
- Grodon, C.; Dijkstra, M.; Evans, R.; Roth, R. Decay of correlation functions in hard-sphere mixtures: Structural crossover. J. Chem. Phys. 2004, 121, 7869–7882. [Google Scholar] [CrossRef] [PubMed]
- Archer, A.J.; Pini, D.; Evans, R.; Reatto, L. Model colloidal fluid with competing interactions: Bulk and interfacial properties. J. Chem. Phys. 2007, 126, 014104. [Google Scholar] [CrossRef] [PubMed]
- Walters, M.C.; Subramanian, P.; Archer, A.J.; Evans, R. Structural crossover in a model fluid exhibiting two length scales: Repercussions for quasicrystal formation. Phys. Rev. E 2018, 98, 012606. [Google Scholar] [CrossRef] [PubMed]
- Cats, P.; Evans, R.; Härtel, A.; van Roij, R. Primitive model electrolytes in the near, and far field: Decay lengths from DFT, and simulations. J. Chem. Phys. 2021, 154, 124504. [Google Scholar] [CrossRef] [PubMed]
- Klix, C.L.; Royall, C.P.; Tanaka, H. Structural and dynamical features of multiple metastable glassy states in a colloidal system with competing interactions. Phys. Rev. Lett. 2010, 104, 165702. [Google Scholar] [CrossRef] [PubMed]
- Tsurusawa, H.; Leocmach, M.; Russo, J.; Tanaka, H. Direct link between mechanical stability in gels and percolation of isostatic particles. Sci. Adv. 2019, 5, eaav6090. [Google Scholar] [CrossRef]
- Ruiz-Franco, J.; Zaccarelli, E. On the role of competing interactions in charged colloids with short-range attraction. Annu. Rev. Condens. Matter Phys. 2021, 12, 51–70. [Google Scholar] [CrossRef]
- Tan, J.; Afify, N.D.; Ferreiro-Rangel, C.A.; Fan, X.; Sweatman, M.B. Cluster formation in symmetric binary SALR mixtures. J. Chem. Phys. 2021, 154, 074504. [Google Scholar] [CrossRef] [PubMed]
- Costa, D.; Munaó, G.; Bomont, J.M.; Malescio, G.; Palatella, A.; Prestipino, S. Microphase versus macrophase separation in the square-well-linear fluid: A theoretical and computational study. Phys. Rev. E 2023, 108, 034602. [Google Scholar] [CrossRef]
- Patsahan, O.; Meyra, A.; Ciach, A. Spontaneous pattern formation in monolayers of binary mixtures with competing interactions. Soft Matter 2024, 20, 1410–1424. [Google Scholar] [CrossRef] [PubMed]
- Bomont, J.M.; Pastore, G.; Costa, D.; Munaó, G.; Malescio, G.; Prestipino, S. Arrested states in colloidal fluids with competing interactions: A static replica study. J. Chem. Phys. 2024, 160, 214504. [Google Scholar] [CrossRef] [PubMed]
- Franz, S.; Jacquin, H.; Parisi, G.; Urbani, P.; Zamponi, F. Static replica approach to critical correlations in glassy systems. J. Chem. Phys. 2013, 138, 12A540. [Google Scholar] [CrossRef] [PubMed]
- Folena, G.; Biroli, G.; Charbonneau, P.; Hu, Y.; Zamponi, F. Equilibrium fluctuations in mean-field disordered models. Phys. Rev. E 2022, 106, 024605. [Google Scholar] [CrossRef]


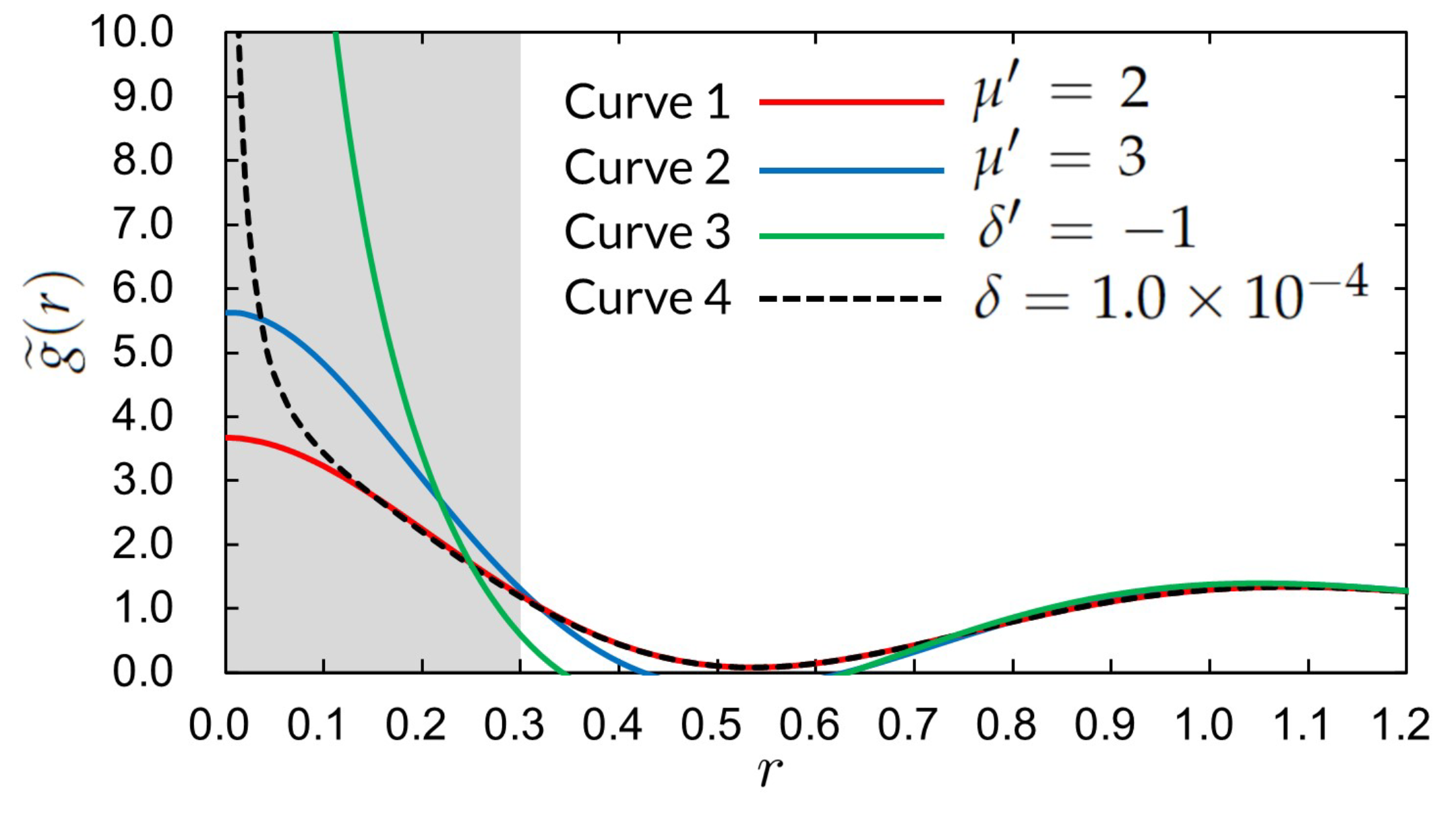
| Equation (30): Divergence | Equation (38): Vanishing | ||
|---|---|---|---|
| Equation (30): divergence | |||
| Equation (39): vanishing | — | ||
| 0.15 | ||||
| (1.21) | 0.14 (1.17) | – | ||
| 0.15 | ||||
| (1.25) | 0.15 (1.21) | |||
| 0.14 | 0.15 | |||
| 0.16 (1.32) | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frusawa, H. Pole Analysis of the Inter-Replica Correlation Function in a Two-Replica System as a Binary Mixture: Mean Overlap in the Cluster Glass Phase. Axioms 2024, 13, 468. https://doi.org/10.3390/axioms13070468
Frusawa H. Pole Analysis of the Inter-Replica Correlation Function in a Two-Replica System as a Binary Mixture: Mean Overlap in the Cluster Glass Phase. Axioms. 2024; 13(7):468. https://doi.org/10.3390/axioms13070468
Chicago/Turabian StyleFrusawa, Hiroshi. 2024. "Pole Analysis of the Inter-Replica Correlation Function in a Two-Replica System as a Binary Mixture: Mean Overlap in the Cluster Glass Phase" Axioms 13, no. 7: 468. https://doi.org/10.3390/axioms13070468
APA StyleFrusawa, H. (2024). Pole Analysis of the Inter-Replica Correlation Function in a Two-Replica System as a Binary Mixture: Mean Overlap in the Cluster Glass Phase. Axioms, 13(7), 468. https://doi.org/10.3390/axioms13070468





