The Unified Description of Abstract Convexity Structures

Abstract

The convexity of space is essential in nonlinear analysis, variational inequalities and optimization theory because it guarantees the existence and uniqueness of solutions to a certain extent. Because of its wide variety of applications, mathematicians have extensively promoted and researched convexity. This paper reviews some representative convexity structures and discusses their relations from their definitions, unifying them in the abstract convex structure. Moreover, applications of main convexity structures including KKM theory and fixed point theory will be reviewed.

1. Introduction

The convexity of spaces plays a vital role in fixed point, selection, KKM theories and optimization problems. The convex structure that we usually assume in the above theories is a convex subset of topological vector spaces. Most of the phenomena in the real world are nonlinear. The requirements of the linear structure are sometimes challenging to achieve, which inspires researchers to generalize the original linear convex structure in nonlinear spaces or topological spaces. Therefore, it is necessary to extend the concept of convexity. Many research results have been achieved. For example, In 1959, Michael [1] proposed the Michael-convex and gave the condition for continuous selectivity. In 1987, Horvath [2] defined $H$–space with topological properties; that is, he replaced the original convexity with contractibility (the spatial structure is $H$–convex structure). In 1990, Tarafdar [3] considered the fixed point theorem in $H$–space and generalized the maximum–minimum inequality. Based on Michael’s research on improving convexity, many convex structures have emerged in topological spaces. For example, van de Vel’s [4] convex structure, Pasicki’s [5,6,7] convex space, Komiya’s convex space [8], Lassonde’s [9] convex space, Horvath’s [10] pseudoconvexity, Joó’s [11] pseudoconvexity, Bielawski’s [12] simplicial convexity and so on.

In 1993, Park and Kim [13] discovered that, in some cases, convex spaces could be substituted by more general spaces, namely generalized convex spaces (or $G$–convex spaces). In 1996, Park and Kim [14] presented a coincidence theorem for admissible mappings in generalized convex spaces and applied it to an abstract variational inequality, a KKM-type theorem, and a fixed-point theorem. In 2001, Park [15] studied the Fan–Browder fixed point theorem in $G$–convex space, and as an application, he gave a generalized form of the KKMF lemma and Nash equilibrium theorem. Studies on the fixed point theory and KKM theory in $G$–convex spaces can be sought out in references [16,17,18,19,20,21].

In addition to the convex structure mentioned above, in 2004, Briec and Horvath [22] considered a convex structure, namely $B$–convex, and studied the extremal programming problem under this convex structure. After that, Hong [23], in 2009, studied the properties of $B$–convex in a finite-dimensional $B$–space and obtained a few relations between the $B$–convex structure, selection properties, and fixed point properties. Many scholars established abundant extended versions of the fixed point theorems and selection theorems in topological spaces without the linear stucture. These theorems are still valid in these convex spaces, provided there are some common features between them.

In 2007, based on the research of Michael, van de Vel and Horvath, Xiang et al. [24,25] reduced the conditions for constructing convex structures to obtain a more general convex structure, i.e., abstract convexity, which included the above convex structures, and further generalized convexity. In order to tackle the above problem, they proposed a new way to ensure the existence of fixed points or the continuous selection of mappings, and the $H_0$–condition was necessary. They established the relationship between abstract convexity, fixed points and selective characteristics. It was proved that if the convex structure $\mathrm{\Xi }$ had selective properties, $\mathrm{\Xi }$ satisfied the $H$–condition. They also proved that if the convex structure $\mathrm{\Xi }$ delimited on the topological space had weak selective properties, $\mathrm{\Xi }$ satisfied the $H_0$–condition. In 2013, Xiang et al. [26] gave further conclusions in a class of generalized convex spaces. They proved that an abstract convex space had KKM properties if and only if it had a strong Fan–Browder characteristic. And a few extended forms of the KKM lemma were established.

In addition to the above theories, Ky Fan inequalities, variational inequalities, and quasi-variational inequalities also depend on the convexity of spaces. They have also been generalized in the concrete abstract convex space by weakening the convexity, compactness, and continuity of the mappings. In 2012, Chen [27] used the extension property of continuous mappings to construct a generalized convex space without linear structure, i.e., $T$–convex space, which was a generalization of $H$–space, and proved that the convex structure satisfied the $H_0$–condition. The KKM lemma and the fixed point theorem have been generalized in this space. In 2017, Chen [28] used the properties of this space, established and proved the KKM lemma, applying it to the fixed point theorem. Based on the above research, Chen [29], in 2020, weakened the compactness, convexity, and continuity of Ky Fan inequality and proved a new version of this inequality by using the classical set-valued analysis method and KKM method. More results can be found in references [30,31,32,33,34].

Currently, most abstract convex structures are applied in studying fixed point theory, KKM theory, and continuous selection theory. However, little research has been conducted on the relationships among these structures. In 2002, Llinares [35] conducted a seminal study on this topic, exploring the relationship between $mc$–space and simplicial convexity, $c$–space, order convexity, $B^{\prime }$–simple convexity, $L$–space, and more. His findings, such as the equivalence of $mc$–space and $L$–space, have significantly advanced our understanding of abstract convex structures.

Inspired by the research above, this paper aims to sort out the relationship between the convex structures mentioned in this paper, unifying them in the abstract convex structure, and review some generalizations of the fixed point theory and the KKM theory in representative convex spaces.

The rest of the paper is organized as follows: Section 2 gives definitions of the various convex structures proposed in recent studies. Section 3 analyzes the properties of various convex structures and the relationship between them from the definitions. Section 4 will describe the generalizations of the above theories in representative convex spaces. This article will be summarized in Section 5.

2. Preliminaries

2.1. Abstract Convexity Space

Definition 1 

([24]). Suppose that V is a topological space and Ξ is a family of subsets of V. $\left(V,\mathrm{\Xi }\right)$ is said to be an abstract convexity structure space or abstract convexity space if Ξ satisfies the following characteristics:

(1) 

$\varnothing \in \mathrm{\Xi }$;

(2) 

Ξ is closed under the intersection operation of its subsets, that is, if nonempty subset $D\subset \mathrm{\Xi }$, then ${\displaystyle \bigcap _{\mathrm{\Lambda }\in D}}\mathrm{\Lambda }$ is in Ξ.

The abstract convex hull of $\mathrm{\Lambda }\subset V$ is defined as $co\left(\mathrm{\Lambda }\right)=\cap \left\{D\in \mathrm{\Xi }:\mathrm{\Lambda }\subset D\right\}$. $\mathrm{\Lambda }\subset V$ is called an abstract convex set if $\mathrm{\Lambda }\in \mathrm{\Xi }$. $\mathrm{\Lambda }$ is an abstract convex set when it fulfills $\mathrm{\Lambda }=co\left(\mathrm{\Lambda }\right)$.

Next, we give some simple examples of abstract convexity spaces.

Example 1. 

Let $V=\left[0,1\right]\cup \left[2,3\right]$ be a subset of R and C be a family of subsets of V. Then $\left(V,C\right)$ is an abstract convex space.

Example 2. 

Suppose that $V=\left\{1,2,3\right\}$ is a finite set, its family of subsets $C=\left\{\varnothing ,\left\{1\right\},\left\{2\right\},\left\{3\right\},\left\{1,2\right\},\left\{1,3\right\},\left\{2,3\right\},\left\{1,2,3\right\}\right\}$. Then $\left(V,C\right)$ is an abstract convex space.

The examples above declare they are not convex sets in R.

Suppose that V is any nonempty set, $\aleph \left(V\right)$ is a family of all nonempty finite subsets of V, and $\left|\mathrm{\Lambda }\right|$ is the number of elements of $\mathrm{\Lambda }$.

2.2. $G$–Convex Space

Definition 2 

([13]). Assume that V is a topological space, D is a nonempty subset of V, and $\mathrm{\Gamma }:\aleph \left(D\right)\to 2^V$ is a nonempty mapping. $\left(V,D;\mathrm{\Gamma }\right)$ is known as a generalized convex space or $G$–convex space if the mapping fulfills the following properties:

(1) 

for any $\mathrm{\Lambda },B\in \aleph \left(D\right)$, $\mathrm{\Lambda }\subset B$ implies $\mathrm{\Gamma }\left(\mathrm{\Lambda }\right)\subset \mathrm{\Gamma }\left(B\right)$;

(2) 

for any $\mathrm{\Lambda }\in \aleph \left(D\right)$, $\left|\mathrm{\Lambda }\right|=n+1$, we can discover a continuous mapping ${\pi }_{\mathrm{\Lambda }}:{∆}_N\to \mathrm{\Gamma }\left(\mathrm{\Lambda }\right)$ such that $J\in \aleph \left(\mathrm{\Lambda }\right)$ indicates ${\pi }_{\mathrm{\Lambda }}\left({∆}_J\right)\subset \mathrm{\Gamma }\left(J\right)$. Where $N=\left\{0,1,\dots ,n\right\}$ and ${∆}_J$ represents the face of the n-dimensional standard simplex ${∆}_N=e_0{e}_1\dots e_n$ corresponding to $J\in \aleph \left(\mathrm{\Lambda }\right)$. That is, if $\mathrm{\Lambda }=\left\{w_0,w_1,\dots ,w_n\right\}$ and $J=\left\{w_{i_0},w_{i_1},\dots ,w_{i_n}\right\}\subset \mathrm{\Lambda }$, then ${∆}_J=\left\{e_{i_0},e_{i_1},\dots ,e_{i_n}\right\}$.

For any $\mathrm{\Lambda }\in \aleph \left(D\right)$, let $\mathrm{\Gamma }\left(\mathrm{\Lambda }\right)={\mathrm{\Gamma }}_{\mathrm{\Lambda }}$. For the $G$–convex space $\left(V,D;\mathrm{\Gamma }\right)$, the subset ℑ of V is called $G$–convex if for each $\mathrm{\Lambda }\in \aleph \left(D\right)$, when $\mathrm{\Lambda }\subset \Im$, then ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}\subset \Im$. Supposing $S\subset V$, the $G$–convex hull is defined as $c{o}^G\left(S\right)=\cap \left\{D\subset V:S\subset D\right\}$, where D is $G$–convex. $G$–convex space $\left(V,D;\mathrm{\Gamma }\right)$ writing $\left(V,\mathrm{\Gamma }\right)$ when $V=D$.

Two concrete examples are given below to better understand $G$–convex spaces.

Example 3. 

Supposing that V is a convex subset in topological vector spaces and ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}=co\left(\mathrm{\Lambda }\right)$, then $\left(V,\mathrm{\Gamma }\right)$ is a $G$–convex space.

Proof. 

Let $\aleph \left(V\right)$ be a family of all nonempty finite subsets of V and $\mathrm{\Lambda }=\left\{w_0,w_1,\dots ,w_n\right\}$ be any finite subset of V. $\mathrm{\Gamma }:\aleph \left(D\right)\to 2^V$ is defined as ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}=co\left(\mathrm{\Lambda }\right)$.

(1)

For any $\mathrm{\Lambda }=\left\{w_1,w_2,\dots ,w_n\right\},B=\left\{b_1,b_2,\dots ,b_m\right\}\in \aleph \left(V\right)$, when $\mathrm{\Lambda }\subset B$, we have $co\left(\mathrm{\Lambda }\right)\subset co\left(B\right)$, i.e., $\mathrm{\Gamma }\left(\mathrm{\Lambda }\right)\subset \mathrm{\Gamma }\left(B\right)$;

(2)

Define ${\pi }_{\mathrm{\Lambda }}:{∆}_N\to co\left(\mathrm{\Lambda }\right)$ as $\pi \left(u\right)={\displaystyle \sum _{l=0}^n}{\mu }_i{w}_l$, where ${\mu }_l\ge 0$ and ${\displaystyle \sum _{l=0}^n}{\mu }_l=1$. For any $T=\left\{w_{l_0},w_{l_1},\dots ,w_{l_k}\right\}\subset \mathrm{\Lambda }$, ${∆}_T=co\left\{e_{l_0},e_{l_1},\dots ,e_{l_k}\right\}$, where ${∆}_T$ represents the face of the n-dimensional standard simplex ${∆}_N=e_0{e}_1\dots e_n$ corresponding to $T\subset \mathrm{\Lambda }$. For any $\kappa \in {∆}_T=co\left\{e_{l_0},e_{l_1},\dots ,e_{l_k}\right\}$, we can obtain ${\pi }_{\mathrm{\Lambda }}\left(\kappa \right)={\displaystyle \sum _{j=0}^k}{\mu }_j{w}_{l_j}\in {\mathrm{\Gamma }}_T$, i.e., ${\pi }_{\mathrm{\Lambda }}\left({∆}_T\right)\subset \mathrm{\Gamma }\left(T\right)$. Hence, we can discover a continuous mapping ${\pi }_{\mathrm{\Lambda }}:{∆}_N\to \mathrm{\Gamma }\left(\mathrm{\Lambda }\right)$ such that $T\in \aleph \left(\mathrm{\Lambda }\right)$ indicates ${\pi }_{\mathrm{\Lambda }}\left({∆}_T\right)\subset \mathrm{\Gamma }\left(T\right)$.

According to Definition 2, $\left(V,\mathrm{\Gamma }\right)$ is a $G$–convex space. □

Example 4. 

Assuming $V=\left\{\left(v,u\right)\in R^2:v^2+u^2=1\right\}$, $\mathrm{\Gamma }:\aleph \left(D\right)\to 2^V$ is defined as $\mathrm{\Gamma }\left(\mathrm{\Lambda }\right)={\displaystyle \widehat{w_0\dots w_n}}$. For any $\mathrm{\Lambda }=\left\{w_0,w_1,\dots w_n\right\}\in \aleph \left(V\right)$, $\left(V,\mathrm{\Gamma }\right)$ is a $G$–convex space.

Proof. 

(1) For any $\mathrm{\Lambda }=\left\{w_1,w_2,\dots ,w_n\right\},B=\left\{b_1,b_2,\dots ,b_m\right\}\in F\left(V\right)$, when $\mathrm{\Lambda }\subset B$, we have $\mathrm{\Gamma }\left(\mathrm{\Lambda }\right)\subset \mathrm{\Gamma }\left(B\right)$;

(2) Define ${\pi }_{\mathrm{\Lambda }}:{∆}_N\to co\left(\mathrm{\Lambda }\right)$ as ${\pi }_{\mathrm{\Lambda }}\left(v\right)=\left(w^{\prime },\sqrt{1-w^{\prime 2}}\right)$, where $w^{\prime }$ is on the arc ${\displaystyle \widehat{w_0\dots w_n}}$. For any $T=\left\{w_{i_0},w_{i_1},\dots ,w_{i_k}\right\}\subset \mathrm{\Lambda }$, ${∆}_T=co\left\{e_{i_0},e_{i_1},\dots ,e_{i_k}\right\}$, where ${∆}_T$ represents the face of the n-dimensional standard simplex ${∆}_N=e_0{e}_1\dots e_n$ corresponding to $T\subset \mathrm{\Lambda }$. For any $v\in {∆}_T=co\left\{e_{i_0},e_{i_1},\dots ,e_{i_k}\right\}$, we can gain ${\pi }_{\mathrm{\Lambda }}\left(v\right)=\left(w^{\prime },\sqrt{1-w^{\prime 2}}\right)\in {\mathrm{\Gamma }}_T$. Therefore, we can discover a continuous mapping ${\pi }_{\mathrm{\Lambda }}:{∆}_N\to \mathrm{\Gamma }\left(\mathrm{\Lambda }\right)$ such that $T\in \aleph \left(\mathrm{\Lambda }\right)$ implies ${\pi }_{\mathrm{\Lambda }}\left({∆}_T\right)\subset \mathrm{\Gamma }\left(T\right)$. □

This example also illustrates that it is not a convex set in the Euclidean space. For other examples of $G$–convex spaces, see [20] and the literature therein.

2.3. $H$–Convex Space

Definition 3 

([2]). Suppose that V is a topological space and $\left\{{\mathrm{\Gamma }}_{\mathrm{\Lambda }}\right\}$ is a given family of non-empty contractible subsets of V. Indexed by all finite subsets Λ, if $\mathrm{\Lambda }\subset B$, ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}\subset {\mathrm{\Gamma }}_B$, then the pair $\left(V,\left\{{\mathrm{\Gamma }}_{\mathrm{\Lambda }}\right\}\right)$ is called an $H$–space. If any finite subset $P\subset \Im$ satisfies ${\mathrm{\Gamma }}_P\subset \Im$, then a subset ℑ of V is called $H$–convex.

The literature [36,37] gives more examples of $H$–spaces.

Example 5. 

The arbitrary Hausdorff topological vector space V is an $H$–space. In fact, for any finite subset $\mathrm{\Lambda }=\left\{w_0,w_1,\dots ,w_n\right\}\subset V$, let ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}=co\left\{w_1,w_2,\dots ,w_n\right\}$ and ℑ be $H$–convex for any convex subset $\Im \subset V$.

Example 6. 

Each contractible space V is an $H$–space. For any finite subset $\mathrm{\Lambda }\subset V$, suppose ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}=V$ and then the only $H$–convex subset is V.

Example 7. 

Assume that $\left(V,\le \right)$ is a topological space with lattice structure such that the ordered interval $\left[{\gamma }_1,{\gamma }_2\right]$ is nonempty or contractible for any ${\gamma }_1,{\gamma }_2\in V$. If $\mathrm{\Lambda }=\left\{w_0,w_1,\dots ,w_n\right\}$, let ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}=\left[w_0\wedge w_1\wedge \cdots \wedge w_n,w_0\vee w_1\vee \cdots \vee w_n\right]$.

2.4. Order Convexity

Definition 4 

([38]). If the partially ordered set $\left(V,\le \right)$ possesses a minimum upper bound for any pair of elements $\left(v,v^{\prime }\right)$, denoted by $v\vee v^{\prime }$, the set V is called semi-lattice, specifically an upper semi-lattice.

An arbitrary nonempty finite subset $T\subset V$ possesses a minimum upper bound, denoted by $supT$. Any two elements $\gamma$ and ${\gamma }^{\prime }$ do not have to be comparable in the partially ordered set $\left(V,\le \right)$, and in the case of $\gamma \le {\gamma }^{\prime }$, the set $\left[\gamma ,{\gamma }^{\prime }\right]=\left\{\kappa \in V:\gamma \le \kappa \le {\gamma }^{\prime }\right\}$ is called an order interval. Suppose that $T\subset V$ is a nonempty finite subset, define $∆\left(T\right)={\displaystyle \bigcup _{w\in T}}\left[w,supT\right]$, then it has the following characteristics:

(1)

$T\subset ∆\left(T\right)$;

(2)

if $T\subset T^{\prime }$, $∆\left(T\right)\subset ∆\left(T^{\prime }\right)$.

A subset $\mathrm{\Psi }\subset V$ is said to be $∆$–convex if $∆\left(T\right)\subset \mathrm{\Psi }$ for any nonempty finite subset $T\subset \mathrm{\Psi }$.

Assume that ℑ is a family of $∆$–convex subsets of V and T is any subset of V. The $∆$–convex hull is defined as $c{o}_{∆}\left(T\right)=\bigcap \left\{\mathrm{\Psi }\in \Im :T\subset \mathrm{\Psi }\right\}$.

The following examples can help us further understand the concept of order convexity.

Example 8. 

Suppose that $V=\left\{\left(\gamma ,1\right):0\le \gamma \le 1\right\}\cup \left\{\left(1,\kappa \right):0\le \kappa \le 1\right\}\subset R^2$ and the partial order of V is ≤ consistent with that in $R^2$, defined as follows:

$$\left(s,t\right)\le \left(q,l\right)\iff q-s\ge 0,l-t\ge 0,l-t\le q-s,$$

for any $\left(s,t\right),\left(q,l\right)\in R^2$. Then V is $∆$–convex.

Proof. 

With the definition of ≤, we are able to gain $supV=\left(1,1\right)$. In fact, for any $\left(s,t\right)\in V$, we have $0\le s\le 1,t=1$ or $s=1,0\le t\le 1$. Furthermore, we get $1-s\ge 0,$$1-t=0,1-t\le 1-s$, which indicates $\left(s,t\right)\le \left(1,1\right)$. The other situation is similar to verify.

For any finite subset $T\subset V$, we can obtain $∆\left(T\right)={\displaystyle \bigcup _{\left(s,t\right)\in T}}\left[\left(s,t\right),\sup \mathrm{T}\right]\subset V$, which shows V is $∆$–convex. □

Example 9. 

Suppose that V is a below set

$$V=\left\{\left(\gamma ,1\right):0\le \gamma \le 1\right\}\cup \left\{\left(\gamma ,\kappa \right):0\le \kappa \le 1,\kappa \ge \gamma -1,\gamma \ge 1\right\}\subset R^2.$$

And the partial order of V is ≤ consistent with that in $R^2$, defined as follows:

$$\left(s,t\right)\le \left(q,l\right)\iff q-s\ge 0,l-t\ge 0,l-t\le q-s,$$

for any $\left(s,t\right),\left(q,l\right)\in R^2$. Then V is $∆$–convex.

The proof is similar to Example 8.

Other non-trivial examples can be found in [38].

2.5. $T$–Convex Space

The following definitions can be found in [27].

Definition 5. 

Assume that U and V are topological spaces. Let Λ be any subset of U and $\xi :\mathrm{\Lambda }\to V$ be any continuous mapping. If there exists a continuous mapping ${\xi }^{\ast }:U\to V$ such that ${\xi }^{\ast }\left(\kappa \right)=\xi \left(\kappa \right)$ for all $\kappa \in \mathrm{\Lambda }$, then ξ can extend (or expand) from Λ to U.

Definition 6. 

Suppose that U and V are topological spaces. If any subset Λ of U and any continuous mapping $\xi :\mathrm{\Lambda }\to V$, ξ can extend from Λ to U, then Λ has an extension property about U.

Definition 7. 

Assume that U is a topological space. Let $\left\{T_{\mathrm{\Lambda }}\right\}$ be a given family of non-empty subsets of U with the extension property with respect to U. Indexed by all finite subsets Λ, if $\mathrm{\Lambda }\subset B$, and $T_{\mathrm{\Lambda }}\subset T_B$, then the pair $\left(U,\left\{T_{\mathrm{\Lambda }}\right\}\right)$ is called a T-space. A subset ℑ of U is called T-convex if any finite subset $P\subset \Im$ satisfies $T_P\subset \Im$. Let $\left(U,\left\{T_{\mathrm{\Lambda }}\right\}\right)$ be a T-space. Define the T-convex hull as below:

$$c{o}^T\left(\mathrm{\Lambda }\right)=\cap \left\{M\subset U:\mathrm{\Lambda }\subset M\right\}.$$

where M is a T-convex set. It is clear that a subset Λ of U is T-convex when it fulfills $\mathrm{\Lambda }=c{o}^T\left(\mathrm{\Lambda }\right)$.

2.6. $Michael$–Convex

Assume that V is an arbitrary set. For any $i\le n$, define ${\partial }_i:V^n\to V^{n-1}$ as follows.

${\partial }_i\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_{n-1}\right)=\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_{i-1},{\gamma }_{i+1},\dots ,{\gamma }_{n-1}\right)$.

Definition 8 

([1]). The convex structure on the metric space V with measures ζ assigns each positive integer n to the subset $M_n$ of $V^n$, and the mapping $k_n:M_n\times {∆}_{n-1}\to V$ such that

(1) 

if $\gamma \in M_1$, then $k_1\left(\gamma ,1\right)=\gamma$;

(2) 

if $\gamma \in M_n\left(n\ge 2\right)$ and $i\le n$, then ${\partial }_i\gamma \in M_{n-1}$ and for any $t\in {∆}_{n-1},t_i=0$, $k_n\left(\gamma ,t\right)=k_{n-1}\left({\partial }_i\gamma ,{\partial }_{i}t\right)$;

(3) 

if $\gamma \in M_n\left(n\ge 2\right)$, ${\gamma }_l={\gamma }_{l+1}$ and $t\in {∆}_{n-1}$ for some $l<n$, then $k_n\left(\gamma ,t\right)=k_{n-1}\left({\partial }_l\gamma ,t^{\ast }\right)$, where $t^{\ast }=\left(t_0,\dots t_{i-1},t_l+t_{l+1},t_{l+2},\dots ,t_{n-1}\right)$;

(4) 

if $\gamma \in M_n$, the mapping $t\to k_n\left(\gamma ,t\right)$ from Δ to V is continuous, and

(5) 

for all $\epsilon >0$, there is a neighbourhood $U_{\epsilon }$ on the diagonal of V, such that for all n and $\gamma ,u\in M_n$, $\left({\gamma }_l,u_l\right)\in V_{\epsilon }$, $l=0,1,\dots ,n-1$, and $\rho \left(k_n\left(\gamma ,t\right),k_n\left(u,t\right)\right)<\epsilon$ hold for all $t\in {∆}_{n-1}$.

For a subset S of a space V with convex structure, if $S^n\subset M_n$ for all n, then the convex hull of S is defined as $co\left(S\right)=\left\{k_n\left(\gamma ,t\right):\gamma \in S^n,t\in {∆}_{n-1},n=1,2,\dots \right\}$, where ${∆}_n$ denote the standard $n$–simplex.

2.7. Pasicki’s $S$–Contractible Space

Definition 9 

([5,6,7]). If there is a mapping $S:V\times I\times V\to V$ such that for any $\gamma \in V$, $\left\{S\left(\gamma ,t,·\right)\right\}$ is a homotopy connecting the identity mapping to the constant-valued function $S\left(\gamma ,1,u\right)=\gamma$, the topological space V is known as S-contractible.

For any nonempty set $\mathrm{\Lambda }\subset V$, define the $S$–convex hull of $\mathrm{\Lambda }$ as follows.

$$c{o}^S\left(\mathrm{\Lambda }\right)=\bigcap \left\{D\subset V:\mathrm{\Lambda }\subset Dandforany\gamma \in \mathrm{\Lambda },t\in I,S\left(\gamma ,t,D\right)\subset D\right\}.$$

If $\mathrm{\Lambda }=\varnothing$, then $c{o}^S\left(\mathrm{\Lambda }\right)=\varnothing$. If $c{o}^S\left(\mathrm{\Lambda }\right)=\mathrm{\Lambda }$, $\mathrm{\Lambda }$ is said to be $S$–convex.

2.8. Komiya’s Convex Space

The below definitions can be sought out in [8].

Definition 10. 

Let V be an arbitrary set, and the mapping $p:2^V\to 2^V$ be a convex hull operator on V, which satisfies the following characteristics:

(1) 

$p\left(\varnothing \right)=\varnothing$;

(2) 

$\gamma \in V$, $p\left(\left\{\gamma \right\}\right)=\left\{\gamma \right\}$;

(3) 

$\mathrm{\Lambda }\subset V$, $p\left(\mathrm{\Lambda }\right)=\bigcup \left\{p\left(\mathrm{\Xi }\right):\mathrm{\Xi }\in \aleph \left(\mathrm{\Lambda }\right)\right\}$;

(4) 

$p\left(p\left(\mathrm{\Lambda }\right)\right)=p\left(\mathrm{\Lambda }\right)$.

Definition 11. 

Let V be a topological space, the mapping $p:2^V\to 2^V$ be a convex hull operator on V, and $\mathrm{\Psi }=\left\{{\phi }_F:F\in \aleph \left(V\right)\right\}$. $\left(V,p,\mathrm{\Psi }\right)$ is called a convex space, where $\left|F\right|=n+1$ and ${\phi }_F:{∆}_n\to p\left(F\right)$ is the homomorphism of the convex hull, i.e., ${\phi }_F\left({∆}_m\right)=p\left(\mathrm{\Lambda }\right)$. $\mathrm{\Lambda }\subset F$ and $\left|\mathrm{\Lambda }\right|=m+1$.

2.9. Bielawski’s Simplicial Convexity

The definitions can be found in [12].

Definition 12. 

Assume that V is an arbitrary set and Ξ is a family of subsets of V. Ξ is called a convexity on V when it fulfills the following:

(1) 

$V\in \mathrm{\Xi }$;

(2) 

${\left\{{\mathrm{\Lambda }}_i\right\}}_{i\in J}\subset \mathrm{\Xi }$, then ${\displaystyle \bigcap _{i\in J}}{\mathrm{\Lambda }}_i\in \mathrm{\Xi }$.

Definition 13. 

A mapping p is called convex prehull on V if a mapping $p:2^V\to 2^V$ satisfies the following properties:

(1) 

for any $\mathrm{\Lambda }\subset V$, $\mathrm{\Lambda }\subset p\left(\mathrm{\Lambda }\right)$;

(2) 

for any $\mathrm{\Lambda },B\subset V$, when $\mathrm{\Lambda }\subset B$, $p\left(\mathrm{\Lambda }\right)\subset p\left(B\right)$.

Suppose that V is a topological space, for any $\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right)\in V^{n+1}$, define a continuous mapping $\mathrm{\Psi }\left[{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right]:{∆}_n\to V$ as $\mathrm{\Psi }=\left\{\mathrm{\Psi }\left[{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right]:\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right)\in V^{n+1},n\in N\right\}$ which fulfills the following properties:

(1)

for all $\gamma \in V$, $\mathrm{\Psi }\left[\gamma \right]\left(1\right)=\gamma$;

(2)

for all $n\le 1$, $\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right)\in V^{n+1}$, $\kappa \in {∆}_n$, $i=0,1,\dots ,n$, then ${\lambda }_i\left(\kappa \right)=0\Rightarrow \mathrm{\Psi }\left[{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right]\left(\kappa \right)=\mathrm{\Psi }\left[{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_{i-1},{\gamma }_{i+1},\dots ,{\gamma }_n\right]\left({\partial }_i\kappa \right)$.

where ${\partial }_i\kappa =\left({\kappa }_0,{\kappa }_1,\dots ,{\kappa }_{i-1},{\kappa }_{i+1},\dots ,{\kappa }_n\right)$.

Definition 14. 

The simplicial convexity $C\left(\mathrm{\Psi }\right)$ of the topological space V determined by Ψ is determined by the hull $p_{\mathrm{\Psi }}:2^V\to 2^V$, defined as follows:

$$p_{\mathrm{\Psi }}\left(A\right)=\left\{\mathrm{\Psi }\left[a_0,a_1,\dots ,a_n\right]\left(u\right):n\in N,\left(a_0,a_1,\dots ,a_n\right)\in A^{n+1},u\in {∆}_n\right\}.$$

Then $C\left(\mathrm{\Psi }\right)=\left\{A\subset V:p_{\mathrm{\Psi }}\left(A\right)=A\right\}$.

Remark 1. 

In simplicial convexity, $p_{\mathrm{\Psi }}\left(\left\{v\right\}\right)=\left\{\mathrm{\Psi }\left[v\right]\left(1\right)\right\}=\left\{v\right\}$ for any $v\in V$.

Remark 2. 

According to Proposition (0.4) in [12], if Ξ is a convexity on V, then the function $c{o}_{\mathrm{\Xi }}:2^V\to 2^V$ defined by

$$c{o}_{\mathrm{\Xi }}\left(\mathrm{\Lambda }\right)=\bigcap \left\{B\in \mathrm{\Xi }:\mathrm{\Lambda }\subset B\right\}$$

is a convex hull on V and the convexity ${\mathrm{\Xi }}_h=\left\{\mathrm{\Lambda }\subset V:c{o}_{\mathrm{\Xi }}\left(\mathrm{\Lambda }\right)=\mathrm{\Lambda }\right\}$ is equal to Ξ.

Remark 3. 

Consider the unit sphere S as the following set of complex numbers $\left\{e^{i\phi }:\phi \in \left[0,2\pi \right]\right\}$. Suppose that $\mathrm{\Xi }=\left\{\left\{e^{i\phi }:\phi \in \left[\alpha ,\beta \right]\right\}:0\le \alpha <\beta <2\pi \right\}\cup \left\{S,\varnothing \right\}$. According to Proposition (1.5) in [12], it implies that there exists a simplicial convexity $C\left(\mathrm{\Psi }\right)$ such that $\mathrm{\Xi }\subset C\left(\mathrm{\Psi }\right)$.

2.10. Joó’s Pseudoconvexity

Definition 15 

([11]). Assume that V is a topological space, and the convex hull operator on V is defined as the operator in the Komiya convex space. $\mathrm{\Psi }=\left\{{\phi }_T:T\in \aleph \left(V\right)\right\}$, $\left(V,p,\mathrm{\Psi }\right)$ is called a pseudoconvex space, where ${\phi }_T:{∆}_n\to p\left(T\right)$ is a continuous surjective mapping, and $\left|T\right|=n+1$ such that ${\phi }_T$ reflects the convex hull into a convex hull, i.e., for each face ${∆}_J$ of the n-dimensional standard simplex ${∆}_n=e_0{e}_1\dots e_n$ corresponding to $J\in \aleph \left(T\right)$, we have ${\phi }_T\left({∆}_J\right)=p\left(J\right)$.

Remark 4. 

Joó [11] defined the following convexity on $R^{n+1}$. Let $u=\left(u_0,u_1,\dots ,u_n\right)$ and $v=\left(v_0,v_1,\dots ,v_n\right)\in R^{n+1}$. We shall give the interval $〈u,v〉$ joining them as a polygon with at most $n+1$ pairwise orthogonal segments as follows: If $u_n\ge v_n$, then let $I_n=\left\{\left(u_0,u_1,\dots ,u_{n-1},t\right):u_n\ge t\ge v_n\right\}$ and $u^{\prime }=\left(u_0,u_1,\dots ,u_{n-1},v_n\right)$ be the other endpoint of $I_n$. If $u_n\le v_n$, then let $I_n=\left\{\left(v_0,v_1,\dots ,v_{n-1},t\right):u_n\le t\le v_n\right\}$ and $v^{\prime }=\left(v_0,v_1,\dots ,v_{n-1},u_n\right)$. In the first case, we get $I_{n-1}$ analogously to $I_n$; if, for example, $u_{n-1}\le v_{n-1}$, then $I_{n-1}=\left\{\left(v_0,v_1,\dots ,v_{n-2},t,v_n\right):u_{n-1}\le t\le v_{n-1}\right\}$ and $v^{″}=\left(v_0,v_1,\dots ,v_{n-2},u_{n-1},v_n\right)$, if $u_{n-1}\ge v_{n-1}$, then $I_{n-1}=\left\{\left(u_0,u_1,\dots ,u_{n-2},t,v_n\right):u_{n-1}\ge t\ge v_{n-1}\right\}$ and $u^{″}=\left(u_0,u_1,\dots ,u_{n-2},v_{n-1},v_n\right)$. In the second case ($u_n\le v_n$), we construct $I_{n-1}$ analogously, and in the third step, $I_{n-2}$, etc. Finally, the segments $I_0,I_1,\dots ,I_n$, parallel to the axis $u_0,u_1,\dots ,u_n$, respectively, will join u and v (possibly not in the order of the indices). Now let a set $K\subset R^{n+1}$ be convex if $u,v\in K$ implies $〈u,v〉\subset K$. The space $R^{n+1}$ with the convexity above is a pseudoconvex space.

2.11. Horvath’s Pseudoconvex Space

Definition 16 

([10]). Suppose that V is a topological space. A mapping $S:V\times I\times V\to V$ fulfills

(1) 

for any $\gamma ,\kappa \in V$, $S\left(\gamma ,0,\kappa \right)=u$, $S\left(\gamma ,1,\kappa \right)=\gamma$.

$\mathrm{\Xi }\subset V$ is called $S$–convex if for all $\left(\gamma ,\kappa ,t\right)\in \mathrm{\Xi }\times I\times \mathrm{\Xi }$, $S\left(\gamma ,\kappa ,t\right)\in \mathrm{\Xi }$. Let $c{o}_S\left(\mathrm{\Lambda }\right)=\bigcap \left\{U:\mathrm{\Lambda }\subset U\subset VandUisS-convex\right\}$.

If the mapping S satisfies (1) and the following condition:

(2) 

for any $\mathrm{\Lambda }\in \aleph \left(V\right)$, $S{|}_{C_S\left(\mathrm{\Lambda }\right)\times I\times C_S\left(\mathrm{\Lambda }\right)}$ is continuous,

then $\left(V,S\right)$ is said to be a pseudoconvex space.

Remark 5. 

Pasicki’s $S$–contractible space is almost identical to Horvath’s pseudoconvex space. Horvath pointed out that every contractible space V is a pseudoconvex space, which can establish an $H$–space structure. In fact, for each finite subset $\mathrm{\Lambda }\subset V$, let ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}=C_h\left\{\mathrm{\Lambda }\right\}$, and $C_h\left\{\mathrm{\Lambda }\right\}$ be the $H$–convex hull of Λ.

2.12. $B^{\prime }$–Simplicial Convexity

Definition 17 

([39]). The topological space V has a $B^{\prime }$–simplicial convexity if, for each $n\in N$ and $\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right)\in V^{n+1}$, there is a continuous mapping $\mathrm{\Psi }\left[{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right]:{∆}_n\to V$ satisfying for all $n\ge 1$, $\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right)\in V^{n+1}$, $\left({\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right)\in {∆}_n$, if ${\kappa }_i=0$, then $\mathrm{\Psi }\left[{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right]\left({\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right)=\mathrm{\Psi }\left[{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_{i-1},{\gamma }_{i+1},\dots ,{\gamma }_n\right]\left({\partial }_i\kappa \right)$, where ${\partial }_i\kappa =\left({\kappa }_0,{\kappa }_1,\dots ,{\kappa }_{i-1},{\kappa }_{i+1},\dots ,{\kappa }_n\right)$.

Remark 6. 

A subset $Z\subset V$ is called a $B^{\prime }$–simplicial convex set if and only if, for all $n\in N$ and $\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right)\in Z^{n+1}$, it is satisfied that $\mathrm{\Psi }\left[{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right]\left(\kappa \right)\in Z$ for all $\kappa \in {∆}_n$.

2.13. $L$–Space

Definition 18 

([39]). The $L$–structure on V is provided by the nonempty set-valued mapping $\mathrm{\Gamma }:\aleph \left(V\right)\to 2^V$, such that for each $\mathrm{\Lambda }=\left\{w_0,w_1,\dots ,w_n\right\}\in \aleph \left(V\right)$, there exists a continuous mapping ${\xi }_{\mathrm{\Lambda }}:{∆}_n\to \mathrm{\Gamma }\left(\mathrm{\Lambda }\right)$ such that for all $K\subset \left\{0,1,\dots ,n\right\}$, if ${∆}_K=co\left\{e_{i_k}:i_k\in K\right\}$, then ${\xi }_{\mathrm{\Lambda }}\left({∆}_K\right)\subseteq \mathrm{\Gamma }\left(\left\{w_i:i\in K\right\}\right)$. $\left(V,\mathrm{\Gamma }\right)$ is called a $L$–convex space when for all $\mathrm{\Lambda }\in \aleph \left(W\right)$, $\mathrm{\Gamma }\left(\mathrm{\Lambda }\right)\subset W$.

Remark 7. 

It should be emphasized that the above definition implicitly assigns to each $\mathrm{\Lambda }\in \aleph \left(V\right)$ an order on the elements of Λ, i.e., if $\left|\mathrm{\Lambda }\right|=n+1$, a bijection $\varphi :\mathrm{\Lambda }\to \left\{e_0,e_1,\dots ,e_n\right\}$.

Remark 8. 

Let $\mathrm{\Gamma }:\aleph \left(V\right)\to 2^V$. If for $\mathrm{\Lambda }\in \aleph \left(V\right)$, $\left|\mathrm{\Lambda }\right|=n+1$ and there exists a bijection ${\varphi }_0$ and ${\xi }_{\mathrm{\Lambda },{\varphi }_0}:{∆}_n\to \mathrm{\Gamma }\left(\mathrm{\Lambda }\right)$ satisfying the condition

$$\forall K\subset \left\{0,1,\dots ,n\right\},{\xi }_{\mathrm{\Lambda },{\varphi }_0}\left({∆}_K\right)\subset \mathrm{\Gamma }\left(\left\{{\varphi }_0^{-1}\left(e_i\right)|i\in K\right\}\right),$$

then for every bijection $\varphi :\mathrm{\Lambda }\to \left\{e_0,e_1,\dots ,e_n\right\}$, there exists ${\xi }_{\mathrm{\Lambda },\varphi }:{∆}_n\to \mathrm{\Gamma }\left(\mathrm{\Lambda }\right)$ satisfying

$$\forall K\subset \left\{0,1,\dots ,n\right\},{\xi }_{\mathrm{\Lambda },\varphi }\left({∆}_K\right)\subset \mathrm{\Gamma }\left(\left\{{\varphi }^{-1}\left(e_i\right)|i\in K\right\}\right).$$

Indeed, it suffices to define ${\xi }_{\mathrm{\Lambda },\varphi }\left({\displaystyle \sum _{i\in K}}{\lambda }_i{e}_i\right)={\xi }_{\mathrm{\Lambda },{\varphi }_0}\left({\displaystyle \sum _{i\in K}}{\lambda }_i\left({\varphi }_0\circ {\varphi }^{-1}\right)\left(e_i\right)\right)$.

2.14. $K$–Convex Structure

Definition 19 

([40]). The $K$–convex structure on the set V is provided by the mapping $K:V\times V\times \left[0,1\right]\to V$, and then $\left(V,K\right)$ is called $K$–convex space.

Remark 9. 

The $K$–convex structure is based on the idea of considering functions joining pairs of points. That is, the segments used in usual convexity are substituted for an alternative path previously fixed on V. The function that defines this set is called $K$–convex function and V is said to have a $K$–convex structure.

2.15. $mc$–Space

Definition 20 

([41]). The topological space V is an $mc$–space (or has an $mc$–structure). If for any nonempty finite subset $\mathrm{\Lambda }=\left\{w_0,w_1,\dots ,w_n\right\}\in \aleph \left(V\right)$, there is a family element $\left\{b_0,b_1,\dots ,b_n\right\}\subset V$ and the family mapping $P_i^{\mathrm{\Lambda }}:V\times \left[0,1\right]\to V$ satisfying the following conditions:

(1) 

for any $v\in V$, $P_i^{\mathrm{\Lambda }}\left(v,0\right)=v$, $P_i^{\mathrm{\Lambda }}\left(v,1\right)=b_i$, $i=0,1,\dots n$;

(2) 

a mapping $G_{\mathrm{\Lambda }}:{\left[0,1\right]}^n\to V$, defined as $G_{\mathrm{\Lambda }}\left(l_0,l_1,\dots ,l_{n-1}\right)=P_0^{\mathrm{\Lambda }}\left(\dots \left(P_{n-1}^{\mathrm{\Lambda }}\left(P_n^{\mathrm{\Lambda }}\left(b_n.1\right),l_{n-1}\right),\dots ,l_0\right)\right)$, is continuous.

Remark 10. 

The $mc$–space is based on the idea of substituting the segment that joins any pair of points (or the convex hull of a finite set of points) by an arc, path, or set that fulfills the same role. In particular, the idea is to associate to any finite family of points a family of functions whose composition is continuous. The image of this composition generates a set associated to the finite family of points in a similar manner to how the usual convex hull operator associates a set to each finite family of points.

Remark 11. 

Note that if V is a convex subset of a topological vector space and we consider functions $P_i^A\left(v,l\right)=\left(1-l\right)v+l{w}_i$, then they define an $mc$–structure on V. In this case, $b_i=w_i$, and functions $P_i^{\mathrm{\Lambda }}\left(v,l\right)$ represent the segment joining $w_i$ and v when $l\in \left[0,1\right]$. Therefore, $mc$–spaces are extensions of convex sets. Moreover, the image of the composition $G_{\mathrm{\Lambda }}\left({\left[0,1\right]}^n\right)$ in this particular case represents the usual convex hull of Λ.

Researchers who are interested in $L$–spaces and $mc$–spaces can refer to references [42,43,44] and references therein.

In order to analyze the properties of these convexities, we give the definitions of the convex space fulfilling the $H$–condition and the $H_0$–condition.

Definition 21 

([24]). $\left(U,\mathrm{\Xi }\right)$ fulfills the $H$–condition if the convex structure Ξ has the following characteristic: for each $\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}\subset U$, there exists a continuous mapping $\xi :{∆}_N\to {\displaystyle \overline{co}}\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}$ such that $\xi \left({∆}_J\right)\subset {\displaystyle \overline{co}}\left\{{\kappa }_j:j\in J\right\}$ for any nonempty set $J\subset N$, where ${∆}_J$ represents the face of the n-dimensional standard simplex ${∆}_N=e_0{e}_1\dots e_n$ corresponding to $J\subset N$. And ${\displaystyle \overline{co}}\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}$ represents the closure of the convex hull $\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}$ in the convex structure Ξ.

Definition 22 

([25]). $\left(U,\mathrm{\Xi }\right)$ fulfills the $H_0$–condition if the convex structure Ξ has the following characteristic: for each $\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}\subset U$, there exists a continuous mapping $\xi :{∆}_N\to co\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}$ such that $\xi \left({∆}_J\right)\subset co\left\{{\kappa }_j:j\in J\right\}$ for any nonempty set $J\subset N$, where ${∆}_J$ represents the face of the n-dimensional standard simplex ${∆}_N=e_0{e}_1\dots e_n$ corresponding to $J\subset N$. And $co\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}$ represents the convex hull $\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}$ in the convex structure Ξ.

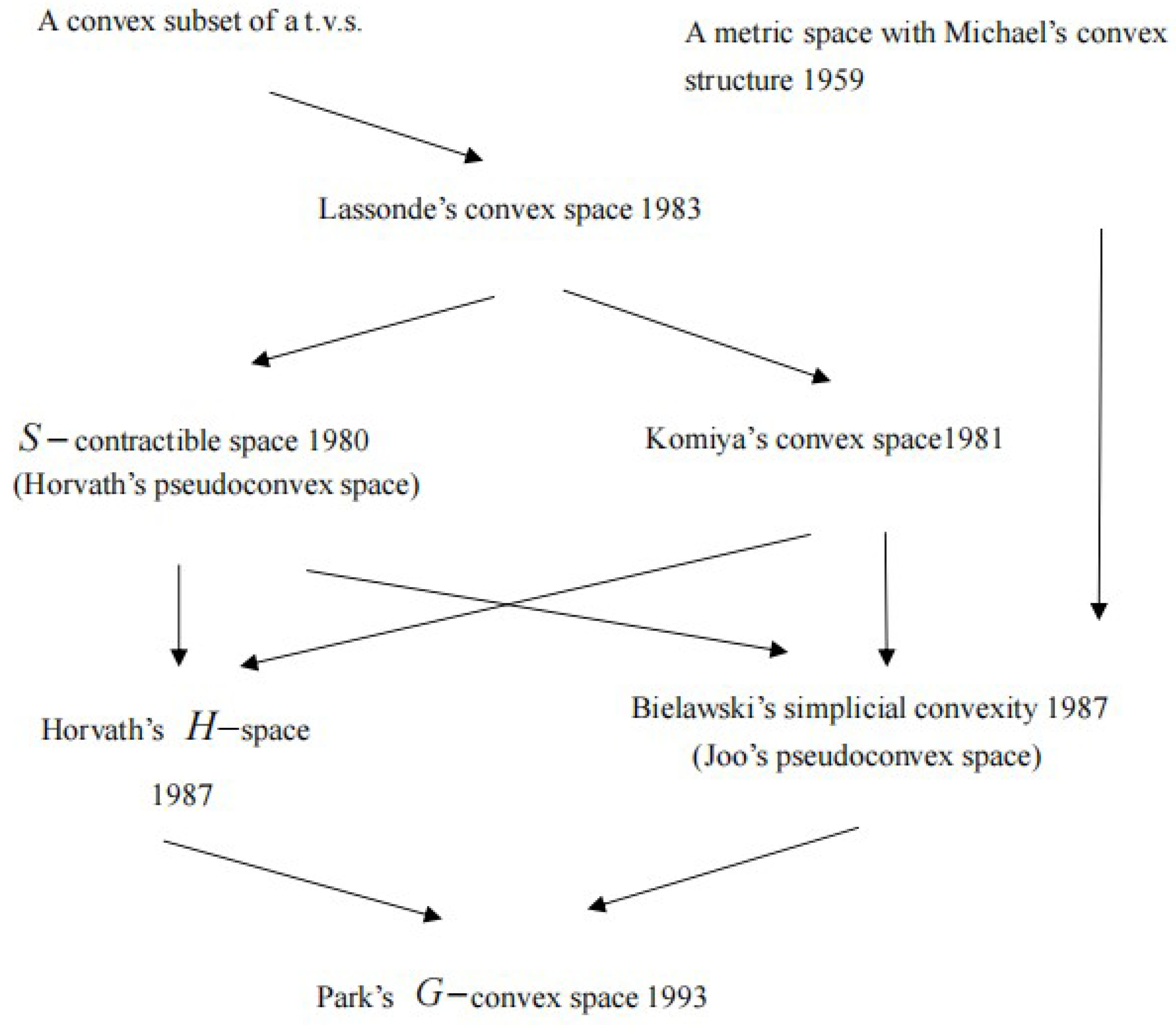
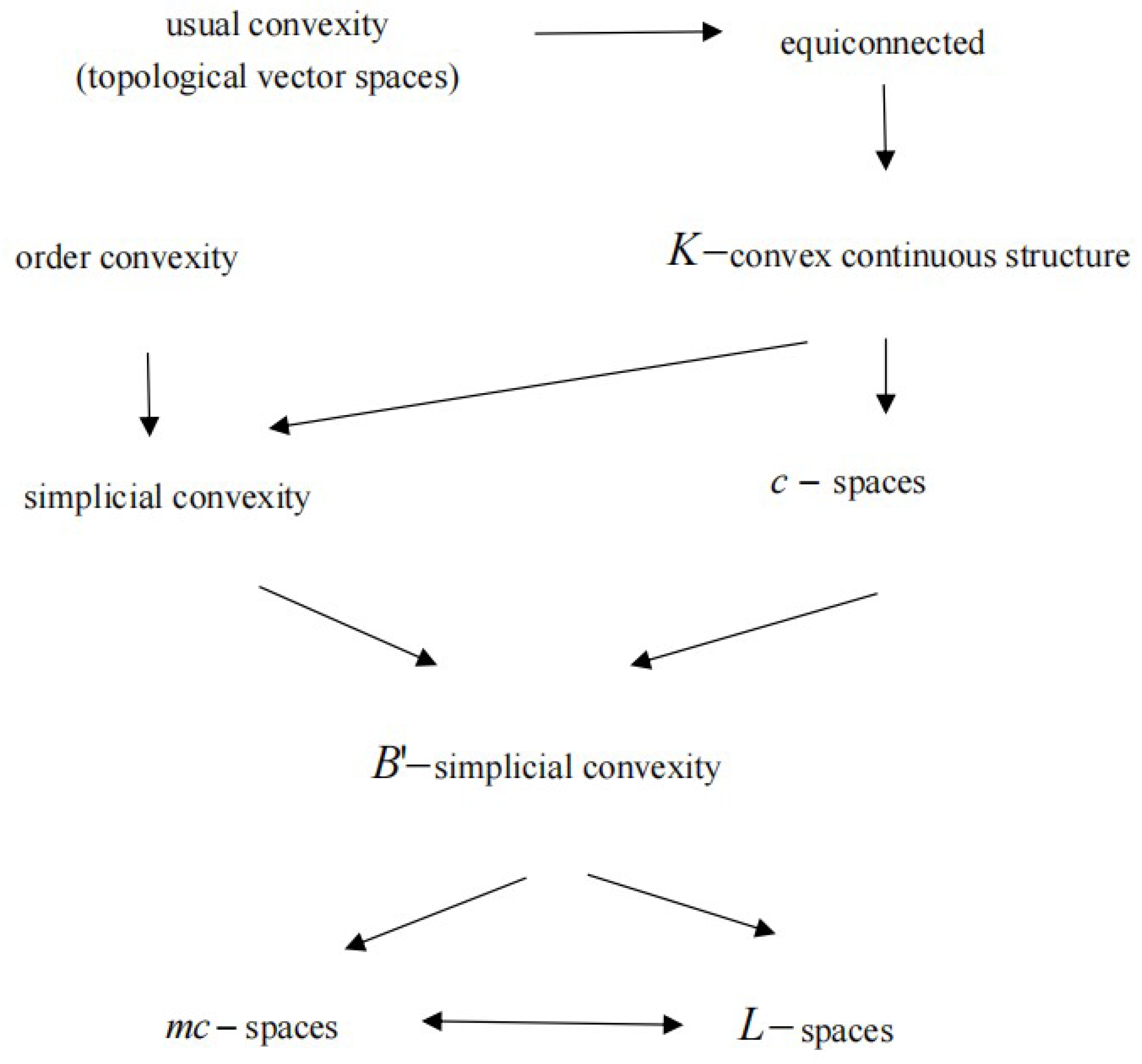
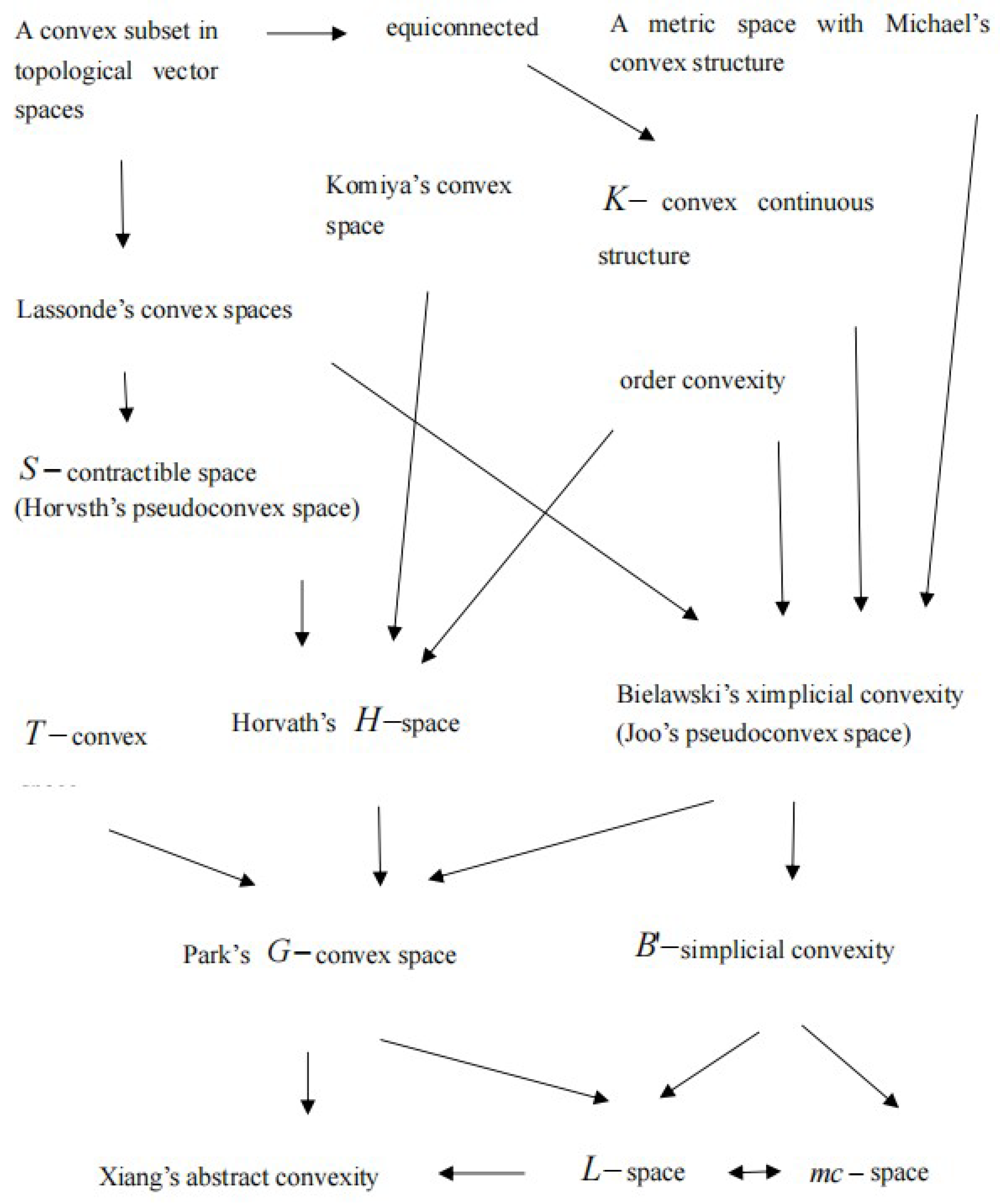
3. The Relation between the Various Convexities

This section will analyze the relationship between the above mentioned convex structures, some of which have already been concluded.

Lemma 1 

([27]). A $T$–convex space $\left(V,\left\{T_{\mathrm{\Lambda }}\right\}\right)$ satisfies the $H_0$–condition.

The following conclusion can be discovered in the references [13,19].

Theorem 1 

([13]). An $H$–space $\left(V,\left\{{\mathrm{\Gamma }}_A\right\}\right)$ is a $G$–convex space.

Theorem 2. 

A topological semi-lattice $\left(V,\le \right)$ with the path-connected interval is a $G$–convex space.

The proof is given in [19].

Theorem 3. 

A $T$–convex space $\left(V,\left\{T_{\mathrm{\Lambda }}\right\}\right)$ is a $G$–convex space.

Proof. 

Assume D is a nonempty subset of V and ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}=T_{\mathrm{\Lambda }}$. From Definition 7 and Lemma 1, we are able to acquire the following results:

(1)

for any $\mathrm{\Lambda },B\in \aleph \left(D\right)$, when $\mathrm{\Lambda }\subset B$, ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}\subset {\mathrm{\Gamma }}_B$;

(2)

for any $\mathrm{\Lambda }\in F\left(D\right)$, $\left|\mathrm{\Lambda }\right|=n+1$, we are capable of discovering a continuous mapping ${\varphi }_{\mathrm{\Lambda }}:{∆}_N\to \mathrm{\Gamma }\left(\mathrm{\Lambda }\right)$ such that $J\in \aleph \left(\mathrm{\Lambda }\right)$ indicates ${\varphi }_{\mathrm{\Lambda }}\left({∆}_J\right)\subset \mathrm{\Gamma }\left(J\right)$.

Therefore, we are capable of drawing a conclusion. □

Theorem 4. 

An $L$–space $\left(V,\mathrm{\Gamma }\right)$ is an abstract convex space.

Proof. 

Suppose that $\mathrm{\Xi }=\left\{W\subset V:WisL-convexsubsetofV\right\}$. It only needs to verify that $\left(V,\mathrm{\Xi }\right)$ satisfies the definition of abstract convex space:

(1)

$\varnothing \in \mathrm{\Xi }$;

(2)

for a nonempty subset $D\subset \mathrm{\Xi }$, it needs to be verified that ${\displaystyle \bigcap _{\mathrm{\Lambda }\in D}}\mathrm{\Lambda }\subset \mathrm{\Xi }$. For any finite subset $L\subset {\displaystyle \bigcap _{\mathrm{\Lambda }\in D}}\mathrm{\Lambda }$, we have $L\subset \mathrm{\Lambda }$ for any $\mathrm{\Lambda }\in D$. Because $\mathrm{\Lambda }\in D\subset \mathrm{\Xi }$, i.e., $\mathrm{\Lambda }$ is a $L$–convex set, we can obtain $\mathrm{\Gamma }\left(Ł\right)\subset \mathrm{\Lambda }$. Thus, $\mathrm{\Gamma }\left(L\right)\subset {\displaystyle \bigcap _{\mathrm{\Lambda }\in D}}\mathrm{\Lambda }$, and furthermore, ${\displaystyle \bigcap _{\mathrm{\Lambda }\in D}}\mathrm{\Lambda }\subset \mathrm{\Xi }$.

□

Theorem 5. 

A $G$–convex space $\left(V,D;\mathrm{\Gamma }\right)$ is an abstract convex space.

The verification is similar to Theorem 4.

In the definition of $L$–space, there is no requirement for the monotonicity of the set-valued mapping $\mathrm{\Gamma }$. According to the definition of $G$–convex space, $G$–convex space is a special $L$–space.

In [13], Park gives the relationship between the partially convex structures, as shown in Figure 1.

In [35], Llinares proves and gives the relationship between the above partially convex structures, as shown in Figure 2.

To understand the relationship between these convex structures more clearly, we will now present the relationship between the convex structures in Figure 3.

Figure 3 illustrates how these convex structures are unified in the abstract convex structure.

The fixed point theory, KKM theory, and continuous selection theory are generally related to the convexity of the space. When certain conditions of the convexity of the space are satisfied, the space will have the fixed point property or the continuous selection property.

Xiang et al. [24,25,26] gave the relationship between abstract convexity, the fixed point property, and continuous selection property.

Property 1. 

If $\left(V,\mathrm{\Xi }\right)$ is selective about any standard simplex, $\left(V,\mathrm{\Xi }\right)$ fulfills the $H$–condition.

Property 2. 

If $\left(V,\mathrm{\Xi }\right)$ is selective about any compact Hausdorff space, $\left(V,\mathrm{\Xi }\right)$ satisfies the $H$–condition.

Property 3. 

If $\left(V,\mathrm{\Xi }\right)$ has weak selectivity about any standard simplex, $\left(V,\mathrm{\Xi }\right)$ satisfies the $H_0$–condition.

Property 4. 

If $\left(V,\mathrm{\Xi }\right)$ has weak selectivity about any compact topological space, $\left(V,\mathrm{\Xi }\right)$ satisfies the $H_0$–condition.

Property 5. 

Suppose that $\left(V,\mathrm{\Xi }\right)$ is an $l.c.$ complete metric space; then V possesses selective properties about any compact space if and only if $\left(V,\mathrm{\Xi }\right)$ fulfills the $H$–condition.

Property 6. 

Suppose that $\left(V,\mathrm{\Xi }\right)$ is an $l.c.$ metric space such that every single set is a convex set, and U is a convex and compact subset of $\left(V,\mathrm{\Xi }\right)$. If $\left(V,\mathrm{\Xi }\right)$ possesses the weak selective properties, then U has the fixed point property.

Property 7. 

Assume that $\left(V,\mathrm{\Xi }\right)$ is an $l.c.$ complete metric space with a convex structure Ξ, which fulfills the $H$–condition when Ξ is one of the below convex structures:

(1) 

$H$–convex structure;

(2) 

a convex structure on a topological semi-lattice space;

(3) 

Michael’s convex strcture;

(4) 

$B$–convex structure.

Property 8. 

Assume $\left(V,\mathrm{\Xi }\right)$ is a binary pair, when Ξ is one of the below convex structures, Ξ fulfills the $H_0$–condition:

(1) 

$H$–convex structure;

(2) 

a convex structure on a topological semi-lattice space;

(3) 

Michael’s convex strcture;

(4) 

$B$–convex structure;

(5) 

$G$–convex structure.

4. KKM Theory and Fixed Point Theory in Partially Convex Spaces

This section will briefly describe the extension of KKM theory and fixed point theory in partially convex spaces. First, we give the KKM theory in partially convex spaces.

4.1. KKM Theory in Partially Convex Spaces

Knaster et al. [45], in 1929, proposed the outstanding KKM lemma, an essential result of the intersection of non-empty sets. The intersection points can be fixed points, equilibrium points, saddle points, or solutions to other equilibrium problems. The existence of these points is inseparable from the convexity of space. After the researchers generalized the convexity of Euclidean space, the KKM theory, fixed point theory, and continuous selection theory were generalized in these generalized convex spaces. Although these spatial convexities do not have a linear structure, the conclusion is still established.

Lemma 2 

([45]). [KKM lemma] Suppose that $P_0,P_1,\dots ,P_n$ is $n+1$ closed sets in simplex $\sigma =co\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right)$. If for any $l_0,l_1,\dots ,l_k$, $k=0,1,\dots ,n$, $co\left({\gamma }_{l_0},{\gamma }_{l_1},\dots ,{\gamma }_{l_k}\right)\subset {\displaystyle \bigcup _{m=0}^k}{P}_{l_m}$, then ${\displaystyle \bigcap _{l=0}^n}{P}_l\ne \varnothing$, where $\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_n\right)\subset R^n$.

Ky Fan [46], in 1961, popularized the above lemma to arbitrary topological vector spaces and obtained the KKMF lemma, which has since become the basic theory for solving nonlinear problems.

Lemma 3 

([46]). [KKMF lemma] Assume that V is a set of the Hausdorff linear topological space Λ. For any $\gamma \in V$, if $\xi \left(\gamma \right)$ is a closed set, then there exists ${\gamma }_0\in V$ such that $\xi \left({\gamma }_0\right)$ is compact. For any $\left\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\right\}\subset V$, $co\left\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\right\}\subset {\displaystyle \bigcup _{i=1}^n}\xi \left({\gamma }_i\right)$, then ${\displaystyle \bigcap _{\gamma \in V}}\xi \left(\gamma \right)\ne \varnothing$.

Assume that V is a topological space and $\xi :V\to 2^V$ is a set-valued mapping. If for any finite subset $\left\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\right\}\subset V$, $co\left\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\right\}\subset {\displaystyle \bigcup _{i=1}^n}\xi \left({\gamma }_i\right)$, then $\xi$ is called a KKM mapping.

After that, the researchers grasped the convexity condition in space and proposed many convex spaces without a linear structure, in which the KKM lemma was studied, and the definition of KKM mappings was given.

4.1.1. KKM Theory in $G$–Convex Space

The KKM theory mainly studies KKM mapping and its applications, which was named for the first time by Park [47]. In 1993, after Park proposed the notion of generalized convex space or $G$–convex space, the theory was widely studied in this space. Due to the limited space of the paper, only the KKM theorems of partially convex space are given here. Interested readers can refer to references [48,49,50] and the references therein.

The following theorem is a new version of KKM lemma in $G$–convex space, as presented in [48].

Theorem 6. 

Suppose that $\left(V,D;\mathrm{\Gamma }\right)$ is a $G$–convex space, and the set-valued mapping $\xi :\aleph \left(D\right)\to 2^V$ is both compactly closed and a KKM mapping. ${\left\{\xi \left(\kappa \right)\right\}}_{\kappa \in D}$ has the finite intersection property. Further, when ξ is a compactly closed value and ${\displaystyle \bigcap _{\kappa \in M}}\xi \left(\kappa \right)$ is compact for some $M\in \aleph \left(D\right)$, then ${\displaystyle \bigcap _{\kappa \in D}}\xi \left(\kappa \right)\ne \varnothing$.

Compared with the KKMF lemma, the KKM theorem is extended from topological vector spaces to $G$–convex spaces without a linear structure, which strengthens the conditions satisfied by the set-value mapping and still obtains the conclusion that the set intersection is non-empty. In [48], it is pointed out that, for the sake of simplicity, other forms can be obtained by taking M as a single point set. See [48] for more details.

In addition to this form, we can find other forms of generalizing the KKM lemma in $G$–convex spaces. Ref. [49] obtains the KKM theorem from the Ky Fan-type matching theorem with open coverage. Then, it gives the KKM-type theorem for the admissible mapping class (see [13] for definition). More details can be found in the literature [49].

By reviewing the references on the KKM theorems in $G$–convex spaces, we find that Ding, Park, and Tan et al. have made significant contributions to the study of this theory, which can be found in [50,51,52,53,54,55,56], in which the references are more important, covering the generalized forms, proof methods, and applications of KKM theory in $G$–convex spaces.

The authors of these papers have studied the KKM theorem and its equivalence with the fixed point theorem (mainly Browder’s fixed point theorem) in $G$–convex spaces and applied it to verifying Nash’s equilibrium theorem in game theory. And various generalized equilibrium problems have been solved under these theorems. Not only that, the coincidence theorem, the continuous selection theorem, and the minimax inequality have also been generalized in this space.

4.1.2. KKM Theory in $H$–Space

In 1987, Horvath [2] proposed the concept of $H$–space with the contractibility of topological spaces and generalized the KKM lemma in this space.

In 1988, Bardaro and Ceppitelli [37] defined the $H-KKM$ mapping. They established and proved the KKM theorem in $H$–spaces.

Definition 23. 

Suppose that $\left(V,\left\{{\mathrm{\Gamma }}_A\right\}\right)$ is an $H$–space; the mapping $\xi :V\to 2^V$ is said to be an $H-KKM$ mapping. If for all subsets $\mathrm{\Lambda }\subset V$, ${\mathrm{\Gamma }}_{\mathrm{\Lambda }}\subset {\displaystyle \bigcup _{\gamma \in \mathrm{\Lambda }}}\xi \left(\gamma \right)$.

Theorem 7. 

Assume that $\left(V,\left\{{\mathrm{\Gamma }}_A\right\}\right)$ is an $H$–space. The set-valued mapping $\xi :V\to 2^V$ is an $H-KKM$ mapping and fulfills the following conditions:

(1) 

for any $\gamma \in V$, $\xi \left(\gamma \right)$ is compactly closed, i.e., for each compact subset $B\subset V$, $B\cap \xi \left(\gamma \right)$ is closed in B;

(2) 

there exists a compact set $T\subset V$ and an $H$–compact set $P\subset V$ such that the weak $H$–convex set Φ fulfills $P\subset \mathrm{\Phi }\subset V$, ${\displaystyle \bigcap _{\gamma \in \mathrm{\Phi }}}\left(\xi \left(\gamma \right)\cap \mathrm{\Phi }\right)\subset T$.

Then ${\displaystyle \bigcap _{\gamma \in V}}\xi \left(\gamma \right)\ne \varnothing$.

Theorem 7 not only generalizes the linear convexity to $H$–convexity but also adopts the concepts of compactly closed, $H$–compact set, and weak $H$–convexity to establish the KKM theorem.

In 1992, Chang et al. [57] established the KKM theorem in Horvath’s $H$–space.

A definition of a generalized KKM mapping is defined in [57].

Definition 24. 

Suppose that $\left(V,\left\{{\mathrm{\Gamma }}_A\right\}\right)$ is an $H$–space, Φ is a nonempty set and $\xi :\mathrm{\Phi }\to 2^V$ is a set-valued mapping. If for any finite set $\left\{{\kappa }_1,{\kappa }_2,\dots ,{\kappa }_n\right\}\subset \mathrm{\Phi }$, there exists $\left\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\right\}\subset V$ such that ${\mathrm{\Gamma }}_{\left\{{\gamma }_{i_1},{\gamma }_{i_2},\dots ,{\gamma }_{i_k}\right\}}\subset {\displaystyle \bigcup _{j=1}^k}\xi \left({\kappa }_{i_j}\right)$ for any $\left\{{\gamma }_{i_1},{\gamma }_{i_2},\dots ,{\gamma }_{i_k}\right\}\subset \left\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\right\}$, $\left(1\le k\le n\right)$, then ξ is called a generalized KKM (or $G-KKM$) mapping.

The below theorem in $H$–space is in [57].

Theorem 8. 

Assume that $\left(V,\left\{{\mathrm{\Gamma }}_A\right\}\right)$ is an $H$–space, Ψ is a nonempty set and the $G-KKM$ mapping $\xi :\mathrm{\Psi }\to 2^V$ fulfills the following conditions:

(1) 

for any $\kappa \in \mathrm{\Psi }$, $\xi \left(\kappa \right)$ is compactly closed in V;

(2) 

for any $\kappa \in \mathrm{\Psi }$, $\xi \left(\kappa \right)$ is compactly open in V.

Then $\left\{\xi \left(\kappa \right):\kappa \in \mathrm{\Psi }\right\}$ possesses the finite intersection characteristic. Further, If there exists ${\kappa }_0$ such that $\xi \left({\kappa }_0\right)$ is a compact set, which is added to condition (1), then ${\displaystyle \bigcap _{\kappa \in \mathrm{\Psi }}}\xi \left(\kappa \right)\ne \varnothing$.

The reference [57] gives an example to show that the conclusion may not hold when conditions (1) or (2) are satisfied, and Chang et al. have obtained other results regarding the intersection of sets by Theorem 8, which is used as an application to establish the minimum–maximum inequality and the coincidence theorem.

In the KKM theorem of $H$–space, given in the literature [37,57,58,59], the conditions of closed compactness and the KKM mapping are essential. Most of the applications of the theorem in each piece of the literature are the coincidence theorems, minimax inequalities and fixed point theorems.

4.1.3. KKM Theory in Topological Ordered Space

In 1996, after Horvath and Ciscar [38] proposed the notion of semilattice convex in partial topological spaces, they studied the KKM theorem of topological semilattice under this framework. They used it to prove the existence of the maximum element of weak preference relationships.

Theorem 9. 

Suppose that U is a topological semi-lattice with path-connected intervals and $\left\{R_i:l=0,1,\dots ,n\right\}$ is a family of closed subsets of U. If there exists $\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}\subset U$, $∆\left(\left\{{\kappa }_{l_0},{\kappa }_{l_1},\dots ,{\kappa }_{l_k}\right\}\right)\subseteq {\displaystyle \bigcup _{j=0}^k}{R}_{l_j}$ for any $\left\{l_0,l_1,\dots ,l_k\right\}\subset \left\{0,1,\dots ,n\right\}$. Then ${\displaystyle \bigcap _{l=0}^n}{R}_l\ne \varnothing$.

Horvath and Ciscar established the KKM theorem in the form of open sets in partial order topological spaces. And it only needed to change the condition of the closed subset family to the open subset family.

The KKM theorem for topological semi-lattice forms does not involve a set-valued mapping. However, it directly extends the KKM Lemma and replaces the well-known convexity with a semi-lattice convex.

Luo [60] combined the concept of the transferable closed set to establish the general KKM theorem, from which the general Ky Fan inequality is obtained and used to verify the general Fan–Browder fixed point theorem; as an application, he verified the existence of the Nash equilibria.

Theorem 10. 

Suppose that Ψ is a topological semi-lattice with path-connected intervals and ${\mathrm{\Psi }}_0\subset \mathrm{\Psi }$ is a nonempty set. The binary relation $R\subset {\mathrm{\Psi }}_0\times \mathrm{\Psi }$ fulfills the following characteristics:

(1) 

$\zeta :{\mathrm{\Psi }}_0\to 2^{\mathrm{\Psi }}$ is transferable closed values, $\zeta \left(\kappa \right)=\left\{\gamma \in \mathrm{\Psi }:\left(\kappa ,\gamma \right)\in R\right\}$ for each $\kappa \in {\mathrm{\Psi }}_0$;

(2) 

there exists ${\kappa }_0\in {\mathrm{\Psi }}_0$ such that cl $\zeta \left({\kappa }_0\right)$ is compact;

(3) 

for any nonempty finite subset $\mathrm{\Lambda }\subset {\mathrm{\Psi }}_0$, ${\displaystyle \bigcup _{\kappa \in \mathrm{\Lambda }}}\left[\kappa ,sup\mathrm{\Lambda }\right]\subset {\displaystyle \bigcup _{\kappa \in \mathrm{\Lambda }}}\zeta \left(\kappa \right)$.

Then ${\displaystyle \bigcap _{\kappa \in \mathrm{\Lambda }}}\zeta \left(\kappa \right)\ne \varnothing$.

Theorem 10 generalized the KKMF lemma and adopted the definition of a transferable closed set as one of the conditions for set-valued mapping. At the same time, $co\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}$ was replaced by a semi-lattice convex.

The KKM theorem established in topological ordered space is mainly used to generalize Ky Fan inequality, Fan–Browder fixed point theorem, the existence of the largest element and maximal element, and as an application of these conclusions, the existence theorem of Nash equilibrium points is also generalized in this space. Refer to the literature [60,61,62,63,64,65,66] for more details.

4.2. Fixed Point Theory in Partially Convex Space

4.2.1. Fixed Point Theory in $G$–Convex Space

The fixed point theorem is fundamental in many research fields, such as differential equations, topology, functional analysis, optimal control, and game theory. The earlier fixed point theorem was proposed by Brouwer [67] in 1910.

Theorem 11. 

A continuous mapping $\xi :{∆}_N\to {∆}_N$ has a fixed point.

The $n$–dimensional simplex can be a unit sphere or a compact convex subset in $R^n$. The Brouwer fixed point theorem was later developed from a single-valued mapping to a set-valued mapping, see [68,69].

Regarding the development process of the theory, the author Park gave a detailed explanation in [54]. In [54], he pointed out that one of the applications of the Kakutani fixed point theorem was to prove the existence of Nash equilibria in finite games and the existence of economic equilibria, which was the beginning of the theory of set-value mapping related to economic equilibria in game theory and economic theory.

The existence of fixed points mainly depends on a certain compactness and convexity of the subsets in topological spaces and a certain continuity of mappings. Many scholars have made many generalizations on fixed point theorems; see [68,69,70,71,72,73]. Moreover, Park gave a detailed description of the history of the development of the Brouwer fixed-point theorem in the literature [54]. Readers who are interested can refer to reference [54] and the references therein. Here, we mainly furnish the generalization of the partial fixed-point theorem in $G$–convex space.

Theorem 12 

([16]). Suppose that $\left(U,D;\mathrm{\Gamma }\right)$ is an $LG$–space, and $\zeta :U\to 2^U$ is an upper semicontinuous mapping with compact values. For any $\kappa \in U$, $\zeta \left(\kappa \right)$ is a nonempty closed $G$–convex set. Then ζ possesses a fixed point, i.e., there exists ${\kappa }^{\ast }\in U$ satisfying ${\kappa }^{\ast }\in \zeta \left({\kappa }^{\ast }\right)$.

Remark 12. 

A $G$–convex space $\left(\mathrm{\Phi },D;\mathrm{\Gamma }\right)$ is known as an $LG$–space (or local $G$–convex space) if $\left(\mathrm{\Phi },T\right)$ is a uniform space, such that D is dense in Φ, and there is a set of basis ${\left\{{\mathrm{\Psi }}_{\lambda }\right\}}_{\lambda \in I}$ of the uniform T such that for each $\lambda \in I$, $\left\{\kappa \in \mathrm{\Phi }:C\cap {\mathrm{\Psi }}_{\lambda }\left[\kappa \right]\ne \varnothing \right\}$ is $G$–convex when $C\subset \mathrm{\Phi }$ is $G$–convex, where ${\mathrm{\Psi }}_{\lambda }\left[\kappa \right]=\left\{{\kappa }^{\prime }\in \mathrm{\Phi }:\left(\kappa ,{\kappa }^{\prime }\right)\in {\mathrm{\Psi }}_{\lambda }\right\}$.

Comparing Theorem 12 with the Fan–Glicksberg fixed-point theorem, we can find that the compactness of the set and the upper semi-continuity condition of the mapping are invariant when we study the theorem in the local $G$–convex space. Here, the linear convex in the usual vector space is extended to $G$–convex, and the conclusion still holds.

Ding [74], Balaj [75] and Park et al. have researched much on the generalizations of the fixed point theorem in $G$–convex spaces, but most of the results have yet to be obtained directly. However, they are obtained by applying the KKM theorem in $G$–convex spaces.

4.2.2. Fixed Point Theory in $H$–Space

Horvath [36] generalized the theorem in [69] in $H$–space.

Theorem 13. 

Assume that $\left(V,\left\{{\mathrm{\Gamma }}_{\mathrm{\Lambda }}\right\}\right)$ is an $H$–space. $\mathrm{\Lambda },B:V\to 2^V$ fulfills the following conditions:

(1) 

for any $\gamma \in V$, ${\mathrm{\Lambda }}^{-1}\left(\gamma \right)$ is an open set, $\mathrm{\Lambda }\left(\gamma \right)\ne \varnothing$ and $\mathrm{\Lambda }\left(\gamma \right)\subseteq B\left(\gamma \right)$;

(2) 

for any $\gamma \in V$, $B\left(\gamma \right)$ is $H$–convex;

(3) 

there exists ${\gamma }_0\in V$ such that $V\backslash {\mathrm{\Lambda }}^{-1}\left({\gamma }_0\right)$ is compact.

Then there exists ${\gamma }^{\ast }\in V$ such that ${\gamma }^{\ast }\in B\left({\gamma }^{\ast }\right)$.

Ding et al. [59] furnished the below theorem in $H$–metric spaces.

Theorem 14. 

Assume that U is an $H$–convex subset of the $H$–metric space $\left(V,\zeta ,\mathrm{\Gamma }\right)$. $\mathrm{\Lambda }:U\to 2^U$ fulfills that $\mathrm{\Lambda }\left(\kappa \right)$ has finite metric closed values for any $\kappa \in U$. If there exists a finite subset $\left\{{\kappa }_0,{\kappa }_1,\dots ,{\kappa }_n\right\}\subset U$ such that $U={\displaystyle \bigcup _{l=0}^n}\mathrm{\Lambda }\left({\kappa }_l\right)$ and for any $\gamma \in U$, ${\mathrm{\Lambda }}^{-1}\left(\gamma \right)=\left\{\kappa \in U:\gamma \in \mathrm{\Lambda }\left(\kappa \right)\right\}$ is an admissible set. Then, there exists ${\kappa }^{\ast }\in U$ such that ${\kappa }^{\ast }\in \mathrm{\Lambda }\left({\kappa }^{\ast }\right)$.

The above two theorems are studied in $H$–space and $H$–metric space, respectively, and the conditions for set-valued mapping are different. Theorem 13 gives the relationship between the two set-valued mappings and draws conclusions based on certain assumptions. Theorem 14 assumes that the set-valued mapping has finite metric closure values and adds the condition that the set is admissible.

For more research on the fixed point theorem for $H$–space, see [76].

4.2.3. Fixed Point Theory in Topological Ordered Space

After Horvath and Ciscar [38] proposed the notion of semi-lattice convex in topological spaces, they obtained the fixed point theorem by utilizing the established KKM theorem in topological spaces with path-connected intervals.

Theorem 15. 

Suppose that Φ is a compact topological semi-lattice possessing path-connected intervals. The binary relation $R\subseteq \mathrm{\Phi }\times \mathrm{\Phi }$ fulfills the following characteristics:

(1) 

$\mathrm{\Phi }={\displaystyle \bigcup _{\kappa \in \mathrm{\Phi }}}\mathrm{int}{R}^{-1}\left(\kappa \right)$;

(2) 

for any $\kappa \in \mathrm{\Phi }$, $R\left(\kappa \right)$ is nomempty. If ${\kappa }_1,{\kappa }_2\in R\left(\kappa \right)$, then $\left[{\kappa }_1,{\kappa }_1\vee {\kappa }_2\right]\subseteq R\left(\kappa \right)$.

Then there exists ${\kappa }^{\ast }\in \mathrm{\Phi }$ such that ${\kappa }^{\ast }\in R\left({\kappa }^{\ast }\right)$.

Unlike the fixed point theorem in topological vector spaces, theorem 15 is obtained because the conditions established in topological ordered spaces changed from set-valued mapping to a binary relationship.

Luo [60] also generalized the Fan–Browder fixed point theorem.

Theorem 16. 

Suppose that Φ is a topological semi-lattice with path-connected intervals. A nonempty multi-valued mapping $\zeta :\mathrm{\Phi }\to 2^{\mathrm{\Phi }}$ possesses closed $∆$–convex values and the local intersection characteristic. If there exists ${\kappa }^{\ast }\in \mathrm{\Phi }$ such that cl $\left(\mathrm{\Phi }\backslash {\zeta }^{-1}\left({\kappa }^{\ast }\right)\right)$ is compact, then ζ has a fixed point.

The above theorem extends the fixed point theorem from topological vector spaces to topological ordered spaces with path-connected intervals. Discussing the fixed point theorem in topological ordered spaces, the condition of topological ordered spaces with the path-connected intervals is essential, and the set-valued mapping is generally defined according to the binary relationship in this space. Luo [63], AI-Homidan, et al. [64,65] continue to study the existence theorem of fixed points for multi-valued mappings.

5. Conclusions

In this paper, we introduce several convex structures, analyze the relations between the T-convex space, G-convex space, L-space and abstract convex space and prove they are contained in abstract convexity spaces. Moreover, we give the relations of convex structures in Figure 3. Then, we review the generalizations of the fixed point theory and the KKM theory in G-convex space, H-convex space and topological ordered space. In this paper, the relations of these convex structures are sorted out, thus helping researchers interested in convexity theory to explore the nature of convexity. However, the limitation of this paper is that it does not consider specific examples of applications of convex structures in actual issues. This topic can be discussed in future research.