On the Extremal Weighted Mostar Index of Bicyclic Graphs

Abstract

Let G be a simple connected graph with edge set $E\left(G\right)$ and vertex set $V\left(G\right)$. The weighted Mostar index of a graph G is defined as $w^{+}Mo\left(G\right)={\displaystyle \sum _{e=uv\in E\left(G\right)}}(d_G\left(u\right)+d_G\left(v\right))|n_u\left(e\right)-n_v\left(e\right)|$, where $n_u\left(e\right)$ denotes the number of vertices closer to u than to v for an edge $uv$ in G. In this paper, we obtain the upper bound and lower bound of the weighted Mostar index among all bicyclic graphs and characterize the corresponding extremal graphs.

1. Introduction

All graphs considered in this paper are finite, undirected, connected and simple. We refer the readers to [1] for the terminology and notations. Let G be a connected graph with edge set $E\left(G\right)$ and vertex set $V\left(G\right)$. Call u a pendant vertex in G, if $d_G\left(u\right)=1$. Call $uv$ a pendant edge in G, if $d_G\left(u\right)=1$ or $d_G\left(v\right)=1$. A connected graph is called a unicyclic graph if the number of edges equals the number of vertices. A connected graph is called a bicyclic graph if the number of edges is 1 more than the number of vertices. A cycle with k edges is called a k-cycle. For $u,v\in V\left(G\right),d_G(u,v)$ denotes the distance between u and v in G, namely the length of the shortest path connecting u and v. For $e=uv\in E\left(G\right)$, the distance between the edge e and the vertex x, denoted by $d_G(e,x)$, is defined as $d_G(e,x)=min\{d_G(u,x),d_G(v,x)\}.$ For $e_1,e_2\in E\left(G\right)$, the distance between $e_1$ and $e_2$, denoted by $d_G(e_1,e_2)$, is defined as the least distance between one vertex in $e_1$ and the other vertex in $e_2$. For $e=uv\in E\left(G\right)$, $n_u\left(e\right)$ denotes the number of vertices closer to u than to v for an edge $uv$ in G.

The Mostar index [2] of a graph G is defined as

$${\displaystyle Mo\left(G\right)=\sum _{e=uv\in E\left(G\right)}|n_u\left(e\right)-n_v\left(e\right)|.}$$

Some properties and applications of the Mostar index have been reported in [3,4,5,6,7,8,9,10,11,12,13]. The weighted Mostar index [14] of a graph G is defined as

$$w^{+}Mo\left(G\right)=\sum _{e=uv\in E\left(G\right)}(d_G\left(u\right)+d_G\left(v\right))|n_u\left(e\right)-n_v\left(e\right)|.$$

This topological index has been extensively studied in the mathematical literature. Kandan [15] computed the weighted Mostar index for a conical and generalized gear graph. Asmat [16] obtained the upper bound of the weighted Mostar index for trees with a given diameter and the corresponding extremal graph. Zhen [17] obtained the extremal values of the weighted Mostar index among trees and unicyclic graphs with a given order.

In this paper, we obtain the upper bound and lower bound of the weighted Mostar index among all bicyclic graphs and characterize the corresponding extremal graphs.

Theorem 1.

Let G be a bicyclic graph with order $n\ge 12$, then

$$w^{+}Mo\left(G\right)\ge \left\{\begin{array}{c}4n+6,n\mathit{is}\mathit{even},\hfill \\ 4n+10,n\mathit{is}\mathit{odd},\hfill \end{array}\right.$$

with the equality if and only if $G\cong {\mathsf{\Theta }}_{n-3,2,2}$ (See Figure 1).

Theorem 2.

Let G be a bicyclic graph with order $n\ge 8$, then

$$w^{+}Mo\left(G\right)\le n^3-3n^2+2n-4,$$

with the equality if and only if $G\cong B_2$ (See Figure 2).

Theorem 1 is proved in Section 3. The proof mainly refers to the proof of the lower bound of Mostar index for bicyclic graphs in [12]. We extend this method to the weighted Mostar index and improve this method. Theorem 2 is proved in Section 4. The method of proving the upper bound of Mostar index for bicyclic graphs by defining the deficit of edges in [12] is not applicable here. We use a method different from that in [12] to find the upper bound of weighted Mostar index among all bicyclic graphs.

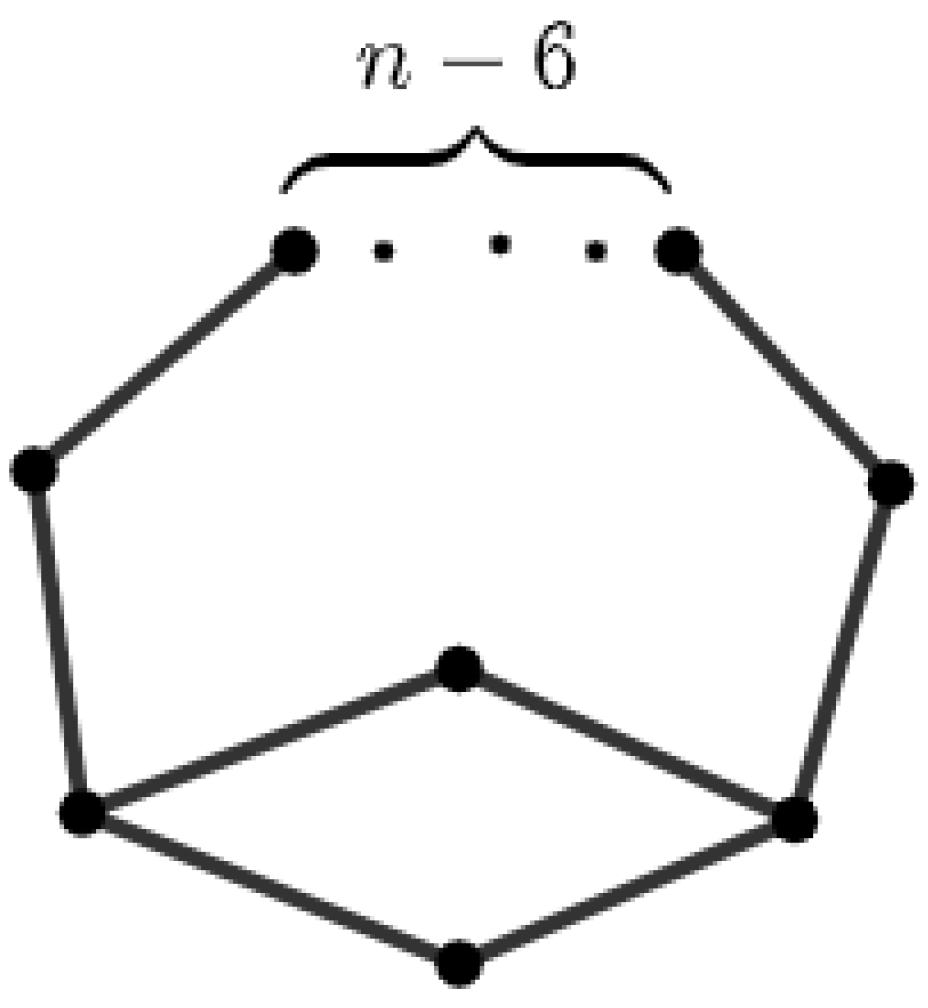
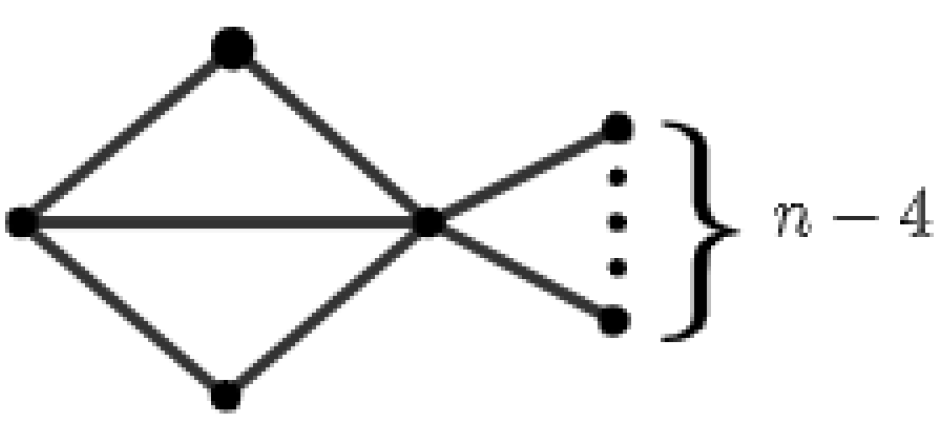
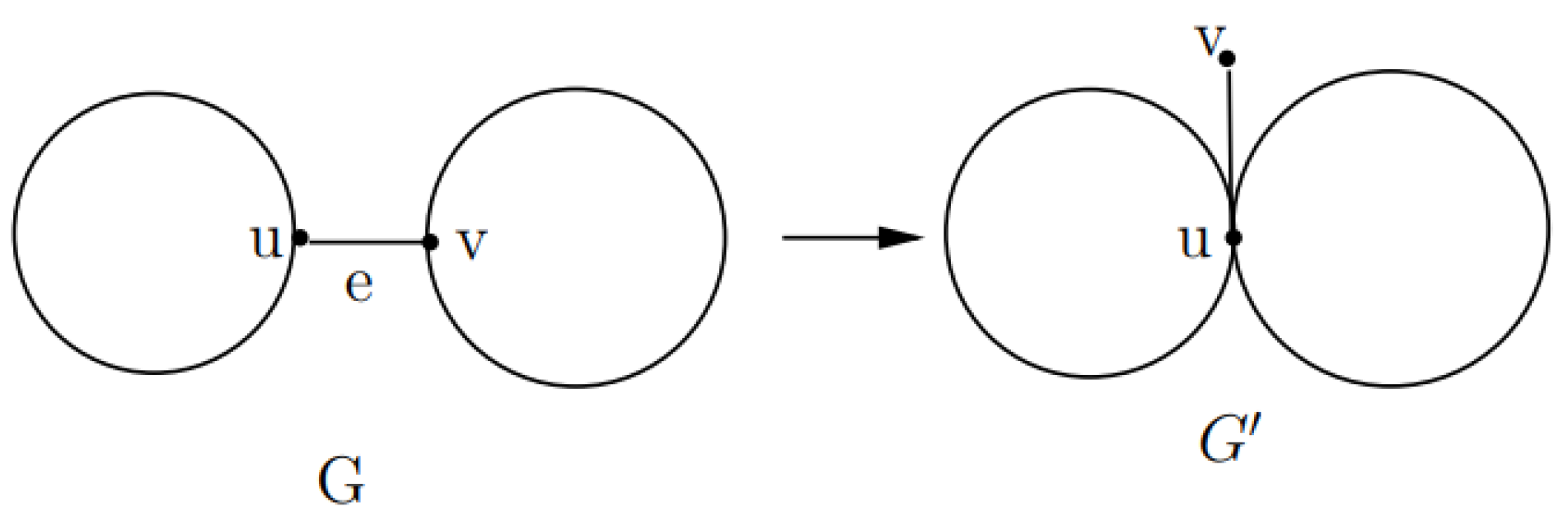
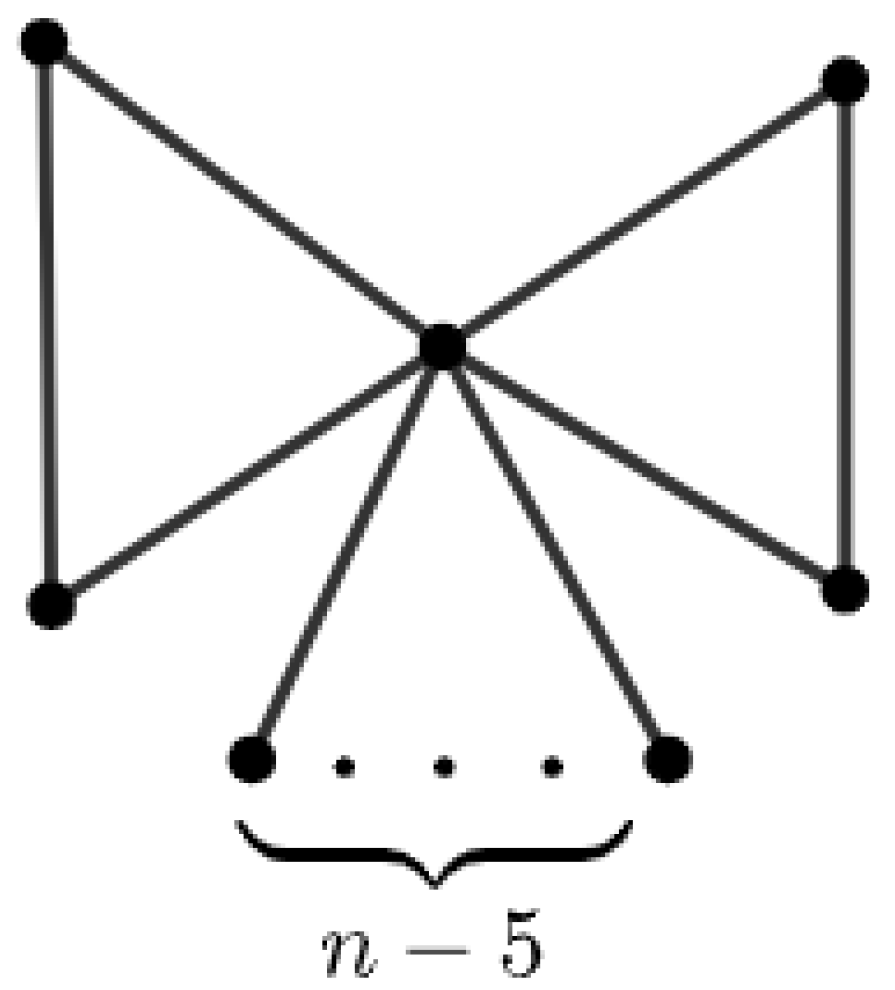
2. Preliminaries

For convenience, we denote by ${\varphi }_G\left(e\right)=|n_u\left(e\right)-n_v\left(e\right)|$ the contribution of the edge $e=uv$ to the Mostar index of graph G, and by ${\mathsf{\Phi }}_G\left(e\right)=(d_G\left(u\right)+d_G\left(v\right))|n_u\left(e\right)-n_v\left(e\right)|$ the contribution of the edge $e=uv$ to the weighted Mostar index of graph G.

Let G be a unicyclic graph with order n. Let C be the unique cycle in G and $\left|C\right|=k$. For $w\in V\left(C\right)$, denote by $T_w$ the component of $\left(G-\left\{e_1,e_2\right\}\right)$ which contains w, where $e_1$ and $e_2$ are the two edges incident to w in C. Let e be an edge in C. If k is even, there exists an edge $\overline{e}$ in C such that $d(e,\overline{e})={\displaystyle \frac{k}{2}}-1$, then $\overline{e}$ is called the parallel edge of e. If k is odd, there exists a vertex $w_e$ in C such that $d(e,w_e)={\displaystyle \frac{k-1}{2}}$, then $w_e$ is called the symmetric vertex of e. Conversely, if $w_e=v$, define $e=e_v$, then say that e is symmetric about v.

Theta graph ${\mathsf{\Theta }}_{a,b,c}$ consists of two vertices, $v_1$ and $v_2$, which are connected by three internally disjoint paths, $P_a$, $P_b$, and $P_c$ of lengths a, b, and c, respectively. We assume that $a\ge b\ge c$.

Lemma 1.

([2]) Let G be a connected graph with order n, and $e=uv\in E\left(G\right)$, then

$${\varphi }_G\left(e\right)=|n_u\left(e\right)-n_v\left(e\right)|\le n-2,$$

with the equality if and only if e is a pendant edge in G.

Lemma 2.

Let G be a connected graph, and $e=uv$ be a cut edge but not a pendant edge in G. Let $G^{\prime }$ be the graph obtained from G by contracting the edge $e=uv$ into a vertex u, and adding a pendant edge $uv$ to this vertex (see Figure 3). Then $w^{+}Mo\left(G^{\prime }\right)>w^{+}Mo\left(G\right)$.

Proof. 

It is clear that $d_{G^{\prime }}\left(u\right)+d_{G^{\prime }}\left(v\right)=d_G\left(u\right)+d_G\left(v\right)$. By Lemma 1, we have ${\varphi }_{G^{\prime }}\left(uv\right)>{\varphi }_G\left(uv\right)$, then ${\mathsf{\Phi }}_{G^{\prime }}\left(uv\right)>{\mathsf{\Phi }}_G\left(uv\right)$. The sum of the degrees of the two end vertices of each edge (except $e=uv$) incident to u or v becomes larger, but the contribution to the Mostar index stays unchanged, so the contribution to the weighted Mostar index becomes larger. Furthermore, for the remaining edges, the contributions to the weighted Mostar index stay unchanged. Thus, $w^{+}Mo\left(G^{\prime }\right)>w^{+}Mo\left(G\right)$. □

Lemma 3.

([11]) Let G be a unicyclic graph with order n, and C be the unique cycle in G.

(1)

If $\left|C\right|$ is even and $e\in E\left(C\right)$, then

$${\varphi }_G\left(e\right)={\varphi }_G\left(\overline{e}\right)=\left|\left|G_1\right|-\left|G_2\right|\right|=n-2min\left\{\left|G_1\right|,\left|G_2\right|\right\},$$

where $G_1$ and $G_2$ are the two components of $G-\left\{e,\overline{e}\right\}$.

(2)

If $\left|C\right|$ is odd and $e\in E\left(C\right)$, then

$${\varphi }_G\left(e\right)=\left|\left|G_1\right|-\left|G_2\right|\right|=n-\left|T_{w_e}\right|-2min\left\{\left|G_1\right|,\left|G_2\right|\right\},$$

where $G_1$ and $G_2$ are the two components of $G-\left\{e\right\}-T_{w_e}$.

3. Proof of Theorem 1

In this section, we start by calculating the weighted Mostar index of graph ${\mathsf{\Theta }}_{n-3,2,2}$ to find the bicyclic graph with the minimum weighted Mostar index.

Lemma 4.

If n is odd, then $w^{+}Mo\left({\mathsf{\Theta }}_{n-3,2,2}\right)=4n+10$; if n is even, then $w^{+}Mo\left({\mathsf{\Theta }}_{n-3,2,2}\right)=4n+6$.

Proof. 

If n is odd, then $a=n-3$ is even. For each edge e of ${\mathsf{\Theta }}_{n-3,2,2}$, we have $\varphi \left(e\right)=1$. Thus, $w^{+}Mo\left({\mathsf{\Theta }}_{n-3,2,2}\right)=30+4(n-5)=4n+10$. If n is even, then $a=n-3$ is odd. The central edge on $P_a$ has a contribution of 0 and each remaining edge of ${\mathsf{\Theta }}_{n-3,2,2}$ has a contribution of 1 to $Mo\left({\mathsf{\Theta }}_{n-3,2,2}\right)$. Thus, $w^{+}Mo\left({\mathsf{\Theta }}_{n-3,2,2}\right)=30+4(n-6)=4n+6$. □

A path $P:=v_0{v}_1,...v_r$ in a graph G is called a pendant path if one of the two vertices of $v_0$ and $v_r$ is a pendant vertex and the other one has degree at least 3, and each remaining vertex of P has degree 2.

Lemma 5.

Let G be a bicyclic graph with order $n\ge 12$. If G has at least two pendant paths or one pendant path with order at least 3, then $w^{+}Mo\left(G\right)>w^{+}Mo\left({\mathsf{\Theta }}_{n-3,2,2}\right)$.

Proof. 

Let G be a bicyclic graph with order $n\ge 12$, if G has at least two pendant paths, then $w^{+}Mo\left(G\right)\ge 2\times 3(n-2)>4n+10$. If G has one pendant path with order at least 3, then $w^{+}Mo\left(G\right)\ge 3(n-2)+4(n-4)>4n+10$. □

Lemma 6.

Let G be a bicyclic graph with order $n\ge 12$. If G has no pendant path or only one pendant path with order 2, then $w^{+}Mo\left(G\right)\ge w^{+}Mo\left({\mathsf{\Theta }}_{n-3,2,2}\right)$, with the equality if and only if $G\cong {\mathsf{\Theta }}_{n-3,2,2}$.

Proof. 

Let G be a bicyclic graph with order $n\ge 12$. If G has no pendant path or only one pendant path with order 2, then G consists of a graph $G^{\prime }$ which has no pendant edge, and possibly an extra vertex attached to $G^{\prime }$ by a single edge. Hence, $\left|V\left(G\right)\right|=|V\left(G^{\prime }\right)|$ or $\left|V\left(G\right)\right|=|V\left(G^{\prime }\right)|+1$.

Suppose that $G^{\prime }$ has exactly two cycles, $C_a$ and $C_b$, with lengths a and b, respectively. Let $u_1$ and $u_2$ be the two terminal vertices on the path of length t connecting the two cycles, where $u_1$ is in $C_a$ and $u_2$ is in $C_b$. Clearly, $\left|V\right(G^{\prime }\left)\right|=a+b+t-1$. If $t=0$, then $u_1=u_2$. Let $e_1$,$e_2$ be the edges incident with $u_1$ in $C_a$, and let $f_1$,$f_2$ be the edges incident with $u_2$ in $C_b$. We distinguish three cases.

Case 1: If $G\cong G^{\prime }$, then $n=a+b+t-1$, ${\varphi }_G\left(e_1\right)={\varphi }_G\left(e_2\right)=n-a$, ${\varphi }_G\left(f_1\right)={\varphi }_G\left(f_2\right)=n-b$. For each of these four edges, the sum of degrees of the end vertices is at least 5, so we have

$$w^{+}Mo\left(G\right)\ge 10(n-a)+10(n-b)=10n+10t-10\ge 10n-10>4n+10.$$

Case 2: If $G\ncong G^{\prime }$, and the pendant edge is attached to any vertex on the path, then $n=a+b+t$, ${\varphi }_G\left(e_1\right)={\varphi }_G\left(e_2\right)=n-a$, ${\varphi }_G\left(f_1\right)={\varphi }_G\left(f_2\right)=n-b$. We have

$$w^{+}Mo\left(G\right)\ge 10(n-a)+10(n-b)=10n+10t\ge 10n>4n+10.$$

Case 3: If $G\ncong G^{\prime }$, and the pendant edge is attached to any vertex on one cycle, say $C_a$, then $n=a+b+t$, ${\varphi }_G\left(e_1\right)$,${\varphi }_G\left(e_2\right)\ge n-a-2$, ${\varphi }_G\left(f_1\right)={\varphi }_G\left(f_2\right)=n-b$. We have

$$w^{+}Mo\left(G\right)\ge 10(n-a-2)+10(n-b)=10n+10t-20\ge 10n-20>4n+10.$$

Suppose that $G^{\prime }\cong {\mathsf{\Theta }}_{a,b,c}$, let $P_a$,$P_b$,$P_c$ be the three paths of ${\mathsf{\Theta }}_{a,b,c}$, and $v_1$,$v_2$ be the two vertices of degree 3 of ${\mathsf{\Theta }}_{a,b,c}$. Let $e_1$,$e_2$,$e_3$ be the edges incident with $v_1$, where $e_1$ is in $P_a$, $e_2$ is in $P_b$, and $e_3$ is in $P_c$. $\varphi \left[\varphi \left(e_1\right),\varphi \left(e_2\right),\varphi \left(e_3\right)\right]$ denotes the contribution of the three edges to $Mo\left(G^{\prime }\right)$. By symmetry, the edges incident with $v_2$ have the same contribution.

In ${\mathsf{\Theta }}_{a,b,c}$, for $e_1=v_1{v}_3$, the number of vertices closer to $v_1$ than to $v_3$ is equal to the number of vertices closer to $v_3$ than to $v_1$ on $P_a$ and $P_c$. The remaining $b-1$ vertices on $P_b$ are all closer to $v_1$ than to $v_3$, then $\varphi \left(e_1\right)=b-1$.

For $e_3=v_1{v}_4$, the number of vertices closer to $v_1$ than to $v_4$ is equal to the number of vertices closer to $v_4$ than to $v_1$ on $P_a$ and $P_c$. If $b+c$ is even, among the remaining $b-1$ vertices on $P_b$, ${\displaystyle \frac{b+c}{2}}-1$ vertices are closer to $v_1$ than to $v_4$, and ${\displaystyle \frac{b-c}{2}}$ vertices are closer to $v_4$ than to $v_1$, then $\varphi \left(e_3\right)=c-1$. Similarly, if $b+c$ is odd, we can also obtain $\varphi \left(e_3\right)=c-1$.

For $e_2=v_1{v}_5$, the number of vertices closer to $v_1$ than to $v_5$ is equal to the number of vertices closer to $v_5$ than to $v_1$ on $P_b$ and $P_c$. If $b\ge c+2$, then $a-1$ vertices on $P_a$ are all closer to $v_1$ than to $v_5$, thus $\varphi \left(e_2\right)=a-1$. If $b=c+1$, let $u_i$ be any vertex on $P_a$, where i denotes the length of the path from $v_2$ to $u_i$ on $P_a$, and $1\le i\le a-1$. Note that if $a-i<c+i$, then $d(u_i,v_1)<d(u_i,v_5)$ and if $a-i\ge c+i$, then $d(u_i,v_1)=d(u_i,v_5)$, so among the $a-1$ vertices on $P_a$, $a-1-⌊{\displaystyle \frac{a-c}{2}}⌋$ vertices are closer to $v_1$ than to $v_5$, and no vertex is closer to $v_5$ than to $v_1$, thus $\varphi \left(e_2\right)=a-1-⌊{\displaystyle \frac{a-c}{2}}⌋=⌊{\displaystyle \frac{a+c-1}{2}}⌋$. If $b=c$, then $\varphi \left(e_2\right)=\varphi \left(e_3\right)=c-1$.

Case 1: $a\ge b\ge c+2$. In ${\mathsf{\Theta }}_{a,b,c}$, we have $\varphi \left[b-1,a-1,c-1\right]$. If $G\cong G^{\prime }$, then $n=a+b+c-1$. Considering the contributions of the six edges incident to $v_1$ and $v_2$ in ${\mathsf{\Theta }}_{a,b,c}$ to $w^{+}Mo\left(G\right)$, we obtain

$$w^{+}Mo\left(G\right)\ge 10(b-1)+10(a-1)+10(c-1)=10n-20>4n+10.$$

If $G\ncong G^{\prime }$, then $n=a+b+c$, ${\varphi }_G\left(e_1\right)\ge b-2$, ${\varphi }_G\left(e_2\right)\ge a-2$, ${\varphi }_G\left(e_3\right)\ge c-2$. Considering the contributions of the pendant edge and the six edges incident to $v_1$ and $v_2$ in ${\mathsf{\Theta }}_{a,b,c}$ to $w^{+}Mo\left(G\right)$, we know that

$$w^{+}Mo\left(G\right)\ge 10(b-2)+10(a-2)+10(c-2)+4(n-2)=14n-68>4n+10.$$

Case 2: $a\ge b=c+1$. In ${\mathsf{\Theta }}_{a,c+1,c}$, we have $\varphi \left[c,⌊{\displaystyle \frac{a+c-1}{2}}⌋,c-1\right]$. If $G\cong G^{\prime }$, then $n=a+2c$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& \ge 10c+10⌊{\displaystyle \frac{a+c-1}{2}}⌋+10(c-1)\hfill \\ & \ge 10c+10\left({\displaystyle \frac{a+c-2}{2}}\right)+10(c-1)\hfill \\ & =5n+15c-20.\hfill \end{array}\end{array}$$

If $c\ge 2$, then $w^{+}Mo\left(G\right)\ge 5n+10>4n+10$. If $c=1$, then $b=2$, thus $G\cong {\mathsf{\Theta }}_{a,2,1}$. When n is odd, $a=n-2$ is odd, then we have

$$w^{+}Mo\left({\mathsf{\Theta }}_{a,2,1}\right)=10+10\times {\displaystyle \frac{a-1}{2}}+4(a-3)=9n-25>4n+10.$$

When n is even, $a=n-2$ is even, then we find

$$w^{+}Mo\left({\mathsf{\Theta }}_{a,2,1}\right)=10+10\times {\displaystyle \frac{a}{2}}+4(a-2)=9n-16>4n+10.$$

If $G\ncong G^{\prime }$, then $n=a+2c+1$, ${\varphi }_G\left(e_1\right)\ge c-1$, ${\varphi }_G\left(e_2\right)\ge ⌊{\displaystyle \frac{a+c-1}{2}}⌋-1$, ${\varphi }_G\left(e_3\right)\ge c-2$. We obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& \ge 10(c-1)+10(⌊{\displaystyle \frac{a+c-1}{2}}⌋-1)+10(c-2)+4(n-2)\hfill \\ & \ge 9n+15c-63\hfill \\ & \ge 9n-48\hfill \\ & >4n+10.\hfill \end{array}\end{array}$$

Case 3: $a\ge b=c\ge 2$. In ${\mathsf{\Theta }}_{a,c,c}$, we have $\varphi \left[c-1,c-1,c-1\right]$. If $G\cong G^{\prime }$, it is clear that the contribution of each edge incident to $v_1$ or $v_2$ to $Mo\left(G\right)$ is $c-1$. Each central edge on the path with an odd length has a contribution of 0 and each remaining edge has a contribution of at least 1 to $Mo\left(G\right)$. Thus, if $c\ge 3$, then

$$w^{+}Mo\left(G\right)\ge 30(c-1)+4[(n+1)-9]=30c+4n-62>4n+10.$$

If $c=2$, then $G\cong {\mathsf{\Theta }}_{n-3,2,2}$.

If $G\ncong G^{\prime }$, then $n=a+2c$, ${\varphi }_G\left(e_1\right)$,${\varphi }_G\left(e_2\right)$,${\varphi }_G\left(e_3\right)\ge c-2$. We obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& \ge 30(c-2)+4(n-2)=4n+30c-68.\hfill \end{array}\end{array}$$

If $c\ge 3$, then $w^{+}Mo\left(G\right)\ge 4n+22>4n+10.$ If $c=2$ and the pendant edge is incident to $v_1$ or $v_2$, then ${\varphi }_G\left(e_1\right)={\varphi }_G\left(e_2\right)={\varphi }_G\left(e_3\right)=2$, thus

$$w^{+}Mo\left(G\right)\ge 5(n-2)+12\times 3=5n+26>4n+10.$$

If $c=2$ and the pendant edge is incident to the center vertex of $P_c$, then we have ${\varphi }_G\left(e_1\right)={\varphi }_G\left(e_2\right)=2$, ${\varphi }_G\left(e_3\right)=0$, thus

$$w^{+}Mo\left(G\right)\ge 4(n-2)+10+10=4n+12>4n+10.$$

If $c=2$ and the pendant edge is incident to a vertex x in $V\left(P_a\right)\setminus \left\{v_1,v_2\right\}$, where $d(x,v_1)\le d(x,v_2)$, then ${\varphi }_G\left(e_1\right)=0$, ${\varphi }_G\left(e_2\right)={\varphi }_G\left(e_3\right)=2$, thus

$$w^{+}Mo\left(G\right)\ge 4(n-2)+10+10=4n+12>4n+10.$$

□

Finally, Theorem 1 can be proved by Lemmas 4–6.

4. Proof of Theorem 2

Based on the definition of bicyclic graphs, bicyclic graphs can be divided into two types: ${\mathcal{B}}_n^1$ is the set of bicyclic graphs of order n with exactly two cycles. ${\mathcal{B}}_n^2$ us the set of bicyclic graphs of order n with three cycles. In this section, for every type of bicyclic graph, we obtain the bicyclic graph with the maximum weighted Mostar index.

$G_1·G_2$ denotes the graph obtained from $G_1$ and $G_2$ by identifying one vertex. $S_{n,k}$ denotes the unicyclic graph on n vertices with a cycle of length k, where $n-k$ pendant vertices are incident to a fixed vertex on the cycle, and we call the fixed vertex the center vertex of $S_{n,k}$.

Theorem 3.

Let $G\in {\mathcal{B}}_n^1$ and $n\ge 5$, then $w^{+}Mo\left(G\right)\le n^3-3n^2+2n-12$, with the equality if and only if $G\cong B_1$ (see Figure 4).

Proof. 

Let $G\cong H_1·H_2$, where $H_1$ is a unicyclic graph of order $n_1$ with $k_1$-cycle, and $H_2$ is a unicyclic graph of order $n_2$ with $k_2$-cycle. By Lemma 2, we can easily obtain $w^{+}Mo(H_1·H_2)\le w^{+}Mo(H_1^{\prime }·H_2)$, where $H_1^{\prime }$ is a unicyclic graph of order $n_1$ with $k_1$-cycle, and all cut edges are pendant edges. Let C be the unique cycle of $H_1^{\prime }$. Note that

$$\sum _{e\in E(H_1^{\prime }·H_2)\setminus E\left(C\right)}{\mathsf{\Phi }}_{H_1^{\prime }·H_2}\left(e\right)\le \sum _{e\in E(S_{n_1,k}·H_2)\setminus E\left(C\right)}{\mathsf{\Phi }}_{S_{n_1,k}·H_2}\left(e\right).$$

Let u be the common vertex of $H_1^{\prime }$ and $H_2$, and let p be the number of pendant edges attached at u in $H_1^{\prime }$. D denotes the sum of the degrees of all vertices on C, and ${\delta }_e$ denotes the sum of the degrees of the end vertices of the edge e.

If $k_1$ is odd, $e_u$ is the symmetric edge of u on C, and let $F=E\left(C\right)\setminus \left\{e_u\right\}$. It is clear that $n=n_2-1+p+k_1+{\displaystyle \sum _{e\in F}}(\left|T_{w_e}\right|-1)$. By Lemma 3, we obtain

$$\varphi \left(e_u\right)\le n-(n_2+p)-2\times {\displaystyle \frac{k_1-1}{2}}=n-k_1-(n_2+p-1).$$

For each $e\in F$, we obtain $\varphi \left(e\right)\le n-\left|T_{w_e}\right|-2\times {\displaystyle \frac{k_1-1}{2}}=n-k_1-(\left|T_{w_e}\right|-1)$. By ${\delta }_{e_u}\ge 4$ and $\left|T_{w_e}\right|-1\ge 0$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{e\in E\left(C\right)}{\mathsf{\Phi }}_{H_1^{\prime }·H_2}\left(e\right)& \le {\delta }_{e_u}\left[n-k_1-(n_2+p-1)\right]+\sum _{e\in F}{\delta }_e\left[n-k_1-(\left|T_{w_e}\right|-1)\right]\hfill \\ & =2D(n-k_1)-{\delta }_{e_u}(n_2+p-1)-\sum _{e\in F}{\delta }_e(\left|T_{w_e}\right|-1)\hfill \\ & \le 2D(n-k_1)-4\left[n-k_1-\sum _{e\in F}(\left|T_{w_e}\right|-1)\right]-\sum _{e\in F}{\delta }_e(\left|T_{w_e}\right|-1)\hfill \\ & =(2D-4)(n-k_1)+\sum _{e\in F}(4-{\delta }_e)(\left|T_{w_e}\right|-1)\hfill \\ & \le (2D-4)(n-k_1),\hfill \end{array}\end{array}$$

with the equality if and only if $H_1^{\prime }\cong S_{n_1,k_1}$.

If $k_1$ is even, by Lemma 3, for each $e\in E\left(C\right)$, we find $\varphi \left(e\right)\le n-2\times {\displaystyle \frac{k_1}{2}}=n-k_1$. Then

$$\sum _{e\in E\left(C\right)}{\mathsf{\Phi }}_{H_1^{\prime }·H_2}\left(e\right)\le 2D(n-k_1),$$

with the equality if and only if $H_1^{\prime }\cong S_{n_1,k_1}$.

Thus, we have $w^{+}Mo(H_1^{\prime }·H_2)\le w^{+}Mo(S_{n_1,k_1}·H_2)$, with the equality if and only if $H_1^{\prime }\cong S_{n_1,k_1}$, where the common vertex of $S_{n_1,k_1}$ and $H_2$ is the center vertex of $S_{n_1,k_1}$.

Let $C^{\prime }$ denote the unique cycle of $S_{n_1,k_1-1}$ and f be a pendant edge of $S_{n_1,k_1-1}$,

$E_1=E\left(C\right)$, $E_2=E\left(C^{\prime }\right)\cup \left\{f\right\}$. Note that

$$\sum _{e\in E(S_{n_1,k_1}·H_2)\setminus E_1}{\mathsf{\Phi }}_{S_{n_1,k_1}·H_2}\left(e\right)\le \sum _{e\in E(S_{n_1,k_1-1}·H_2)\setminus E_2}{\mathsf{\Phi }}_{S_{n_1,k_1-1}·H_2}\left(e\right).$$

If $k_1$ is odd, then $k_1-1$ is even, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{e\in E_1}{\mathsf{\Phi }}_{S_{n_1,k_1}·H_2}\left(e\right)& =[2d\left(u\right)+2\times 2(k_1-1)-4](n-k_1)\hfill \\ & =[2d\left(u\right)+4k_1-8](n-k_1),\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{e\in E_2}{\mathsf{\Phi }}_{S_{n_1,k_1-1}·H_2}\left(e\right)& =[2d\left(u\right)+2+2\times 2(k_1-2)](n-k_1+1)+[d\left(u\right)+2](n-2)\hfill \\ & =[2d\left(u\right)+4k_1-6](n-k_1+1)+[d\left(u\right)+2](n-2).\hfill \end{array}\end{array}$$

Then,

$$\sum _{e\in E_2}{\mathsf{\Phi }}_{S_{n_1,k_1-1}·H_2}\left(e\right)-\sum _{e\in E_1}{\mathsf{\Phi }}_{S_{n_1,k_1}·H_2}\left(e\right)=2(n-k_1)+2d\left(u\right)+4k_1-6+[d\left(u\right)+2](n-2)>0.$$

If $k_1$ is even, then $k_1-1$ is odd, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{e\in E_1}{\mathsf{\Phi }}_{S_{n_1,k_1}·H_2}\left(e\right)& =[2d\left(u\right)+2\times 2(k_1-1)](n-k_1)\hfill \\ & =[2d\left(u\right)+4k_1-4](n-k_1),\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{e\in E_2}{\mathsf{\Phi }}_{S_{n_1,k_1-1}·H_2}\left(e\right)& =[2d\left(u\right)+2+2\times 2(k_1-2)-4](n-k_1+1)+[d\left(u\right)+2](n-2)\hfill \\ & =[2d\left(u\right)+4k_1-10](n-k_1+1)+[d\left(u\right)+2](n-2).\hfill \end{array}\end{array}$$

By $d\left(u\right)\ge 4$, then

$$\sum _{e\in E_2}{\mathsf{\Phi }}_{S_{n_1,k_1-1}·H_2}\left(e\right)-\sum _{e\in E_1}{\mathsf{\Phi }}_{S_{n_1,k_1}·H_2}\left(e\right)=-6(n-k_1)+2d\left(u\right)+4k_1-10+[d\left(u\right)+2](n-2)>0.$$

So $w^{+}Mo(S_{n_1,k_1}·H_2)<w^{+}Mo(S_{n_1,k_1-1}·H_2)<...<w^{+}Mo(S_{n_1,3}·H_2)$.

Thus, $w^{+}Mo(H_1·H_2)\le w^{+}Mo(S_{n_1,3}·H_2)$, with the equality if and only if $H_1\cong S_{n_1,3}$, where the common vertex of $S_{n_1,3}$ and $H_2$ is the center vertex of $S_{n_1,3}$. By symmetry, we have $w^{+}Mo(H_1·H_2)\le w^{+}Mo(S_{n_1,3}·S_{n_2,3})$, with the equality if and only if $H_1\cong S_{n_1,3}$ and $H_2\cong S_{n_2,3}$, where the common vertex of $S_{n_1,3}$ and $S_{n_2,3}$ is the center vertex of $S_{n_1,3}$ and $S_{n_2,3}$.

Hence, $B_1$ is the bicyclic graph with the maximum weighted Mostar index in ${\mathcal{B}}_n^1$, and it is clear that

$$w^{+}Mo\left(B_1\right)=4(n+1)(n-3)+n(n-2)(n-5)=n^3-3n^2+2n-12.$$

This completes the proof of Theorem 3. □

Theorem 4.

Let $G\in {\mathcal{B}}_n^2$ and $n\ge 8$, then $w^{+}Mo\left(G\right)\le n^3-3n^2+2n-4$, with the equality if and only if $G\cong B_2$.

Proof. 

Let $G\in {\mathcal{B}}_n^2$ and $n\ge 8$, then G contains a subgraph isomorphic to ${\mathsf{\Theta }}_{a,b,c}$, and we assume that $a\ge b\ge c$. If G is the bicyclic graph with the maximum weighted Mostar index, by Lemma 2.2, we know that all cut edges are pendant edges. We distinguish five cases.

Case 1: $a+c\ge 5$.

Let p denote the number of pendant edges in G. We have $n=a+b+c-1+p\ge p+6$ by $b\ge 2$. For each edge e in $P_a\cup P_c$, we have $\mathsf{\Phi }\left(e\right)\le (p+6)[n-(a+c\left)\right]\le n(n-5)$; for each edge e in $P_b$, we have $\mathsf{\Phi }\left(e\right)\le (p+5)[n-(b+c\left)\right]\le (n-1)(n-3)$; for each pendant edge e, we have $\mathsf{\Phi }\left(e\right)\le (p+4)(n-2)\le {(n-2)}^2$. Since these equations cannot hold at the same time, we know that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& <(a+c)n(n-5)+b(n-1)(n-3)+[n-(a+b+c-1)]{(n-2)}^2\hfill \\ & =n^3-3n^2-(a+c)n-b-4(a+c)+4\hfill \\ & <n^3-3n^2+2n-4.\hfill \end{array}\end{array}$$

Case 2: $a=3$, $b=3$, $c=1$.

Let $v_1$ and $v_2$ be two vertices of degree 3 of ${\mathsf{\Theta }}_{3,3,1}$. Clearly, $\mathsf{\Phi }\left(v_1{v}_2\right)\le n(n-6)$; for each edge e (except $v_1{v}_2$) incident to $v_1$ or $v_2$ in ${\mathsf{\Theta }}_{3,3,1}$, we have $\mathsf{\Phi }\left(e\right)\le (n-1)(n-4)$; for each remaining edge e in ${\mathsf{\Theta }}_{3,3,1}$, we have $\mathsf{\Phi }\left(e\right)\le (n-2)(n-6)$; for each pendant edge e, we have $\mathsf{\Phi }\left(e\right)\le {(n-2)}^2$. We reveal

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& <n(n-6)+4(n-1)(n-4)+2(n-2)(n-6)+(n-6){(n-2)}^2\hfill \\ & =n^3-3n^2-14n+16\hfill \\ & <n^3-3n^2+2n-4.\hfill \end{array}\end{array}$$

Case 3: $a=3$, $b=2$, $c=1$.

Let $v_1$ and $v_2$ be two vertices of degree 3 of ${\mathsf{\Theta }}_{3,2,1}$. $v_3$ is the vertex of degree 2 on $P_b$, $v_4$ is the neighbor of $v_1$ on $P_a$, and $v_5$ is the neighbor of $v_2$ on $P_a$. If there is at least one pendant edge attached at the vertices of degree 2 of ${\mathsf{\Theta }}_{3,2,1}$, then $\mathsf{\Phi }\left(v_1{v}_2\right)\le n(n-5)$, $\mathsf{\Phi }\left(v_1{v}_3\right),\mathsf{\Phi }\left(v_2{v}_3\right)<n(n-4)$, $\mathsf{\Phi }\left(v_1{v}_4\right),\mathsf{\Phi }\left(v_2{v}_5\right)<n(n-4)$, $\mathsf{\Phi }\left(v_4{v}_5\right)\le (n-1)(n-5)$; for each pendant edge e, we have $\mathsf{\Phi }\left(e\right)\le {(n-2)}^2$. We find

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& <n(n-5)+4n(n-4)+(n-1)(n-5)+(n-5){(n-2)}^2\hfill \\ & =n^3-3n^2-3n-15\hfill \\ & <n^3-3n^2+2n-4.\hfill \end{array}\end{array}$$

If there is no pendant edge attached at vertices of degree 2 of ${\mathsf{\Theta }}_{3,2,1}$, then we have $\mathsf{\Phi }\left(v_1{v}_2\right)\le (n+1)(n-5)$, $\mathsf{\Phi }\left(v_1{v}_3\right),\mathsf{\Phi }\left(v_2{v}_3\right)\le n(n-4)$, $\mathsf{\Phi }\left(v_1{v}_4\right),\mathsf{\Phi }\left(v_2{v}_5\right)\le n(n-4)$, $\mathsf{\Phi }\left(v_4{v}_5\right)\le 4(n-5)$; for each pendant edge e, we have $\mathsf{\Phi }\left(e\right)\le (n-1)(n-2)$. We obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& <(n+1)(n-5)+4n(n-4)+4(n-5)+(n-5)(n-1)(n-2)\hfill \\ & =n^3-3n^2+n-35\hfill \\ & <n^3-3n^2+2n-4.\hfill \end{array}\end{array}$$

Case 4: $a=2$, $b=2$, $c=2$.

If there is at least one pendant edge attached at the vertices of degree 2 of ${\mathsf{\Theta }}_{2,2,2}$, then for each edge e in ${\mathsf{\Theta }}_{2,2,2}$, we have $\mathsf{\Phi }\left(e\right)<n(n-4)$; for each pendant edge e, we have $\mathsf{\Phi }\left(e\right)\le {(n-2)}^2$. We obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& <6n(n-4)+(n-5){(n-2)}^2\hfill \\ & =n^3-3n^2-20\hfill \\ & <n^3-3n^2+2n-4.\hfill \end{array}\end{array}$$

If all pendant edges are attached at $v_1$, where $v_1$ is a vertex of degree 3 of ${\mathsf{\Theta }}_{2,2,2}$, then for each edge e incident to $v_1$ in ${\mathsf{\Theta }}_{2,2,2}$, we have $\mathsf{\Phi }\left(e\right)=n(n-4)$; for each remaining edge e in ${\mathsf{\Theta }}_{2,2,2}$, we have $\mathsf{\Phi }\left(e\right)=5(n-6)$; for each pendant edge e, we have $\mathsf{\Phi }\left(e\right)=(n-1)(n-2)$. We find

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& =3n(n-4)+3\times 5(n-6)+(n-5)(n-1)(n-2)\hfill \\ & =n^3-5n^2+20n-100\hfill \\ & <n^3-3n^2+2n-4.\hfill \end{array}\end{array}$$

If all pendant edges are attached at $v_1$ and $v_2$, where $v_1$ and $v_2$ are the vertices of degree 3 of ${\mathsf{\Theta }}_{2,2,2}$, then for each edge e in ${\mathsf{\Theta }}_{2,2,2}$, we have $\mathsf{\Phi }\left(e\right)\le (n-1)(n-6)$; for each pendant edge e, we have $\mathsf{\Phi }\left(e\right)\le {(n-2)}^2$. We have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& <6(n-1)(n-6)+(n-5){(n-2)}^2\hfill \\ & =n^3-3n^2-18n+16\hfill \\ & <n^3-3n^2+2n-4.\hfill \end{array}\end{array}$$

Case 5: $a=2$, $b=2$, $c=1$.

Let $v_1$ and $v_2$ be two vertices of degree 3 of ${\mathsf{\Theta }}_{2,2,1}$, and let $v_3$ and $v_4$ be two vertices of degree 2 of ${\mathsf{\Theta }}_{2,2,1}$. $p_j$ denotes the number of pendant edges attached at $v_j$, where $j=1,2,3,4$. It is clear that $n={\displaystyle \sum _{j=1}^4}{p}_j+4$. Without a loss of generality, we assume that $p_1\ge p_2$, $p_3\ge p_4$, then

$$\mathsf{\Phi }\left(v_1{v}_3\right)=(p_1+p_3+5)\left|p_1+p_4+1-p_3\right|\le (p_1+p_3+5)(n-p_2-3),$$

$$\mathsf{\Phi }\left(v_1{v}_4\right)=(p_1+p_4+5)\left(p_1+p_3+1-p_4\right)\le (p_1+p_4+5)(n-p_2-3),$$

$$\mathsf{\Phi }\left(v_2{v}_3\right)=(p_2+p_3+5)\left|p_2+p_4+1-p_3\right|\le (p_2+p_3+5)(n-p_1-3),$$

$$\mathsf{\Phi }\left(v_2{v}_4\right)=(p_2+p_4+5)\left(p_2+p_3+1-p_4\right)\le (p_2+p_4+5)(n-p_1-3),$$

$$\mathsf{\Phi }\left(v_1{v}_2\right)=(p_1+p_2+6)(p_1-p_2),$$

for each pendant edge e, we have

$$\mathsf{\Phi }\left(e\right)\le n(n-2).$$

By $n={\displaystyle \sum _{j=1}^4}{p}_j+4\ge 8$, $p_2,p_3,p_4\ge 0$, and $0\le p_1\le n-4$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{+}Mo\left(G\right)& \le (p_1+p_3+5)(n-p_2-3)+(p_1+p_4+5)(n-p_2-3)+(p_2+p_3+5)(n-p_1-3)\hfill \\ & +(p_2+p_4+5)(n-p_1-3)+(p_1+p_2+6)(p_1-p_2)+n(n-2)(n-4)\hfill \\ & =2(p_1+p_2+p_3+p_4+10)(n-3)-p_2(2p_1+p_3+p_4+10)\hfill \\ & -p_1(2p_2+p_3+p_4+10)+p_1(p_1+p_2+6)-p_2(p_1+p_2+6)+n^3-6n^2+8n\hfill \\ & =n^3-6n^2+8n+2(n+6)(n-3)+p_1(p_1-p_2-p_3-p_4-4)\hfill \\ & -p_2(3p_1+p_2+p_3+p_4+16)\hfill \\ & \le n^3-4n^2+14n-36+p_1(p_1-4)\hfill \\ & \le n^3-4n^2+14n-36+(n-4)(n-8)\hfill \\ & =n^3-3n^2+2n-4,\hfill \end{array}\end{array}$$

with the equality if and only if $p_2=p_3=p_4=0$, and $p_1=n-4$, i.e., $G\cong B_2$.

This completes the proof of Theorem 4. □

Finally, Theorem 2 can be proved by Theorems 3 and 4.

5. Conclusions and a Further Research Problem

In this paper, firstly, by dividing the bicyclic graphs into two types according to the number of pendant paths, we determine the lower bound of the weighted Mostar index among all bicyclic graphs with order $n\ge 12$ and characterize the corresponding extremal graphs. Secondly, we divide the bicyclic graphs into two types based on the definition of bicyclic graphs and Theta graph, and find its upper bound for every type of bicyclic graph, then we obtain the upper bound of the weighted Mostar index for bicyclic graphs with order $n\ge 8$ and the graph that achieves the upper bound. Based on the bicyclic graphs, we can consider the related research of tricyclic graphs. The following is a further research problem:

Problem 1. Among all tricyclic graphs with order n, identify the graphs with the largest and smallest weighted Mostar index.