Extreme Behavior of Competing Risks with Random Sample Size
Abstract
1. Introduction
2. Main Results
2.1. Limit Theorem for Case (I) with Independent Sample Size
- (i).
- (ii).
- The following limit distribution holdsprovided that one of the following four conditions is satisfied (notation: , the right endpoint of )
- (a).
- When is one of the same p-types of , and is one of the same p-types of .
- (b).
- When is one of the same p-types of , and is one of the same p-types of for . In addition, Equation (11) holds with and .
- (c).
- When is one of the same p-types of , and is one of the same p-types of for . In addition, Equation (11) holds with and or and .
- (d).
2.2. Limit Theorem for Case (II) with Non-Independent Sample Size
3. Extension and Examples
3.1. Extreme Limit Theory for Competing Minima Risks
- (i).
- (ii).
- The following limit distribution holdsprovided that one of the conditions (a)∼(d) in Theorem 2 holds.
3.2. Examples
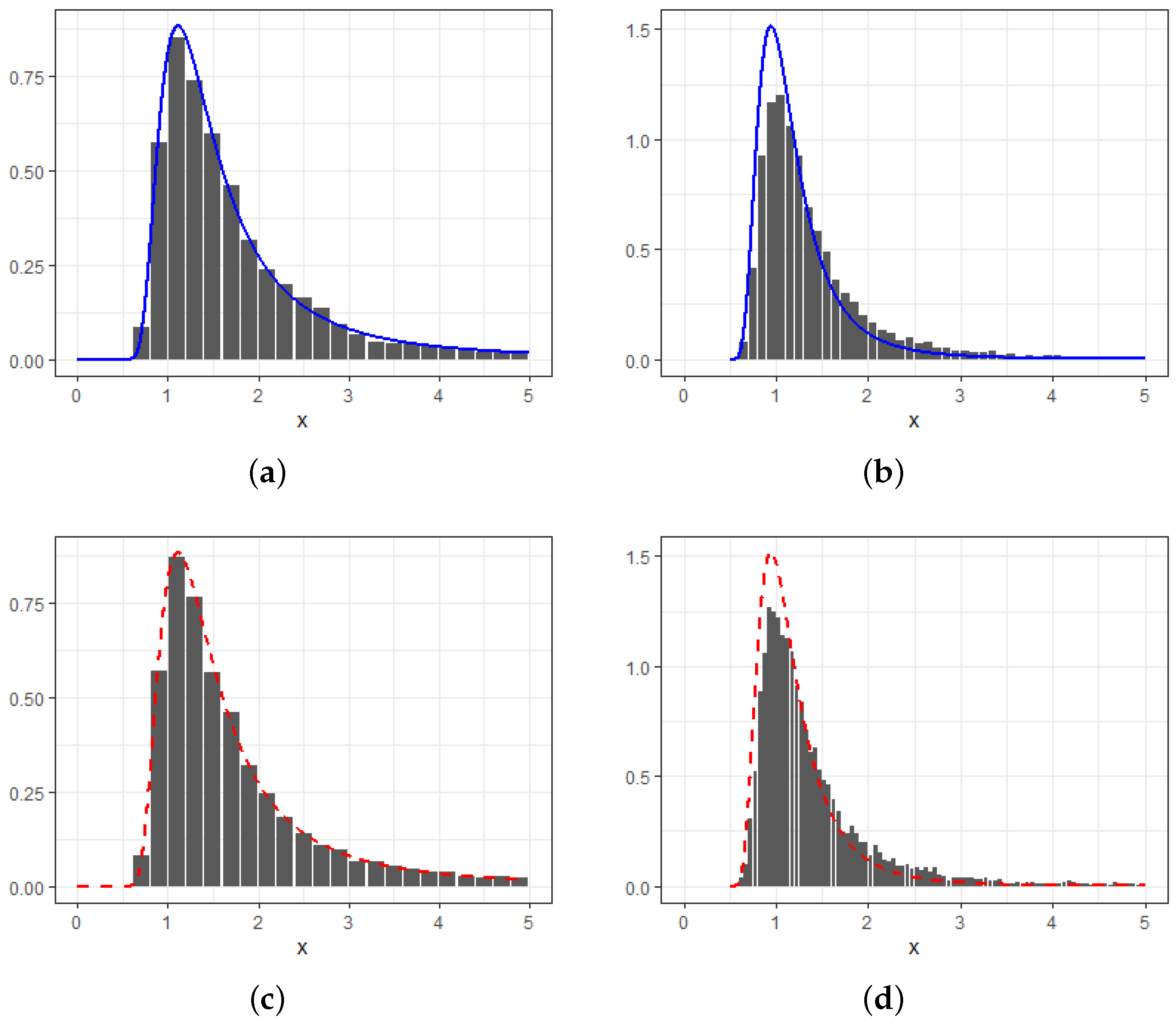
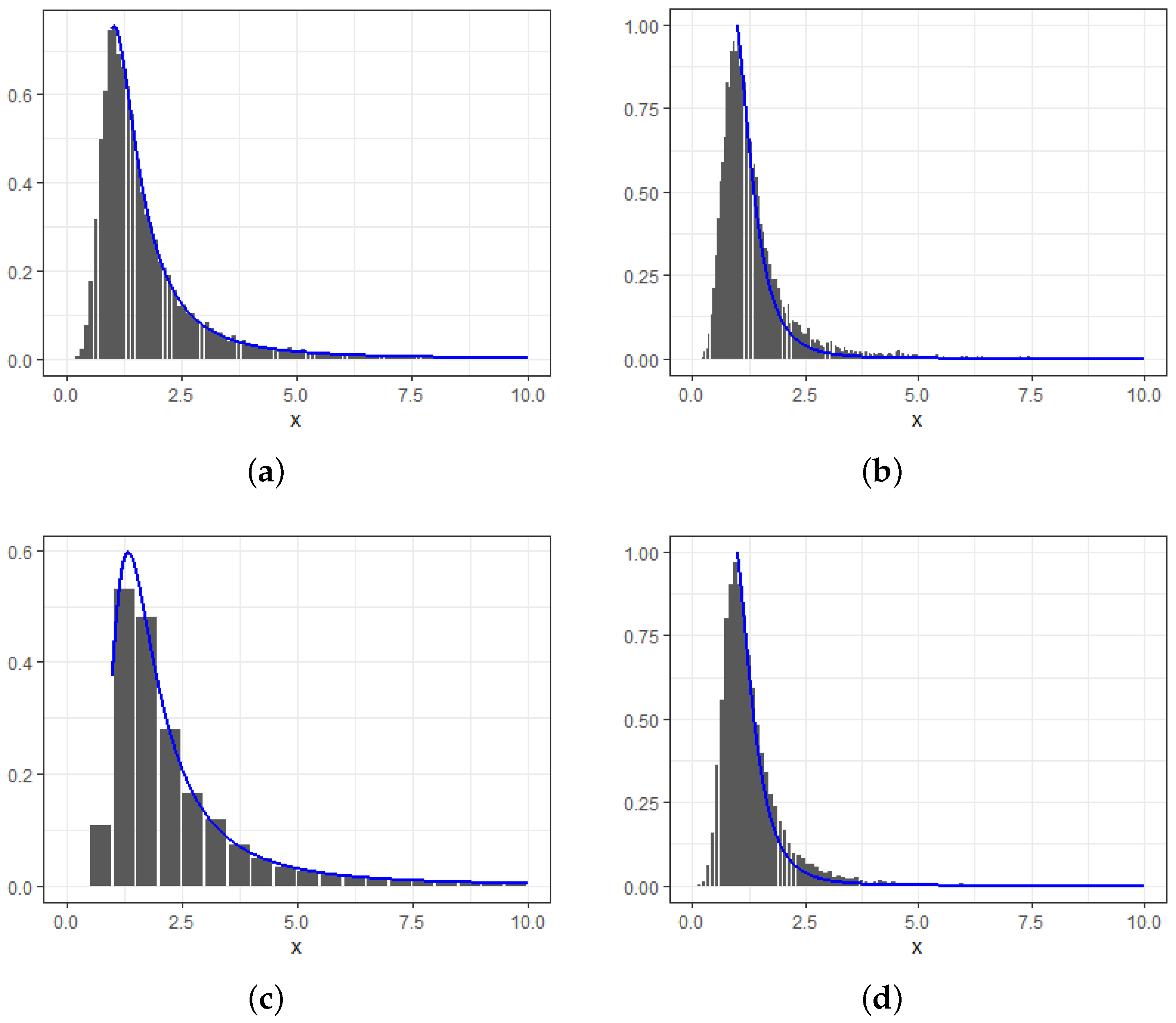
4. Numerical Studies
- For or with , we have
- For with , we have
- For or with , we have
- For with , we have
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Theorems 1∼4
- (a).
- Since and are one of the same p-types of and , respectively, we have, for ,We thus obtain Equation (A6).
- (b).
- For being one of the same p-types of , and being one of the same p-types of with , we have, forholds for all . Therefore, Equation (A6) follows.
- (c).
- For being one of the same p-types of , and being the same p-type of with , we have, for or and anyWe have thus .
- (d).
- For being one of the same p-types of , we have, for or , and anyindicating that .
References
- Leadbetter, M.R.; Lindgren, G.; Rootzén, H. Extremes and Related Properties of Random Sequences and Processes; Springer: New York, NY, USA, 1983. [Google Scholar]
- Embrechts, P.; Kluppelberg, C.; Mikosch, T. Modelling Extremal Events; Stochastic Modelling and Applied Probability; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Beirlant, J.; Teugels, J.L. Limit distributions for compounded sums of extreme order statistics. J. Appl. Probab. 1992, 29, 557–574. [Google Scholar] [CrossRef]
- Pantcheva, E. Limit Theorems for Extreme Order Statistics under Nonlinear Normalization; Springer: Berlin/Heidelberg, Germany, 1985; pp. 284–309. [Google Scholar]
- Nasri-Roudsari, D. Limit distributions of generalized order statistics under power normalization. Commun. Stat.-Theory Methods 1999, 28, 1379–1389. [Google Scholar] [CrossRef]
- Barakat, H.M.; Khaled, O.M.; Rakha, N.K. Modeling of extreme values via exponential normalization compared with linear and power normalization. Symmetry 2020, 12, 1876. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, Z. New extreme value theory for maxima of maxima. Stat. Theory Relat. Fields 2021, 5, 232–252. [Google Scholar] [CrossRef]
- Hu, K.; Wang, K.; Constantinescu, C.; Zhang, Z.; Ling, C. Extreme Limit Theory of Competing Risks under Power Normalization. arXiv 2023, arXiv:2305.02742. [Google Scholar]
- Chen, Y.; Guo, K.; Ji, Q.; Zhang, D. “Not all climate risks are alike”: Heterogeneous responses of financial firms to natural disasters in China. Financ. Res. Lett. 2023, 52, 103538. [Google Scholar] [CrossRef]
- Cui, Q.; Xu, Y.; Zhang, Z.; Chan, V. Max-linear regression models with regularization. J. Econom. 2021, 222, 579–600. [Google Scholar] [CrossRef]
- Zhang, Z. Five critical genes related to seven COVID-19 subtypes: A data science discovery. J. Data Sci. 2021, 19, 142–150. [Google Scholar] [CrossRef]
- Soliman, A.A. Bayes Prediction in a Pareto Lifetime Model with Random Sample Size. J. R. Stat. Soc. Ser. 2000, 49, 51–62. [Google Scholar] [CrossRef]
- Korolev, V.; Gorshenin, A. Probability models and statistical tests for extreme precipitation based on generalized negative binomial distributions. Mathematics 2020, 8, 604. [Google Scholar] [CrossRef]
- Barakat, H.; Nigm, E. Convergence of random extremal quotient and product. J. Stat. Plan. Inference 1999, 81, 209–221. [Google Scholar] [CrossRef]
- Peng, Z.; Jiang, Q.; Nadarajah, S. Limiting distributions of extreme order statistics under power normalization and random index. Stochastics 2012, 84, 553–560. [Google Scholar] [CrossRef]
- Tan, Z.Q. The limit theorems for maxima of stationary Gaussian processes with random index. Acta Math. Sin. 2014, 30, 1021–1032. [Google Scholar] [CrossRef]
- Tan, Z.; Wu, C. Limit laws for the maxima of stationary chi-processes under random index. Test 2014, 23, 769–786. [Google Scholar] [CrossRef]
- Galambos, J. The Asymptotic Theory of Extreme Order Statistics; Wiley Series in Probability and Mathematical Statistics; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Barakat, H.; Nigm, E. Extreme order statistics under power normalization and random sample size. Kuwait J. Sci. Eng. 2002, 29, 27–41. [Google Scholar]
- Dorea, C.C.; GonÇalves, C.R. Asymptotic distribution of extremes of randomly indexed random variables. Extremes 1999, 2, 95–109. [Google Scholar] [CrossRef]
- Peng, Z.; Shuai, Y.; Nadarajah, S. On convergence of extremes under power normalization. Extremes 2013, 16, 285–301. [Google Scholar] [CrossRef]
- Hashorva, E.; Padoan, S.A.; Rizzelli, S. Multivariate extremes over a random number of observations. Scand. J. Stat. 2021, 48, 845–880. [Google Scholar] [CrossRef]
- Shi, P.; Valdez, E.A. Multivariate negative binomial models for insurance claim counts. Insur. Math. Econ. 2014, 55, 18–29. [Google Scholar] [CrossRef]
- Ribereau, P.; Masiello, E.; Naveau, P. Skew generalized extreme value distribution: Probability-weighted moments estimation and application to block maxima procedure. Commun. Stat.-Theory Methods 2016, 45, 5037–5052. [Google Scholar] [CrossRef]
- Berman, S.M. Limiting distribution of the maximum term in sequences of dependent random variables. Ann. Math. Stat. 1962, 33, 894–908. [Google Scholar] [CrossRef]
- Freitas, A.; Hüsler, J.; Temido, M.G. Limit laws for maxima of a stationary random sequence with random sample size. Test 2012, 21, 116–131. [Google Scholar] [CrossRef]
- Abd Elgawad, M.; Barakat, H.; Qin, H.; Yan, T. Limit theory of bivariate dual generalized order statistics with random index. Statistics 2017, 51, 572–590. [Google Scholar] [CrossRef]
- Grigelionis, B. On the extreme-value theory for stationary diffusions under power normalization. Lith. Math. J. 2004, 44, 36–46. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, L.; Hu, K.; Wen, C.; Tan, Z.; Ling, C. Extreme Behavior of Competing Risks with Random Sample Size. Axioms 2024, 13, 568. https://doi.org/10.3390/axioms13080568
Bai L, Hu K, Wen C, Tan Z, Ling C. Extreme Behavior of Competing Risks with Random Sample Size. Axioms. 2024; 13(8):568. https://doi.org/10.3390/axioms13080568
Chicago/Turabian StyleBai, Long, Kaihao Hu, Conghua Wen, Zhongquan Tan, and Chengxiu Ling. 2024. "Extreme Behavior of Competing Risks with Random Sample Size" Axioms 13, no. 8: 568. https://doi.org/10.3390/axioms13080568
APA StyleBai, L., Hu, K., Wen, C., Tan, Z., & Ling, C. (2024). Extreme Behavior of Competing Risks with Random Sample Size. Axioms, 13(8), 568. https://doi.org/10.3390/axioms13080568






