Dynamics of a New Four-Thirds-Degree Sub-Quadratic Lorenz-like System
Abstract
:1. Introduction
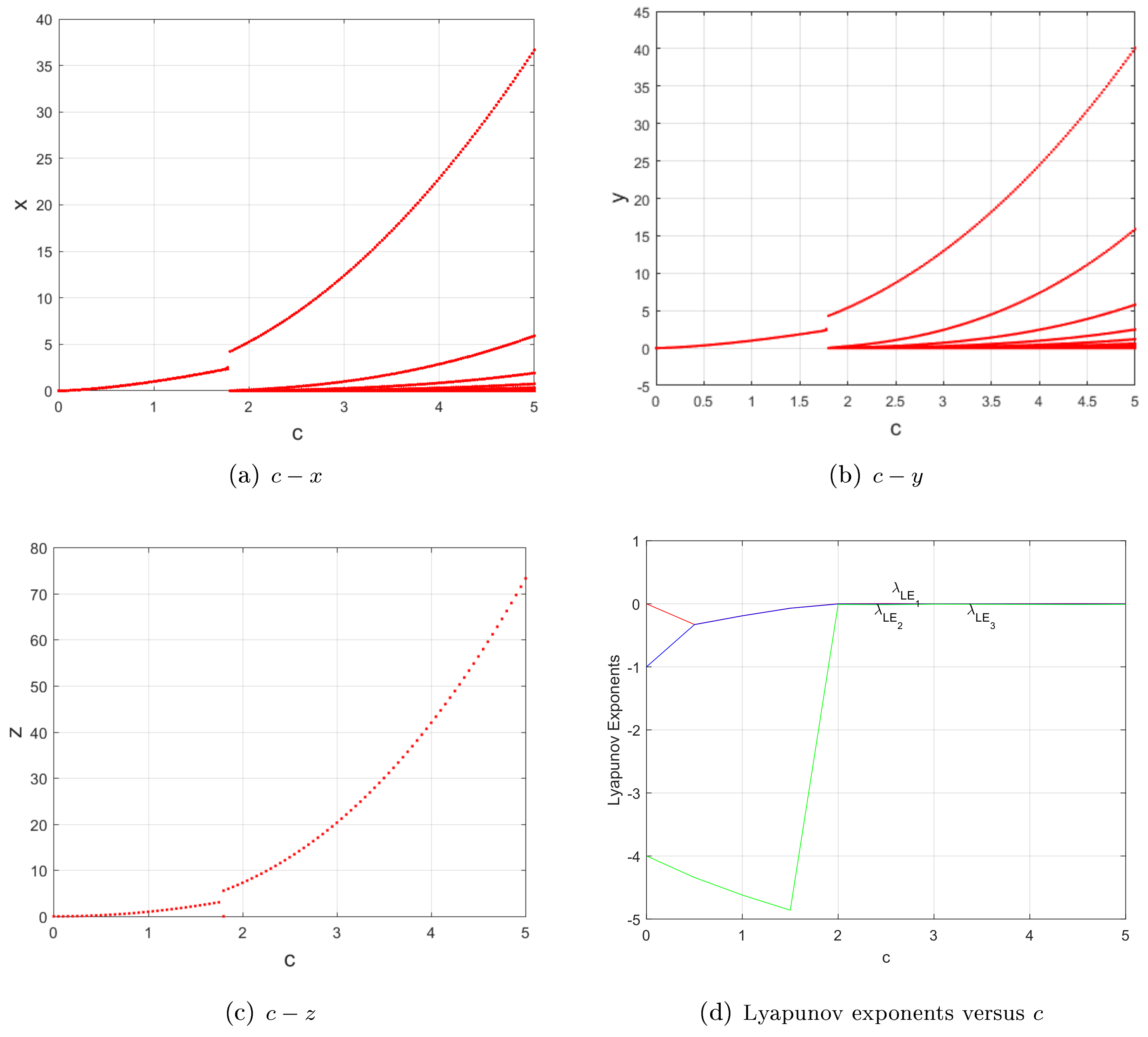
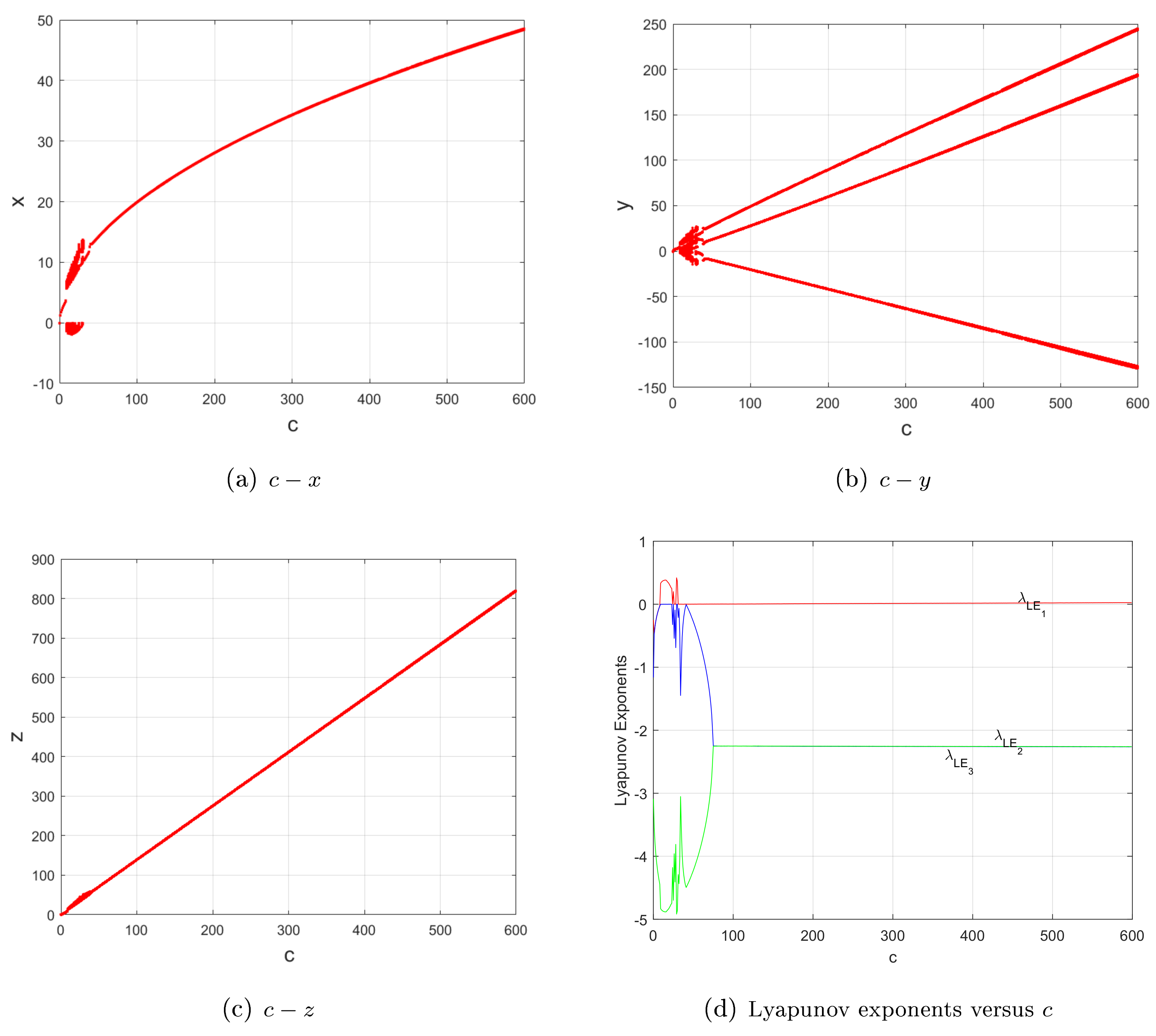
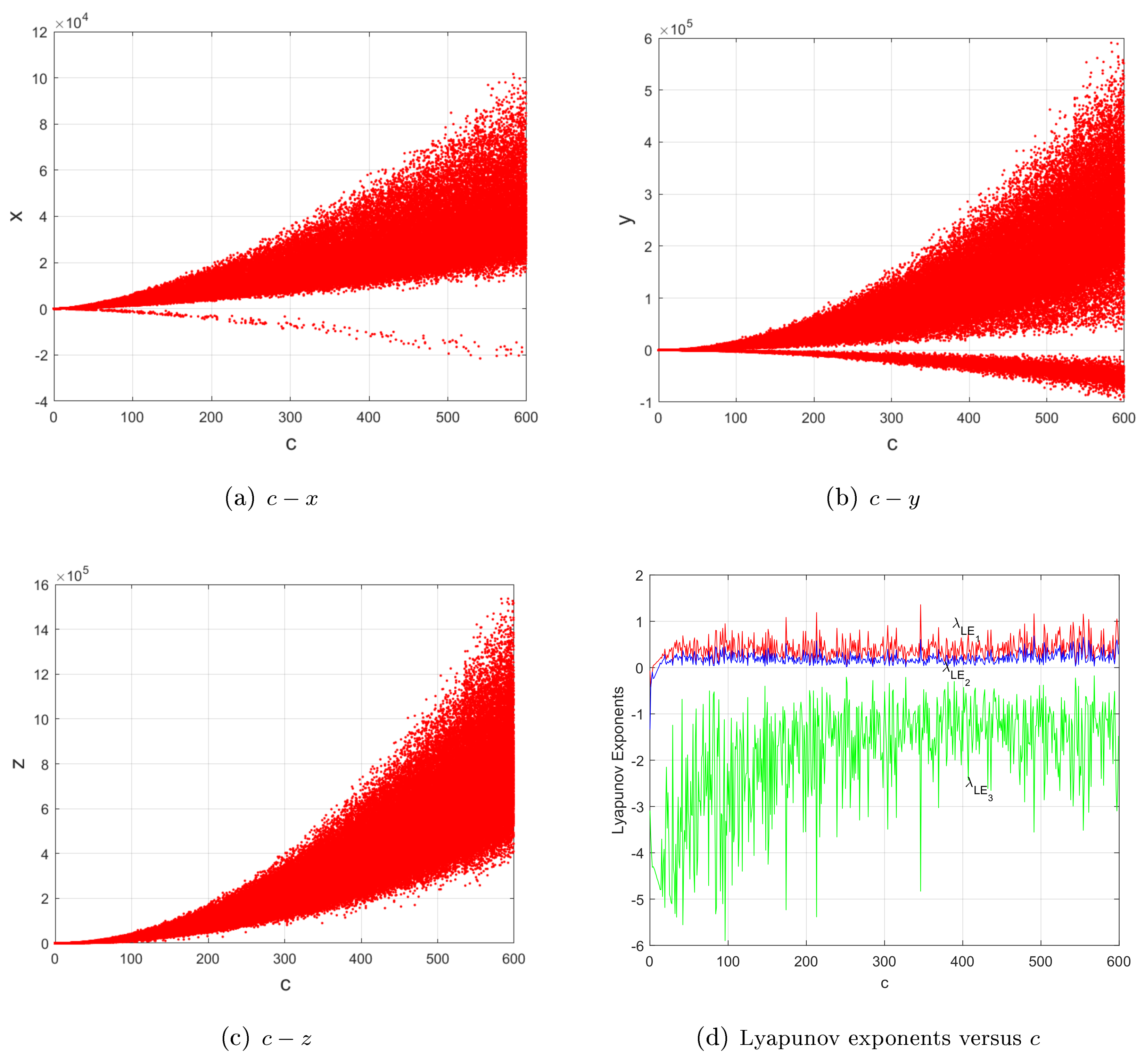
2. New Four-Thirds-Degree Lorenz-like System and Its Main Dynamics
3. Hopf Bifurcation
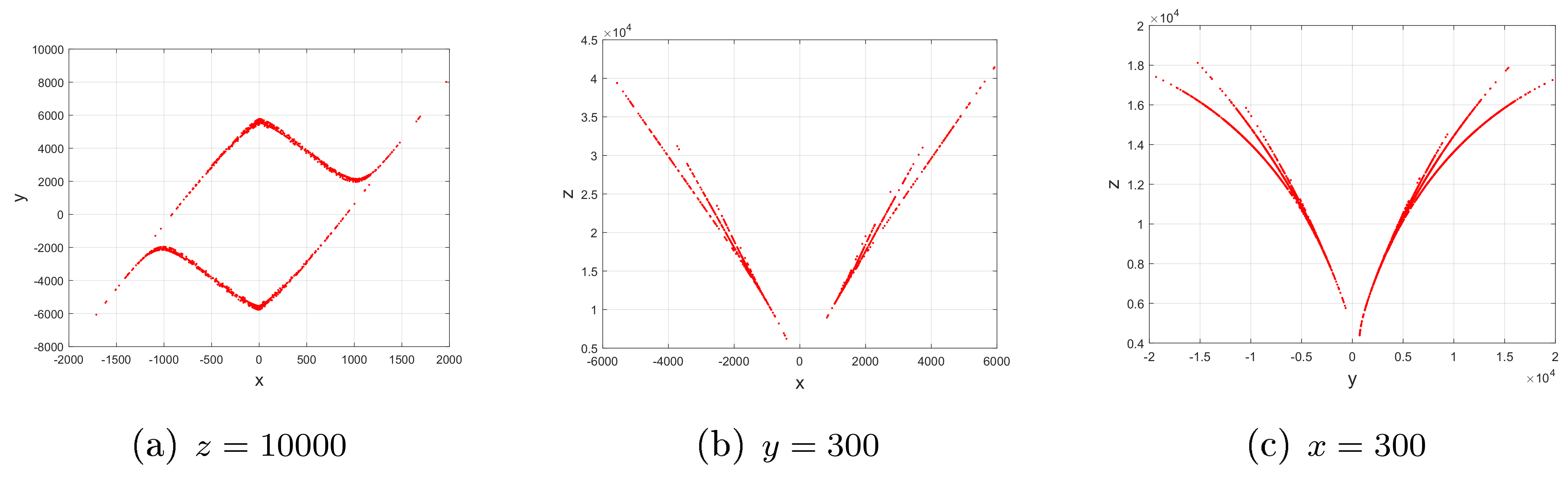
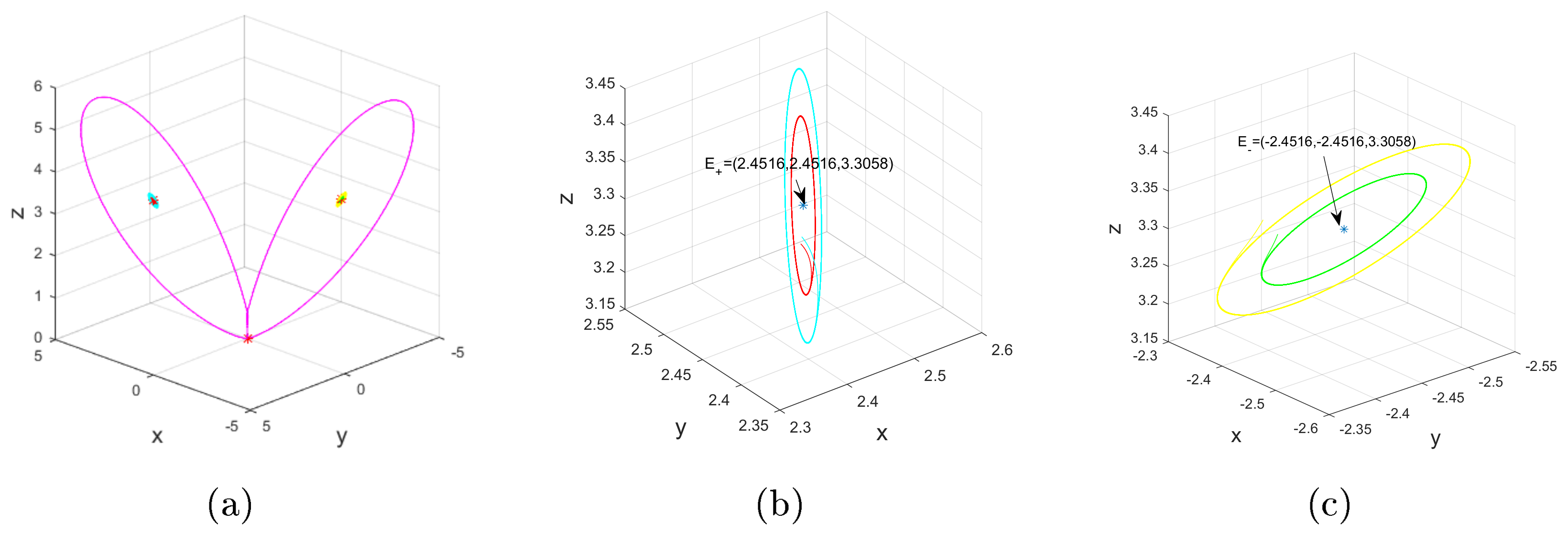
4. Existence of Heteroclinic Orbit
4.1.
- 1.
- Assume , and . is one of the stationary points.
- 2.
- If and , , then we arrive at and , . Namely, .
4.2.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smale, S. Mathematical problems for the next century. Math. Intell. 1998, 20, 7–15. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Afraimovich, V.S.; Bykov, V.V.; Shilnikov, L.P. The origin and structure of Lorenz attractor. Sov. Phys. Dokl. 1977, 22, 253–255. [Google Scholar]
- Tucker, W. The Lorenz attractor exists. Comptes Rendus l’Académie Sci. Ser. I Math. 1999, 328, 1197–1202. [Google Scholar] [CrossRef]
- Viana, M. What’s new on Lorenz strange attractors? Math. Intell. 2000, 22, 6–19. [Google Scholar] [CrossRef]
- Stewart, I. Mathematics: The Lorenz attractor exists. Nature 2000, 406, 948–949. [Google Scholar] [CrossRef] [PubMed]
- Shilnikov, L.P.; Shilnikov, A.L.; Turaev, D.V.; Chua, L.O. Methods of Qualitative Theory in Nonlinear Dynamics Part I, II; World Scientific: Singapore, 2001. [Google Scholar]
- Letellier, C.; Mendes, E.M.A.M.; Malasoma, J. Lorenz-like systems and Lorenz-like attractors: Definition, examples, and equivalences. Phys. Rev. E 2023, 108, 044209. [Google Scholar] [CrossRef]
- Kokubu, H.; Roussarie, R. Existence of a singularly degenerate heteroclinic cycle in the Lorenz system and its dynamical consequences: Part I. J. Dyn. Differ. Equ. 2004, 16, 513–557. [Google Scholar] [CrossRef]
- Messias, M. Dynamics at infinity and the existence of singularly degenerate heteroclinic cycles in the Lorenz system. J. Phys. A Math. Theor. 2009, 42, 115101. [Google Scholar] [CrossRef]
- Llibre, J.; Zhang, X. Invariant algebraic surfaces of the Lorenz system. J. Math. Phys. 2002, 43, 1622–1645. [Google Scholar] [CrossRef]
- Liao, X.; Yu, P.; Xie, S.; Fu, Y. Study on the global property of the smooth Chua’s system. Int. J. Bifurc. Chaos 2006, 16, 2815–2841. [Google Scholar] [CrossRef]
- Liao, X. New Research on Some Mathematical Problems of Lorenz Chaotic Family; Huazhong University of Science & Technology Press: Wuhan, China, 2017. [Google Scholar]
- Chen, G. Generalized Lorenz systems family. arXiv 2020, arXiv:2006.04066. [Google Scholar]
- Pasini, A.; Pelino, V. A unified view of Kolmogorov and Lorenz systems. Phys. Lett. A 2000, 275, 435–446. [Google Scholar] [CrossRef]
- Pelino, V.; Maimone, F.; Pasini, A. Energy cycle for the lorenz attractor. Chaos Solitons Fractals 2014, 64, 67–77. [Google Scholar] [CrossRef]
- Liang, X.; Qi, Q. Mechanical analysis of Chen chaotic system. Chaos Solitons Fractals 2017, 98, 173–177. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. On differences and similarities in the analysis of Lorenz, Chen, and Lu systems. Appl. Math. Comput. 2015, 256, 334–343. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Mokaev, T.N.; Kuznetsova, O.A.; Kudryashova, E.V. The Lorenz system: Hidden boundary of practical stability and the Lyapunov dimension. Nonlinear Dyn. 2020, 102, 713–732. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, G. Constructing an autonomous system with infinitely many chaotic attractors. Chaos 2017, 27, 071101. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Q. Dynamics of a new Lorenz-like chaotic system. Nonl. Anal. RWA 2010, 11, 2563–2572. [Google Scholar] [CrossRef]
- Wang, H.; Ke, G.; Pan, J.; Hu, F.; Fan, H. Multitudinous potential hidden Lorenz-like attractors coined. Eur. Phys. J. Spec. Top. 2022, 231, 359–368. [Google Scholar] [CrossRef]
- Wang, H.; Pan, J.; Ke, G. Revealing more hidden attractors from a new sub-quadratic Lorenz-like system of degree . Int. J. Bifurc. Chaos 2024, 34, 2450071. [Google Scholar] [CrossRef]
- Sprott, J.C. A proposed standard for the publication of new chaotic systems. Int. J. Bifurc. Chaos 2011, 21, 2391–2394. [Google Scholar] [CrossRef]
- Llibre, J.; Messias, M.; Silva, P.R. On the global dynamics of the Rabinovich system. J. Phys. A Math. Theor. 2008, 41, 275210. [Google Scholar] [CrossRef]
- Wang, H.; Ke, G.; Pan, J.; Su, Q. Conjoined Lorenz-like attractors coined. Miskolc Math. Notes 2023. [Google Scholar]
- Ke, G. Creation of three-scroll hidden conservative Lorenz-like chaotic flows. Adv. Theory Simulations 2024. [Google Scholar] [CrossRef]
- Wang, H.; Ke, G.; Hu, F.; Pan, J.; Dong, G.; Chen, G. Pseudo and true singularly degenerate heteroclinic cycles of a new 3D cubic Lorenz-like system. Results Phys. 2024, 56, 107243. [Google Scholar] [CrossRef]
- Wang, H.; Pan, J.; Ke, G. Multitudinous potential homoclinic and heteroclinic orbits seized. Electron. Res. Arch. 2024, 32, 1003–1016. [Google Scholar] [CrossRef]
- Wang, H.; Pan, J.; Ke, G.; Hu, F. A pair of centro-symmetric heteroclinic orbits coined. Adv. Cont. Discr. Mod. 2024, 2024, 14. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Q. Dynamics of a hyperchaotic Lorenz-type system. Nonlinear Dyn. 2014, 77, 569–581. [Google Scholar] [CrossRef]
- Li, T.; Chen, G.; Chen, G. On homoclinic and heteroclinic orbits of the Chen’s system. Int. J. Bifurc. Chaos 2006, 16, 3035–3041. [Google Scholar] [CrossRef]
- Tigan, G.; Constantinescu, D. Heteroclinic orbits in the T and the Lü system. Chaos Solitons Fractals 2009, 42, 20–23. [Google Scholar] [CrossRef]
- Liu, Y.; Pang, W. Dynamics of the general Lorenz family. Nonlinear Dyn. 2012, 67, 1595–1611. [Google Scholar] [CrossRef]
- Tigan, G.; Llibre, J. Heteroclinic, homoclinic and closed orbits in the Chen system. Int. J. Bifurc. Chaos 2016, 26, 1650072. [Google Scholar] [CrossRef]
- Kuzenetsov, Y.A. Elements of Applied Bifurcation Theory, 3rd ed.; Springer: New York, NY, USA, 2004; Volume 112. [Google Scholar]
- Sotomayor, J.; Mello, L.F.; Braga, D.C. Lyapunov coefficients for degenerate Hopf bifurcations. arXiv 2007, arXiv:0709.3949. [Google Scholar]




| b | a | c | Property of |
|---|---|---|---|
| <0 | <0 | <0 | A 1D and a 2D |
| >0 | A 3D | ||
| >0 | <0 | A 2D and a 1D | |
| >0 | A 1D and a 2D | ||
| >0 | <0 | <0 | A 2D and a 1D |
| >0 | A 1D and a 2D | ||
| >0 | <0 | A 3D | |
| >0 | A 2D and a 1D |
| z | a | Property of |
|---|---|---|
| >0 | <0 | A 1D , a 1D and a 1D |
| >0 | A 2D and a 1D | |
| <0 | <0 | A 2D and a 1D |
| >0 | A 1D , a 1D and a 1D |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, G.; Pan, J.; Hu, F.; Wang, H. Dynamics of a New Four-Thirds-Degree Sub-Quadratic Lorenz-like System. Axioms 2024, 13, 625. https://doi.org/10.3390/axioms13090625
Ke G, Pan J, Hu F, Wang H. Dynamics of a New Four-Thirds-Degree Sub-Quadratic Lorenz-like System. Axioms. 2024; 13(9):625. https://doi.org/10.3390/axioms13090625
Chicago/Turabian StyleKe, Guiyao, Jun Pan, Feiyu Hu, and Haijun Wang. 2024. "Dynamics of a New Four-Thirds-Degree Sub-Quadratic Lorenz-like System" Axioms 13, no. 9: 625. https://doi.org/10.3390/axioms13090625






