Mathematical Model for the Control of Red Palm Weevil
Abstract
:1. Introduction
2. Mathematical Formulation
Positivity and Boundedness
3. Model Analysis
3.1. Equilibrium Points
3.2. Basic Reproduction Number
3.3. Stability of the RPW System
- The eigenvalues of at the extinction equilibrium point are , , , ; thus, is always unstable. Therefore, the entire population cannot become extinct at the same time.
- The eigenvalues of at the weevil-free equilibrium point are , , , and ; thus, is locally stable if and .
- One of the eigenvalues of is positive; so, , the palm tree extinction equilibrium point, is unstable.
- The eigenvalues of the Jacobian matrix at the infected palm tree extinction equilibrium point are , , , and . Therefore, is unstable.
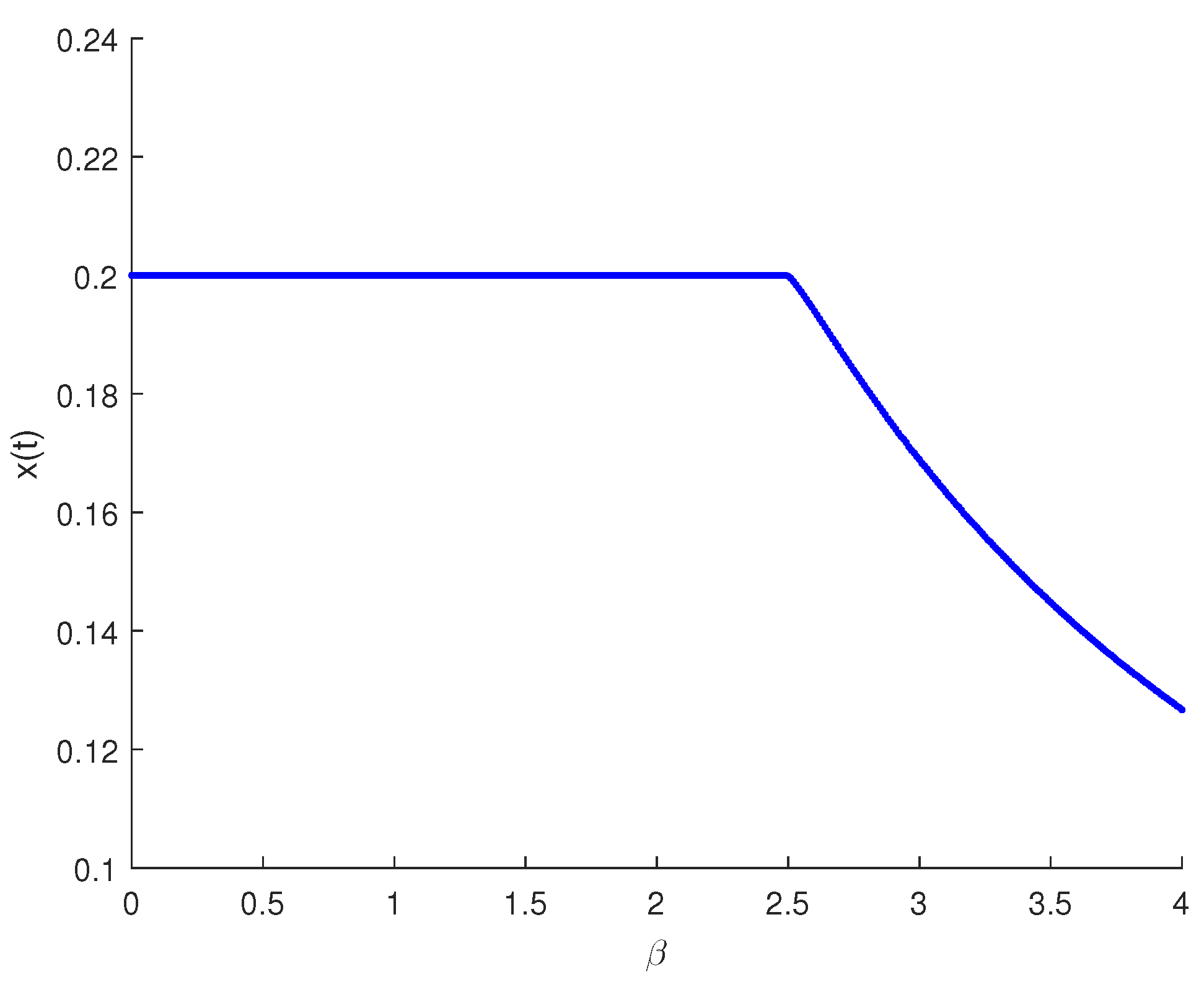
4. Model Analysis Optimization of the Biological Control
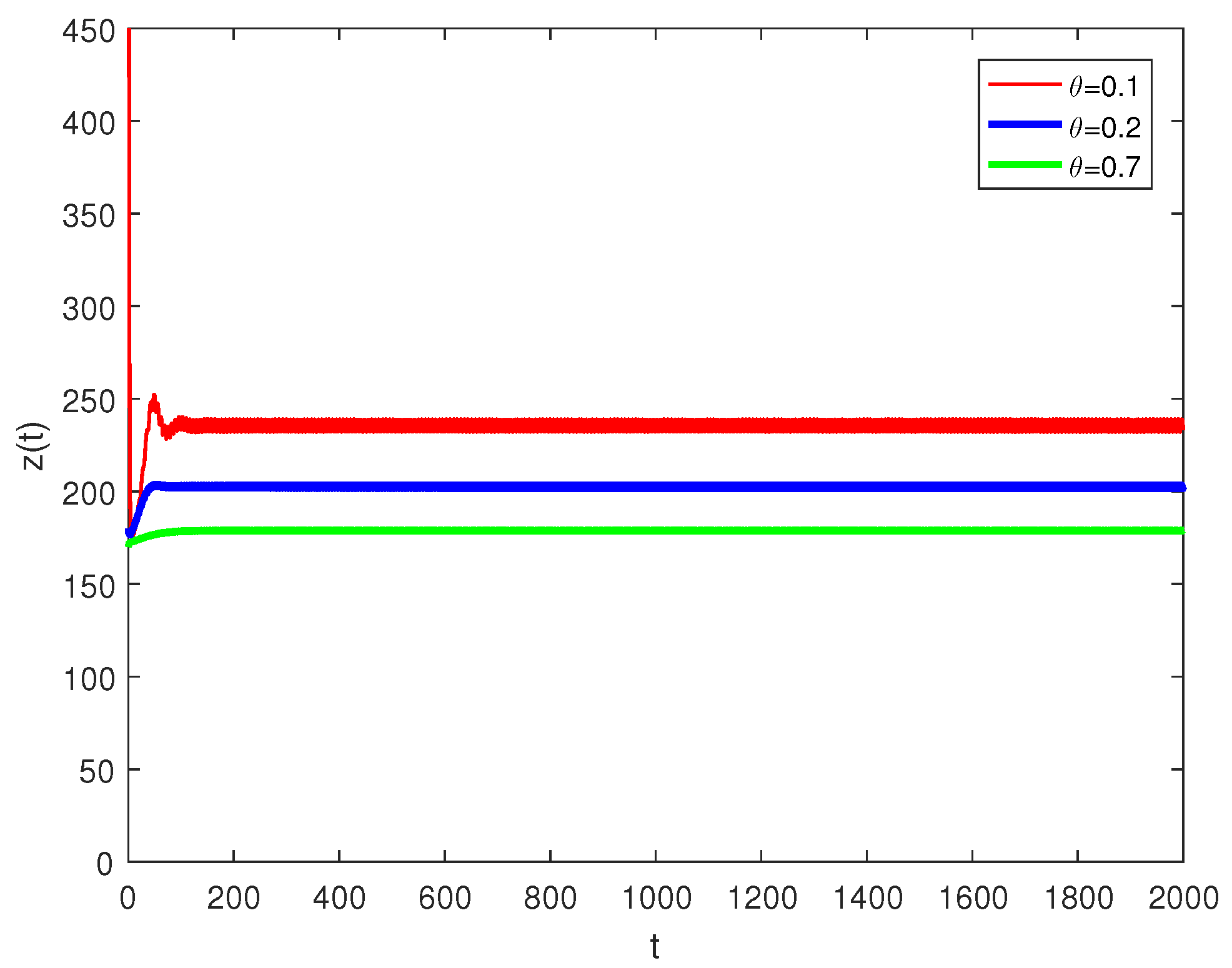
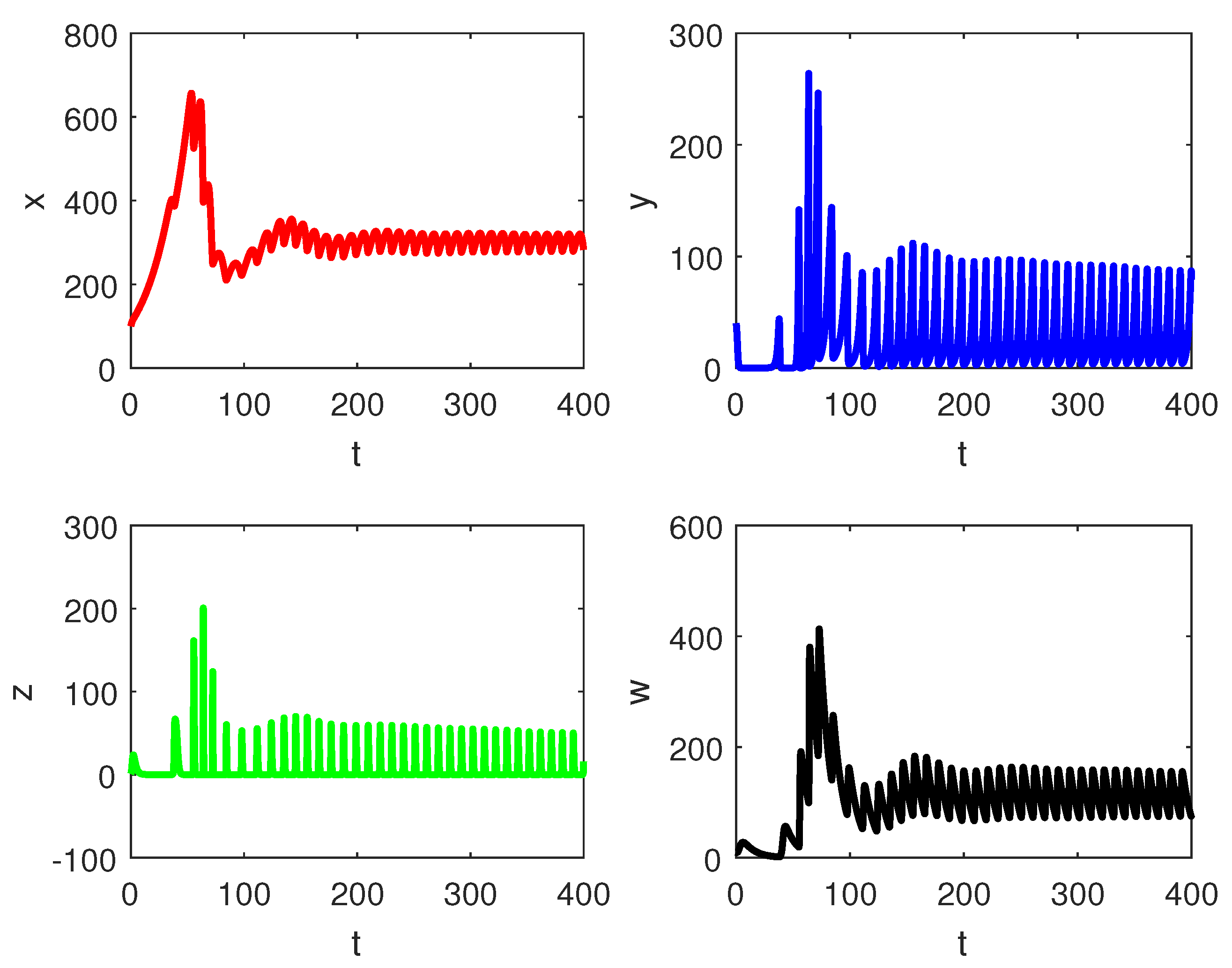
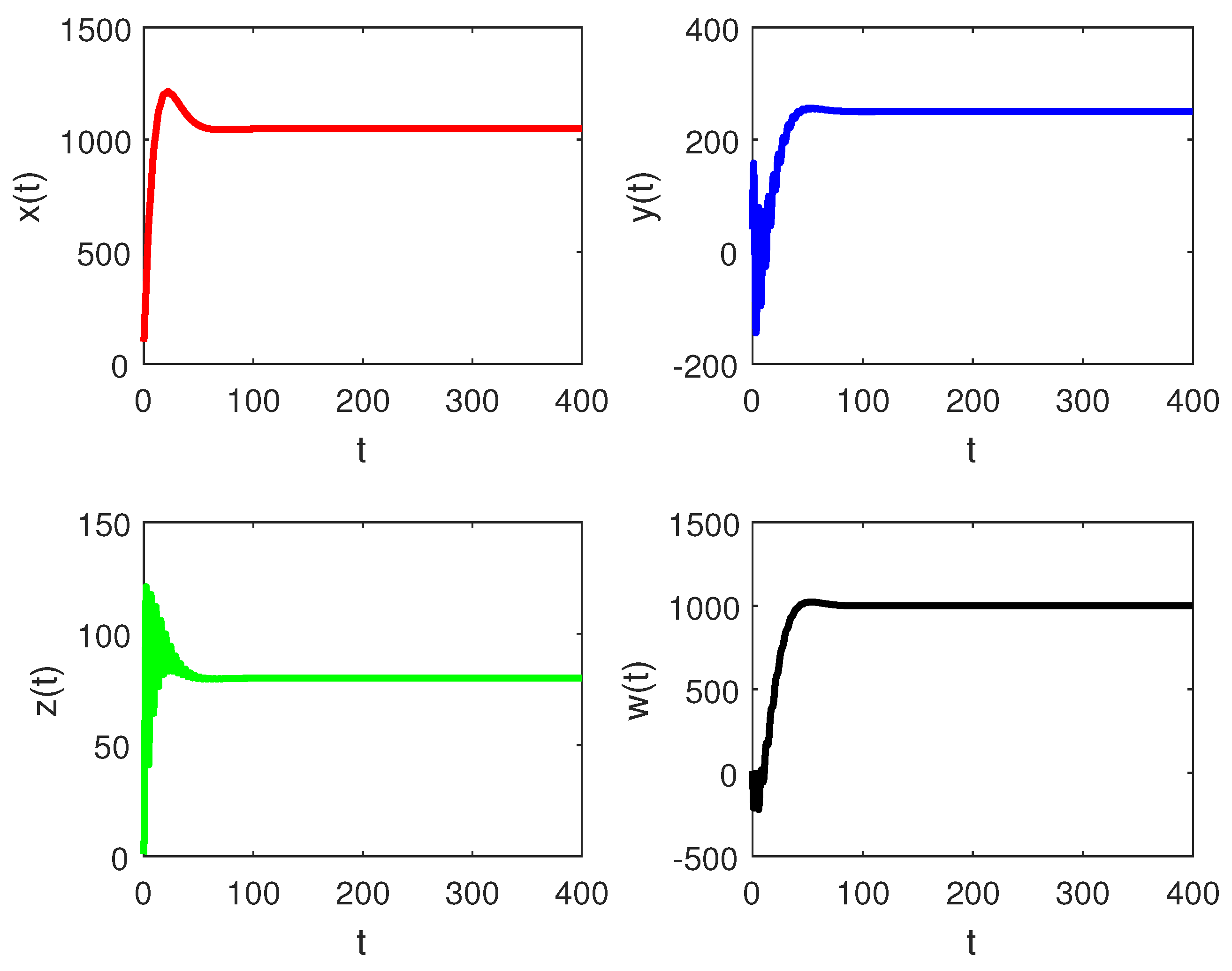
5. Numerical Simulations
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aldawood, A.; Rasool, K. Rearing optimization of red palm weevil: Rhynchophorus ferrugineus (Coleoptera: Curculionidae) on date palm: Phoenix dactylifera. Fla. Entomol. 2011, 94, 756. [Google Scholar] [CrossRef]
- Abdel-Banat, B.; El-Shafie, H. Management of the Red Palm Weevil in Date Palm Plantations in Al-Ahsa Oasis of Saudi Arabia. Plant Health Cases 2023, 2023, phcs20230001. [Google Scholar] [CrossRef]
- Seman-Kamarulzaman, A.F.; Pariamiskal, F.A.; Azidi, A.N.; Hassan, M. A Review on Digestive System of Rhynchophorus ferrugineus as Potential Target to Develop Control Strategies. Insects 2023, 14, 506. [Google Scholar] [CrossRef] [PubMed]
- Hoddle, M.S.; Antony, B.; El-Shafie, H.A.; Chamorro, M.L.; Milosavljević, I.; Löhr, B.; Faleiro, J.R. Taxonomy, Biology, Symbionts, Omics, and Management of Rhynchophorus Palm Weevils (Coleoptera: Curculionidae: Dryophthorinae). Annu. Rev. Entomol. 2024, 69, 455–479. [Google Scholar] [CrossRef] [PubMed]
- Manee, M.M.; Alqahtani, F.H.; Al-Shomrani, B.M.; El-Shafie, H.A.; Dias, G.B. Omics in the Red Palm Weevil Rhynchophorus ferrugineus (Olivier) (Coleoptera: Curculionidae): A Bridge to the Pest. Insects 2023, 14, 255. [Google Scholar] [CrossRef]
- Al-Khayri, J. Date palm Phoenix dactylifera micropropagation. In Protocols for Micropropagation of Woody Trees and Fruits; Springer: Berlin/Heidelberg, Germany, 2007; pp. 509–526. [Google Scholar]
- Eldin, H.A.; Waleed, K.; Samir, M.; Tarek, M.; Sobeah, H.; Salam, M.A. A survey on detection of Red Palm Weevil inside palm trees: Challenges and applications. In Proceedings of the 9th International Conference on Software and Information Engineering, Cairo, Egypt, 11–13 November 2020; pp. 119–125. [Google Scholar]
- Mashal, M.M.; Obeidat, B.F. The efficacy assessment of emamectin benzoate using micro injection system to control red palm weevil. Heliyon 2019, 5, e01833. [Google Scholar] [CrossRef]
- Refaat, E.S.M.; El Shazly, M.; El Deeb, M.; Eliwa, A. Study the effect of mechanical injection technique on controlling red palm weevil. Zagazig J. Agric. Res. 2017, 44, 1889–1900. [Google Scholar]
- Abbas, M.S.T. IPM of the red palm weevil, Rhynchophorus ferrugineus. In Integrated Management of Arthropod Pests and Insect Borne Diseases; Springer: Berlin/Heidelberg, Germany, 2010; pp. 209–233. [Google Scholar]
- Chihaoui-Meridja, S.; Harbi, A.; Abbes, K.; Chaabane, H.; La Pergola, A.; Chermiti, B.; Suma, P. Systematicity, persistence and efficacy of selected insecticides used in endotherapy to control the red palm weevil Rhynchophorus ferrugineus (Olivier, 1790) on Phoenix canariensis. Phytoparasitica 2020, 48, 75–85. [Google Scholar] [CrossRef]
- El-Juhany, L.I. Degradation of date palm trees and date production in Arab countries: Causes and potential rehabilitation. Aust. J. Basic Appl. Sci. 2010, 4, 3998–4010. [Google Scholar]
- Hoddle, M.; Al-Abbad, A.H.; El-Shafie, H.; Faleiro, J.; Sallam, A.; Hoddle, C. Assessing the impact of areawide pheromone trapping, pesticide applications, and eradication of infested date palms for Rhynchophorus ferrugineus (Coleoptera: Curculionidae) management in Al Ghowaybah, Saudi Arabia. Crop Prot. 2013, 53, 152–160. [Google Scholar] [CrossRef]
- Milosavljević, I.; El-Shafie, H.A.; Faleiro, J.R.; Hoddle, C.D.; Lewis, M.; Hoddle, M.S. Palmageddon: The wasting of ornamental palms by invasive palm weevils, Rhynchophorus spp. J. Pest Sci. 2019, 92, 143–156. [Google Scholar] [CrossRef]
- Sarwar, M. Biological control of red palm weevil Rhynchophorus Ferrugineus (Coleoptera: Curculionidae) by the natural enemies. Int. J. Res. Biol. Pharm. 2016, 2, 22–35. [Google Scholar]
- El Sadawy, H.A.; Namaky, A.H.E.; Al Omari, F.; Bahareth, O.M. Susceptibility of Rhynchophorus Ferrugineus (Olivier) (Coleoptera: Curculionidae) to entomopathogenic nematodes with regard to its immune response. Biol. Control 2020, 148, 104308. [Google Scholar] [CrossRef]
- Rehman, G.; Mamoon-ur Rashid, M. Evaluation of entomopathogenic nematodes against red palm weevil, Rhynchophorus ferrugineus (Olivier) (Coleoptera: Curculionidae). Insects 2022, 13, 733. [Google Scholar] [CrossRef]
- El-Shahed, M.; Al-Dubiban, A.M. Mathematical Modelling of Lesser Date Moth Using Sex Pheromone Traps and Natural Enemies. Math. Probl. Eng. 2021, 2021, 8835321. [Google Scholar] [CrossRef]
- El-Shahed, M.; Al-Dububan, A.M. Deterministic and Stochastic Fractional Order Model for Lesser Date Moth. Comput. Syst. Sci. Eng. 2022, 40, 749–764. [Google Scholar] [CrossRef]
- El-Shahed, M.; Al-Nujiban, A.; Abdel-Baky, N.F. Stochastic Modelling of Red Palm Weevil Using Chemical Injection and Pheromone Traps. Axioms 2022, 11, 334. [Google Scholar] [CrossRef]
- Ben Dhahbi, A.; Chargui, Y.; Boulaaras, S.M.; Ben Khalifa, S. A one-sided competition mathematical model for the sterile insect technique. Complexity 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Ben Dhahbi, A.; Chargui, Y.; Boulaaras, S.M.; Ben Khalifa, S.; Koko, W.; Alresheedi, F. Mathematical modelling of the sterile insect technique using different release strategies. Math. Probl. Eng. 2020, 2020, 8896566. [Google Scholar] [CrossRef]
- Solano-Rojas, Y.; Gámez, M.; López, I.; Garay, J.; Varga, Z.; Cabello, T. Conservation Strategy for Palm Groves: Optimal Chemical Control Model for Red Palm Weevil, Rhynchophorus ferrugineus. Agronomy 2021, 11, 920. [Google Scholar] [CrossRef]
- Alnafisah, Y.; El-Shahed, M. Optimal control of red palm weevil model incorporating sterile insect technique, mechanical injection, and pheromone traps. Alex. Eng. J. 2024, 93, 382–391. [Google Scholar] [CrossRef]
- Gulati, P.; Chauhan, S.; Mubayi, A.; Singh, T.; Rana, P. Dynamical analysis, optimum control and pattern formation in the biological pest (EFSB) control model. Chaos Solitons Fractals 2021, 147, 110920. [Google Scholar] [CrossRef]
- Barik, M.; Chauhan, S.; Misra, O.P.; Bhatia, S.K. Optimal control using linear feedback control and neutralizing antibodies for an HIV model with dynamical analysis. J. Appl. Math. Comput. 2022, 68, 4361–4389. [Google Scholar] [CrossRef]
- Molter, A.; Bezerra, J.I.; Rafikova, E.; Nava, D.E.; Rafikov, M. Dynamics and biological control of the sugarcane borer with two parasitoids. Ecol. Model. 2023, 481, 110371. [Google Scholar] [CrossRef]
- Rodrigues, L.R.; Gabrielli, F. State Feedback as a Strategy for Control and Analysis of COVID-19. arXiv 2024, arXiv:2405.17735. [Google Scholar]
- Farman, M.; Saleem, M.U.; Tabassum, M.F.; Ahmad, A.; Ahmad, M.O. A linear control of composite model for glucose insulin glucagon pump. Ain Shams Eng. J. 2019, 10, 867. [Google Scholar] [CrossRef]
- Di Giamberardino, P.; Iacoviello, D. A linear quadratic regulator for nonlinear SIRC epidemic model. In Proceedings of the 2019 23rd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 9–11 October 2019; pp. 733–738. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Anderson, B.D.; Moore, J.B. Optimal Control: Linear Quadratic Methods; Courier Corporation: Washington, DC, USA, 2007. [Google Scholar]
- Bernstein, D.S. Nonquadratic cost and nonlinear feedback control. Int. J. Robust Nonlinear Control. 1993, 3, 211–229. [Google Scholar] [CrossRef]
- Asri, S.; Rodrigues, L. Data-Driven LQR using Reinforcement Learning and Quadratic Neural Networks. arXiv 2023, arXiv:2311.10235. [Google Scholar]
- Ismail, A.I.; Hassaballa, A.A.; Almadini, A.M.; Daffalla, S. Analyzing the Spatial Correspondence between Different Date Fruit Cultivars and Farms’ Cultivated Areas, Case Study: Al-Ahsa Oasis, Kingdom of Saudi Arabia. Appl. Sci. 2022, 12, 5728. [Google Scholar] [CrossRef]
- Ali-Bob, M. Management of the red palm weevil Rhynchophorus ferrugineus (Olivier) using sustainable options in Saudi Arabia. Arab. J. Plant Prot. 2019, 37, 2019. [Google Scholar] [CrossRef]
- Abbas, M.K.; Hou, Y.; Wu, S.Y.; Batt, M.A. Evaluation of some control methods against the red palm weevil, Rhynchophorus ferrugineus Olivier (Coleoptera: Curculionidae) infesting date palm trees. Menoufia J. Plant Prot. 2024, 9, 223–229. [Google Scholar] [CrossRef]
- Fenton, A.; Norman, R.; Fairbairn, J.P.; Hudson, P.J. Modelling the efficacy of entomopathogenic nematodes in the regulation of invertebrate pests in glasshouse crops. J. Appl. Ecol. 2000, 37, 309–320. [Google Scholar] [CrossRef]
- Mohanny, K.M.; Mohamed, G.S.; Abdo, O.M. Laboratory study of life table and demographic parameters of Red Palm Weevil (Rhynchophorus ferrugineus, Coleoptera: Dryophthoridae) on sugarcane slices. SVU-Int. J. Agric. Sci. 2020, 2, 93–103. [Google Scholar] [CrossRef]
- Mehdi, M.Z.; Wakil, W.; Jan, H.; Raza, M.M.; Shah, Q.; Zia-ul-Haq, M. Evaluation of entomopathogenic nematode and fungi alone and their combination against red palm weevil, Rhynchophorus ferrugineus (Olivier). J. Entomol. Zool. Stud. 2018, 6, 2038–2042. [Google Scholar]
- Alwaneen, W.S.; Wakil, W.; Kavallieratos, N.G.; Qayyum, M.A.; Tahir, M.; Rasool, K.G.; Husain, M.; Aldawood, A.S.; Shapiro-Ilan, D. Efficacy and persistence of entomopathogenic fungi against Rhynchophorus ferrugineus on date palm: Host to host transmission. Agronomy 2024, 14, 642. [Google Scholar] [CrossRef]
- Fenton, A.; Norman, R.; Fairbairn, J.P.; Hudson, P.J. Evaluating the efficacy of entomopathogenic nematodes for the biological control of crop pests: A nonequilibrium approach. Am. Nat. 2001, 158, 408–425. [Google Scholar] [CrossRef]
- Mushanyu, J.; Chazuka, Z.; Mudzingwa, F.; Ogbogbo, C. Modelling the impact of detection on COVID-19 transmission dynamics in Ghana. RMS Res. Math. Stat. 2021, 8, 1953722. [Google Scholar] [CrossRef]
- Gatyeni, S.P.; Chirove, F.; Nyabadza, F. Modelling the potential impact of stigma on the transmission dynamics of COVID-19 in South Africa. Mathematics 2022, 10, 3253. [Google Scholar] [CrossRef]
- Birkhoff, G.; Rota, G. Ordinary Differential Equation; John Wiley and Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Hassan, K.; Mustafa, A.; Hama, M. An Eco-Epidemiological Model Incorporating Harvesting Factors. Symmetry 2021, 13, 2179. [Google Scholar] [CrossRef]
- Brauer, F. Boundedness of solutions of predator-prey systems. Theor. Popul. Biol. 1979, 15, 268–273. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- La Salle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361–404. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.P.; Santra, P.K.; Mahapatra, G.S. Global stability and analysing the sensitivity of parameters of a multiple-susceptible population model of SARS-CoV-2 emphasising vaccination drive. Math. Comput. Simul. 2023, 203, 741–766. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Rafikov, M.; de Holanda Limeira, E. Mathematical modelling of the biological pest control of the sugarcane borer. Int. J. Comput. Math. 2012, 89, 390–401. [Google Scholar] [CrossRef]
- Rafikov, M.; Silveira, J.C. On dynamical behavior of the sugarcane borer–Parasitoid agroecosystem. Ecol. Complex. 2014, 18, 67–73. [Google Scholar] [CrossRef]
- Shehab, B.; Ammr, M. THE INFLUENCE OF PREY AND PREDATOR DENSITY ON THE PREDACIOUS BEHAVIOR OF Chrysoperla mutata (MACLACHLAN) LARVAE FEEDING ON DUBAS NYMPHS Ommatissus lybicus DEBERG. Iraqi J. Sci. 2008, 49, 40–49. [Google Scholar]
- Al-Rawy, M.A.; Hamad, B.S.; Abdullatif, A.M. Factors affecting the effectiveness of Chrysoperla mutata (McL.) larvae feeding on dubas nymphs Ommatissus lybicus DeBerg. J. Educ. Sci. Stud. 2013, 1, 387–398. [Google Scholar]


| Parameter | Description | Value | Source |
|---|---|---|---|
| r | The growth rate of susceptible date palm trees | 0.038 | [35] |
| k | The carrying capacity of the date palm farm | 30000 | [36] |
| Red palm weevil infection rate | 0.025 | [36] | |
| Recovery rate of infected palm trees as a result of aluminum phosphide fumigation | 0.5 | [37] | |
| The rate of predation by larvae on the interior of the infected palm trunk | 0.08 | [38] | |
| Palm tree mortality rate as a result of red palm weevil infestation | 0.008 | [36] | |
| The rate of increase in the number of larvae as a result of eggs | 0.17 | [39] | |
| Predation intensity between larvae and entomopathogenic nematode | 0.7 | [40] | |
| The mortality rate of larvae | 0.15 | [41] | |
| Entomopathogenic nematodes mortality rate. | 0.1 | [42] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqahtani, Z.; Almuneef, A.; El-Shahed, M. Mathematical Model for the Control of Red Palm Weevil. Axioms 2024, 13, 637. https://doi.org/10.3390/axioms13090637
Alqahtani Z, Almuneef A, El-Shahed M. Mathematical Model for the Control of Red Palm Weevil. Axioms. 2024; 13(9):637. https://doi.org/10.3390/axioms13090637
Chicago/Turabian StyleAlqahtani, Zuhur, Areej Almuneef, and Moustafa El-Shahed. 2024. "Mathematical Model for the Control of Red Palm Weevil" Axioms 13, no. 9: 637. https://doi.org/10.3390/axioms13090637
APA StyleAlqahtani, Z., Almuneef, A., & El-Shahed, M. (2024). Mathematical Model for the Control of Red Palm Weevil. Axioms, 13(9), 637. https://doi.org/10.3390/axioms13090637







