The Edge Odd Graceful Labeling of Water Wheel Graphs

Abstract

A graph, $G=(V,E)$, is edge odd graceful if it possesses edge odd graceful labeling. This labeling is defined as a bijection $g:E\left(G\right)\to \{1,3,\dots ,2m-1\}$, from which an injective transformation is derived, $g^{*}:V\left(G\right)\to \{1,2,3,\dots ,2m-1\}$, from the rule that the image of $u\in V\left(G\right)$ under $g^{*}$ is ${\sum }_{uv\in E\left(G\right)}g\left(uv\right)\mathrm{mod}\left(2m\right)$. The main objective of this manuscript is to introduce new classes of planar graphs, namely water wheel graphs, $W{W}_n$; triangulated water wheel graphs, $T{W}_n$; closed water wheel graphs, $C{W}_n$; and closed triangulated water wheel graphs, $C{T}_n$. Furthermore, we specify conditions for these graphs to allow for edge odd graceful labelings.

1. Introduction

Graph labeling, a significant aspect of graph theory, pertains to the process of assigning labels or values to the vertices or edges of a graph, typically in accordance with defined rules or constraints. These labels may signify different attributes or features related to the elements of the graph. By systematically assigning labels to either vertices or edges, graph labeling facilitates a methodical examination, understanding, and investigation of the structure and characteristics inherent to graphs. The applications of graph labeling extend across diverse fields, encompassing network design, communication systems, computer networks, social networks, bioinformatics, and data analysis [1,2,3,4]. The notions and terminology in this manuscript are standard and can be found in any book on graph theory; for example, see [5].

Vertex graph coloring is a type of graph labeling and defined as a process that entails the assignment of colors to the vertices of a graph in such a way that neighboring vertices are assigned distinct colors. Vertex coloring is widely considered to be one of the most extensively studied and prominent topics within the field of graph theory, as stated by Alon [5]. A dynamic survey of graph labeling by Gallian [6] provides intensive background on the topic of graph labeling.

In formal terms, the graceful labeling of a graph $G=(V,E)$ with n vertices and m edges can be defined by an injective function, f, that maps the set of vertices, V, to the set $\{0,1,2,...,m\}$. In this labeling, each edge $xy$ is assigned a label $\left|g\right(x)-g(y\left)\right|$, ensuring that all edges have distinct labels [7,8]. Similarly, the edge graceful labeling of a graph $G=(V,E)$ of order n and size m can be defined by an injective function, f, that maps the set of edges, E, to the set $\{0,1,2,...,m\}$ such that the derived function $g^{*}$ from the set of vertices, V, to the set $\{0,1,2,...,n-1\}$ defined as $g^{*}\left(u\right)={\sum }_{uv\in E\left(G\right)}g\left(uv\right)\mathrm{mod}m$ is a bijection [9].

Let G be a graph of order n and size m; the edge odd graceful labeling of G is a bijection, $g:E\left(G\right)\to \{1,3,\dots ,2m-1\}$, in such a way that the derived transformation $g^{*}:V\left(G\right)\to \{1,2,3,\dots ,2m-1\}$ given by $g^{*}\left(u\right)={\sum }_{uv\in E\left(G\right)}g\left(uv\right)\mathrm{mod}\left(2m\right)$ is an injective function [10]. A graph that possesses this labeling is referred to as an edge odd graceful graph.

The goal of this manuscript is to introduce new classes of planar graphs, namely, water wheel graphs $W{W}_n$; closed water wheel graphs, $C{W}_n$; triangulated water wheel graphs, $T{W}_n$; and closed triangulated water wheel graphs, $C{T}_n$. Furthermore, we specify conditions for these graphs to allow edge odd graceful labelings. This study builds upon the ongoing research trend focusing on the edge labeling of graphs, as seen in previous works such as [10,11,12,13].

2. The Main Results

This section introduces the definitions and constructions of the new classes of graphs and the main results.

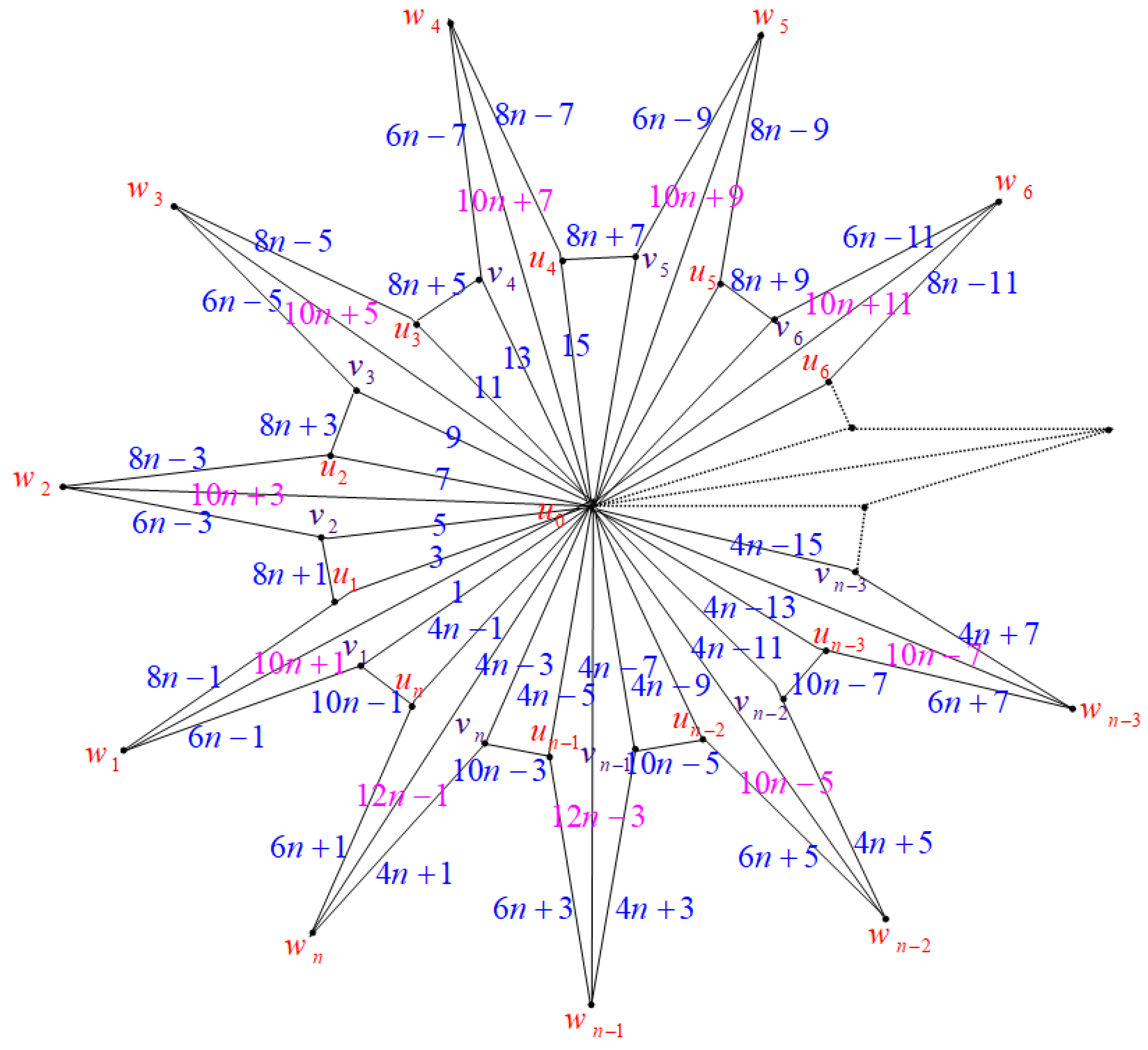
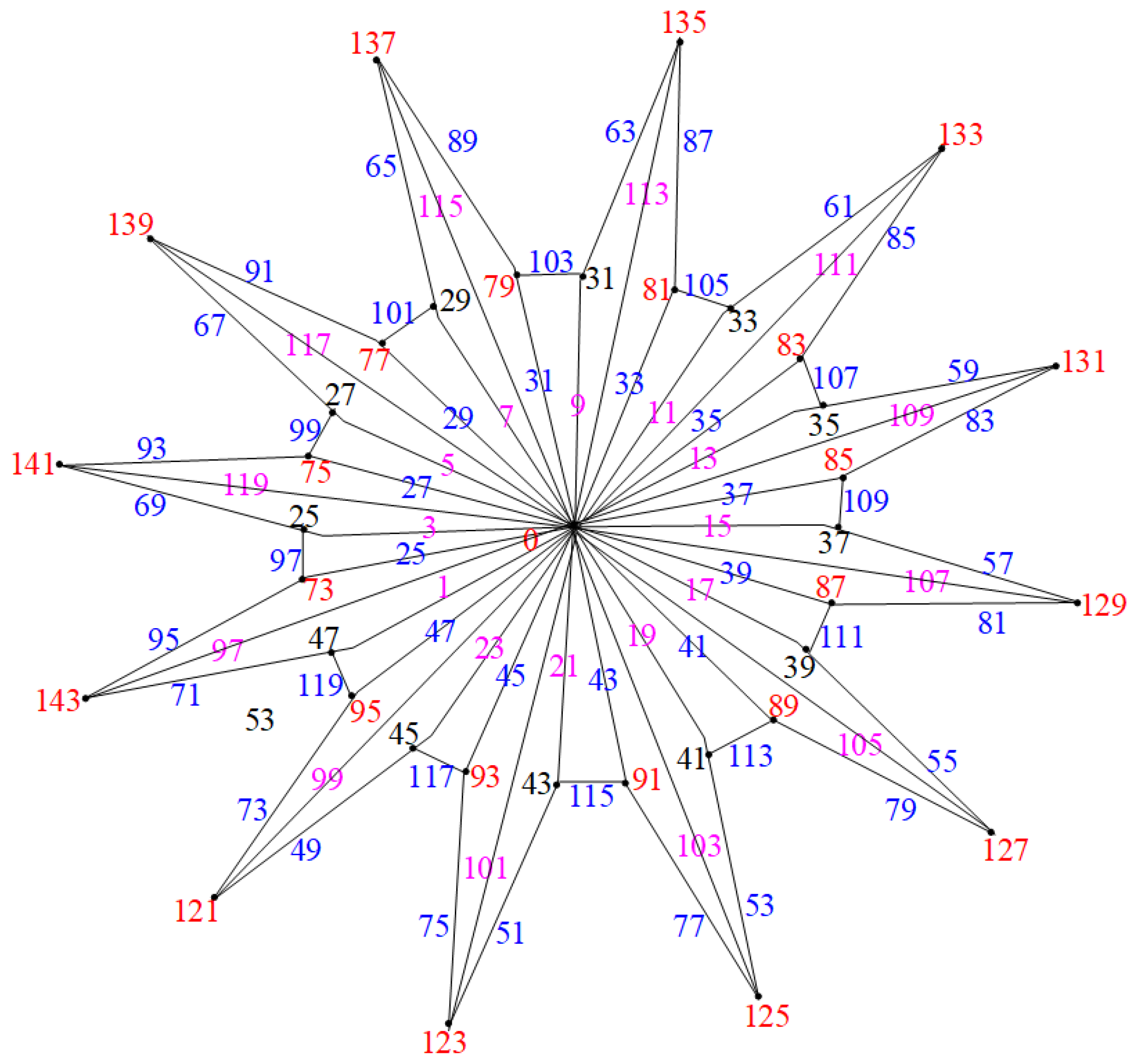
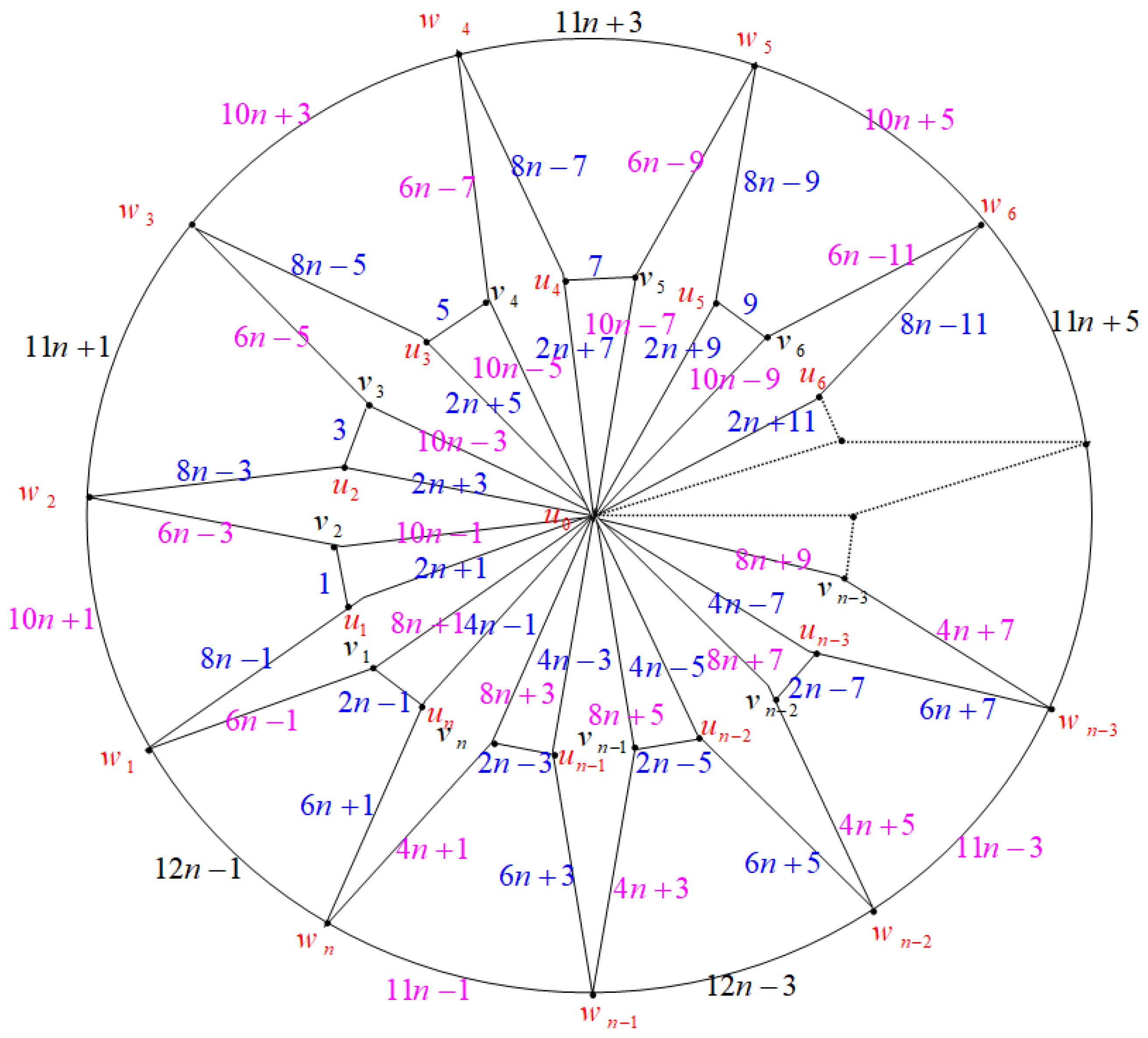
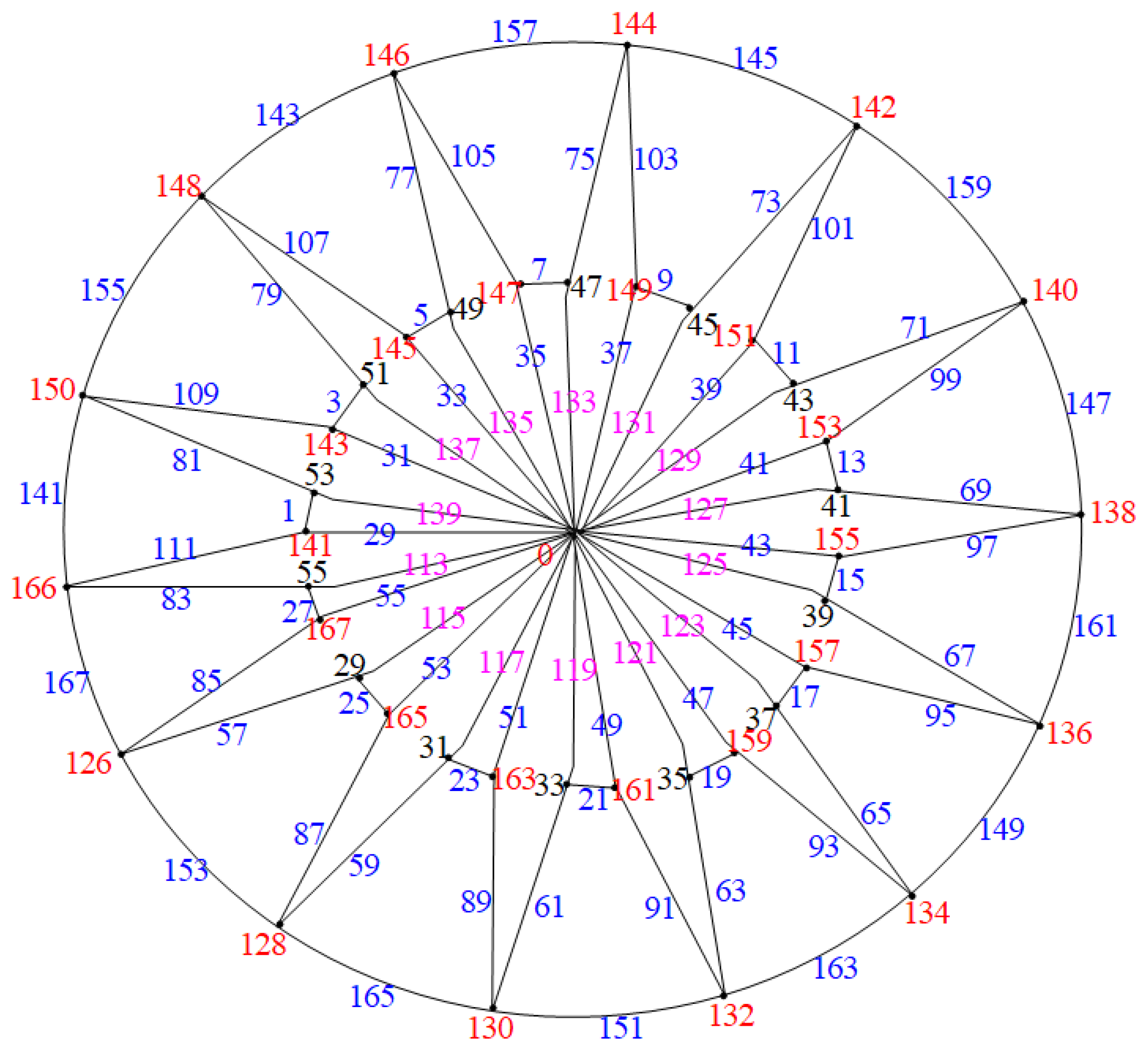
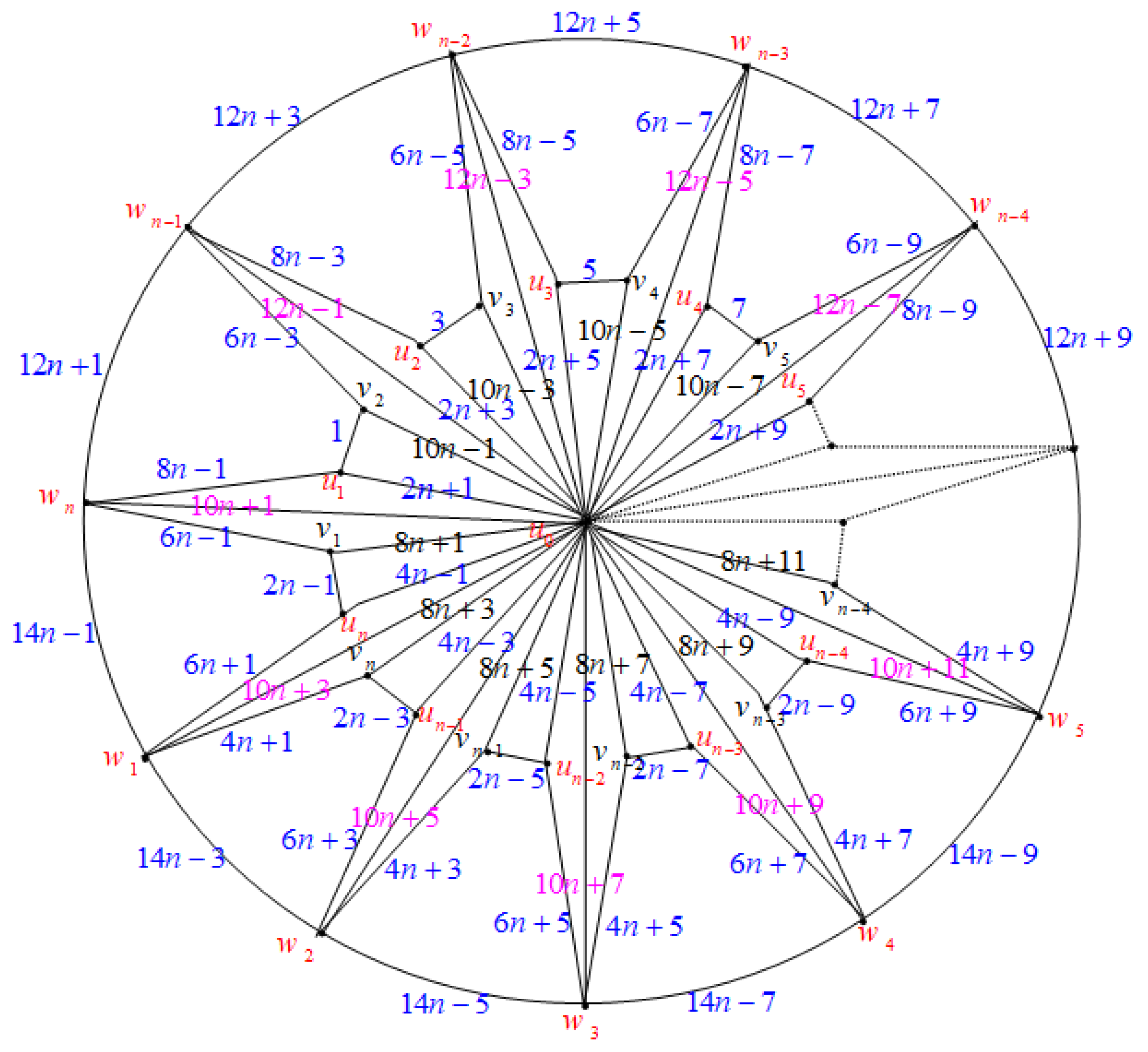
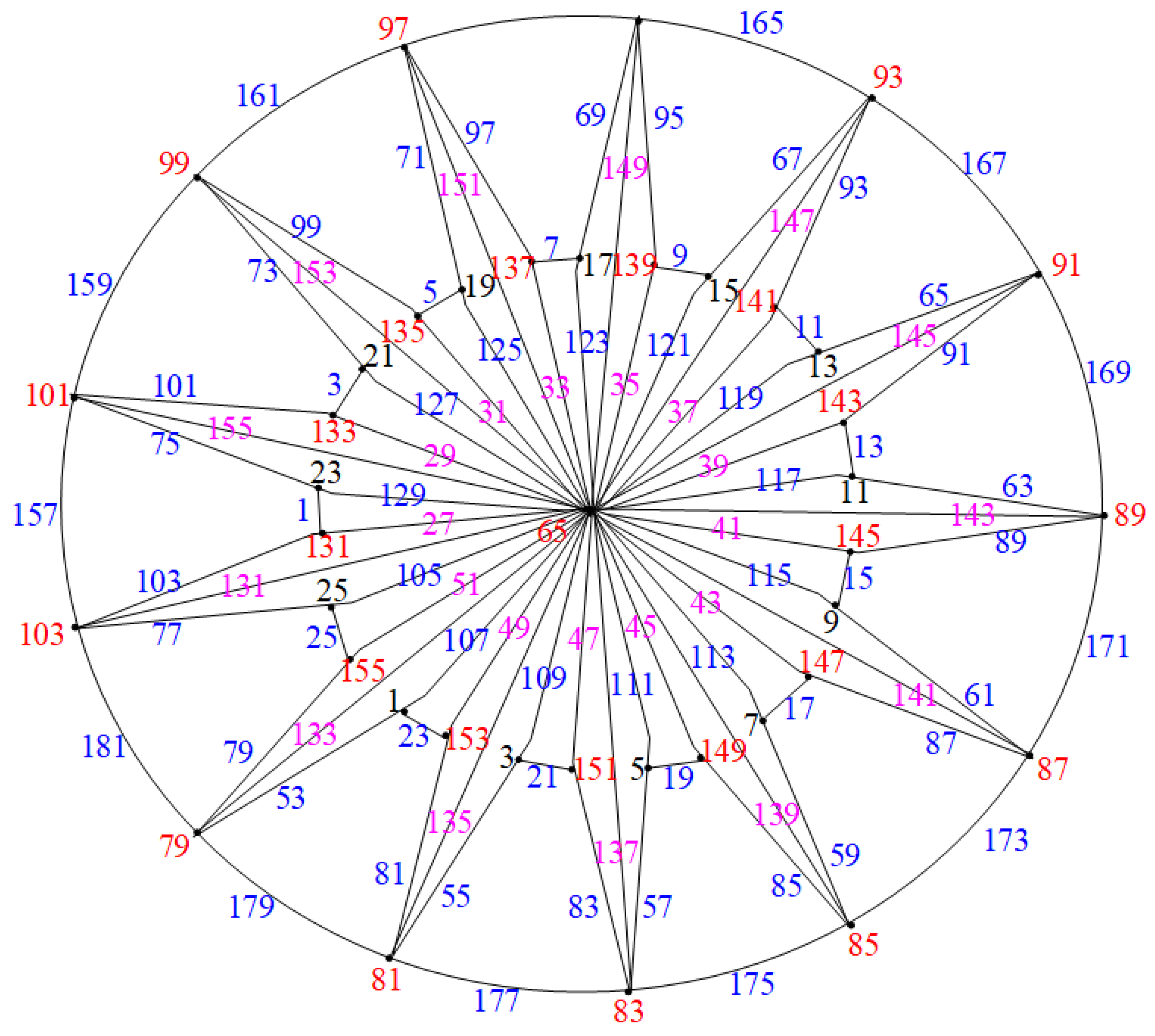
2.1. Water Wheel Graphs ($W{W}_n$ Graphs)

Definition 1. 

For $n\ge 3,$ a water wheel graph, $W{W}_n,$ is a graph with

• A vertex set $V\left(W{W}_n\right)=$$\left\{u_0\right\}\cup \left\{u_i,v_i,w_i:1\le i\le n\right\}$;
• An edge set $E\left(W{W}_n\right)=\left\{u_0{u}_i,u_0{v}_i,u_i{w}_i,v_i{w}_i:1\le i\le n\right\}\cup \left\{u_i{v}_{i+1}\right.$:$1\le i\le n-1\}\cup \left\{u_n{v}_1\right\}$.

Theorem 1. 

The water wheel graph, $W{W}_n,$ is edge odd graceful.

Proof. 

Let the vertex set of $W{W}_n$ be $\{u_0,u_1,u_2,\dots ,u_n,v_1,v_2,v_3,\dots ,v_n,w_1,w_2,w_3,\dots ,w_n\}$; then, $\left|E\left(W{W}_n\right)\right|=5n=m$. We show the edge odd labeling of these graphs in two cases.

Case (1): Consider the graph $W{W}_n$ when $n\equiv 1\mathrm{mod}\left(10\right)$, as illustrated in Figure 1.

The mapping

$$g:E\left(W{W}_n\right)\to \{1,3,\dots ,10n-1\},$$

which assigns odd integers to the edges, can be defined as follows:

$$\begin{array}{cccc}& g\left(u_0{v}_i\right)=2i-1,\hspace{0.17em}1\le i\le n;\hfill & & g\left(u_0{u}_i\right)=2n+2i-1,\hspace{0.17em}1\le i\le n;\hfill \\ & g\left(v_i{w}_i\right)=6n-2i+1,\hspace{0.17em}1\le i\le n;\hfill & & g\left(u_i{w}_i\right)=8n-2i+1,\hspace{0.17em}1\le i\le n;\hfill \\ & g\left(u_i{v}_{i+1}\right)=8n+2i-1,\hspace{0.17em}1\le i\le n-1;\hfill & & g\left(u_n{v}_1\right)=10n-1.\hfill \end{array}$$

This assigns labels to the vertices mod $\left(10n\right)$ with the following mappings:

$$\begin{array}{cccc}& g^{*}\left(u_i\right)=(8n+2i-1)\mathrm{mod}\left(10n\right),1\le i\le n;\hfill & & g^{*}\left(v_1\right)=6n-1;\hfill \\ & g^{*}\left(v_i\right)=(4n+2i-3)\mathrm{mod}\left(10n\right),2\le i\le n;\mathrm{and}\hfill \\ & g^{*}\left(w_i\right)=(4n-4i+2)\mathrm{mod}\left(10n\right),1\le i\le n.\hfill \end{array}$$

For the center vertex, we have

$$g^{*}\left(u_0\right)={\displaystyle \frac{n}{2}}(1+2n-1+2n+1+4n-1)\equiv 4n^2\equiv 4n\mathrm{mod}\left(10n\right).$$

Hence, when $n\equiv 1$(mod 10), the graphs $W{W}_n$ are edge odd graceful. To illustrate this, consider the example in Figure 2.

Case (2): Consider the graph $W{W}_n$ when $n\equiv k\mathrm{mod}\left(10\right),k\ne 1$, as illustrated in Figure 3.

The mapping

$$g:E\left(W{W}_n\right)\to \{1,3,\dots ,10n-1\},$$

which assigns odd integers to the edges, can be defined as follows:

$$\begin{array}{ccc}& g\left(u_i{v}_{i+1}\right)=2i-1,1\le i\le n-1;\hfill & \hfill g\left(u_n{v}_1\right)=2n-1;\\ & g\left(u_0{u}_i\right)=2n+2i-1,1\le i\le n;\hfill & \hfill g\left(v_i{w}_i\right)=6n-2i+1,1\le i\le n;\\ & g\left(u_i{w}_i\right)=8n-2i+1,1\le i\le n;\hfill & \hfill g\left(u_0{v}_1\right)=8n+1\mathrm{and}\\ & g\left(u_0{v}_i\right)=10n-2i+3,2\le i\le n.\hfill \end{array}$$

This assigns labels to the vertices $\mathrm{mod}\left(10n\right)$ as follows:

$$\begin{array}{cc}& g^{*}\left(u_i\right)=(2i-1)\mathrm{mod}\left(10n\right),1\le i\le n;\hfill \\ & g^{*}\left(v_i\right)=(6n-2i+1)\mathrm{mod}\left(10n\right),1\le i\le n;\hfill \\ & g^{*}\left(w_i\right)=(4n-4i+2)\mathrm{mod}\left(10n\right),1\le i\le n,\hfill \end{array}$$

and for the center vertex, we have

$$g^{*}\left(u_0\right)={\displaystyle \frac{n}{2}}(2n+1+4n-1+8n+1+10n-1)\equiv 12n^2\mathrm{mod}\left(10n\right).$$

Furthermore,

$$\begin{array}{cccc}& \mathrm{when}n\equiv 0\mathrm{mod}\left(10\right)\mathrm{or}n\equiv 5\mathrm{mod}\left(10\right),\hfill & & \mathrm{we}\mathrm{get}{g}^{*}\left(u_0\right)=0;\hfill \\ & \mathrm{when}n\equiv 2\mathrm{mod}\left(10\right)\mathrm{or}n\equiv 7\mathrm{mod}\left(10\right),\hfill & & \mathrm{we}\mathrm{get}{g}^{*}\left(u_0\right)=4n;\hfill \\ & \mathrm{when}n\equiv 3\mathrm{mod}\left(10\right)\mathrm{or}n\equiv 8\mathrm{mod}\left(10\right),\hfill & & \mathrm{we}\mathrm{get}{g}^{*}\left(u_0\right)=6n;\hfill \\ & \mathrm{when}n\equiv 4\mathrm{mod}\left(10\right)\mathrm{or}n\equiv 9\mathrm{mod}\left(10\right),\hfill & & \mathrm{we}\mathrm{get}{g}^{*}\left(u_0\right)=8n;\hfill \\ & \mathrm{when}n\equiv 6\mathrm{mod}\left(10\right),\hfill & & \mathrm{we}\mathrm{get}{g}^{*}\left(u_0\right)=2n.\hfill \end{array}$$

Hence, when $n\equiv k\left(\mathrm{mod}10\right),k\ne 1$, the graphs $W{W}_n$ are edge odd graceful. To illustrate this, consider the example in Figure 4. □

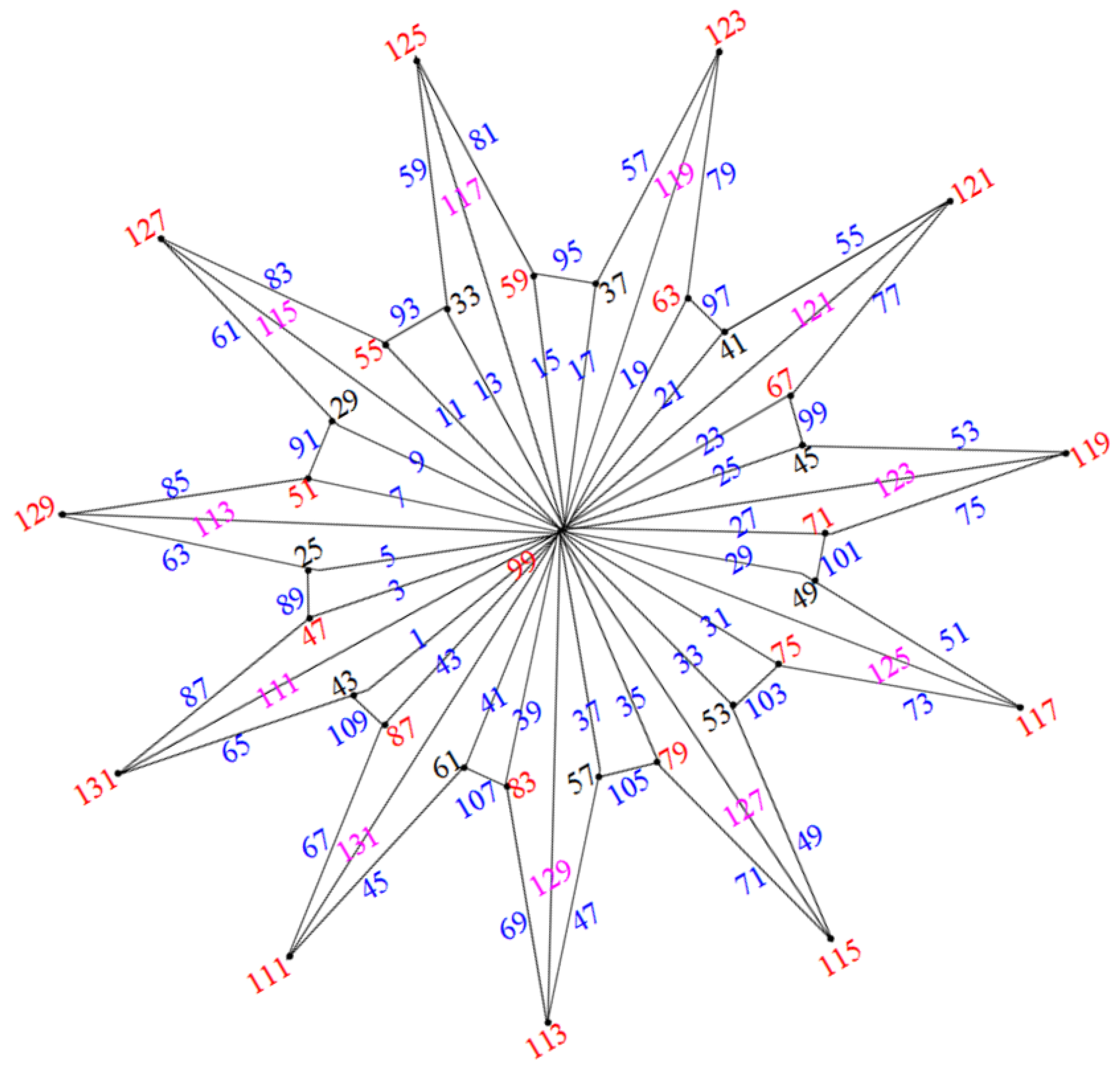
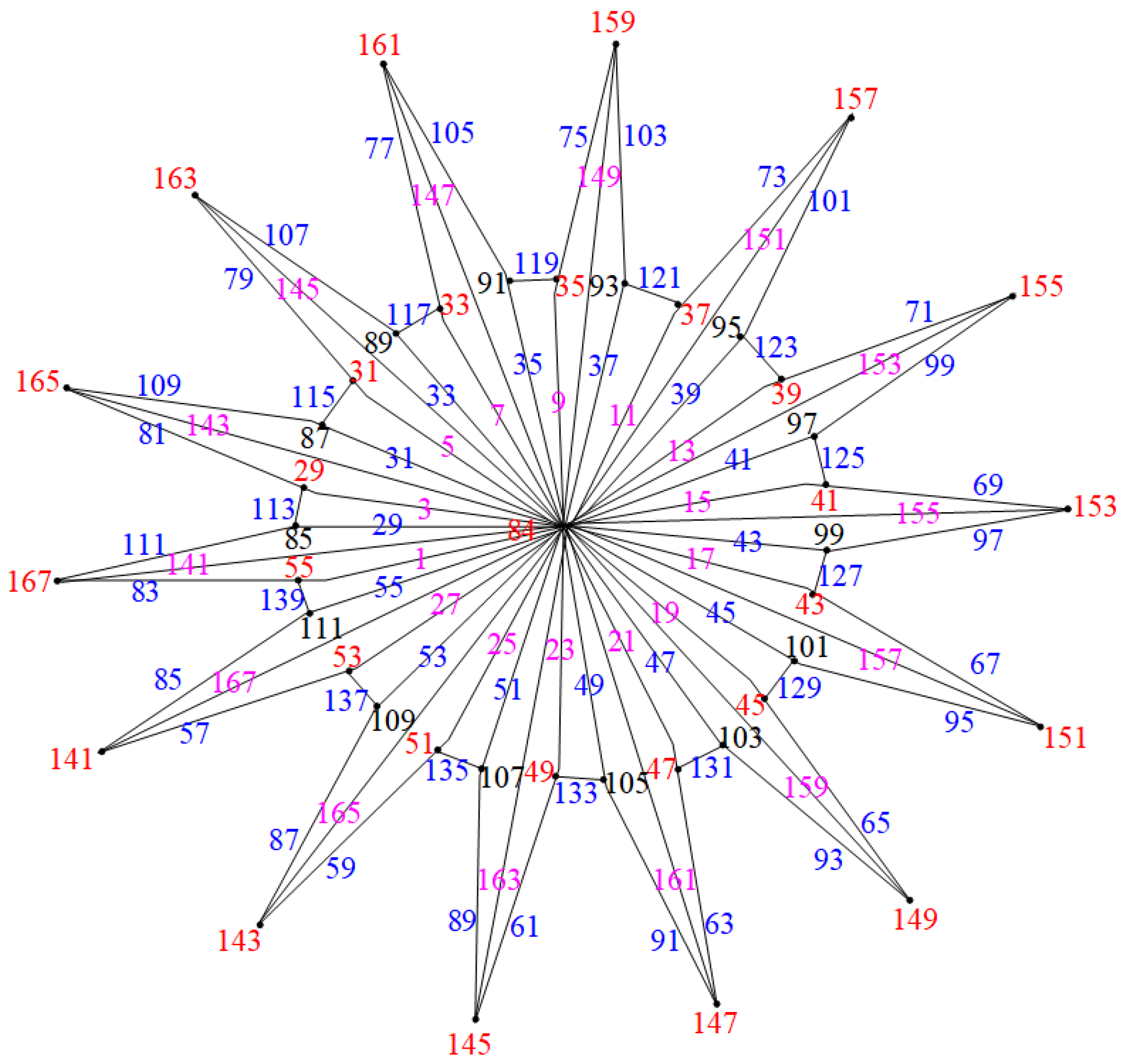
2.2. Triangulated Water Wheel Graphs ($T{W}_n$ Graphs)

Definition 2. 

For $n\ge 3$, a triangulated water wheel graph $T{W}_n$ is obtained by adding edges $u_0{w}_i,$ for all $1\le i\le n,$ to the $W{W}_n$ graph.

Theorem 2. 

Any triangulated water wheel graph, $T{W}_n,$ is edge odd graceful.

Proof. 

Let the vertex set of $T{W}_n$ be $\left\{u_0,u_1,u_2,\dots ,u_n,v_1,v_2,v_3,\dots ,v_n,w_1,w_2,w_3,\dots ,w_n\right\}$; then, $\left|E\left(T{W}_n\right)\right|=6n=m$. We show the edge odd graceful labeling of these graphs in two cases.

Case (1): Consider the graph $T{W}_n$ when n is odd, as illustrated in Figure 5.

The mapping

$$g:E\left(T{W}_n\right)\to \{1,3,\dots ,12n-1\},$$

which assigns odd integers to the edges, can be defined as follows:

$$\begin{array}{cc}& g\left(u_0{v}_i\right)=4i-3,1\le i\le n;\hfill \\ & g\left(u_0{u}_i\right)=4i-1,1\le i\le n;\hfill \\ & g\left(v_i{w}_i\right)=6n-2i+1,1\le i\le n;\hfill \\ & g\left(u_i{w}_i\right)=8n-2i+1,1\le i\le n;\hfill \\ & g\left(u_i{v}_{i+1}\right)=8n+2i-1,1\le i\le n-1;\hfill \\ & g\left(u_n{v}_1\right)=10n-1;\hfill \\ & g\left(u_0{w}_i\right)=10n+2i-1,1\le i\le n.\hfill \end{array}$$

This assigns labels to the vertices $\mathrm{mod}\left(12n\right)$ as follows:

$$\begin{array}{cc}& g^{*}\left(u_i\right)=(4n+4i-1)\left(\mathrm{mod}12n\right),1\le i\le n;\hfill \\ & g^{*}\left(v_1\right)=4n-1;\hfill \\ & g^{*}\left(v_i\right)=(2n+4i-5)\left(\mathrm{mod}12n\right),2\le i\le n;\hfill \\ & g^{*}\left(w_i\right)=(12n-2i+1)\left(\mathrm{mod}12n\right),1\le i\le n,\hfill \end{array}$$

and for the center vertex, we have

$$g^{*}\left(u_0\right)=n(1+4n-1)+{\displaystyle \frac{n}{2}}(10n+1+12n-1)\equiv 15n^2\left(\mathrm{mod}12n\right).$$

Furthermore,

$$\begin{array}{cc}& \mathrm{when}n\equiv 1\left(\mathrm{mod}4\right),\mathrm{we}\mathrm{get}{g}^{*}\left(u_0\right)=3n;\hfill \\ & \mathrm{when}n\equiv 3\left(\mathrm{mod}4\right),\mathrm{we}\mathrm{get}{g}^{*}\left(u_0\right)=9n.\hfill \end{array}$$

Hence, when n is odd, the graphs $T{W}_n$ are edge odd graceful.To illustrate this, consider the examples in Figure 6 and Figure 7.

Case (2): Consider the graph $T{W}_n$ when n is even, as illustrated in Figure 8.

The mapping

$$g:E\left(T{W}_n\right)\to \{1,3,\dots ,12n-1\},$$

which assigns odd integers to the edges, can be defined as follows:

$$\begin{array}{cc}& g\left(u_0{v}_i\right)=2i-1,1\le i\le n;\hfill \\ & g\left(u_0{u}_i\right)=2n+2i-1,1\le i\le n;\hfill \\ & g\left(v_i{w}_i\right)=6n-2i+1,1\le i\le n;\hfill \\ & g\left(u_i{w}_i\right)=8n-2i+1,1\le i\le n;\hfill \\ & g\left(u_i{v}_{i+1}\right)=8n+2i-1,1\le i\le n-1;\hfill \\ & g\left(u_n{v}_1\right)=10n-1;\hfill \\ & g\left(u_0{w}_i\right)=10n+2i-1,1\le i\le n.\hfill \end{array}$$

This assigns labels to the vertices $\mathrm{mod}\left(12n\right)$ as follows:

$$\begin{array}{cc}& g^{*}\left(u_i\right)=(6n+2i-1)\left(\mathrm{mod}12n\right),\hspace{0.17em}1\le i\le n;\hfill \\ & g^{*}\left(v_1\right)=4n-1;\hfill \\ & g^{*}\left(v_i\right)=(2n+2i-3)\left(\mathrm{mod}12n\right),\hspace{0.17em}2\le i\le n;\hfill \\ & g^{*}\left(w_i\right)=(12n-2i+1)\left(\mathrm{mod}12n\right),\hspace{0.17em}1\le i\le n,\hfill \end{array}$$

and for the center vertex, we have

$$g^{*}\left(u_0\right)={\displaystyle \frac{n}{2}}(1+2n-1)+{\displaystyle \frac{n}{2}}(2n+1+4n-1)+{\displaystyle \frac{n}{2}}(10n+1+12n-1)\equiv 15n^2\left(\mathrm{mod}12n\right).$$

Furthermore,

$$\begin{array}{cc}& \mathrm{when}n\equiv 0\left(\mathrm{mod}4\right),\mathrm{we}\mathrm{obtain}{g}^{*}\left(u_0\right)=0;\hfill \\ & \mathrm{when}n\equiv 2\left(\mathrm{mod}4\right),\mathrm{we}\mathrm{obtain}{g}^{*}\left(u_0\right)=6n.\hfill \end{array}$$

Hence, when n is even, the graphs $T{W}_n$ are edge odd graceful. To illustrate this, consider the examples in Figure 9 and Figure 10. □

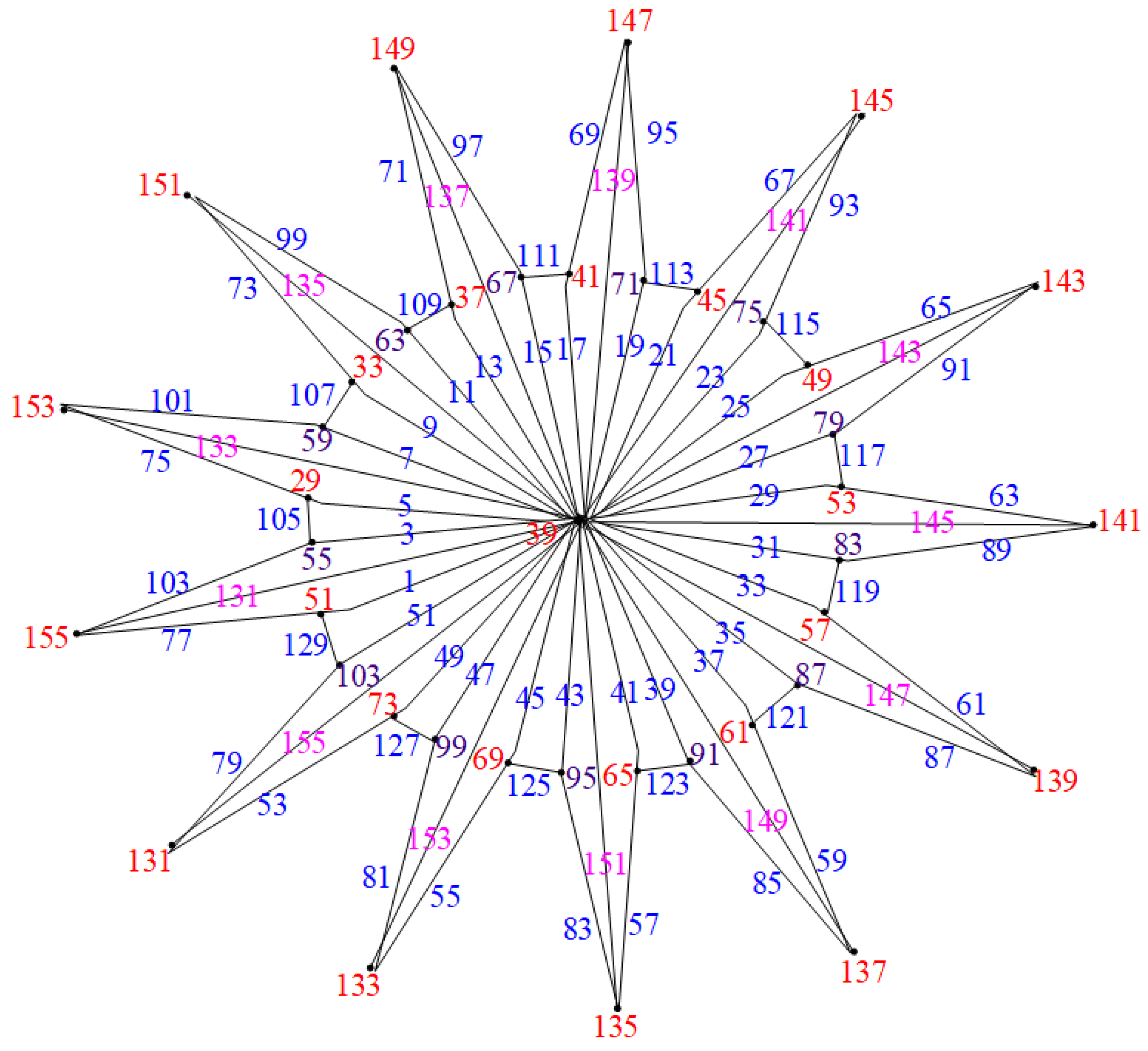
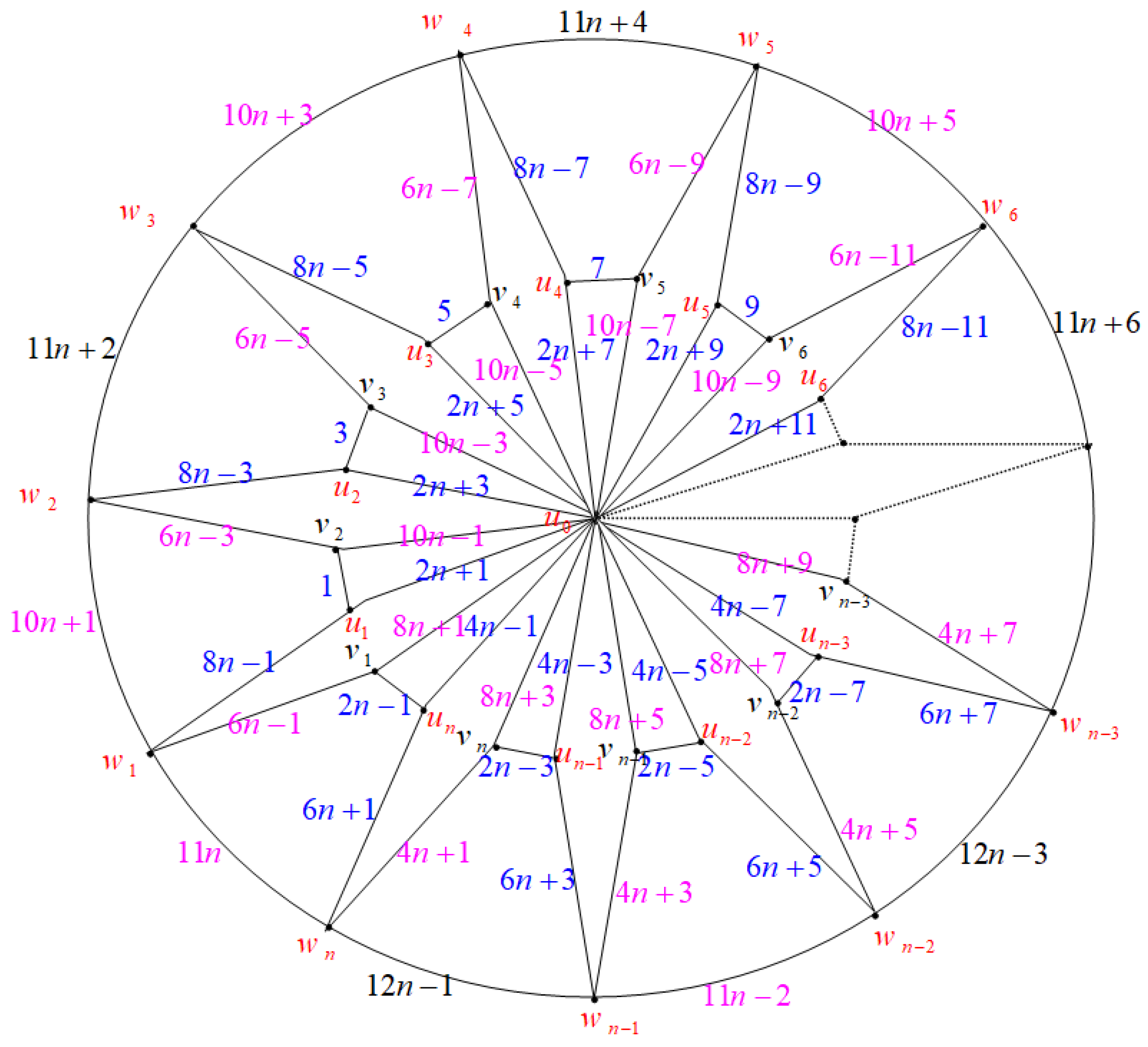
2.3. Closed Water Wheel Graphs ($C{W}_n$ Graphs)

Definition 3. 

For $n\ge 3,$ a closed water wheel graph, $C{W}_n,$ is obtained by adding edges $w_1{w}_n$ and $w_i{w}_{i+1},1\le$$i\le n-1$, to the $W{W}_n$ graph.

Theorem 3. 

Any closed water wheel graph, $C{W}_n,$ is edge odd graceful.

Proof. 

Let the vertex set of $C{W}_n$ be $\left\{u_0,u_1,u_2,\dots ,u_n,v_1,v_2,v_3,\dots ,v_n,w_1,w_2,w_3,\dots ,w_n\right\}$; then, $\left|E\left(C{W}_n\right)\right|=6n=m$. We show the edge odd graceful labeling of these graphs in two cases.

Case (1): Consider the graph $C{W}_n$ when n is odd, as illustrated in Figure 11.

The mapping

$$g:E\left(C{W}_n\right)\to \{1,3,\dots ,12n-1\},$$

which assigns odd integers to the edges, can be defined as follows:

$$\begin{array}{cccc}& g\left(u_i{v}_{i+1}\right)=2i-1,\hspace{0.17em}1\le i\le n-1;\hfill & & g\left(u_n{v}_1\right)=2n-1;\hfill \\ & g\left(u_0{u}_i\right)=2n+2i-1,\hspace{0.17em}1\le i\le n;\hfill & & g\left(v_i{w}_i\right)=6n-2i+1,\hspace{0.17em}1\le i\le n;\hfill \\ & g\left(u_i{w}_i\right)=8n-2i+1,\hspace{0.17em}1\le i\le n;\hfill & & g\left(u_0{v}_1\right)=8n+1;\hfill \\ & g\left(u_0{v}_i\right)=10n-2i+3,\hspace{0.17em}2\le i\le n;\hfill & & g\left(w_{2i-1}{w}_{2i}\right)=10n+2i-1,\hspace{0.17em}1\le i\le {\displaystyle \frac{n+1}{2}};\hfill \\ & g\left(w_{2i}{w}_{2i+1}\right)=11n+2i,\hspace{0.17em}1\le i\le {\displaystyle \frac{n-1}{2}};\hfill & & g\left(w_n{w}_1\right)=11n.\hfill \end{array}$$

This assigns labels to the vertices $\mathrm{mod}\left(12n\right)$ as follows:

$$\begin{array}{cc}& g^{*}\left(u_i\right)=(10n+2i-1)\left(\mathrm{mod}12n\right),\hspace{0.17em}1\le i\le n;\hfill \\ & g^{*}\left(v_i\right)=(4n-2i+1)\left(\mathrm{mod}12n\right),\hspace{0.17em}1\le i\le \mathrm{and}\hfill \\ & g^{*}\left(w_i\right)=(11n-2i+1)\left(\mathrm{mod}12n\right),\hspace{0.17em}1\le i\le n,\hfill \end{array}$$

and for the center vertex, we have

$$g^{*}\left(u_0\right)={\displaystyle \frac{n}{2}}(2n+1+4n-1)+{\displaystyle \frac{n}{2}}(8n+1+10n-1)\equiv 12n^2\left(\mathrm{mod}12n\right)\equiv 0.$$

Hence, when n is odd, the graphs $C{W}_n$ are edge odd graceful. To illustrate this, consider the example in Figure 12.

Case (2): Consider the graph $C{W}_n$ when n is even, as illustrated in Figure 13.

The mapping

$$g:E\left(C{W}_n\right)\to \{1,3,\dots ,12n-1\},$$

which assigns odd integers to the edges, can be defined as follows:

$$\begin{array}{cccc}& g\left(u_i{v}_{i+1}\right)=2i-1,1\le i\le n-1;\hfill & & g\left(u_n{v}_1\right)=2n-1;\hfill \\ & g\left(u_0{u}_i\right)=2n+2i-1,1\le i\le n;\hfill & & g\left(v_i{w}_i\right)=6n-2i+1,1\le i\le n;\hfill \\ & g\left(u_i{w}_i\right)=8n-2i+1,1\le i\le n;\hfill & & g\left(u_0{v}_i\right)=10n-2i+3,2\le i\le n,\hfill \\ & g\left(u_0{v}_1\right)=8n+1;\hfill & & g\left(w_{2i-1}{w}_{2i}\right)=10n+2i-1,1\le i\le {\displaystyle \frac{n}{2}};\hfill \\ & g\left(w_{2i}{w}_{2i+1}\right)=11n+2i-1,1\le i\le {\displaystyle \frac{n}{2}}-1;\hfill & & g\left(w_n{w}_1\right)=12n-1.\hfill \end{array}$$

This assigns labels to the vertices $\mathrm{mod}\left(12n\right)$ as follows:

$$\begin{array}{cc}& g^{*}\left(u_i\right)=(10n+2i-1)\left(\mathrm{mod}12n\right),1\le i\le n;\hfill \\ & g^{*}\left(v_i\right)=(4n-2i+1)\left(\mathrm{mod}12n\right),1\le i\le n;\hfill \\ & g^{*}\left(w_1\right)=12n-2;g^{*}\left(w_i\right)=(11n-2i)\left(\mathrm{mod}12n\right),2\le i\le n,\hfill \end{array}$$

and for the center vertex, we have

$$g^{*}\left(u_0\right)={\displaystyle \frac{n}{2}}(2n+1+4n-1)+{\displaystyle \frac{n}{2}}(8n+1+10n-1)\equiv 15n^2\left(\mathrm{mod}12n\right)\equiv 0.$$

Hence, when n is even, the graphs $C{W}_n$ are edge odd graceful. To illustrate this, consider the example in Figure 14. □

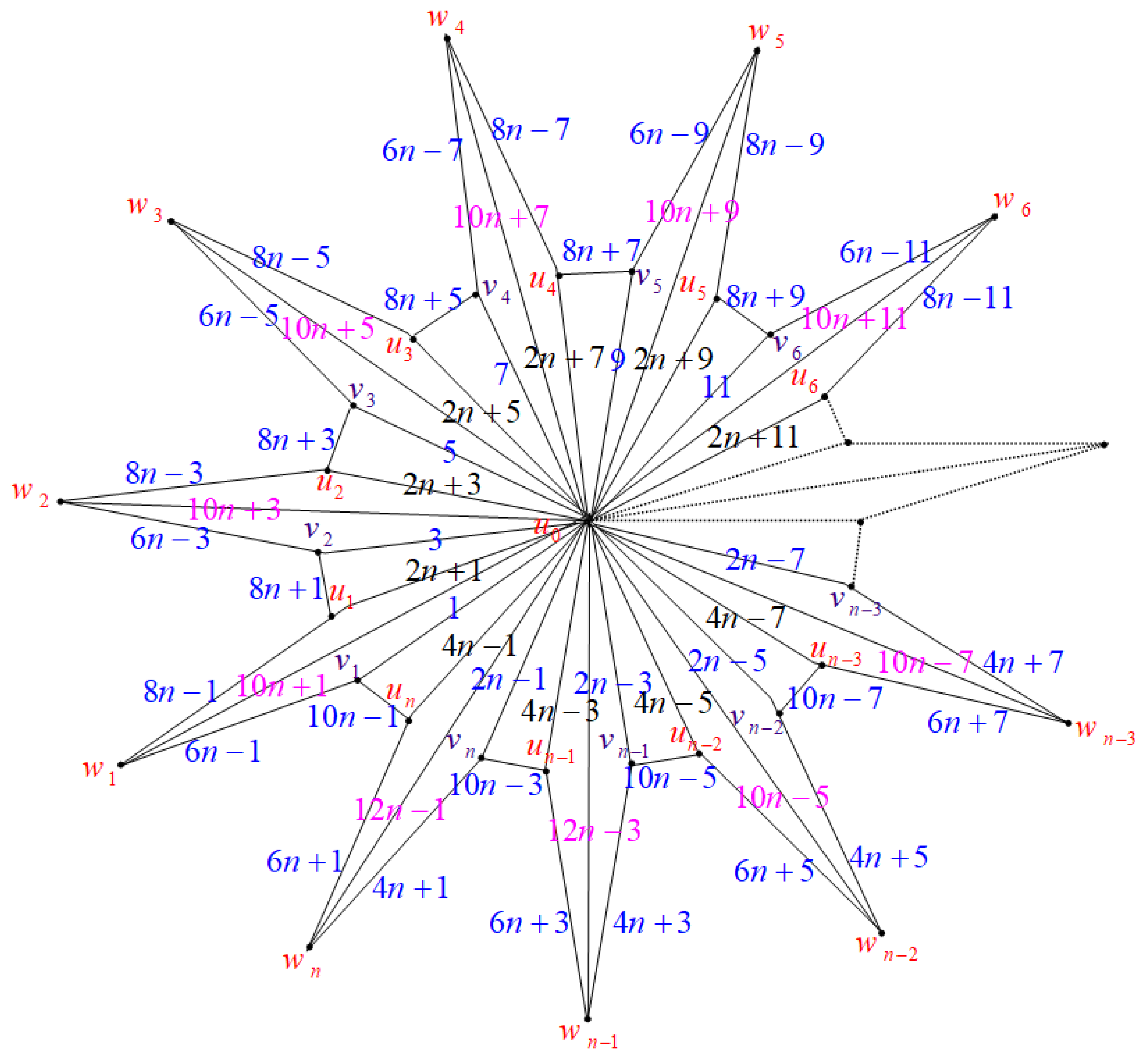
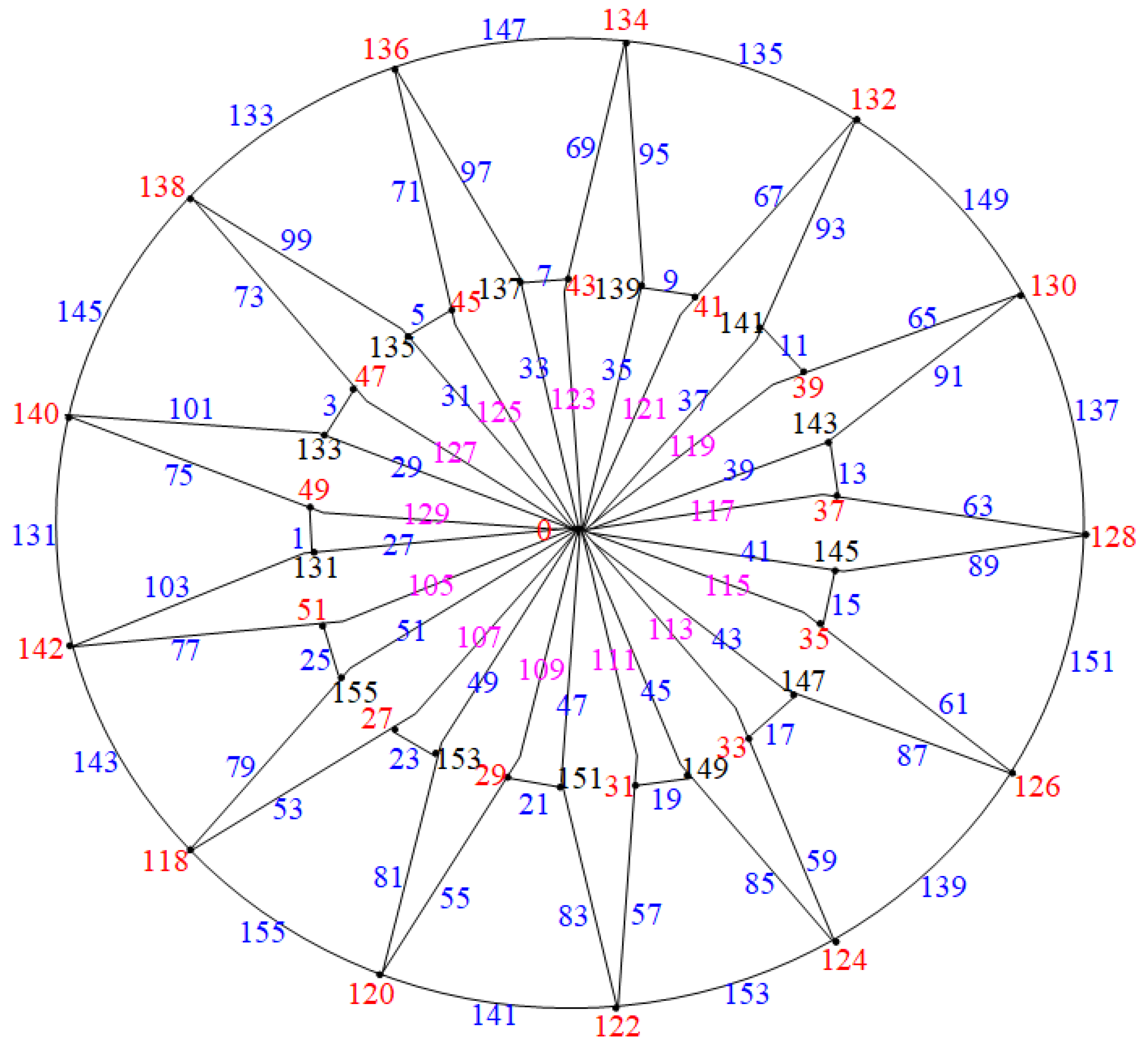
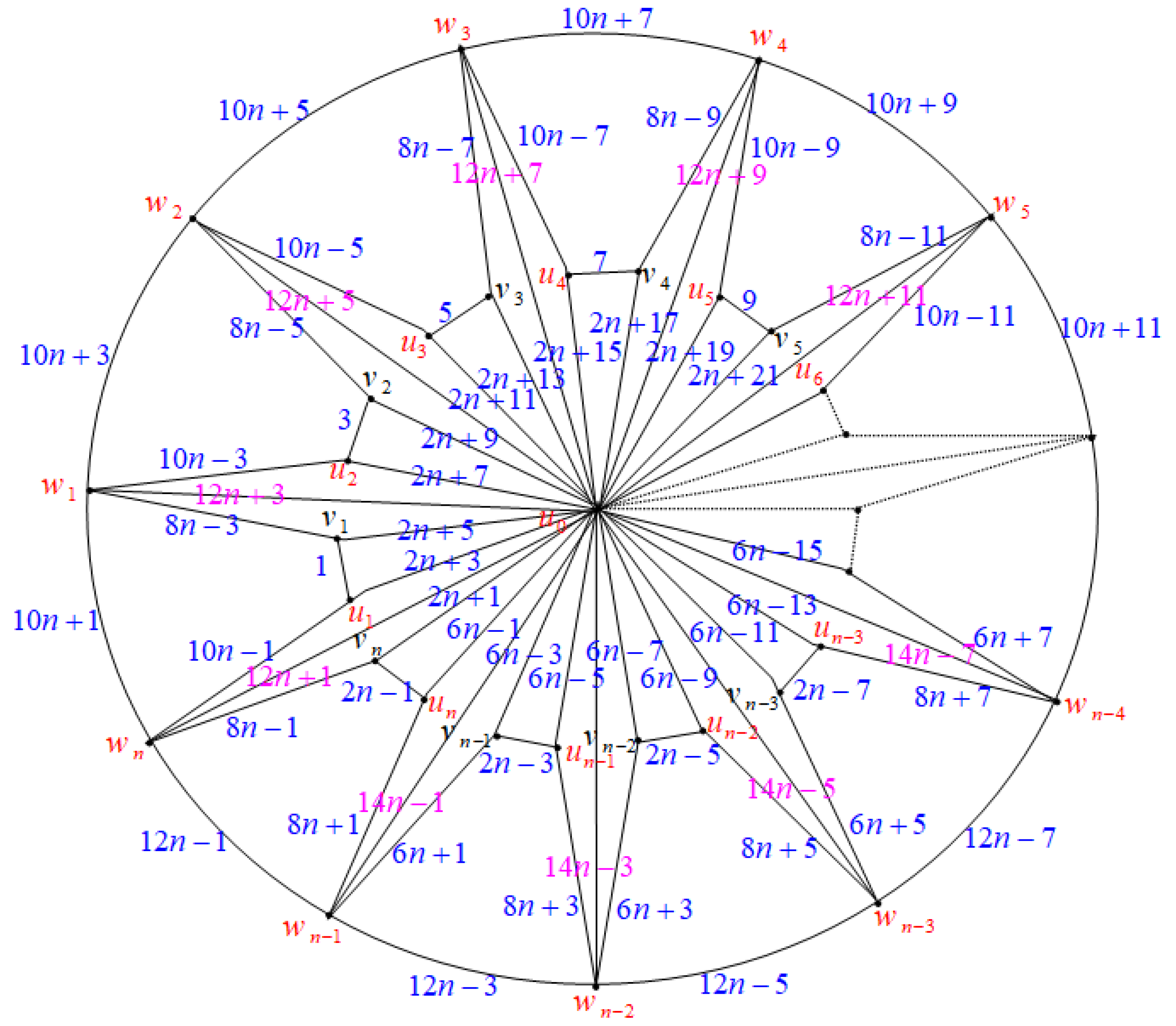
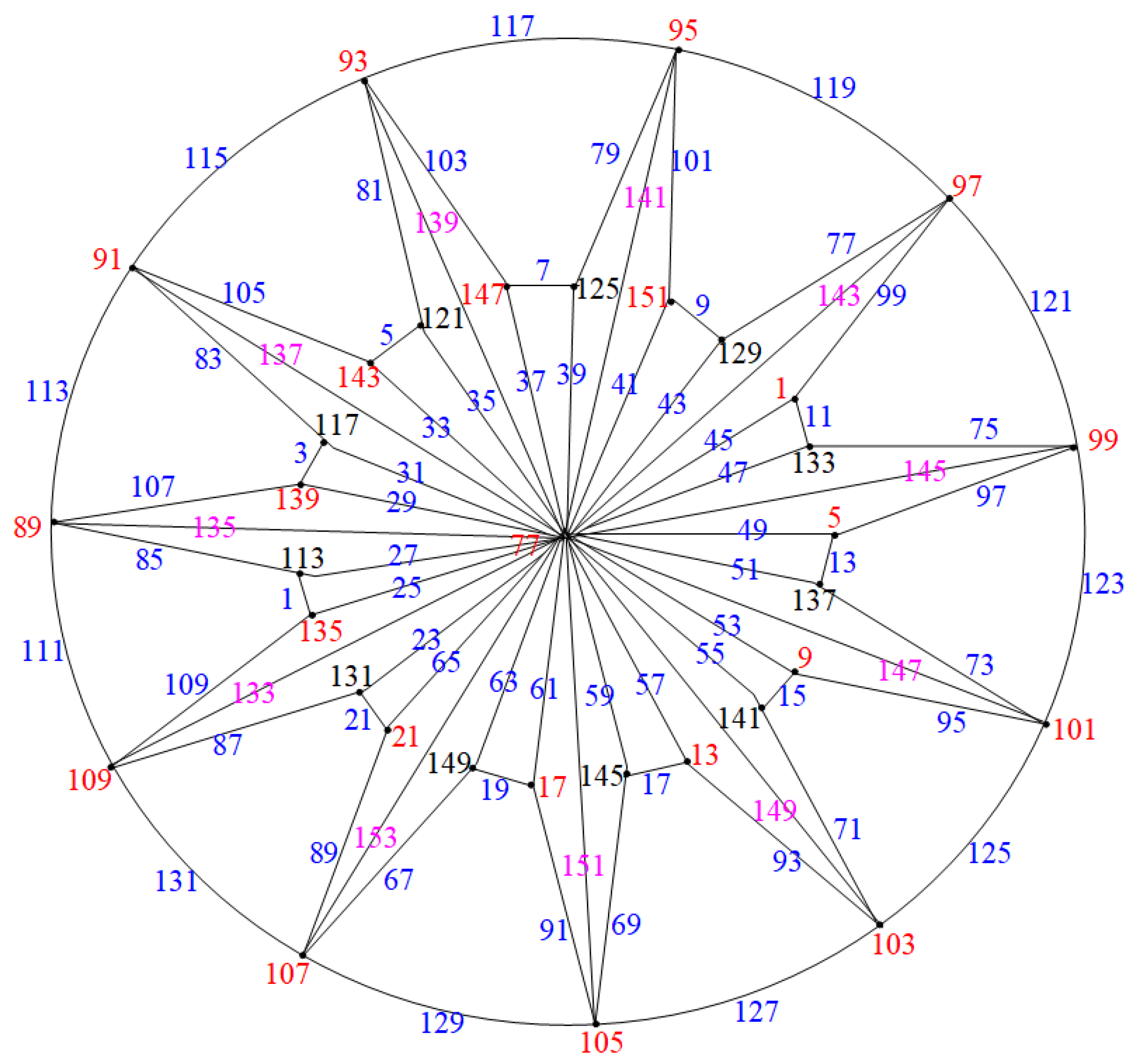
2.4. Closed Triangulated Water Wheel Graphs ($C{T}_n$ Graphs)

Definition 4. 

For $n\ge 3,$ a closed triangulated water wheel graph, $C{T}_n,$ is obtained by adding edges $w_1{w}_n$ and $w_i{w}_{i+1},\hspace{0.17em}1\le$$i\le n-1$, to the $T{W}_n$ graph.

Theorem 4. 

Any closed triangulated water wheel graph, $C{T}_n,$ is edge odd graceful.

Proof. 

Let the vertex set of $C{T}_n$ be $\{u_0,u_1,u_2,\dots ,u_n,v_1,v_2,v_3,\dots ,v_n,w_1,w_2,w_3,\dots ,w_n\}$; then, $\left|E\left(C{T}_n\right)\right|=7n=m$. We show the edge odd graceful labeling of these graphs in two cases.

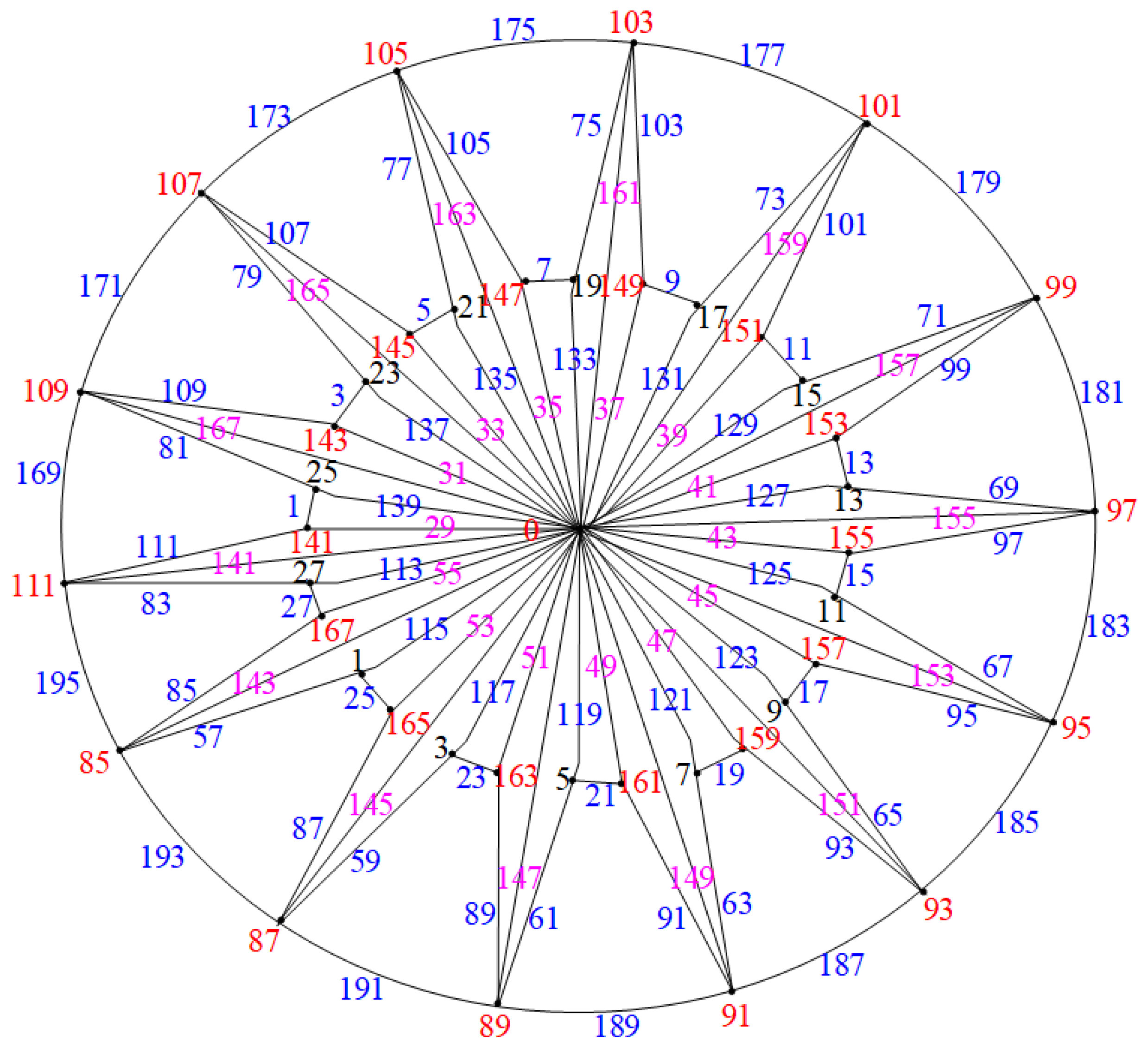
• Case (1): Consider the graph $C{T}_n$ when $n\equiv 11\mathrm{mod}14$, as illustrated in Figure 15.

The mapping

$$g:E\left(C{T}_n\right)\to \{1,3,\dots ,14n-1\},$$

which assigns odd integers to the edges, can be defined as follows:

$$\begin{array}{cccc}& g\left(u_i{v}_i\right)=2i-1,\hspace{0.17em}1\le i\le n;\hfill & & g\left(u_0{u}_i\right)=2n+4i-1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(u_0{u}_n\right)=6n-1;\hfill & & g\left(u_0{v}_i\right)=2n+4i+1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(u_0{v}_n\right)=2n+1;\hfill & & g\left(v_{n-i}{w}_{n-i}\right)=6n+2i-1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(v_n{w}_n\right)=8n-1;\hfill & & g\left(u_{i+1}{w}_i\right)=10n-2i-1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(u_n{w}_{n-1}\right)=8n+1;\hfill & & g\left(w_i{w}_{i+1}\right)=10n+2i+1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(w_1{w}_n\right)=10n+1;\hfill & & g\left(u_0{w}_i\right)=12n+2i+1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(u_0{w}_n\right)=12n+1.\hfill \end{array}$$

This assigns labels to the vertices $\mathrm{mod}\left(14n\right)$ as follows:

$$\begin{array}{cc}& g^{*}\left(u_i\right)=(12n+4i-1)\left(\mathrm{mod}14n\right),1\le i\le n-1,\hfill \\ & g^{*}\left(u_n\right)=2n-1;g^{*}\left(v_i\right)=(10n+4i-1)\left(\mathrm{mod}14n\right),1\le i\le n-1;\hfill \\ & g^{*}\left(v_n\right)=12n-1\mathrm{and}{g}^{*}\left(w_i\right)=(8n+2i-1)\left(\mathrm{mod}14n\right),1\le i\le n,\hfill \end{array}$$

and for the center vertex, we have

$$g^{*}\left(u_0\right)={\displaystyle \frac{n}{2}}(12n+1+14n-1)+n(2n+1+6n-1)\equiv 21n^2\left(\mathrm{mod}14n\right)\equiv 7n.$$

Hence, when $n\equiv 11\mathrm{mod}14$, the graphs $C{T}_n$ are edge odd graceful. To illustrate this, consider the example in Figure 16.

Case (2): Consider the graph $C{T}_n$ when $n\equiv k\mathrm{mod}14,k\ne 11$, as illustrated in Figure 17.

The mapping

$$g:E\left(C{T}_n\right)\to \{1,3,\dots ,14n-1\},$$

which assigns odd integers to the edges, can be defined as follows:

$$\begin{array}{cc}& g\left(u_i{v}_{i+1}\right)=2i-1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(u_n{v}_1\right)=2n-1;\hfill \\ & g\left(u_0{u}_i\right)=2n+2i-1,\hspace{0.17em}1\le i\le n;\hfill \\ & g\left(v_{n-(i-1)}{w}_i\right)=4n+2i-1,\hspace{0.17em}1\le i\le n;\hfill \\ & g\left(u_{n-(i-1)}{w}_i\right)=6n+2i-1,\hspace{0.17em}1\le i\le n;\hfill \\ & g\left(u_0{v}_1\right)=8n+1,\hfill \\ & g\left(u_0{v}_{n-(i-1)}\right)=8n+2i+1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(u_0{w}_n\right)=10n+1;\hfill \\ & g\left(u_0{w}_i\right)=10n+2i+1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(w_i{w}_{i+1}\right)=14n-2i-1,\hspace{0.17em}1\le i\le n-1;\hfill \\ & g\left(w_n{w}_1\right)=14n-1.\hfill \end{array}$$

This assigns labels to the vertices $\mathrm{mod}\left(14n\right)$ as follows:

$$\begin{array}{cc}& g^{*}\left(u_i\right)=(10n+2i-1)\left(\mathrm{mod}14n\right),1\le i\le n;\hfill \\ & g^{*}\left(v_i\right)=(2n-2i+1)\left(\mathrm{mod}14n\right),1\le i\le n\mathrm{and}\hfill \\ & g^{*}\left(w_i\right)=(6n+2i-1)\left(\mathrm{mod}14n\right),1\le i\le n,\hfill \end{array}$$

and for the center vertex, we have

$$\begin{array}{cc}& g^{*}\left(u_0\right)={\displaystyle \frac{n}{2}}(2n+1+4n-1)+{\displaystyle \frac{n}{2}}(8n+1+10n-1)+{\displaystyle \frac{n}{2}}(10n+1+12n-1)\equiv \hfill \\ & 23n^2\left(\mathrm{mod}14n\right).\hfill \end{array}$$

Furthermore,

$$\begin{array}{cccc}& n\equiv 0\mathrm{mod}14,g^{*}\left(u_0\right)=0;\hfill & & n\equiv 1\mathrm{mod}14,g^{*}\left(u_0\right)=9n;\hfill \\ & n\equiv 2\mathrm{mod}14,g^{*}\left(u_0\right)=4n;\hfill & & n\equiv 3\mathrm{mod}14,g^{*}\left(u_0\right)=13n;\hfill \\ & n\equiv 4\mathrm{mod}14,g^{*}\left(u_0\right)=8n;\hfill & & n\equiv 5\mathrm{mod}14,g^{*}\left(u_0\right)=3n;\hfill \\ & n\equiv 6\mathrm{mod}14,g^{*}\left(u_0\right)=12n;\hfill & & n\equiv 7\mathrm{mod}14,g^{*}\left(u_0\right)=7n;\hfill \\ & n\equiv 8\mathrm{mod}14,g^{*}\left(u_0\right)=2n;\hfill & & n\equiv 9\mathrm{mod}14,g^{*}\left(u_0\right)=11n;\hfill \\ & n\equiv 10\mathrm{mod}14,g^{*}\left(u_0\right)=6n;\hfill & & n\equiv 12\mathrm{mod}14,g^{*}\left(u_0\right)=10n;\hfill \\ & n\equiv 13\mathrm{mod}14,g^{*}\left(u_0\right)=5n.\hfill \end{array}$$

Hence, when $n\equiv k\mathrm{mod}14,k\ne 11$, the graphs $C{T}_n$ are edge odd graceful. To illustrate this, consider the examples in Figure 18 and Figure 19. □

3. Conclusions

This study contributes to the current research trend in the field of graph labeling, specifically focusing on edge graceful labeling. It introduces novel classes of graphs, namely water wheel graphs, $W{W}_n$; closed water wheel graphs, $C{W}_n$; triangulated water wheel graphs, $T{W}_n$; and closed triangulated water wheel graphs, $C{T}_n$. Additionally, this study provides precise criteria for the property of edge odd gracefulness in these graphs.