A Systematic Overview of Fuzzy-Random Option Pricing in Discrete Time and Fuzzy-Random Binomial Extension Sensitive Interest Rate Pricing
Abstract
:1. Introduction
1.1. Preliminary Considerations
- Fuzzy random option pricing (FROP). Broadly, it is based on traditional option pricing models, with the uncertainty in various parameters, such as volatility, the observed price of the underlying asset, or discount rates, being represented via fuzzy numbers (FNs) [20].
- Option pricing with Sugeno’s fuzzy measures and Choquet’s integral. By integrating these analytical tools with traditional option pricing formulas, this approach enables the modeling of Knightian uncertainty. It addresses market friction issues such as liquidity shortages and the risk of issuer defaults [22].
- The fuzzy pay-off method [23] is centered around real option pricing. It is undoubtedly one of the most modern approaches in fuzzy option pricing, as the first works date back to the late 2000s.
- Nonparametric option pricing. Contributions in this stream leverage tools such as fuzzy neural networks and fuzzy expert systems for option pricing, capitalizing on their ability to serve as universal function approximators [21].
1.2. Research Objectives
2. A Systematic Bibliographical Revision of Fuzzy-Random Option Pricing in Discrete Time
2.1. Materials and Methods

| Reference | Year | Moves Calibration | Uncertain Parameters | Option Type | Shape of the Fuzzy Quantities |
|---|---|---|---|---|---|
| Yoshida [34] | 2003 | Cox et al. [16] | Moves | American style | TFNs |
| Muzzioli and Torricelli [35] | 2004 | Up and down moves may be independent and following Cox et al. [16] | Moves | Application to stock option markets/European style | TFNs |
| Lee et al. [36] | 2005 | Cox et al. [16] | Moves | Stock market application/European style | Triangular and symmetric FNs |
| Buckley and Eslami [37] | 2007 | Moves are calibrated from a symmetric ± a% | Subjacent asset price, strike price, discount rate, and moves | European style | TFNs |
| Muzzioli and Reynaerts [38] | 2007 | Moves are independent | Moves | European style | TFNs |
| Buckley and Eslami [39] | 2008 | Moves are calibrated from a symmetric ± a% | Initial asset price, strike price, interest rate, and moves | European style | TFNs |
| Muzzioli and Reynaerts [40] | 2008 | Cox et al. [16] | Moves | American style | Trapezoidal/TFNs |
| Liao and Ho [41] | 2010 | Moves may be independent and following Cox et al. [16] | Initial asset price and moves | Real options/capital budgeting | TFNs |
| Wang, Wang, and Watada [42] | 2010 | Cox et al. [16] | Cash-flows and strike price | Real options/capital budgeting | TFNs |
| Zmeskal [43] | 2010 | Cox et al. [16], but the use of alternatives such as Rendleman and Bartter [17] is suggested | Initial asset price, strike price, interest rate, and moves | American/Value of a company | TrFNs |
| Tolga, Kahraman, and Demircan [44] | 2010 | Trinomial moves are calibrated with [45] | Present value of cash-flows. Moves and probabilities are crisp | Real options/capital budgeting | TrFNs |
| Allenotor and Thulasiram [46] | 2011 | Trinomial moves are calibrated with [45] | Present value of cash-flows. Moves and probabilities are crisp | Real options/capital budgeting | TrFNs/and trapezoidal linguistic variables |
| Ho and Liao [47] | 2011 | Moves can be independently calibrated, but with Cox et al. [16] | Strike price and moves | Real options by taxonomy | TFNs |
| Yu et al. [48] | 2011 | Cox et al. [16] | Moves | European | TFNs |
| Elahi and Azziz [49] | 2012 | Moves may be independent | Price, strike price, and moves | Asian financial options | Not defined |
| Tolga, Tuysuz, and Kahraman [50] | 2013 | Trinomial moves are calibrated with [45] | Present value of cash-flows. Moves and probabilities are crisp | Real options/capital budgeting | TrFNs |
| Cruz-Aranda, Ortiz, and Cabrera-Llanos [51] | 2014 | Cox et al. [16] | Moves | Real options/capital budgeting | TFNs |
| Muzzioli and de Baets [20] | 2016 | Review on fuzzy-random option pricing | Stock markets | ---- | |
| Anzilli and Facchinetti [52] | 2017 | Cox et al. [16] | Moves | Real options/life insurance guarantees | TFNs |
| Anzilli, Facchinetti, and Pirotti [53] | 2018 | Cox et al. [16] | Moves | Life insurance guarantees | Adaptive FNs |
| Xu, Liu, and Xu [54] | 2018 | Cox et al. [16] | Recovery rate and moves | Vulnerable options of American style | TFNs |
| Zhang and Watada [55] | 2018 | Cox et al. [16] | Moves | American options on stock indices | Adaptive FNs |
| D’Amato et al. [56] | 2019 | Moves are independently fitted | Moves | Real options/capital budgeting | TFNs |
| Cruz-Aranda and Terán-Bustamente [57] | 2019 | Cox et al. [16] | Moves | Real options/capital budgeting | TFNs |
| Meenakshi and Felbin [58] | 2019 | Moves are independently fitted | Initial asset price, strike price, interest rate, and moves | American style | TrFNs |
| Shang et al. [59] | 2020 | Moves are independently fitted | Moves | Real options/capital budgeting | Parabolic FNs |
| Chrysafis and Papadopoulos [60] | 2021 | Cox et al. [16] | Initial asset price, interest rate, and moves | Real options/capital budgeting | Empirical FNs |
| Meenakshi and Kennedy [61] | 2021 | Moves are independently fitted | Initial asset price, strike price, interest rate, and moves | European style | TrFNs |
| Meenakshi and Kennedy [62] | 2021 | Cox et al. [16] | Initial asset price, strike price, interest rate, and moves | American style | Octogonal FNs |
| Wang, Wang, and Tang [63] | 2022 | Moves are independently fitted | Moves | Financial options | TrFNs |
| Zmeskal, Dluhošová, Gurný, and Kresta [64] | 2022 | Cox et al. [16] | Initial asset price, strike price, interest rate, and moves | Real options, multimode | TrFNs |
| Zmeškal, Dluhošová, Gurný, and Guo [27] | 2022 | Binomial lattice by [11] | Bond spot prices and interest rate volatilities | Options on bond games | Adaptive FNs |
| Andrés-Sánchez [21] | 2023 | Cox et al. [16] | Initial asset price, strike price, interest rate, and moves | European style | TFNs |
| Ersen, Tas, and Ugurlu [65] | 2023 | Trinomial moves are calibrated with [45] | Present value of cash-flows. Moves and probabilities are crisp | Real options/capital budgeting | Trapezoidal/intuitionistic FNs |
| Zhang and Yin [66] | 2023 | Cox et al. [16] | Moves | Real options/capital budgeting | Symmetric/TFNs |
| Agustina, Sumarti, and Sidarto [67] | 2024 | Binomial moves by Cox et al. [16] and trinomial moves by Kamrad and Ritchken [66] | Moves | European Style | Adaptive FNs |
| Andrés-Sánchez [68] | 2024 | Cox et al. [16] and Rendleman and Bartter [17] | Moves | European Style/Option on Indexes | Empirical intuitionistic FNs/triangular intuitionistic FNs |
2.2. Analysis of the Content of the Reviewed Papers
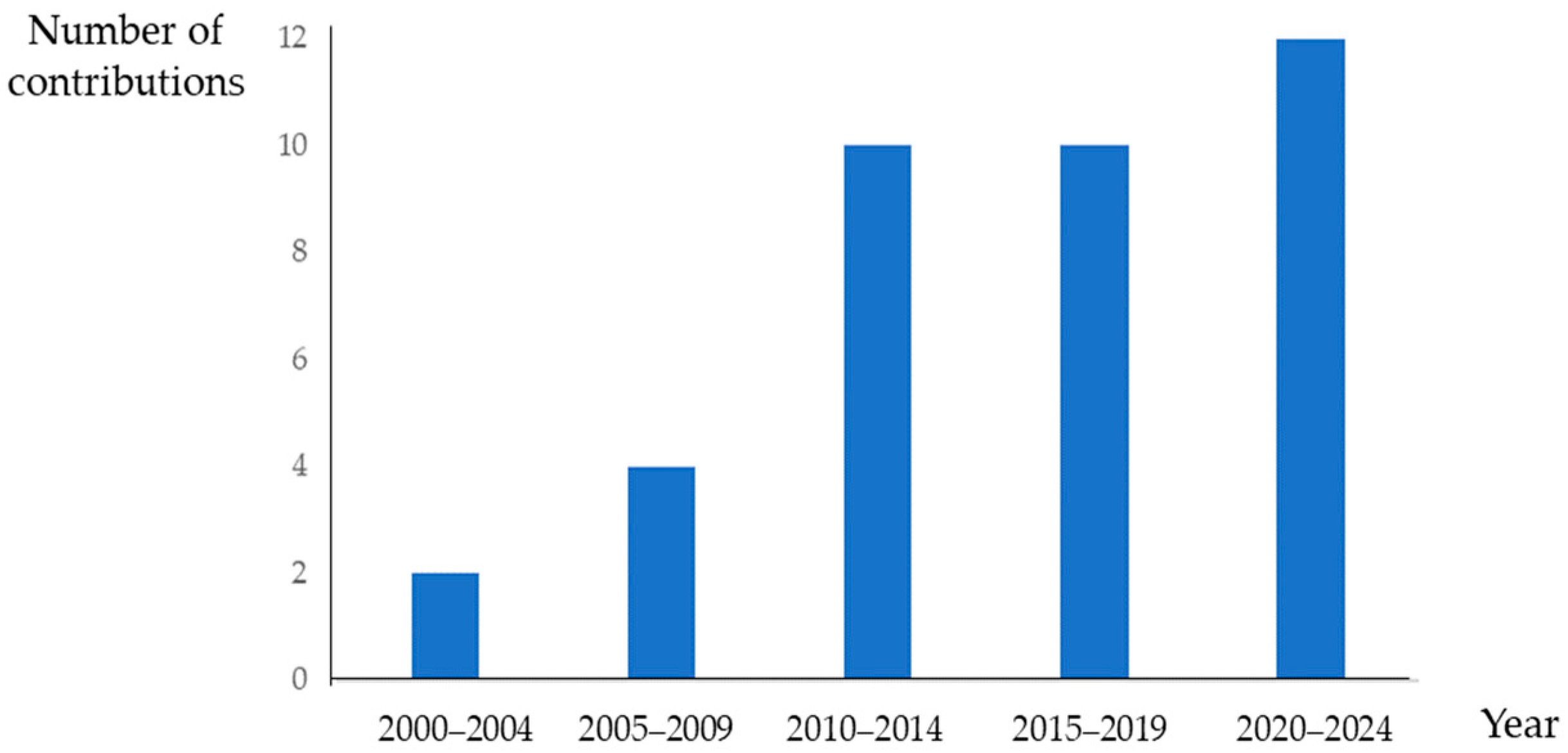
2.3. Quantitative Analysis of the Contributions of FROPDT
- From 2010 to 2019, among the 18 studies reviewed, a large number analyzed the application of FROPDT in real options valuation [41,42,44,45,46,50,52,53,56,57]. By definition, real options, which arise from specific investment projects, do not involve empirical applications with large datasets. During this decade, FROPDT applications emerged in other areas, such as business valuation [43], life insurance guarantees [52,53], and vulnerable options [54]. Only in [55] is there an extensive application using market data.
- From 2020 onwards, the trend is similar to that of the previous decade. The application of FROPDT in real option pricing is an established topic [22,59,60,65,66]. There are studies addressing issues related to the implementation of option valuation using the binomial approach [61,62,63,67] and others exploring the valuation of options not analyzed in previous decades, such as bond games [27]. Only in [67,68] is there an empirical application using market data.
3. Binomial Lattice of the Term Structure of Interest Rates
3.1. Pricing Sensitive Interest-Rate Assets with a Binomial Lattice
3.2. Pricing Sensitive Interest-Rate Assets with the Ho-Lee Model
4. Binomial Lattices with an Additive Interest-Rate Model and Fuzzy Volatility
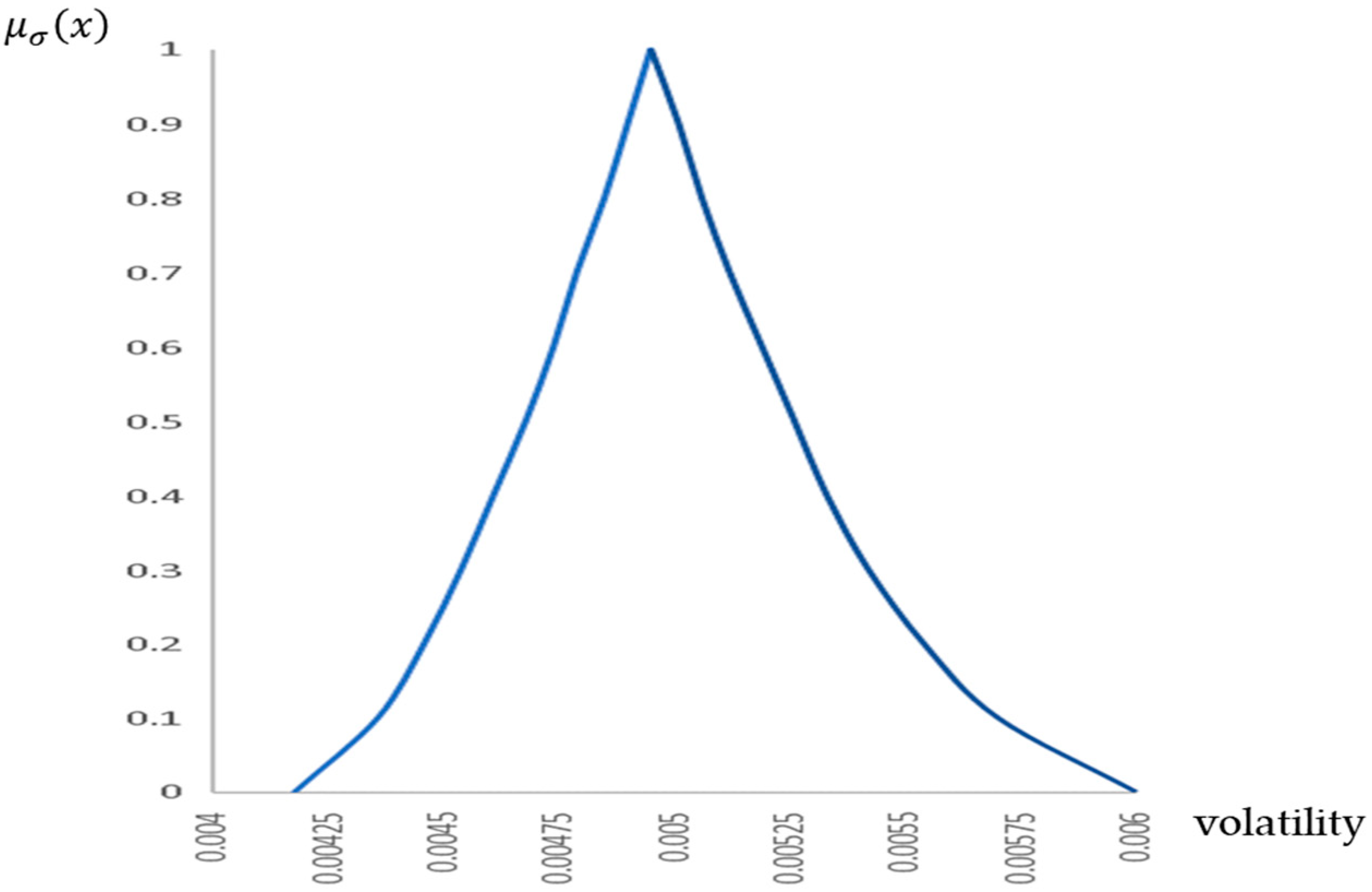
4.1. Fitting the Volatility of the Short-Term Interest Rates with Fuzzy Numbers
4.2. Pricing Interest-Rate Sensitivity Assets with a Fuzzy Ho and Lee Model of the Temporal Structure of Interest Rates
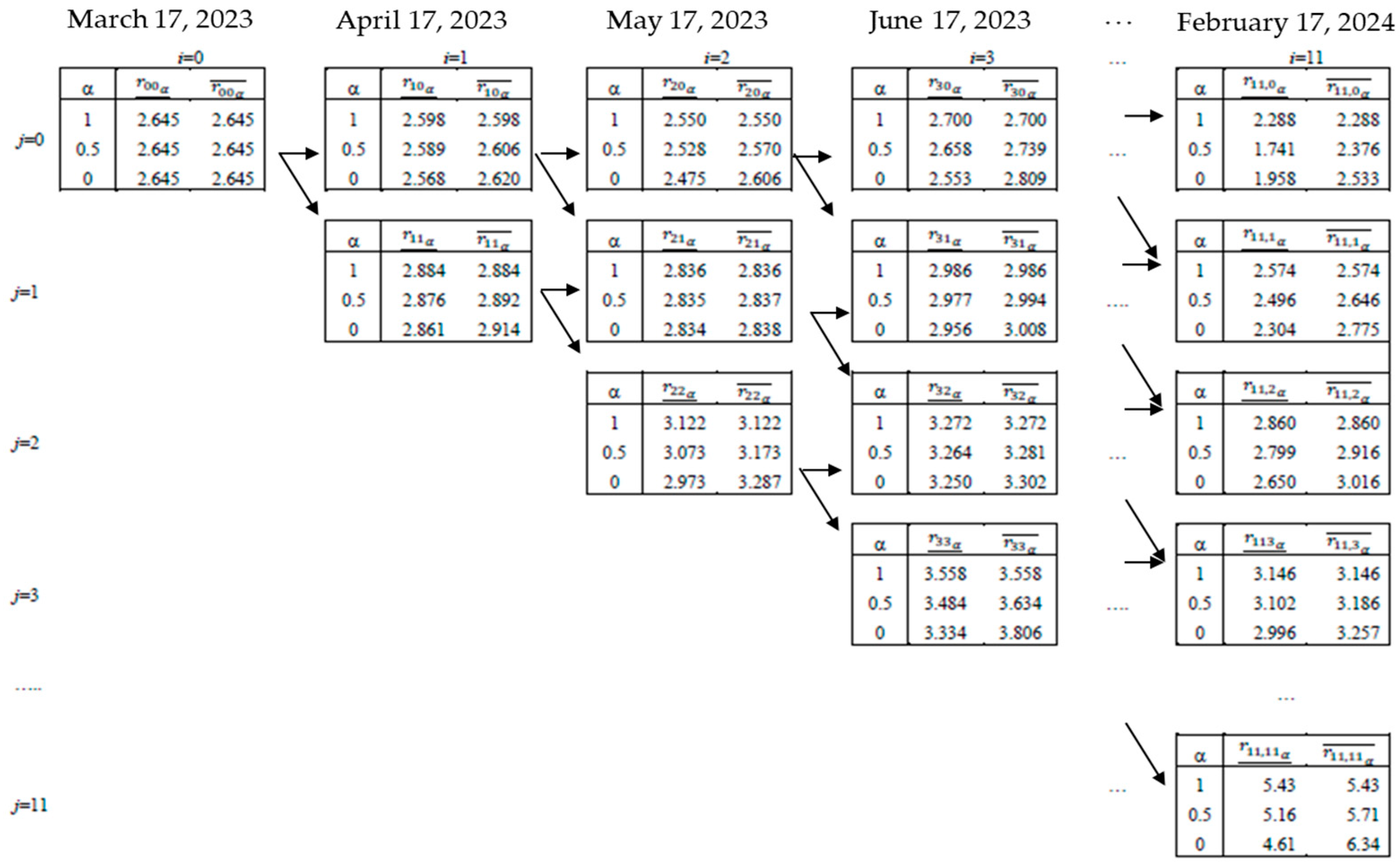
Empirical Application 1
4.3. Adjusting a Triangular Fuzzy Number to Variables Linked to a Fuzzy Pricing of Interest-Sensitive Instruments with Ho and Lee’s Binomial Lattice
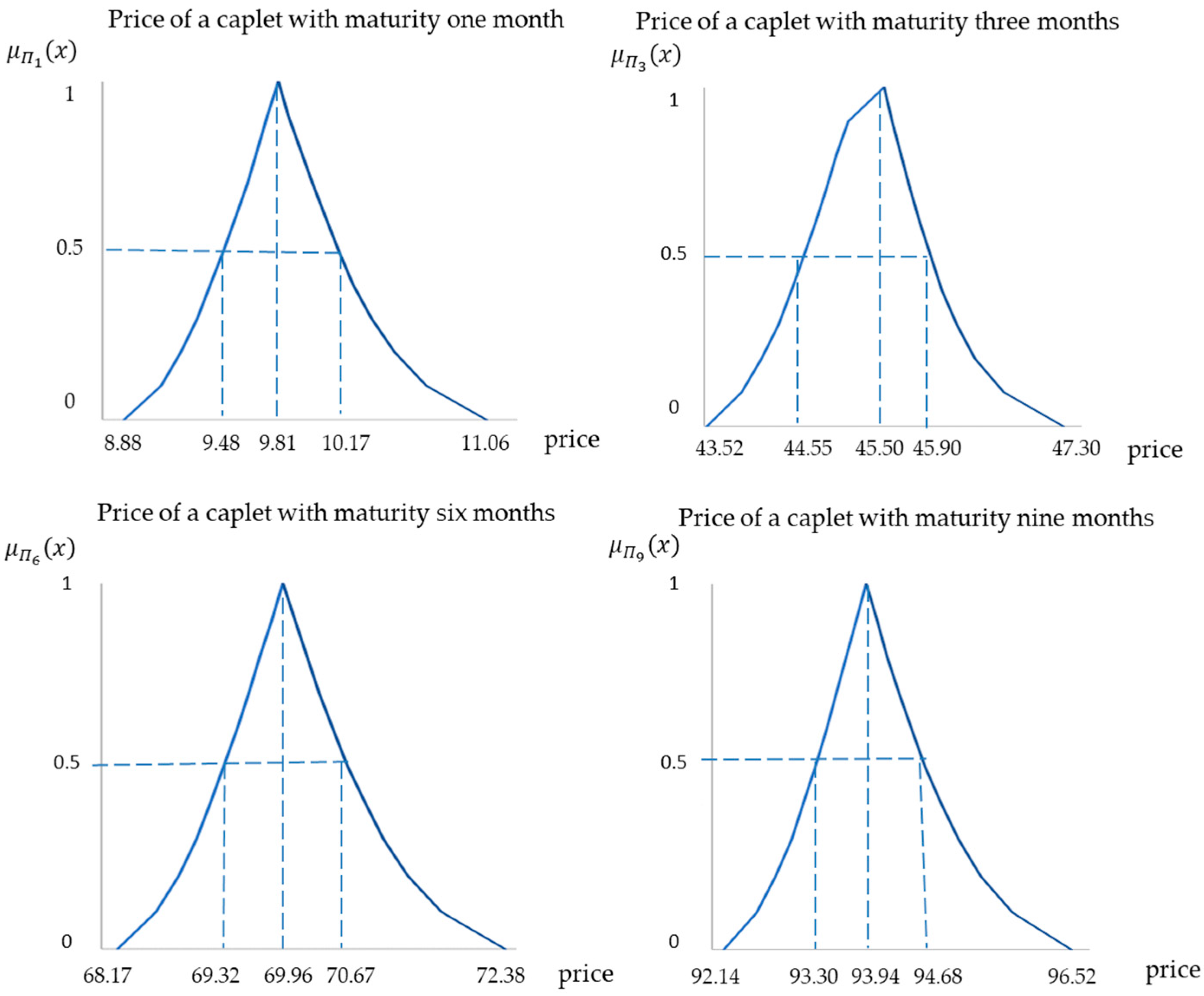
Empirical Application 2
5. Discussion
6. Conclusions and Further Research
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FROP | Fuzzy-Random Option Pricing |
| FROPDT | Fuzzy-Random Option Pricing in Discrete Time |
| FN | Fuzzy Number |
| TFN | Triangular Fuzzy Number |
| TrFN | Trapezoidal Fuzzy Number |
Appendix A
| α | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.00031 | 0.00031 | 0.00495 | 0.00495 | 0.00495 | 0.00495 | 0.00% | 0.00% |
| 0.9 | 0.00031 | 0.00032 | 0.00490 | 0.00501 | 0.00488 | 0.00506 | 0.48% | 0.99% |
| 0.8 | 0.00031 | 0.00032 | 0.00485 | 0.00506 | 0.00480 | 0.00516 | 0.98% | 1.92% |
| 0.7 | 0.00030 | 0.00032 | 0.00479 | 0.00512 | 0.00472 | 0.00527 | 1.47% | 2.78% |
| 0.6 | 0.00030 | 0.00033 | 0.00474 | 0.00519 | 0.00464 | 0.00537 | 1.94% | 3.53% |
| 0.5 | 0.00029 | 0.00033 | 0.00468 | 0.00526 | 0.00457 | 0.00547 | 2.37% | 4.15% |
| 0.4 | 0.00029 | 0.00034 | 0.00461 | 0.00533 | 0.00449 | 0.00558 | 2.72% | 4.59% |
| 0.3 | 0.00029 | 0.00034 | 0.00454 | 0.00542 | 0.00441 | 0.00568 | 2.93% | 4.76% |
| 0.2 | 0.00028 | 0.00035 | 0.00446 | 0.00554 | 0.00433 | 0.00579 | 2.89% | 4.50% |
| 0.1 | 0.00027 | 0.00036 | 0.00436 | 0.00570 | 0.00426 | 0.00589 | 2.31% | 3.43% |
| 0 | 0.00026 | 0.00038 | 0.00418 | 0.00600 | 0.00418 | 0.00600 | 0.00% | 0.00% |
| α-cuts of one-month interest rates | ||||||||||
| α | ||||||||||
| 1 | 0.02598 | 0.02598 | 0.02700 | 0.02700 | 0.02515 | 0.02515 | 0.02379 | 0.02379 | 0.02288 | 0.02288 |
| 0.9 | 0.02596 | 0.02599 | 0.02695 | 0.02705 | 0.02506 | 0.02525 | 0.02365 | 0.02393 | 0.02271 | 0.02305 |
| 0.8 | 0.02594 | 0.02601 | 0.02691 | 0.02709 | 0.02496 | 0.02534 | 0.02350 | 0.02407 | 0.02253 | 0.02322 |
| 0.7 | 0.02593 | 0.02602 | 0.02685 | 0.02714 | 0.02486 | 0.02543 | 0.02335 | 0.02421 | 0.02234 | 0.02339 |
| 0.6 | 0.02591 | 0.02604 | 0.02680 | 0.02719 | 0.02475 | 0.02553 | 0.02318 | 0.02435 | 0.02214 | 0.02357 |
| 0.5 | 0.02589 | 0.02606 | 0.02674 | 0.02724 | 0.02463 | 0.02563 | 0.02300 | 0.02451 | 0.02192 | 0.02376 |
| 0.4 | 0.02587 | 0.02607 | 0.02667 | 0.02729 | 0.02449 | 0.02574 | 0.02280 | 0.02467 | 0.02167 | 0.02395 |
| 0.3 | 0.02584 | 0.02609 | 0.02659 | 0.02735 | 0.02434 | 0.02586 | 0.02257 | 0.02485 | 0.02139 | 0.02418 |
| 0.2 | 0.02581 | 0.02612 | 0.02649 | 0.02743 | 0.02414 | 0.02600 | 0.02227 | 0.02506 | 0.02103 | 0.02444 |
| 0.1 | 0.02576 | 0.02615 | 0.02636 | 0.02752 | 0.02387 | 0.02618 | 0.02186 | 0.02533 | 0.02053 | 0.02477 |
| 0 | 0.02568 | 0.02620 | 0.02610 | 0.02767 | 0.02335 | 0.02649 | 0.02108 | 0.02580 | 0.01958 | 0.02533 |
| α-cuts of one-month interest rates | ||||||||||
| α | ||||||||||
| 1 | 0.02598 | 0.02598 | 0.02700 | 0.02700 | 0.02515 | 0.02515 | 0.02379 | 0.02379 | 0.02288 | 0.02288 |
| 0.9 | 0.02595 | 0.02600 | 0.02691 | 0.02707 | 0.02497 | 0.02529 | 0.02352 | 0.02399 | 0.02255 | 0.02313 |
| 0.8 | 0.02592 | 0.02602 | 0.02682 | 0.02714 | 0.02479 | 0.02542 | 0.02325 | 0.02419 | 0.02222 | 0.02337 |
| 0.7 | 0.02589 | 0.02604 | 0.02673 | 0.02720 | 0.02461 | 0.02555 | 0.02298 | 0.02439 | 0.02189 | 0.02362 |
| 0.6 | 0.02586 | 0.02607 | 0.02664 | 0.02727 | 0.02443 | 0.02569 | 0.02271 | 0.02459 | 0.02156 | 0.02386 |
| 0.5 | 0.02583 | 0.02609 | 0.02655 | 0.02734 | 0.02425 | 0.02582 | 0.02244 | 0.02479 | 0.02123 | 0.02411 |
| 0.4 | 0.02580 | 0.02611 | 0.02646 | 0.02740 | 0.02407 | 0.02596 | 0.02217 | 0.02499 | 0.02090 | 0.02435 |
| 0.3 | 0.02577 | 0.02613 | 0.02637 | 0.02747 | 0.02389 | 0.02609 | 0.02190 | 0.02519 | 0.02057 | 0.02460 |
| 0.2 | 0.02574 | 0.02615 | 0.02628 | 0.02754 | 0.02371 | 0.02622 | 0.02163 | 0.02540 | 0.02024 | 0.02484 |
| 0.1 | 0.02571 | 0.02618 | 0.02619 | 0.02760 | 0.02353 | 0.02636 | 0.02135 | 0.02560 | 0.01991 | 0.02509 |
| 0 | 0.02568 | 0.02620 | 0.02610 | 0.02767 | 0.02335 | 0.02649 | 0.02108 | 0.02580 | 0.01958 | 0.02533 |
| Error (%) | ||||||||||
| 1 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| 0.9 | 0.06% | 0.03% | 0.16% | 0.08% | 0.34% | 0.16% | 0.55% | 0.25% | 0.70% | 0.32% |
| 0.8 | 0.11% | 0.05% | 0.31% | 0.15% | 0.68% | 0.32% | 1.09% | 0.51% | 1.39% | 0.64% |
| 0.7 | 0.16% | 0.08% | 0.46% | 0.22% | 1.00% | 0.48% | 1.61% | 0.75% | 2.06% | 0.95% |
| 0.6 | 0.20% | 0.10% | 0.60% | 0.29% | 1.30% | 0.62% | 2.09% | 0.97% | 2.70% | 1.22% |
| 0.5 | 0.24% | 0.12% | 0.71% | 0.35% | 1.56% | 0.74% | 2.52% | 1.16% | 3.26% | 1.46% |
| 0.4 | 0.27% | 0.14% | 0.80% | 0.40% | 1.76% | 0.84% | 2.86% | 1.30% | 3.71% | 1.64% |
| 0.3 | 0.29% | 0.15% | 0.85% | 0.42% | 1.87% | 0.88% | 3.06% | 1.37% | 3.98% | 1.72% |
| 0.2 | 0.28% | 0.14% | 0.82% | 0.40% | 1.82% | 0.85% | 2.99% | 1.32% | 3.90% | 1.64% |
| 0.1 | 0.22% | 0.11% | 0.65% | 0.32% | 1.44% | 0.66% | 2.37% | 1.02% | 3.11% | 1.27% |
| 0 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| α-cuts of one-month interest rates | ||||||||||
| α | ||||||||||
| 1 | 0.02884 | 0.02884 | 0.03558 | 0.03558 | 0.04231 | 0.04231 | 0.04952 | 0.04952 | 0.05434 | 0.05434 |
| 0.9 | 0.02879 | 0.02888 | 0.03544 | 0.03572 | 0.04203 | 0.04259 | 0.04910 | 0.04995 | 0.05382 | 0.05485 |
| 0.8 | 0.02874 | 0.02893 | 0.03530 | 0.03587 | 0.04175 | 0.04288 | 0.04868 | 0.05038 | 0.05330 | 0.05538 |
| 0.7 | 0.02869 | 0.02898 | 0.03515 | 0.03601 | 0.04146 | 0.04318 | 0.04824 | 0.05083 | 0.05277 | 0.05593 |
| 0.6 | 0.02864 | 0.02903 | 0.03500 | 0.03617 | 0.04115 | 0.04350 | 0.04779 | 0.05130 | 0.05222 | 0.05651 |
| 0.5 | 0.02859 | 0.02909 | 0.03484 | 0.03634 | 0.04083 | 0.04384 | 0.04731 | 0.05181 | 0.05162 | 0.05713 |
| 0.4 | 0.02853 | 0.02915 | 0.03466 | 0.03653 | 0.04048 | 0.04421 | 0.04678 | 0.05238 | 0.05098 | 0.05783 |
| 0.3 | 0.02846 | 0.02923 | 0.03446 | 0.03675 | 0.04008 | 0.04465 | 0.04618 | 0.05304 | 0.05025 | 0.05863 |
| 0.2 | 0.02838 | 0.02931 | 0.03423 | 0.03702 | 0.03960 | 0.04518 | 0.04546 | 0.05384 | 0.04937 | 0.05961 |
| 0.1 | 0.02828 | 0.02944 | 0.03391 | 0.03738 | 0.03896 | 0.04591 | 0.04450 | 0.05493 | 0.04820 | 0.06094 |
| 0 | 0.02809 | 0.02966 | 0.03334 | 0.03806 | 0.03783 | 0.04726 | 0.04280 | 0.05695 | 0.04612 | 0.06341 |
| α-cuts of one-month interest rates | ||||||||||
| α | ||||||||||
| 1 | 0.02884 | 0.02884 | 0.03558 | 0.03558 | 0.04231 | 0.04231 | 0.04952 | 0.04952 | 0.05434 | 0.05434 |
| 0.9 | 0.02876 | 0.02892 | 0.03536 | 0.03583 | 0.04186 | 0.04280 | 0.04885 | 0.05027 | 0.05351 | 0.05524 |
| 0.8 | 0.02869 | 0.02900 | 0.03513 | 0.03607 | 0.04141 | 0.04330 | 0.04818 | 0.05101 | 0.05269 | 0.05615 |
| 0.7 | 0.02861 | 0.02908 | 0.03491 | 0.03632 | 0.04096 | 0.04379 | 0.04751 | 0.05175 | 0.05187 | 0.05706 |
| 0.6 | 0.02854 | 0.02917 | 0.03468 | 0.03657 | 0.04052 | 0.04429 | 0.04684 | 0.05249 | 0.05105 | 0.05797 |
| 0.5 | 0.02846 | 0.02925 | 0.03446 | 0.03682 | 0.04007 | 0.04478 | 0.04616 | 0.05324 | 0.05023 | 0.05887 |
| 0.4 | 0.02839 | 0.02933 | 0.03423 | 0.03707 | 0.03962 | 0.04528 | 0.04549 | 0.05398 | 0.04941 | 0.05978 |
| 0.3 | 0.02831 | 0.02941 | 0.03401 | 0.03731 | 0.03917 | 0.04578 | 0.04482 | 0.05472 | 0.04858 | 0.06069 |
| 0.2 | 0.02824 | 0.02950 | 0.03379 | 0.03756 | 0.03872 | 0.04627 | 0.04415 | 0.05547 | 0.04776 | 0.06160 |
| 0.1 | 0.02816 | 0.02958 | 0.03356 | 0.03781 | 0.03828 | 0.04677 | 0.04347 | 0.05621 | 0.04694 | 0.06250 |
| 0 | 0.02809 | 0.02966 | 0.03334 | 0.03806 | 0.03783 | 0.04726 | 0.04280 | 0.05695 | 0.04612 | 0.06341 |
| Error (%) | ||||||||||
| α | ||||||||||
| 1 | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| 0.9 | 0.10% | 0.12% | 0.24% | 0.30% | 0.40% | 0.50% | 0.51% | 0.63% | 0.57% | 0.71% |
| 0.8 | 0.19% | 0.24% | 0.47% | 0.58% | 0.80% | 0.97% | 1.03% | 1.23% | 1.16% | 1.37% |
| 0.7 | 0.29% | 0.35% | 0.70% | 0.85% | 1.20% | 1.40% | 1.55% | 1.78% | 1.73% | 1.98% |
| 0.6 | 0.37% | 0.45% | 0.92% | 1.09% | 1.57% | 1.79% | 2.04% | 2.27% | 2.28% | 2.51% |
| 0.5 | 0.45% | 0.54% | 1.11% | 1.29% | 1.90% | 2.12% | 2.48% | 2.67% | 2.78% | 2.95% |
| 0.4 | 0.50% | 0.61% | 1.25% | 1.44% | 2.17% | 2.35% | 2.83% | 2.96% | 3.19% | 3.27% |
| 0.3 | 0.53% | 0.64% | 1.34% | 1.51% | 2.32% | 2.46% | 3.04% | 3.08% | 3.42% | 3.40% |
| 0.2 | 0.52% | 0.61% | 1.30% | 1.45% | 2.26% | 2.35% | 2.98% | 2.94% | 3.37% | 3.23% |
| 0.1 | 0.41% | 0.48% | 1.02% | 1.13% | 1.79% | 1.82% | 2.37% | 2.27% | 2.68% | 2.50% |
| 0 | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| 1 Month | 3 Months | 6 Months | 9 Months | |||||
|---|---|---|---|---|---|---|---|---|
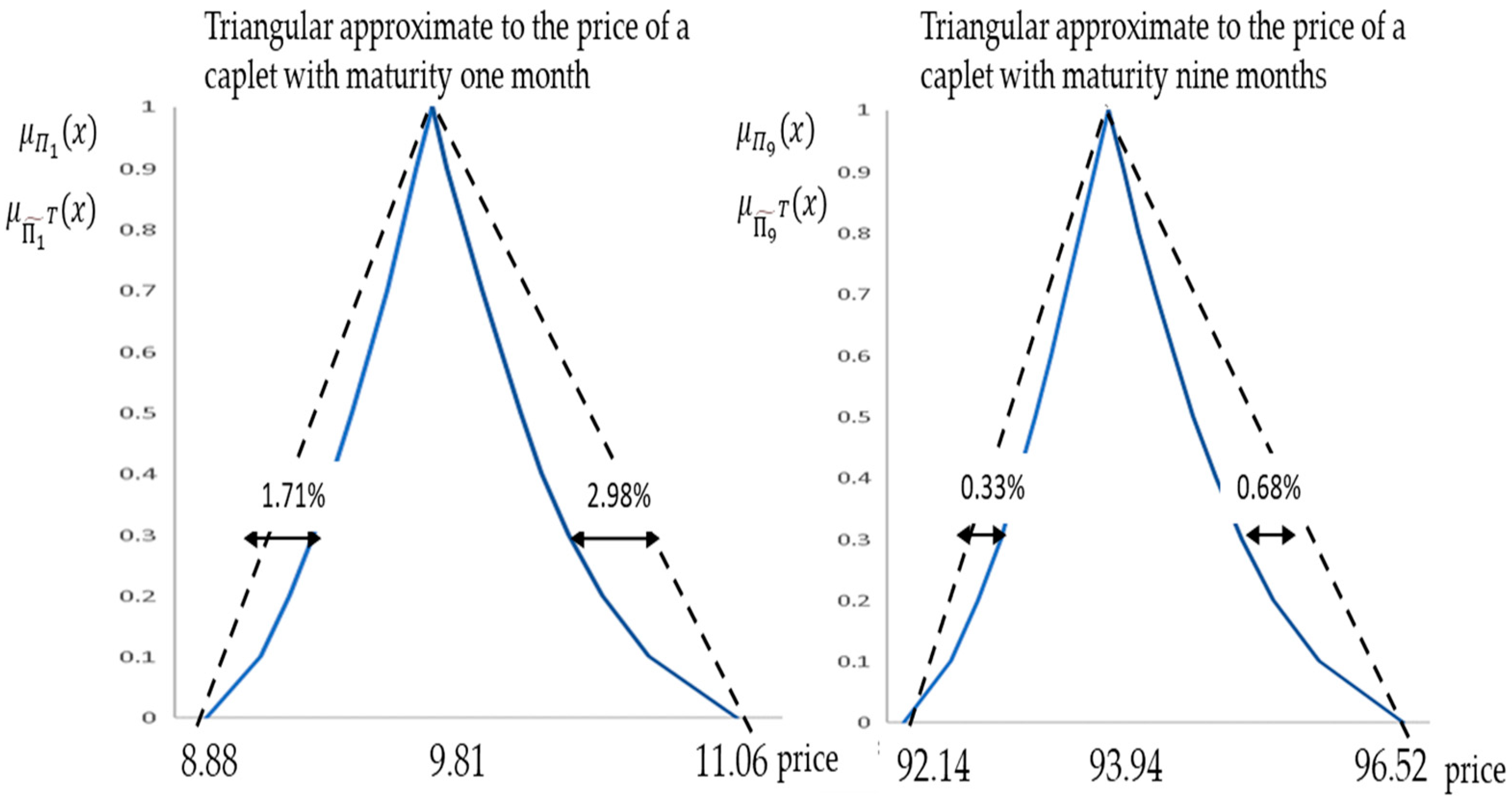
| = | (8.88, 9.81, 11.06) | (43.52, 45.40, 47.30) | (68.17, 69.96, 72.38) | (92.14, 93.94, 96.52) | ||||
| α | ||||||||
| 1 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| 0.9 | 0.29% | 0.60% | 0.43% | 0.22% | 0.08% | 0.16% | 0.06% | 0.14% |
| 0.8 | 0.59% | 1.17% | 0.26% | 0.43% | 0.16% | 0.32% | 0.12% | 0.27% |
| 0.7 | 0.88% | 1.70% | 0.10% | 0.64% | 0.24% | 0.47% | 0.18% | 0.39% |
| 0.6 | 1.15% | 2.18% | 0.06% | 0.82% | 0.31% | 0.60% | 0.23% | 0.49% |
| 0.5 | 1.40% | 2.57% | 0.21% | 0.99% | 0.37% | 0.72% | 0.28% | 0.58% |
| 0.4 | 1.60% | 2.85% | 0.34% | 1.12% | 0.42% | 0.80% | 0.31% | 0.65% |
| 0.3 | 1.71% | 2.98% | 0.44% | 1.21% | 0.45% | 0.84% | 0.33% | 0.68% |
| 0.2 | 1.67% | 2.84% | 0.48% | 1.21% | 0.43% | 0.81% | 0.32% | 0.65% |
| 0.1 | 1.32% | 2.19% | 0.41% | 0.93% | 0.34% | 0.63% | 0.25% | 0.51% |
| 0 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
References
- Zimmermann, H.; Hafner, W. Amazing discovery: Vincenz Bronzin’s option pricing models. J. Bank. Financ. 2007, 31, 531–546. [Google Scholar] [CrossRef]
- Constantinides, G.M. Black–Merton–Scholes Option Pricing: A 50-Year Celebration—Looking Ahead. J. Invest. Manag. 2024, 22, 11–15. [Google Scholar]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. Available online: http://www.jstor.org/stable/1831029 (accessed on 12 September 2024). [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Merton, R.C. Applications of option-pricing theory: Twenty-five years later. Am. Econ. Rev. 1998, 88, 323–349. Available online: http://www.jstor.org/stable/116838 (accessed on 12 September 2024).
- Chen, R.R. Understanding and Managing Interest Rate Risks; World Scientific: Singapore, 1996; Volume 1. [Google Scholar]
- Vasicek, O. An equilibrium characterization of the term structure. J. Financ. Econ. 1977, 5, 177–188. [Google Scholar] [CrossRef]
- Brennan, M.J.; Schwartz, E.S. A continuous time approach to the pricing of bonds. J. Bank. Financ. 1979, 3, 133–155. [Google Scholar] [CrossRef]
- Dothan, L.U. On the term structure of interest rates. J. Financ. Econ. 1978, 6, 59–69. [Google Scholar] [CrossRef]
- Cox, J.C.; Ingersoll, J.E., Jr.; Ross, S.A. An intertemporal general equilibrium model of asset prices. Econom. J. Econom. Soc. 1985, 53, 363–384. [Google Scholar] [CrossRef]
- Ho, T.S.; Lee, S.B. Term structure movements and pricing interest rate contingent claims. J. Financ. 1986, 41, 1011–1029. [Google Scholar] [CrossRef]
- Black, F.; Derman, E.; Toy, W. A one-factor model of interest rates and its application to treasury bond options. Financ. Anal. J. 1990, 46, 33–39. [Google Scholar] [CrossRef]
- Hull, J.; White, A. One-factor interest-rate models and the valuation of interest-rate derivative securities. J. Financ. Quant. Anal. 1993, 28, 235–254. [Google Scholar] [CrossRef]
- Hull, J.C. Options Futures and other Derivatives; Pearson Education India: Tamil Nadu, India, 2008. [Google Scholar]
- Trigeorgis, L. A log-transformed binomial numerical analysis method for valuing complex multioption investments. J. Financ. Quant. Anal. 1991, 26, 309–326. [Google Scholar] [CrossRef]
- Cox, J.; Ross, S.; Rubinstein, M. Option Pricing: A Simplified Approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Rendleman, R.J., Jr.; Bartter, B.J. Two state option pricing. J. Financ. 1979, 34, 1092–1110. [Google Scholar] [CrossRef]
- Jamshidian, F. Forward induction and construction of yield curve diffusion models. J. Fixed Income 1991, 1, 62–74. [Google Scholar] [CrossRef]
- Veronesi, P. Fixed Income Securities: Valuation, Risk, and Risk Management; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Muzzioli, S.; De Baets, B. Fuzzy approaches to option price modeling. IEEE Trans. Fuzzy Syst. 2017, 25, 392–401. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J. A systematic review of the interactions of fuzzy set theory and option pricing. Expert Syst. Appl. 2023, 223, 119868. [Google Scholar] [CrossRef]
- Cherubini, U.; Della Lunga, G. Fuzzy value-at-risk: Accounting for market liquidity. Econ. Notes 2001, 30, 293–312. [Google Scholar] [CrossRef]
- Collan, M.; Fuller, R.; Mezei, R. A Fuzzy Pay-Off Method for Real Option Valuation. J. Appl. Math. Decis. Sci. 2009, 2009, 238196. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J. Fuzzy Random Option Pricing in Continuous Time: A Systematic Review and an Extension of Vasicek’s Equilibrium Model of the Term Structure. Mathematics 2023, 11, 2455. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J. A Fuzzy-Random Extension of Jamshidian’s Bond Option Pricing Model and Compatible One-Factor Term Structure Models. Axioms 2023, 12, 668. [Google Scholar] [CrossRef]
- Jamshidian, F. An exact bond option formula. J. Financ. 1989, 44, 205–209. [Google Scholar] [CrossRef]
- Zmeškal, Z.; Dluhošová, D.; Gurný, P.; Guo, H. Soft bond game options valuation in discrete time using a fuzzy-stochastic approach. Int. J. Fuzzy Syst. 2022, 24, 2215–2228. [Google Scholar] [CrossRef]
- Sfiris, D.S.; Papadopoulos, B.K. Nonasymptotic fuzzy estimators based on confidence intervals. Inf. Sci. 2014, 279, 446–459. [Google Scholar] [CrossRef]
- Dubois, D.; Folloy, L.; Mauris, G.; Prade, H. Probability–possibility transformations, triangular fuzzy sets, and probabilistic inequalities. Reliab. Comput. 2004, 10, 273–297. [Google Scholar] [CrossRef]
- Kreinovich, V.O.; Kosheleva, S.N.; Shahbazova, S.N. Why triangular and trapezoid membership functions: A simple explanation. In Fuzziness and Soft Computing; Shahbazova, S., Sugeno, M., Eds.; Springer: Cham, Switzerland, 2020; Volume 391, pp. 25–31. [Google Scholar]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Moher, D. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, 71. [Google Scholar] [CrossRef]
- Zupic, I.; Čater, T. Bibliometric methods in management and organization. Organ. Res. Methods 2015, 18, 429–472. [Google Scholar] [CrossRef]
- Meyer, D.E.; Mehlman, D.W.; Reeves, E.S.; Origoni, R.B.; Evans, D.; Sellers, D.W. Comparison study of overlap among 21 scientific databases in searching pesticide information. Online Rev. 1983, 7, 33–43. [Google Scholar] [CrossRef]
- Yoshida, Y. A discrete-time model of American put option in an uncertain environment. Eur. J. Oper. Res. 2003, 151, 153–166. [Google Scholar] [CrossRef]
- Muzzioli, S.; Torricelli, C. A multiperiod binomial model for pricing options in a vague world. J. Econ. Dyn. Control 2004, 28, 861–887. [Google Scholar] [CrossRef]
- Lee, C.F.; Tzeng, G.-H.; Wang, S.-Y. A fuzzy set approach for generalized CRR model: An empirical analysis of S&P 500 index options. Rev. Quant. Financ. Account. 2005, 25, 255–275. [Google Scholar] [CrossRef]
- Buckley, J.J.; Eslami, E. Pricing stock options using fuzzy sets. Iran. J. Fuzzy Syst. 2015, 266, 131–143. [Google Scholar]
- Muzzioli, S.; Reynaerts, H. Option Pricing in the Presence of Uncertainty. In Perception-based Data Mining and Decision Making in Economics and Finance; Batyrshin, I., Kacprzyk, J., Sheremetov, L., Zadeh, L.A., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2007; Volume 36. [Google Scholar] [CrossRef]
- Buckley, J.J.; Eslami, E. Pricing Options, Forwards and Futures Using Fuzzy Set Theory. Fuzzy Eng. Econ. Appl. 2008, 233, 339–357. [Google Scholar] [CrossRef]
- Muzzioli, S.; Reynaerts, H. American option pricing with imprecise risk-neutral probabilities. Int. J. Approx. Reason. 2008, 44, 1303–1321. [Google Scholar] [CrossRef]
- Liao, S.H.; Ho, S.H. Investment project valuation based on a fuzzy binomial approach. Inf. Sci. 2010, 180, 2124–2133. [Google Scholar] [CrossRef]
- Wang, B.; Wang, S.; Watada, J. Real options analysis based on fuzzy random variables. Int. J. Innov. Comput. Inf. Control 2010, 6, 1689–1698. [Google Scholar]
- Zmeskal, Z. Generalized soft binomial American real option pricing model (fuzzy-stochastic approach). Eur. J. Oper. Res. 2010, 207, 1096–1103. [Google Scholar] [CrossRef]
- Tolga, A.Ç.; Kahraman, C.; Demircan, M.L. A Comparative Fuzzy Real Options Valuation Model using Trinomial Lattice and Black-Scholes Approaches: A Call Center Application. J. Mult. Valued Log. Soft Comput. 2010, 16, 135–154. [Google Scholar]
- Hull, J.; White, A. Numerical procedures for implementing term structure models I: Single-factor models. J. Deriv. 1994, 2, 7–16. [Google Scholar] [CrossRef]
- Allenotor, D.; Thulasiram, R.K. Grid resources valuation with fuzzy real option. Int. J. High Perform. Comput. Netw. 2011, 7, 1–7. [Google Scholar] [CrossRef]
- Ho, S.H.; Liao, S.H. A fuzzy real option approach for investment. Expert Syst. Appl. 2011, 38, 15296–15302. [Google Scholar] [CrossRef]
- Yu, S.-E.; Huarng, K.-H.; Leon Li, M.-Y.; Chen, C.-Y. A novel option pricing model via fuzzy binomial decision tree. Int. J. Innov. Comput. Inf. Control 2011, 7, 709–718. [Google Scholar]
- Elahi, Y.; Aziz MI, A. Efficient pricings for binomial Asian option under fuzzy environment. Far East J. Math. Sci. 2012, 63, 133–140. Available online: https://www.pphmj.com/abstract/6564.htm (accessed on 12 September 2024).
- Tolga, A.C.; Tuysuz, F.; Kahraman, C. A fuzzy multi-criteria decision analysis approach for retail location selection. Int. J. Inf. Technol. Decis. Mak. 2013, 12, 729–755. [Google Scholar] [CrossRef]
- Cruz Aranda, F.; Ortiz Arango, F.; Cabrera Llanos, A.I. Project valuation of a distribution centre of an auxiliary rail freight terminal: Using real options with fuzzy logic and binomial trees. J. Appl. Econ. Sci. 2016, 12, 894–905. Available online: https://www.ceeol.com/search/article-detail?id=534332 (accessed on 12 September 2024).
- Anzilli, L.; Facchinetti, G. New definitions of mean value and variance of fuzzy numbers: An application to the pricing of life insurance policies and real options. Int. J. Approx. Reason. 2017, 91, 96–113. [Google Scholar] [CrossRef]
- Anzilli, L.; Facchinetti, G.; Pirotti, T. Pricing of minimum guarantees in life insurance contracts with fuzzy volatility. Inf. Sci. 2018, 460, 578–593. [Google Scholar] [CrossRef]
- Xu, W.J.; Liu, G.F.; Yu, X.J. A Binomial Tree Approach to Pricing Vulnerable Option in a Vague World. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2018, 26, 143–162. [Google Scholar] [CrossRef]
- Zhang, H.; Watada, J. Fuzzy Levy-GJR-GARCH American option pricing model based on an infinite pure jump process. IEICE Trans. Inf. Syst. 2018, 101, 1843–1859. [Google Scholar] [CrossRef]
- D’Amato, M.; Zrobek, S.; Bilozor, M.R.; Walacik, M.; Mercadante, G. Valuing the effect of the change of zoning on underdeveloped land using fuzzy real option approach. Land Use Policy 2019, 86, 365–374. [Google Scholar] [CrossRef]
- Cruz Aranda, F.; Terán Bustamante, A. Valuation of an investment project in research and development in the pharmaceutical industry. Contaduría Y Adm. 2019, 64, 90. [Google Scholar] [CrossRef]
- Meenakshi, K.; Felbin, C. Problem of Pricing American Fuzzy Put Option Buyers Model for general Trapezoidal Fuzzy Numbers. Recent Trends Parallel Comput. 2016, 25, 402–416. [Google Scholar] [CrossRef]
- Shang, T.C.; Yang, L.; Liu, P.H.; Shang, K.T.; Zhang, Y. Financing mode of energy performance contracting projects with carbon emissions reduction potential and carbon emissions ratings. Energy Policy 2020, 144, 111632. [Google Scholar] [CrossRef]
- Chrysafis, K.A.; Papadopoulos, B.K. Decision Making for Project Appraisal in Uncertain Environments: A Fuzzy-Possibilistic Approach of the Expanded NPV Method. Symmetry 2021, 13, 27. [Google Scholar] [CrossRef]
- Meenakshi, K.; Kennedy, F.C. A study of european fuzzy put option buyers model on future contracts involving general trapezoidal fuzzy numbers. Glob. Stoch. Anal. 2021, 8, 47–59. [Google Scholar]
- Meenakshi, K.; Kennedy, F.C. On some properties of American fuzzy put option model on fuzzy future contracts involving general linear octagonal fuzzy numbers. Adv. Appl. Math. Sci. 2021, 21, 331–342. [Google Scholar]
- Wang, G.X.; Wang, Y.Y.; Tang, J.M. Fuzzy Option Pricing Based on Fuzzy Number Binary Tree Model. IEEE Trans. Fuzzy Syst. 2021, 30, 3548–3558. [Google Scholar] [CrossRef]
- Zmeskal, Z.; Dluhosova, D.; Gurny, P.; Kresta, A. Generalized soft multimode real options model (fuzzy-stochastic approach). Expert Syst. Appl. 2022, 192, 116388. [Google Scholar] [CrossRef]
- Ersen, H.Y.; Tas, O.; Ugurlu, U. Solar Energy Investment Valuation With Intuitionistic Fuzzy Trinomial Lattice Real Option Model. IEEE Trans. Eng. Manag. 2023, 70, 2584–2593. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yin, J.B. Assessment of investment decisions in bulk shipping through fuzzy real options analysis. Marit. Econ. Logist. 2023, 25, 122–139. [Google Scholar] [CrossRef]
- Agustina, F.; Sumarti, N.; Sidarto, K.A. Construction of the bino-trinomial method using the fuzzy set approach for option pricing. J. Indones. Math. Soc. 2024, 30, 179–204. [Google Scholar] [CrossRef]
- Kamrad, B.; Ritchken, P. Multinomial Approximating Models for Options with k State Variables. Manag. Sci. 1991, 37, 197–210. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J.D. Modeling Up-and-Down Moves of Binomial Option Pricing with Intuitionistic Fuzzy Numbers. Axioms 2024, 13, 503. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy statistics: Hypothesis testing. Soft Comput. 2005, 9, 512–518. [Google Scholar] [CrossRef]
- Chrysafis, K.A.; Papadopoulos, B.K. On theoretical pricing of options with fuzzy estimators. J. Comput. Appl. Math. 2009, 223, 552–566. [Google Scholar] [CrossRef]
- Buckley, J.J.; Qu, Y. On using α-cuts to evaluate fuzzy equations. Fuzzy Sets Syst. 1990, 38, 309–312. [Google Scholar] [CrossRef]
- Andres-Sanchez, J. Pricing European Options with Triangular Fuzzy Parameters: Assessing Alternative Triangular Approximations in the Spanish Stock Option Market. Int. J. Fuzzy Syst. 2018, 20, 1624–1643. [Google Scholar] [CrossRef]
- Jiménez, M.; Rivas, J.A. Fuzzy number approximation. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1998, 6, 69–78. [Google Scholar] [CrossRef]
- Andrés-Sánchez, J.; Puchades, L.G.V. Life settlement pricing with fuzzy parameters. Appl. Soft Comput. 2023, 148, 110924. [Google Scholar] [CrossRef]
- Black, F.; Karasinski, P. Bond and Option pricing when Short rates are Lognormal. Financ. Anal. J. 1991, 47, 52–59. [Google Scholar] [CrossRef]
- Derman, E.; Kani, I. Riding on a smile. Risk 1994, 7, 32–39. [Google Scholar]
- Capotorti, A.; Figà-Talamanca, G. SMART-or and SMART-and fuzzy average operators: A generalized proposal. Fuzzy Sets Syst. 2020, 395, 1–20. [Google Scholar] [CrossRef]
- Muzzioli, S.; Ruggieri, A.; De Baets, B. A comparison of fuzzy regression methods for the estimation of the implied volatility smile function. Fuzzy Sets Syst. 2015, 266, 131–143. [Google Scholar] [CrossRef]




| Journal | Number of Items |
|---|---|
| Expert Systems with Applications | 3 |
| European Journal of Operational Research IEEE Transactions of Fuzzy Systems Information Sciences International Journal of Approximate Reasoning Journal of Innovative Computing, Information and Control | 2 |
| Advances and Applications in Mathematical Sciences; Axioms; Contaduría y Administración; Energy Policy; Far East Journal of Mathematical Sciences; Fuzzy Engineering Economics with Applications (book); Global and Stochastic Analysis; IEICE Transactions on Information and Systems; IEEE Transactions on Engineering Management; International Journal of Fuzzy Systems; International Journal of High Performance Computing and Networking; International Journal of Information Technology & Decision Making; International Journal of Uncertainty Fuzziness and Knowledge-Based Systems; Iranian Journal of Fuzzy Systems; Journal of Economic Dynamics & Control; Journal of Applied Economic Sciences; Journal of Marine Science and Technology-Taiwan; Journal of the Indonesian Mathematical Society; Land Use Policy; Maritime Economics & Logistics; Perception-Based Data Mining and Decision Making in Economics and Finance; Recent Trends in Parallel Computing; Review of Quantitative Finance and Accounting; Symmetry-Basel | 1 |
| Authors | Year | Title | Journal | SCOPUS | WoS |
|---|---|---|---|---|---|
| Muzzioli and Torricelli [35] | 2004 | A multiperiod binomial model for pricing options in a vague world. | Journal of Economic Dynamics & Control | 67 | 72 |
| Zmeskal [43] | 2010 | Generalized soft binomial American real option pricing model (fuzzy-stochastic approach). | European Journal of Operational Research | 55 | 64 |
| Ho and Liao [47] | 2011 | A fuzzy real option approach for investment. | Expert Systems With Applications | 55 | 56 |
| Yoshida [34] | 2003 | A discrete-time model of American options in an uncertain environment. | European Journal of Operational Research | 43 | 40 |
| Muzzioli and Reynaerts [39] | 2008 | American option pricing with imprecise risk-neutral probabilities. | International Journal of Approximate Reasoning | 39 | 34 |
| Liao and Ho [41] | 2010 | Investment project valuation based on a fuzzy-binomial approach. | Information Sciences | 37 | 35 |
| Muzzioli and de Baets [20] | 2017 | Fuzzy approaches to option price modeling. | IEEE Transactions on Fuzzy Systems | 38 | 38 |
| Lee et al. [36] | 2005 | A fuzzy set approach for the generalized CRR model: an empirical analysis of S&P 500 index options. | Review of Quantitative Finance and Accounting | 33 | NO |
| Yu et al. [48] | 2011 | Model construction of option pricing based on fuzzy theory. | Journal of Marine Science and Technology-Taiwan | 18 | 33 |
| Shang et al. [59] | 2020 | Financing mode of energy performance contracting projects with carbon emissions reduction potential and carbon emissions ratings. | Energy Policy | 25 | 19 |
| D’Amato et al. [56] | 2019 | Valuing the effect of the change in zoning on underdeveloped land using the fuzzy real options approach. | Land Use Policy | 19 | 12 |
| Chrysafis and Papadopoulos [60] | 2021 | Decision making for project appraisal in uncertain environments: a fuzzy-possibilistic approach of the expanded NPV method. | Symmetry | 18 | 17 |
| Andrés-Sánchez [69] | 2023a | A systematic review of the interactions of fuzzy set theory and option pricing. | Expert Systems with Applications | 12 | 13 |
| Month (maturity) | 1 month (17 April 2023) | 2 months (17 May 2023) | 3 months (17 June 2023) | 4 months (17 July 2023) | 5 months (17 August 2023) | 6 months (17 September 2023) |
| spot rate | 2.645 | 2.693 | 2.741 | 2.838 | 2.935 | 3.032 |
| price | 99.780 | 99.552 | 99.317 | 99.059 | 98.785 | 98.495 |
| Month (maturity) | 7 months (17 October 2023) | 8 months (17 November 2023) | 9 months (17 December 2023) | 10 months (17 January 2024) | 11 months (17 February 2023) | 12 months (17 March 2023) |
| spot rate | 3.081 | 3.129 | 3.178 | 3.227 | 3.275 | 3.324 |
| price | 98.219 | 97.935 | 97.645 | 97.347 | 97.042 | 96.731 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrés-Sánchez, J.d. A Systematic Overview of Fuzzy-Random Option Pricing in Discrete Time and Fuzzy-Random Binomial Extension Sensitive Interest Rate Pricing. Axioms 2025, 14, 52. https://doi.org/10.3390/axioms14010052
Andrés-Sánchez Jd. A Systematic Overview of Fuzzy-Random Option Pricing in Discrete Time and Fuzzy-Random Binomial Extension Sensitive Interest Rate Pricing. Axioms. 2025; 14(1):52. https://doi.org/10.3390/axioms14010052
Chicago/Turabian StyleAndrés-Sánchez, Jorge de. 2025. "A Systematic Overview of Fuzzy-Random Option Pricing in Discrete Time and Fuzzy-Random Binomial Extension Sensitive Interest Rate Pricing" Axioms 14, no. 1: 52. https://doi.org/10.3390/axioms14010052
APA StyleAndrés-Sánchez, J. d. (2025). A Systematic Overview of Fuzzy-Random Option Pricing in Discrete Time and Fuzzy-Random Binomial Extension Sensitive Interest Rate Pricing. Axioms, 14(1), 52. https://doi.org/10.3390/axioms14010052






