Collocation Method for the Time-Fractional Generalized Kawahara Equation Using a Certain Lucas Polynomial Sequence
Abstract
1. Introduction
- The employment of the introduced Lucas polynomial sequence in numerical analysis is new.
- Derivations of some new theoretical results, such as the high-order and operational matrices of derivatives of the utilized Horadam sequence of polynomials.
- A new study for the convergence analysis of the proposed double expansion.
2. An Overview of Lucas Polynomial Sequences
3. Some New Formulas of
- The analytic form of .
- The inversion formula of .
- The expressions of the high-order derivatives of as combinations of their original ones.
4. A Collocation Approach for the Time-Fractional Generalized KDE
5. The Convergence and Error Analysis
6. Illustrative Examples
7. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and Caputo derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Li, C.; Zhao, Z. Introduction to fractional integrability and differentiability. Eur. Phys. J. Spec. Top. 2011, 193, 5–26. [Google Scholar] [CrossRef]
- Li, C.; Dao, X.; Guo, P. Fractional derivatives in complex planes. Nonlinear Anal. 2009, 71, 1857–1869. [Google Scholar] [CrossRef]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Magin, R. Fractional Calculus in Bioengineering, part 1. Crit. Rev. Biomed. Eng. 2004, 32. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and MEDIA; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Gasmi, B.; Moussa, A.A.; Mati, Y.; Alhakim, L.A.; Akgül, A. New exact traveling wave solutions to the Kawahara equation using the tanh (ξ) expansion method. Int. J. Appl. Comput. Math. 2023, 9, 98. [Google Scholar] [CrossRef]
- Varol, D. Solitary and periodic wave solutions of the space-time fractional extended Kawahara equation. Fractal Fract. 2023, 7, 539. [Google Scholar] [CrossRef]
- Zafar, H.; Ali, A.; Khan, K.; Sadiq, M.N. Analytical solution of time fractional Kawahara and modified Kawahara equations by homotopy analysis method. Int. J. Appl. Comput. Math. 2022, 8, 94. [Google Scholar] [CrossRef]
- Karunakar, P.; Chakraverty, S. Solution of interval-modified Kawahara differential equations using homotopy perturbation transform method. In Wave Dynamics; World Scientific: Singapore, 2022; pp. 193–202. [Google Scholar]
- Arifeen, S.U.; Ali, I.; Ahmad, I.; Shaheen, S. Computational study of time-fractional non-linear Kawahara equations using quintic B-spline and Galerkin’s method. Partial Differ. Equ. Appl. Math. 2024, 12, 100779. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Alweldi, A.M. On the modified Laplace homotopy perturbation method for solving damped modified Kawahara equation and its application in a fluid. Symmetry 2023, 15, 394. [Google Scholar] [CrossRef]
- Wang, X. Analytical and numerical studies of the modified Kawahara equation with dual-power law nonlinearities. Numer. Algorithms 2024, 1–33. [Google Scholar] [CrossRef]
- Al-Essa, L.A.; Ur Rahman, M. A survey on fractal fractional nonlinear Kawahara equation: Theoretical and computational analysis. Sci. Rep. 2024, 14, 6990. [Google Scholar] [CrossRef] [PubMed]
- Nirmala, A.N.; Kumbinarasaiah, S. A rapid numerical method for nonlinear generalized time-fractional Kawahara equations via domination polynomials of complete graph. Phys. Scr. 2024, 99, 125264. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, J. Numerical investigation of fractional Kawahara equation via Haar scale wavelet method. Contemp. Math. 2024, 5, 478–491. [Google Scholar] [CrossRef]
- Horadam, A.F. Extension of a synthesis for a class of polynomial sequences. Fibonacci Quart. 1996, 34, 68–74. [Google Scholar] [CrossRef]
- Keskin, R.; Siar, Z. Some new identities concerning the Horadam sequence and its companion sequence. Commun. Korean Math. Soc. 2019, 34, 1–16. [Google Scholar]
- Djordjevic, S.S.; Djordjevic, G.B. Generalized Horadam polynomials and numbers. An. Ştiinţ. Univ. Ovidius Constanţa Ser. Mat. 2018, 26, 91–101. [Google Scholar] [CrossRef]
- Singh, P.K.; Ray, S.S. A numerical approach based on Pell polynomial for solving stochastic fractional differential equations. Numer. Algorithms 2024, 97, 1513–1534. [Google Scholar] [CrossRef]
- El-Sayed, A.A. Pell-Lucas polynomials for numerical treatment of the nonlinear fractional-order Duffing equation. Demonstr. Math. 2023, 56, 20220220. [Google Scholar] [CrossRef]
- Postavaru, O. An efficient numerical method based on Fibonacci polynomials to solve fractional differential equations. Math. Comput. Simul. 2023, 212, 406–422. [Google Scholar] [CrossRef]
- Angadi, L.M. Wavelet based Galerkin method for the numerical solution of singular boundary value problems using Fibonacci wavelets. J. Sci. Res. 2025, 17, 227–234. [Google Scholar] [CrossRef]
- Gupta, R.; Saha Ray, S. A new effective coherent numerical technique based on shifted Vieta–Fibonacci polynomials for solving stochastic fractional integro-differential equations. Comput. Appl. Math. 2023, 42, 256. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alqubori, O.M.; Atta, A.G. A collocation approach for the nonlinear fifth-order KdV equations using certain shifted Horadam polynomials. Mathematics 2025, 13, 300. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Hesthaven, J.; Gottlieb, S.; Gottlieb, D. Spectral Methods for Time-Dependent Problems; Cambridge University Press: Cambridge, UK, 2007; Volume 21. [Google Scholar]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation: Chelmsford, MA, USA, 2001. [Google Scholar]
- Abd-Elhameed, W.M.; Al-Harbi, M.S.; Amin, A.K.; Ahmed, H.M. Spectral treatment of high-order Emden–Fowler equations based on modified Chebyshev polynomials. Axioms 2023, 12, 99. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Baleanu, D.; Agarwal, P.; Moussa, H. Approximating system of ordinary differential-algebraic equations via derivative of Legendre polynomials operational matrices. Int. J. Mod. Phys. C 2023, 34, 2350036. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Lopes, A.M.; Babatin, M.M. Shifted fractional Jacobi collocation method for solving fractional functional differential equations of variable order. Chaos Solitons Fract. 2020, 134, 109721. [Google Scholar] [CrossRef]
- Hafez, R.M. Numerical solution of linear and nonlinear hyperbolic telegraph type equations with variable coefficients using shifted Jacobi collocation method. Comput. Appl. Math. 2018, 37, 5253–5273. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alqubori, O.M.; Al-Harbi, A.K.; Alharbi, M.H.; Atta, A.G. Generalized third-kind Chebyshev tau approach for treating the time fractional cable problem. Electron. Res. Arch. 2024, 32, 6200–6224. [Google Scholar] [CrossRef]
- Haq, S.; Noreen, A.; Akbar, T.; Arifeen, S.U.; Ghafoor, A.; Khan, Z.A. Numerical solution of seventh order KdV equations via quintic B-splines collocation method. Alex. Eng. J. 2025, 114, 497–506. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Al-Sady, A.M.; Alqubori, O.M.; Atta, A.G. Numerical treatment of the fractional Rayleigh–Stokes problem using some orthogonal combinations of Chebyshev polynomials. AIMS Math. 2024, 9, 25457–25481. [Google Scholar] [CrossRef]
- Alsuyuti, M.M.; Doha, E.H.; Ezz-Eldien, S.S.; Youssef, I.K. Spectral Galerkin schemes for a class of multi-order fractional pantograph equations. J. Comput. Appl. Math. 2021, 384, 113157. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alsuyuti, M.M. New spectral algorithm for fractional delay pantograph equation using certain orthogonal generalized Chebyshev polynomials. Commun. Nonlinear Sci. Numer. Simul. 2024, 141, 108479. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Ahmed, H.M. Tau and Galerkin operational matrices of derivatives for treating singular and Emden–Fowler third-order-type equations. Int. J. Mod. Phys. C 2022, 33, 2250061. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, X.; Zhang, H. A time–space spectral tau method for the time fractional cable equation and its inverse problem. Appl. Numer. Math. 2018, 130, 95–111. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Boulaaras, S.; Sweilam, N.H. Numerical solution of the fractional-order logistic equation via the first-kind Dickson polynomials and spectral tau method. Math. Methods Appl. Sci. 2023, 46, 8004–8017. [Google Scholar] [CrossRef]
- Napoli, A.; Abd-Elhameed, W.M. An innovative harmonic numbers operational matrix method for solving initial value problems. Calcolo 2017, 54, 57–76. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Moussa, H. Pseudo-spectral matrices as a numerical tool for dealing BVPs, based on Legendre polynomials’ derivatives. Alex. Eng. J. 2023, 66, 301–313. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Al-Harbi, M.S.; Atta, A.G. New convolved Fibonacci collocation procedure for the FitzHugh–Nagumo non-linear equation. Nonlinear Eng. 2024, 13, 20220332. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. Legendre operational matrix of fractional derivatives and its applications in solving the fractional differential equations. Appl. Math. Model. 2010, 34, 768–779. [Google Scholar]
- Ahmed, H.M. Enhanced shifted Jacobi operational matrices of derivatives: Spectral algorithm for solving multiterm variable-order fractional differential equations. Bound. Value Probl. 2023, 2023, 108. [Google Scholar] [CrossRef]
- Ahmed, H.M. A new first finite class of classical orthogonal polynomials operational matrices: An application for solving fractional differential equations. Contemp. Math. 2023, 974–994. [Google Scholar] [CrossRef]
- Biswas, C.; Das, S.; Singh, A.; Altenbach, H. Solution of variable-order partial integro-differential equation using Legendre wavelet approximation and operational matrices. ZAMM-J. Appl. Math. Mech. 2023, 103, e202200222. [Google Scholar] [CrossRef]
- Shloof, A.M.; Senu, N.; Ahmadian, A.; Nouh, M.I.; Salahshour, S. A novel fractal-fractional analysis of the stellar helium burning network using extended operational matrix method. Phys. Scr. 2023, 98, 034004. [Google Scholar] [CrossRef]
- Pourbabaee, M.; Saadatmandi, A. The construction of a new operational matrix of the distributed-order fractional derivative using Chebyshev polynomials and its applications. Int. J. Comput. Math. 2021, 98, 2310–2329. [Google Scholar] [CrossRef]
- Saldır, O.; Sakar, M.G.; Erdogan, F. Numerical solution of time-fractional Kawahara equation using reproducing kernel method with error estimate. Comput. Appl. Math. 2019, 38, 198. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alqubori, O.M.; Atta, A.G. A collocation procedure for treating the time-fractional FitzHugh–Nagumo differential equation using shifted Lucas polynomials. Mathematics 2024, 12, 3672. [Google Scholar] [CrossRef]
- Koepf, W. Hypergeometric Summation, 2nd ed.; Springer Universitext Series; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Andrews, G.E.; Askey, R.; Roy, R. Special Functions; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Abd-Elhameed, W.M.; Youssri, Y.H.; Amin, A.K.; Atta, A.G. Eighth-kind Chebyshev polynomials collocation algorithm for the nonlinear time-fractional generalized Kawahara equation. Fractal Fract. 2023, 7, 652. [Google Scholar] [CrossRef]
- Luke, Y.L. Inequalities for generalized hypergeometric functions. J. Approx. Theory 1972, 5, 41–65. [Google Scholar] [CrossRef]
- Jameson, G.J.O. The incomplete gamma functions. Math. Gaz. 2016, 100, 298–306. [Google Scholar] [CrossRef]

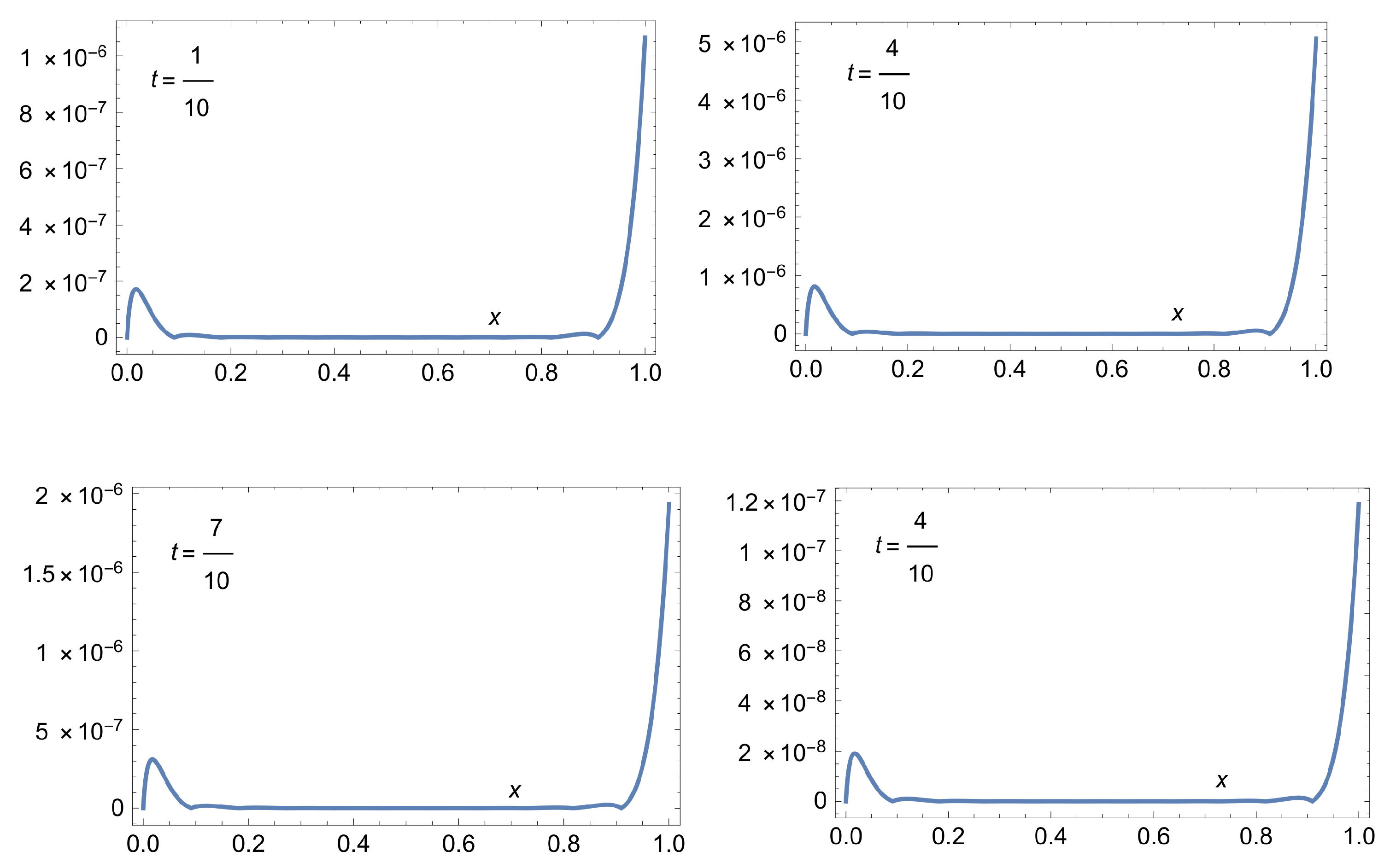
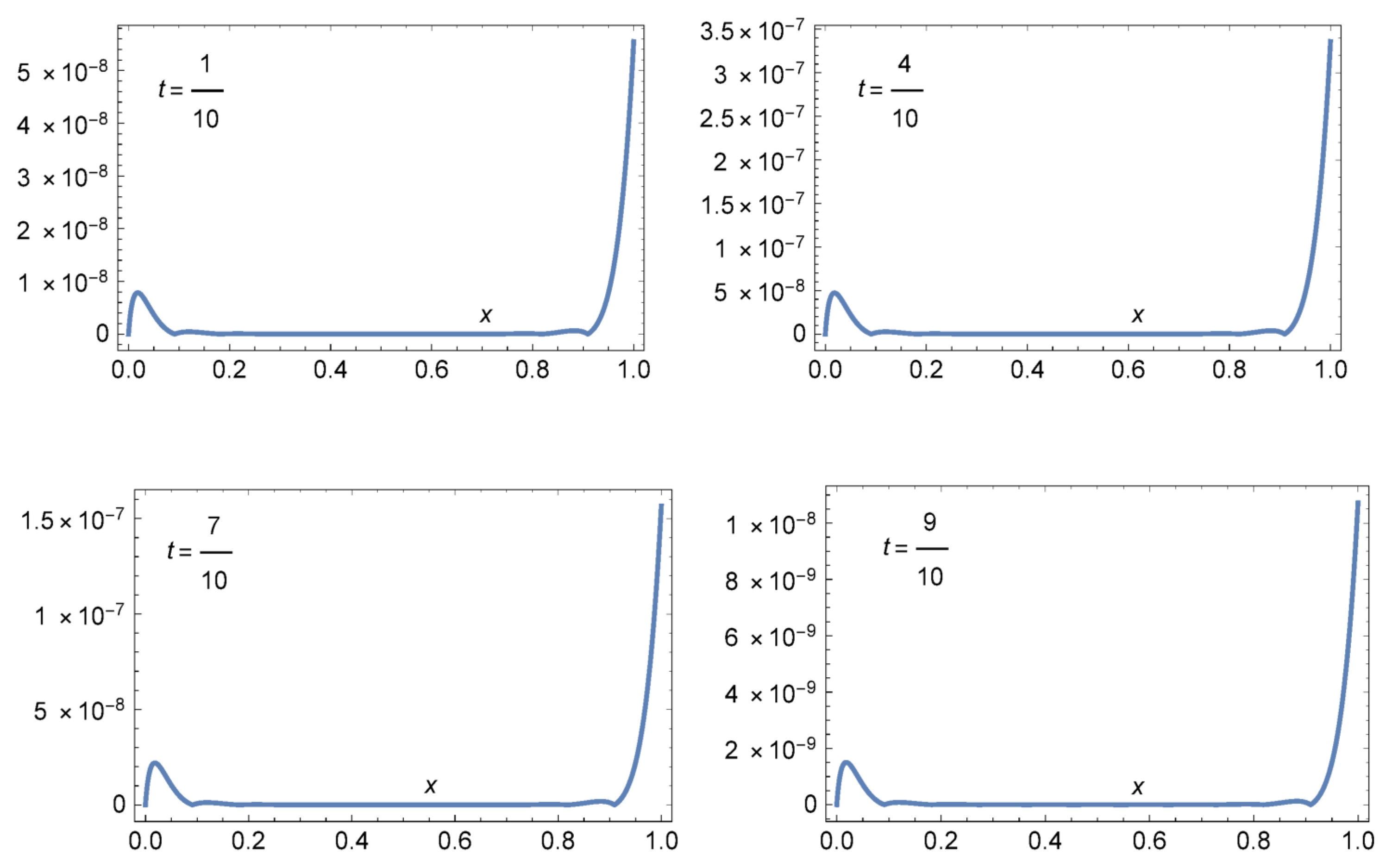
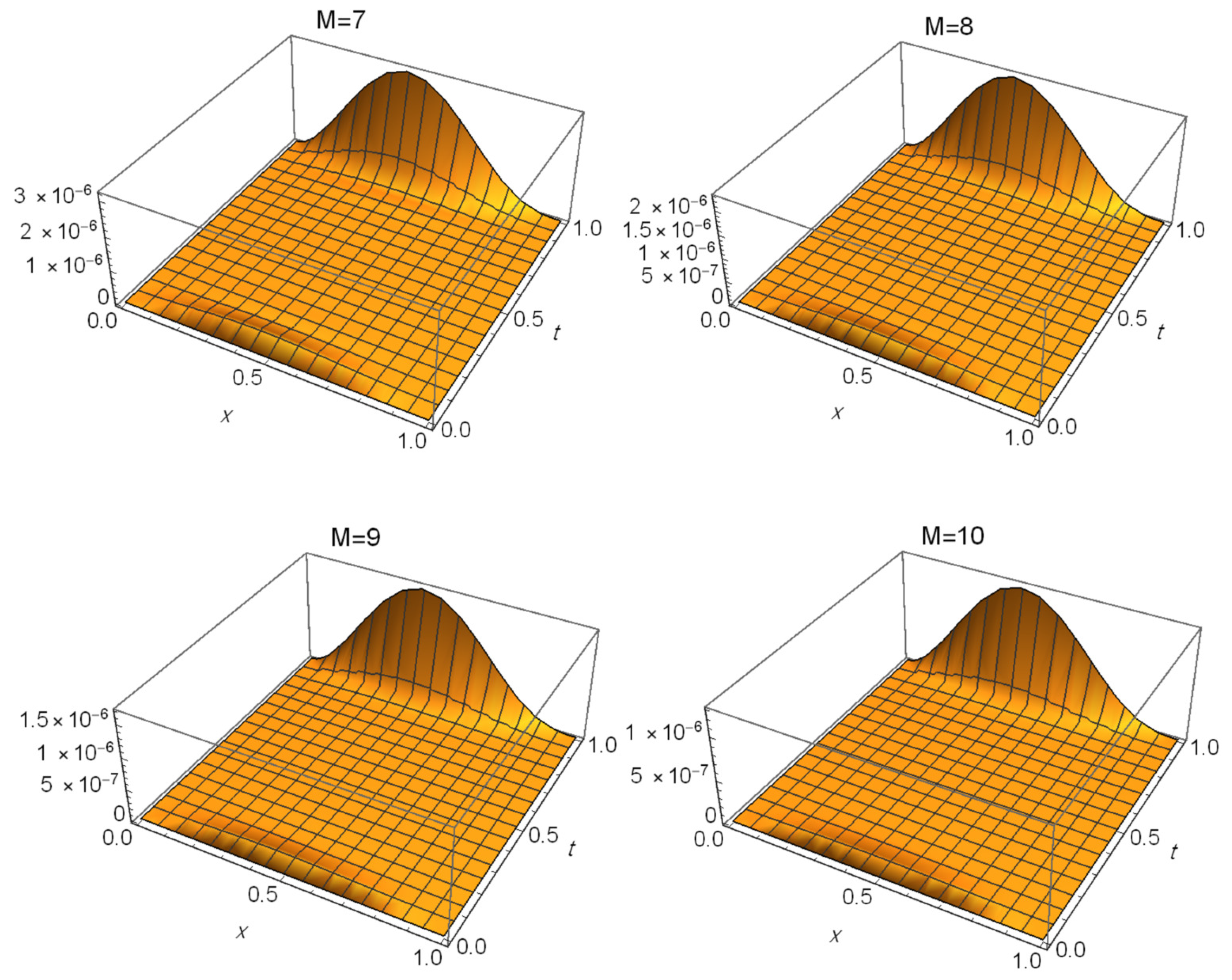
| (0.1, 0.1) | 1.38172 | 9.39553 | 4.40408 |
| (0.2, 0.2) | 5.6496 | 1.45969 | 1.25069 |
| (0.3, 0.3) | 3.8616 | 2.30332 | 9.78697 |
| (0.4, 0.4) | 5.51946 | 1.13216 | 2.85139 |
| (0.5, 0.5) | 1.5361 | 9.11035 | 4.00171 |
| (0.6, 0.6) | 1.1336 | 2.9774 | 2.52177 |
| (0.7, 0.7) | 8.73609 | 6.51013 | 3.62756 |
| (0.8, 0.8) | 8.17378 | 7.40989 | 4.7107 |
| (0.9, 0.9) | 1.09754 | 9.7457 | 6.21363 |
| Method in [51] | Our Method | Method in [51] | Our Method | Method in [51] | Our Method | |
| (0.1, t) | 6.36 | 1.38172 | 5.66 | 9.39553 | 4.92 | 5.00897 |
| (0.2, t) | 1.79 | 3.8989 | 1.59 | 2.65122 | 1.38 | 1.4134 |
| (0.3, t) | 2.70 | 5.88305 | 2.41 | 4.00043 | 2.09 | 2.13262 |
| (0.4, t) | 3.03 | 6.58352 | 2.70 | 4.47677 | 2.34 | 2.38648 |
| (0.5, t) | 2.74 | 5.95898 | 2.44 | 4.0521 | 2.12 | 2.16101 |
| (0.6, t) | 2.02 | 4.421075 | 1.80 | 3.00633 | 1.56 | 1.60246 |
| (0.7, t) | 1.16 | 2.58006 | 1.03 | 1.75445 | 8.99 | 9.35108 |
| (0.8, t) | 4.50 | 1.03006 | 4.00 | 7.0045 | 3.48 | 3.73307 |
| (0.9, t) | 7.12 | 1.71464 | 6.34 | 1.16598 | 5.51 | 6.21363 |
| z | ||||||
|---|---|---|---|---|---|---|
| 0.1 | 6.56903 | 5.74638 | 3.72786 | 1.64911 | 3.39914 | 4.54984 |
| 0.2 | 1.85363 | 1.62151 | 1.05193 | 4.65317 | 9.54927 | 1.2782 |
| 0.3 | 2.79693 | 2.44669 | 1.58727 | 4.65317 | 1.43938 | 1.92666 |
| 0.4 | 3.12993 | 2.73802 | 1.77627 | 7.85731 | 1.61144 | 2.15696 |
| 0.5 | 2.833 | 2.47828 | 1.60778 | 7.11206 | 1.4571 | 1.95037 |
| 0.6 | 2.10183 | 1.83867 | 1.19285 | 5.27661 | 1.07429 | 1.43797 |
| 0.7 | 1.22658 | 1.07302 | 6.96172 | 3.07955 | 6.16875 | 8.25706 |
| 0.8 | 4.89695 | 4.28383 | 2.77937 | 1.22961 | 2.38728 | 3.19545 |
| 0.9 | 8.15143 | 7.13133 | 4.64319 | 2.05545 | 3.7767 | 5.05522 |
| Method in [51] | Our Method | Method in [51] | Our Method | Method in [51] | Our Method | |
| (0.1, t) | 7.73 | 8.70227 | 7.98 | 5.91726 | 8.26 | 3.15499 |
| (0.2, t) | 1.57 | 2.43683 | 1.66 | 1.65698 | 1.75 | 8.83338 |
| (0.3, t) | 1.95 | 3.63484 | 2.10 | 2.47164 | 2.26 | 1.31732 |
| (0.4, t) | 2.17 | 3.99944 | 2.12 | 2.71964 | 2.32 | 1.44899 |
| (0.5, t) | 2.09 | 3.53402 | 1.86 | 2.40324 | 2.00 | 1.27976 |
| (0.6, t) | 1.64 | 2.53687 | 1.46 | 1.72524 | 1.44 | 9.18057 |
| (0.7, t) | 1.00 | 1.41757 | 8.90 | 9.64113 | 8.20 | 5.12531 |
| (0.8, t) | 4.10 | 5.35954 | 3.64 | 3.64548 | 3.18 | 1.93545 |
| (0.9, t) | 6.83 | 8.36451 | 6.07 | 5.6901 | 5.27 | 3.01595 |
| z | ||||
|---|---|---|---|---|
| 0.1 | 6.81302 | 3.61427 | 1.47142 | 4.53549 |
| 0.2 | 1.90786 | 1.01209 | 4.12041 | 1.26997 |
| 0.3 | 2.84596 | 1.50968 | 6.14636 | 1.89416 |
| 0.4 | 3.13167 | 1.66115 | 6.76329 | 2.08391 |
| 0.5 | 2.76754 | 1.4679 | 5.97675 | 1.84108 |
| 0.6 | 1.98696 | 1.05377 | 4.29084 | 1.3213 |
| 0.7 | 1.11052 | 5.88874 | 2.39807 | 7.38075 |
| 0.8 | 4.19985 | 2.22663 | 9.06843 | 2.78951 |
| 0.9 | 6.55692 | 3.47544 | 1.41483 | 4.35778 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd-Elhameed, W.M.; Al-Harbi, A.K.; Alqubori, O.M.; Alharbi, M.H.; Atta, A.G. Collocation Method for the Time-Fractional Generalized Kawahara Equation Using a Certain Lucas Polynomial Sequence. Axioms 2025, 14, 114. https://doi.org/10.3390/axioms14020114
Abd-Elhameed WM, Al-Harbi AK, Alqubori OM, Alharbi MH, Atta AG. Collocation Method for the Time-Fractional Generalized Kawahara Equation Using a Certain Lucas Polynomial Sequence. Axioms. 2025; 14(2):114. https://doi.org/10.3390/axioms14020114
Chicago/Turabian StyleAbd-Elhameed, Waleed Mohamed, Abdulrahman Khalid Al-Harbi, Omar Mazen Alqubori, Mohammed H. Alharbi, and Ahmed Gamal Atta. 2025. "Collocation Method for the Time-Fractional Generalized Kawahara Equation Using a Certain Lucas Polynomial Sequence" Axioms 14, no. 2: 114. https://doi.org/10.3390/axioms14020114
APA StyleAbd-Elhameed, W. M., Al-Harbi, A. K., Alqubori, O. M., Alharbi, M. H., & Atta, A. G. (2025). Collocation Method for the Time-Fractional Generalized Kawahara Equation Using a Certain Lucas Polynomial Sequence. Axioms, 14(2), 114. https://doi.org/10.3390/axioms14020114








