Abstract
Hierarchy analysis of the knowledge graphs aims to discover the latent structure inherent in knowledge base data. Drawing inspiration from topic modeling, which identifies latent themes and content patterns in text corpora, our research seeks to adapt these analytical frameworks to the hierarchical exploration of knowledge graphs. Specifically, we adopt a non-parametric probabilistic model, the nested hierarchical Dirichlet process, to the field of knowledge graphs. This model discovers latent subject-specific distributions along paths within the tree. Consequently, the global tree can be viewed as a collection of local subtrees for each subject, allowing us to represent subtrees for each subject and reveal cross-thematic topics. We assess the efficacy of this model in analyzing the topics and word distributions that form the hierarchical structure of complex knowledge graphs. We quantitatively evaluate our model using four common datasets: Freebase, Wikidata, DBpedia, and WebRED, demonstrating that it outperforms the latest neural hierarchical clustering techniques such as TraCo, SawETM, and HyperMiner. Additionally, we provide a qualitative assessment of the induced subtree for a single subject.
MSC:
68T09; 68T30; 68Q15; 68Q10
1. Introduction
Knowledge graphs (KGs) are gaining more attention due to their potential to integrate with large language models, addressing issues such as hallucination and token limitations. A KG [1] comprises entities and relations, where entities are regarded as nodes and relations as different types of edges. In semantic-oriented interpretation, KGs are composed of triples in the format ⟨subject, predicate, object⟩, which serve as the fundamental units of graphs.
Relations, in KGs, represent the connections between entities, which can be categorized into various types based on their nature and context. Hierarchical relationships, such as Is-A and Part-Of, capture taxonomic and compositional structures, respectively. Associative relationships describe general associations, while causal relationships define cause–effect links. Temporal and spatial relationships capture time and location dependencies, whereas functional, ownership, and membership relationships depict roles, control, and group inclusion. Additionally, dependency and social relationships represent dependencies and interpersonal or professional connections, respectively. These diverse relationship types enrich KGs, enabling more sophisticated queries and insights.
Various factors motivate learning hierarchies from KGs. A key advantage of hierarchical configurations lies in their ability to emulate the innate human tendency to categorize and arrange data for enhanced comprehension and recall, which is particularly beneficial for tasks such as reasoning. The hierarchical structure facilitates the identification of relationships between various entities/concepts portraying parent–child associations among them. Hierarchical KGs streamline the categorization and organization of knowledge, enabling efficient navigation and reinforcement through semantic inference. The existing KGs commonly include hierarchy-like information, for example ⟨England, /location/location/contains, Pontefract/Lancaster⟩ within Freebase [2], or offer an ontology that hierarchically organizes information about classes and concepts, DBpedia [3].
Although some research endeavors have explored hierarchical structures [4,5], they often necessitate supplementary data or alternative methodologies to gather hierarchical insights. The quest for a method capable of autonomously and effectively replicating the semantic hierarchy remains a persisting challenge. A crucial consideration in hierarchy analysis for KGs is discovering significant relationships among nodes and identifying a hierarchical configuration immerse within the graph. This challenge is further amplified by the need to accurately capture semantic meanings of the nodes and edges in the KG [6,7]. This procedure frequently involves using algorithms like hierarchical clustering and graph embedding methods to reveal underlying patterns in KGs.
In our previous work [8], a subject of a triple is described as a single path in the tree built by the nested Chinese Restaurant process (nCRP). Each subject is represented by a singular path in the tree and ‘composed’ of the topics on the path. It is a fundamental drawback in the proposed approach for subject modeling because a specific sequence of topics is expected to encompass the entire thematic content of the subject. Such an approach presents a combinatorial challenge as the nCRP aims to delineate a corpus’s thematic essence with increasing levels of specificity. Consequently, similar topics may reappear at different points in the tree to reflect their relevance to the subject theme. For instance, although the tree has already learned the separate topics of two subjects, ‘artist’ and ‘writer,’ when a subject emerges that combines these two, it generates a new composite topic rather than referencing the two pre-existing topics. Due to the exponential increase in nodes, mastering deeper levels of learning becomes demanding, leading to the truncation of nCRP trees, typically at the third tier. As a result, each subject is represented by a few topics that encapsulate its thematic content, potentially blending multiple themes and resulting in a broader and more complex tree structure during inference. The development of a hierarchical topic model that permits a subject to use topics in various branches of the tree representing a hierarchy is what we are aiming at.
To overcome the mentioned issues, we are investigating novel and manageable methods for extracting hierarchical information from KGs. Our strategy is to adopt a non-parametric probabilistic model for the hierarchical clustering of KG data. It uncovers the latent subject-specific distributions on paths within the hierarchy or tree, constructing a subtree denoting each subject. An entire tree is a collection of local subtrees representing individual subjects. The method allows one to identify cross-thematic topics while keeping individual topics in separate subtrees. Therefore, the proposed method here clusters subject entities, corresponding predicates, and object entities, providing insight into their distributions across subtrees. We accomplish that by adapting the nested hierarchical Dirichlet process (nHDP).
We quantitatively evaluate our model using four datasets: Freebase, Wikidata, DBpedia, and WebRED. We demonstrate that it outperforms the latest neural-network-based hierarchical clustering techniques, such as TraCo, SawETM, and HyperMiner. Additionally, we provide a qualitative assessment of the induced subtrees for subjects.
Overall, our contributions presented in this work are as follows:
- Adapting the nHDP to analyze and construct hierarchy based on knowledge graphs by replacing documents with subjects, words with predicates, and objects;
- Proposing a set of new coverage measures to evaluate hierarchies;
- Evaluating, both quantitatively and qualitatively, hierarchical structures by conducting experiments on four real-world datasets such as Freebase, Wikidata, DBpedia, and WebRed;
- Obtaining a first-rate performance of the proposed nHDP_KG method, surpassing other neural-network-based hierarchical clustering techniques, including TraCo, SawETM, and HyperMiner.
2. Related Work
2.1. Hierarchy of Knowledge Graphs
The hierarchy of knowledge graphs has been a topic of interest in various research studies. hTransM [9] proposes a hierarchy-constrained approach for link prediction in knowledge graphs, emphasizing the importance of hierarchical structures in enhancing prediction performance. HAKE [10] introduces hierarchy-aware knowledge graph embedding (HAKE) to model semantic hierarchies in knowledge graphs. This path-based paper [4] creates a hierarchical structure of subject clusters, utilizing taxonomy induction. HamQA [11], a hierarchy-aware multi-hop question answering framework on knowledge graphs to align hierarchical information between question contexts and knowledge graphs. These studies collectively highlight the significance of hierarchy in knowledge graphs and propose various methods to leverage hierarchical structures for improved representation and prediction.
Two categories of hierarchical topic models exist. The first category comprises traditional models like hLDA [12] and its variations [13], which use Gibbs sampling or variational inference for parameter estimation. However, these models struggle with large datasets due to high computational costs. The second category consists of neural models such as TraCo, SawETM, and HyperMiner. TraCo [14] is a novel neural hierarchical topic model designed to address key challenges in topic modeling. TraCo leverages a new transport plan dependency (TPD) approach to model the dependencies between hierarchical topics as optimal transport plans, ensuring sparse and balanced dependencies. This method enhances the affinity between parent and child topics while maintaining diversity among sibling topics. Additionally, TraCo incorporates a context-aware disentangled decoder (CDD), which decodes documents using topics at each level individually and incorporates contextual semantic biases. This ensures that topics at different levels capture distinct semantic granularities, thereby improving the rationality of topic hierarchies. Through extensive experiments on benchmark datasets, TraCo demonstrates superior performance over state-of-the-art baselines in terms of the affinity, rationality, and diversity of topic hierarchies. SawETM [15] is a novel hierarchical topic model that addresses limitations of existing models by capturing dependencies and semantic similarities between topics across different layers. Unlike traditional models that assume topics are independent, SawETM uses the Sawtooth Connection technique to link topics across layers, enhancing coherence and depth in topic hierarchies. Additionally, it integrates a robust inference network within a deep hierarchical VAE framework, combining deterministic and stochastic paths to improve text data modeling. This design prevents common issues like posterior collapse and enables SawETM to discover rich, multi-layered topic representations. Experiments demonstrate that SawETM outperforms other models, providing deeper and more interpretable topics and better document representations. HyperMiner [16] introduces a novel method for topic modeling that addresses the shortcomings of Euclidean embedding spaces by utilizing hyperbolic space, renowned for its tree-like characteristics conducive to hierarchical data representation. By measuring distances between words and topics in this space, HyperMiner captures the underlying semantic hierarchies more effectively. General words, which frequently co-occur with others, are positioned near the center, while specific words are placed near the boundary, reflecting their unique contextual relationships. Additionally, hyperbolic space allows for the incorporation of prior structural knowledge, preserving hierarchical relations through distance constraints. Our contributions include leveraging hyperbolic space for enhanced semantic hierarchy mining and designing a graph-based learning scheme to guide the creation of meaningful topic taxonomies. Extensive experiments show that HyperMiner outperforms baseline methods in topic quality and document representation.
2.2. Knowledge Graph Embedding
Knowledge graph embedding is a method to map knowledge graphs from discrete graph space to continuous vector space. It is powerful to allow knowledge graphs to be easily integrated with deep learning algorithms. TransE [17] is based on the idea that when translated by valid predicates, subject embeddings should be positioned near object embeddings. This concept is formalized through an objective function that is optimized using stochastic gradient descent to derive the embeddings. DistMult [18] is a bilinear model that captures interactions between entities and relations in a knowledge graph. It represents relations as diagonal matrices and computes scores using the dot product of entity embeddings and relation matrices. ComplEx [19] extends DistMult by modeling relations as complex-valued vectors. It is capable of capturing both asymmetric and symmetric relations in the knowledge graph by utilizing complex-valued embeddings. RotatE [20] is a geometric model that represents relations as rotations in the complex vector space. It captures compositionality and symmetry within the knowledge graph by rotating entity embeddings based on relation embeddings. HolE [21] is a bilinear model that represents relations as circular correlations between the embeddings of entities. It captures the compositional nature of relations in the knowledge graph by computing circular correlations between entity embeddings.
3. Hierarchy Construction as Topic Modeling
We define a knowledge graph (KG), , as a collection of triples. Each fact triple is composed of a subject entity s that is linked to an object entity o via a predicate p. Formally, where is a triple, and , , and are the sets of subjects, predicates, and objects in , respectively. KGs are rarely bipartite regarding and . In other words, entities can take on the role of both subjects and objects in , thus, .
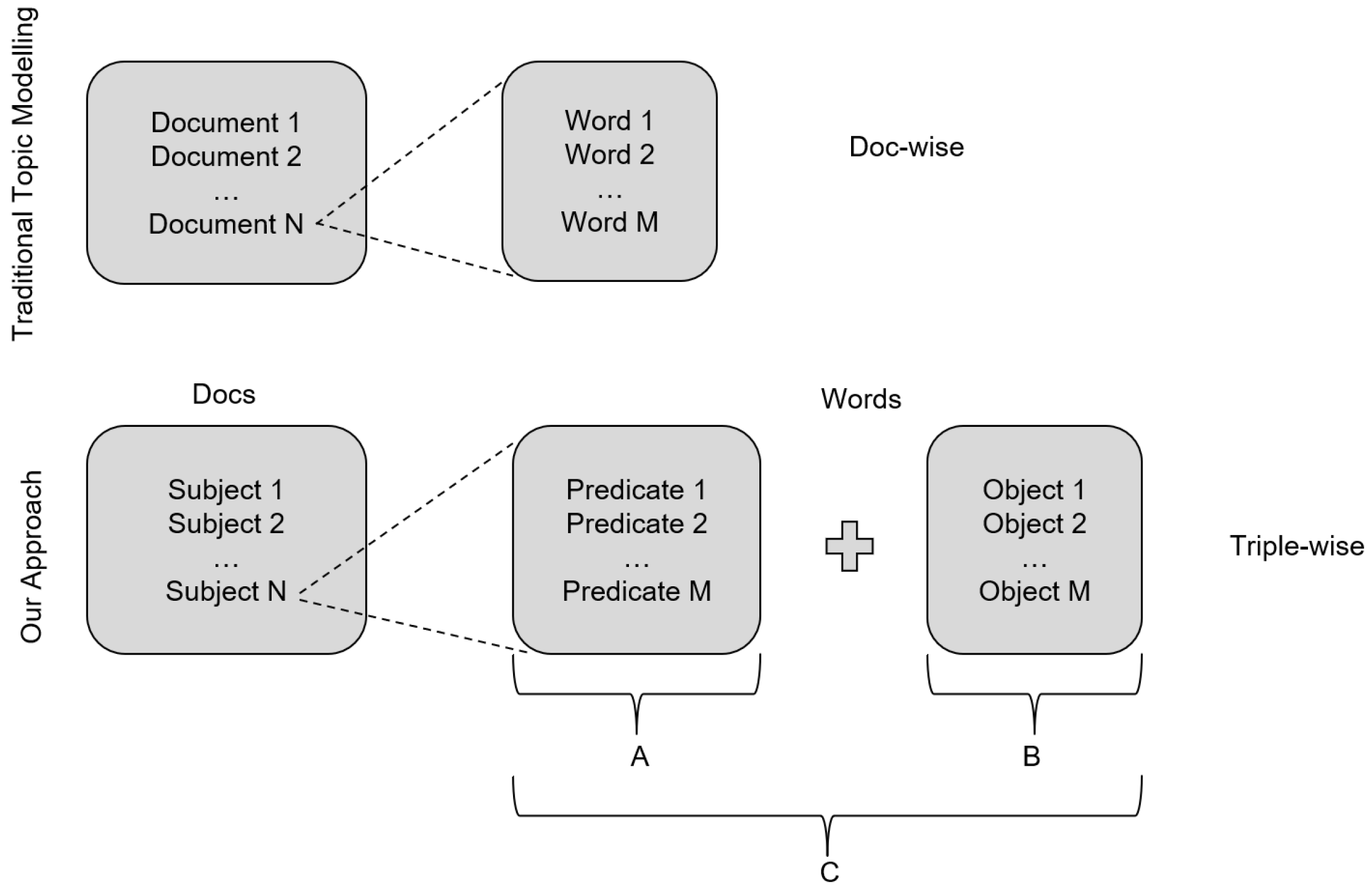
The essential aspect of the proposed method is to treat a hierarchy construction task as topic modeling. To accomplish that, we convert graph triples into documents and words. As in Figure 1, a subject is a document in topic modeling terminology and is described by all its predicates and objects . Furthermore, the predicates and objects are treated as words in the topic modeling problem.
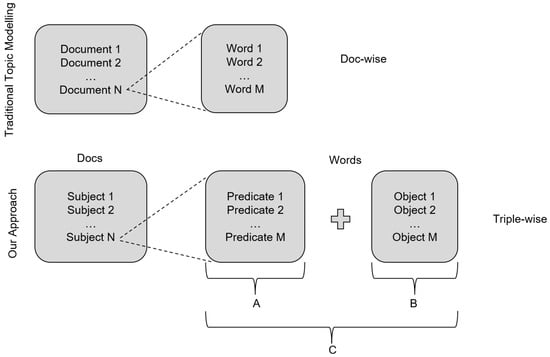
Figure 1.
‘Conversion’ of triple components into documents and words related to them: a given subject, i.e., document, is represented by words (C) composed of both predicates (A) and objects (B) of all triples containing the subject.
In the presented work, we use the following convention: a subject is described by words ; here, is the set of words describing . The set of all subjects is denoted as , and words, , belong to the set of all words, called vocabulary , which means .
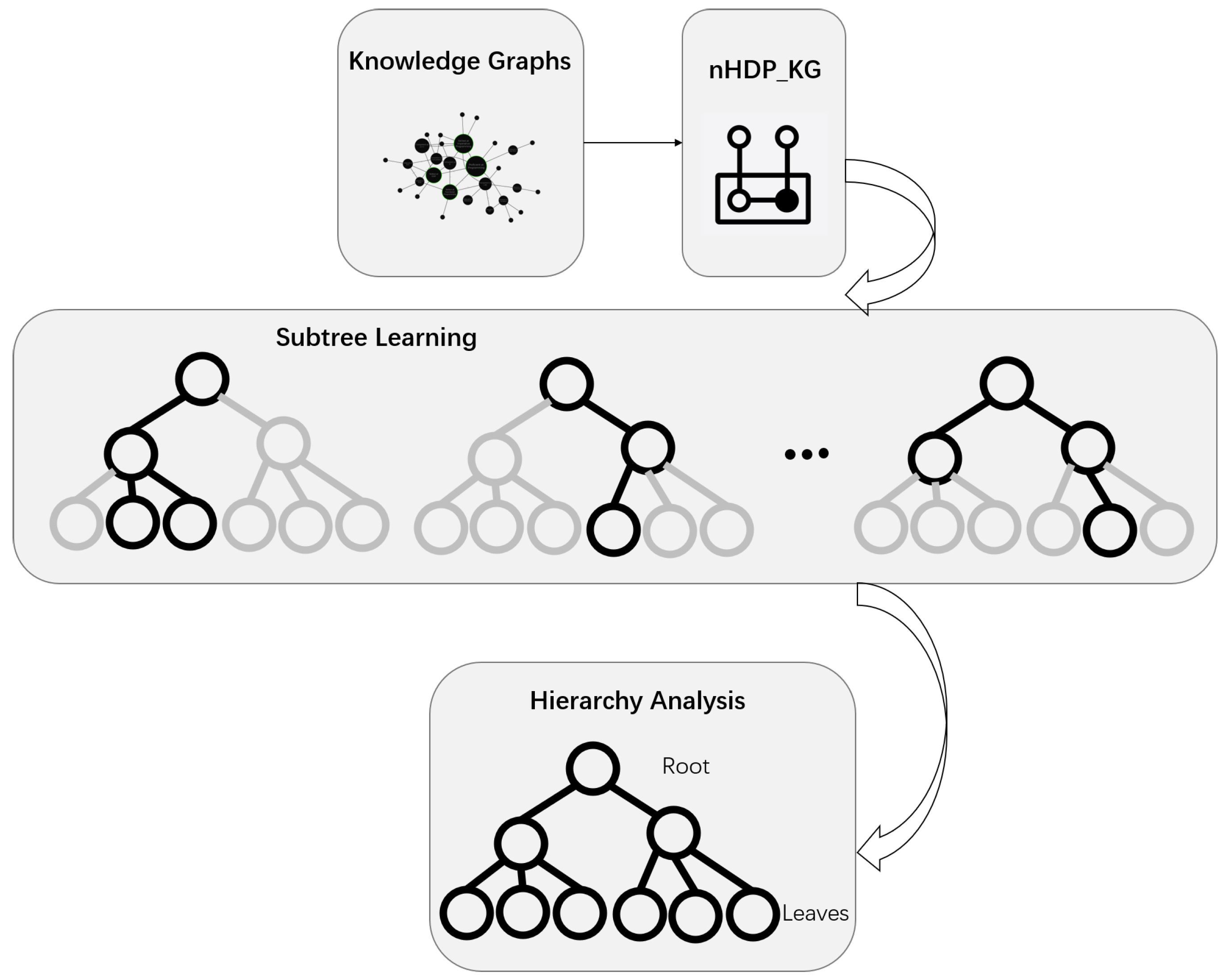
We aim to develop a hierarchical representation of a KG in which the global tree structure captures general topics at the root level and specific topics at the leaf level. Nodes in this tree represent collections of entities with shared semantics. Unlike nCRP, where topics are restricted to a single path, our proposed approach, called hereafter nHDP_KG, allows each subject entity to access the entire tree. A subject-specific distribution over paths assigns higher probabilities to particular subtrees, reflecting the relevance of certain topics to the subject. This reveals subject-specific distributions on hierarchical paths, with subtrees representing individual subjects. A complete tree comprises localized subtrees associated with the individual subjects. This approach facilitates the identification of cross-thematic topics while preserving the distinctiveness of individual topics in separate subtrees. The proposed method clusters subject entities and associated words and offers insight into their distributions across subtrees. To achieve this, we employ the nested hierarchical Dirichlet process (nHDP). The overall workflow is depicted in Figure 2.
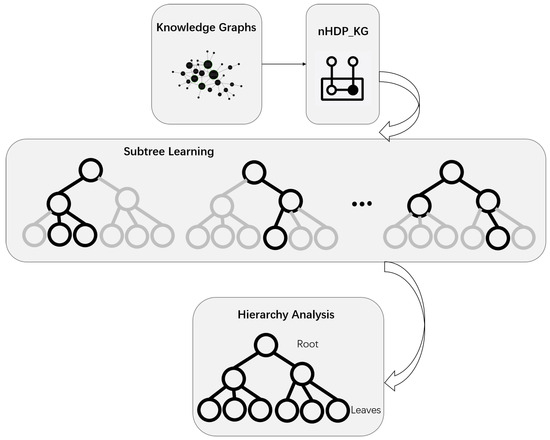
Figure 2.
nHDP_KG Workflow.
4. Description of Proposed Method
The proposed method uses a nested hierarchical Dirichlet process (nHDP), which extends the hierarchical Dirichlet process (HDP), i.e., a Bayesian nonparametric model used in machine learning, to infer distributions over distributions. The nHDP expands upon the HDP by allowing a flexible tree-structured exchangeable random partition to model hierarchical clustering.
Let us describe nHDP via a sequence of short descriptions of necessary concepts.
4.1. Dirichlet Process
The Dirichlet process (DP) [22,23] is a stochastic process used in Bayesian nonparametric models to represent distributions over data. The mixture models divide a data set into categories based on statistical characteristics that all members within a cell share. The parameters of the mixture and a reasonable number of traits for describing the data can be learned using Dirichlet process priors. Mathematically, it is defined as
where the data are represented with a family of distributions and the corresponding parameters . These parameters are drawn from the discrete, theoretically infinite distribution G, which the DP permits to exist. The data W are divided as a result of this discreteness in accordance with how the atoms are distributed among the chosen parameters . where is a scaling parameter, and is a base probability measure.
4.2. Hierarchical Dirichlet Process
The hierarchical Dirichlet process (HDP) [23,24] is a multi-level variation of the DP. It relies on the notion that the base distribution on the continuous space might be discrete. This is advantageous since a discrete distribution enables the placement of probability mass on a subset of atoms (data points) through multiple draws from the DP in advance. As a result, various data groups with different probability distributions can share the same atoms. It is necessary to create a distinct base, yet the atoms are unknown. By obtaining the base from a DP prior, the HDP models these atoms. As a result, groupings go through a hierarchical procedure:
Similar to the DP, inference requires explicit representations of the HDP. The representation is based on two levels of Sethuraman’s stick-breaking construction [25]. Sample G is as in the following construction
Here, can be understood as the percentage of a unit-length stick that is broken from the rest. Furthermore, then sample is according to the following equation:
This form is the same as the previous equation with the crucial difference that G is discrete, which causes atoms to repeat. All random variables in this representation are i.i.d., which helps variational inference techniques.
4.3. Adapted Nested Hierarchical Dirichlet Process
The nHDP_KG, an adapted framework from nHDP [23], allows each subject, i.e., s from , to use the entire hierarchical structure while acquiring subject-specific distributions over semantically related topics. Each subject is represented by a primary trajectory corresponding to its core themes, along with branches that incorporate additional topics. The process of constructing a subject’s topic distribution is divided into two stages: first, developing the subject’s distribution over paths within the tree, and second, defining the word distribution conditioned on reaching specific nodes along these paths.
4.3.1. Global Tree: Distribution on Paths
All subject entities share a global tree drawn according to the stick-breaking construction via nHDP.
This tree is just an endless collection of Dirichlet processes with a continuous base distribution and an inter-DP transition rule. This rule states that a path is followed from a root Dirichlet process by drawing for where is a constant root index, and indexes the DP connected to the topic . With the nested HDP, we use each Dirichlet process in a global tree as a base distribution for a local DP drawn independently for each entity rather than following pathways according to the global tree.
Then, for each subject s, a local tree will be constructed. For each , the corresponding can be drawn as per the DP,
as was discussed, the In contrast, will have various probability weights on the same atoms. Therefore, the probability of a path in the tree will vary for each subject; it will have the same nodes as T, while each subject will have its unique distribution on the tree. A stick-breaking construction to represent this subject-specific DP is
The HDP samples distribution with base measure . This results in a subject-specific distribution over paths in the globally shared tree T.
The key difference from the HTM is that now each subject has its own distribution over the shared hierarchical topic structure rather than all subjects sharing the same tree distribution.
4.3.2. Local Tree: Generating a Subject
A technique exists for choosing word-specific paths that are thematically compatible with the tree for subject s, meaning they frequently reuse the same path while allowing for off-shoots.
The process goes as follows:
- For each node in the tree T, draw a beta-distributed random variable that acts as a stochastic switch.
- To generate a word n in a subject s, start at the root node and recursively traverse down the tree according to until reaching some node . With probability , emit the topic at this node. Otherwise, continue traversing down the tree according to .
This recursive process generates a path and selects a node and topic for each word.
The probability of a word being assigned topic is
where the first term is the probability of path according to , and the second term is the probability of selecting topic at that node.
This process allows each word to follow its own path in the tree according to the subject-specific distribution , capturing unique topic combinations within a subject.
4.4. Stochastic Variational Inference
A method of stochastic variational inference is applied to approximate the posterior inference of the nested hierarchical Dirichlet process (nHDP). The process involves the optimization of local variational parameters for a specific group of individuals, followed by a progression along the natural gradient of the overall variational parameters. More inference details can be found in [23].
4.4.1. Greedy Subtree Selection
For each subject, a subtree is selected from the global tree T using a greedy algorithm that maximizes the variational objective function. Starting from the root, nodes are sequentially added based on their activation status, where an activated node is one whose parent is in the subtree but the node itself is not.
4.4.2. Stochastic Updates for Local Variables
Index Pointer. is the index pointer to the atom in global DP for the th break in . The prior is . The updates for it are
Topic Indicator. is the topic indicator for word n in subject s, is the prior distribution. The variational distribution on the path for word is
where the prior term is the tree-structured prior of the nHDP,
Stick Proportion. is the stick proportion for local DP for node ; is the prior distribution. The variational parameter updates for the subject-level stick-breaking proportions are
In textual terms, the statistic concerning the first parameter denotes the anticipated quantity of words in subject s that either traverse or halt at node . The statistic related to the second parameter signifies the anticipated quantity of words from subject s whose trajectories traverse the same ancestor but subsequently transition to a node with an index exceeding j based on the indicators from the subject-level stick-breaking construction of .
Switch Probability. is the switch probability for node i, is the prior distribution. The variational parameter updates for the switching probabilities are similar to those of the subject-level stick-breaking process but collect the statistics from in a slightly different way,
The statistic for the first parameter represents the anticipated word count related to the topic at node . On the other hand, the statistic for the second parameter indicates the expected number of words that transit through node without ending there. The first parameter statistic denotes the projected word quantity associated with the topic at node . The second parameter statistic signifies the anticipated number of words that traverse through node but do not stop there.
4.4.3. Stochastic Updates for Global Variables
Once the subtree is selected and the local subject-specific variational parameters are updated for each subject s in mini-batch m, we adjust the global q distribution parameters, including the topics and the global stick-breaking proportions , using the natural gradient.
Topic Probability. is the topic probability vector for node i, is the prior distribution. To update the Dirichlet q distributions on each topic stochastically, start by constructing the vector containing the necessary statistics based on the information in sub-batch m.
For each w from 1 to , the vector represents the anticipated quantity of words with index w derived from topic across subjects indexed by . The modification for the corresponding q distribution is then calculated.
Stick Proportion. is the stick proportion for the global DP for node i. is the prior distribution. The sufficient statistics for the q distribution on from the subjects in mini-batch m are gathered along with . This process is carried out as a first step. This step is essential for the estimation of the q distribution on . The sufficient statistics collected from the subjects in mini-batch m are crucial for this estimation.
The initial value increases the count of subjects in mini-batch m containing atom in their subtree. The subsequent value increases the occurrence of an atom with a higher index value in the same Dirichlet process used by a subject in sub-batch m. The global variational parameters are updated based on these values.
5. Experiment Setup
The proposed methodology has been evaluated on four datasets: FB15k-237, DBpedia, Wikidata, and WebRED. Evaluation of the obtained models (hierarchies) was performed based on hierarchy topic quality, simple coverage, subject-based coverage, and vocabulary-based coverage (see Section 5.2 for a detailed description of the used metrics).
5.1. Dataset
Some numerical details of the used datasets are presented in Table 1.

Table 1.
Data Statistics.
FB15k-237: The FB15k-237 dataset [26], derived from the FB15k dataset [17], was created by eliminating duplicate and reverse triples. It is based on a Freebase version from approximately 2013. It consists of 272,115 triples built using 14,541 different entities and 237 predicates. Due to the resource restriction for a fair comparison, we randomly extracted triples containing 10,000 subjects for our hierarchical clustering analysis. This process has resulted in a subset with 10,000 subjects, 197,497 triples, 22,982 entities, and 237 predicates.
DBpedia: The DBpedia dataset [3] was created by randomly querying DBpedia for entities in various classes such as ‘Politician’, ‘CelestialBody’, ‘MusicalWork’, ‘WrittenWork’, ‘Film’, ‘Scientist’, ‘Artwork’, ‘NaturalPlace’, ‘Building’, ‘Infrastructure’, ‘PopulatedPlace’, ‘Artist’, ‘Software’, and ’Athlete’. A total of 75 entities were extracted for each class, resulting in 908 subjects, 57,191 triples, 31,202 entities, and 345 predicates. The goal of this dataset was to test a model on a hierarchy different from WordNet taxonomy. The hierarchy of DBpedia classes were obtained from the DBpedia ontology mapping available on the DBpedia website http://mappings.dbpedia.org/server/ontology/classes/ (accessed on 13 March 2025).
Wikidata: The dataset Wikidata5m [27] is a large-scale KG containing millions of entities, each aligned with a corresponding Wikipedia page. This dataset combines information from Wikidata and Wikipedia, allowing for the evaluation of link prediction on entities that have not been seen before. The dataset is provided in three parts: a graph, a corpus, and aliases. The inductive data splits are used in our paper. Due to the resource restriction and a fair comparison, we randomly extracted triples containing 10,000 subjects. This process has yielded a dataset with 10,000 subjects, 44,896 triples, 27,608 entities, and 374 predicates.
WebRED: WebRED [28] is a dataset designed for relation extraction, sourced from various publicly available internet texts covering diverse domains and writing styles. The dataset includes approximately 200 million weakly supervised examples for supervised pre-training and 110,000 human-annotated examples for fine-tuning and model evaluation. As before, to ensure a fair comparison under resource constraints, 10,000 subjects were randomly selected for hierarchical clustering analysis. The resulting dataset consists of 10,000 subjects, 45,712 triples, 16,595 entities, and 428 predicates.
5.2. Evaluation Metrics
5.2.1. Hierarchy Topic Quality
A comprehensive method for constructing coherence measures in hierarchical tree structures to enhance the interpretability of hierarchical topics has been introduced in [29]. The topic coherence is calculated within branches and levels of the tree. It leads to two measures Branch Topic Quality (BTQ) and Level Topic Quality (LTQ). They are aggregated to obtain Hierarchical Topic Quality (HTQ), which serves as a metric for assessing and benchmarking topic models.
The above-mentioned measures are an extension of the unifying framework presented in [30]. The original framework defines coherence measures using four sets: segmentation (S), confirmation measure (M), probability estimation (P), and aggregation (). Based on these, a configuration space is created.
The authors of [29] made a modification by adding a hierarchical word set (). The new configuration space is . They also adapted the input of the segmentation set to account for hierarchical structures. In this method, hierarchical word sets () include words () from both parent and child nodes at a specific branch b () and words () from all nodes at a particular level l ().
For our experiments, we use an open source implementation of the configuration space for computing coherence of words representing a topic https://github.com/piskvorky/gensim/blob/develop/gensim/models/coherencemodel.py (accessed on 13 March 2025). The measure’s segmentation (), probability estimation (), and confirmation measure () are utilized, using a sliding window of size 110 and combining indirect cosine measures with normalized pointwise mutual information (NPMI) [29]. The confirmation measures are aggregated with a diversity term to produce BTQ and LTQ as below. The arithmetic mean of BTQ and LTQ yields the hierarchical topic quality (HTQ) for the entire topic model. The equations are summarized as below:
5.2.2. Coverage
To evaluate the constructed hierarchies more thoroughly, we propose a set of new coverage measures based on the work presented in [31]. The proposed metrics are Simple Coverage, Coverage based on Subjects, and Coverage based on Vocabulary.
A coverage evaluation process requires some preprocessing. If a given topic is represented by an ordered set of words , we replace in a subject (set of words describing it, Section 3) all occurrences of top words from with the first word .
Simple Coverage—SimCov: The hierarchy tree should organize topics from general to specific. Higher-level topics, closer to the root node, should encompass a broad range of subjects, while lower-level topics, closer to the leaf nodes, should exhibit narrower coverage. The coverage is calculated as follows:
where is a topic z, is the number of times the word appears in a subject s from , and k is the number of topics at level L. The average coverage of all topics at the same level reflects the model’s coverage capability. As the tree becomes deeper, with each successive level moving closer to the leaves, the coverage score should decrease accordingly.
Coverage based on Subjects—SubCov: Based on the idea of simple coverage we focus on evaluating coverage of all topics at a given level. The value of the coverage is calculated using the following equations:
where is the frequency of co-occurrence of the first word with a word across all subjects; and are the number of occurrences of the word and , respectively, and k is the number of topics at level L. Pointwise mutual information () calculates the similarity between word pairs across all subjects. The PMI score is computed for each topic in the tree. The average coherence of all topics at the same level is calculated to assess the model’s coverage.
As a tree goes deeper, the coverage score is expected to decrease with lower levels, aligning with the assumption that more specific topics have narrower coverage.
Coverage based on Vocabulary—VocCov: In contrast to the two previous approaches, from the perspective of words describing the specific topics, the number of top words in higher-level topics should be less than that in lower-level topics. Now, the equations are
where this time is the frequency of co-occurrence of the first word and a word in the whole vocabulary; and is the number of times the words and occurs, and k is the number of topics at level L. Pointwise mutual information () is employed to calculate the similarity of pairs in the whole vocabulary. The PMI score for each topic in the tree is computed.
The average coherence of all topics at the same level is used to reflect the coverage of the model. As the tree goes deeper, the level decreases, and the coverage score should increase as per the assumption.
5.3. Experiment Environment
For our experiments, the nHDP_KG model was configured with a batch size of 20 and 1000 iterations. The hyperparameter beta0, which controls the Dirichlet base distribution, was set to 1, and the maximum depth of generated hierarchies was set to 3. In practice, the number of topics is dataset-dependent and varies based on the desired depth of topic exploration.
6. Experiment Results
The results of the conducted experiments have been evaluated. The evaluation is performed quantitatively and qualitatively.
6.1. Quantitative Evaluation
Hierarchical Topic Quality: The comparison of the performance of the proposed method for constructing a hierarchy based on KGs with other approaches on the diverse datasets (FB15k-237, WikiData, DBpedia, and WebRED) is shown in Table 2. The nHDP_KG and hLDA methods do not require embedding of triples, while the latest three models were used with five different embeddings: TransE, DistMult, ComplEx, RotatE, and HoIE. The used metrics are branch topic quality (BTQ), level topic quality (LTQ), and hierarchical topic quality (HTQ).

Table 2.
Performance comparison for various models over datasets (best performance in bold).
The nHDP_KG consistently displayed a better performance across all datasets, with HTQ values ranging from 0.795 to 0.484, demonstrating the highest performance on FB15k-237 and the lowest on WebRED and surpassing other models. In contrast, hLDA exhibited a notably lower performance with HTQ values of 0.627 on FB15k-237 and 0.244 on WebRED, indicating its inferior effectiveness on these datasets.
The Traco model, employing various embeddings, exhibited varying levels of performance: TransE embedding performed relatively well on FB15k-237 (HTQ = 0.385) but poorly on WikiData (HTQ = 0.014) and WebRED (HTQ = 0.190). Similarly, DistMult, ComplEx, RotatE, and HoIE embeddings displayed comparable trends, showcasing optimal performance on FB15k-237 and a noticeable decline on WikiData.
SawETM demonstrated overall superior performance compared to TraCo, except on DBpedia, particularly with TransE and DistMult embeddings. TransE led to the highest HTQ of 0.626 on FB15k-237 among all embeddings for this model. Performance decreased on WikiData, with the highest HTQ values of 0.203 for TransE and HoIE.
HyperMinor generally exhibited the best performance among models utilizing embeddings on FB15k-237. DistMult embedding attained the highest HTQ on FB15k-237 (0.692) and sustained a relatively strong performance across other datasets. TransE, ComplEx, RotatE, and HoIE embeddings also demonstrated robust outcomes, with HTQ values consistently surpassing those observed for TraCo and SawETM across all datasets.
In conclusion, in general, the nHDP_KG model outperformed other models across all datasets. HyperMinor consistently achieved high HTQ values across various datasets, particularly with the DistMult embedding. TraCo and SawETM models displayed varying performance, with SawETM generally outperforming TraCo. The hLDA model exhibited the least effectiveness in this evaluation.
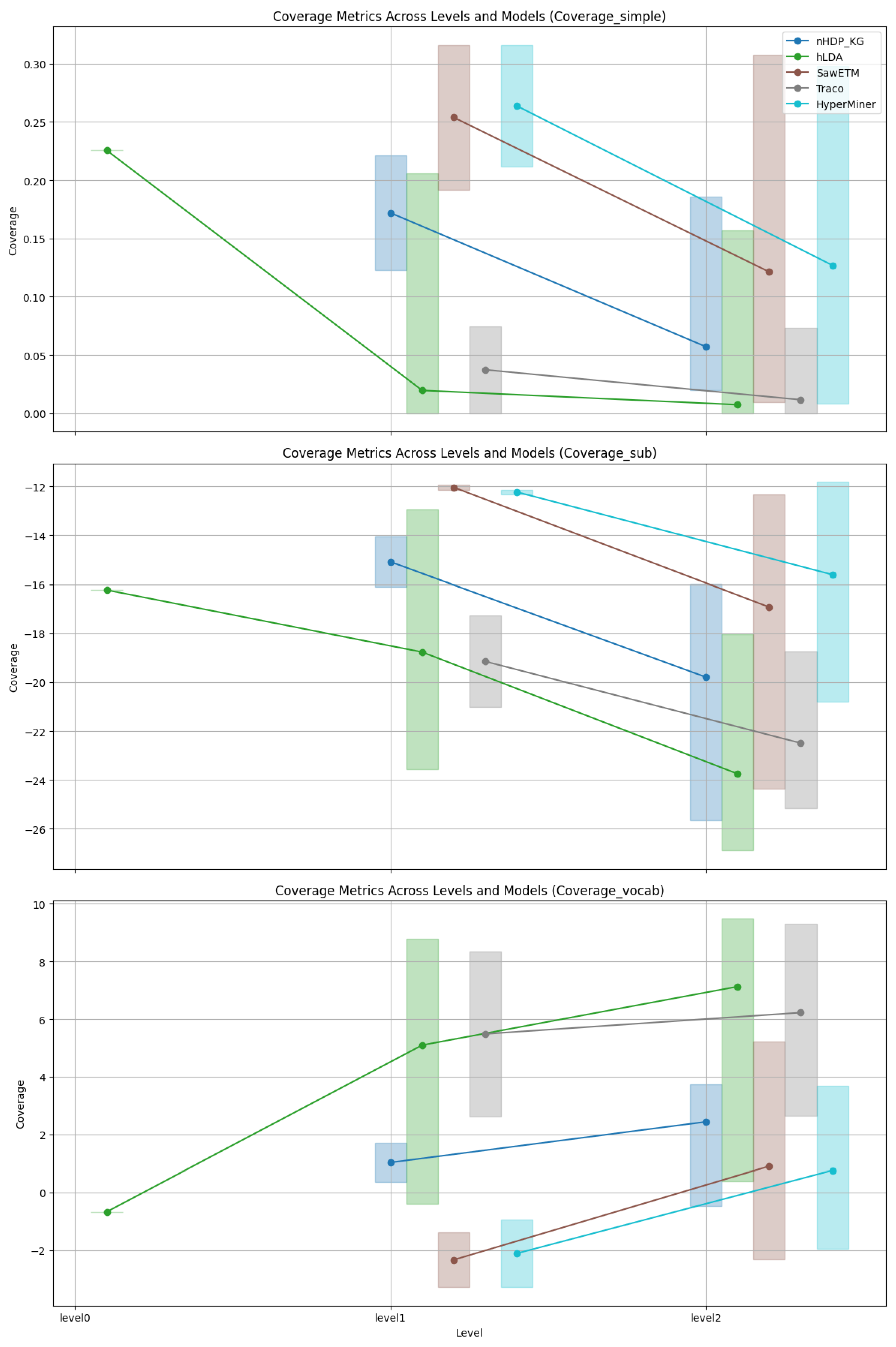
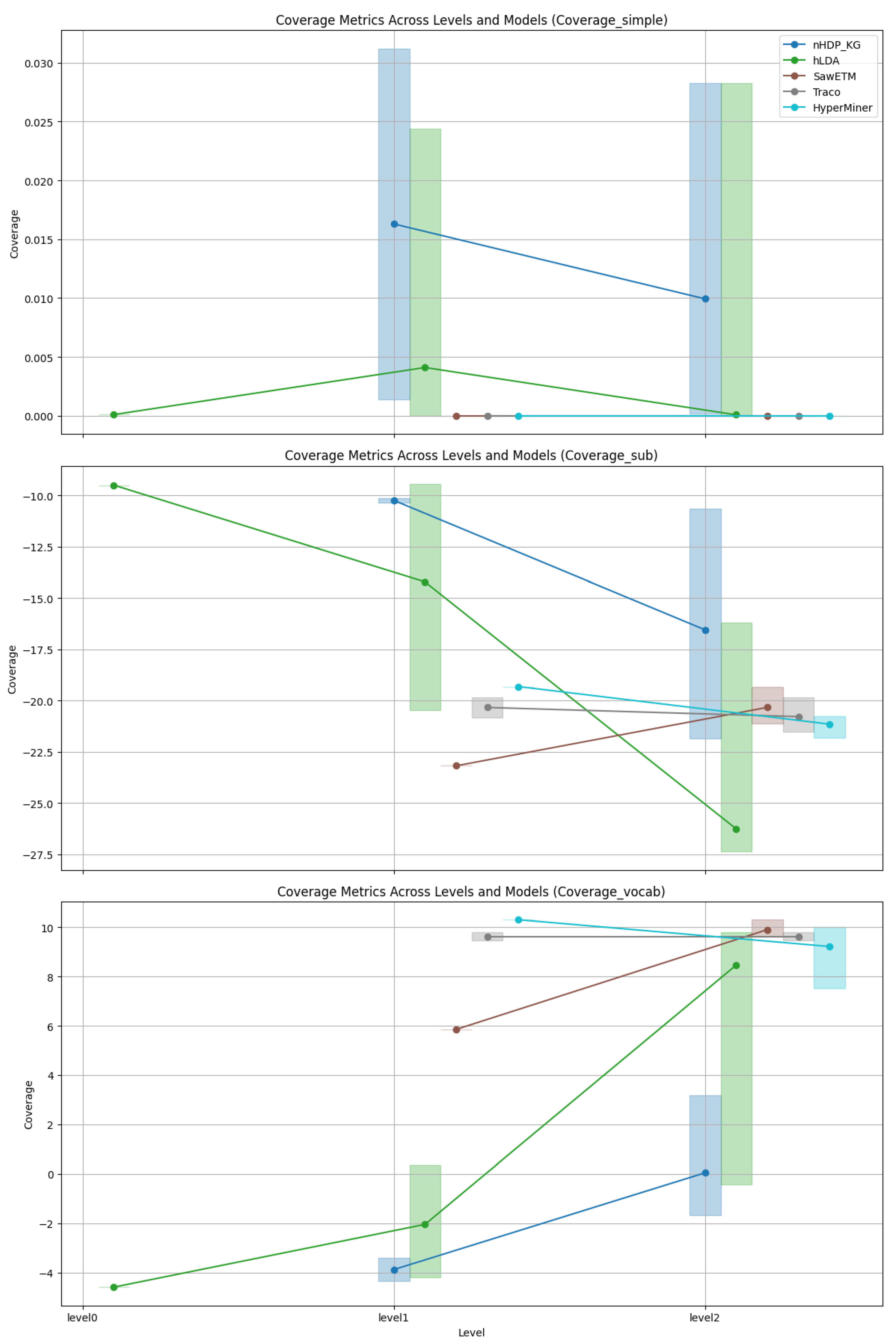
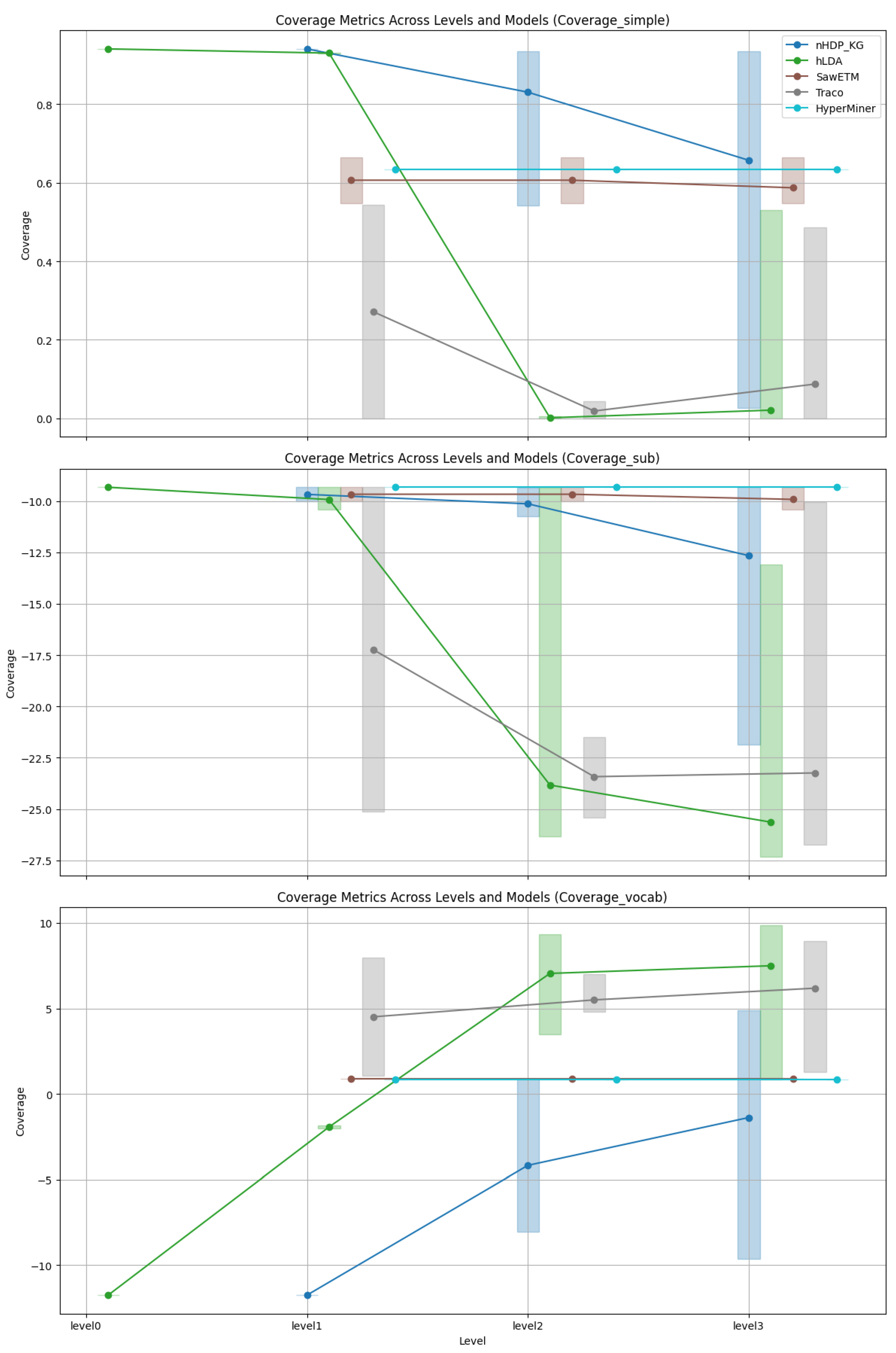
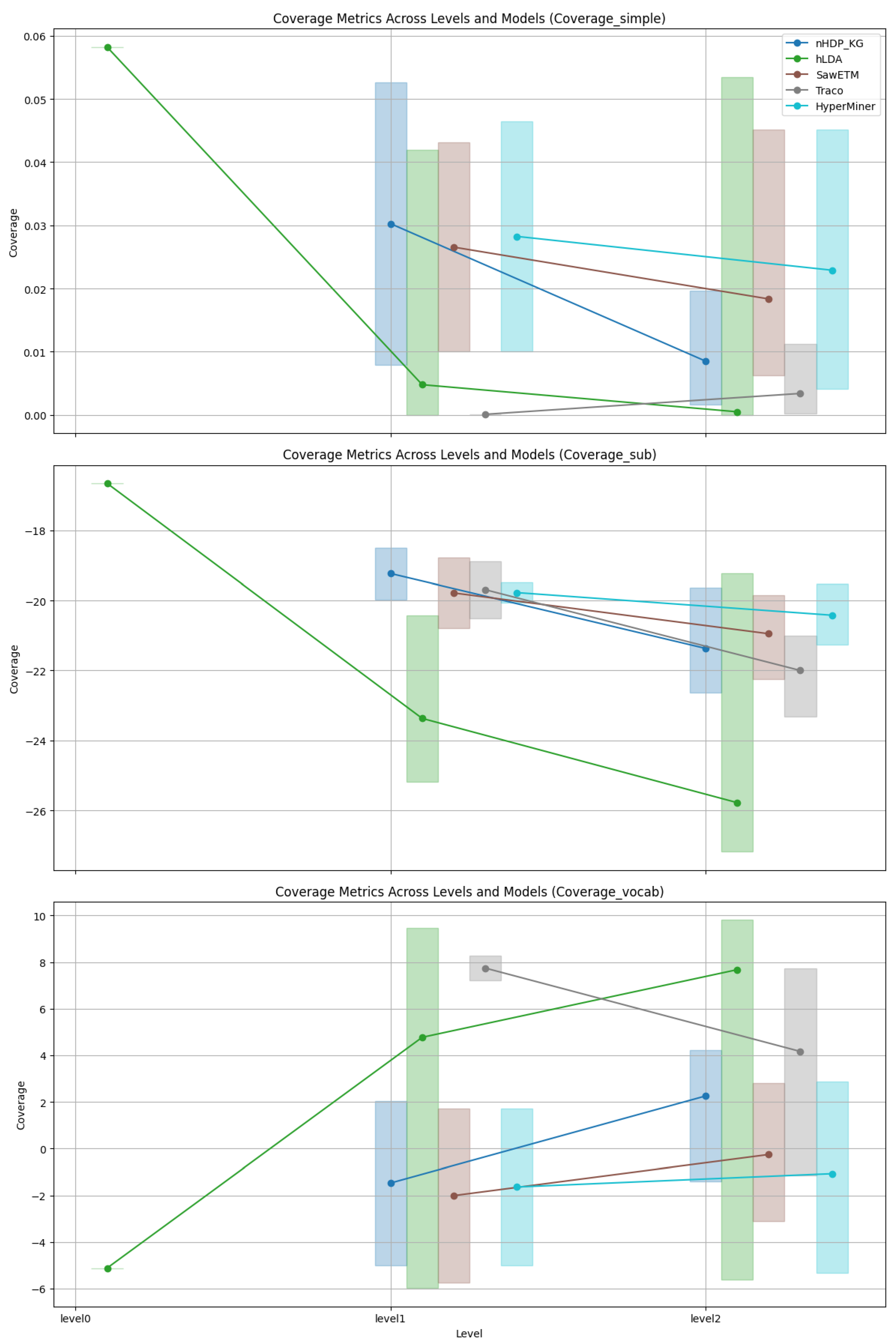
Coverage: As depicted in Figure 3, Figure 4, Figure 5 and Figure 6 an analysis was conducted to observe the patterns in coverage measurements at different levels of hierarchy for various models across all datasets. The coverage scores are presented within a minimum and maximum value range, with the average coverage score indicated by dots for all levels of the constructed hierarchies. It is noteworthy that for hLDA, we have root level values due to the inherent characteristics of the technique.
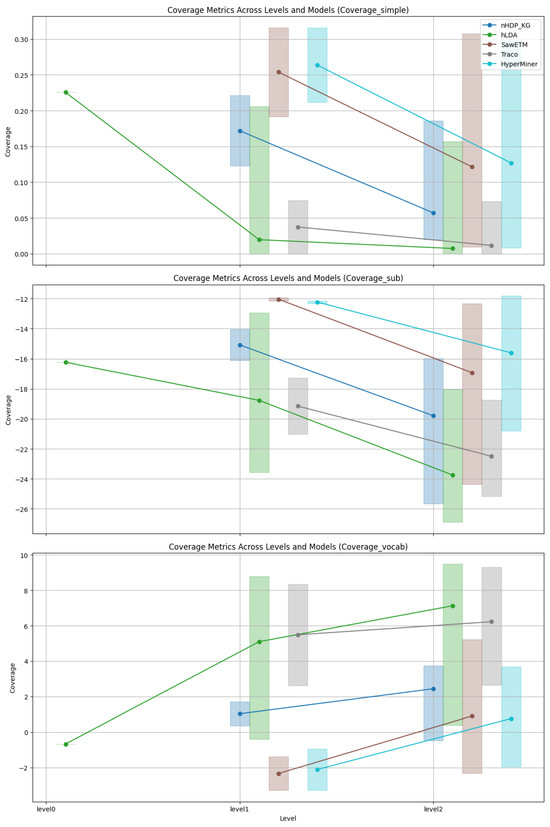
Figure 3.
Coverage trends of FB15k-237.
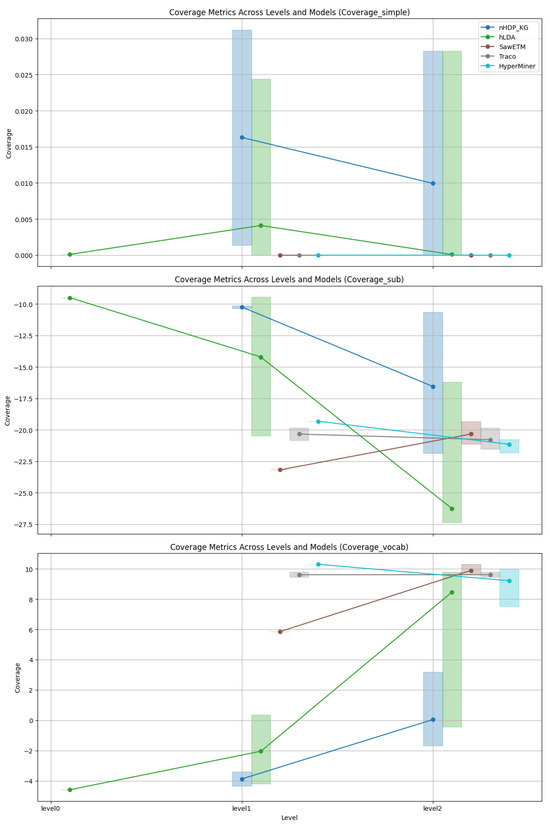
Figure 4.
Coverage trends of Wikidata.
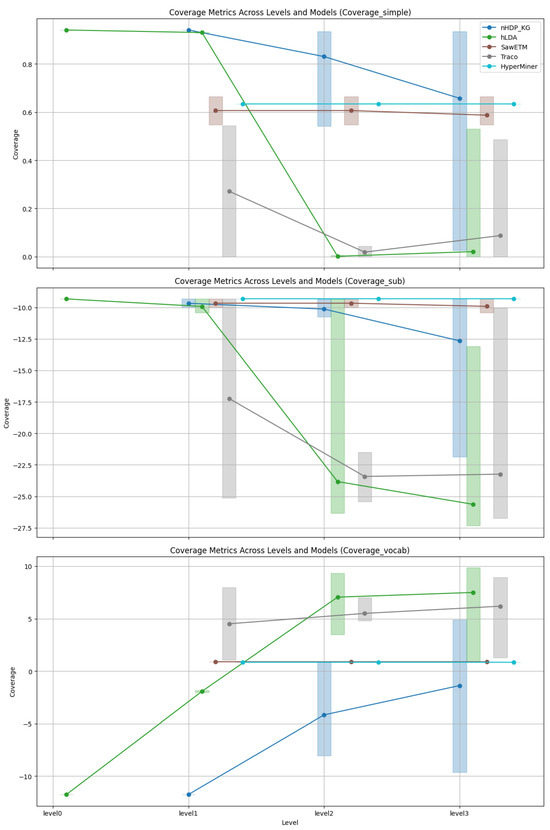
Figure 5.
Coverage trends of DBpedia.
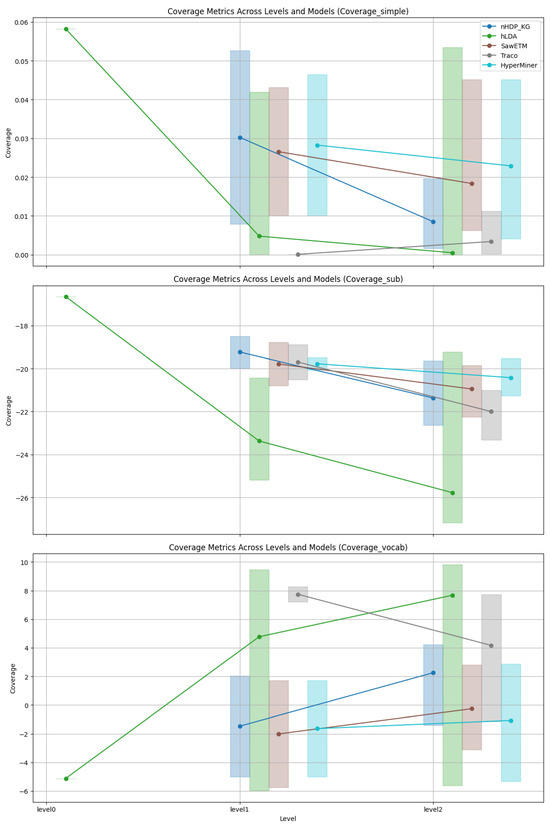
Figure 6.
Converge trends of WebRED.
Figure 3, Figure 4, Figure 5 and Figure 6 show the coverage values. Each figure includes the range and mean values of coverage at different tree levels. Only our method provides the coverage value at the tree top; the other methods provide values at levels one and two. The bars represent variation in coverage, and dots (connected via lines) denote mean values.
The visual representations in Figure 3 illustrate the coverage trends for FB15k-237. The results from nHDP_KG, SaWETM, and HyperMiner show a clear decline in SimCov and SubCov as coverage levels increase, while VocCov demonstrates an upward trend, consistent with our initial assumptions. In contrast, hLDA and TraCo display relatively stable performance with only minor fluctuations across all metrics at levels 1 and 2.
In Figure 4, the coverage trends for Wikidata are depicted. The metric SimCov shows a decline in both nHDP_KG and hLDA from level1 to level2, while SawETM, TraCo, and HyperMiner display consistent levels without a decreasing trend. Regarding the SubCov metric, nHDP_KG and hLDA exhibit a continuous decrease across levels, whereas TraCo and HyperMiner demonstrate less pronounced but still evident reductions, with SawETM displaying an unexpected increase. Conversely, the VocCov metric indicates an upward trend for nHDP_KG and hLDA, suggesting enhanced vocabulary coverage at higher hierarchical levels. On the other hand, SaWETM and TraCo show relatively stable trends with slight improvements, while HyperMiner exhibits variability but ultimately lower coverage at level 2.
In Figure 5, the graph depicts the trends in coverage for Dbpedia. The metrics SimCov and SubCov show a clear decreasing trend as levels increase for nHDP_KG and hLDA, whereas SawETM and HyperMiner exhibit a relatively consistent coverage. TraCo, on the other hand, does not display any noticeable coverage trend in this context. Conversely, nHDP_KG and hLDA demonstrate an increasing trend in the VocCov metric, suggesting enhanced vocabulary coverage at higher levels. Additionally, TraCo shows a slight increase across all levels, while SawETM and HyperMiner maintain a more stable performance.
Figure 6 illustrates the coverage trends for WebRED. The nHDP_KG model shows a sharp decline in the SimCov metric as levels increase, while other models demonstrate more stable or slightly decreasing trends. However, TraCo does not efficiently capture the hierarchy. In the SubCov metric, nHDP_KG exhibits a consistent decrease across levels, while the other models display moderate declines. On the other hand, in the VocCov metric, nHDP_KG shows an increasing trend, indicating enhanced vocabulary coverage at higher levels. In contrast, other models show more stability or slight increases in this metric, with TraCo showing a decline.
In summary, nHDP_KG and hLDA successfully generate hierarchical trees that align with our coverage expectation regarding values of coverage for different levels of a hierarchy (Section 5.2.2), demonstrating their ability to capture the intended topic structure. In contrast, other models appear to be weaker in this regard.
6.2. Qualitative Evaluation
To illustrate constructed hierarchies, we show a subtree representing specific subjects. The subtree nodes are derived from predicates and objects characterized by subject entities, i.e., elements of triples . The ultimate goal is to analyze the distribution pattern of these terms within the context of subject-based hierarchical clustering.
Before we present a more detailed analysis, let us look at Table 3 and Table 4. They represent two subjects Gene Wilder and Primetime Emmy Award for Outstanding Lead Actress in a Comedy Series ‘linked’ to the same subtree. The column nodeID indicates—with nodes in bold—parts of the subtree containing relevant predicates and objects. It starts with the top—(1,)—and then with nodes at lower levels: (1, 1) would indicate the first node (from left) at level one, while (1, 1, 2)—for example—the second node at level two attached to node (1, 1). The next column contains words (predicates and objects) associated with the nodes and subtrees. As can be seen, most of them are predicates, which appear more frequently across multiple subjects; objects are much less frequent, so they are much less present in the subtree. Moreover, it has to be said that many different subjects exist in the datasets, and the relatively small size of constructed hierarchy trees means that a single subtree is ‘shared’ among many subjects. At the same time it is observed—looking of Table 3 and Table 4—that different parts of the subtree are associated with different subjects.

Table 3.
Top 5 word distributions for the topic: Gene Wilder.

Table 4.
Top 5 word distribution for the topic: Primetime Emmy Award for Outstanding Lead Actress in a Comedy Series.
Table 3 includes the top five word distribution results for Gene Wilder. It contains a hierarchical representation of Gene Wilder’s career and achievements. Wilder’s roles in films, nominations, awards, musical contributions, and other aspects of his career are linked with a branch of the subtree described by nodes (1,), (1, 1), (1, 1, 1), and (1, 1, 3). The predicates in italics and with a dot are found in the Original_Triples describing Gene Wilder.
Each level represents a different level of detail throughout the subtrees, from broad categories such as people/person/profession or /film/actor/film./film/performance/film to finer details such as specific award_nominnee or nominated_for. For instance, a triple indicating a film performance ⟨…, p =/film/actor/film/film/performance/film, o =/m/0bsb1d⟩ would be categorized under the film performance subtree (1, 1, 3), while an award nomination triple ⟨…, p =/award/award_nominee/award_nominations./award/award_nomination/award, o =/m/09qvc0⟩ falls under the awards subtree (1, 1, 1). This hierarchical structuring of triples into subtrees facilitates a comprehensive and nuanced analysis of Gene Wilder’s career, illustrating the interconnectedness of his professional achievements in a detailed manner.
Table 4 provides a hierarchical representation of the entity Primetime Emmy Award for Outstanding Lead Actress in a Comedy Series, encompassing its multifaceted properties and objects. The hierarchical structure, indicated by the nodes (1,), (1, 2), (1, 2, 1), (1, 2, 4), organizes various predicates into a branch of the subtree. For example, the subtree under (1, 1) highlights categories related to professions, awards, and film performances, while (1, 2) includes financial and demographic attributes such as currency and ethnicity. The subtree (1, 2, 1) expands on geographical and administrative details, such as locations and time zones. Compared with Original_Triples, the node (1, 2, 4) contains predicates of all (except one) triples describing the subject Primetime Emmy Award for Outstanding Lead Actress in a Comedy Series. Again, the hierarchical organization allows for a comprehensive and nuanced analysis of the subject.
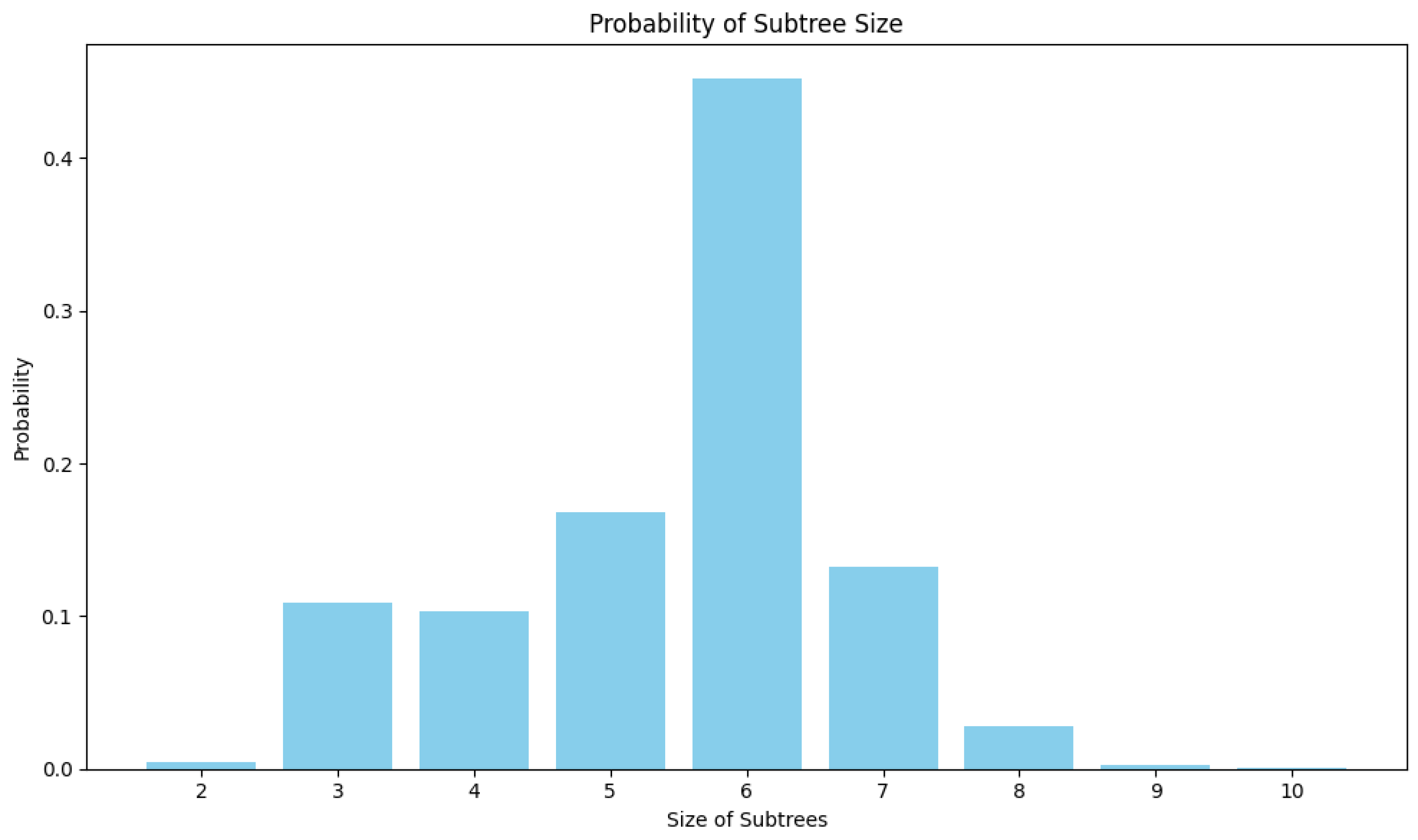
An interesting aspect of subtrees representing subjects in the constructed hierarchies is their size. A single subject can be represented by a very small subtree composed of two nodes or a large subtree of even ten nodes. Figure 7 presents the distribution of subtree sizes over all subjects. As it is seen, most of the subjects are depicted as six-node subtrees.
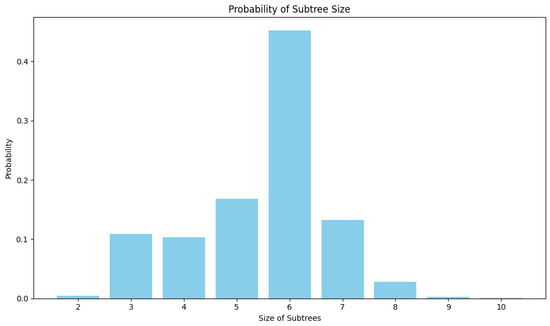
Figure 7.
Overall subtree size distribution.
6.3. Discussion and Limitation
Due to the nature of the technique, the performance of nHDP_KG is influenced by the choice of hyperparameters. For example, the base Dirichlet distribution is chosen as 1; other hyperparameters are selected as default: for the top-level DP concentration, , and for the second-level DP concentration, . For switching probabilities U, the beta distribution for the tree level prior is set to , and . The modification of the base Dirichlet parameter leads to changes in the inferred hierarchy.
Although the nHDP is designed to handle large datasets efficiently by a stochastic variational inference algorithm, it can still be a concern for computational complexity, particularly as the number of subjects and topics increase and deeper hierarchical structures are explored. Managing such a large number of topics and hierarchical trees could result in high computational demands during the inference and learning phases.
The complexity of the approach can be estimated on a step by step basis:—for tree construction and maintenance, it mainly depends on the tree size T, . For stochastic variational inference for the subtree for each subject with a minibatch —the time complexity is by selecting a sparse subtree and updating parameters based on word counts for each subject. For global tree parameters updates based on the minibatch statistics—the complexity depends on the tree size T and the vocabulary size V, . The overall complexity of our approach is .
For the comparison, the complexity of the deep-learning-based approach could be estimated in the following way: the embedding parameters depend on the encoder and decoder size; so, for n-dimensional embeddings for E entities, R relationships, and H hidden units, the estimated time complexity would be . We can see that even when our computational cost looks high, it depends on the data and vocabulary. In the case of deep learning, the complexity is heavily dependent on the embedding dimensions and model architecture, including hidden units and layers. In practice, our nHDP_KG usually took a few hours without GPU, yet the deep-learning-based models took 1–2 days with GPU. Using a parallel-based implementation could improve nHDP’s scalability. In the case of large data sizes, the inference for each subject can be performed simultaneously, i.e., the tree construction and updates for large T could be parallelized.
Furthermore, the quality of knowledge graphs (KGs) is paramount for our technique. We focused on exploring graph data with rich semantic information, i.e., graphs with many types of relations between nodes. The results confirm that the proposed approach works better for KGs with a higher ratio of triples to subjects, i.e., graphs with ‘enough’ predicates and objects to describe the subjects. Such a behavior can be explained by the nature of nHDP, which relies on the statistical analysis of relations to capture their distributions.
7. Conclusions
In conclusion, our study effectively applies the nested hierarchical Dirichlet process (nHDP) to analyze knowledge graphs, revealing subject-specific distributions and representing global knowledge graphs as local subtrees. Through quantitative evaluation of multiple models on various datasets, the proposed model outperforms the existing neural-network-based hierarchical clustering techniques, indicating its potential to advance the organization of large-scale knowledge bases. Additionally, qualitative assessment showcases the model’s ability to generate meaningful subtrees, providing insights into the structure and relationships within knowledge graphs and demonstrating the robustness and versatility of our approach.
Author Contributions
Conceptualization, Y.Z. and M.Z.R.; methodology, Y.Z. and Z.Y.; formal analysis, Y.Z. and Z.Y.; experiments and validation, Y.Z. and W.X.; writing—original draft preparation, Y.Z. and M.Z.R.; writing—review and editing, Z.Y., W.X., Z.Y. and M.Z.R.; supervision, Z.Y. and M.Z.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Discovery Grant from the Natural Science and Engineering Research Council of Canada (NSERC) grant number 2017-06245.
Data Availability Statement
The paper utilized several datasets, all of which were accessed on 30 March 2025. They are as follows: wikidata: https://deepgraphlearning.github.io/project/wikidata5m; WebRED: https://github.com/google-research-datasets/WebRED; freebase: https://paperswithcode.com/dataset/fb15k-237; The authors prepared one dataset, and the details are as follows: dbpedia: https://github.com/yujia0223/hkg/tree/main/data/dbpedia; dbpedia original source: https://www.dbpedia.org/resources/.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ji, S.; Pan, S.; Cambria, E.; Marttinen, P.; Philip, S.Y. A survey on knowledge graphs: Representation, acquisition, and applications. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 494–514. [Google Scholar] [CrossRef] [PubMed]
- Bollacker, K.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A Collaboratively Created Graph Database for Structuring Human Knowledge. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 12–19 June 2008; pp. 1247–1250. [Google Scholar]
- Lehmann, J.; Isele, R.; Jakob, M.; Jentzsch, A.; Kontokostas, D.; Mendes, P.N.; Hellmann, S.; Morsey, M.; Van Kleef, P.; Auer, S.; et al. Dbpedia–a large-scale, multilingual knowledge base extracted from wikipedia. Semantic Web 2015, 6, 167–195. [Google Scholar] [CrossRef]
- Pietrasik, M.; Reformat, M. Path based hierarchical clustering on knowledge graphs. arXiv 2021, arXiv:2109.13178. [Google Scholar]
- Pietrasik, M.; Reformat, M. A Simple Method for Inducing Class Taxonomies in Knowledge Graphs. In Proceedings of the European Semantic Web Conference; Springer: Cham, Germany, 2020; pp. 53–68. [Google Scholar]
- Croft, W. On two mathematical representations for “semantic maps”. Z. Sprachwiss. 2022, 41, 67–87. [Google Scholar] [CrossRef]
- Jalving, J.; Shin, S.; Zavala, V.M. A graph-based modeling abstraction for optimization: Concepts and implementation in plasmo. Math. Program. Comput. 2022, 14, 699–747. [Google Scholar] [CrossRef]
- Zhang, Y.; Pietrasik, M.; Xu, W.; Reformat, M. Hierarchical Topic Modelling for Knowledge Graphs. In Proceedings of the European Semantic Web Conference; Springer: Cham, Germany, 2022; pp. 270–286. [Google Scholar]
- Li, M.; Wang, Y.; Zhang, D.; Jia, Y.; Cheng, X. Link prediction in knowledge graphs: A hierarchy-constrained approach. IEEE Trans. Big Data 2018, 8, 630–643. [Google Scholar] [CrossRef]
- Zhang, Z.; Cai, J.; Zhang, Y.; Wang, J. Learning hierarchy-aware knowledge graph embeddings for link prediction. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3065–3072. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, Q.; Huang, X.; Duan, K.; Tan, Q.; Jiang, Z. Hierarchy-Aware Multi-Hop Question Answering Over Knowledge Graphs. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 2519–2527. [Google Scholar]
- Griffiths, T.; Jordan, M.; Tenenbaum, J.; Blei, D. Hierarchical topic models and the nested Chinese restaurant process. Adv. Neural Inf. Process. Syst. 2003. Available online: https://proceedings.neurips.cc/paper_files/paper/2003/file/7b41bfa5085806dfa24b8c9de0ce567f-Paper.pdf (accessed on 30 March 2025).
- Kim, J.H.; Kim, D.; Kim, S.; Oh, A. Modeling Topic Hierarchies with the Recursive Chinese Restaurant Process. In Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012; pp. 783–792. [Google Scholar]
- Wu, X.; Pan, F.; Nguyen, T.; Feng, Y.; Liu, C.; Nguyen, C.D.; Luu, A.T. On the Affinity, Rationality, and Diversity of Hierarchical Topic Modeling. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024. [Google Scholar]
- Duan, Z.; Wang, D.; Chen, B.; Wang, C.; Chen, W.; Li, Y.; Ren, J.; Zhou, M. Sawtooth Factorial Topic Embeddings Guided Gamma Belief Network. In Proceedings of the International Conference on Machine Learning. PMLR, Virtual, 18–24 July 2021; pp. 2903–2913. [Google Scholar]
- Xu, Y.; Wang, D.; Chen, B.; Lu, R.; Duan, Z.; Zhou, M. Hyperminer: Topic taxonomy mining with hyperbolic embedding. Adv. Neural Inf. Process. Syst. 2022, 35, 31557–31570. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. Adv. Neural Inf. Process. Syst. 2013. Available online: https://proceedings.neurips.cc/paper_files/paper/2013/file/1cecc7a77928ca8133fa24680a88d2f9-Paper.pdf (accessed on 30 March 2025).
- Yang, B.; Yih, W.t.; He, X.; Gao, J.; Deng, L. Embedding entities and relations for learning and inference in knowledge bases. arXiv 2014, arXiv:1412.6575. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex Embeddings for Simple Link Prediction. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 19–24 June 2016; pp. 2071–2080. [Google Scholar]
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, J. Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv 2019, arXiv:1902.10197. [Google Scholar]
- Nickel, M.; Rosasco, L.; Poggio, T. Holographic Embeddings of Knowledge Graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Ferguson, T.S. A Bayesian Analysis of Some Nonparametric Problems. Ann. Stat. 1973, 1, 209–230. [Google Scholar] [CrossRef]
- Paisley, J.; Wang, C.; Blei, D.M.; Jordan, M.I. Nested hierarchical Dirichlet processes. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 256–270. [Google Scholar] [CrossRef] [PubMed]
- Whye Teh, Y.; Jordan, M.I.; Blei, D.M. Hierarchical Dirichlet Processes. J. Am. Stat. Assoc. 2006, 101, 1566–1581. [Google Scholar] [CrossRef]
- Sethuraman, J. A constructive definition of Dirichlet priors. Stat. Sin. 1994, 4, 639–650. [Google Scholar]
- Toutanova, K.; Chen, D. Observed vs. Latent Features for Knowledge Base and Text Inference. In Proceedings of the 3rd Workshop on Continuous Vector Space Models and Their Compositionality, Beijing, China, 31 July 2015; pp. 57–66. [Google Scholar]
- Wang, X.; Gao, T.; Zhu, Z.; Zhang, Z.; Liu, Z.; Li, J.; Tang, J. KEPLER: A unified model for knowledge embedding and pre-trained language representation. Trans. Assoc. Comput. Linguist. 2021, 9, 176–194. [Google Scholar] [CrossRef]
- Ormandi, R.; Saleh, M.; Winter, E.; Rao, V. WebRED: Effective Pretraining and Finetuning for Relation Extraction on the Web. arXiv 2021, arXiv:2102.09681. [Google Scholar]
- Marius, M.K.N.C.J.; Burkhardt, K.S. Hierarchical Topic Evaluation: Statistical vs. Neural Models. In Proceedings of the Bayesian Deep Learning Workshop, NeurIPS, Virtual, 10 December 2021. [Google Scholar]
- Röder, M.; Both, A.; Hinneburg, A. Exploring the Space of Topic Coherence Measures. In Proceedings of the 8th ACM International Conference on Web Search and Data Mining, Shanghai, China, 2–6 February 2015; pp. 399–408. [Google Scholar]
- Almars, A.M.; Ibrahim, I.A.; Zhao, X.; Al-Maskari, S. Evaluation Methods of Hierarchical Models. In Proceedings of the Advanced Data Mining and Applications: 14th International Conference, ADMA 2018, Nanjing, China, 16–18 November 2018; Springer: Cham, Germany, 2018; pp. 455–464. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).