Generation of Julia Sets for a Novel Class of Generalized Rational Functions via Generalized Viscosity Iterative Method

Abstract

This article investigates and analyzes the diverse patterns of Julia sets generated by new classes of generalized exponential and sine rational functions. Using a generalized viscosity approximation-type iterative method, we derive escape criteria to visualize the Julia sets of these functions. This approach enhances existing algorithms, enabling the visualization of intricate fractal patterns as Julia sets. We graphically illustrate the variations in size and shape of the images as the iteration parameters change. The new fractals obtained are visually appealing and attractive. Moreover, we observe fascinating behavior in Julia sets when certain input parameters are fixed, while the values of n and m vary. We believe the conclusions of this study will inspire and motivate researchers and enthusiasts with a strong interest in fractal geometry.

1. Introduction

Fractal geometry challenges the traditional notion that nature adheres to simple geometric forms, instead unveiling its true complexity through intricate, irregular patterns. By embracing self-similarity across scales, fractal geometry provides a powerful framework for analyzing shapes that defy classical classification. It reveals structured, yet seemingly chaotic, patterns inherent in the natural world, offering a unique perspective on its richness and complexity. This holistic approach deepens our understanding of the principles underlying various natural phenomena. Fractal analysis spans numerous disciplines, from science to art, expanding our perception of the world and highlighting the interconnectedness of diverse patterns. For further insights, see [1,2,3]. The allure of fractals, particularly Julia and Mandelbrot sets, has captivated mathematicians for decades. The foundation of Julia sets traces back to the early 20th-century work of the French mathematician Gaston Julia [4].

The construction of fractals, including Mandelbrot and Julia sets, is founded on various fixed-point iterative methods. Techniques such as Mann iteration, Picard iteration, and others (see [5,6,7,8,9,10]) have been extensively applied by mathematicians to analyze the behavior and patterns of polynomials, complex sine and cosine functions, and transcendental functions. These approaches reveal that the shape, color, and other characteristics of fractals can vary significantly depending on the iterative method applied to the same function (see [11,12]). In addition to Julia sets, iteration schemes play a key role in generating other fractals, including biomorphs, iterated function system fractals, inversion fractals, and root-finding fractals (see [13,14]).

In 2000, Moudafi [15] explored the convergence properties of the viscosity method in the framework of semi-nonexpansive mappings, providing valuable insights into iterative techniques. These advancements have greatly enriched the study and applications of fractals, enhancing our understanding of their intricate structures. More recently, Nandal et al. [16] proposed a generalized version of viscosity approximation-type iterative methods in the context of Hilbert spaces, significantly expanding both the theoretical foundation and practical applications of this approach.

The study revealed the untapped potential of the method for fractal generation. This intriguing connection suggests that the generalized viscosity approximation-type iterative method can not only solve complex problems in optimization and nonlinear analysis but also serve as a powerful tool for exploring and constructing fractals, such as Julia sets and related structures. Furthermore, the generalized viscosity approximation-type iterative method is a significant extension of classical fixed-point methods, including Halpern’s iteration and other iterative techniques.

The method allows for the more efficient and flexible exploration of fractal structures, revealing intricate, self-similar patterns that are difficult to achieve with more traditional methods, and the convergence properties of the generalized viscosity approximation method help in generating fractals with greater precision, making it possible to visualize even subtle variations in the fractal patterns as Julia sets. Julia sets are remarkable mathematical formations generated through iterative processes, showcasing intricate and mesmerizing fractal patterns. These sets arise by repeatedly applying a function to complex numbers, with each iteration determining whether a particular number stays bounded or escapes to infinity.

In recent studies, Kumari et al. [17,18] and Iqbal et al. [19] investigated the application of generalized viscosity approximation-type iterative methods in fractal generation, emphasizing their potential in producing Mandelbrot and Julia sets. In their subsequent research, these methods were applied to analyze and visualize the intricate dynamics of Julia and Mandelbrot sets, contributing to a deeper understanding of these captivating fractal structures. Building on this work, the present study adapts the existing viscosity approximation-type iterative method to establish escape criteria for the new generalized exponential rational function $Q\left(z\right)=\hslash e^{z^n}+{\displaystyle \frac{\wp }{z^m}}+\vartheta$ and the generalized sine rational function $W\left(z\right)=\hslash sin\left(z^n\right)+{\displaystyle \frac{\wp }{z^m}}+\vartheta ,$ where $n\ge 2,$$m,n\in \mathbb{N},$$\hslash ,\wp ,\vartheta \in \mathbb{C}.$ These functions are analytic except at $z=0.$

The structure of the paper is organized as follows: Section 2 introduces the fundamental definitions and preliminary results necessary to achieve the goals of this study. Section 3 establishes the main theorems used to derive a general escape criterion, which is crucial for generating Julia sets through a viscosity approximation-type iterative method. Section 4 details the algorithms implemented and presents visual illustrations of Julia sets generated using MATLAB R2019a (9.6.0.1072779, 64-bit) for various parameter values, along with a comprehensive discussion of the results. Finally, Section 5 concludes the paper with a summary of the key findings.

2. Preliminaries

This section presents some fundamental definitions and essential results that are necessary to accomplish the objectives of this article.

Definition 1

(Julia set [4]). Let $W:\mathbb{C}\to \mathbb{C}$ be a complex-valued function. The filled Julia set of W is defined as

$$\begin{array}{c}\hfill f_W=\{z\in \mathbb{C}:\{|W^p{\left(z\right)\left|\right\}}_{p=0}^{\infty }\mathit{is}\mathit{bounded}\}.\end{array}$$

where $W^p$ denotes the $p^{th}$ compositional iterate of W. The Julia set is the boundary of the filled Julia set.

Definition 2.

Let $W:\mathbb{C}\to \mathbb{C}$ be a complex-valued function and $z_0\in \mathbb{C}$ an initial point. Define the following sequence:

$$\begin{array}{c}\hfill z_{p+1}=W\left(z_p\right),p\ge 0,\end{array}$$

(1)

The escape time for $z_0$ is the minimum integer p such that $|z_p|>R$, where R is a predefined escape radius. If $|z_p|>R,$ the point is said to escape to infinity under iteration. If the point does not escape within a maximum number of iterations K, it is assumed to belong to the filled Julia set.

Definition 3

([15]). Let $\left\{z_p\right\}$ denote the sequence of iterates, with $z_0\in \mathbb{C}$ as the initial point. The sequence $\left\{z_p\right\}$ is said to follow the viscosity approximation method if

$$\begin{array}{c}\hfill z_{p+1}={\xi }_{p}g\left(z_p\right)+(1-{\xi }_p)W\left(z_p\right),p\ge 0,\end{array}$$

(2)

where ${\xi }_p\in (0,1),$ g, and W are self-mappings on $\mathbb{C}$, with g being a contraction mapping.

This iterative process, introduced by Moudafi [15] in $2000,$ combines the contraction mapping g with the operator W through a convex combination that evolves with each iteration.

A novel generalized viscosity approximation-type iterative method was studied by Nandal et al. [16]. This approach can be described in the complex plane as follows: starting from an initial point $z_0\in \mathbb{C},$ the sequence $\left\{z_p\right\}$ is defined by

$$\left\{\begin{array}{c}{z}_{p+1}={\mathcal{J}}_{{\lambda }_p}^{B_1}{T}_j^p{T}_{j-1}^p\cdots T_2^p{T}_1^p{y}_p,\hfill \\ y_p={\zeta }_{p}g\left(z_n\right)+(1-{\zeta }_p){\mathcal{J}}_{{\mu }_p}^{B_2}{U}_p{z}_p,\hfill \end{array}\right.$$

(3)

where $U_p=(1-{\xi }_p)I+{\xi }_{p}U,$ and $T_l^p=(1-{\rho }_p^l)I+{\rho }_p^l{T}_l,$ for $l=1,2,\cdots ,j,$ with ${\zeta }_i,{\xi }_j,{\rho }_j^l\in (0,1),$ the resolvent operators ${\mathcal{J}}_{{\lambda }_p}^{B_1}={(I+{\lambda }_p{B}_1)}^{-1}$ and ${\mathcal{J}}_{{\mu }_p}^{B_2}={(I+{\mu }_p{B}_2)}^{-1}$ are associated with monotone operators $B_1$ and $B_2,$ respectively, with ${\lambda }_p,{\mu }_p\in (0,\infty ).$

Consider the following new class of complex functions $Q,W:\mathbb{C}\to \mathbb{C},$ which are analytic except at $z=0$ as

$$\begin{array}{c}\hfill Q\left(z\right)=\hslash e^{z^n}+{\displaystyle \frac{\wp }{z^m}}+\vartheta ,\end{array}$$

(4)

and

$$\begin{array}{c}\hfill W\left(z\right)=\hslash sin\left(z^n\right)+{\displaystyle \frac{\wp }{z^m}}+\vartheta ,\end{array}$$

(5)

where $n\ge 2,$$m,n\in \mathbb{N},$ and $\hslash ,\wp ,\vartheta \in \mathbb{C}.$

The key to generating fractals and establishing escape criteria lies in running the algorithms effectively. It is well known that $|sin(z^n\left)\right|\le 1$ for certain values of $z\in \mathbb{C}$. The Maclaurin series expansions for the exponential and sine functions are given by

$$\begin{array}{c}\hfill |e^{z^n}|=\left|\sum _{p=0}^{\infty }{\displaystyle \frac{z^{np}}{p!}}\right|>\left|\sum _{p=1}^{\infty }{\displaystyle \frac{z^{np}}{p!}}\right|=|z^n|\left|\sum _{p=1}^{\infty }{\displaystyle \frac{z^{n(p-1)}}{p!}}\right|>\left|\tau \right||z^n|\end{array}$$

(6)

where $0<\left|\tau \right|\le 1$ except the values of $z\in \mathbb{C}$ for which $\left|\tau \right|=0,$ and

$$\begin{array}{c}\hfill |sin\left(z^n\right)|=\left|\sum _{p=0}^{\infty }{\displaystyle \frac{{(-1)}^p{z}^{n(2p+1)}}{(2p+1)!}}\right|=|z^n||\sum _{p=0}^{\infty }{\displaystyle \frac{{(-1)}^p{z}^{2pn}}{(2p+1)!}}{\displaystyle |}\ge \left|\psi \right||z^n|,\end{array}$$

(7)

where $0<\left|\psi \right|\le 1$ except the values of $z\in \mathbb{C}$ for which $\left|\psi \right|=0$ (see the details [5]).

3. Main Results

In this section, we construct an escape time algorithm based on the iteration scheme (3) to analyze the newly introduced generalized exponential and sine rational functions.

Assume $j=2,$ and let the sequences be constant, given by ${\zeta }_p=\zeta ,{\xi }_p=\xi ,{\rho }_p^1=\rho ,$${\rho }_p^2=\sigma ,{\lambda }_p=\lambda ,{\mu }_p=\mu ,T_1^p=V,T_2^p=S,$ where $\zeta ,\xi ,\rho ,\sigma \in (0,1)$, and $\lambda ,\mu \in (0,\infty ).$ Suppose that the function $g\left(z\right)=rz+s$ is a contraction mapping with $r,s\in \mathbb{C}$ and $\left|r\right|<1,$ and define $B_1\left(z\right)=\omega z$ and $B_2\left(z\right)=\eta z,$ where $\omega ,\eta \in \mathbb{R}.$ Accordingly, we have ${\mathcal{J}}_{\lambda }^{B_1}\left(z\right)={\displaystyle \frac{z}{1+\omega \lambda }}$ and ${\mathcal{J}}_{\mu }^{B_2}\left(z\right)={\displaystyle \frac{z}{1+\eta \mu }}.$ Furthermore, let $U=V=Q=W$ and $S=g,$ where Q and W are defined in (4) and (5), respectively. Under these assumptions, the iterative scheme given by (3) takes the following form:

$$\left\{\begin{array}{c}{z}_{p+1}={\mathcal{J}}_{\lambda }^{B_1}{S}_{\sigma }{V}_{\rho }{y}_p,\hfill \\ y_p=\zeta g\left(z_p\right)+(1-\zeta ){\mathcal{J}}_{\mu }^{B_2}{U}_{\xi }{z}_p,\hfill \end{array}\right.$$

(8)

where $U_{\xi }=(1-\xi )I+\xi U,$$V_{\rho }=(1-\rho )I+\rho V,$ and $S_{\sigma }=(1-\sigma )I+\sigma S.$

3.1. Escape Criteria for $Q\left(z\right)=\hslash e^{z^n}+{\displaystyle \frac{\wp }{z^m}}+\vartheta .$

In this subsection, we derive the escape criterion for the function $Q\left(z\right)=\hslash e^{z^n}+{\displaystyle \frac{\wp }{z^m}}+\vartheta$ using (8).

Theorem 1.

Let $z_0\in \mathbb{C},$$|z_0{|\ge max\{\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{m+n}}}\}>max\{{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}},$${\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\tau }_2-1\left)\right|(1+\sigma (r-1))|}}\right)}^{{\displaystyle \frac{1}{n-1}}}\}$, where $\zeta ,\xi ,\rho ,\sigma \in (0,1)$, and let $g\left(z\right)=rz+s$ be a complex contraction mapping with $r,s\in \mathbb{C}$ and $\left|r\right|<1.$ Then, the sequence $\left\{z_p\right\}$ defined by the iteration in (8), satisfies $|z_p|\to \infty ,$ as $p\to \infty .$

Proof. 

From the definition of $U_{\xi }{z}_p,$ we have

$$|U_{\xi }{z}_p|=|((1-\xi )z_p+\xi U\left(z_p\right)|,p\ge 0.$$

For $p=0$ and using (6), we obtain

$$\begin{array}{ccc}\hfill |U_{\xi }{z}_0|& =& |(1-\xi )z_0+\xi \left(\hslash e^{z_0^n}+{\displaystyle \frac{\wp }{z_0^m}}+\vartheta \right)|\hfill \\ & \ge & \xi \left|\left(\hslash e^{z_0^n}+{\displaystyle \frac{\wp }{z_0^m}}+\vartheta \right)\right|-(1-\xi )\left|z_0\right|\hfill \\ & \ge & \xi |\left(\hslash e^{z_0^n}+{\displaystyle \frac{\wp }{z_0^m}}\right)|-\xi |\vartheta |-(1-\xi )|z_0|\hfill \\ & \ge & \xi |\hslash ||{\tau }_1\left|\right|z_0^n|-\xi |{\displaystyle \frac{\wp }{z_0^m}}|-\xi |\vartheta |-(1-\xi )|z_0|\hfill \end{array}$$

Our assumption $|z_0{|\ge max\{\left|\vartheta \right|,\left|b\right|,|\wp |}^{{\displaystyle \frac{1}{n+m}}}\}$ yields that $-\left|\vartheta \right|\ge -|z_0|$ and $-|\wp |\ge -|z_0{|}^{n+m},$ and we obtain

$$\begin{array}{ccc}\hfill |U_{\xi }{z}_0|& \ge & \xi |\hslash ||{\tau }_1\left|\right|z_0^n|-\xi {\displaystyle \frac{|z_0{|}^{n+m}}{|z_0^m|}}-\xi |z_0|-(1-\xi )|z_0|.\hfill \\ & \ge & \xi |\hslash ||{\tau }_1\left|\right|z_0^n|-\xi |z_0^n|-\xi |z_0|-(1-\xi )|z_0|\hfill \\ & \ge & \xi |\hslash ||{\tau }_1\left|\right|z_0^n|-\xi |z_0^n|-|z_0|,\hfill \\ & =& |z_0|\left(\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)|z_0^{n-1}|-1\right),\hfill \end{array}$$

and thus,

$$\begin{array}{c}\hfill |U_{\xi }{z}_0|\ge |z_0|\left(\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)|z_0^{n-1}|-1\right).\end{array}$$

(9)

Using (8) and (9), we have

$$\begin{array}{ccc}\hfill |y_0|& =& |\zeta g\left(z_0\right)+(1-\zeta ){\mathcal{J}}_{\mu }^{B_2}{U}_{\xi }{z}_0|\hfill \\ & =& |\zeta (r{z}_0+s)+(1-\zeta ){\displaystyle \frac{U_{\xi }{z}_0}{1+\eta \mu }}|\hfill \\ & \ge & (1-\zeta )\left|{\displaystyle \frac{U_{\xi }{z}_0}{1+\eta \mu }}\right|-\zeta \left|(r{z}_0+s)\right|\hfill \\ & \ge & (1-\zeta ){\displaystyle \frac{|U_{\xi }{z}_0|}{|1+\eta \mu |}}-\zeta \left|r\right||z_0|-\zeta |s|,since-|s|\ge -|z_0|\hfill \\ & \ge & (1-\zeta ){\displaystyle \frac{|z_0|\left(\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)|z_0^{n-1}|-1\right)}{|1+\eta \mu |}}-\zeta \left|r\right||z_0|-\zeta |z_0|\hfill \\ & \ge & |z_0|\left({\displaystyle \frac{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)|z_0{|}^{n-1}-(1-\zeta )}{|1+\eta \mu |}}-\zeta (1+|r\left|\right)\right).\hfill \end{array}$$

Thus, we have

$$\begin{array}{c}\hfill |y_0|\ge |z_0|\left({\displaystyle \frac{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)|z_0{|}^{n-1}-(1-\zeta )}{|1+\eta \mu |}}-\zeta (1+|r\left|\right)\right).\end{array}$$

(10)

Our assumption $|z_0|>{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}}$ gives

$${\displaystyle \frac{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)|z_0{|}^{n-1}-(1-\zeta )}{|1+\eta \mu |}}-\zeta (1+|r\left|\right)>1.$$

From (10), we obtain

$$\begin{array}{c}\hfill |y_0|>|z_0|.\end{array}$$

(11)

Now, based on the construction of $V_{\rho },$ we have

$$\begin{array}{ccc}\hfill |V_{\rho }{y}_0|& =& |(1-\rho )y_0+\rho V\left(y_0\right)|\hfill \\ & =& |(1-\rho )y_0+\rho \left(\hslash e^{y_0^n}+{\displaystyle \frac{\wp }{y_0^m}}+\vartheta \right)|\hfill \\ & \ge & \rho \left|\left(\hslash e^{y_0^n}+{\displaystyle \frac{\wp }{y_0^m}}+\vartheta \right)\right|-(1-\rho )\left|y_0\right|\hfill \\ & \ge & \rho |\left(\hslash e^{y_0^n}+{\displaystyle \frac{\wp }{y_0^m}}\right){\displaystyle |}-\rho \left|\vartheta \right|-(1-\rho )|y_0|\hfill \\ & \ge & \rho |\hslash ||{\tau }_2\left|\right|y_0^n|-\rho |{\displaystyle \frac{\wp }{y_0^m}}|-\rho |\vartheta |-(1-\rho )|y_0|\hfill \\ & \ge & \rho |\hslash ||{\tau }_2\left|\right|y_0^n|-\rho {\displaystyle \frac{|\wp |}{|y_0^m|}}-\rho \left|\vartheta \right|-(1-\rho )|y_0|.\hfill \end{array}$$

(12)

From (11), we have $|y_0|>|z_0|$, which implies that $-|z_0|>-|y_0|$ and $-{\displaystyle \frac{1}{|y_0|}}>-{\displaystyle \frac{1}{|z_0|}},$ and (12) becomes

$$\begin{array}{c}\hfill |V_{\rho }{y}_0|\ge \rho |\hslash \left|\right|{\tau }_2\left|\right|z_0^n|-\rho {\displaystyle \frac{|\wp |}{|z_0^m|}}-\rho \left|\vartheta \right|-(1-\rho )|z_0|.\end{array}$$

(13)

The assumption $|z_0{|\ge max\{\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{n+m}}}\}$ yields that $-\left|\vartheta \right|\ge -|z_0|,$ and $-|\wp |\ge -|z_0{|}^{n+m},$ and therefore, we obtain

$$\begin{array}{ccc}\hfill |V_{\rho }{y}_0|& \ge & \rho |\hslash ||{\tau }_2\left|\right|z_0^n|-\rho |z_0^n|-\rho |z_0|-(1-\rho )|z_0|\hfill \\ & \ge & \rho |\hslash ||{\tau }_2\left|\right|z_0^n|-\rho |z_0^n|-|z_0|,\hfill \\ & =& |z_0|\left(\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)|z_0^{n-1}|-1\right).\hfill \end{array}$$

(14)

Now, based on the construction of $S_{\sigma }{V}_{\rho },$ we have

$$\begin{array}{ccc}\hfill S_{\sigma }{V}_{\rho }{y}_0& =& [(1-\sigma )I+\sigma S]\left(V_{\rho }{y}_0\right)\hfill \\ & =& (1-\sigma )V_{\rho }{y}_0+\sigma (r{V}_{\rho }{y}_0+s)\hfill \\ & =& (1+\sigma (r-1))V_{\rho }{y}_0+\sigma s.\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill S_{\sigma }{V}_{\rho }{y}_0=(1+\sigma (r-1))V_{\rho }{y}_0+\sigma s.\end{array}$$

(15)

Further, from (8), consider

$$\begin{array}{c}\hfill |z_1|={\displaystyle |}{\mathcal{J}}_{\lambda }^{B_1}{S}_{\sigma }{V}_{\rho }{y}_0|.\end{array}$$

From (15), we have

$$\begin{array}{ccc}\hfill |z_1|& =& \left|{\mathcal{J}}_{\lambda }^{B_1}((1+\sigma (r-1))V_{\rho }{y}_0+\sigma s)\right|\hfill \\ & =& \left|{\displaystyle \frac{((1+\sigma (r-1))V_{\rho }{y}_0+\sigma s)}{1+\omega \lambda }}\right|\hfill \\ & \ge & {\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}|V_{\rho }{y}_0|-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}\left|s\right|\hfill \\ & \ge & {\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}|V_{\rho }{y}_0|-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}\left|z_0\right|.\hfill \end{array}$$

From (14), we have

$$\begin{array}{c}\hfill |z_1|\ge |z_0|\left({\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}\left(\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)|z_0^{n-1}|-1\right)-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}\right).\end{array}$$

(16)

Our assumptions $|z_0|>{\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)\left|(1+\sigma (r-1))\right|}}\right)}^{{\displaystyle \frac{1}{n-1}}}$ give

$${\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}\left(\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)|z_0^{n-1}|-1\right)-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}>1.$$

Thus, there exists $\Omega >0$ such that

$$\begin{array}{c}\hfill {\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}\left(\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)|z_0^{n-1}|-1\right)-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}>\Omega +1>1.\end{array}$$

(17)

Using (16) and (17), we have

$$\begin{array}{c}\hfill |z_1|>(1+\Omega )|z_0|.\end{array}$$

In particular, $|z_1|>|z_0|.$ Continuing this procedure, we obtain $|z_p{|>(1+\Omega )}^p\left|z_0\right|.$ Hence, $|z_p|\to \infty ,$ as $p\to \infty .$ □

In the proof of Theorem 1, we rely solely on the fact that $|z_0{|\ge max\{\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{n+m}}}\}>max\{{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}},{\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)\left|(1+\sigma (r-1))\right|}}\right)}^{{\displaystyle \frac{1}{n-1}}}\}.$ Therefore, this result can be refined to yield the following corollary.

Corollary 1.

Let $|z_0{|\ge max{\displaystyle \{}|\vartheta |,|s|,|\wp |}^{{\displaystyle \frac{1}{n+m}}},{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}},{\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)\left|(1+\sigma (r-1))\right|}}\right)}^{{\displaystyle \frac{1}{n-1}}}\}.$ Then, $|z_p|\to \infty ,$ as $p\to \infty .$

3.2. Escape Criteria for $W\left(z\right)=\hslash sin\left(z^n\right)+{\displaystyle \frac{\wp }{z^m}}+\vartheta$

In this subsection, we derive the escape criterion for $W\left(z\right)=\hslash sin\left(z^n\right)+{\displaystyle \frac{\wp }{z^m}}+\vartheta$ using (8).

Theorem 2.

Let $z_0\in \mathbb{C}$, $|z_0{|\ge max\{\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{m+n}}}\}>max{\displaystyle \{}{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}},$${\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\omega }_2-1\left)\right|(1+\sigma (r-1))|}}\right)}^{{\displaystyle \frac{1}{n-1}}}\}$, where $\zeta ,\xi ,\rho ,\sigma \in (0,1),$ and let $g\left(z\right)=rz+s$ be a complex contraction mapping with $r,s\in \mathbb{C}$ and $\left|r\right|<1.$ Then, $|z_p|\to \infty ,$ as $p\to \infty ,$ where $\left\{z_p\right\}$ is defined in (8).

Proof. 

Based on the construction of $U_{\xi }{z}_p,$ we have

$$|U_{\xi }{z}_p|=|((1-\xi )I+\xi U)\left(z_p\right)|,p\ge 0.$$

For $p=0$ and using (7), we obtain

$$\begin{array}{ccc}\hfill |U_{\xi }{z}_0|& =& |(1-\xi )z_0+\xi U\left(z_0\right)|\hfill \\ & =& |(1-\xi )z_0+\xi \left(\hslash sin\left(z_0^n\right)+{\displaystyle \frac{\wp }{z_0^m}}+\vartheta \right)|\hfill \\ & \ge & \xi \left|\left(\hslash sin\left(z_0^n\right)+{\displaystyle \frac{\wp }{z_0^m}}+r\right)\right|-(1-\xi )\left|z_0\right|\hfill \\ & \ge & \xi |\left(\hslash sin\left(z_0^n\right)+{\displaystyle \frac{\wp }{z_0^m}}\right)|-\xi |\vartheta |-(1-\xi )|z_0|\hfill \\ & \ge & \xi |\hslash ||{\psi }_1\left|\right|z_0^n|-\xi |{\displaystyle \frac{\wp }{z_0^m}}|-\xi |\vartheta |-(1-\xi )|z_0|\hfill \\ & \ge & \xi |\hslash ||{\psi }_1\left|\right|z_0^n|-\xi {\displaystyle \frac{|\wp |}{|z_0^m|}}-\xi \left|\vartheta \right|-(1-\xi )|z_0|.\hfill \end{array}$$

Our assumption $|z_0{|\ge max\{\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{n+m}}}\}$ yields that $-\left|s\right|\ge -|z_0|,$ and $-\left|\vartheta \right|\ge -|z_0|,$ and $-|\wp |\ge -|z_0{|}^{n+m},$ and we obtain

$$\begin{array}{ccc}\hfill |U_{\xi }{z}_0|& \ge & \xi |\hslash ||{\psi }_1\left|\right|z_0^n|-\xi |z_0^n|-\xi |z_0|-(1-\xi )|z_0|\hfill \\ & \ge & \xi |\hslash ||{\psi }_1\left|\right|z_0^n|-\xi |z_0^n|-|z_0|,\hfill \\ & =& |z_0|\left(\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)|z_0^{n-1}|-1\right),\hfill \end{array}$$

and thus,

$$\begin{array}{c}\hfill |U_{\xi }{z}_0|\ge |z_0|\left(\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)|z_0^{n-1}|-1\right).\end{array}$$

(18)

Using (8) and (18), we have

$$\begin{array}{ccc}\hfill |y_0|& =& |\zeta g\left(z_0\right)+(1-\zeta ){\mathcal{J}}_{\mu }^{B_2}{U}_{\xi }{z}_0|\hfill \\ & =& |\zeta (r{z}_0+s)+(1-\zeta ){\displaystyle \frac{U_{\xi }{z}_0}{1+\eta \mu }}|\hfill \\ & \ge & (1-\zeta ){\displaystyle \frac{|U_{\xi }{z}_0|}{|1+\eta \mu |}}-\zeta \left|r\right||z_0|-\zeta |s|\hfill \\ & \ge & (1-\zeta ){\displaystyle \frac{|z_0|\left(\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)|z_0^{n-1}|-1\right)}{|1+\eta \mu |}}-\zeta \left|r\right||z_0|-\zeta |z_0|\hfill \\ & \ge & |z_0|\left({\displaystyle \frac{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)|z_0{|}^{n-1}-(1-\zeta )}{|1+\eta \mu |}}-\zeta (1+|r\left|\right)\right).\hfill \end{array}$$

Thus, we have

$$\begin{array}{c}\hfill |y_0|\ge |z_0|\left({\displaystyle \frac{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)|z_0{|}^{n-1}-(1-\zeta )}{|1+\eta \mu |}}-\zeta (1+|r\left|\right)\right).\end{array}$$

(19)

Our assumption $|z_0|>{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}}$ gives

$${\displaystyle \frac{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)|z_0{|}^{n-1}-(1-\zeta )}{|1+\eta \mu |}}-\zeta (1+|r\left|\right)>1.$$

From (19), we obtain

$$\begin{array}{c}\hfill |y_0|>|z_0|.\end{array}$$

(20)

Now, based on the construction of $V_{\rho },$ we have

$$\begin{array}{ccc}\hfill |V_{\rho }{y}_0|& =& |(1-\rho )y_0+\rho V\left(y_0\right)|\hfill \\ & =& |(1-\rho )y_0+\rho \left(\hslash sin\left(y_0^n\right)+{\displaystyle \frac{\wp }{y_0^m}}+\vartheta \right)|\hfill \\ & \ge & \rho \left|\left(\hslash sin\left(y_0^n\right)+{\displaystyle \frac{\wp }{y_0^m}}+\vartheta \right)\right|-(1-\rho )\left|y_0\right|\hfill \\ & \ge & \rho |\left(\hslash sin\left(y_0^n\right)+{\displaystyle \frac{\wp }{y_0^m}}\right)|-\rho |\vartheta |-(1-\xi )|y_0|\hfill \\ & \ge & \rho |\hslash ||{\psi }_2\left|\right|y_0^n|-\rho |{\displaystyle \frac{\wp }{y_0^m}}|-\rho |\vartheta |-(1-\rho )|y_0|\hfill \\ & \ge & \rho |\hslash ||{\psi }_2\left|\right|y_0^n|-\rho {\displaystyle \frac{|\wp |}{|y_0^m|}}-\rho \left|\vartheta \right|-(1-\rho )|y_0|.\hfill \end{array}$$

(21)

From (20), we have $|y_0|>|z_0|$, which implies that $-|z_0|>-|y_0|$ and $-{\displaystyle \frac{1}{|y_0|}}>-{\displaystyle \frac{1}{|z_0|}},$ and Equation (21) becomes

$$\begin{array}{c}\hfill |V_{\rho }{y}_0|\ge \rho |\hslash \left|\right|{\psi }_2\left|\right|z_0^n|-\rho {\displaystyle \frac{|\wp |}{|z_0^m|}}-\rho \left|\vartheta \right|-(1-\rho )|z_0|.\end{array}$$

(22)

The assumption $|z_0{|\ge max\{\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{n+m}}}\}$ yields that $-\left|\vartheta \right|\ge -|z_0|,$ and $-|\wp |\ge -|z_0{|}^{n+m},$ and therefore, we obtain

$$\begin{array}{ccc}\hfill |V_{\rho }{y}_0|& \ge & \rho |\hslash ||{\psi }_2\left|\right|z_0^n|-\rho |z_0^n|-\rho |z_0|-(1-\rho )|z_0|\hfill \\ & \ge & \rho |\hslash ||{\psi }_2\left|\right|z_0^n|-\rho |z_0^n|-|z_0|,\hfill \\ & =& |z_0|\left(\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)|z_0^{n-1}|-1\right).\hfill \end{array}$$

(23)

Now, based on the construction of $S_{\sigma }{V}_{\rho },$ we have

$$\begin{array}{ccc}\hfill S_{\sigma }{V}_{\rho }{y}_0& =& [(1-\sigma )I+\sigma S]\left(V_{\rho }{y}_0\right)\hfill \\ & =& (1-\sigma )V_{\rho }{y}_0+\sigma (r{V}_{\rho }{y}_0+s)\hfill \\ & =& (1+\sigma (r-1))V_{\rho }{y}_0+\sigma s.\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill S_{\sigma }{V}_{\rho }{y}_0=(1+\sigma (r-1))V_{\rho }{y}_0+\sigma s.\end{array}$$

(24)

Further, from (8), consider

$$\begin{array}{c}\hfill |z_1|=|{\mathcal{J}}_{\lambda }^{B_1}{S}_{\sigma }{V}_{\rho }{y}_0|.\end{array}$$

From (24), we have

$$\begin{array}{ccc}\hfill |z_1|& =& \left|{\mathcal{J}}_{\lambda }^{B_1}((1+\sigma (r-1))V_{\rho }{y}_0+\sigma s)\right|\hfill \\ & =& \left|{\displaystyle \frac{((1+\sigma (r-1))V_{\rho }{y}_0+\sigma s)}{1+\omega \lambda }}\right|\hfill \\ & \ge & {\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}|V_{\rho }{y}_0|-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}\left|s\right|\hfill \\ & \ge & {\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}|V_{\rho }{y}_0|-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}\left|z_0\right|.\hfill \end{array}$$

From (23), we have

$$\begin{array}{c}\hfill |z_1|\ge |z_0|\left({\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}\left(\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)|z_0^{n-1}|-1\right)-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}\right).\end{array}$$

(25)

Our assumptions $|z_0|>{\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)\left|(1+\sigma (r-1))\right|}}\right)}^{{\displaystyle \frac{1}{n-1}}}$ give

$${\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}\left(\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)|z_0^{n-1}|-1\right)-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}>1.$$

Thus, there exist $\phi >0$ such that

$$\begin{array}{c}\hfill {\displaystyle \frac{\left|\right(1+\sigma (r-1)\left)\right|}{|1+\omega \lambda |}}\left(\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)|z_0^{n-1}|-1\right)-{\displaystyle \frac{\sigma }{|1+\omega \lambda |}}>\phi +1>1.\end{array}$$

(26)

Using (25) and (26), we have

$$\begin{array}{c}\hfill |z_1|>(1+\phi )|z_0|.\end{array}$$

In particular, $|z_1|>|z_0|.$ Continuing this procedure, we obtain $|z_p{|>(1+\phi )}^p\left|z_0\right|.$ Hence, $|z_p|\to \infty ,$ as $p\to \infty .$ □

In the proof of Theorem 2, we relied solely on the fact that $|z_0{|\ge max\{\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{n+m}}}\}>max{\displaystyle \{}{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}},{\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)\left|(1+\sigma (r-1))\right|}}\right)}^{{\displaystyle \frac{1}{n-1}}}\}.$ So, we can refine it and obtain the following corollary.

Corollary 2.

Let $|z_0{|\ge max{\displaystyle \{}|\vartheta |,|s|,|\wp |}^{{\displaystyle \frac{1}{n+m}}},{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}},{\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)\left|(1+\sigma (r-1))\right|}}\right)}^{{\displaystyle \frac{1}{n-1}}}\}.$ Then, $|z_p|\to \infty ,$ as $p\to \infty .$

4. Graphical Examples

To visualize fractals, specific convergence conditions are crucial, serving as the foundation for effectively executing the algorithm and generating the desired fractal structures. We construct and analyze Julia sets corresponding to various parameter values, examining how these variations influence the resulting patterns. The Julia sets are computed using the generalized viscosity approximation-type iterative method given in (8), with a maximum of 70 iterations applied throughout this work. All fractal visualizations are produced using MATLAB R2019a (9.6.0.1072779, 64-bit), which enables the generation of non-classical Julia sets across distinct orbits. To carry out these visualizations, we develop two dedicated algorithms: one for the Julia set of $Q\left(z\right)=\hslash e^{z^n}+{\displaystyle \frac{\wp }{z^m}}+\vartheta$, and another for $W\left(z\right)=\hslash sin\left(z^n\right)+{\displaystyle \frac{\wp }{z^m}}+\vartheta$, where $n\ge 2,$$m,n\in \mathbb{N}$ and $\hslash ,\wp ,\vartheta \in \mathbb{C}.$ By varying the input parameters along with the values of n and m, we present the resulting Julia sets produced by Algorithms 1 and 2.

Algorithm 1 Julia set generation for $Q\left(z\right)=\hslash e^{z^n}+{\displaystyle \frac{\wp }{z^m}}+\vartheta .$

Input: $Q\left(z\right)=\hslash e^{z^n}+{\displaystyle \frac{\wp }{z^m}}+\vartheta ,$ where $n\ge 2,$ $\hslash ,\wp ,\vartheta \in \mathbb{C},$ $A\subset \mathbb{C}$-area in which we draw

the set; K-maximal number of iterations; $\zeta ,\xi ,\sigma ,\rho \in (0,1)$; $g\left(z\right)=rz+s$, where $r,s\in \mathbb{C}$

with $\left|r\right|<1;$ colormap $[0..C\text{-}1]$-color with C colors.

Output: Julia set for area A

for $z_0\in A$ do

R = ${max{\displaystyle \{}\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{m+n}}},{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\tau }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}},$

${\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\tau }_2|-1)\left|(1+\sigma (r-1))\right|}}\right)}^{{\displaystyle \frac{1}{n-1}}}\}$

k=0

while $k\le K$ do

$z_{p+1}={\displaystyle \frac{(1+\sigma (r-1)))[(1-\rho )y_p+\rho Q\left(y_p\right)]+\sigma s}{(1+\omega \lambda )}},$

$y_p=\xi g\left(z_p\right)+(1-\xi ){\displaystyle \frac{\Re }{(1+\eta \mu )}},$

$\Re =\zeta z_p+(1-\zeta )Q\left(z_p\right),$  $p\ge 0$, where $0<\zeta ,\xi ,\rho ,\sigma <1.$

if $|z_{k+1}|\ge R$ then break end if

k=k+1

$j=[(C-1){\displaystyle \frac{k}{K}}]$

color $z_0$ with colormap $\left[j\right]$

Algorithm 2 Julia set generation for $W\left(z\right)=\hslash sin\left(z^n\right)+{\displaystyle \frac{\wp }{z^m}}+\vartheta$.

Input: $W\left(z\right)=\hslash sin\left(z^n\right)+{\displaystyle \frac{\wp }{z^m}}+\vartheta ,$ where $n\ge 2,$ $\hslash ,\wp ,\vartheta \in \mathbb{C},$ $A\subset \mathbb{C}$-area in which we

draw the set; K-maximal number of iterations; $\zeta ,\xi ,\sigma ,\rho \in (0,1)$; $g\left(z\right)=rz+s$, where

$r,s\in \mathbb{C}$ with $\left|r\right|<1;$ colormap $[0..C-1]$-color with C colors.

Output: Julia set for area A

for $z_0\in A$ do

R = ${max{\displaystyle \{}\left|\vartheta \right|,\left|s\right|,|\wp |}^{{\displaystyle \frac{1}{m+n}}},{\left({\displaystyle \frac{(1+\zeta (1+\left|r\right|\left)\right)|1+\eta \mu |+(1-\zeta )}{(1-\zeta )\xi \left(\right|\hslash \left|\right|{\psi }_1|-1)}}\right)}^{{\displaystyle \frac{1}{n-1}}},$

${\left({\displaystyle \frac{1}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)}}+{\displaystyle \frac{(\sigma +|1+\omega \lambda \left|\right)}{\rho \left(\right|\hslash \left|\right|{\psi }_2|-1)\left|(1+\sigma (r-1))\right|}}\right)}^{{\displaystyle \frac{1}{n-1}}}\}$

k=0

while $k\le K$ do

$z_{p+1}={\displaystyle \frac{(1+\sigma (r-1)))[(1-\rho )y_p+\rho W\left(y_p\right)]+\sigma s}{(1+\omega \lambda )}},$

$y_p=\xi g\left(z_p\right)+(1-\xi ){\displaystyle \frac{\Re }{(1+\eta \mu )}},$

$\Re =\zeta z_p+(1-\zeta )W\left(z_p\right),$  $p\ge 0$, where $0<\zeta ,\xi ,\rho ,\sigma <1.$

if $|z_{k+1}|\ge R$ then break end if

k=k+1

$j=[(C-1){\displaystyle \frac{k}{K}}]$

color $z_0$ with colormap $\left[j\right]$

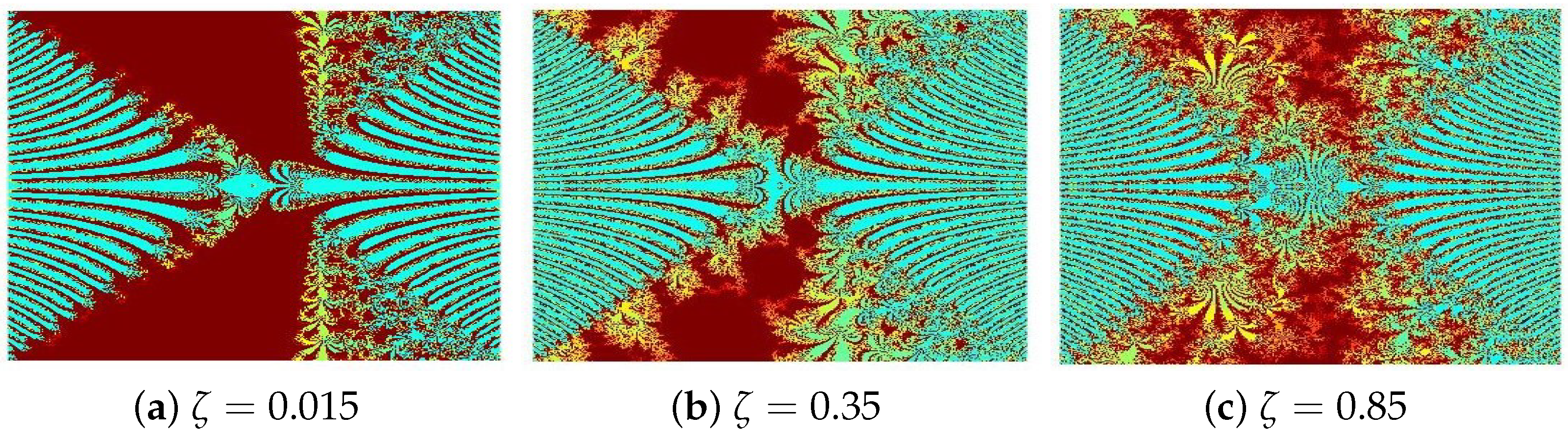
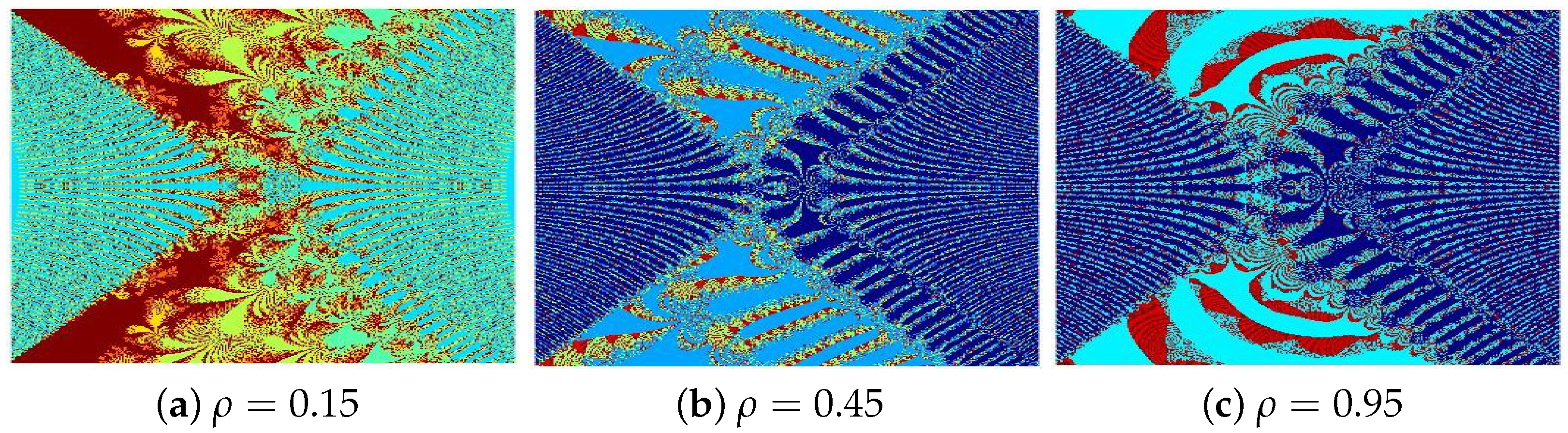
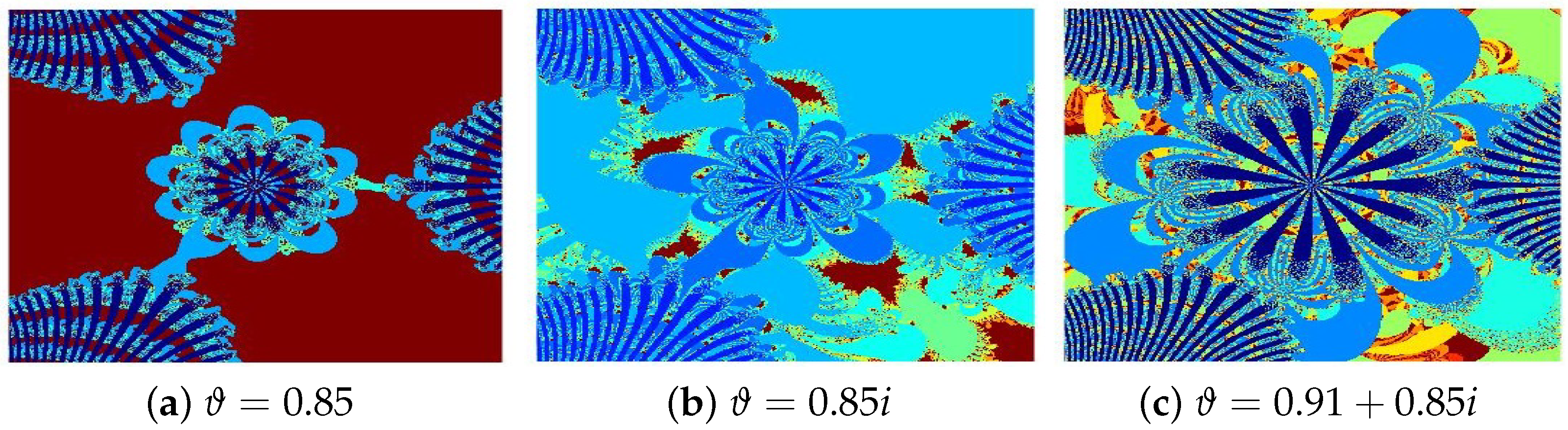
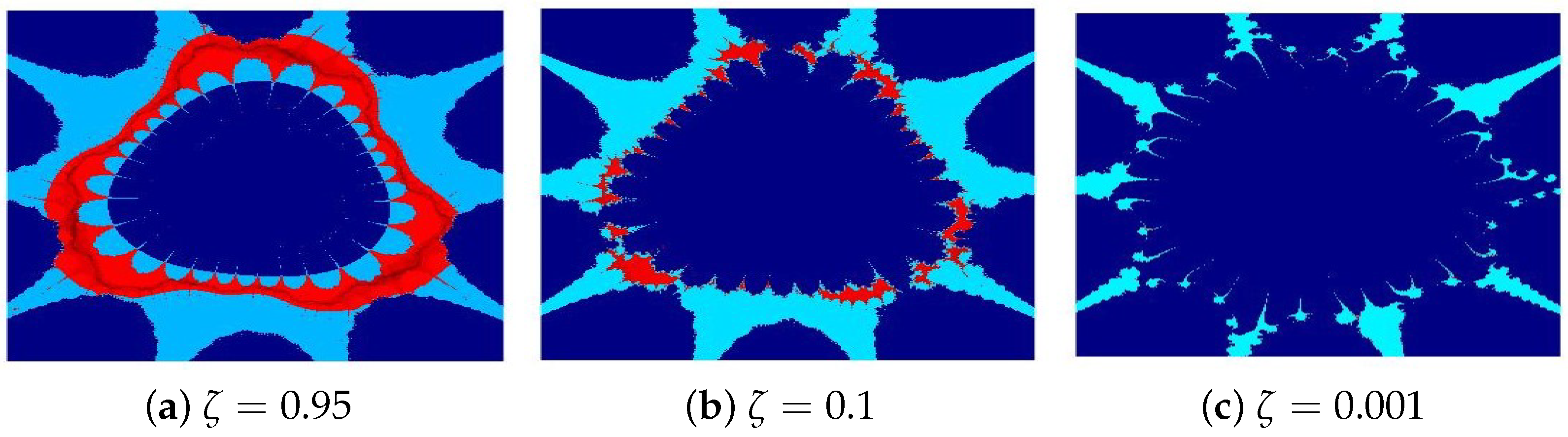
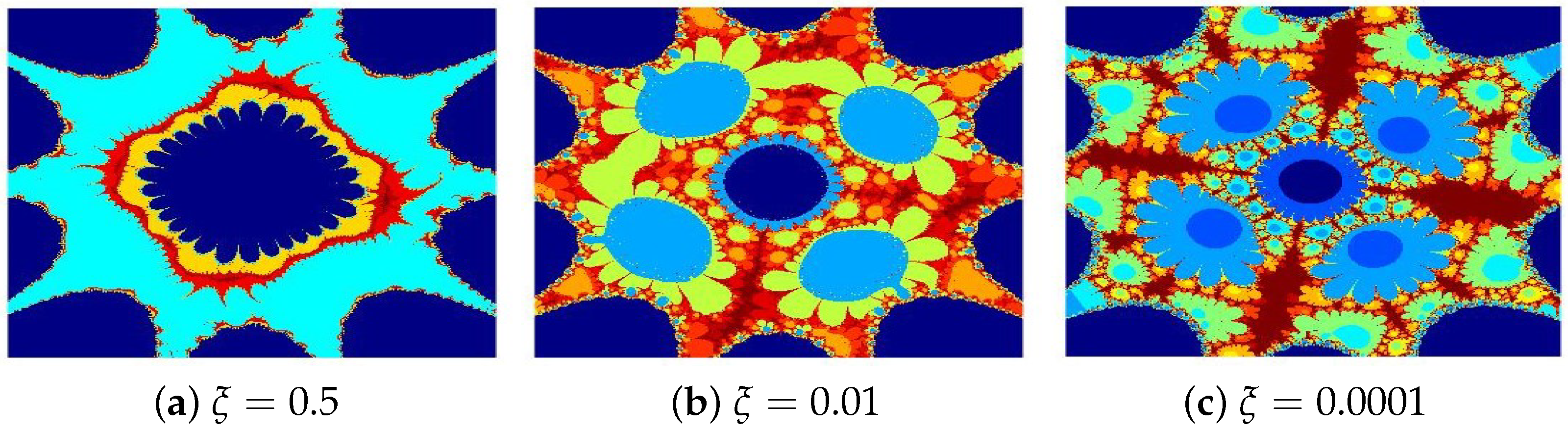
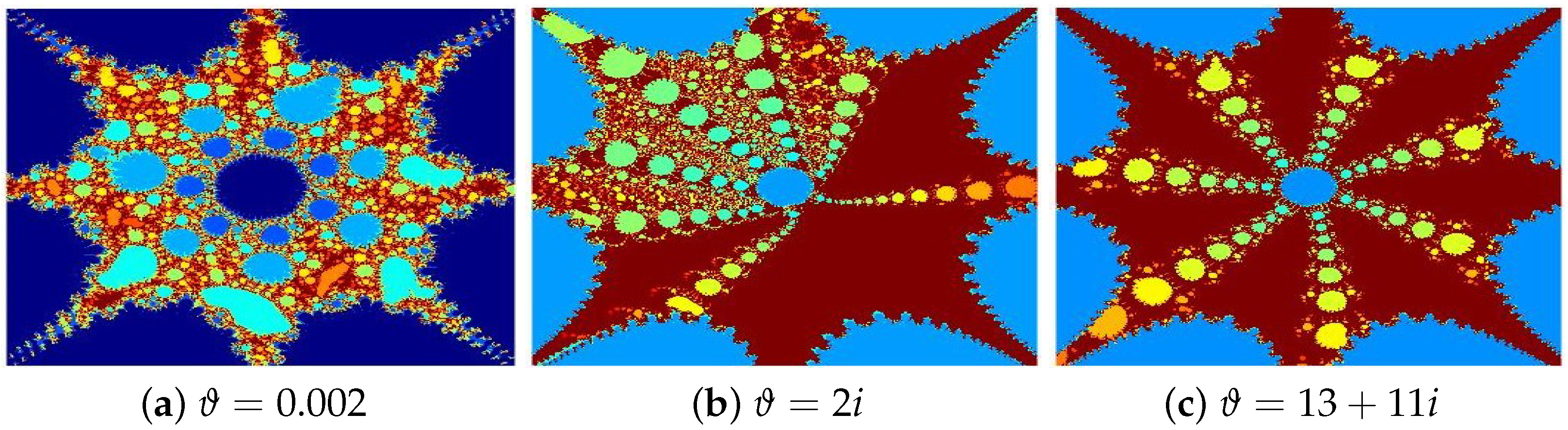
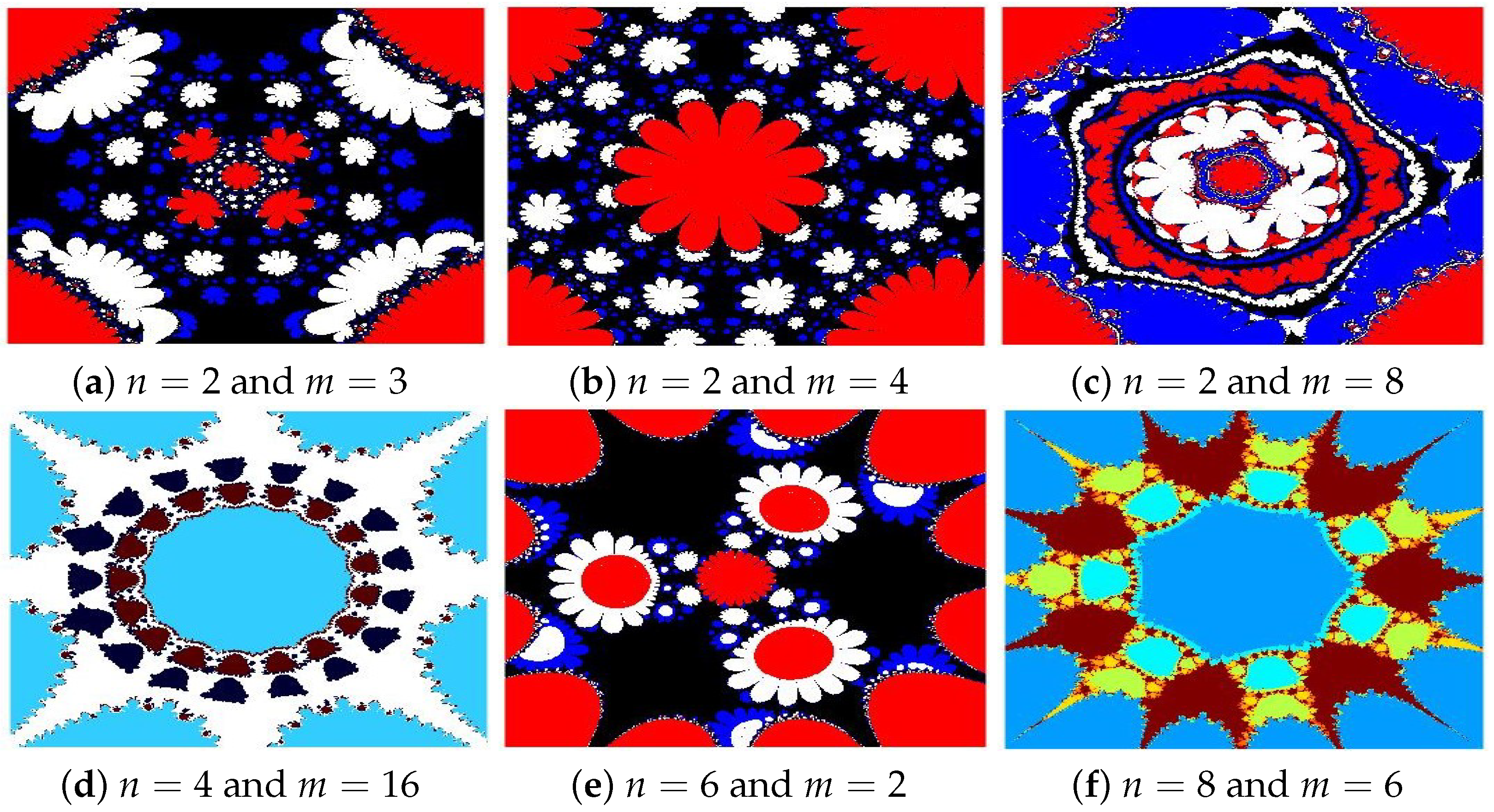
4.1. Julia Sets for $Q\left(z\right)=\hslash e^{z^n}+{\displaystyle \frac{\wp }{z^m}}+\vartheta$

This subsection presents the Julia sets corresponding to the generalized exponential rational function for different input values. The execution times for generating these images are also provided in seconds.

In the first example, we generate Julia sets using Algorithm 1 for the functions $Q\left(z\right)$ and $g\left(z\right)$. The parameter values used for this illustration are $n=2,m=1,\hslash =7,$$\wp =3.1,\vartheta =9.1,r=0.75,s=1.5,\omega =0.25,\eta =0.5,\lambda =0.3,\mu =0.2,|{\tau }_1|=0.75,$$|{\tau }_2|=0.55.$ The resulting images are organized into four groups. In each group, three of the parameters from $\zeta ,\xi ,\rho ,\sigma$ are held fixed, while the fourth is varied:

• In Figure 1, $\xi =0.15,\rho =0.25,\sigma =0.35$ are fixed, and $\zeta$ is varying: (a)$0.015,$ (b) $0.35,$ and (c) $0.85.$
• In Figure 2, $\zeta =0.015,\rho =0.25,\sigma =0.45$ are fixed, and $\xi$ is varying: (a)$0.001,$ (b) $0.05,$ and (c) $0.15.$
• In Figure 3, $\zeta =0.75,\xi =0.65,\sigma =0.25$ are fixed and $\rho$ is varying: (a)$0.15,$ (b) $0.45,$ and (c) $0.95.$
• In Figure 4, $\zeta =0.01,\xi =0.02,\rho =0.002$ are fixed and $\sigma :$ is varying: (a)$0.25,$ (b) $0.55,\mathrm{and}$(c) $0.95.$

In Figure 1, Figure 2, Figure 3 and Figure 4a–c, for $n=2$ and $m=1,$ we fix the values of three parameters from $\zeta ,\xi ,\rho ,\sigma$ and vary the remaining one. It is clear that the four parameters $\zeta ,\xi ,\rho$ and $\sigma$ play a significant role in determining the shape, size, and color of the sets. As shown in these figures, an increase in any of the parameters leads to an expansion of the set, accompanied by changes in its shape. The image generation time for each iteration is also recorded.

In the second example, we generate Julia sets using Algorithm 1 for the functions $Q\left(z\right)$ and $g\left(z\right)$. The parameter values used for this illustration are $n=3,m=5,$$r=0.5-0.1i,s=1.5+0.2i,\zeta =0.75,\xi =0.83,\rho =0.87,\sigma =0.95,\omega =0.2,\eta =0.3,$$\lambda =0.3,\mu =0.15,|{\tau }_1|=0.175,|{\tau }_2|=0.15.$ The resulting images are organized into three groups. In each group, two of the parameters from $\hslash ,\wp ,\vartheta$ are held fixed, while the fourth is varied:

• In Figure 5, with $\wp =16,\vartheta =0.9$ fixed, ℏ is varied as follows: (a)$0.015,$ (b) $1.5i,$ (c) $0.5-0.1i.$
• In Figure 6, with $\hslash =0.5-0.7i,\vartheta =2.3$ fixed, ℘ is varied as follows: (a)$0.5,$ (b) $0.05i,\mathrm{and}$(c) $0.31-0.51i.$
• In Figure 7, with $\hslash =0.13,\wp =0.5$ fixed, $\vartheta$ is varied as follows: (a)$0.85,$ (b) $0.85i,$ and (c) $0.91+0.85i.$

In Figure 5, Figure 6 and Figure 7a–c, with $n=3$ and $m=5$, we present Julia sets generated by fixing two of the parameters $\hslash ,\wp$ or $\vartheta$, while varying the third. Specifically, in subfigures (a), the parameters are set as purely real, in (b) as purely imaginary, and in (c) as complex values. These variations highlight the significant influence of $\hslash ,\wp$, and $\vartheta$ on the geometry, scale, and coloration of the Julia sets particularly around the edges of the characteristic leaf-like structures. The resulting patterns resemble traditional Rangoli designs, floral motifs, or intricate stained glass artwork. The execution times for each image are recorded per iteration to support the detailed performance analysis.

In the third example, we generate Julia sets using Algorithm 1 for the function $Q\left(z\right)$. The parameter values used for this illustration are $n=3,m=5,\hslash =0.13,\wp =16,$$\vartheta =0.91+0.85i,\zeta =0.0075,\xi =0.0083,\rho =0.0087,\sigma =0.0095,\omega =0.2,\eta =0.3,$$\lambda =0.3,\mu =0.15,|{\tau }_1|=0.175,|{\tau }_2|=0.15.$ The resulting images are organized into two groups. In each group, one of the parameters from r and s is held fixed, while the second is varied:

• In Figure 8, $s=16$ is fixed, and r is varied: (a)$0.85,$ (b) $0.85i,$ and (c) $0.75-0.1i.$
• In Figure 9, $r=0.085+0.91i$ is fixed, and s is varied: (a)$75,$ (b) $105i,$ and (c) $231-31i.$

In Figure 8a–c and Figure 9a–c, with $n=3$ and $m=5$, we display Julia sets produced by fixing one of the parameters r or s, while varying the other. In subfigures (a), both r and s are set as purely real, in (b) as purely imaginary, and in (c) as complex values. These variations clearly demonstrate that the parameters r and s significantly affect the structure, scale, and color distribution of the Julia sets, particularly along the contours of the leaf-like formations. The generated patterns resemble traditional Rangoli designs, floral arrangements, or delicate stained glass artwork.

In this example, we showcase the diversity of Julia sets generated using the generalized viscosity approximation-type iterative method for $Q\left(z\right)$ and $g\left(z\right).$ These sets are illustrated in Figure 10a–l, with the parameters used for their generation specified as follows:

(a)

$n=2,m=1,Q\left(z\right)=105e^{z^2}+{\displaystyle \frac{106}{z}}+91,g\left(z\right)=(0.005-0.01i)z+(0.005+0.001i),\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.71,\xi =0.81,\rho =0.88,$$\sigma =0.95,$

(b)

$n=2,m=1,Q\left(z\right)=105i{e}^{z^2}+{\displaystyle \frac{106i}{z}}+91i,g\left(z\right)=(0.005-0.01i)z+(0.005+0.001i),\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.071,\xi =0.081,\rho =0.088,$$\sigma =0.095,$

(c)

$n=2,m=1,Q\left(z\right)=(15+105i)e^{z^2}+{\displaystyle \frac{15-106i}{z}}+(8+91i),g\left(z\right)=(0.005-0.01i)z+(0.005+0.001i),\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.0071,\xi =0.0081,\rho =0.0088,$$\sigma =0.0095,$

(d)

$n=2,m=3,Q\left(z\right)=0.0015e^{z^2}+{\displaystyle \frac{16}{z^3}}+0.9,g\left(z\right)=(0.5-0.1i)z+1.5+0.01i,\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.71,\xi =0.81,\rho =0.88,$$\sigma =0.95,$

(e)

$n=3,m=3,Q\left(z\right)=0.13e^{z^3}+{\displaystyle \frac{0.17}{z^3}}+(0.91+0.85i),g\left(z\right)=(0.5-0.1i)z+(261.5+12i),\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.0071,\xi =0.00081,\rho =0.0088,\sigma =0.0095,$

(f)

$n=5,m=10,Q\left(z\right)=15i{e}^{z^5}+{\displaystyle \frac{17i}{z^{10}}}+0.91,g\left(z\right)=0.5z+361.5-0.42i,\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.071,\xi =0.081,\rho =0.088,\sigma =0.095,$

(g)

$n=8,m=8,Q\left(z\right)=11e^{z^8}+{\displaystyle \frac{19}{z^8}}+0.91,g\left(z\right)=0.5z+361.5-0.42i,\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.071,\xi =0.081,\rho =0.088,\sigma =0.095,$

(h)

$n=9,m=14,Q\left(z\right)=15e^{z^9}+{\displaystyle \frac{16}{z^{14}}}+0.9,g\left(z\right)=0.5z+241-0.4i,\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.071,\xi =0.081,\rho =0.088,\sigma =0.095,$

(i)

$n=14,m=16,Q\left(z\right)=15e^{z^{14}}+{\displaystyle \frac{16}{z^{16}}}+0.9,g\left(z\right)=0.5z+241-0.4i,\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.071,\xi =0.081,\rho =0.088,\sigma =0.095,$

(j)

$n=21,m=25,Q\left(z\right)=15e^{z^{21}}+{\displaystyle \frac{16}{z^{25}}}+0.9,g\left(z\right)=0.5z+261-0.4i,\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.071,\xi =0.081,\rho =0.088,\sigma =0.095,$

(k)

$n=21,m=6,Q\left(z\right)=15e^{z^{21}}+{\displaystyle \frac{6}{z^6}}+0.9,g\left(z\right)=0.5z+261-0.4i,\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.071,\xi =0.081,\rho =0.088,\sigma =0.095,$

(l)

$n=85,m=8,Q\left(z\right)=15e^{z^{85}}+{\displaystyle \frac{16}{z^8}}+0.9,g\left(z\right)=0.5z+261-0.4i,\eta =0.15,\omega =0.3,\mu =0.2,\lambda =0.3,|{\tau }_1|=0.18,|{\tau }_2|=0.15,\zeta =0.071,\xi =0.081,\rho =0.088,\sigma =0.095.$

In Figure 10a–e, we observe distinct behavioral changes in the Julia sets when varying the parameters in the generalized exponential rational function via Algorithm 1. Adjusting the values of parameter $\hslash ,\wp ,\vartheta ,a,$ and b as purely real, purely imaginary, and complex lead to noticeable differences in the color, shape, and size of the Julia sets. The resulting images display intricate and beautiful fractal patterns. Figure 10f–l illustrate Julia sets for $m=n=$ even/odd, while the other parameters remain fixed as described in Figure 10f–l. From these images, it is clear that as n and m increase, and the sets evolve into circular shapes, with petal counts corresponding to the values of n and m. Furthermore, the number of petals increases as n and m increase. The generated Julia sets are strikingly complex, resembling traditional Rangoli patterns, floral shapes, or intricate glass art. Additionally, the image generation time is recorded, showing an increase with each iteration.

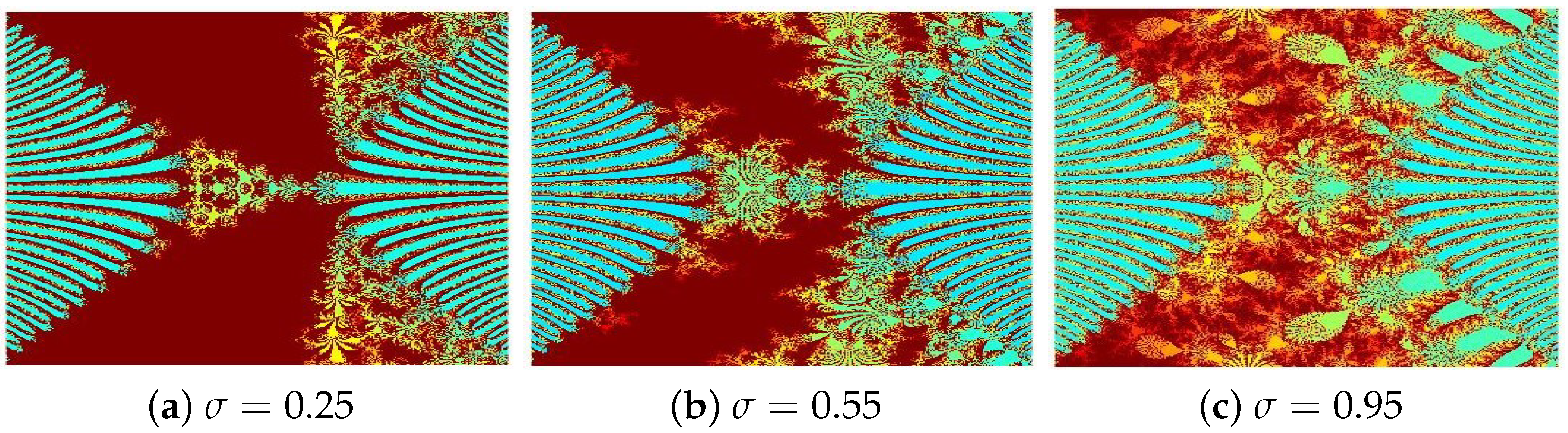
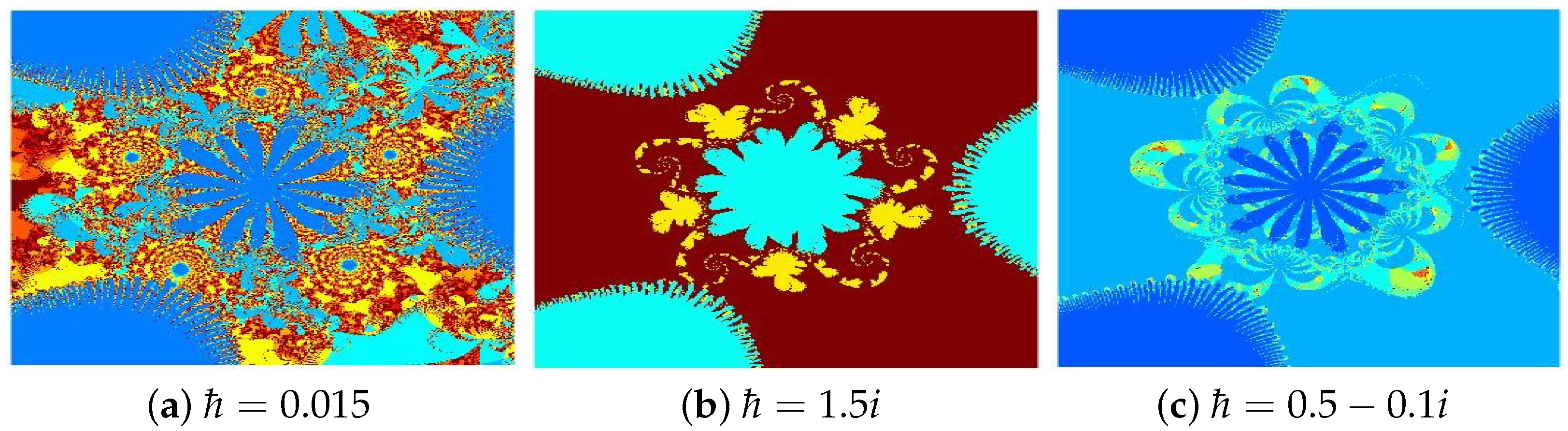
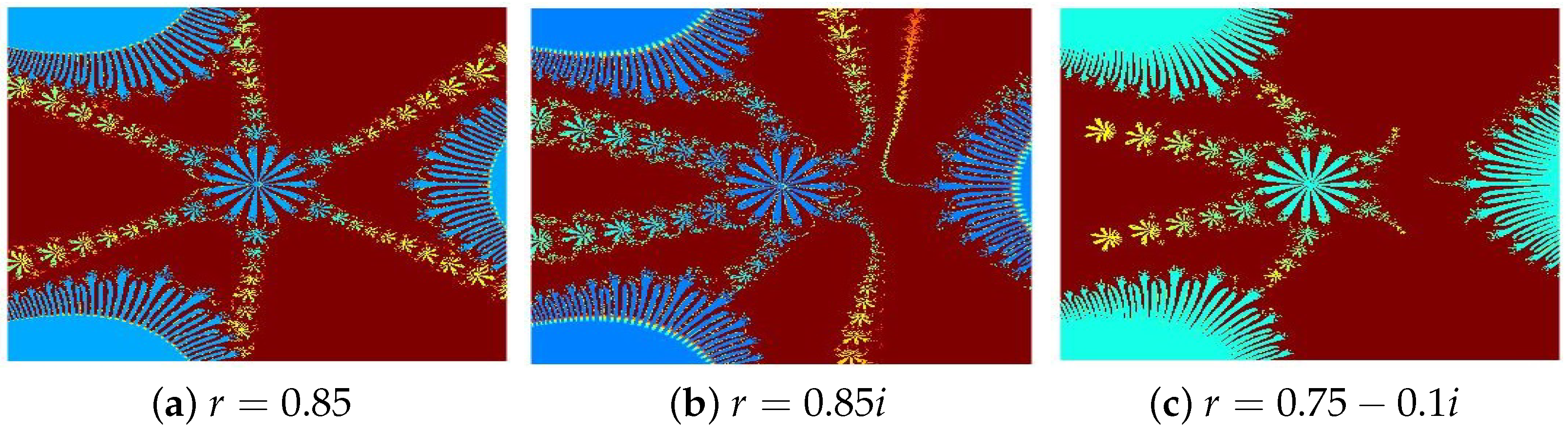
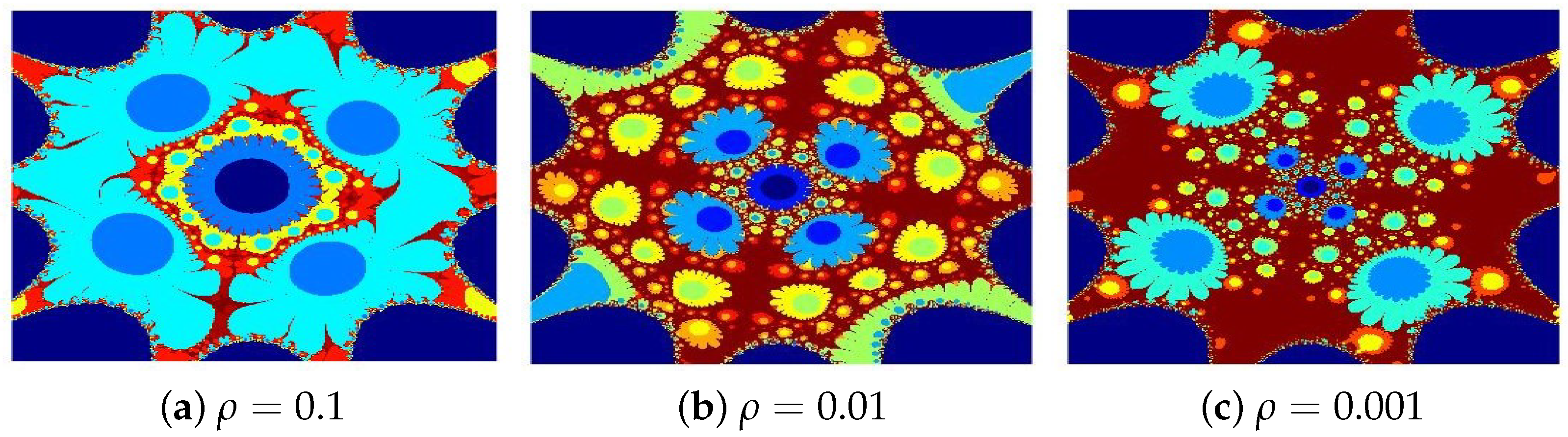
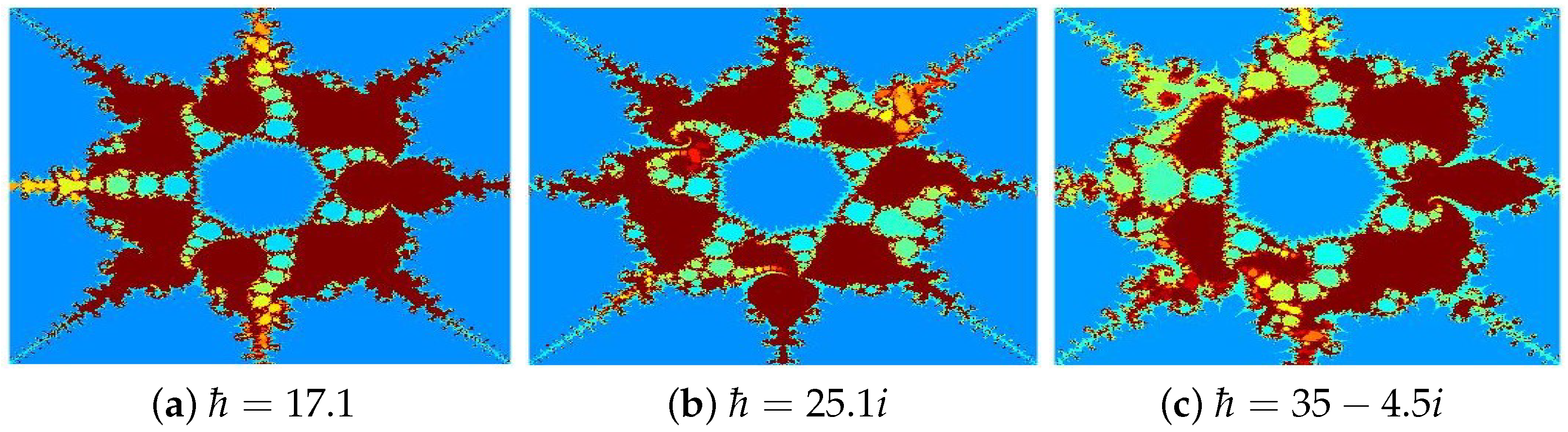
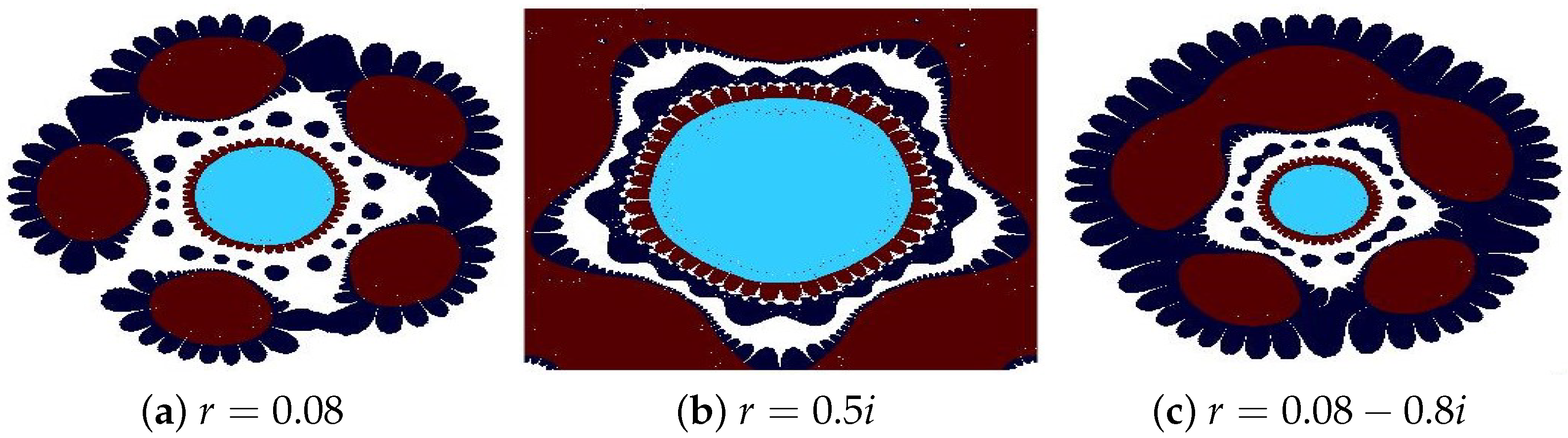
4.2. Julia Sets for $W\left(z\right)=\hslash sin\left(z^n\right)+{\displaystyle \frac{\wp }{z^m}}+\vartheta$

The Julia sets corresponding to the generalized sine rational function for different input values are illustrated in this subsection.

In the first example, we generate Julia sets via Algorithm 2 for the function $W\left(z\right)$ and a complex contraction mapping $g\left(z\right)$. The parameter values used for this illustration are $n=5,m=3,\hslash =0.01+0.1i,\wp =14+12i,\vartheta =1.7,r=0.08,s=-0.7i,\omega =0.58,$$\eta =2.1,\lambda =0.7,\mu =0.5,|{\psi }_1|=0.85,|{\psi }_2|=0.45.$ The generated images are categorized into four groups. In each group, three parameters of $\zeta ,\xi ,\rho ,\sigma$ are held fixed, while the fourth is varied:

• In Figure 11, $\xi =0.65,\rho =0.75,\sigma =0.85$ are fixed, and $\zeta$ is varied as (a)$0.95,$ (b) $0.1,$(c) $0.001.$
• In Figure 12, $\zeta =0.005,\rho =0.007,\sigma =0.008$ are fixed, and $\xi$ is varied as (a)$0.5,$ (b) $0.01,$ and (c) $0.001.$
• In Figure 13, $\zeta =0.00015,\xi =0.0002,\sigma =0.0003$ are fixed, and $\rho$ is varied as (a)$0.1,$ (b) $0.001,$ and (c) $0.0001.$
• In Figure 14, $\zeta =0.0015,\xi =0.002,\rho =0.005$ are fixed, and $\sigma$ is varied as (a)$0.75,$ (b) $0.05,$ and (c) $0.005.$

From Figure 11, Figure 12, Figure 13 and Figure 14a–c, for the fixed values $n=5$ and $m=3,$ we observe the impact of varying one parameter from the set $\zeta ,\xi ,\rho ,\sigma$ while keeping the other three constant. It is evident that these four parameters play a crucial role in shaping the structure of the Julia sets. Specifically, as the values of $\zeta ,\xi ,\rho ,\sigma$ increase, notable changes occur in the size and form of the fractal bulbs. As illustrated in Figure 11, Figure 12, Figure 13 and Figure 14, the bulb size enlarges with increasing parameter values, accompanied by distinct transformations in shape and visual appearance.

In the second example, the parameters selected for this illustration are as follows: $n=6,m=4,r=0.05-0.1i,s=1.5i,\omega =0.5,\eta =1.3,\lambda =0.2,\mu =0.15,|{\psi }_1|=0.175,$$|{\psi }_2|=0.15,$$\zeta =0.001,\xi =0.003,\rho =0.006$, and $\sigma =0.009.$ The generated images are categorized into three groups. In each group, two parameters from $\hslash ,\wp ,\vartheta$ are fixed, while the third is varied:

• In Figure 15, the parameters $\wp =7.5,\vartheta =1.2$ are fixed, while ℏ is varied as (a)$17.1,$ (b) $25.1i,$ and (c) $35-4.5i.$
• In Figure 16, the parameters $\hslash =0.3+0.4i,\vartheta =0.7$ are fixed, while ℘ is varied as (a)$0.5,$ (b) $5i,$ and (c) $8.1+3.5i.$
• In Figure 17, the parameters $\hslash =1.3,\wp =0.1$ are fixed, while $\vartheta$ is varied as (a)$0.002,$ (b) $2i,$ and (c) $13+11i.$

In the third example, the parameters used to generate the Julia sets in this example are the following: $n=6,m=4,\hslash =0.01+0.8i,\wp =(0.17+0.3i),\vartheta =0.5+0.3i,\omega =0.85,\eta =1.85,\lambda =0.82,\mu =0.75,|{\psi }_1|=0.85,|{\psi }_2|=0.45,$$\zeta =0.005,\xi =0.006,\rho =0.007$, and $\sigma =0.008.$ The generated images are categorized into four groups. In each group, we fix one of the parameter from $r,s,$ while the second is varied:

• In Figure 18, the parameter $s=1.5i$ is fixed, while r is varied as (a)$0.08,$ (b) $0.5i$ and (c)$0.08-0.8i.$
• In Figure 19, the parameter $r=0.8+0.5i$ is fixed, while s is varied as (a)$3.5,$(b) $-4.5i$ and (c)$81-21i.$

In Figure 18a–c and Figure 19a–c, Julia sets are displayed for varying parameter configurations: (a) where r, and s are fixed as purely real, (b) as purely imaginary, and (c) as complex values. The central circular region of the Julia sets undergoes noticeable changes, with the surrounding area also transforming in shape and size. These changes often lead to portions detaching from the central structure, forming new, smaller circular regions that bear a resemblance to the original central part.

In this example, we demonstrate the diversity of Julia sets produced using the generalized viscosity approximation-type iterative method for $W\left(z\right).$ The resulting sets are displayed in Figure 20a–f, generated using the following parameter values:

(a)

$n=2,m=3,W\left(z\right)=0.001e^{z^2}+{\displaystyle \frac{17}{z^3}}+0.7i,g\left(z\right)=(0.13-0.15i)z+3.8i,\eta =2.85,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,$$\sigma =0.009,$

(b)

$n=2,m=4,W\left(z\right)=0.001e^{z^2}+{\displaystyle \frac{17}{z^3}}+0.7i,g\left(z\right)=(0.13-0.15i)z+3.8i,\eta =2.85,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,$$\sigma =0.009,$

(c)

$n=2,m=8,W\left(z\right)=0.001e^{z^2}+{\displaystyle \frac{17}{z^3}}+0.7i,g\left(z\right)=(0.13-0.15i)z+3.8i,\eta =2.85,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,$$\sigma =0.009,$

(d)

$n=4,m=16,W\left(z\right)=0.1i{e}^{z^4}+{\displaystyle \frac{24}{z^{16}}}+0.7i,g\left(z\right)=0.08z+3.8i,\eta =0.185,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,$$\sigma =0.009,$

(e)

$n=6,m=2,W\left(z\right)=0.001e^{z^6}+{\displaystyle \frac{17}{z^2}}+0.7i,g\left(z\right)=(0.13-0.15i)z+3.8i,\eta =2.85,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,$$\sigma =0.009,$

(f)

$n=8,m=6,W\left(z\right)=0.1e^{z^8}+{\displaystyle \frac{14}{z^6}}+0.7i,g\left(z\right)=(0.13-0.15i)z+3.8i,\eta =2.85,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,$$\sigma =0.009,$

(g)

$n=3,m=18,W\left(z\right)=0.1e^{z^3}+{\displaystyle \frac{0.017}{z^{18}}}+0.7i,g\left(z\right)=(0.13-0.15i)z+3.8i,\eta =0.085,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,\sigma =0.009,$

(h)

$n=18,m=14,W\left(z\right)=0.001e^{z^{18}}+{\displaystyle \frac{0.0001}{z^{14}}}+0.7i,g\left(z\right)=0.8z-3.8i,\eta =0.00085,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,$$\sigma =0.009,$

(i)

$n=75,m=6,W\left(z\right)=0.001e^{z^{75}}+{\displaystyle \frac{17}{z^6}}+0.7i,g\left(z\right)=(0.13-0.15i)z+3.8i,\eta =0.185,\omega =0.81,\mu =0.72,\lambda =0.7,|w_1|=0.85,|w_2|=0.45,\zeta =0.006,\xi =0.007,\rho =0.008,\sigma =0.009,$

In Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19a–c, we examine Julia sets generated under different parameter conditions: in (a), the parameters ℏ, $\wp ,\vartheta ,r$, and s are fixed as purely real values; in (b), they are set as purely imaginary; and in (c), they take complex values. These variations demonstrate that ℏ, $\wp ,\vartheta ,r$, and s play a crucial role in shaping the structure, scale, and coloration of the Julia sets. Further analysis reveals that adjusting the values of n and m also has a profound effect on the geometry and intricacy of the fractals. As n and m increase, the Julia sets exhibit greater complexity, undergoing significant transformations in their overall form (see Figure 20a–f). The resulting patterns display mesmerizing fractal designs, reminiscent of traditional Rangoli art, floral motifs, or delicate stained glass. The computational time for generating each image is recorded, highlighting the balance between algorithmic efficiency and visual richness. Each parameter adjustment not only deepens the fractal’s complexity but also enhances its artistic beauty, producing images that are both mathematically profound and aesthetically stunning. Key observations from this study include the following:

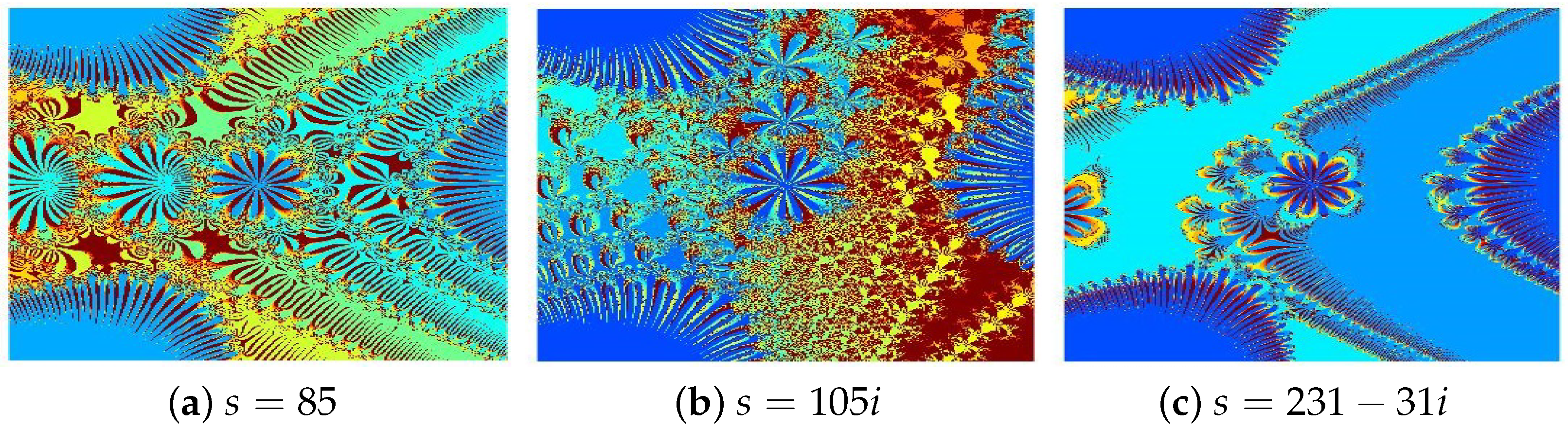
• The parameters $\zeta ,\xi ,\rho ,\sigma ,\hslash ,\wp ,\vartheta ,r$ and s are critical in determining the fractals’ structure, scale, and visual properties.
• The convergence criteria used in the iterative schemes significantly influence the image resolution and pixel quality.
• All presented fractals exhibit remarkable innovation and visual appeal, stemming from the sophisticated interplay of the functions $Q\left(z\right)$ and $W\left(z\right)$. The resulting designs are not only mathematically significant but also artistically captivating, showcasing the harmonious fusion of computation and creativity.

5. Conclusions

We have established an escape criterion based on a generalized viscosity approximation-type iterative method, specifically designed for generalized exponential and sine rational functions. Leveraging this framework, we constructed and visualized intricate Julia sets as fractals. These visualizations were implemented through Algorithms 1 and 2, using MATLAB to explore and analyze the dynamic behavior of Julia sets under varying parameter configurations. The resulting non-classical fractals revealed complex and aesthetically rich structures. The results demonstrate that the parameters $\zeta ,\xi ,\rho ,\sigma ,\hslash ,\wp ,\vartheta ,r,s$, along with the exponents n and m play a pivotal role in determining the size, intricacy, and visual characteristics of these fractals. Notably, even minor adjustments to these parameters can lead to substantial transformations in the fractal’s morphology, coloration, and scale. Looking ahead, we plan to expand this study by generating corresponding Mandelbrot sets, incorporating transformations such as replacing c by $log{c}^t$ within the generalized functions. Additionally, we intend to enhance our analytical approach by incorporating performance metrics such as generation time and ANI (Average Number of Iterations). Beyond the theoretical implications, this work holds significant practical value, particularly in the textile industry, where the generated fractal patterns can be applied to innovative design and printing techniques, offering new possibilities for artistic and commercial applications.