Closed-Form Meromorphic Solutions of High-Order and High-Dimensional Differential Equations
Abstract
:1. Introduction
2. The Extended Complex Method
3. Application of the Extended Complex Method to the fSK Equation
4. Utilization of the Extended Complex Method to the (3+1)-Dimensional gSW Equation
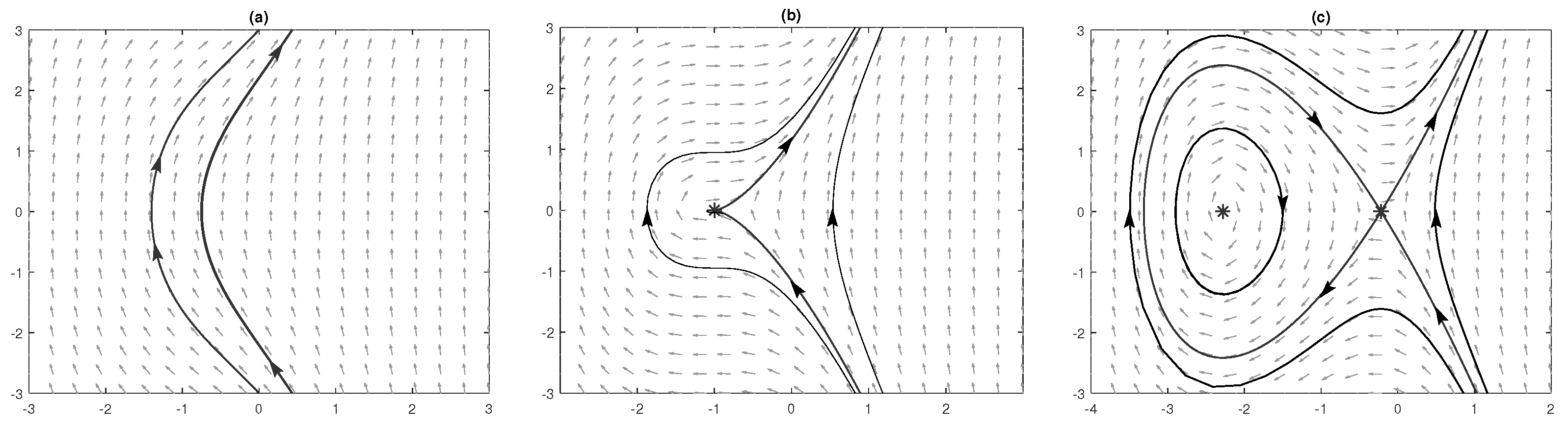
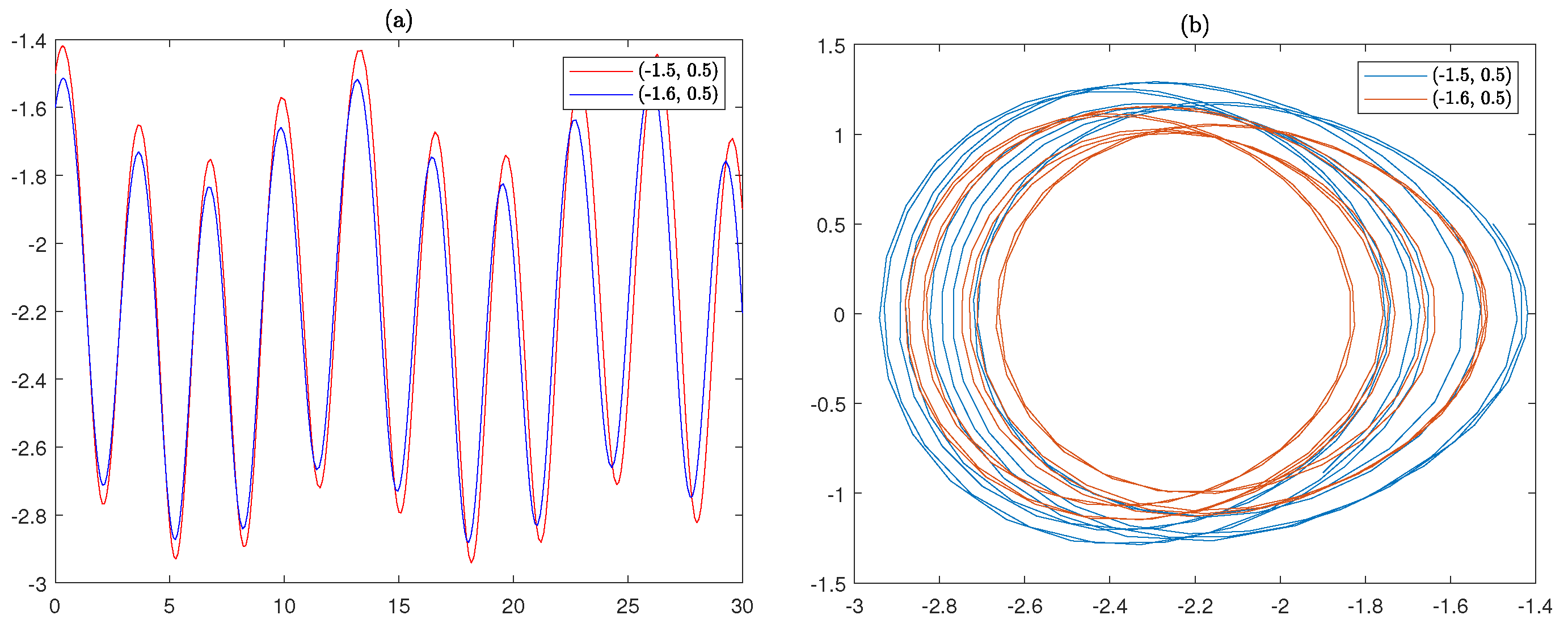
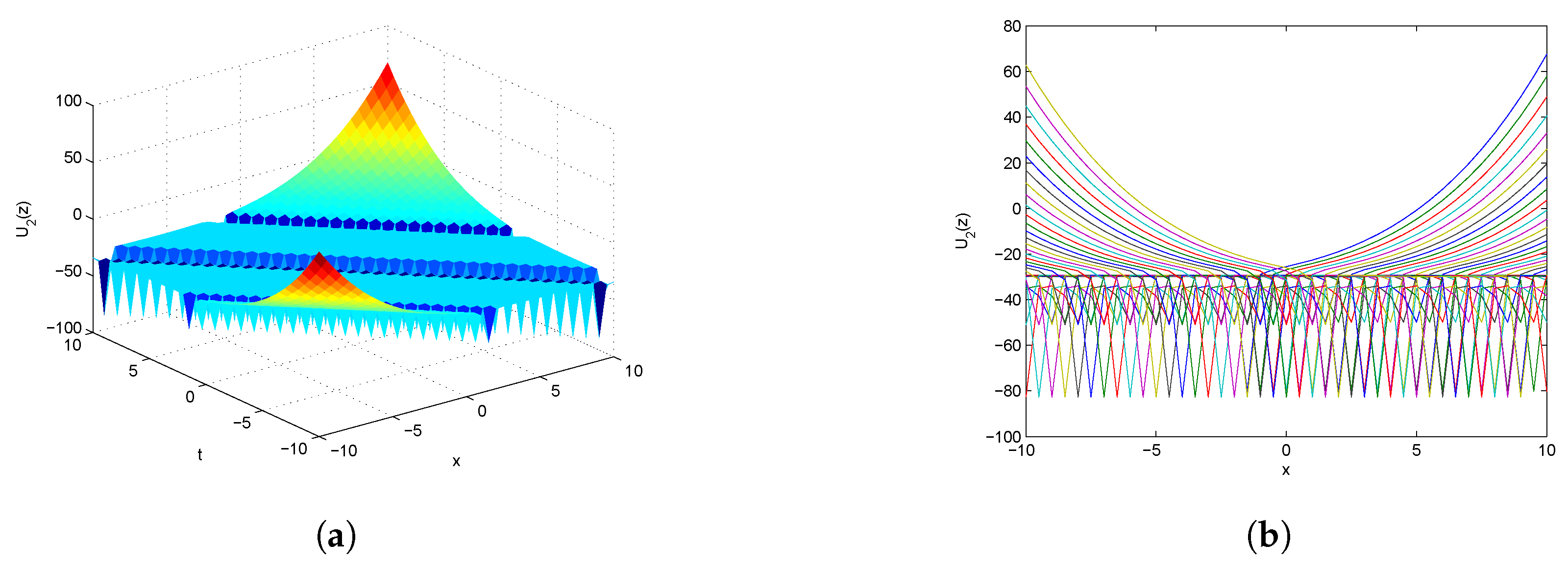
5. Dynamics Analysis
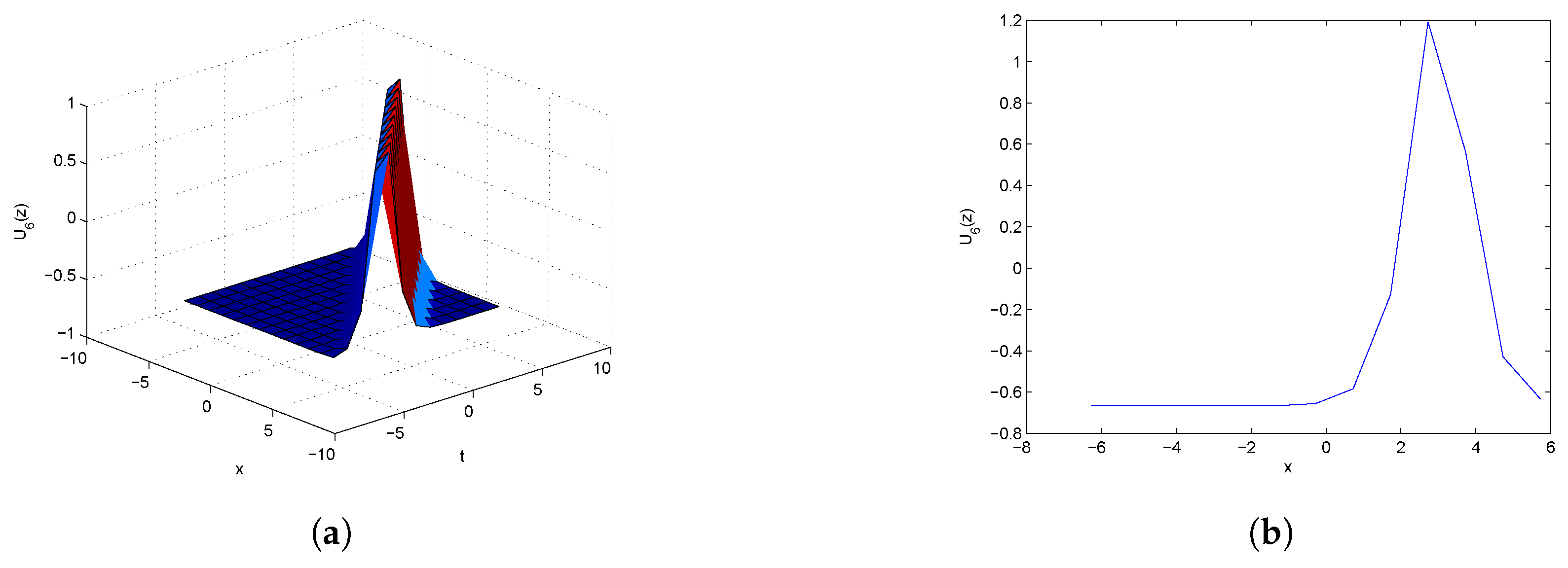
5.1. Dynamics Behavior of the (3+1)-Dimensional gSW Equation
5.2. Chaos Behavior of the (3+1)-Dimensional gSW Equation
5.3. Dynamic Structure of the Solutions to the fSK Equation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, Y.; Peng, L.; Huang, Z.; Lai, Y. Soliton, breather, lump, interaction solutions and chaotic behavior for the (2+1)-dimensional KPSKR equation. Chaos Soliton. Fract. 2024, 187, 115351. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, X.; Huang, Z.; Peng, L.; Lai, Y.; Aminakbari, N. Soliton and lump and travelling wave solutions of the (3+1) dimensional KPB like equation with analysis of chaotic behaviors. Sci. Rep. 2024, 14, 20966. [Google Scholar] [CrossRef] [PubMed]
- Liu, J. Lump-type solutions and interaction solutions for the (2+1)-dimensional generalized fifth-order KdV equation. Appl. Math. Lett. 2018, 86, 36–41. [Google Scholar] [CrossRef]
- Liu, J.; Ye, Q. Stripe solitons and lump solutions for a generalized Kadomtsev-Petviashvili equation with variable coefficients in fluid mechanics. Nonlinear Dyn. 2019, 96, 23–29. [Google Scholar] [CrossRef]
- Gu, Y.; Lai, Y. Analytical investigation of the fractional Klein-Gordon equation along with analysis of bifurcation, sensitivity and chaotic behaviors. Mod. Phys. Lett. B 2025, 39, 2550124. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Ali, K.K.; Liu, J. New optical soliton solutions for fokas-lenells dynamical equation via two various methods. Mod. Phys. Lett. B 2021, 35, 2150196. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. New solitary wave solutions to the (2+1)-dimensional Calogero-Bogoyavlenskii-Schiff and the Kadomtsev-Petviashvili hierarchy equations. Indian J. Phys. 2017, 135, 327–336. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. On the novel wave behaviors to the coupled nonlinear Maccari’s system with complex structure. Optik 2017, 131, 1036–1043. [Google Scholar] [CrossRef]
- Hosseini, K.; Zabihi, A.; Samadani, F.; Ansari, R. New explicit exact solutions of the unstable nonlinear Schrödinger’s equation using the expa and hyperbolic function methods. Opt. Quant. Electron. 2018, 50, 82. [Google Scholar] [CrossRef]
- Hosseini, K.; Manafian, J.; Samadani, F.; Foroutan, M.; Mirzazadeh, M.; Zhou, Q. Resonant optical solitons with perturbation terms and fractional temporal evolution using improved tan (ϕ(η)/2)-expansion method and exp function approach. Optik 2018, 158, 933–939. [Google Scholar] [CrossRef]
- Hosseini, K.; Samadani, F.; Kumar, D.; Faridi, M. New optical solitons of cubic-quartic nonlinear Schrödinger equation. Optik 2018, 157, 1101–1105. [Google Scholar] [CrossRef]
- Hosseini, K.; Yazdani Bejarbaneh, E.; Bekir, A.; Kaplan, M. New exact solutions of some nonlinear evolution equations of pseudoparabolic type. Opt. Quant. Electron. 2017, 49, 241. [Google Scholar] [CrossRef]
- Ali, K.K.; Rezazadeh, H.; Talarposhti, R.A.; Bekir, A. New soliton solutions for resonant nonlinear Schródinger’s equation having full nonlinearity. Int. J. Mod. Phys. B 2020, 34, 2050032. [Google Scholar] [CrossRef]
- Ali, K.K.; Wazwaz, A.M.; Mehanna, M.S.; Osman, M.S. On short-range pulse propagation described by (2+1)-dimensional Schródinger’s hyperbolic equation in nonlinear optical fibers. Phys. Scr. 2020, 95, 75203. [Google Scholar] [CrossRef]
- Roshid, H.; Rahman, M. The exp(-ϕ(ξ))-expansion method with application in the (1+1)-dimensional classical Boussinesq equations. Results Phys. 2014, 4, 150–155. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M. The exp(-ϕ(ξ))-expansion method for finding traveling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Kadkhoda, N.; Jafari, H. Analytical solutions of the Gerdjikov-Ivanov equation by using exp(-φ(ξ))-expansion method. Optik 2017, 139, 72–76. [Google Scholar] [CrossRef]
- Aminakbari, N.; Gu, Y.; Dang, G. Study on soliton behaviors of the complex nonlinear Fokas-Lenells equation utilizing different methods. Mod. Phys. Lett. B 2024, 38, 2450340. [Google Scholar] [CrossRef]
- Gu, Y.; Jiang, C.; Lai, Y. Analytical Solutions of the fractional Hirota-Satsuma coupled KdV equation along with analysis of bifurcation, sensitivity and chaotic behaviors. Fractal Fract. 2024, 8, 585. [Google Scholar] [CrossRef]
- Yuan, W.; Xiong, W.; Lin, J.; Wu, Y. All meromorphic solutions of an auxiliary ordinary differential equation and its applications. Acta Math. Sci. 2015, 35, 1241–1250. [Google Scholar] [CrossRef]
- Yuan, W.; Meng, F.; Huang, Y.; Wu, Y. All traveling wave exact solutions Of the variant Boussinesq equations. Appl. Math. Comput. 2015, 268, 865–872. [Google Scholar] [CrossRef]
- Gu, Y.; Yuan, W.; Aminakbari, N.; Lin, J. Meromorphic solutions of some algebraic differential equations related Painlevé equation IV and its applications. Math. Meth. Appl. Sci. 2018, 41, 3832–3840. [Google Scholar] [CrossRef]
- Ye, F.; Tian, J.; Zhang, X.; Jiang, C.; Ouyang, T.; Gu, Y. All traveling wave exact solutions of the Kawahara equation using the complex method. Axioms 2022, 11, 330. [Google Scholar] [CrossRef]
- Bergweiler, W.; Rippon, P.; Stallard, G. Dynamics of meromorphic functions with direct or logarithmic singularities. Proc. Lond. Math. Soc. 2008, 97, 368–400. [Google Scholar] [CrossRef]
- Conte, R.; Ng, T.W.; Wu, C. Closed-form meromorphic solutions of some third order boundary layer ordinary differential equations. Bull. Sci. Math. 2022, 174, 103096. [Google Scholar] [CrossRef]
- Eremenko, A. Meromorphic traveling wave solutions of the Kuramoto-Sivashinsky equation. J. Math. Phys. 2006, 2, 278–286. [Google Scholar]
- Kudryashov, N.A. Meromorphic solutions of nonlinear ordinary differential equations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2778–2790. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Sinelshchikov, D.I.; Demina, M.V. Exact solutions of the generalized Bretherton equation. Phys. Lett. A 2011, 375, 1074–1079. [Google Scholar] [CrossRef]
- Yuan, W.; Li, Y.; Lin, J. Meromorphic solutions of an auxiliary ordinary differential equation using complex method. Math. Meth. Appl. Sci. 2013, 36, 1776–1782. [Google Scholar] [CrossRef]
- Yuan, W.; Wu, Y.; Chen, Q.; Huang, Y. All meromorphic solutions for two forms of odd order algebraic differential equations and its applications. Appl. Math. Comput. 2014, 240, 240–251. [Google Scholar] [CrossRef]
- Yuan, W.; Huang, Z.; Fu, M.; Lai, J. The general solutions of an auxiliary ordinary differential equation using complex method and its applications. Adv. Differ. Equ. 2014, 2014, 147. [Google Scholar] [CrossRef]
- Sawada, K.; Kotera, T. A method for finding N-soliton solutions of the K.d.V. equation and K.d.V.-Like Equation. Progr. Theoret. Phys. 1974, 51, 1355–1367. [Google Scholar] [CrossRef]
- Tang, Y.; Ma, W.; Xu, W. Grammian and Pfaffian solutions as well as Pfaffianization for a (3+1)-dimensional generalized shallow water equation. Chin. Phys. B 2012, 21, 070212. [Google Scholar] [CrossRef]
- Liu, C.; Dai, Z. Exact soliton solutions for the fifth-order Sawada-Kotera equation. Appl. Math. Comput. 2008, 206, 272–275. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A.; Mohyud-Din, S.T. Extended generalized Riccati equation mapping method for the fifth-order Sawada-Kotera equation. AIP Adv. 2013, 3, 52104. [Google Scholar] [CrossRef]
- Guo, Y.; Li, D.; Wang, J. The new exact solutions of the fifth-order Sawada-Kotera equation using three wave method. Appl. Math. Lett. 2019, 94, 232–237. [Google Scholar] [CrossRef]
- Gu, J.; Zhang, Y.; Dong, H. Dynamic behaviors of interaction solutions of (3+1)-dimensional shallow water wave equation. Comput. Math. Appl. 2018, 76, 1408–1419. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D. Analytical soliton solutions to the generalized (3+1)-dimensional shallow water wave equation. Mod. Phys. Lett. B 2022, 36, 2150540. [Google Scholar] [CrossRef]
- Shi, F.; Qi, M.; Wang, K. Multi-kink solitons, resonant soliton molecules and multi-lumps solutions to the (3+1)-dimensional shallow water wave equation. Mod. Phys. Lett. B 2025, 39, 2550039. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, H.; Zhang, X.; Yang, H. Rational solutions and lump solutions to the generalized (3+1)-dimensional shallow water-like equation. Comput. Math. Appl. 2017, 73, 246–252. [Google Scholar] [CrossRef]
- Lang, S. Elliptic Functions, 2nd ed.; Springer: New York, NY, USA, 1987. [Google Scholar]
- Kivshar, Y.S.; Luther-Davies, B. Dark optical solitons: Physics and applications. Phys. Rep. 1998, 298, 81–197. [Google Scholar] [CrossRef]



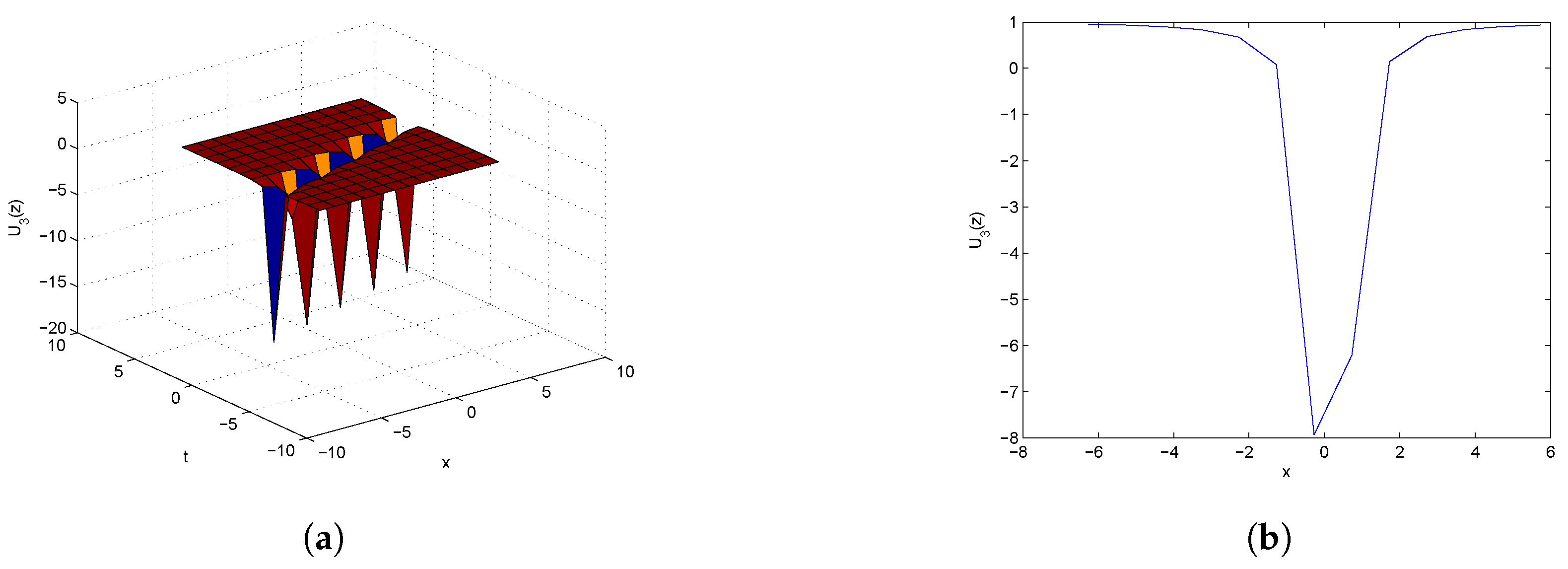

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, H.; Gu, Y. Closed-Form Meromorphic Solutions of High-Order and High-Dimensional Differential Equations. Axioms 2025, 14, 334. https://doi.org/10.3390/axioms14050334
Tu H, Gu Y. Closed-Form Meromorphic Solutions of High-Order and High-Dimensional Differential Equations. Axioms. 2025; 14(5):334. https://doi.org/10.3390/axioms14050334
Chicago/Turabian StyleTu, Hongqiang, and Yongyi Gu. 2025. "Closed-Form Meromorphic Solutions of High-Order and High-Dimensional Differential Equations" Axioms 14, no. 5: 334. https://doi.org/10.3390/axioms14050334
APA StyleTu, H., & Gu, Y. (2025). Closed-Form Meromorphic Solutions of High-Order and High-Dimensional Differential Equations. Axioms, 14(5), 334. https://doi.org/10.3390/axioms14050334





