The Three Laws of Thought, Plus One: The Law of Comparisons

Abstract

The rules of logic are nearly 2500 years old and date back to Plato and Aristotle who set down the three laws of thought: identity, non-contradiction, and excluded middle. The use of language and logic has been adequate for us to develop mathematics, prove theorems, and create scientific knowledge. However, the laws of thought are incomplete. We need to extend our logical system by adding to the very old laws of thought an essential yet poorly understood law. It is a necessary law of thought that resides in our biology even deeper than the other three laws. It is related to the rudiments of how we as living beings, and even nonliving things, respond to influences as stimuli. It helps us discriminate between being ourselves and sensing that there is something else that is not ourselves that even amoebas seem to know. It is the intrinsic ability to sense and distinguish. This fourth law is the law of comparisons. Although it has been missing from our logical deductions it underlies the other three laws of thought because without it we cannot know what is and what is not.

The original three laws of thought, defined by Plato (Figure 1), comprise the most basic requirements for identification and reasoning:

First, that nothing can become greater or less, either in number or magnitude, while remaining equal to itself. Second, that without addition or subtraction there is no increase or diminution of anything, but only equality. Third, that what was not before cannot be afterwards, without becoming and having become.

Figure 1. Plato (Left) Holding the Timaeus and Aristotle Holding the Ethics, a Painting by Raphael Sanzio at the School of Athens.

Figure 1. Plato (Left) Holding the Timaeus and Aristotle Holding the Ethics, a Painting by Raphael Sanzio at the School of Athens.

We turn now to the modern way of introducing these three laws:

The Three Laws, Plus One

Law 1: The Law of Identity

Two entities x and y are identical if they share the same properties.

A necessary and sufficient condition for two entities x and y to be identical (be the same) is that they share the same properties: $\forall x\forall y[x=y\to \forall P(Px\leftrightarrow Py]$ and $\forall x\forall y[\forall P(Px\leftrightarrow Py)\to x=y]$. In other words: for all x and all y, the statement x is y implies that for every property P, if x has that property, then y has that property and conversely. It is also true that for all properties, if x and y have the same properties, then they are identical.

If x is not identical to y for all y, then it is identical with x, enabling one to make the distinction of x from all y ≠ x. According to Leibnitz, the law of identity is the first primitive truth of reason that is affirmative. Yet, one can discern from the statement of this law that identity in itself has no meaning unless one thinks of it in terms relative to other things. Thus satisfying the law of identity involves the even more basic implicit assumption that entities must be compared with all other entities to know if they are identical with themselves or there are other entities identical with them. Because it is not possible to know if an entity is identical with itself unless it is previously known from memory, it is necessary that it should be compared with itself. Comparisons are necessary and sufficient to satisfy the law of identity.

One may conclude that to know something is identical only with itself, we must compare it with all other things for all the properties it has. After numerous comparison of x with other y, we learn to characterize x by remembering it according to the properties it has and their intensities. We also need to compare property P with every other property Q as to which is possessed by x and which is not.

Law 2: The Law of Noncontradiction

Either x or not x is true and there is no other possibility.

This means that opposite assertions cannot be true at the same time. Here again, two entities are involved, x and not x, and to determine which it is, distinction between them needs to be made through comparison. In logic, to show that x holds is equivalent to showing that not x does not hold.

Law 3: The Law of the Excluded Middle

An entity x has or does not have a property P. Conversely, a property P is either possessed by an entity x or it is not possessed by x.

This law does not allow for different degrees of the property P. To talk about degrees of properties is clearly different from the black and white distinctions that Laws 2 and 3 require. Further, to identify x, as in Law 1, we have to know not only what properties it has, but also to what extent it has these properties.

Thus it appears that knowledge about comparisons must precede these three laws, and we must introduce a new law that precedes them. Once we admit that comparisons are a biological talent and that we need to be more precise about understanding things, we can elaborate deterministic outcomes into all shades of gray, which in fact we human beings are able to detect.

Law 4: The Law of Quantitative Comparison [1,2,3,4]

Given two entities x and y both having a property P. Either x has P more than y, less than y or is indifferent to y. When x and y are closely similar (homogeneously close) it is possible be using expert judgment to estimate the dominance of one over another numerically and derive priorities from such comparisons.

Let 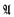be a finite set of n entities. Let 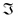be a set of properties or attributes with respect to which entities in 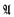are compared by estimating the similarity between one entity and another. A property is a feature that an object or individual possesses even if we are ignorant of this fact, whereas an attribute is a special concept assigned to some entity under consideration. Sometimes erroneously an attribute is referred to as a property.

When two entities in 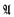are compared according to a property P in 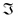, we say that we are performing binary comparisons. Let >_P be a binary relation 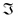representing “more preferred than” or “dominates” with respect to a property P in 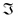. Let ~_P be the binary relation “indifferent to” with respect to a property P in 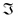. Hence, given two entities, A_i , A_j in 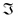, either $A_i>{}_{P}A_j$ or $A_j>{}_{P}A_i$ or $A_i{~}_P{A}_j$ for all P in 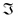. We use 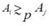to indicate more preferred or indifferent. A given family of binary relations >_P with respect to a property P in 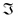is a primitive concept. We have used this kind of relation to derive the notion of priority or importance both with respect to one or several properties.

Surprisingly we found a similarity between the foregoing axioms and those given by Arthur Schopenhauer [4] who was not equipped to develop a mathematical theory to use them. He listed them in the following way in his On the Fourfold Root of the Principle of Sufficient Reason, §33:

• A subject is equal to the sum of its predicates, or a = a.
• No predicate can be simultaneously attributed and denied to a subject, or a ≠ ~a.
• Of every two contradictorily opposite predicates, one must belong to every subject.
• Truth is the reference of a judgment to something outside it as its sufficient reason or ground.

Because the brain works with electricity, that is quantitative in nature, we need to talk about the use of mathematics that derives from making comparisons. This mathematics cannot be intrinsically based on the use of Cartesian axes to represent independent and dependent variables measured with arbitrary units applied uniformly, particularly because properties do not arise in our understanding as space and time that are endowed with homogeneity throughout.

Had the mathematics of relative measurement been known long ago, our understanding of the world would (not “might”) have been different because it deals with interdependence in a natural way. Later, for example, we shall see how the inverse square laws of nature are an intrinsic part of the Fourier transform of our neural firings in the real number domain. Relative measurement applies to things that do not change as well as to things that do. If the world began with the big bang, everything was energy with dynamic behavior over time. Accurate measurement did not last long. When Descartes invented the ideas of axes and scales with arbitrary units, he assumed that the world was fixed and he could study it by using the axes. However, the world of human behavior changes, and situations change.