Robust Mixture Modeling Based on Two-Piece Scale Mixtures of Normal Family

Abstract

In this paper, we examine the finite mixture (FM) model with a flexible class of two-piece distributions based on the scale mixtures of normal (TP-SMN) family components. This family allows the development of a robust estimation of FM models. The TP-SMN is a rich class of distributions that covers symmetric/asymmetric and light/heavy tailed distributions. It represents an alternative family to the well-known scale mixtures of the skew normal (SMSN) family studied by Branco and Dey (2001). Also, the TP-SMN covers the SMN (normal, t, slash, and contaminated normal distributions) as the symmetric members and two-piece versions of them as asymmetric members. A key feature of this study is using a suitable hierarchical representation of the family to obtain maximum likelihood estimates of model parameters via an EM-type algorithm. The performances of the proposed robust model are demonstrated using simulated and real data, and then compared to other finite mixture of SMSN models.

1. Introduction

Finite mixture models are highly demanded in machine-learning analysis, due to their properties, computational tractability, and for being a good approximation for continuous densities [1]. They are also an important statistical tool for many applications in clustering, discriminant analysis, image processing and satellite imaging [2]. Beyond the already known results provided for the finite mixture of normal distributions (FM-NOR) model in the literature [1], recent developments cover symmetric/asymmetric and light/heavy tailed distributions. One of these is the novel class of finite mixture of multivariate skew-normal mixture (FM-SN) models [3,4], which provides some advantages over the normal mixtures: the normal components allow an arbitrarily close modeling of any distribution by increasing the number of components, and, in the context of supervised learning, groups of observations represented by asymmetrically distributed data can lead to the wrong classification. The components of skew-normal mixture models, however, capture skewness due to their flexibility [1]. In addition, a robust extension of the FM-SN model to robust finite mixture of skew-t (FM-ST) has been done in the influential works of [3,5,6,7]. The FM-ST components, too, capture both skewness and extreme observations due to their flexibility [8].

The SMSN family is a rich and very strong flexible class of distributions which covers the light/heavy-tailed distributions; e.g., skew-normal (SN), skew-t (ST), skew-slash (SSL) and skew contaminated-normal (SCN) distributions, and has been widely considered in many statistical models, especially FM models (see e.g., [5,9,10,11,12,13,14,15]). The SMSN family is an extension of the skewed version of the well-known symmetric scale mixtures of the normal (SMN) family which contains the light/heavy-tailed members: the normal (N), t (T), slash (SL) and contaminated-normal (CN) distributions [16]. Lange et al. [17], Lange and Sinsheimer [18], and Maleki and Nematollahi [19] used the SMN family in an application of robust statistical modeling. A two-piece distribution based on the symmetrical distributions with various scales is an alternative approach to model atypical data (see e.g., [10,20,21,22,23,24]). In our approach, we have used the two-piece distributions based on the SMN family. This family, called the two-piece distributions based on the scale mixtures of normal (TP-SMN), and analogy of the SMSN family, contains the light/heavy-tailed members: the two-piece normal (TP-N), two-piece t (TP-T), two-piece slash (TP-SL) and two-piece contaminated-normal (TP-CN) distributions as its members.

In this paper, we consider the TP-SMN family of distributions as a two-component mixture of truncated SMN distributions on a special two partition of the real domain ($\mathbb{R}$), and then propose the finite mixture of this family, called FM-TP-SMN models. It represents an alternative family to the well-known scale mixtures of skew normal (SMSN) family studied by [25]. We have also used a hierarchical representation of the FM-TP-SMN and implemented an expectation-maximization (EM)-type algorithm for finding the maximum likelihood (ML) estimates of the proposed model. Studies by [21,23], show that by truncating the distribution in two partitions, makes it possible to obtain a better fit of empirical distribution because, the subjacent process of the complete likelihood is modeled. This way, the “two-piece” modeling is a direct competitor against the FM-SMSN family of distributions [21].

The rest of this paper is organized as follows. In Section 2, we review some main properties of the TP-SMN family and represent this family as a two-component mixture of the truncated SMN distributions. In Section 3, the FM-TP-SMN model is introduced and the ML estimates of the proposed model parameters via an EM-type algorithm are provided. In Section 4, numerical studies with an application of the proposed models and estimates are considered. Some conclusions and ideas for future research are offered in Section 5.

2. The Two-Piece Scale Mixtures of Normal Distributions

In this section, we analyze some necessary properties of the TP-SMN family of distributions for our proposed FM model.

The well-known SMN family introduced by [16] (the basis of the robust asymmetric TP-SMN family), has the following probability density function (PDF) and stochastic representation. Let $X\sim SMN(\mu ,\sigma ,\mathit{\nu })$, then its PDF is

$$f_{SMN}(x|\mu ,\sigma ,\mathit{\nu })={\int }_0^{\infty }\varphi (x|\mu ,u^{-1}{\sigma }^2)dH(u|\mathit{\nu }),x\in \mathbb{R},$$

(1)

and its stochastic representation is

$$X=\mu +\sigma U^{-1/2}W,$$

(2)

where $\varphi (·|\mu ,{\sigma }^2)$ represents the density of $N(\mu ,{\sigma }^2)$ distribution, $H(·|\mathit{\nu })$ is the cumulative distribution function (CDF) of the scale mixing random variable U, which can be indexed by a scalar or vector of parameters $\mathit{\nu }$, and W is a standard normal random variable that is independent of U.

The TP-SMN is a rich family of distributions that covers the asymmetric light-tailed TP-N (also called the epsilon-skew-normal; [26]), the asymmetric heavy-tailed TP-T, TP-SL and TP-CN distributions, and their corresponding symmetric members. Note that symmetric members of the TP-SMN and SMSN classes are the SMN family. In terms of density, for $y\in \mathbb{R}$ this family can be represented as

$$g(x|\mu ,\sigma ,\gamma ,\mathit{\nu })=\left\{\begin{array}{cc}2(1-\gamma )f_{SMN}(x|\mu ,\sigma (1-\gamma ),\mathit{\nu }),\hfill & y\le \mu ,\hfill \\ 2{\gamma }_{SMN}(x|\mu ,\sigma \gamma ,\mathit{\nu }),\hfill & y>\mu ,\hfill \end{array}\right.$$

(3)

where $0<\gamma <1$ is the slant parameter, $f_{SMN}(·|\mu ,\sigma ,\mathit{\nu })$ is given by (1) and is denoted by $Y\sim TP-SMN(\mu ,\sigma ,\gamma ,\mathit{\nu })$ with $E(Y)=\mu -b\sigma (1-2\gamma )$ and $Var(Y)={\sigma }^2[c_2{k}_2(\mathit{\nu })-b^2{c}_1^2]$, for which $b=\sqrt{2/\pi }{k}_1(\mathit{\nu })$, $c_r={\gamma }^{r+1}+{(-1)}^r{(1-\gamma )}^{r+1}$, $k_r(\mathit{\nu })=E(U^{-r/2})$, and U is the scale mixing random variable in (2).

Different TP-SMN member distributions in (3) are obtained by several distributions for scale mixing random variable U in (2), as follows:

• Two-piece normal (TP-N): $U=1$ with probability one,
• Two-piece t (TP-T): $U\sim Gamma(\nu /2,\nu /2)$, i.e., $\mathit{\nu }=\nu$,
• Two-piece slash (TP-SL): $U\sim Beta(\nu ,1)$, i.e., $\mathit{\nu }=\nu$,
• Two-piece contaminated normal (TP-CN): $h(u|\mathit{\nu })=\nu I_{(u=1)}+(1-\nu )I_{(u=1)}$, i.e., $\mathit{\nu }={(\nu ,\tau )}^{\top }$.

For more details and statistical properties of the TP-SMN family, see [20,23].

Further, the two-piece distributions can be represented as the two-component mixture with separated supports, i.e., left and right half basic distributions [20] (Equation (4)), especially when $Y\sim TP-SMN(\mu ,\sigma ,\gamma ,\mathit{\nu })$ with PDF given in (3), two-component mixture left and right half SMN distributions with special component probabilities as follows:

$$g(x|\mu ,{\sigma }_1,{\sigma }_2,\mathit{\nu })=2\frac{{\sigma }_1}{{\sigma }_1+{\sigma }_2}{f}_{SMN}(y|\mu ,{\sigma }_1,\mathit{\nu })I_{(-\infty ,\mu ]}(y)+2\frac{{\sigma }_1}{{\sigma }_1+{\sigma }_2}{f}_{SMN}(x|\mu ,{\sigma }_2,\mathit{\nu })I_{(\mu ,+\infty )}(y).$$

(4)

Note in Equation (4) that, the scale parameter $\sigma$ and slant parameter $\gamma$ in Equation (3) are recovered in the form of $\sigma ={\sigma }_1+{\sigma }_2$ and $\gamma ={\sigma }_2/({\sigma }_1+{\sigma }_2)$.

By using auxiliary (latent) variables $S_j$, $j=1,2$; in terms of the components of the mixture in Equation (4), the TP-SMN random variable can have the following stochastic representation

$$\left\{\begin{array}{c}Y|S_1=1\sim SMN(\mu ,{\sigma }_1,\mathit{\nu })I_A(y_i),\hfill \\ Y|S_2=1\sim SMN(\mu ,{\sigma }_2,\mathit{\nu })I_{A^c}(y_i),\hfill \end{array}\right.$$

(5)

where $A=(-\infty ,\mu )$ and $SMN(·)I_A(·)$ denotes the truncated SMN distribution on the interval A, and $\mathbf{S}={(S_1,S_2)}^{\top }$ has a multinomial distribution with following probability mass function (PMF):

$$P(\mathbf{S}=\mathbf{s})={\left(\frac{{\sigma }_2}{{\sigma }_1+{\sigma }_2}\right)}^{z_1}{\left(\frac{{\sigma }_2}{{\sigma }_1+{\sigma }_2}\right)}^{z_2};s_1,s_2=0,1,$$

(6)

and is denoted by $\mathbf{S}\sim M(1,{\sigma }_1/({\sigma }_1+{\sigma }_2),{\sigma }_2/({\sigma }_1+{\sigma }_2))$. Note that each component-label is a Bernoulli random variable $S_k\sim Binomial(1,{\sigma }_k/({\sigma }_1+{\sigma }_2))$; $k=1,2$, such that $S_1+S_2=1$.

3. Finite Mixtures TP-SMN

In this section, we introduce the finite mixture of TP-SMN (FM-TP-SMN) model and obtain the ML estimates of this model’s parameters.

3.1. FM-TP-SMN Model

Here, we consider a distribution represented as a g-component mixture of TP-SMN distributions. In terms of density, this mixture distribution is characterized by the following density:

$$f(y|\Theta )=\sum _{j=1}^g{\pi }_{j}g(y|{\mu }_j,{\sigma }_j,{\gamma }_j,{\mathit{\nu }}_j),y\in \mathbb{R},$$

(7)

where $\Theta ={({\pi }_1,\dots ,{\pi }_g,{\mu }_1,\dots ,{\mu }_g,{\sigma }_1,\dots ,{\sigma }_g,{\gamma }_1,\dots ,{\gamma }_g,{\mathit{\nu }}_1,\dots ,{\mathit{\nu }}_g)}^{\top }$, for which ß $={({\pi }_1,\dots ,{\pi }_g)}^{\top }$ with ${\pi }_j>0$, $j=1,\dots ,g$, ${\sum }_{j=1}^g{\pi }_j=1$, and, for $j=1,\dots ,g$, $g(y|{\mu }_j,{\sigma }_j,{\gamma }_j,{\mathit{\nu }}_j)$ is an $TP-SMN({\mu }_j,{\sigma }_j,{\gamma }_j,{\mathit{\nu }}_j)$-component density as defined in (1). Also, we write $Y\sim FM-TP-SMN(\Theta )$ to say that a random variable Y has an FM-TP-SMN distribution as defined by (7).

Concerning the parameter ${\mathit{\nu }}_j$ of the mixing distribution $H(·|{\mathit{\nu }}_j)$, for $j=1,\dots ,g$, it is worth noting that it can be a vector of parameters, e.g. the contaminated normal distribution. Thus, for computational convenience we assume that ${\mathit{\nu }}_1=\cdots ={\mathit{\nu }}_g=\mathit{\nu }$ (see also [5]).

In terms of the components of the mixtures, Equation (7) can be equivalently obtained by

$$Y|Z_j=1\sim TP-SMN({\mu }_j,{\sigma }_j,{\gamma }_j,\mathit{\nu }),j=1,\dots ,g,$$

(8)

where $Z={(Z_1,\dots ,Z_g)}^{\top }\sim Multinomial(1,{\pi }_1,\dots ,{\pi }_g)$ is a multinomial (component-label) vector with probability mass function $P(Z_1=z_1,\dots ,Z_m=z_m)={\pi }_1^{z_1}{\pi }_2^{z_2}\cdots {\pi }_g^{z_g}$, $z_j=0,1$; $j=1,\dots ,g$, ${\sum }_{j=1}^g{z}_j=1$.

Since only one component of $\mathit{Z}$ can be equal to one (remaining ones are zero), events $\{Z_j=1\}$ and $\{Z_j=1,Z_r=0;\forall j\ne r\}$ are equivalent, indicating thus that the distribution of Y corresponds to the i-th component of the mixture; for further details, see e.g., [1].

Remark 1.

Let $Y\sim FM-TP-SMN(\Theta )$, then the mean and variance of Y are, respectively, given by

$$E[Y]=\sum _{j=1}^g{\pi }_{j}E[Y|Z_j=1]=\sum _{j=1}^g{\pi }_{j}E[X_j],$$

and

$$Var[Y]=\sum _{j=1}^g{\pi }_j\{Var[Y|Z_j=1]+{(E[Y|Z_j=1]-E[Y])}^2\}=\sum _{j=1}^g{\pi }_j\{Var[X_j]+{(E[X_j]-\overline{\mu })}^2\},$$

where $X_j\sim TP-SMN({\mu }_j,{\sigma }_j,{\gamma }_j,\mathit{\nu })$, $j=1,\dots ,g$, and $\overline{\mu }={\sum }_{j=1}^g{\pi }_{j}E[X_j]$ (see e.g., [2]).

The FM-TP-ESN densities in (7) are an extremely flexible class which includes the finite mixtures of SMN densities as special case, when ${\epsilon }_j=0$, $j=1,\dots ,g$.

For each i.i.d. sample in the form of $\mathbf{Y}={(Y_1,\dots ,Y_n)}^{\top }$, by considering the PDF (7), the log-likelihood function is

$$\ell (\Theta |\mathbf{Y})=\sum _{i=1}^n\log \left(\sum _{j=1}^g{\pi }_{j}g(y|{\mu }_j,{\sigma }_j,{\gamma }_j,\mathit{\nu })\right).$$

(9)

3.2. ML Estimates of Model Parameters

We can utilize a (latent) indicator (allocation) variables ${\mathbf{Z}}_i={(Z_{i1},\dots ,Z_{ig})}^{\top }$, $i=1,\dots ,n$, to assign observations belonging to different components of the mixture ($j=1,\dots ,g$), so in terms of $Z_{ij}$, we can conclude that

$$Y_i|Z_{ij}=1{\sim }^{ind.}TP-SMN({\mu }_j,{\sigma }_j,{\gamma }_j,\mathit{\nu }),P(Z_{ij}=1)={\pi }_j;i=1,\dots ,n,j=1,\dots ,g,$$

and so using Equations (2) and (5) with $S_{ij}={(S_{ij1},S_{ij2})}^{\top }$, $i=1,\dots ,n$, we have that

$$\begin{array}{ccc}\hfill Y_i|U_{ij},Z_{ij}=1,S_{ijk}=1& {\sim }^{ind.}& N({\mu }_j,u_{ij}^{-1/2}{\sigma }_j^2)I_{A_j}{(y_i)}^{2-k}{I}_{A_j^c}{(y_i)}^{k-1},\hfill \\ \hfill U_{ij}|Z_{ij}=1,S_{ijk}=1& {\sim }^{ind.}& H(u_{ij}|\mathit{\nu }),\hfill \\ \hfill S_{ij}|Z_{ij}=1& {\sim }^{iid.}& M\left(1,\frac{{\sigma }_{1j}}{{\sigma }_{1j}+{\sigma }_{2j}},\frac{{\sigma }_{2j}}{{\sigma }_{1j}+{\sigma }_{2j}}\right),\hfill \\ \hfill Z_i& {\sim }^{iid.}& M(n,{\pi }_1,\dots ,{\pi }_g),\hfill \end{array}$$

(10)

for $i=1,\dots ,n$; $j=1,\dots ,g$; $k=1,2$, $A_j=(-\infty ,{\mu }_j]$ and $N(·)I_A(·)$ denotes the truncated normal distribution on the interval A.

The above hierarchical representation of the FM-TP-SMN model will be used to obtain the ML estimates via an ECME-algorithm. This algorithm is a generalization of the ECM-algorithm introduced by [27], which is an extension of the EM-algorithm [28]. It can be obtained by replacing some CM-steps, which maximize the constrained expected complete-data log-likelihood function, with steps that maximize the corresponding constrained actual likelihood function. As [27,29] indicated, the joint ML estimates obtained by ECME-algorithms are much more efficient than other EM-type algorithms.

Let $\mathbf{C}=\{\mathbf{Y},\mathbf{S},\mathbf{Z}\}$ denotes the complete data, where $\mathbf{Y}={(Y_1,\dots ,Y_n)}^{\top }$ is the observed sample $\mathbf{S}={({\mathbf{S}}_1^{\top },\dots ,{\mathbf{S}}_n^{\top })}^{\top }$ and $\mathbf{Z}={({\mathbf{Z}}_1^{\top },\dots ,{\mathbf{Z}}_n^{\top })}^{\top }$ are the latent or unobserved variables from the FM-TP-SMN model with vector of parameters $\Theta ={({\pi }_1,\dots ,{\pi }_g,{\mu }_1,\dots ,{\mu }_g,{\sigma }_{11},\dots ,{\sigma }_{1g},{\sigma }_{21},\dots ,{\sigma }_{2g},\mathit{\nu })}^{\top }$. Considering the hierarchical representation (10), the completed (augmented) likelihood function is given by

$$L_C(\Theta )=\prod _{i=1}^n\prod _{j=1}^g\prod _{k=1}^2{(\varphi (y_i|{\mu }_j,u_{ijk}^{-1}{\sigma }_k^2)h(u_{ijk}|\mathit{\nu })p({\mathbf{z}}_i|{\pi }_1,\dots ,{\pi }_g)p({\mathbf{s}}_i|{\sigma }_{1j},{\sigma }_{2j})I_{A_j}{(y_i)}^{2-k}{I}_{A_j^c}{(y_i)}^{k-1})}^{z_{ij}{s}_{ijk}},$$

where $A_j=(-\infty ,{\mu }_j]$. After ignoring constants and using auxiliary (latent) variables the completed log-likelihood function is in the form:

$$\ell (\Theta )=-{\sum }_{i=1}^n{\sum }_{j=1}^g{z}_{ij}\log \left({\sigma }_{1j}+{\sigma }_{2j}\right)-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^g{\sum }_{k=1}^2\frac{z_{ij}{s}_{ijk}{u}_{ijk}}{{\sigma }_{kj}^2}{(y_i-{\mu }_j)}^2+{\sum }_{i=1}^n{\sum }_{j=1}^g{\sum }_{k=1}^2{z}_{ij}{s}_{ijk}\log h(u_{ijk}|\mathit{\nu }).$$

(11)

Quantities ${\widehat{z}}_{ij}=E[Z_{ij}|\widehat{\Theta },y_i]$, ${\widehat{s}}_{ijk}=E[S_{ijk}|\widehat{\Theta },y_i,Z_{ij}=1]$ and ${\widehat{w}}_{ijk}=E[Z_{ij}{S}_{ijk}{U}_{ijk}|\widehat{\Theta },y_i]$, must be defined, and using known properties of conditional expectation and PDF in (4), we obtain ${\widehat{w}}_{ijk}={\widehat{z}}_{ij}{\widehat{s}}_{ijk}{\widehat{\kappa }}_{ijk}$, where ${\widehat{\kappa }}_{ijk}=E[U_{ijk}|\widehat{\Theta },y_i,Z_{ij}=1,S_{ijk}=1]$, $i=1,\dots ,n$, $j=1,2$, and

$$\begin{array}{ccc}\hfill {\widehat{z}}_{ij}& =& E[Z_{ij}|\widehat{\Theta },y_i]=\frac{{\pi }_{j}g(y_i|{\widehat{\mu }}_j,{\widehat{\sigma }}_{1j},{\widehat{\sigma }}_{2}j,\widehat{\mathit{\nu }})}{{\sum }_{j=1}^g{\pi }_{j}g(y_i|{\widehat{\mu }}_j,{\widehat{\sigma }}_{1j},{\widehat{\sigma }}_{2j},\widehat{\mathit{\nu }})};i=1,\dots ,n,j=1,\dots ,g,\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\widehat{s}}_{ij1}& =& \frac{2\left(\frac{{\sigma }_{1j}}{{\widehat{\sigma }}_{1j}+{\widehat{\sigma }}_{2j}}\right)f_{SMN}(y_i|{\widehat{\mu }}_j,{\widehat{\sigma }}_{1j},\widehat{\mathit{\nu }})I_{(-\infty ,{\widehat{\mu }}_j]}(y_i)}{g(y_i|{\widehat{\mu }}_j,{\widehat{\sigma }}_{1j},{\widehat{\sigma }}_{2j},\widehat{\mathit{\nu }})}=I_{(-\infty ,{\widehat{\mu }}_j]}(y_i),\hfill \end{array}$$

(13)

where $g(·|·)$ is the TP-SMN PDF defined in Equation (4), and ${\widehat{s}}_{ij2}=1-{\widehat{s}}_{ij1}$, and the conditional expectation ${\widehat{\kappa }}_{ij}$ for the TP-SMN distribution members are given by:

• Two-piece normal (TP-N): ${\widehat{\kappa }}_{ijk}=1$,
• Two-piece t (TP-T): ${\widehat{\kappa }}_{ijk}=\frac{\widehat{\nu }+1}{\widehat{\nu }+d_{ijk}}$,
• Two-piece slash (TP-SL): ${\widehat{\kappa }}_{ij}=\frac{2\widehat{\nu }+1}{d_{ijk}}\frac{P_1(\widehat{\nu }+3/2,d_{ijk}/2)}{P_1(\widehat{\nu }+1/2,d_{ijk}/2)}$,
• Two-piece contaminated Normal (TP-CN): ${\widehat{\kappa }}_{ij}=\frac{{\widehat{\tau }}^{3/2}\widehat{\nu }{e}^{-\widehat{\tau }{d}_{ijk}/2}+(1-\widehat{\nu })e^{-d_{ijk}/2}}{{\widehat{\tau }}^{1/2}\widehat{\nu }{e}^{-\widehat{\tau }{d}_{ijk}/2}+(1-\widehat{\nu })e^{-d_{ijk}/2}}$,

where $d_{ijk}={\left(\frac{y_i-{\widehat{\mu }}_j}{{\widehat{\sigma }}_{kj}}\right)}^2$ and $P_x(a,b)$ denotes the distribution function of the $Gamma(a,b)$ distribution evaluated at x.

Now, the expectation step (E-step) at the $(r+1)$th iteration of the ECME-algorithm requires the calculation of $Q(\Theta |{\widehat{\Theta }}^r)=E_{\Theta }[{\ell }_c(\Theta )|{\widehat{\Theta }}^r,\mathbf{y}]$. So,

E-step.

$$Q(\Theta |{\widehat{\Theta }}^r)=-n\sum _{j=1}^g\log ({\sigma }_{1j}+{\sigma }_{2j})-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^g\sum _{k=1}^2\frac{{\widehat{w}}_{ijk}}{{\sigma }_{kj}^2}{(y_i-{\mu }_j)}^2+\sum _{i=1}^n\sum _{j=1}^g\sum _{k=1}^{2}E[Z_{ij}{S}_{ijk}\log h(U_{ijk}|\mathit{\nu })|{\widehat{\Theta }}^r,y_i].$$

For the conditionally maximizing steps (CM-steps) at the $(r+1)$-th iteration of the ECME-algorithm we have:

CM-steps.

Update ${\pi }_j$, $j=1,\dots ,g$, as:

$${\pi }_j^{(r+1)}=\frac{{\sum }_{i=1}^n{\widehat{z}}_{ij}^{(r)}}{n}.$$

(14)

Update ${\mu }_j$, $j=1,\dots ,g$, as:

$${\mu }_j^{(r+1)}=\frac{{\sum }_{i=1}^n{\widehat{\alpha }}_{ij}^{(r)}{y}_i}{{\widehat{\alpha }}_{ij}^{(r)}},$$

(15)

where ${\widehat{\alpha }}_{ij}^{(r)}={\sum }_{k=1}^2{\widehat{w}}_{ijk}^{(r)}/{\sigma }_{kj}^{2(r)}$.

Update ${\widehat{\sigma }}_{kj}^{(k+1)}$; $k=1,2$; $j=1,\dots ,g$, by solving the following stressed cubic equations

$${\sigma }_{kj}^3+p{\sigma }_{kj}+q=0;k=1,2,$$

(16)

where $p=-\frac{{\sum }_{i=1}^n{\widehat{w}}_{ijk}^{(r)}{(Y_i-{\mu }_j^{(r+1)})}^2}{{\widehat{z}}_{ij}^{(r)}}$, for which $q=p{\sigma }_{2j}{I}_{(k=1)}+p{\sigma }_{1j}{I}_{(k=2)}$. Note that $p,q<0$, so this cubic equation has unique just root in the $(0,+\infty )$ interval.

CML-step of the ECME-algorithm.

$${\mathit{\nu }}^{(k+1)}=argma{x}_{\mathit{\nu }}\ell ({\widehat{\Theta }}_{-\mathit{\nu }}^{(r+1)},\mathit{\nu }|\mathbf{Y}),$$

(17)

where $\ell (·|\mathbf{Y})$ is the log-likelihood function given in (9) and ${\widehat{\Theta }}_{-\mathit{\nu }}^{(r+1)}$ denotes the $(r+1)$-th update of $\widehat{\Theta }$ except $\mathit{\nu }$.

The ECME-algorithm iterates until a sufficient convergence rule is satisfied, e.g., if $|\ell ({\widehat{\Theta }}^{(r+1)}|\mathbf{y})/\ell ({\widehat{\Theta }}^{(r)}|\mathbf{y})-1|\le ϵ$, under the determined tolerance $ϵ$.

4. Numerical Studies

In this section, we assess the performance of the proposed FM model using simulated and real datasets. The implementations of the algorithms were based on the R software [30] version 3.5.1 with a core i7 760 processor 2.8 GHz, and a relative tolerance of ${10}^{-5}$ was used for convergence of the ECME-algorithms. A sample copy of the R code is available up on request from the authors and will be available in an R package specialize to this proposed model.

4.1. Simulations

In this section, we have three simulations. In the first, we showed the robustness of the FM-TP-SMN models to classify heterogeneous data; in the second, we showed the misspecification of the proposed FM-TP-SMN models; and in the third simulation we considered suitability of the asymptotic properties for proposed model estimates.

4.1.1. Clustering

The FM models are useful for clustering the observations by allocating them into groups of observations that are similar in some sense. In fact, by considering the estimated (posterior) probabilities, we can assign such observation points to given groups. However, some atypical data have an undesirable effect to suitable clustering (see e.g., [1,2,8]). In our models, we consider the skewness and use the clustering as a base on them to show the robustness on the clustering of atypical data in components. We generated 1000 samples from the FM-TP-SMN with two components and for each sample, and considered the k-means clustering while we have ignored the true classification on these classifications.

We simulated 1000 samples with sample sizes $n=100,350,800$, from the FM-TP-SMN models with parameters ${\pi }_1=0.75$, ${\mu }_1=10$, ${\mu }_2=15$, ${\sigma }_1=2$, ${\sigma }_2=4$, ${\gamma }_1=0.1$, ${\gamma }_2=0.7$ and ${\gamma }_1={\gamma }_2=0.5$ (FM-Normal model), for which $\mathit{\nu }=4$ for TP-T and TP-SL, and $\mathit{\nu }=(0.3,0.3)$ for TP-CN. According to the FM-TP-SMN estimated (posterior) probabilities given in (12) and the threshold value 0.5, we allocated the observations to some specific component. For each sample $t=1,\dots ,1000$, the mean value rate of the correct allocations are given in

Table 1. Mean of true allocations rates for fitted finite mixture two-piece distributions based on the scale mixtures of normal (FM-TP-SMN) models.

True Model	Sample Size	Fitted Model
		FM-Normal	FM-TP-N	FM-TP-T	FM-TP-CN	FM-TP-SL
FM-TP-T	100	0.3745	0.7026	0.7674	0.8026	0.7902
	350	0.2836	0.7693	0.8372	0.8462	0.8450
	800	0.2231	0.7990	0.8418	0.8490	0.8469
FM-TP-CN	100	0.6023	0.6512	0.7835	0.7941	0.7829
	350	0.6258	0.7654	0.8542	0.8622	0.8510
	800	0.6395	0.7810	0.8599	0.8665	0.8563
FM-TP-SL	100	0.5374	0.7735	0.7810	0.7747	0.7840
	350	0.5903	0.8235	0.8420	0.8250	0.8491
	800	0.6034	0.8264	0.8437	0.8281	0.8507

, which shows that clustering based on the FM-TP-T, FM-TP-SL and FM-TP-CN are more reasonability than the ordinary FM-Normal model clustering, in the presence of atypical data. Also note that in the case of the true model (FM-TP-T), the FM-TP-CN also outperforms the other models.

4.1.2. Misspecification

For this section, we simulated 2000 samples with lengths $n=150$ from FM-SN (asymmetric and light tailed components) and FM-ST (asymmetric and heavy tailed components) separately, with parameters of the previous simulation structure and with $({\lambda }_1,{\lambda }_2)=(-2,3)$. Then, we fitted various proposed FM-TP-SMN models to these data. In

Table 2. The number of times (out of 2000) the true FM models chosen under seven proposed hypotheses.

Condition Examined	True Model:	FM-SN		FM-ST
	Criteria:	AIC	BIC	AIC	BIC
FM-TP-N vs. FM-Normal		1934	1958	1986	1975
FM-TP-T vs. FM-Normal		1511	1645	2000	2000
FM-TP-SL vs. FM-Normal		1387	1410	1823	1865
FM-TP-CN vs. FM-Normal		1503	1532	1746	1732
FM-TP-T vs. FM-TP-N		83	92	1861	1883
FM-TP-SL vs. FM-TP-N		112	123	1821	1793
FM-TP-CN vs. FM-TP-N		143	196	1732	1746

, various FM-TP-SMN models were first compared with the ordinary FM-NOR model (symmetric and light tailed components) and then various competitors within the FM-TP-SMN models (asymmetric components). The results in the first of four rows of Table 2 demonstrate that the number of preferred models belongs to the class of FM-TP-SMN models against the FM-NOR model. Also, the number of preferred models to fit the FM-SN is FM-TP-N, and in this case other preferred models except the FM-TP-N model are models which have similarities with it (for example FM-TP-T with large values of degree of freedom $\nu$), i.e., preferred fitted models to the FM-SN with asymmetric and light tailed components are the FM-TP-SMN models with light tailed components. In the cases of FM-ST with asymmetric but heavy tailed components, also the FM-TP-SMN models with heavy tailed components were preferred. In this and the real application parts, the model selection criteria to choose the best model are: logarithm of the maximized likelihood function (log-like) which is $\ell (\widehat{\Theta }|\mathbf{y})$, Akaike information criteria (AIC); [31], Bayesian information criteria (BIC); [32], in the form of

$$AIC=2k-2\ell (\widehat{\Theta }|\mathbf{y})\mathrm{and}BIC=k\log n-2\ell (\widehat{\Theta }|\mathbf{y}),$$

respectively, where k is the number of the model parameters.

4.1.3. Asymptotical results

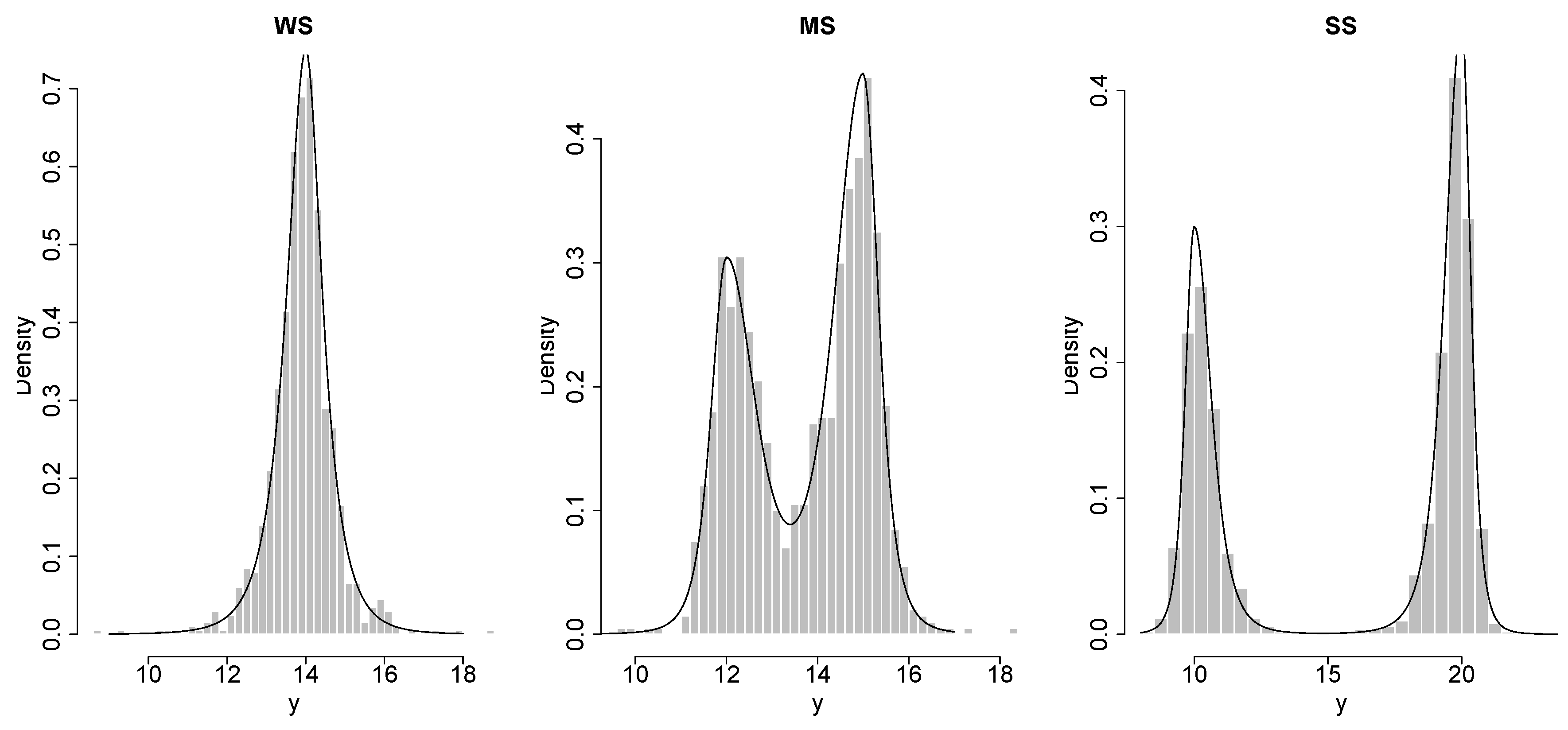
For this section, we simulated 400 samples each one with sample sizes $n=150$, 600, 1000, 2000, 4000, from some FM-TP-T models with two components which are weak separated (WS), medium separated (MS) and strong separated (SS) of components, i.e., little, medium and large overlap of components respectively (see Figure 1), for which ${\pi }_1=0.4$, ${\mu }_1=10$, ${\mu }_2=15$, ${\sigma }_1=1$, ${\sigma }_2=1$, ${\gamma }_1=0.65$, ${\gamma }_2=0.35$, $\mathit{\nu }=4$ and $({\mu }_1,{\mu }_2)=(-0.2,0.2)$ for WS data; $({\mu }_1,{\mu }_2)=(-1.5,1.5)$ for MS data; and $({\mu }_1,{\mu }_2)=(-5,5)$ for SS data.

Using the proposed ECME algorithm to find the ML estimates we focus on the evaluation of Monte-Carlo average of biasness (MC-bias) and mean squared error (MSE) defined as of the ML estimates in each j-th sample, $j=1,\dots ,400$, respectively given in

Table 3. Monte-Carlo average bias (MC-bias) and mean squared error (MSE) for maximum likelihood (ML) estimates in the weak separated components (WS) FM-TP-true (T) model.

Measure	Parameter	Sample Size
		$\mathit{n}=\mathbf{150}$	$\mathit{n}=\mathbf{600}$	$\mathit{n}=\mathbf{1000}$	$\mathit{n}=\mathbf{2000}$	$\mathit{n}=\mathbf{4000}$
MC-Bias	${\pi }_1$	−1.64533 × 10${}^{-2}$	2.50755 × 10${}^{-3}$	−1.849 × 10${}^{-5}$	8.427 × 10${}^{-6}$	3.452 × 10${}^{-7}$
	${\mu }_1$	3.48475 × 10${}^{-2}$	−9.48375 × 10${}^{-4}$	−2.287 × 10${}^{-3}$	7.427 × 10${}^{-4}$	6.584 × 10${}^{-4}$
	${\mu }_2$	3.93636 × 10${}^{-1}$	−1.98365 × 10${}^{-2}$	−3.276 × 10${}^{-3}$	9.4978 × 10${}^{-4}$	−6.436 × 10${}^{-4}$
	${\sigma }_1$	−4.98656 × 10${}^{-1}$	3.44827 × 10${}^{-2}$	6.487 × 10${}^{-3}$	−6.775 × 10${}^{-3}$	−7.864 × 10${}^{-3}$
	${\sigma }_2$	4.57463 × 10${}^{-1}$	4.03741 × 10${}^{-2}$	−6.284 × 10${}^{-3}$	−6.103 × 10${}^{-3}$	9.903 × 10${}^{-4}$
	${\gamma }_1$	1.57363 × 10${}^{-2}$	1.93845 × 10${}^{-3}$	1.574 × 10${}^{-6}$	1.427 × 10${}^{-6}$	5.047 × 10${}^{-7}$
	${\gamma }_2$	1.40384 × 10${}^{-2}$	1.73644 × 10${}^{-3}$	2.037 × 10${}^{-6}$	6.948 × 10${}^{-7}$	4.765 × 10${}^{-7}$
	$\nu$	1.14024 × 10${}^2$	1.36253 × 10${}^{-1}$	−6.017 × 10${}^{-2}$	1.284 × 10${}^{-2}$	−1.201 × 10${}^{-2}$
MSE	${\pi }_1$	7.15248 × 10${}^{-3}$	7.35733 × 10${}^{-4}$	3.854 × 10${}^{-4}$	6.036 × 10${}^{-5}$	6.729 × 10${}^{-5}$
	${\mu }_1$	1.10375 × 10${}^{-1}$	8.99164 × 10${}^{-2}$	3.927 × 10${}^{-3}$	2.889 × 10${}^{-4}$	2.960 × 10${}^{-4}$
	${\mu }_2$	1.97364 × 10${}^0$	1.23473 × 10${}^{-1}$	4.920 × 10${}^{-2}$	3.276 × 10${}^{-3}$	3.328 × 10${}^{-3}$
	${\sigma }_1$	1.69475 × 10${}^0$	1.11763 × 10${}^0$	2.118 × 10${}^{-1}$	3.2849 × 10${}^{-3}$	3.453 × 10${}^{-3}$
	${\sigma }_2$	1.67568 × 10${}^1$	1.43855 × 10${}^1$	4.548 × 10${}^{-1}$	6.786 × 10${}^{-2}$	6.903 × 10${}^{-2}$
	${\gamma }_1$	8.00264 × 10${}^{-3}$	3.49566 × 10${}^{-4}$	2.801 × 10${}^{-4}$	6.104 × 10${}^{-5}$	6.003 × 10${}^{-5}$
	${\gamma }_2$	1.98374 × 10${}^{-2}$	8.20183 × 10${}^{-3}$	2.102 × 10${}^{-4}$	6.352 × 10${}^{-5}$	6.102 × 10${}^{-5}$
	$\nu$	0.97803 × 10${}^2$	5.46093 × 10${}^{-1}$	1.112 × 10${}^{-1}$	1.684 × 10${}^{-2}$	1.521 × 10${}^{-2}$

,

Table 4. MC-Bias and MSE for ML estimates in the medium separated components (MS) FM-TP-T model.

Measure	Parameter	Sample Size
		$\mathit{n}=\mathbf{150}$	$\mathit{n}=\mathbf{600}$	$\mathit{n}=\mathbf{1000}$	$\mathit{n}=\mathbf{2000}$	$\mathit{n}=\mathbf{4000}$
MC-Bias	${\pi }_1$	5.03746 × 10${}^{-3}$	−4.21374 × 10${}^{-3}$	−1.40712 × 10${}^{-3}$	−5.83744 × 10${}^{-4}$	6.10927 × 10${}^{-5}$
	${\mu }_1$	2.18723 × 10${}^{-2}$	−1.72451 × 10${}^{-3}$	−6.28474 × 10${}^{-4}$	2.99837 × 10${}^{-5}$	−2.48576 × 10${}^{-5}$
	${\mu }_2$	−1.30284 × 10${}^{-2}$	8.29374 × 10${}^{-4}$	6.99386 × 10${}^{-4}$	3.95645 × 10${}^{-5}$	−3.43927 × 10${}^{-5}$
	${\sigma }_1$	1.25344 × 10${}^{-2}$	1.28374 × 10${}^{-4}$	−5.98375 × 10${}^{-5}$	−4.99380 × 10${}^{-5}$	−5.99837 × 10${}^{-6}$
	${\sigma }_2$	1.27364 × 10${}^{-2}$	−2.04634 × 10${}^{-3}$	−1.47364 × 10${}^{-3}$	2.98476 × 10${}^{-4}$	6.97484 × 10${}^{-5}$
	${\gamma }_1$	−1.10264 × 10${}^{-2}$	−1.02172 × 10${}^{-3}$	−4.93846 × 10${}^{-5}$	−6.10283 × 10${}^{-7}$	7.98375 × 10${}^{-7}$
	${\gamma }_2$	−0.78725 × 10${}^{-2}$	−0.90273 × 10${}^{-3}$	5.97367 × 10${}^{-5}$	5.83753 × 10${}^{-7}$	9.01274 × 10${}^{-7}$
	$\nu$	2.40926 × 10${}^0$	1.12027 × 10${}^{-1}$	3.98365 × 10${}^{-2}$	−2.48462 × 10${}^{-3}$	−2.83765 × 10${}^{-4}$
MSE	${\pi }_1$	5.85644 × 10${}^{-3}$	6.45364 × 10${}^{-4}$	3.57464 × 10${}^{-5}$	6.20183 × 10${}^{-5}$	7.10993 × 10${}^{-5}$
	${\mu }_1$	1.08744 × 10${}^{-1}$	9.37436 × 10${}^{-1}$	1.03764 × 10${}^{-2}$	2.57463 × 10${}^{-4}$	2.03464 × 10${}^{-4}$
	${\mu }_2$	2.03937 × 10${}^{-1}$	2.00713 × 10${}^{-1}$	4.67483 × 10${}^{-2}$	3.47367 × 10${}^{-3}$	3.24536 × 10${}^{-3}$
	${\sigma }_1$	3.46357 × 10${}^{-1}$	2.47464 × 10${}^{-1}$	2.23433 × 10${}^{-1}$	3.39283 × 10${}^{-3}$	6.58475 × 10${}^{-4}$
	${\sigma }_2$	8.38474 × 10${}^{-1}$	6.37364 × 10${}^{-1}$	4.38475 × 10${}^{-1}$	6.87364 × 10${}^{-2}$	6.00836 × 10${}^{-2}$
	${\gamma }_1$	1.84746 × 10${}^{-2}$	4.03847 × 10${}^{-4}$	3.11972 × 10${}^{-4}$	7.00374 × 10${}^{-5}$	6.21002 × 10${}^{-5}$
	${\gamma }_2$	2.04464 × 10${}^{-2}$	7.64533 × 10${}^{-3}$	2.30283 × 10${}^{-4}$	5.89472 × 10${}^{-5}$	7.00353 × 10${}^{-5}$
	$\nu$	6.47465 × 10${}^1$	5.87957 × 10${}^{-1}$	1.93845 × 10${}^{-2}$	1.74534 × 10${}^{-2}$	1.48375 × 10${}^{-2}$

and

Table 5. MC-Bias and MSE for ML estimates estimates in the strong separated components (SS) FM-TP-T model.

Measure	Parameter	Sample Size
		$\mathit{n}=\mathbf{150}$	$\mathit{n}=\mathbf{600}$	$\mathit{n}=\mathbf{1000}$	$\mathit{n}=\mathbf{2000}$	$\mathit{n}=\mathbf{4000}$
MC-Bias	${\pi }_1$	5.13426 × 10${}^{-3}$	5.60483 × 10${}^{-3}$	−1.40712 × 10${}^{-3}$	−6.26826 × 10${}^{-4}$	−6.95662 × 10${}^{-5}$
	${\mu }_1$	−1.90273 × 10${}^{-2}$	−1.24751 × 10${}^{-3}$	1.20183 × 10${}^{-3}$	3.45342 × 10${}^{-5}$	2.74634 × 10${}^{-5}$
	${\mu }_2$	1.15379 × 10${}^{-2}$	−3.06344 × 10${}^{-3}$	1.47333 × 10${}^{-3}$	4.28144 × 10${}^{-5}$	3.35242 × 10${}^{-5}$
	${\sigma }_1$	−1.03046 × 10${}^{-2}$	-8.34452 × 10${}^{-5}$	6.73645 × 10${}^{-5}$	−4.87354 × 10${}^{-5}$	−7.28374 × 10${}^{-6}$
	${\sigma }_2$	−1.38724 × 10${}^{-2}$	−1.27844 × 10${}^{-3}$	−1.00904 × 10${}^{-3}$	3.49383 × 10${}^{-4}$	9.88365 × 10${}^{-5}$
	${\gamma }_1$	−0.58746 × 10${}^{-2}$	0.34452 × 10${}^{-3}$	5.09847 × 10${}^{-5}$	−5.46353 × 10${}^{-7}$	8.73645 × 10${}^{-7}$
	${\gamma }_2$	−0.60273 × 10${}^{-2}$	−0.24533 × 10${}^{-3}$	6.08422 × 10${}^{-5}$	5.27363 × 10${}^{-7}$	8.69384 × 10${}^{-7}$
	$\nu$	2.37264 × 10${}^0$	0.99775 × 10${}^{-1}$	4.65635 × 10${}^{-2}$	−1.74632 × 10${}^{-2}$	−2.46354 × 10${}^{-3}$
MSE	${\pi }_1$	2.94256 × 10${}^{-3}$	3.83748 × 10${}^{-4}$	2.67464 × 10${}^{-4}$	7.78374 × 10${}^{-5}$	9.73646 × 10${}^{-5}$
	${\mu }_1$	5.01324 × 10${}^{-3}$	4.11293 × 10${}^{-4}$	1.69837 × 10${}^{-4}$	8.32847 × 10${}^{-6}$	2.37462 × 10${}^{-6}$
	${\mu }_2$	5.73648 × 10${}^{-3}$	5.03744 × 10${}^{-4}$	8.98474 × 10${}^{-5}$	6.26353 × 10${}^{-6}$	3.03733 × 10${}^{-6}$
	${\sigma }_1$	3.48373 × 10${}^{-2}$	1.20385 × 10${}^{-3}$	1.65464 × 10${}^{-4}$	1.92736 × 10${}^{-6}$	1.82037 × 10${}^{-6}$
	${\sigma }_2$	7.92746 × 10${}^{-2}$	5.38474 × 10${}^{-3}$	1.16354 × 10${}^{-3}$	1.98274 × 10${}^{-5}$	1.48263 × 10${}^{-5}$
	${\gamma }_1$	3.26354 × 10${}^{-3}$	4.24846 × 10${}^{-4}$	2.63846 × 10${}^{-4}$	6.03947 × 10${}^{-5}$	8.48375 × 10${}^{-5}$
	${\gamma }_2$	2.73145 × 10${}^{-3}$	3.38475 × 10${}^{-4}$	9.83746 × 10${}^{-5}$	5.64544 × 10${}^{-5}$	8.66555 × 10${}^{-5}$
	$\nu$	1.28736 × 10${}^2$	3.01763 × 10${}^{-1}$	9.02635 × 10${}^{-2}$	7.27647 × 10${}^{-3}$	8.83645 × 10${}^{-3}$

by

$$M{C}_{B}ias(\xi )=\left(\frac{1}{400}\sum _{j=1}^{400}{\widehat{\xi }}_j^{(i)}\right)-{\xi }_j,MSE(\xi )=\frac{1}{400}\sum _{j=1}^{400}{({\xi }_j-{\widehat{\xi }}_j^{(i)})}^2,$$

where ${\widehat{\xi }}_j^{(i)}$ is the ML estimate of the parameter ${\xi }_j$ in the i-th sample.

These results in Table 3, Table 4 and Table 5 are obtained from the different fitted FM-TP-SMN models and show the performance of the proposed models as well as their parameters estimates. As the sample size increased we naturally observed that the Monte-Carlo average bias of ML estimates and MSE were tending toward zero.

4.2. Applications

In this section, we apply the FM-TP-SMN models on some various real data sets to show the performance of the proposed models and estimates in applications.

BMI Data

We considered the body mass index (BMI) data set collected for men aged between 18 and 80 years. The BMI data set was gathered with the National Health and Nutrition Examination Survey in the US National Center for Health Statistics (NCHS) of the Center for Disease Control (CDC). A strong relationship between the obesity problem and many chronic diseases has attracted attention in recent years, that is, most people with an obesity problem will have chronic diseases. The ratio of body weight in kilograms and height in squared meters (BMI) is a measure to determine the rate of relationship between overweight and obesity. In this way, a person with BMI > 25 is considered overweighed, while BMI > 30 is considered obese.

This dataset had 4579 participants with BMI records, but for modeling with finite mixture models, participants with weights within 39.50–70.00 kg and 95.01–196.80 kg with 1069 and 1054 participants were considered in the first and second subgroups respectively. Lin et al. [7] were first analyzed this dataset by considering the reports in 1999–2000 and 2001–2002, and were fitted the FM-normal, FM-T, FM-SN and FM-ST, always with two components, and then [5,13] fitted the FM-SMSN models to this dataset. The results, obtained by [13], were general and involved the results by [5,7]. So we fitted the proposed FM-TP-SMN models to this dataset and compared obtained results in the [13].

Table 6. ML estimation results for fitting FM-TP-SMN models to the body mass index (BMI) data.

Parameter	Fitted Model
	FM-Normal	FM-TP-N	FM-TP-T	FM-TP-SL	FM-TP-CN
${\pi }_1$	0.391	0.5400	0.4600	0.5374	0.5282
${\mu }_1$	21.412	20.7520	20.744	20.7982	21.0629
${\mu }_2$	32.548	30.1324	30.155	30.0169	29.9851
${\sigma }_1$	2.0176	5.0343	5.0303	4.2785	1.5215
${\sigma }_2$	6.4180	7.4040	7.4038	6.3213	2.4601
${\gamma }_1$	–	0.6798	0.6806	0.6709	0.6302
${\gamma }_2$	–	0.8695	0.8673	0.8771	0.8785
$\nu$	–	–	7.9939	2.1950	(0.971, 0.081)

contains the ML estimates of the FM-TP-SMN models with two components, and the Log-likelihood, AIC and BIC criterions of the proposed FM-TP-SMN models and FM-SMSN taken from Table 1 due to [13] appear in

Table 7. Model selection criteria for fitting FM-TP-SMN and FM-scale mixtures of the skew normal (SMSN) models to the BMI data. The best values are marked in bold.

Criterion	Fitted Model
	FM-Normal	FM-TP-N	FM-SN	FM-TP-T	FM-ST	FM-TP-SL	FM-SSL	FM-TP-CN	FM-SCN
Log-like	−6911.76	−6870.30	−6979.47	−6856.65	−6869.03	−6857.14	−6867.99	−6871.65	−6865.25
AIC	13833.35	13754.72	13972.95	13729.41	13754.06	13730.41	13751.98	13812.31	13748.51
BIC	13961.61	13763.79	13821.22	13737.61	13782.33	13735.85	13780.24	13775.89	13776.77

.

As noted by Lin et al. [4] and Prates et al. [13], the criteria values in Table 7 indicate that the heavy tailed FM-SMSN models (FM-ST, FM-SCN and FM-SSL) had a better fit than the ordinary FM-NOR and FM-SN models, and also the FM-SSL and FM-ST were the best fitted models. Such results are for the FM-TP-SMN (with corresponding FM-SMSN counterparts) models, while the FM-TP-SMN models were more reasonable than FM-TP-SMN models. However, the FM-TP-SL and FM-TP-T were the best models. In Figure 2, we plot the fitted FM-TP-T and FM-ST densities curved on the histogram of BMI data.

4.3. UScrime Data

As a further application of the FM-TP-SMN models and proposed methodology, we consider the effect of punishment regimes on crime rates [33,34], which is of high interest to criminologists. This has been studied using aggregate data of 47 US states for 1960 given in this data frame, and we consider the 13th column of this data frame which is due to income inequality. The data are available under the UScrime function in the MASS R package.

Table 8. ML estimation results and model selection criteria for fitting FM-TP-SMN models to the UScrime data. The best values are marked in bold.

Criterion	Fitted Model
	FM-Normal	FM-TP-N	FM-SN	FM-TP-T	FM-ST	FM-TP-SL	FM-SSL	FM-TP-CN	FM-SCN
${\pi }_1$	0.615	0.463	0.607	0.462	0.607	0.463	0.607	0.509	0.582
${\mu }_1$	166.674	173.927	175.448	173.924	174.558	173.931	175.350	170.931	175.390
${\mu }_2$	237.632	246.160	227.951	246.060	228.018	245.998	227.888	204.645	224.584
${\sigma }_1$	18.283	20.399	20.170	20.263	19.597	20.294	19.835	18.626	16.362
${\sigma }_2$	20.455	59.464	22.778	59.268	22.634	58.813	22.478	42.728	20.201
${\gamma }_1({\lambda }_1)$	–	0.071	−0.687	0.071	−0.613	0.071	−0.679	0.176	−0.872
${\gamma }_2({\lambda }_2)$	–	0.257	0.555	0.258	0.548	0.259	0.560	0.782	0.579
$\nu$	–	–	–	39.934	100	39.726	37.590	0.745	0.672
$\tau$	–	–	–	–	–	–	–	0.999	0.990
Log-like	−232.226	−228.215	−232.274	−228.865	−231.275	−228.211	−231.265	−229.864	−230.281
AIC	474.452	470.437	478.548	473.734	478.549	472.426	478.531	477.748	478.562
BIC	483.703	483.386	491.499	488.535	491.500	487.228	491.482	494.399	491.513

contains the ML estimates of the FM-TP-SMN models with two components, and the Log-likelihood, AIC and BIC criterions of the proposed FM-TP-SMN and FM- SMSN models.

The log-likelihood values in Table 8 indicate that the FM-TP-N and FM-TP-T are the best models within the FM-TP-SMN models, while the FM-SCN is the best model in the class of the FM-SMSN models. The AIC and BIC criteria chose the FM-TP-N model (asymmetric components) within the FM-TP-SMN models, while they chose the FM-NOR model (symmetric components) in the class of the FM-SMSN models, which has symmetrical components. Among all competitors, the criteria chose the FM-TP-N model belonging to the proposed FM-TP-SMN models, which is more reasonable. In Figure 3 is plotted the histogram of US crime data with the curves of FM-TP-SMN and FM-SMSN models. These graphical visualizations show the suitability of the asymmetrical components and proposed FM-TP-SMN models.

5. Conclusions

We have proposed a flexible family of TP-SMN distributions for application in clustering problems. The TP-SMN family is capable of representing distributions of symmetric/asymmetric and light/heavy tailed forms, which contains the well-known symmetric SMN family and is a reasonable competitor for asymmetric SMSN family as a special case. Estimation of the finite mixtures of the FM-TP-SMN parameters is relatively straightforward via the ECME algorithm with a fast convergence (a few iterations loop). Considering a Bayesian approach and the flexible TP-SMN family in the Autoregressive and ARMA processes from [35,36] can be further topics of research.