Quasinormal Modes of Charged Black Holes in Higher-Dimensional Einstein-Power-Maxwell Theory
Abstract
:1. Introduction
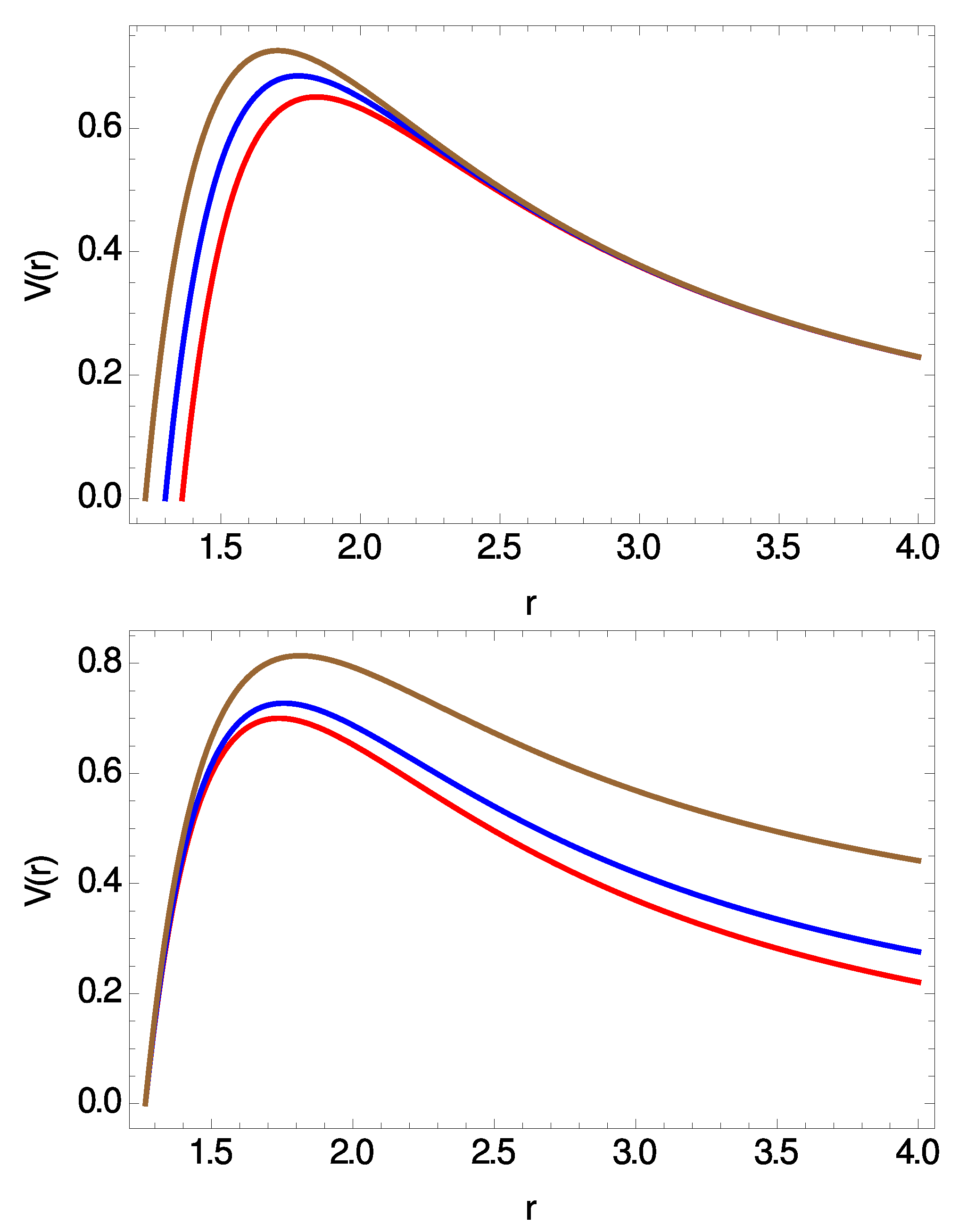
2. The Black Hole Gravitational Background and Scalar Perturbations
2.1. Charged Black Hole Solutions in EpM Theory
2.2. Wave Equation for Scalar Perturbations
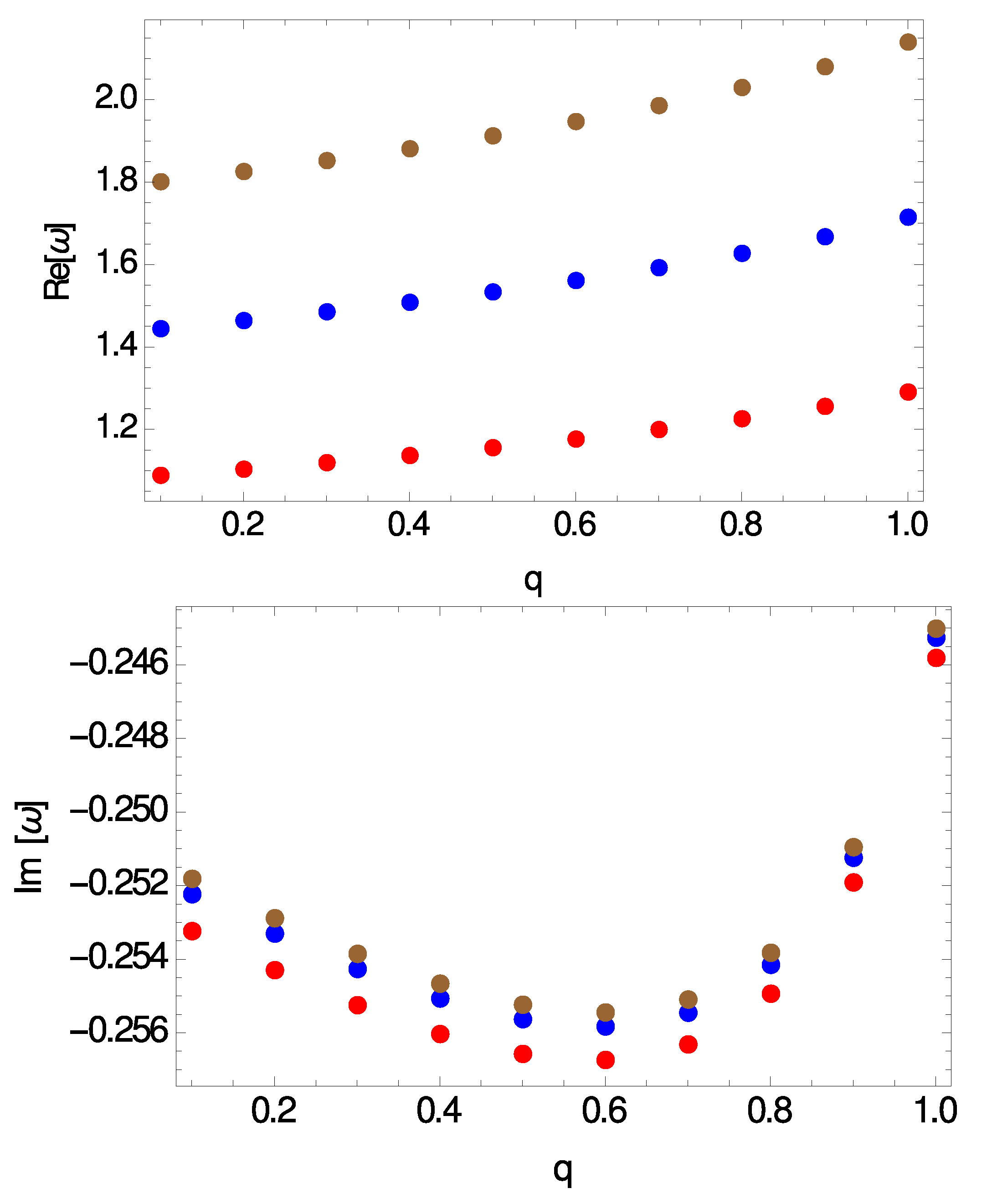
3. Quasinormal Frequencies
Quasinormal Spectrum in the Eikonal Limit
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Herdeiro, C.A.R.; Radu, E. Asymptotically flat black holes with scalar hair: A review. Int. J. Mod. Phys. D 2015, 24, 1542014. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. 2017, 851, L35. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Azulay, R.; Baczko, A.-K.; Baloković, M.; Barrett, J.; Blackburn, L.; Bouman, K.L.; Bower, G.C.; Brinkerink, C.D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. 2019, 875, L2. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. Astrophys. J. 2019, 875, L3. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. 2019, 875, L4. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. 2019, 875, L5. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. 2019, 875, L6. [Google Scholar]
- Event Horizon Telescope web page. Available online: https://eventhorizontelescope.org (accessed on 23 March 2020).
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild singularity. Phys. Rev. 1957, 108, 1063. [Google Scholar] [CrossRef]
- Zerilli, F.J. Effective potential for even parity Regge-Wheeler gravitational perturbation equations. Phys. Rev. Lett. 1970, 24, 737. [Google Scholar] [CrossRef]
- Zerilli, F.J. Gravitational field of a particle falling in a schwarzschild geometry analyzed in tensor harmonics. Phys. Rev. D 1970, 2, 2141. [Google Scholar] [CrossRef]
- Zerilli, F.J. Perturbation analysis for gravitational and electromagnetic radiation in a reissner-nordstroem geometry. Phys. Rev. D 1974, 9, 860. [Google Scholar] [CrossRef]
- Moncrief, V. Gauge-invariant perturbations of Reissner-Nordstrom black holes. Phys. Rev. D 1975, 12, 1526. [Google Scholar] [CrossRef]
- Teukolsky, S.A. Rotating black holes—Separable wave equations for gravitational and electromagnetic perturbations. Phys. Rev. Lett. 1972, 29, 1114. [Google Scholar] [CrossRef] [Green Version]
- Kokkotas, K.D.; Schmidt, B.G. Quasinormal modes of stars and black holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef] [Green Version]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, 83, 793. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon: Oxford, UK, 1985; 646p. [Google Scholar]
- Bohr, N. On the Constitution of Atoms and Molecules. 2. Systems containing only a Single Nucleus. Phil. Mag. Ser. 6 1913, 26, 476. [Google Scholar] [CrossRef] [Green Version]
- Bohr, N. On the Constitution of Atoms and Molecules. Phil. Mag. Ser. 6 1913, 26, 1. [Google Scholar] [CrossRef] [Green Version]
- Corda, C.; Hendi, S.H.; Katebi, R.; Schmidt, N.O. Effective state, Hawking radiation and quasi-normal modes for Kerr black holes. JHEP 2013, 1306, 008. [Google Scholar] [CrossRef] [Green Version]
- Corda, C. Precise model of Hawking radiation from the tunnelling mechanism. Class. Quant. Grav. 2015, 32, 195007. [Google Scholar] [CrossRef] [Green Version]
- Corda, C. Quasi-Normal Modes: The ‘Electrons’ of Black Holes as ‘Gravitational Atoms’? Implications for the Black Hole Information Puzzle. Adv. High Energy Phys. 2015, 2015, 867601. [Google Scholar] [CrossRef]
- Corda, C. Time dependent Schrödinger equation for black hole evaporation: No information loss. Ann. Phys. 2015, 353, 71. [Google Scholar] [CrossRef] [Green Version]
- Heisenberg, W.; Euler, H. Folgerungen aus der Diracschen Theorie des Positrons. Z. Phys. 1936, 98, 714. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. Roy. Soc. Lond. A 1934, 144, 425. [Google Scholar] [CrossRef]
- Bardeen, J.M. Non-singular general-relativistic gravitational collapse. In Proceedings of the International Conference GR5, USSR, Tbilisi, Georgia, 1968; p. 174. [Google Scholar]
- Borde, A. Regular black holes and topology change. Phys. Rev. D 1997, 55, 7615. [Google Scholar] [CrossRef] [Green Version]
- Ayon-Beato, E.; Garcia, A. Regular black hole in general relativity coupled to nonlinear electrodynamics. Phys. Rev. Lett. 1998, 80, 5056. [Google Scholar] [CrossRef] [Green Version]
- Ayon-Beato, E.; Garcia, A. Nonsingular charged black hole solution for nonlinear source. Gen. Rel. Grav. 1999, 31, 629. [Google Scholar] [CrossRef] [Green Version]
- Ayon-Beato, E.; Garcia, A. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. Regular electrically charged structures in nonlinear electrodynamics coupled to general relativity. Class. Quant. Grav. 2004, 21, 4417. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [Green Version]
- Balart, L.; Vagenas, E.C. Regular black hole metrics and the weak energy condition. Phys. Lett. B 2014, 730, 14. [Google Scholar] [CrossRef] [Green Version]
- Balart, L.; Vagenas, E.C. Regular black holes with a nonlinear electrodynamics source. Phys. Rev. D 2014, 90, 124045. [Google Scholar] [CrossRef] [Green Version]
- Reissner, H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie (in German). Ann. Phys. 1916, 355, 106–120. [Google Scholar] [CrossRef] [Green Version]
- Hassaine, M.; Martinez, C. Higher-dimensional charged black holes solutions with a nonlinear electrodynamics source. Class. Quant. Grav. 2008, 25, 195023. [Google Scholar] [CrossRef] [Green Version]
- Gurtug, O.; Mazharimousavi, S.H.; Halilsoy, M. 2+1-dimensional electrically charged black holes in Einstein - power Maxwell Theory. Phys. Rev. D 2012, 85, 104004. [Google Scholar] [CrossRef] [Green Version]
- Mazharimousavi, S.H.; Gurtug, O.; Halilsoy, M.; Unver, O. 2+1 dimensional magnetically charged solutions in Einstein - Power - Maxwell theory. Phys. Rev. D 2011, 84, 124021. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Zou, D.C. (2+1) -Dimensional charged black holes with scalar hair in Einstein–Power–Maxwell Theory. Gen. Rel. Grav. 2017, 49, 73. [Google Scholar] [CrossRef]
- Rincón, Á.; Contreras, E.; Bargueño, P.; Koch, B.; Panotopoulos, G.; Hernández-Arboleda, A. Scale dependent three-dimensional charged black holes in linear and non-linear electrodynamics. Eur. Phys. J. C 2017, 77, 494. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á. Quasinormal modes of black holes in Einstein-power-Maxwell theory. Int. J. Mod. Phys. D 2017, 27, 1850034. [Google Scholar] [CrossRef] [Green Version]
- Rincón, Á.; Panotopoulos, G. Quasinormal modes of scale dependent black holes in (1+2)-dimensional Einstein-power-Maxwell theory. Phys. Rev. D 2018, 97, 024027. [Google Scholar] [CrossRef] [Green Version]
- Rincón, Á.; Contreras, E.; Bargueño, P.; Koch, B.; Panotopoulos, G. Scale-dependent (2+1)-dimensional electrically charged black holes in Einstein-power-Maxwell theory. Eur. Phys. J. C 2018, 78, 641. [Google Scholar] [CrossRef]
- Panotopoulos, G. Charged scalar fields around Einstein-power-Maxwell black holes. Gen. Rel. Grav. 2019, 51, 76. [Google Scholar] [CrossRef]
- Kaluza, T. On the Problem of Unity in Physics. Sitzungsber. Preuss. Akad. Wiss. Berl. (Math. Phys.) 1921, 1921, 966. [Google Scholar]
- Klein, O. Quantum Theory and Five-Dimensional Theory of Relativity. Z. Phys. 1926, 37, 895, (In German and English). [Google Scholar] [CrossRef]
- Nilles, H.P. Supersymmetry, Supergravity and Particle Physics. Phys. Rep. 1984, 110, 1. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory, Vol. 1 & 2; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Polchinski, J. String Theory, Vol. 1 & 2; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Bizon, P.; Chmaj, T.; Schmidt, B.G. Critical behavior in vacuum gravitational collapse in 4+1 dimensions. Phys. Rev. Lett. 2005, 95, 071102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bizon, P.; Chmaj, T.; Rostworowski, A.; Schmidt, B.G.; Tabor, Z. On vacuum gravitational collapse in nine dimensions. Phys. Rev. D 2005, 72, 121502. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P. Black holes in theories with large extra dimensions: A Review. Int. J. Mod. Phys. A 2004, 19, 4899. [Google Scholar] [CrossRef] [Green Version]
- Hod, S. Bohr’s correspondence principle and the area spectrum of quantum black holes. Phys. Rev. Lett. 1998, 81, 4293. [Google Scholar] [CrossRef] [Green Version]
- Kunstatter, G. d-dimensional black hole entropy spectrum from quasinormal modes. Phys. Rev. Lett. 2003, 90, 161301. [Google Scholar] [CrossRef] [Green Version]
- Zhou, K.; Yang, Z.Y.; Zou, D.C.; Yue, R.H. Static spherically symmetric star in Gauss-Bonnet gravity. Chin. Phys. B 2012, 21, 020401. [Google Scholar] [CrossRef] [Green Version]
- Hansraj, S.; Chilambwe, B.; Maharaj, S.D. Exact EGB models for spherical static perfect fluids. Eur. Phys. J. C 2015, 75, 277. [Google Scholar] [CrossRef] [Green Version]
- Tangherlini, F.R. Schwarzschild field in n dimensions and the dimensionality of space problem. Nuovo Cim. 1963, 27, 636. [Google Scholar] [CrossRef]
- Crispino, L.C.B.; Higuchi, A.; Oliveira, E.S.; Rocha, J.V. Greybody factors for nonminimally coupled scalar fields in Schwarzschild–de Sitter spacetime. Phys. Rev. D 2013, 87, 104034. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P.; Pappas, T.; Pappas, N. Greybody factors for scalar fields emitted by a higher-dimensional Schwarzschild–de Sitter black hole. Phys. Rev. D 2014, 90, 124077. [Google Scholar] [CrossRef] [Green Version]
- Pappas, T.; Kanti, P.; Pappas, N. Hawking radiation spectra for scalar fields by a higher-dimensional Schwarzschild–de Sitter black hole. Phys. Rev. D 2016, 94, 024035. [Google Scholar] [CrossRef] [Green Version]
- Panotopoulos, G.; Rincón, Á. Quasinormal modes of five-dimensional black holes in non-commutative geometry. Eur. Phys. J. Plus 2020, 135, 33. [Google Scholar] [CrossRef]
- Muller, C. Lecture Notes in Mathematics: Spherical Harmonics; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Harmark, T.; Natario, J.; Schiappa, R. Greybody Factors for d-Dimensional Black Holes. Adv. Theor. Math. Phys. 2010, 14, 727. [Google Scholar] [CrossRef] [Green Version]
- Poschl, G.; Teller, E. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators. Z. Phys. 1933, 83, 143. [Google Scholar] [CrossRef]
- Ferrari, V.; Mashhoon, B. New approach to the quasinormal modes of a black hole. Phys. Rev. D 1984, 30, 295. [Google Scholar] [CrossRef]
- Cardoso, V.; Lemos, J.P.S. Scalar, electromagnetic and Weyl perturbations of BTZ black holes: Quasinormal modes. Phys. Rev. D 2001, 63, 124015. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Lemos, J.P.S. Quasinormal modes of the near extremal Schwarzschild-de Sitter black hole. Phys. Rev. D 2003, 67, 084020. [Google Scholar] [CrossRef] [Green Version]
- Molina, C. Quasinormal modes of d-dimensional spherical black holes with near extreme cosmological constant. Phys. Rev. D 2003, 68, 064007. [Google Scholar] [CrossRef] [Green Version]
- Panotopoulos, G. Electromagnetic quasinormal modes of the nearly-extremal higher-dimensional Schwarzschild–de Sitter black hole. Mod. Phys. Lett. A 2018, 33, 1850130. [Google Scholar] [CrossRef] [Green Version]
- Birmingham, D. Choptuik scaling and quasinormal modes in the AdS / CFT correspondence. Phys. Rev. D 2001, 64, 064024. [Google Scholar] [CrossRef] [Green Version]
- Fernando, S. Quasinormal modes of charged dilaton black holes in (2+1)-dimensions. Gen. Rel. Grav. 2004, 36, 71. [Google Scholar] [CrossRef] [Green Version]
- Fernando, S. Quasinormal modes of charged scalars around dilaton black holes in 2+1 dimensions: Exact frequencies. Phys. Rev. D 2008, 77, 124005. [Google Scholar] [CrossRef] [Green Version]
- Destounis, K.; Panotopoulos, G.; Rincón, Á. Stability under scalar perturbations and quasinormal modes of 4D Einstein–Born–Infeld dilaton spacetime: Exact spectrum. Eur. Phys. J. C 2018, 78, 139. [Google Scholar] [CrossRef]
- Ovgün, A.; Jusufi, K. Quasinormal Modes and Greybody Factors of f(R) gravity minimally coupled to a cloud of strings in 2+1 Dimensions. Ann. Phys. 2018, 395, 138. [Google Scholar] [CrossRef] [Green Version]
- Rincón, Á.; Panotopoulos, G. Greybody factors and quasinormal modes for a nonminimally coupled scalar field in a cloud of strings in (2+1)-dimensional background. Eur. Phys. J. C 2018, 78, 858. [Google Scholar] [CrossRef] [Green Version]
- Schutz, B.F.; Will, C.M. Black Hole Normal Modes: A Semianalytic Approach. Astrophys. J. 1985, 291, L33. [Google Scholar] [CrossRef] [Green Version]
- Iyer, S.; Will, C.M. Black Hole Normal Modes: A WKB Approach. 1. Foundations and Application of a Higher Order WKB Analysis of Potential Barrier Scattering. Phys. Rev. D 1987, 35, 3621. [Google Scholar] [CrossRef]
- Konoplya, R.A. Quasinormal behavior of the d-dimensional Schwarzschild black hole and higher order WKB approach. Phys. Rev. D 2003, 68, 024018. [Google Scholar] [CrossRef] [Green Version]
- Iyer, S. Black Hole Normal Modes: A Wkb Approach. 2. Schwarzschild Black Holes. Phys. Rev. D 1987, 35, 3632. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Schutz, B.F. Black Hole Normal Modes: A WKB Approach. 3. The Reissner-Nordstrom Black Hole. Phys. Rev. D 1988, 37, 3378. [Google Scholar] [CrossRef] [Green Version]
- Seidel, E.; Iyer, S. Black Hole Normal Modes: A Wkb Approach. 4. Kerr Black Holes. Phys. Rev. D 1990, 41, 374. [Google Scholar] [CrossRef]
- Konoplya, R. Quasinormal modes of the charged black hole in Gauss-Bonnet gravity. Phys. Rev. D 2005, 71, 024038. [Google Scholar] [CrossRef] [Green Version]
- Fernando, S.; Holbrook, C. Stability and quasi normal modes of charged black holes in Born-Infeld gravity. Int. J. Theor. Phys. 2006, 45, 1630. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, S.K. Quasinormal modes of tensor and vector type perturbation of Gauss Bonnet black hole using third order WKB approach. Gen. Rel. Grav. 2007, 39, 567. [Google Scholar] [CrossRef] [Green Version]
- Fernando, S.; Correa, J. Quasinormal Modes of Bardeen Black Hole: Scalar Perturbations. Phys. Rev. D 2012, 86, 064039. [Google Scholar] [CrossRef] [Green Version]
- Santos, V.; Maluf, R.V.; Almeida, C.A.S. Quasinormal frequencies of self-dual black holes. Phys. Rev. D 2016, 93, 084047. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Khoo, F.S.; Kunz, J. Quasinormal modes of Einstein-Gauss-Bonnet-dilaton black holes. Phys. Rev. D 2017, 96, 064008. [Google Scholar] [CrossRef] [Green Version]
- Wolfram Mathematica web page. Available online: http://www.wolfram.com (accessed on 23 March 2020).
- Konoplya, R.A.; Zhidenko, A. Passage of radiation through wormholes of arbitrary shape. Phys. Rev. D 2010, 81, 124036. [Google Scholar] [CrossRef] [Green Version]
- Matyjasek, J.; Opala, M. Quasinormal modes of black holes. The improved semianalytic approach. Phys. Rev. D 2017, 96, 024011. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.A.; Zhidenko, A.; Zinhailo, A.F. Higher order WKB formula for quasinormal modes and grey-body factors: Recipes for quick and accurate calculations. Class. Quant. Grav. 2019, 36, 155002. [Google Scholar] [CrossRef] [Green Version]
- Hatsuda, Y. Quasinormal modes of black holes and Borel summation. Phys. Rev. D 2020, 101, 024008. [Google Scholar] [CrossRef] [Green Version]
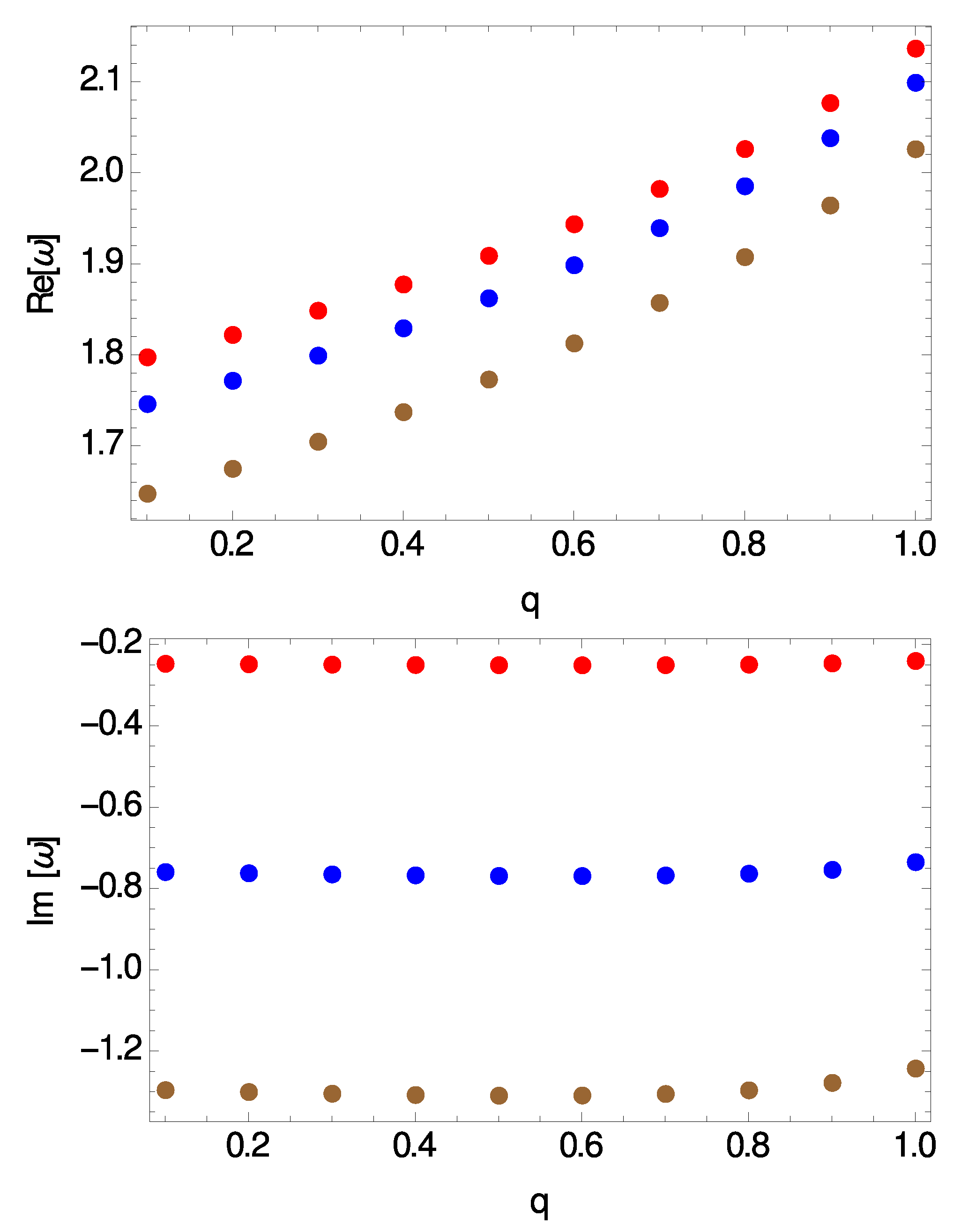
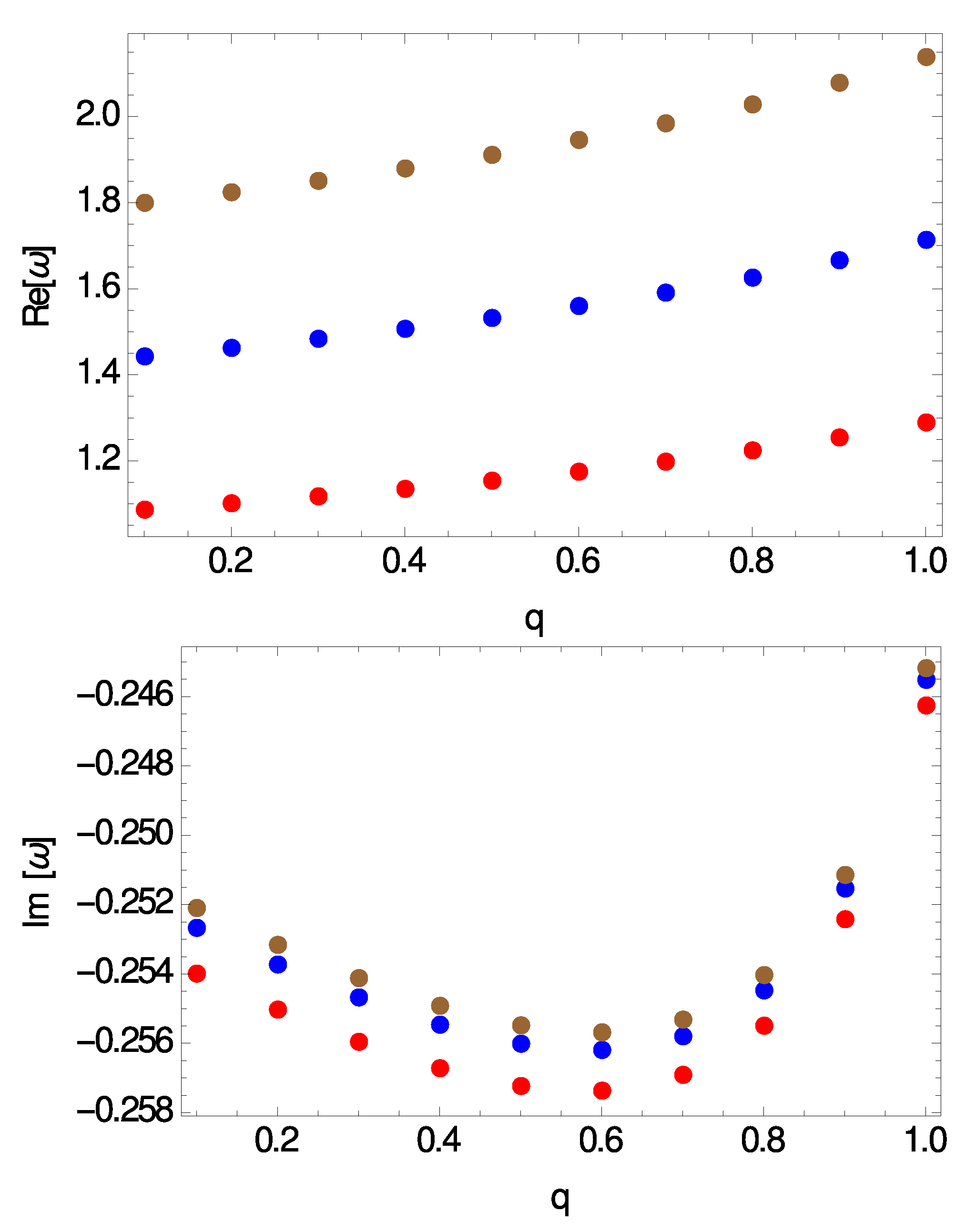
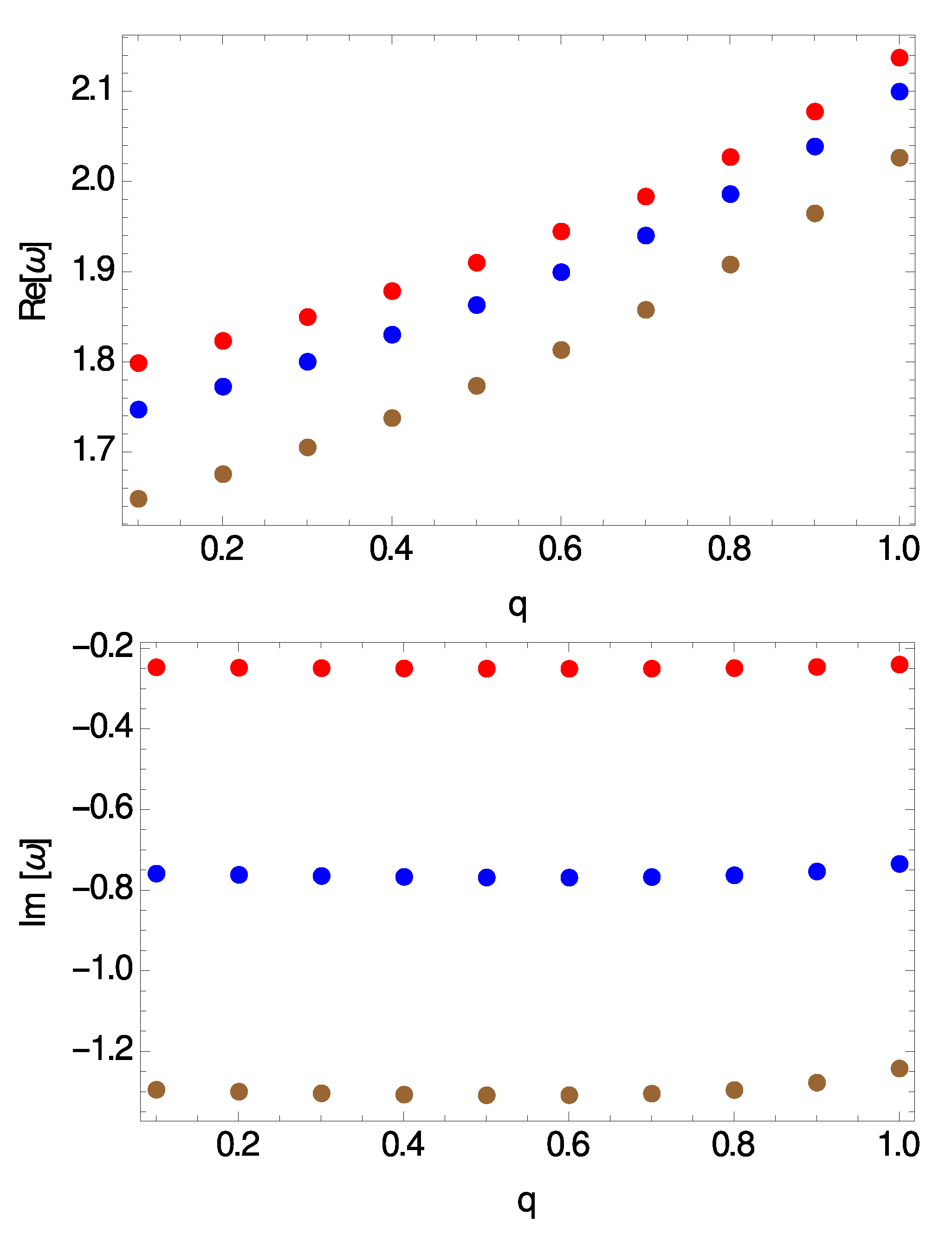


| q | ||
|---|---|---|
| 0.1 | 1.79517-0.25215 i | 1.79650-0.25187 i |
| 0.2 | 1.81978-0.25322 i | 1.82109-0.25294 i |
| 0.3 | 1.84633-0.25418 i | 1.84760-0.25391 i |
| 0.4 | 1.87512-0.25498 i | 1.87637-0.25472 i |
| 0.5 | 1.90660-0.25554 i | 1.90781-0.25529 i |
| 0.6 | 1.94131-0.25574 i | 1.94249-0.25550 i |
| 0.7 | 1.98003-0.25537 i | 1.98117-0.25515 i |
| 0.8 | 2.02383-0.25409 i | 2.02493-0.25388 i |
| 0.9 | 2.07435-0.25120 i | 2.07540-0.25101 i |
| 1.0 | 2.13417-0.24524 i | 2.13516-0.24507 i |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panotopoulos, G. Quasinormal Modes of Charged Black Holes in Higher-Dimensional Einstein-Power-Maxwell Theory. Axioms 2020, 9, 33. https://doi.org/10.3390/axioms9010033
Panotopoulos G. Quasinormal Modes of Charged Black Holes in Higher-Dimensional Einstein-Power-Maxwell Theory. Axioms. 2020; 9(1):33. https://doi.org/10.3390/axioms9010033
Chicago/Turabian StylePanotopoulos, Grigoris. 2020. "Quasinormal Modes of Charged Black Holes in Higher-Dimensional Einstein-Power-Maxwell Theory" Axioms 9, no. 1: 33. https://doi.org/10.3390/axioms9010033
APA StylePanotopoulos, G. (2020). Quasinormal Modes of Charged Black Holes in Higher-Dimensional Einstein-Power-Maxwell Theory. Axioms, 9(1), 33. https://doi.org/10.3390/axioms9010033





